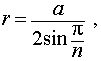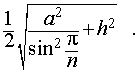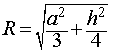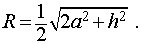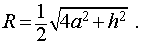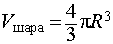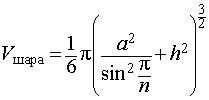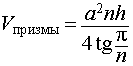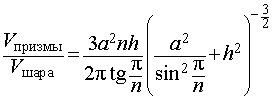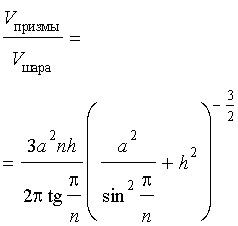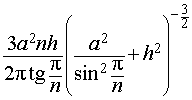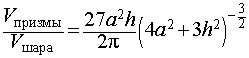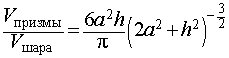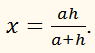Как найти радиус шара вписанного в призму - Исправление недочетов и поиск решений вместе с Examum.ru

1. Многогранник и шар

Шар вписан в призму, если он касается всех граней призмы.

Шар описан около призмы, если все вершины призмы лежат на поверхности шара.

Не во всякую призму можно вписать шар и не около всякой призмы можно описать шар.

Шар вписан в пирамиду, если он касается всех граней пирамиды.

Шар описан около пирамиды, если все вершины пирамиды лежат на поверхности шара.

2. Многогранник и цилиндр

Цилиндр вписан в прямую призму, если основания цилиндра вписаны в основания призмы.

Цилиндр описан около прямой призмы, если его основания описаны около оснований призмы.

Цилиндр вписан в пирамиду, если одно из его оснований принадлежит основанию пирамиды, а другое его основание вписано в сечение пирамиды плоскостью, параллельной ее основанию.

Цилиндр описан около пирамиды, если основание пирамиды вписано в одно из оснований цилиндра, а вершина пирамиды принадлежит другому основанию цилиндра.

3. Многогранник и конус

Конус вписан в призму, если основание конуса вписано в одно из оснований призмы, а вершина конуса принадлежит другому основанию призмы.

Конус описан около призмы, если вершины одного из оснований призмы лежат на поверхности конуса, а все вершины другого основания призмы принадлежат основанию конуса.

Конус вписан в пирамиду, если основание конуса вписано в основание пирамиды, а вершина конуса совпадает с вершиной пирамиды.

Конус описан около пирамиды, если основание конуса описано около основания пирамиды, а вершина конуса совпадает с вершиной пирамиды.

4. Комбинация тел вращения

Шар вписан в конус, если он касается основания конуса в его центре, а боковой поверхности – по окружности. Центр шара находится на оси конуса и равноудален от центра основания и образующей конуса.

Шар описан около конуса, если вершина и окружность основания конуса лежат на поверхности шара. Центр шара лежит на прямой, содержащей ось конуса, и равноудален от вершины и точек окружности основания конуса.

Шар вписан в цилиндр, если он касается оснований цилиндра в их центрах, а боковой поверхности цилиндра по большой окружности шара, параллельной основаниям. Центр шара лежит на середине оси цилиндра, а радиус шара можно найти по формуле:

$LaTeX formula: R_{BPi }=frac{h}{2}$ , где – высота цилиндра.

Шар описан около цилиндра, если окружности оснований цилиндра лежат на поверхности шара.

Не во всякий цилиндр можно вписать шар, но около всякого цилиндра можно описать шар.

При решении задач целесообразно строить вспомогательное сечение, проходящее через ось цилиндра или конуса и центр шара. При этом в сечении цилиндра будет получаться прямоугольник, в сечении конуса – равнобедренный треугольник, в сечении шара – круг с радиусом, равным радиусу шара.

Конус вписан в цилиндр, если основание конуса совпадает с одним из оснований цилиндра, а вершина конуса совпадает с центром другого основания цилиндра.

Конус описан около цилиндра, если одно из оснований цилиндра касается боковой поверхности конуса, а другое основание цилиндра принадлежит основанию конуса.

Пример 1. Шар радиуса касается всех граней прямоугольного параллелепипеда. Найдите объем шара, описанного около этого параллелепипеда.

Решение. Шар можем вписать только в прямоугольный параллелепипед, основание которого является квадрат (рис.9.78). Следовательно, имеем куб с ребром . Найдем диагональ этого куба: , .

Найдем радиус шара, описанного около куба: $LaTeX formula: R=frac{d}{2}=2sqrt{3}$ .

По формуле 9.26 найдем объем шара, описанного около куба: $LaTeX formula: V=frac{4}{3}pi 24sqrt{3}=32sqrt{3}pi$ .

Ответ: .

Пример 2. Все вершины треугольной призмы, основанием которой является треугольник со сторонами ; и , лежат на поверхности шара. Найдите объем шара, если высота призмы равна .

Решение. Так как шар описан около призмы, то все вершины призмы лежат на поверхности шара. Центр шара, с одной стороны, равноудален от вершин призмы, а с другой стороны, равноудален от центров окружностей, описанных около оснований призмы.

На рисунке 9.79: точки и – центры окружностей, описанных около оснований призмы; точка – центр шара; $LaTeX formula: R_{wapa}$ – радиус шара; .

Радиус окружности, описанной около основания призмы, найдем по формуле $LaTeX formula: R=frac{abc}{4S}$ .

Площадь основания призмы найдем по формуле Герона . Получим: .

Тогда $LaTeX formula: AO=R=frac{3cdot 3cdot 4}{4cdot 2sqrt{5}}=frac{9}{2sqrt{5}}$ .

По теореме Пифагора: $LaTeX formula: R^2_{wapa}=AO^2+PO^2$ , $LaTeX formula: R^2_{wapa}=frac{81}{20}+16=frac{401}{20}$ .

Площадь поверхности шара найдем по формуле 9.25 : $LaTeX formula: S=frac{4pi cdot 401}{20}=80,2pi$ .

Ответ: .

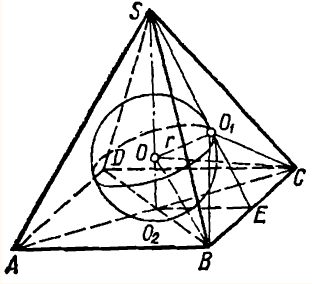
Пример 3. Найдите отношение радиуса шара, описанного около правильного тетраэдра, к радиусу шара, вписанного в этот тетраэдр.

Решение. Пусть ребро тетраэдра равно . Высота правильного тетраэдра опускается в центр правильного треугольника (рис. 9.80), поэтому $LaTeX formula: OA=R=frac{a}{sqrt{3}}$ , $LaTeX formula: OD=r=frac{a}{2sqrt{3}}$ . Центры описанного около правильного тетраэдра и вписанного в него шаров совпадают и лежат на высоте тетраэдра (точка ).

Поскольку точки , , и лежат на поверхности шара, то $LaTeX formula: O_1A=O_1C=O_1B=O_1S=R_{Onuc.}$

Угол – угол наклона боковой грани к плоскости основания ( и – перпендикуляры к ребру ).

Вписанный шар касается всех граней тетраэдра, следовательно, его радиус является перпендикуляром к плоскостям граней, то есть $LaTeX formula: R_{Bnuc.}=O_1O=O_1N$ .

Так как ( $LaTeX formula: angle SNO_1=angle SOD=90^{circ}$ и — общий), то запишем $LaTeX formula: frac{OD}{NO_1}=frac{SD}{SO_1}$ или $LaTeX formula: frac{r}{R_{Bnuc.}}=frac{SD}{R_{Onuc.}}$ , откуда $LaTeX formula: R_{Onuc.}=frac{R_{Bnuc.}cdot SD}{r}$ .

Длину отрезка найдем из теоремы Пифагора: $LaTeX formula: CD=sqrt{a^2-frac{a^2}{4}}=frac{asqrt{3}}{2}$ .

Найдем отношение радиусов описного около тетраэдра и вписанного в тетраэдр шаров:

$LaTeX formula: frac{R_{Onuc.}}{R_{Bnuc.}}=frac{R_{Bnuc.}cdot SD}{rcdot R_{Bnuc.} }=frac{SD}{r}=frac{asqrt{3}}{2}:frac{a}{2sqrt{3}}=frac{asqrt{3}cdot 2sqrt{3}}{2a}=3$ .

Ответ: .

Пример 4. В прямой параллелепипед, одна из диагоналей оснований которого равна и равна стороне основания, вписан цилиндр, высота которого равна . Найдите объем параллелепипеда.

Решение. Окружность можно вписать в квадрат или в ромб. Но диагональ квадрата не может быть равна его стороне. Диагональ ромба может быть равна его стороне, если угол ромба равен $LaTeX formula: 60^{circ}$ . Следовательно, основание параллелепипеда – ромб.

Согласно формуле найдем площадь ромба:

$LaTeX formula: S=12cdot frac{sqrt{3}}{2}=6sqrt{3}$ .

Высота параллелепипеда равна высоте цилиндра: .

Согласно формуле 9.6 найдем объем параллелепипеда:

Ответ: .

Пример 5. Около правильной треугольной пирамиды описан цилиндр, объем которого равен . Найдите объем пирамиды.

Решение. Пусть – радиус основания цилиндра, – высота цилиндра и пирамиды.

Согласно формулам 9.15 и 9.16 запишем: $LaTeX formula: pi R^2h=12sqrt{3}pi$ , $LaTeX formula: R^2h=12sqrt{3}$ .

Так как основание пирамиды – правильный треугольник со стороной , а – радиус окружности, описанной около этого треугольника, то .

Найдем площадь основания пирамиды: $LaTeX formula: S_{o.}=frac{sqrt{3}a^2}{4}=frac{3sqrt{3}R^2}{4}$ .

Согласно формуле 9.11 запишем объем пирамиды: $LaTeX formula: V=frac{1}{3cdot }frac{3sqrt{3}R^2}{4}cdot h=frac{sqrt{3}}{4}cdot R^2h$ . Учитывая, что $LaTeX formula: R^2h=12sqrt{3}$ , получим: $LaTeX formula: V=frac{sqrt{3}}{4}cdot 12sqrt{3}=9$ .

Ответ: .

Пример 6. Конус вписан в треугольную призму, основанием которой является прямоугольный треугольник с катетами см и см, а высота равна см. Найдите площадь боковой поверхности конуса (рис. 9.81).

Решение. 1. Найдем гипотенузу треугольника: (см).

2. Найдем радиус окружности, вписанной в основание призмы:

$LaTeX formula: r=frac{a+b-c}{2}$ , $LaTeX formula: r=frac{5+12-13}{2}=2$ (см).

3. Высота конуса равна высоте призмы: см.

4. По теореме Пифагора найдем образующую конуса:

$LaTeX formula: l=sqrt{r^2+h^2}$ , .

5. По формуле 9.22 найдем боковую поверхность конуса: ( $LaTeX formula: _{CM}\^2$ ).

Ответ: $LaTeX formula: _{CM}\^2$ .

Пример 7. Правильная шестиугольная пирамида вписана в конус, объем которого равен $LaTeX formula: frac{16pi }{3}$ . Найдите площадь боковой поверхности пирамиды, если известно, что радиус основания конуса в два раза меньше его высоты.

Решение. На рисунке 9.82: – высота конуса и высота пирамиды, – радиус основания конуса и радиус окружности, описанной около правильного шестиугольника и .

С учетом формул 9.19 и 9.20 получим: $LaTeX formula: frac{16pi }{3}=frac{1}{3}pi R^2cdot 2R$ , откуда , . Тогда: сторона правильного шестиугольника равна ; .

Найдем радиус окружности, вписанной в шестиугольник: $LaTeX formula: r=frac{3sqrt{3}a^2}{2}$ , $LaTeX formula: r=frac{3sqrt{3}cdot 4}{2}=6sqrt{3}$ .

По теореме Пифагора найдем апофему пирамиды:

$LaTeX formula: CS=sqrt{h^2+r^2}=sqrt{1+108}=sqrt{109}$ .

По формуле 9.13 найдем площадь боковой поверхности пирамиды:

$LaTeX formula: S=frac{1}{2}P_{o.}cdot h_{delta .}$ , $LaTeX formula: S=frac{1}{2}cdot 12cdot sqrt{109}=6sqrt{109}$ .

Ответ: .

Пример 8. Конус, высота которого равна , вписан в шар радиуса . Найдите объем конуса.

Решение. На рисунке 9.83 построено осевое сечение конуса. Так как , а , то .

По теореме Пифагора: . По формулам 9.19 и 9.20 найдем объем конуса: $LaTeX formula: V=frac{1}{3}pi r^2h=frac{pi}{3}(2sqrt{3})^2cdot 6=24pi$ .

Ответ: .

Пример 9. В конус, осевое сечение которого – равносторонний треугольник, вписан шар. Найдите объем конуса, если объем шара равен $LaTeX formula: frac{9pi }{16}$ $LaTeX formula: _{CM}\^3$ .

Решение. Объем шара находят по формуле 9.26 . Радиус шара найдем, решая уравнение $LaTeX formula: frac{4}{3}pi R^3_{wapa}=frac{9pi}{16}$ , откуда получим $LaTeX formula: R_{wapa}=frac{3}{4}$ см. Так как осевым сечением конуса является равносторонний треугольник (рис. 9.84), то центр шара (точка ) лежит на высоте конуса и радиус шара равен радиусу окружности, вписанной в треугольник , т. е. $LaTeX formula: R_{wapa}=r$ .

В свою очередь радиус окружности, вписанной в правильный треугольник со стороной , находят по формуле $LaTeX formula: r=frac{a}{2sqrt{3}}$ . Следовательно, , $LaTeX formula: a=2sqrt{3}cdot frac{3}{4}=frac{3sqrt{3}}{2}$ (см).

Найдем радиус основания конуса и его высоту: $LaTeX formula: R_{kappa .}=frac{1}{2}cdot a=frac{3sqrt{3}}{2}$ (см); $LaTeX formula: h_{kappa .}=sqrt{a^2-frac{a^2}{4}}=frac{sqrt{3}a}{2}$ , $LaTeX formula: h_{kappa .}=frac{sqrt{3}}{2}cdot frac{3sqrt{3}}{2}=frac{9}{4}$ (см).

Согласно формулам 9.19 и 9.20 найдем объем конуса: $LaTeX formula: V=frac{1}{3}pi left ( frac{3sqrt{3}}{2} right )^2cdot frac{9}{4}=frac{81pi}{64}$ ( $LaTeX formula: _{CM}\^3$ ).

Ответ: $LaTeX formula: frac{81pi}{64}$ $LaTeX formula: _{CM}\^3$ .

Пример 10. В цилиндр, площадь поверхности которого равна , вписана сфера. Найдите площадь поверхности сферы.

Решение. Осевое сечение цилиндра – квадрат. Тогда, если радиус основания цилиндра , то его образующая и радиус шара .

Согласно условию задачи: , , , , , .

Тогда и согласно формуле 9.25 получим: $LaTeX formula: S_{cphi .}=4pi sqrt{2}^2=8pi$ .

Ответ: .

1. В любую треугольную пирамиду можно вписать шар и около любой треугольной пирамиды можно описать шар.

2. В любой конус можно вписать шар и около любого конуса можно описать шар.

3. Решая задачи стереометрии, часто вовсе не обязательно изображать сами пространственные фигуры, а достаточно лишь выполнить некоторые фрагменты рисунка.

Объем прямой призмы высоты и периметром основания находят по формуле:

$LaTeX formula: V=S_{o.} cdot h$ . (9.6)

Площадь поверхности прямой призмы находят по формуле:

$LaTeX formula: S_{n.}=2S_{o.}+S_{delta .}$ . (9.7)

Площадь боковой поверхности прямой призмы высоты и периметром основания находят по формуле:

$LaTeX formula: S_{delta .}=P_{o.} cdot h$ . (9.8)

Объем наклонной призмы можно вычислить по формуле:

$LaTeX formula: V=S_{o.} cdot h$ . (9.9)

Площадь поверхности наклонной призмы можно вычислить по формуле:

$LaTeX formula: S_{n.}=2S_{o.}+S_{delta .}$ , (9.10)

Объем пирамиды высоты находят по формуле:

$LaTeX formula: V=frac{1}{3}S_{o.} cdot h$ , (9.11)

Площадь поверхности пирамиды находят по формуле:

$LaTeX formula: S_{n.}=S_{o.}+S_{delta .}$ . (9.12)

Площадь боковой поверхности правильной пирамиды находят по формуле:

$LaTeX formula: S_{delta .}=frac{1}{2}P_{o.} cdot h_{delta .}$ , (9.13)

где $LaTeX formula: h_{delta .}$ – апофема пирамиды.

Объем цилиндра высоты находят по формуле:

$LaTeX formula: V=S_{o.}cdot h$ . (9.15)

Площадь основания цилиндра ( – радиус основания) находят по формуле:

$LaTeX formula: S_{o.}=pi r ^2$ . (9.16)

Площадь поверхности цилиндра находят по формуле:

$LaTeX formula: S_{n.}=2S_{o.}+S_{delta .}$ . (9.17)

Площадь боковой поверхности цилиндра находят по формуле:

$LaTeX formula: S_{delta .}=2pi r l$ , (9.18)

где – радиус основания, – высота, – образующая цилиндра.

Объем конуса высоты находят по формуле:

$LaTeX formula: V=frac{1}{3}S_{o.}cdot h$ . (9.19)

Площадь основания конуса ( – радиус основания) находят по формуле:

$LaTeX formula: S_{o.}=pi r^2$ . (9.20)

Площадь поверхности конуса находят по формуле:

$LaTeX formula: S_{n.}=2S_{o.}+S_{delta .}$ . (9.21)

Площадь боковой поверхности конуса находят по формуле:

$LaTeX formula: S_{delta .}=pi r l$ , (9.22)

где r – радиус основания, l – образующая конуса.

Площадь сферы радиуса находят по формуле:

$LaTeX formula: S_{cphi .}=4pi R^2$ . (9.25)

Объем шара радиуса находят по формуле:

$LaTeX formula: V_{wapa}=frac{4}{3}pi R^3$ . (9.26)

Источник

Призма, вписанная в сферу

Призма, вписанная в сферу. Свойства призмы, вписанной в сферу

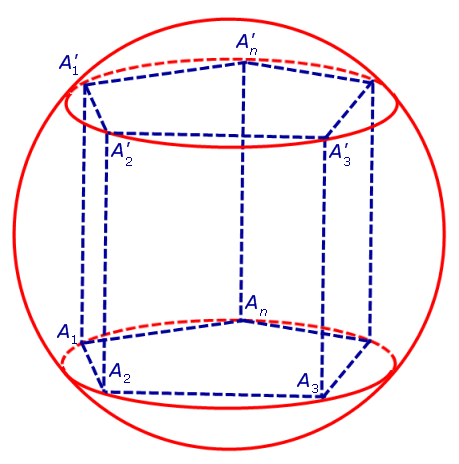
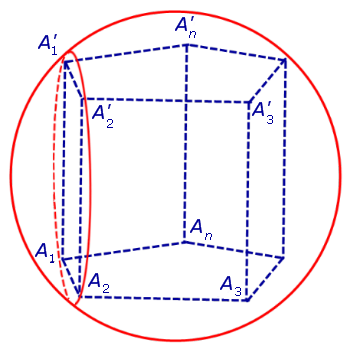
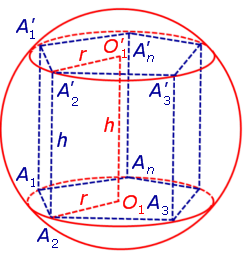
Определение 1. Призмой, вписанной в сферу, называют такую призму, все вершины которой лежат на сфере (рис. 1).

Определение 2. Если призма вписана в сферу, то сферу называют описанной около призмы.

Теорема. Около призмы можно описать сферу тогда и только тогда, когда выполнены следующие два условия:

Призма является прямой призмой;
Около оснований призмы можно описать окружности.

Доказательство. Докажем сначала, что если n – угольная призма A₁A₂ . A_nA’₁A’₂ . A’_n вписана в сферу, то оба условия теоремы выполнены.

Для этого заметим, что плоскость каждого из оснований призмы пересекает сферу по окружности, на которой лежат вершины этого основания. Таким образом, многоугольники, являющиеся основаниями призмы, оказываются вписанными в окружности (рис. 1), то есть второе условие теоремы выполнено.

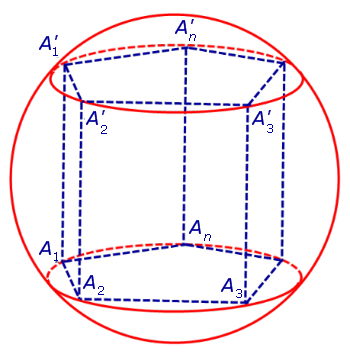
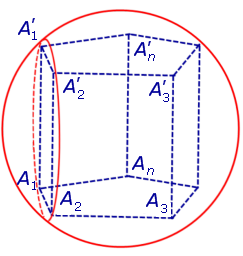
Каждая из боковых граней призмы также вписана в окружность (рис. 2).

Рассмотрим какое-нибудь боковое ребро призмы, например, A₂A’₂. Поскольку это ребро перпендикулярно к ребрам основания A₁A₂ и A₂A₃ , то в силу признака перпендикулярности прямой и плоскости заключаем, что боковое ребро A₂A’₂ перпендикулярно к плоскости основания призмы, то есть призма является прямой призмой.

Таким образом, мы доказали, что, если призма вписана в сферу, то оба условия теоремы выполнены.

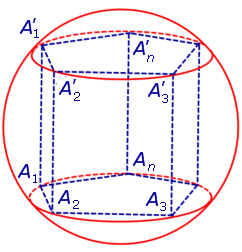
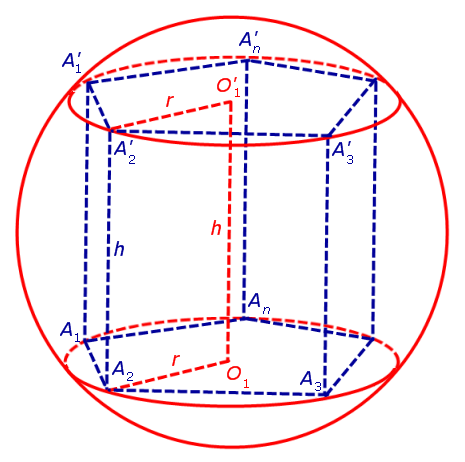
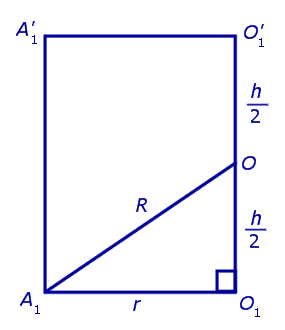
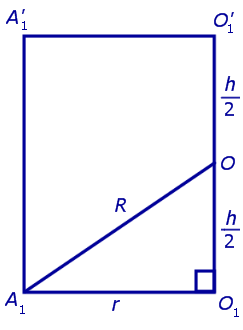
Для этого обозначим символом O₁ центр окружности радиуса r , описанной около нижнего основания призмы, а символом O’₁ обозначим центр окружности, описанной около верхнего основания призмы (рис. 3).

Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы описанных около них окружностей будут равны.

Согласно утверждению 1 из раздела «Призмы, вписанные в цилиндры» отрезок O₁O’₁, соединяющий центры окружностей, описанных около нижнего и верхнего оснований призмы, параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок O₁O’₁ перпендикулярен плоскости основания призмы и равен h.

Обозначим буквой O середину отрезка O₁O’₁ и докажем, что все вершины призмы будут находиться на одном и том же расстояниии от точки O (рис. 4).

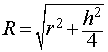(1)

от всех вершин призмы. Отсюда следует, что точка O является центром сферы радиуса R , описанной около призмы.

Следствие 1. Около любой прямой треугольной призмы можно вписать сферу.

Следствие 2. Около любого прямоугольного параллелепипеда (в частности, около куба прямоугольного параллелепипеда (в частности, около куба ) можно описать сферу.

Следствие 3. Около любой правильной призмы можно описать сферу.

Для доказательства следствия 3 достаточно заметить, что правильная n – угольная призма – это прямая призма, основания которой являются правильными n – угольниками, а около любого правильного n – угольника можно описать окружность.

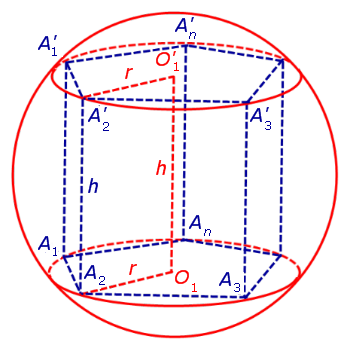
Радиус сферы, описанной около правильной n — угольной призмы

то из формулы (1) получаем выражение для радиуса описанной сферы

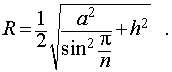(2)

Ответ.

Следствие 6. Радиус сферы, описанной около около правильной шестиугольной призмы с высотой h и ребром основания a равен

Отношение объема правильной n — угольной призмы к объему шара, ограниченного описанной около призмы сферой

Задача 2. Около правильной n — угольной призмы с высотой h и ребром основания a описана сфера. Найти отношение объемов призмы и шара, ограниченного сферой, описанной около данной призмы.

Воспользовавшись формулой (2), выразим объем шара, ограниченного описанной около призмы сферой, через высоту и ребро основания призмы:

Ответ.

Следствие 7. Отношение объема правильной треугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Следствие 8. Отношение объема правильной четырехугольной призмы правильной четырехугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Следствие 9. Отношение объема правильной шестиугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Как найти радиус окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Возможно тебе интересно узнать — как найти длину окружности?

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Радиус описанной сферы и ребро «A» треугольной призмы

Свойства

Зная радиус сферы, описанной вокруг правильной треугольной призмы с равносторонним треугольником в основании, можно найти сторону этого основания и затем посчитать высоту основания, радиусы вписанной и описанной окружностей около него, а также площадь. a=√(6/5) R_1 h=a/√2=√(3/5) R_1 r=a/(2√3)=2√(2/5) R_1 R=a/√3=√(2/5) R_1 S=(√3 a^2)/4=(3√3 〖R_1〗^2)/10

Боковое ребро треугольной призмы в совокупности с радиусом описанной сферы позволяет вычислить диагональ боковой стороны, периметр призмы и площадь боковой, а затем и полной поверхности призмы. d=√(a^2+b^2 )=√(6/5 〖R_1〗^2+b^2 ) P=3(2a+b)=3(2√(6/5) R_1+b) S_(б.п.)=3ab=3b√(6/5) R_1 S_(п.п.)=3b√(6/5) R_1+(3√3 〖R_1〗^2)/5

Чтобы найти объем треугольной призмы через радиус описанной сферы и боковое ребро, нужно подставить в формулу объема необходимое выражение вместо площади основания и умножить его на боковое ребро. V=S_(осн.) b=(3√3 〖R_1〗^2)/10 b

источники:

http://skysmart.ru/articles/mathematic/radius-okruzhnosti

http://geleot.ru/education/math/geometry/calc/prism/radius_sphere_and_edge_a

Источник

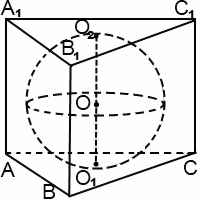
Шар вписанный в призму, касается каждой ее грани. Диаметр вписанного шара равен высоте призмы, а также равен диаметру окружности, вписанной в основание призмы.

Центр шара лежит на середине высоты призмы, проведенной через центр вписанной в основание окружности. Если в основание призмы нельзя вписать окружность либо высота призмы не равна диаметру вписанной в основание окружности, то в такую призму шар вписать нельзя.

Если призма правильная, центр вписанного в нее шара является точкой пересечения бисекторных плоскостей призмы.

При решении задач на шар,вписанный в призму, можно рассмотреть сечение комбинации тел плоскостью, параллельной основаниям. Она представляет собой многоугольник, равный многоугольнику основания, с вписанной в него окружностью, радиус которой равен радиусу шара. Далее используем формулы, связывающие радиус вписанной окружности со сторонами основания, а также то, что центр вписанной в многоугольник окружности является точкой пересечения его биссектрис.

Выразим объем призмы через радиус вписанного шара — R. Объем призмы равен

$[{V_n} = {S_{ocn}} cdot H]$

Площадь основания ищем по формуле S=pr, где p — полупериметр основания, r — радиус вписанной в него окружности. Поскольку в нашем случае r=R и высота призмы H=2R, то

$[{V_n} = pR cdot 2R = 2p cdot {R^2}]$

Но 2p=P — периметру основания. Окончательно имеем

$[{V_n} = P{R^2}]$

Выразим площадь полной поверхности прямой призмы через радиус вписанного в нее шара. Площадь полной поверхности прямой призмы равна сумме площадей оснований и боковой поверхности:

$[{S_{n.n.}} = {S_{bok}} + 2{S_{ocn}}]$

Боковая поверхность

$[{S_{bok}} = PH = 2PR]$

Отсюда

$[{S_{n.n.}} = 2PR + 2pR = 2PR + PR]$

Таким образом, пришли к формуле

$[{S_{n.n.}} = 3PR]$

Источник

Содержание

Вписанные шары

Шар и пирамида

Центр вписанного шара — точка пересечения биссекторных плоскостей, построенных для всех имеющихся в пирамиде двугранных углов; если эти биссекторные плоскости не имеют общей точки, то шар вписать нельзя.

Частный случай: боковые грани пирамиды равнонаклонены к плоскости основания.

Тогда:

шар вписать можно;
центр О шара лежит на высоте пирамиды, конкретнее — это точка пересечения высоты с биссектрисой угла между апофемой и проекцией этой апофемы на плоскость основания.

Шар и прямая призма

В прямую призму можно вписать шар тогда и только тогда, когда:

Центром шара служит середина отрезка, соединяющего центры вписанных в основания окружностей.

$r=R=frac{1}{2}cdot H$
, где r — радиус вписанного шара; R — радиус вписанной в основание окружности; Н — высота призмы.

Шар и цилиндр

В цилиндр можно вписать шар тогда и только тогда, когда осевое сечение цилиндра — квадрат (такой цилиндр иногда называют равносторонним). Центром шара служит центр симметрии осевого сечения цилиндра.

Шар вписан в цилиндр

Рис.1

Объем шара в полтора раза меньше объема описанного вокруг него цилиндра, а площадь поверхности шара — в полтора раза меньше площади полной поверхности того же цилиндра (теорема Архимеда).

Шар и конус

Шар и усечённый конус

В усеченный конус можно вписать шар тогда и только тогда, когда
$R_1+R_2=l$
, где $R_1,;;;R_2$ — радиусы оснований; l — образующая.

Центром шара служит середина отрезка, соединяющего центры оснований.

$r=frac{1}{2}cdot H$
, где r — радиус вписанного шара; Н — высота усеченного конуса.

Источник

ВИДЕОУРОК

Нами ранее уже рассмотрены
простые геометрические тела: призма, пирамида, цилиндр, конус, шар. Но в природе,
техники и геометрии также рассматривают и комбинации указанных геометрических тел.

ПРИМЕР:

Шар называется вписанным в конус, усечённый
конус и цилиндр, если поверхность шара касается плоскости основания этих фигур и
всех их боковых поверхностей.

Шар называется описанным вокруг конуса, если
поверхность шара проходит через вершину конуса, а окружность основания конуса
лежит на поверхности шара.

Шар называется описанным вокруг цилиндра и усечённого конуса, если окружности их
оснований лежат на поверхности шара.

Обратите внимание, что в конус всегда можно вписать шар, а вокруг цилиндра и
усечённого конуса всегда можно описать шар.

Для других объёмных фигур условия вписать в них и описать вокруг них шар должны
быть в каждом случае специально определены.

ЗАДАЧА:

В правильную четырёхугольную пирамиду
вписан куб так, что четыре его вершины находятся на боковых рёбрах пирамиды, а другие
четыре – в плоскости её основания. Найдите ребро куба, если в пирамиде сторона
основания равна а и высота
h.

РЕШЕНИЕ:

На рисунке изображена пирамида SABCD с вписанным в неё кубом MNPQM₁N₁P₁Q₁,
четыре вершины которого лежат на боковых рёбрах пирамиды, а другие – в плоскости
основания.

Обозначим ребро куба через х,
то есть

MN = MM₁ = x.

Рассмотрим подобные ⊿SO₁B и

⊿SON (ON ∥ O₁B).

Из
подобия этих треугольников найдём

Учитывая, что

SO₁ = h, SO = h – x,

получим

откуда

ОТВЕТ:

ЗАДАЧА:

Вокруг шара описан усечённый
конус, образующая которого равна а. Найти
боковую поверхность конуса.

РЕШЕНИЕ:

На рисунке изображёно основное сечение
усечённого конуса с вписанным в него шаром.

По условию задачи ВС = а. Обозначим

О₁В = R, а О₂C = r.

Тогда используя свойство
касательных к окружности, которые выходят из одной и той же самой точки,

О₂С = СМ и О₁В = МВ, или
О₁В + О₂С = СВ = а,

то есть R + r = а. Поэтому, боковая
поверхность усечённого конуса равна

_.
S_бок = π(R + r)а = πа².

Многогранник, описанный вокруг шара.

Шар называется вписанным в многогранник, а
многогранник – описанным вокруг шара, если
плоскости всех граней многогранника касаются шара.

Основные свойства призмы, описанной вокруг шара:

– шар можно вписать в прямую призму, если её основание –
многогранник, в который можно вписать окружность, а высота призмы равна диаметру
этой окружности;

– центр шара будет серединой высоты призмы, которая соединяет
центр окружностей, вписанных в многоугольники оснований призмы.

ЗАДАЧА:

Известно, что в треугольную
призму, стороны основания которой равны

13
см, 14 см и 15 см,

можно вписать шар. Найти радиус этого шара.

РЕШЕНИЕ:

Диаметр вписанного шара равен высоте
призмы и в тоже время равен диаметру окружности, вписанной в основание призмы. Поэтому
радиус окружности, вписанной в основание призмы, равен радиусу шара.

Радиус окружности r,
вписанной в основание призмы, найдём по формуле

где S –
площадь треугольника основания, р – его полупериметр.

По формуле Герона

Поэтому, радиус шара также равен 4
см.

ОТВЕТ: 4 см.

Основные свойства пирамиды, описанной вокруг шара:

– если в пирамиде все двугранные углы при основании равны
между собой, то в эту пирамиду можно вписать сферу; центр сферы принадлежит
высоте пирамиды, точка касания шара с основанием пирамиды совпадает с центром
вписанной в основание окружности, а точки касания с боковыми гранями принадлежат
высотам этих граней;

– в любую правильную пирамиду можно вписать шар; центр шара принадлежит
высоте пирамиды;

– центр шара, вписанного в правильную пирамиду, совпадает
с центром окружности, вписанной в равнобедренный треугольник, боковою стороною которого
будет апофемой правильной пирамиды, а высотою – высота пирамиды; радиус шара равен
радиусу этой окружности.

ЗАДАЧА:

В правильной четырёхугольной пирамиде
центры вписанного и описанного шара совпадают. Определите плоский угол при
вершине пирамиды.

РЕШЕНИЕ:

Дана правильная четырёхугольная
пирамида SАВС и точка
О – центр вписанного в пирамиду и описанного вокруг неё шара.

Точка О₁ – центр окружности, описанной вокруг ∆SВС.
Тогда перпендикуляр из центра шара на плоскость
∆SВС попадаетв
точку О₁, и ОО₁ будет
радиусом вписанного в пирамиду шара.

ОВ = ОС = SО = R –
радиусы описанного шара.

ОО₂ = ОО₁ =
r – радиусы вписанного шара.

Тогда прямоугольные

∆ОО₂В,
∆ОО₁В,
∆ОО₂С и ∆ОО₁С

равны между собой. Из их равенства
выходит, что

ВО₂ = СО₂ = ВО₁ = СО₁ и

∆ВО₂С и ∆ВО₁С равны.

В таком случае

∠ ВО₂С = ∠ ВО₁С = 90°.

Далее SО₁ = ВО₁ =
СО₁ как радиусы окружности, описанной вокруг ∆SВС.

Из равнобедренного ∆ВО₁S по свойству внешнего угла

∠
BSE = ¹/₂∠ BO₁E

Тогда

∠
BSC = ¹/₂∠ BO₁C = 45°.

ОТВЕТ: 45°.

Многогранник, вписанный в шар.

Если шар находится в середине многогранника, то он называется вписанным, а если снаружи многогранника – внешне вписанным.

Шар называется описанным вокруг многогранника,
а многогранник – вписанным в этот шар, если
все вершины многогранника лежат на поверхности шара.

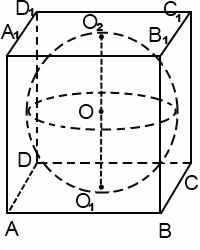
Основные свойства призмы, вписанной в шар:

– шар можно описать вокруг прямой призмы, если её основание
будет многоугольник, вокруг которого можно описать окружность;

– центр шара будет серединой высоты призмы, которая соединяет
центры окружностей, описанных вокруг многоугольников оснований призмы;

– основания призмы вписаны в равные параллельные сечения шара.

ЗАДАЧА:

Вокруг правильной треугольной призмы, сторона основания
которой равна 5√͞͞͞͞͞3 см, описан шар. Радиус шара равен 13
см. Найти высоту призмы.

РЕШЕНИЕ:

Пусть вокруг правильной треугольной
призмы АВСА₁В₁С₁ описан шар.

QВ = R_ABC – радиус окружности, описанной вокруг ∆АВС.

где a = 5√͞͞͞͞͞3 см – сторона основания правильного треугольника АВС.

Тогда

У ∆OQB, OB = R =
13 см – радиус шара, ∠ OQB = 90°.

Имеем

Поскольку точка О –
середина высоты призмы QQ₁ то

QQ₁ = 2×12 = 24
см.

ОТВЕТ: 24 см.

Основные свойства пирамиды, вписанной в шар:

– шар можно описать вокруг пирамиды, если её основанием будет
многоугольник, вокруг которого можно описать окружность; центр шара,
описанного вокруг пирамиды, лежит на перпендикуляре к плоскости основания,
проведённого через центр окружности, описанной вокруг основания;

– центр шара, описанного вокруг правильной пирамиды,
лежит на прямой, которая совпадает с высотой пирамиды;

– центр шара, описанного вокруг правильной пирамиды, совпадает
с центром окружности, описанной вокруг равнобедренного треугольника, боковою
стороной которого будет боковое ребро пирамиды, а высотой – высота пирамиды; радиус шара равен
радиусу этой окружности.

Напомним, что центр описанного шара может принадлежать высоте пирамиды, или
лежать на её продолжении (то есть находиться либо в середине пирамиды, или за её
пределами). Решая задачи способом, предложенным ниже, нет необходимости разглядывать
два случая. При выбранном способе решения место размещения центра шара (в середине
или вне пирамиды) не учитывается.

ЗАДАЧА:

Докажите, что радиус шара R, описанного вокруг правильной пирамиды,
можно найти по формуле

где Н –
высота пирамиды, r – радиус окружности, описанной вокруг основания пирамиды.

РЕШЕНИЕ:

Пусть точка О –
центр шара, описанного вокруг правильной пирамиды с высотой ОК.

По условию QK = R, КА = r – радиус окружности описанной вокруг основания.

Продолжим QK до второго пересечения с шаром в точке Q₁.

Тогда QQ₁ = 2R – диаметр окружности, и поэтому

∠ QAQ₁ = 90° и QQ₁ – гипотенуза прямоугольного треугольника QAQ₁.

∆QKA (∠ K
= 90°),

AQ² = QK² +
AK²,

AQ² = H² +
r².

По свойству катета прямоугольного
треугольника ∆QAQ₁ имеем

AQ² = QQ₁× QK,
то есть AQ² = 2R × H.

Поэтому,

AQ² = H² +
r² и AQ² = 2RH.

Откуда

H² + r² =
2RH,

что и
требовалось доказать.

Применение тригонометрических функций к
решению стереометрических задач.

ЗАДАЧА:

В правильной четырехугольной пирамиде плоский угол при
вершине равняется α. Высота h пирамиды является
диаметром шара. Найти длину кривой пересечения их поверхностей и вычислить ее
при

α
= 0,46 рад, h = 10,7 см.

РЕШЕНИЕ:

Дана правильная
четырехугольная пирамида SABCD и шар O₁, диаметром которой служит
высота пирамиды SO = h, плоский угол при вершине пирамиды ∠ BCD =
α.

Найти длину линии, по которой поверхность шара пересекается
с поверхностью пирамиды.

Искомая линия состоит из четырех ровных дуг кругов, по
которым пересекаются плоскости боковых граней пирамиды с поверхностью шара.

Найдем длину дуги B₁C₁, по
которой грань пирамиды BSC пересекается с
поверхностью шара.

Плоскость грани BSC пересекается с
поверхностью по кругу, центр какого O₂ получим, опустив
из центра шара перпендикуляр O₁O₂ на плоскость этой грани.