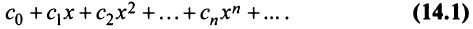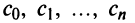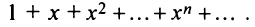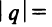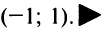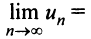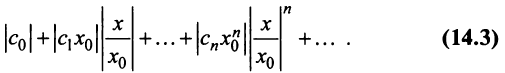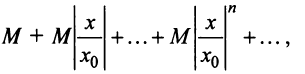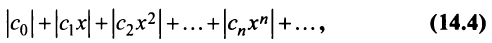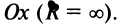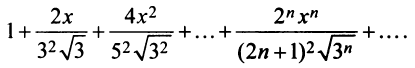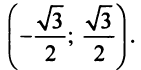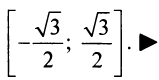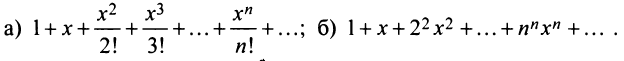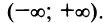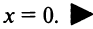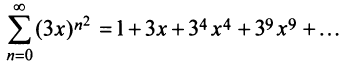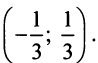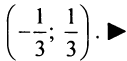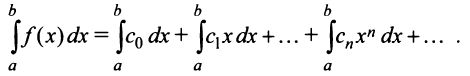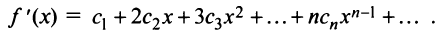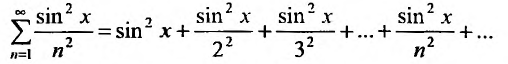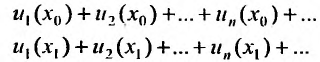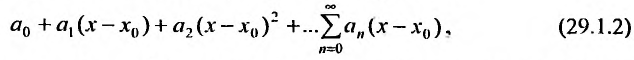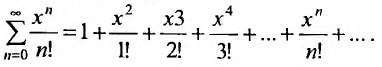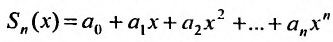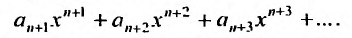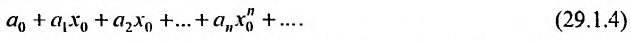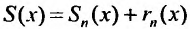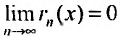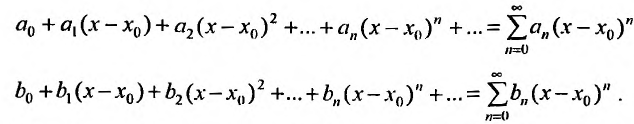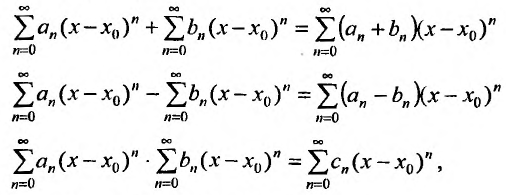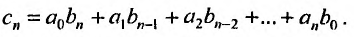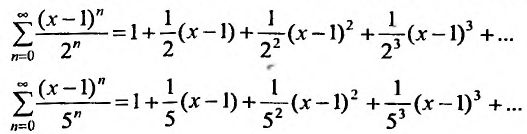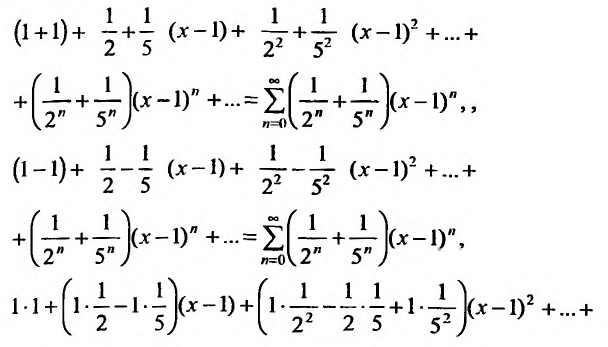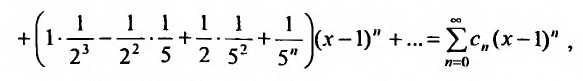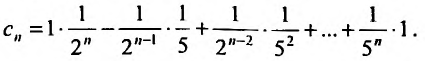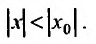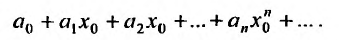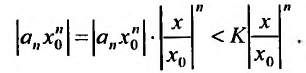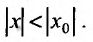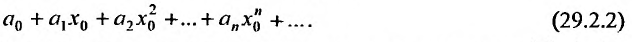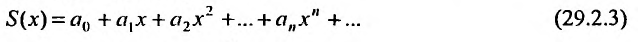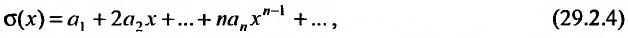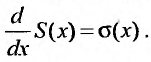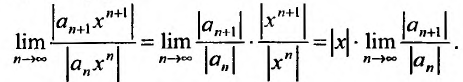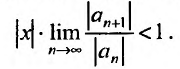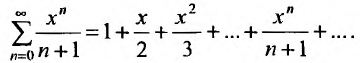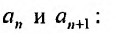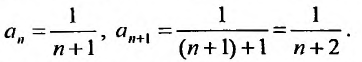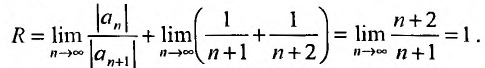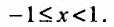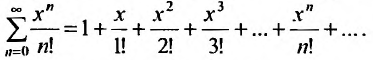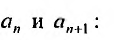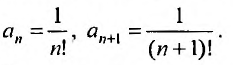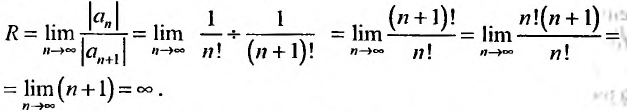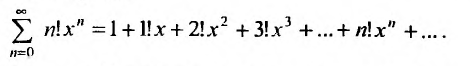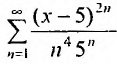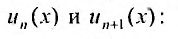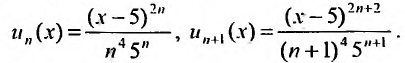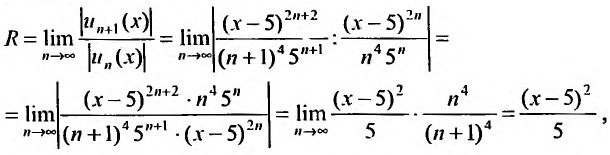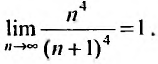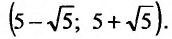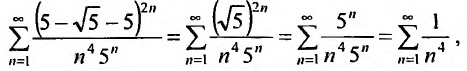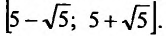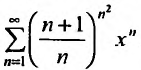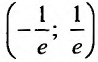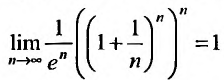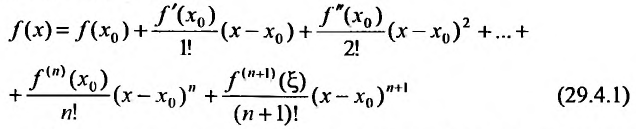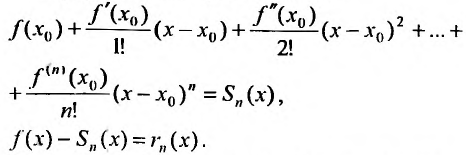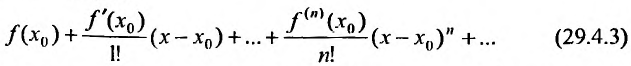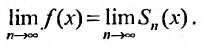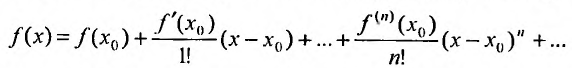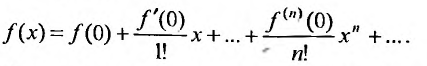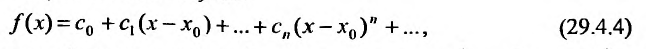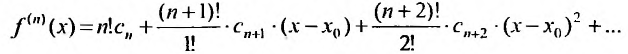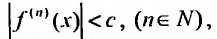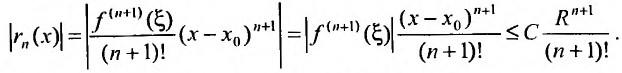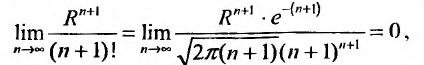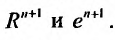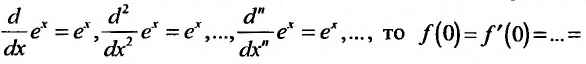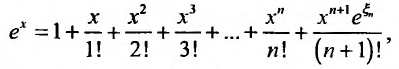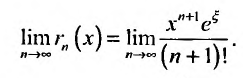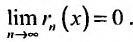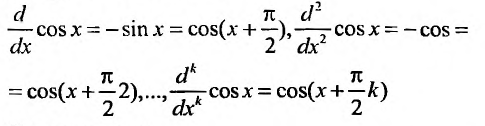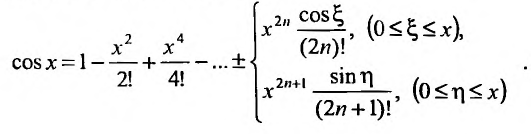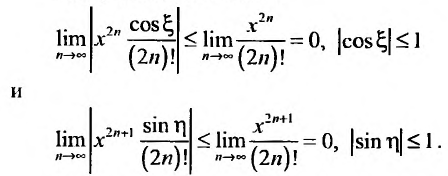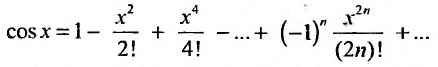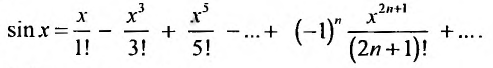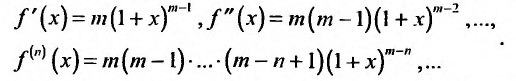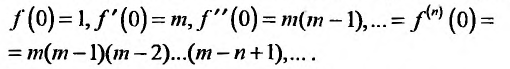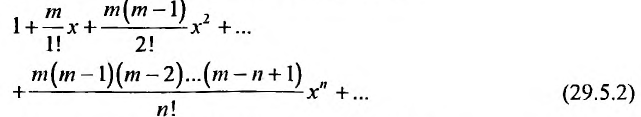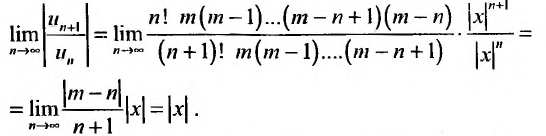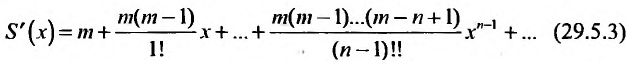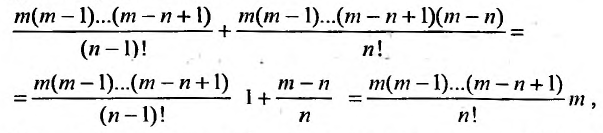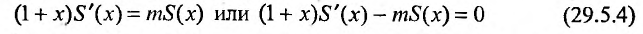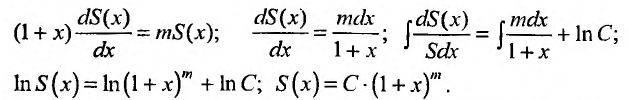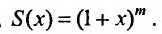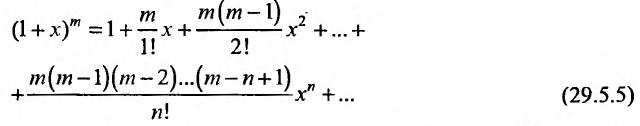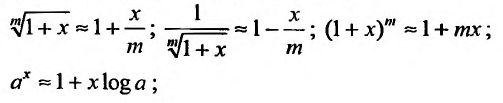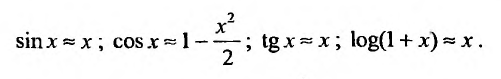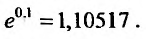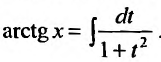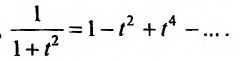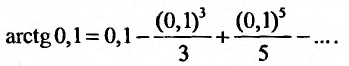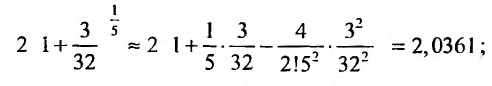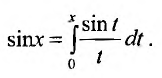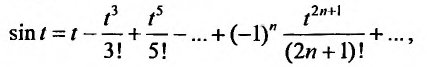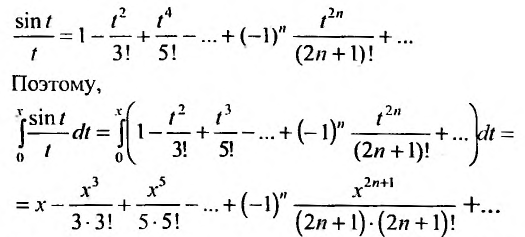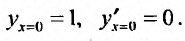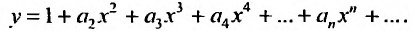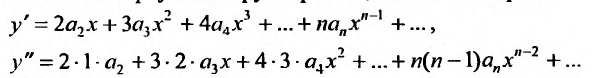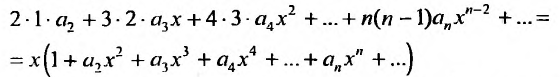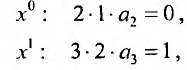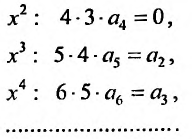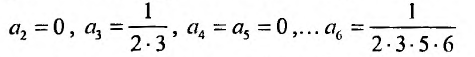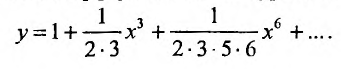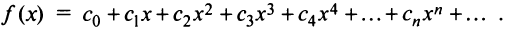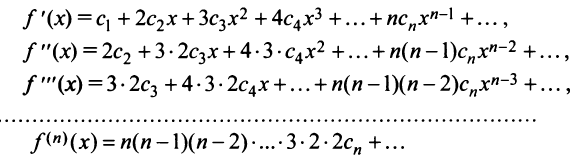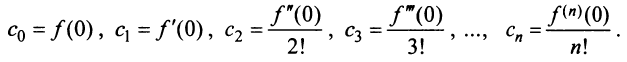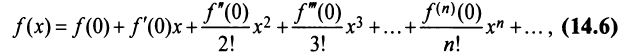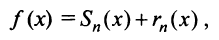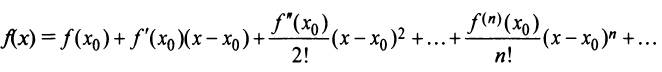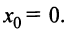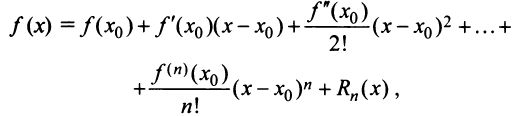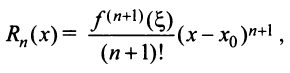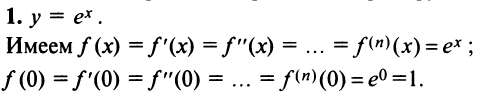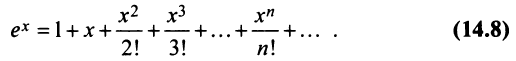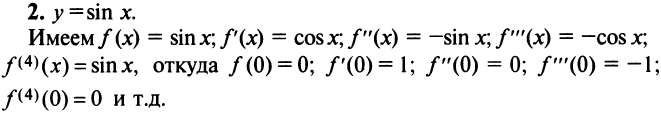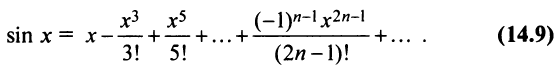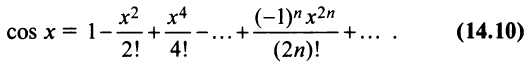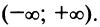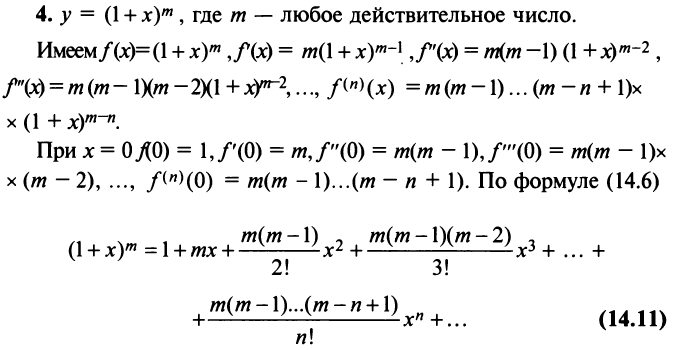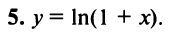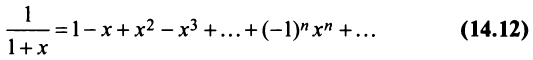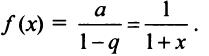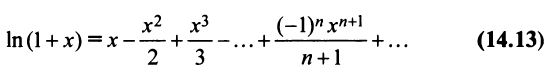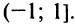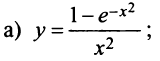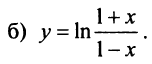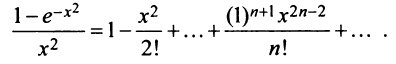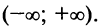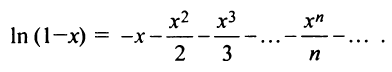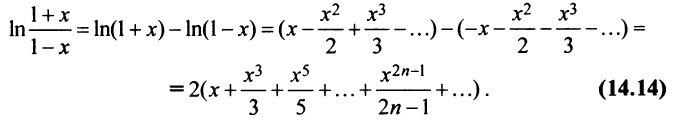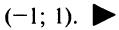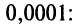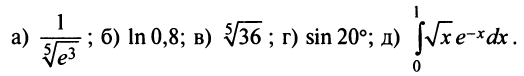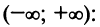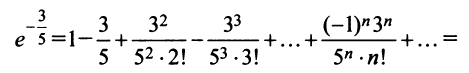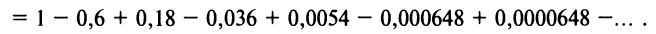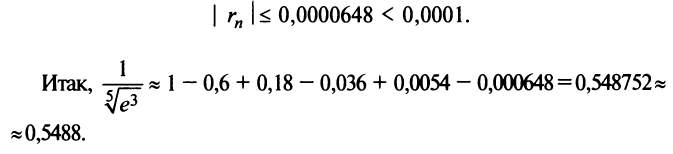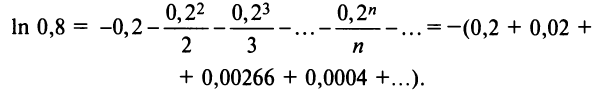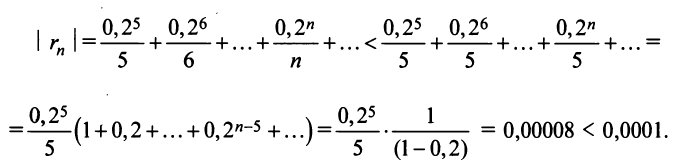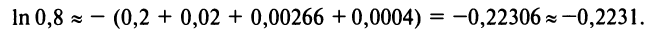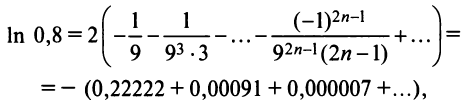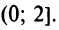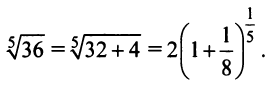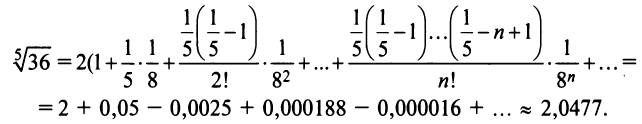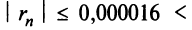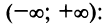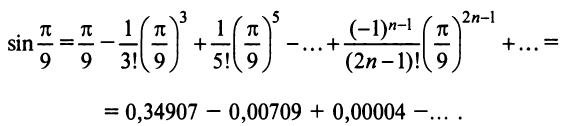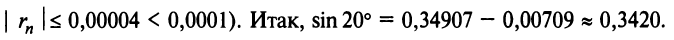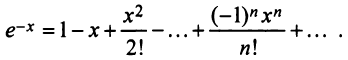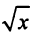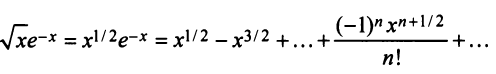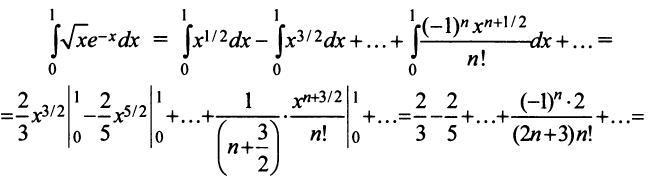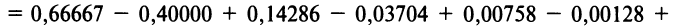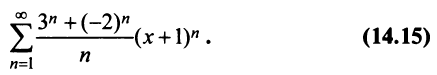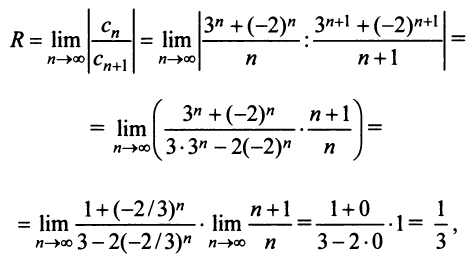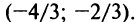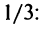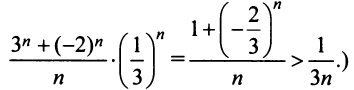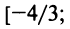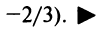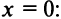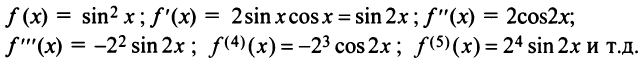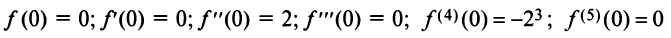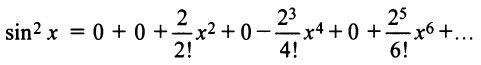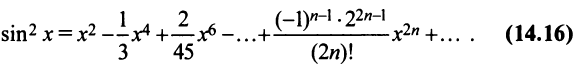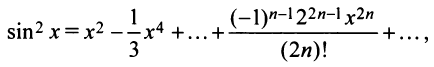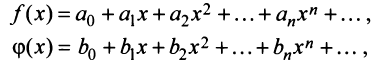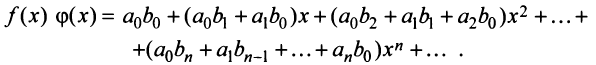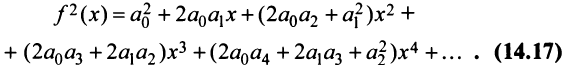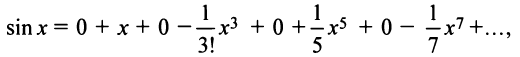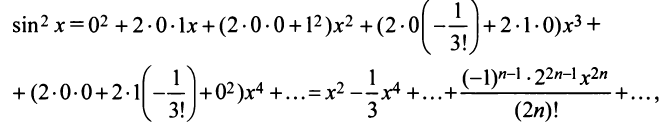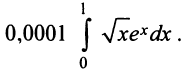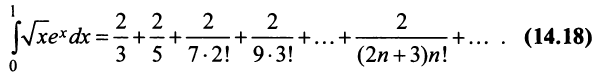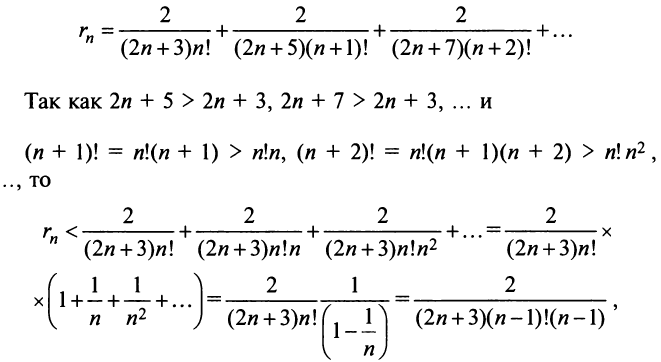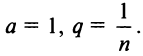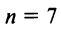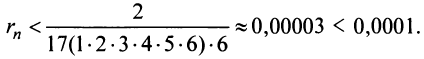Определение
Степенным рядом называется функциональный
ряд
,
элементы которого произведения постоянных
на степенные функции с целыми
показателями степеней от разности
—
коэффициенты степенного ряда (обычно
действительные функции).
В частности, если
,то
мы будем иметь степенной ряд, расположенный
по степеням x
В дальнейшем рассматриваем именно такие
ряды (замена
)
Для удобства n-м элементом
степенного ряда называют элемент
(хотя он стоит на n+1 месте).
Свободный элемент
считается
нулевым элементом ряда.
Рассмотрим ряд
(*)
и докажем очень важную теорему, на
которой будет основано изучение таких
рядов.
Теорема Абеля
Если степенной ряд (*) сходится в точке
,
то он сходится и притом абсолютно, в
интервале
,
т. е. при всяком x ,
удовлетворяющем условию
.
Доказательство:
Заметим, что вследствие сходимости ряда
его
общий элемент
.
Поэтому все элементы этого ряда ограничены
в совокупности, т.е. существует М>0,
такое, что при всяком n
.
Запишем ряд (*) так
и составим ряд их абсолютных величин
элементов этого ряда:
В силу установленного неравенства
каждый элемент здесь меньше соответствующего
элемента геометрической прогрессии со
знаменателем
:
Если
,
то
и прогрессия сходится, поэтому сходится
ряд из абсолютных величин, а значит,
абсолютно сходится сам ряд (*). Теорема
доказана.
Несмотря на то, что
нельзя сразу воспользоваться признаком
сравнения, поскольку в условиях теоремы
не сказано, что ряд в самой точке
сходится абсолютно.
Следствие
Если степенной ряд (*) расходится при
, то он расходится и при всяком х,
большем по абсолютной величине
,
то есть при
Область сходимости степенного ряда
Здесь возможны три случая:
-
Область сходимости состоит только из
одной точки х=0, то есть ряд расходится
для всех значений х, кроме х=0.
Пример
Если х фиксировано и х не равно
0,то, начиная с достаточно большого n,
будет
,
откуда вытекает неравенство
,
означающее, что общий элемент ряда не
стремится к нулю.
-
Область сходимости состоит из всех
точек оси ОХ, то есть ряд сходится
при всех значениях х. Пример
Для любого х, начиная с достаточно
большого n, будет
,
так как
и т.д.
Начиная с номера n,
элементы ряда по абсолютной величине
будут меньше элементов сходящейся
геометрической прогрессии. Следовательно,
при любом х ряд сходится.
-
Область сходимости состоит более чем
из одной точки оси ОХ, причем есть
точки оси, не принадлежащие области
сходимости. Пример
Это геометрическая прогрессия со
знаменателем х. Ряд сходится при
|x|<1 и расходится
при
.
В этом случае на числовой оси наряду с
точками сходимости ряда имеются и точки
его расходимости.
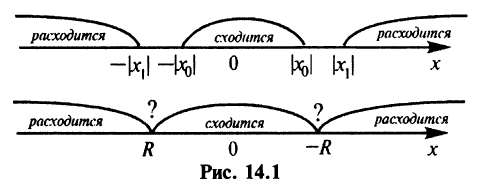
Из теоремы Абеля и ее следствия вытекает,
что все точки сходимости расположены
от начала координат не дальше, чем любая
из точек расходимости. Точки сходимости
будут целиком заполнять некоторый
интервал с центром в начале координат.
Таким образом
Для каждого степенного ряда, имеющего
как точки сходимости , так и точки
расходимости, существует такое
положительное число R,
что для всех х по модулю меньшим R
(
),
ряд абсолютно сходится, а для всех |x|>R
ряд расходится. При x=R
и x=-R различные
варианты:
А) ряд сходится в обеих точках.
Б) ряд сходится в одной из точек.
В) ряд расходится в обеих точках.
Определение
Радиусом сходимости степенного ряда
(*) называется такое число R,
что для любых х, |x|<R,
степенной ряд сходится, а для всех х,
|x|>R,
расходится. Интервал (-R,R)
называется интервалом сходимости.
Считаем, что если ряд расходится для
любого х, кроме х=0, R=0.
Если ряд сходится при всех х, то
считаем
или
.
Для ряда
центр интервала сходимости в точке
( а не х=0) и интервал сходимости
.
Способ отыскания радиуса сходимости
степенного ряда
Отметим, что для нахождения радиуса
сходимости можно исследовать ряд,
составленный из абсолютных величин
элементов исходного ряда, то есть
(**) так как интервалы сходимости ряда
(*) и ряда (**) совпадают. К ряду (**) применим
признак Даламбера.
будет
содержать |x| или
степень |x|
Для тех значений х, при которых
получаемый предел меньше 1, ряд сходится,
а для тех, при которых x>1,
ряд расходится. Отсюда следует, что
значения |x|,
при которых этот предел равен 1, и будет
являться радиусом сходимости ряда.
Может случиться, что найденный предел
при всех х будет равен 0. Это означает,
что ряд (*) сходится при всех х и
.
Наоборот, если для любых х кроме х=0
предел равен бесконечности, то ряд будет
везде расходиться, кроме х=0, то есть
R=0.
Примеры
-
Найти радиус сходимости ряда
,
то есть для всякого х ряд сходится
.
-
Найти радиус сходимости ряда
Если |x|<1 —
ряд сходится
Если |x|>1 –
ряд расходится
При х=1 получаем гармонический ряд,
который расходится.
При х=-1 ряд
сходится условно.
-
Найти радиус сходимости ряда
,
то есть R=1
При |x|<1 –
ряд сходится
При |x|>1 –
ряд расходится
При |x|=1 – ряд
сходится абсолютно.
-
Найти радиус сходимости ряда
Если
ряд сходится, то есть при -2<x-1<2.
Получаем интервал сходимости (-1,3)
с центром х=1.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
From Wikipedia, the free encyclopedia
In mathematics, the radius of convergence of a power series is the radius of the largest disk at the center of the series in which the series converges. It is either a non-negative real number or 
Definition[edit]
For a power series f defined as:
where
- a is a complex constant, the center of the disk of convergence,
- cn is the n-th complex coefficient, and
- z is a complex variable.
The radius of convergence r is a nonnegative real number or 
and diverges if
Some may prefer an alternative definition, as existence is obvious:
On the boundary, that is, where |z − a| = r, the behavior of the power series may be complicated, and the series may converge for some values of z and diverge for others. The radius of convergence is infinite if the series converges for all complex numbers z.[1]
Finding the radius of convergence[edit]
Two cases arise. The first case is theoretical: when you know all the coefficients 
Theoretical radius[edit]
The radius of convergence can be found by applying the root test to the terms of the series. The root test uses the number
«lim sup» denotes the limit superior. The root test states that the series converges if C < 1 and diverges if C > 1. It follows that the power series converges if the distance from z to the center a is less than
and diverges if the distance exceeds that number; this statement is the Cauchy–Hadamard theorem. Note that r = 1/0 is interpreted as an infinite radius, meaning that f is an entire function.
The limit involved in the ratio test is usually easier to compute, and when that limit exists, it shows that the radius of convergence is finite.
This is shown as follows. The ratio test says the series converges if
That is equivalent to
Practical estimation of radius in the case of real coefficients[edit]
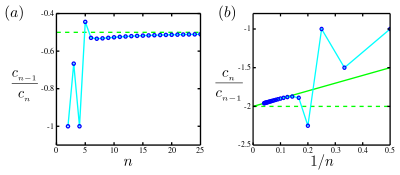
Plots of the function 
The solid green line is the straight-line asymptote in the Domb–Sykes plot,[2] plot (b), which intercepts the vertical axis at −2 and has a slope +1. Thus there is a singularity at 
Usually, in scientific applications, only a finite number of coefficients 


Radius of convergence in complex analysis[edit]
A power series with a positive radius of convergence can be made into a holomorphic function by taking its argument to be a complex variable. The radius of convergence can be characterized by the following theorem:
- The radius of convergence of a power series f centered on a point a is equal to the distance from a to the nearest point where f cannot be defined in a way that makes it holomorphic.
The set of all points whose distance to a is strictly less than the radius of convergence is called the disk of convergence.
A graph of the functions explained in the text: Approximations in blue, circle of convergence in white
The nearest point means the nearest point in the complex plane, not necessarily on the real line, even if the center and all coefficients are real. For example, the function
has no singularities on the real line, since 
The root test shows that its radius of convergence is 1. In accordance with this, the function f(z) has singularities at ±i, which are at a distance 1 from 0.
For a proof of this theorem, see analyticity of holomorphic functions.
A simple example[edit]
The arctangent function of trigonometry can be expanded in a power series:
It is easy to apply the root test in this case to find that the radius of convergence is 1.
A more complicated example[edit]
Consider this power series:
where the rational numbers Bn are the Bernoulli numbers. It may be cumbersome to try to apply the ratio test to find the radius of convergence of this series. But the theorem of complex analysis stated above quickly solves the problem. At z = 0, there is in effect no singularity since the singularity is removable. The only non-removable singularities are therefore located at the other points where the denominator is zero. We solve
by recalling that if z = x + iy and eiy = cos(y) + i sin(y) then
and then take x and y to be real. Since y is real, the absolute value of cos(y) + i sin(y) is necessarily 1. Therefore, the absolute value of ez can be 1 only if ex is 1; since x is real, that happens only if x = 0. Therefore z is purely imaginary and cos(y) + i sin(y) = 1. Since y is real, that happens only if cos(y) = 1 and sin(y) = 0, so that y is an integer multiple of 2π. Consequently the singular points of this function occur at
- z = a nonzero integer multiple of 2πi.
The singularities nearest 0, which is the center of the power series expansion, are at ±2πi. The distance from the center to either of those points is 2π, so the radius of convergence is 2π.
Convergence on the boundary[edit]
If the power series is expanded around the point a and the radius of convergence is r, then the set of all points z such that |z − a| = r is a circle called the boundary of the disk of convergence. A power series may diverge at every point on the boundary, or diverge on some points and converge at other points, or converge at all the points on the boundary. Furthermore, even if the series converges everywhere on the boundary (even uniformly), it does not necessarily converge absolutely.
Example 1: The power series for the function f(z) = 1/(1 − z), expanded around z = 0, which is simply
has radius of convergence 1 and diverges at every point on the boundary.
Example 2: The power series for g(z) = −ln(1 − z), expanded around z = 0, which is
has radius of convergence 1, and diverges for z = 1 but converges for all other points on the boundary. The function f(z) of Example 1 is the derivative of g(z).
Example 3: The power series
has radius of convergence 1 and converges everywhere on the boundary absolutely. If h is the function represented by this series on the unit disk, then the derivative of h(z) is equal to g(z)/z with g of Example 2. It turns out that h(z) is the dilogarithm function.
Example 4: The power series
has radius of convergence 1 and converges uniformly on the entire boundary |z| = 1, but does not converge absolutely on the boundary.[5]
Rate of convergence[edit]
If we expand the function
around the point x = 0, we find out that the radius of convergence of this series is 
So for these particular values the fastest convergence of a power series expansion is at the center, and as one moves away from the center of convergence, the rate of convergence slows down until you reach the boundary (if it exists) and cross over, in which case the series will diverge.
Abscissa of convergence of a Dirichlet series[edit]
An analogous concept is the abscissa of convergence of a Dirichlet series
Such a series converges if the real part of s is greater than a particular number depending on the coefficients an: the abscissa of convergence.
Notes[edit]
- ^ Mathematical Analysis-II. Krishna Prakashan Media. 16 November 2010.
- ^ See Figure 8.1 in: Hinch, E.J. (1991), Perturbation Methods, Cambridge Texts in Applied Mathematics, vol. 6, Cambridge University Press, p. 146, ISBN 0-521-37897-4
- ^ Domb, C.; Sykes, M.F. (1957), «On the susceptibility of a ferromagnetic above the Curie point», Proc. R. Soc. Lond. A, 240 (1221): 214–228, Bibcode:1957RSPSA.240..214D, doi:10.1098/rspa.1957.0078, S2CID 119974403
- ^ Mercer, G.N.; Roberts, A.J. (1990), «A centre manifold description of contaminant dispersion in channels with varying flow properties», SIAM J. Appl. Math., 50 (6): 1547–1565, doi:10.1137/0150091
- ^ Sierpiński, W. (1918). «O szeregu potęgowym, który jest zbieżny na całem swem kole zbieżności jednostajnie, ale nie bezwzględnie». Prace Matematyczno-Fizyczne. 29 (1): 263–266.
References[edit]
- Brown, James; Churchill, Ruel (1989), Complex variables and applications, New York: McGraw-Hill, ISBN 978-0-07-010905-6
- Stein, Elias; Shakarchi, Rami (2003), Complex Analysis, Princeton, New Jersey: Princeton University Press, ISBN 0-691-11385-8
See also[edit]
- Abel’s theorem
- Convergence tests
- Root test
External links[edit]
- What is radius of convergence?
Содержание:
Степенные ряды:
До сих пор мы рассматривали ряды, членами которых были числа, т.е. числовые ряды. Теперь перейдем к рассмотрению рядов, членами которых являются функции, в частности степенные функции
Такие ряды называются степенными, а числа
Область сходимости степенного ряда
Совокупность тех значений 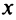
Пример:
Найти область сходимости степенного ряда
Решение:
Данный ряд можно рассматривать как геометрический ряд со знаменателем 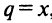
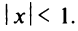
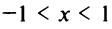
Структура области сходимости степенного ряда устанавливается с помощью теоремы Абеля.
Теорема Абеля. 1) Если степенной ряд сходится при значении 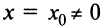
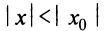
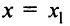
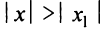
1) По условию ряд (14.1) сходится при 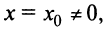
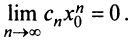
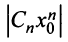
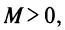
Рассмотрим ряд, составленный из абсолютных величин членов ряда (14.1) 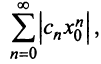
Члены ряда (14.3) согласно неравенству (14.2) меньше соответствующих членов ряда
представляющего геометрический ряд, который сходится, когда его знаменатель 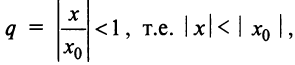
2) По условию ряд (14.1) расходится при 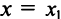
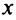
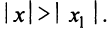
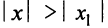
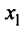
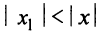
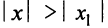
Из теоремы Абеля (см. рис. 14.1) следует, что существует такое число 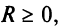
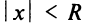
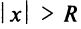
Число 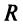
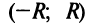
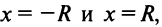
Найдем выражение радиуса сходимости степенного ряда (14.1) через его коэффициенты. Рассмотрим ряд, составленный из абсолютных величин его членов
в котором все коэффициенты 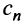
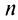
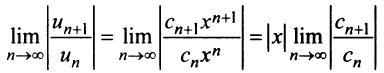
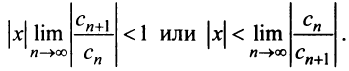
Замечание. Следует отметить, что у некоторых рядов интервал сходимости вырождается в точку 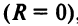
Пример:
Найти область сходимости степенного ряда
Решение:
Найдем радиус сходимости ряда по формуле (14.5) 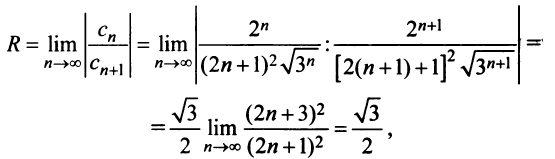
Теперь выясним поведение ряда на концах интервала сходимости. На левом конце при 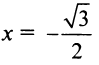
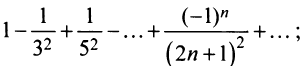
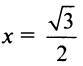
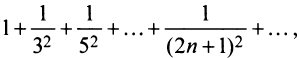
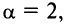
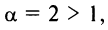
Следует отметить, что сходимость ряда на левом конце ин-тервала сходимости при 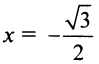
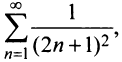
Итак, область сходимости данного ряда
Замечание. При исследовании сходимости на концах интервала сходимости для получающегося ряда с положительными членами применять признак Даламбера не имеет смысла, так как в этом случае всегда будем получать 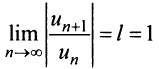
Пример:
Найти области сходимости степенных рядов:
Решение:
а) Радиус сходимости ряда по (14.5)
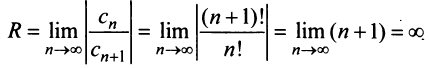
б) Задачу можно решать аналогично предыдущим. Решение упрощается, если заметить, что 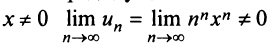
Итак, область сходимости ряда состоит из одной точки
Пример:
Найти область сходимости ряда
Решение:
Найти радиус сходимости по формуле (14.5) в данном случае не представляется возможным, так как коэффициенты ряда 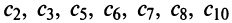
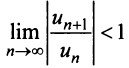
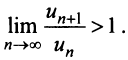
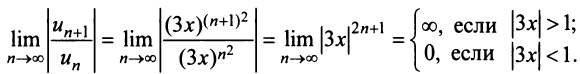
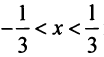
Исследуем сходимость на концах интервала сходимости: при 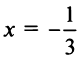
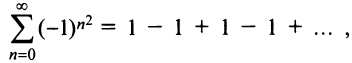
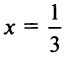
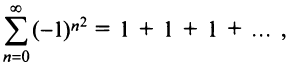
Итак, область сходимости ряда
Свойства степенных рядов. Пусть функция 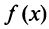
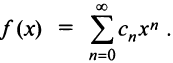
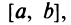
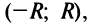
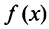
Кроме того, в интервале сходимости степенной ряд можно почленно дифференцировать:
При этом после интегрирования или дифференцирования полученные ряды имеют тот же радиус сходимости
Определение степенного ряда и его сходимости
Понятое функциональной зависимости является одним из важнейших в математике. Всякая функция осуществляет некоторое соответствие между объектами, составляющими область задания этой функции, и объектами, составляющими область её значений. Так можно рассматривать функции, которые ставят в соответствие числам — ряды. Эти функции называются функциональными рядами, т.е. функциональный ряд это выражение
членами которого являются некоторые функции переменной х. Например, ряд
является функциональным рядом.
Придавая в выражении (29.1.1) переменной х некоторые значения 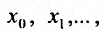
которые могут оказаться, как сходящимися, так и расходящимися.
В простейших случаях для определения сходимости ряда (29.1.1) можно применять к нему известные признаки сходимости числовых рядов, считая х фиксированным.
Определение 29.1.1. Совокупность всех значений переменной х, для которых соответствующие числовые ряды сходятся, называется областью сходимости функционального ряда (29.1.1). Определение 29.1.2. Функциональный ряд вида
где 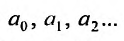
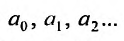
Если в ряде (29.1.2) сделать замену переменного, положив
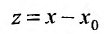
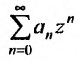
Очевидно, что исследование сходимости ряда (29.1.2) эквивалентно исследованию сходимости ряда (29.1.3). Примером степенного ряда может служить ряд
Сумма п первых членов ряда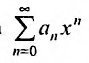
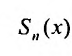
Для степенного ряда можно составить последовательность частичных сумм 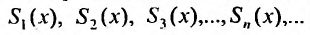
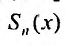
Остатком степенного ряда после n -го его члена (или n -ым остатком) называется ряд, полученный из заданного исключением n его первых членов:
Определение 29.1.3. Степенной ряд называется сходящимся на некотором множестве, если он сходится в любой точке этого множества.
Степенной ряд называется абсолютно сходящимся на некотором множестве, если в каждой точке этого множества сходится ряд из модулей его членов:
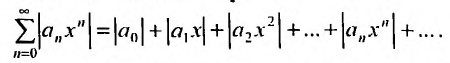
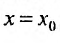
Соответствующий числовой ряд а0 +о,л:0 +… сходится абсолютно, если сходится ряд 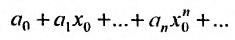
Так как каждой точке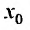
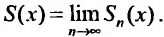
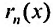
Для сходящегося степенного ряда предел остатка равен нулю:
Степенные ряды можно складывать, вычитать, умножать. Пусть заданы два степенных ряда:
Сумма, разность и произведение заданных степенных рядов определяется формулами:
где
Например, сумма, разность и произведение степенных рядов:
имеет вид:
где
Радиус сходимости, интервал сходимости
Области сходимости степенных рядов устроены довольно просто. Они описываются следующей теоремой.
Теорема 29.2.1 (теорема Абеля). Если степенной ряд
сходится при некотором 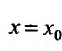
Если же степенной ряд (29.2.1) расходится при 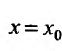
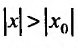
Доказательство. Предположим сначала, что степенной ряд (29.2.1) сходится в точке 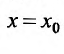
Тогда, в силу необходимого признака сходимости, 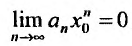
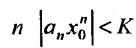
Если 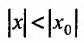
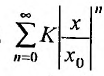
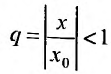
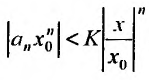
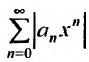
Предположим теперь, что степенной ряд (29.2.1) расходится, при 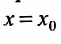
Возьмём тогда некоторое значение х, для которого 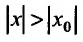
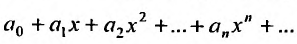
сходится. Но тогда из сходимости этого ряда, в силу первой части доказательства теоремы, вытекает сходимость ряда (29.2.2), что противоречит предположению, о его расходимости. Полученное противоречие означает, что для всех 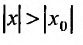
Если ряд (29.2.1) имеет вещественные коэффициенты и переменная х принимает только вещественные значения, то справедливо следующее определение, вытекающее из теоремы Абеля.
Определение 29.2.1. Величина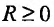
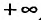
такая, что при всех х, у которых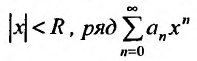
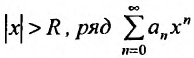
Множество точек х удовлетворяющих соотношению 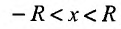
Итак, из определения 29.2.1 и теоремы Абеля следует, что областью сходимости степенного ряда — является интервал сходимости. И если значение 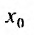
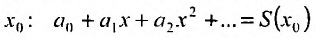
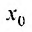
Свойства степенных рядов
Для степенных рядов справедливы следующие свойства:
1) Степенной ряд сходится равномерно внутри интервала сходимости.
2) Внутри интервала сходимости ряда сумма его является непрерывной функцией.
3) Если пределы интегрирования лежат внутри интервала сходимости степенного ряда, то последовательность интегралов от частичных сумм ряда сходится к интегралу от суммы ряда.
4) Если степенной ряд
имеет радиус сходимости R , то и ряд
получаемый в результате почленного дифференцирования ряда (29.2.3) также имеет радиус сходимости R. Производная суммы ряда (29.2.3) равна сумме ряда (29.2.4), т.е.
Вычисление интервала сходимости
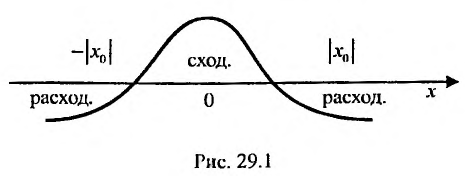
Как уже было сказано в и. 2 областью сходимости степенного ряда является интервал сходимости. Более того, из теоремы Абеля следует, что областью сходимости степенного ряда является интервал с центром в начале координат (рис 29.1).
Действительно, если 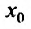
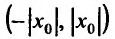
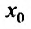
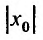
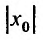
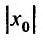
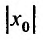
Заметим, что на концах интервала вопрос о сходимости или расходимости решается индивидуально в каждом конкретном случае. У некоторых рядов интервал сходимости может вырождаться в точку, у других охватывать всю ось Ох.
Укажем теперь способ вычисления радиуса сходимости степенного ряда.
Пусть задан степенной ряд 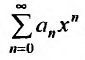
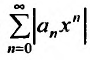
вычислим предел
Если этот предел меньше единицы, то, как следует из признака Д’Аламбера, ряд, составленный из модулей членов ряда (29.2.1) сходится, т.е. ряд сходится если
Если же 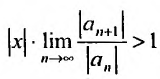
А это означает, что если 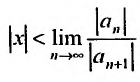
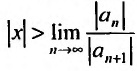
Учитывая определение радиуса сходимости степенного ряда, получим, что радиус сходимости можно вычислить по формуле:
Рассуждая аналогичным образом можно получить еще одну формулу для определения радиуса сходимости:
Если степенной ряд содержит только четные или нечетные степени х, то применяем признак Д’Аламбсра или Коши к ряду, составленному из модулей членов данного ряда.
Пример №1
Найти радиус и интервал сходимости степенного ряда:
Решение:
Выпишем вначале значения
Для определения радиуса сходимости воспользуемся формулой (29.3.1):
Итак, степенной ряд сходится для |х| 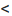
Исследуем сходимость ряда на концах интервала сходимости.
Пусть х =—1. Тогда получим знакочередующийся ряд 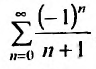
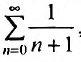
Суммируя вышесказанное, получим интервал сходимости
Пример №2
Найти радиус и интервал сходимости степенного ряда
Решение:
Выпишем вначале значения
Для определения радиуса сходимости воспользуемся формулой (29.3.2):
Так как 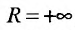
Пример №3
Найти радиус и интервал сходимости степенного ряда:
Решение:
Выпишем вначале значения
Для определения радиуса сходимости воспользуемся формулой (29.3.1):
Так как радиус сходимости равен нулю, то ряд сходится только в одной точке x= 0.
Пример №4
Найти радиус и интервал сходимости степенного ряда
Решение:
Данный ряд содержит только четные степени (а- — 5), коэффициенты при нечетных степенях равны нулю. Поэтому воспользоваться формулами (29.3.1) и (29.3.2) не представляется возможным.
Считая х фиксированным, применим признак Д’Аламбера к ряду, составленному из модулей членов данного ряда. Выпишем значения
Тогда
так как
Ряд сходится, если 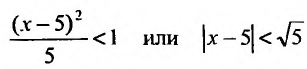
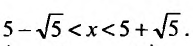
Исследуем сходимость ряда на концах интервала сходимости. Пусть 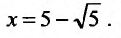
который сходится, как ряд Дирихле, для которого а = 4. При 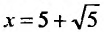
Пример №5
Найти радиус и интервал сходимости степенного ряда
Решение:
Выпишем значение 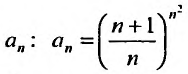
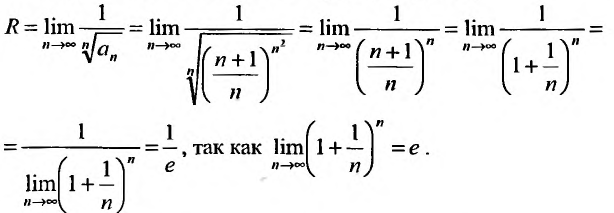
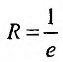
Исследуем его сходимость на концах интервала.
Пусть 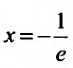
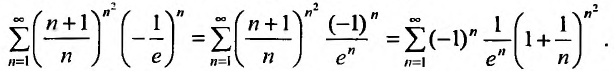
Следовательно, данный ряд расходится. И при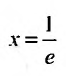
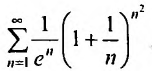
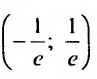
Ряды Тейлора и Маклорена
Как уже отмечалось, сумма сходящегося степенного ряда является некоторой функцией, определенной внутри интервала сходимости. В связи с этим мы рассмотрим задачу разложения некоторой функции в ряд, т.е. будем по заданной функции искать сходящийся ряд того или иного типа, сумма которого в интервале сходимости равнялась бы заданной функции.
Известно, что если функция f имеет на некотором отрезке производные всех порядков, то можно написать формулу Тейлора для любого значения n:
где 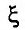
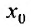
В формуле Тейлора обозначим:
пункта 27.2 (теорема 27.2.1) следует, что если
то степенной ряд
сходится и его суммой будет функция f(х), так как 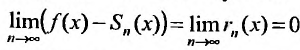
Справедливо и обратное утверждение, что если степенной ряд (29.4.3) сходится, то выполняется (29.4.2).
Определение 29.4.1. Представление функции f в виде ряда
называется разложением этой функции в ряд Тейлора. Если же 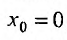
Следует заметить, что остаточный член в формуле Тейлора для функции J не обязательно является остатком ряда Тейлора для этой функции. Поэтому из сходимости ряда Тейлора для функции f , еще не следует сходимость именно к этой функции. При разложении функции в ряд Тейлора необходимо проверять условие (29.4.2). Однако сели разложение функции в какой-либо степенной ряд вообще возможно, то оно является разложением в ряд Тейлора, т.е. справедлива следующая теорема.
Теорема 29.4.1. Пусть
и стоящий справа ряд сходится в интервале 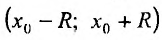
Доказательство. Так как степенной ряд в интервале сходимости можно почленно дифференцировать, то n-ую производную функции (29.4.4) можно представить в виде:
Полагая в последнем тождестве 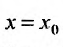
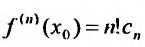
Из доказанной теоремы вытекает, что в одной и той же области, для одной и той же функции существует единственное разложение.
На практике, для разложения функции в ряд Тейлора, удобно пользоваться следующей теоремой.
Теорема 29.4.2. Если при любых х, удовлетворяющих неравенству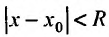
то ряд Тейлора, для этой функции, сходится в интервале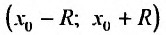
Доказательство. Из условия теоремы следует, что функцию f можно представить формулой Тейлора с остаточным членом в форме Лагранжа, т.е.
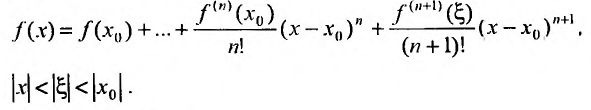
Переходя к пределу при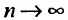
Воспользовавшись асимптотической формулой Стерлинга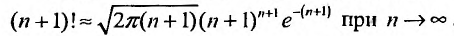
так как стспснно-показательная функция 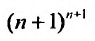
Тогда из неравенства (29.4.6) получим: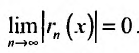
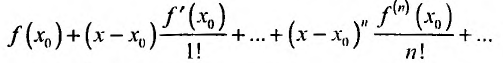
Разложение некоторых элементарных функций в ряд Маклорена
Из пункта 29.4 следует, что для того чтобы некоторая функция разлагалась в ряд Тейлора нужно, чтобы она имела производные любого порядка и чтобы либо 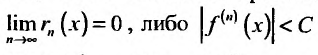
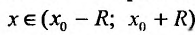
1. Разложение функции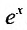
Находим производные данной функции и их значения при х=0. Так как
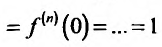
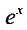
где 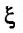
Вычислим предел остаточного члена, для любого х:
Выражение 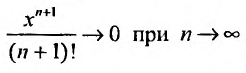
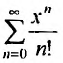
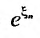
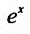
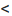
Следовательно, ряд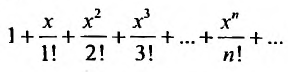
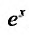
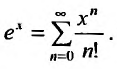
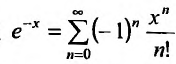
2. Разложение функций cos х и sin х. Для функции cos x имеем:
Следовательно,
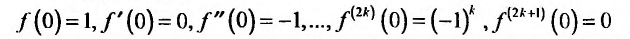
Маклорена с остаточным членом в форме Лагранжа для функции cosx имеет вид:
Ясно, что для любого X
Поэтому, функция cos л- разлагается в ряд Маклорена вида:
Аналогично получается разложение в ряд Маклорена функции sinx:
3. Биномиальный ряд.
Найдем разложение в степенной ряд функции
где m -произвольное действительное число.
Дифференцируя равенство (29.5.1) n раз, получим:
Значения функции и се производных при х = 0 равны:
Следовательно, ряд Маклорена имеет вид:
Если m- целое, то выражение (29.5.2) содержит конечное число членов. Если же m- нецелое, то выражение (29.5.2)- бесконечный ряд, называемый биномиальным.
Определим вначале радиус сходимости этого ряда, для чего применим признак Д’Аламбсра к ряду, составленному из модулей его членов:
Следовательно, при |х| 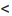
Покажем теперь, что ряд (29.5.2) сходится к функции 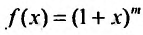
Умножим обе части (29.5.3) на 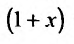
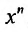
Эта сумма, как показано, равна произведению коэффициента при 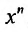
С другой стороны, вычисляя производную отношения
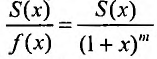
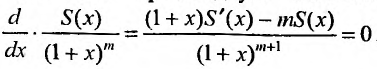
Решая дифференциальное уравнение 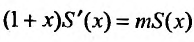
Пусть x = 0, тогда S(0) = С. Из (29.5.2) следует, что S(0) = 1, тогда С = 1.
Следовательно,
Итак, разложение
имеет место при всех х, удовлетворяющих условию 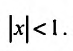
Применение рядов в приближенных вычислениях
Разложения функций в ряд Маклорена позволяют во многих случаях вычислить с большой степенью точности значения этих функций, заменяя ее конечным числом членов разложения. Чем меньше х, тем меньше членов можно брать в этом разложении для вычисления f(х) с желаемой точностью. Если х весьма мало, то достаточно ограничится первыми двумя членами, отбросив все остальные. Например, при х близких к нулю можно пользоваться следующими приближенными формулами:
Например, вычислим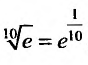
Имеем, 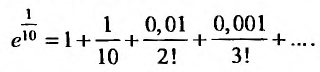
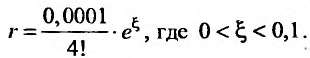
Иногда при вычислении значений функций удобно пользоваться почленным дифференцированием или интегрированием рядов.
Например, известно, что
С другой стороны,
Следовательно,
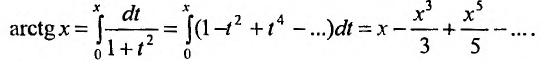
Этот ряд знакочередующийся. Поэтому, его остаток не превосходит первого «отброшенного» члена. Удерживая в разложении первых два слагаемых, получим значение arctg 0,1 = 0,09967 с пятью верными знаками.
При помощи биномиальною ряда можно быстро и довольно точно вычислять значение корней из чисел.
Пример №6
Вычислить 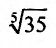
Решение:
Представим, этот корень в виде
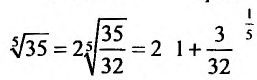
следующим член 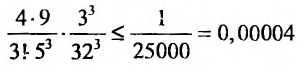
В общем случае можно записать:
где 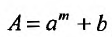
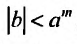
Кроме того, биномиальный ряд является основой многих дальнейших разложений функций в ряды. Например, можно найти разложение в ряд Маклорена функции:
При помощи рядов можно вычислять определенные интегралы.
Например, вычислим интегральный синус:
Имеем
тогда
Подставляя вместо x, те или иные конкретные значения переменной, мы можем вычислять интересующие нас значения интегрального синуса.
При помощи разложении в степенные ряды можно приближенно интегрировать разнообразные дифференциальные уравнения.
Например, найдем решение уравнения 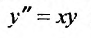
Будем искать решение этого уравнения в виде степенного ряда: 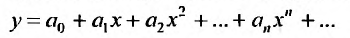
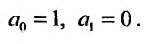
Вычислим первую и вторую производные от этого ряда:
и подставив у, 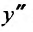
приравняем коэффициенты при равных степенях .г, предварительно умножив правую часть на х:
Получаем систему уравнений, из которой находим:
Замечаем, что отличными от нуля будут лишь те коэффициенты, у которых индекс и степень делятся на 3. Получим решение заданного дифференциального уравнения в виде:
- Заказать решение задач по высшей математике
Ряд Маклорена
Предположим, что функция 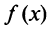
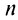
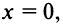
Выразим коэффициенты ряда через 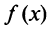
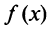
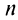
Полагая в полученных равенствах 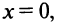
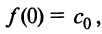
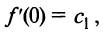
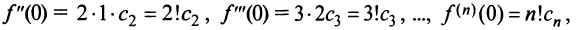
Подставляя значения коэффициентов 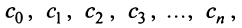
называемый рядом Маклорена.
Следует отметить, что не все функции могут быть разложены в ряд Маклорена. Может оказаться, что ряд Маклорена, составленный формально для функции 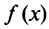
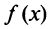
Так же как и для числовых рядов, сумму 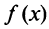
где 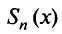
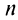
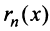
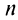
Тогда на основании свойства 4 сходящихся рядов (см. §13.1) можно сформулировать теорему.
Теорема. Для того чтобы ряд Маклорена сходился к функции 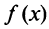
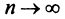
для всех значений 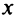
Можно доказать, что если функция 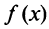
Замечание. Ряд Маклорена является частным случаем ряда Тейлора:
при
Ряд Тейлора тесно связан с формулой Тейлора.
где 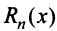
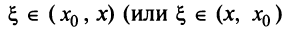
Очевидно, что при выполнении условия (14.7) остаток 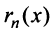
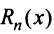
Разложение в ряд Маклорена некоторых функций
По формуле (13.6)
Область сходимости ряда 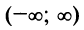
Очевидно, что производные четного порядка 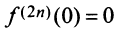
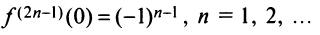
Область сходимости ряда
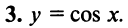
Область сходимости ряда
Интервал сходимости ряда 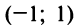
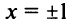
Ряд (14.11) называется биномиальным. Если 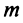
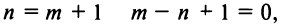
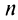
Получить разложение для этой функции можно проще, не вычисляя непосредственно коэффициенты ряда (14.6) с помощью производных.
Рассмотрим геометрический ряд
со знаменателем 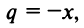
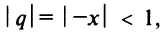
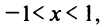
Интегрируя почленно равенство (14.12) в интервале 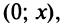
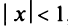
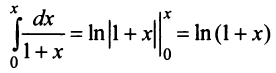
Область сходимости ряда (после выяснения сходимости на концах интервала сходимости) есть
Можно доказать, что ряды, приведенные в формулах (14.8) — (14.13), сходятся к функциям, для которых они составлены.
При разложении более сложных функций используют непосредственно формулу (14.6) либо таблицу простейших разложений (14.8) — (14.13).
Пример №7
Разложить в ряд функции:
Решение:
а) Так как по (14.8)
то, заменяя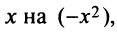
и, наконец,
Область сходимости ряда
б) В разложении 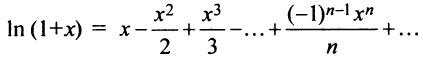
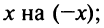
Теперь
Область сходимости ряда
Применение рядов в приближенных вычислениях
Степенные ряды имеют самые разнообразные приложения. С их помощью вычисляют с заданной степенью точности значения функций, определенных интегралов, которые являются «неберущимися» или слишком сложными для вычислений, интегрируются дифференциальные уравнения.
Пример №8
Вычислить приближенно с точностью до
Решение:
а) Для вычисления 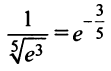
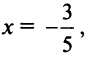
Взяв первые шесть членов разложения, на основании следствия из теоремы Лейбница (см. § 13.4) для сходящегося знакочередующегося ряда мы допустим погрешность 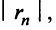
б) Для вычисления 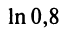
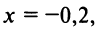
Если в качестве 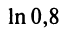
(Мы учли, что сумма сходящегося геометрического ряда в
скобках равна 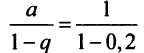
Следует отметить, что для вычисления логарифмов более удобным является ряд (14.14), который сходится быстрее ряда (14.13). Действительно, пусть 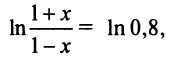
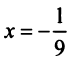
т.е. для вычисления 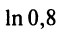
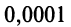
в) Представим 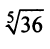
Так как 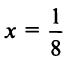
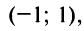
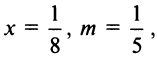
(Для обеспечения данной точности расчета необходимо взять 4 члена, так как по следствию из признака Лейбница для сходящегося знакочередующегося ряда погрешность 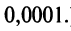
г) Для вычисления 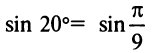
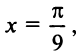
(Необходимо взять два члена, так как при этом погрешность
д)«Точное» интегрирование здесь невозможно, так как интеграл «неберущийся». Заменив 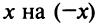
Умножая полученный ряд на
и почленно интегрируя в интервале 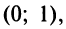
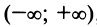
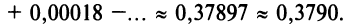
Пример №9
Исследовать сходимость ряда
Решение:
Радиус сходимости ряда (14.15), заданного по степеням 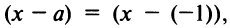
т.е. 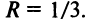
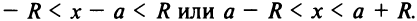
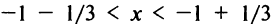
Исследуем сходимость ряда (14.15) на концах этого интервала. При 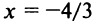
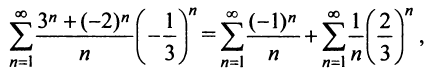
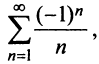
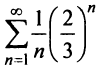
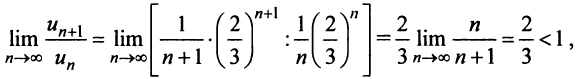
При 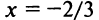
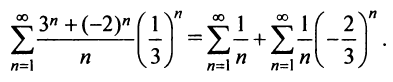
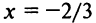
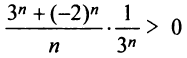
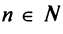
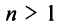
Итак, область сходимости степенного ряда (14.15)
Пример №10
Разложить в ряд Маклорена функцию
Решение:
Первый способ. Применим метод непосредственного разложения по формуле (14.6).
Вначале найдем производные до «-го порядка и вычислим их значения при
При 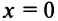
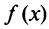
и т.д. Теперь по формуле (14.6) запишем ряд
или
Второй способ. Учитывая, что 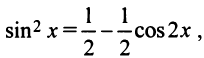
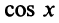
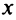

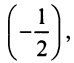
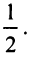
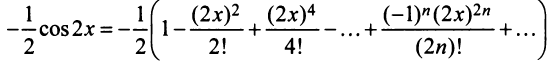
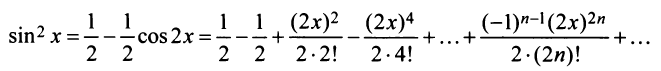
т.е. то же разложение (14.16).
Третий способ. Разложение функции 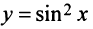
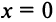
то произведение функций разлагается в той же окрестности в степенной ряд
В частности, при 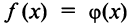
Для функции 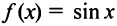
находим по формуле (14.17)
т.е. получили то же разложение (14.16).
Область сходимости ряда, как нетрудно убедиться, есть 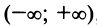
Пример №11
Вычислить с точностью до
Решение:
Выражение данного интеграла в виде числового ряда находится
Вычисление интеграла свелось не к нахождению суммы сходящегося знакочередующегося ряда, при вычислении которой погрешность оценивается с помощью следствия из теоремы Лейбница, а к определению суммы ряда с положительными членами с неизвестной оценкой погрешности.
Поступим следующим образом. Предположим, что для оценки суммы ряда мы взяли 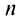
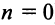
ибо выражение в круглых скобках представляет сумму сходящегося геометрического ряда (13.5) при
При
(Легко вычислить, что при любых 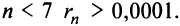
- Элементы матричного анализа
- Уравнение линии
- Функции нескольких переменных
- Комплексные числ
- Линейные дифференциальные уравнения второго порядка
- Системы дифференциальных уравнений
- Числовые ряды
- Знакопеременные ряды





![{displaystyle C=limsup _{nto infty }{sqrt[{n}]{|c_{n}(z-a)^{n}|}}=limsup _{nto infty }left({sqrt[{n}]{|c_{n}|}}right)|z-a|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c67486298c59df5fc7583a5cc253024ebc9045ea)
![{displaystyle r={frac {1}{limsup _{nto infty }{sqrt[{n}]{|c_{n}|}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb0428211dc308307cbbd69ed6151785382c549b)