Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?
Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.
Задача.
Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).
Решение:
Подставив координаты вершин треугольника в уравнение окружности
получим систему уравнений
Вычтем из первого уравнения системы второе:
Теперь из второго уравнения системы вычтем третье:
Приравняем правые части равенств b=-2a+10 и b=3a-20:
Подставим в первое уравнение системы a=6 и b=-2:
a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности
Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин.
Уравнение описанной окружности
Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?
Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.
Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).
Подставив координаты вершин треугольника в уравнение окружности
получим систему уравнений
Вычтем из первого уравнения системы второе:
Теперь из второго уравнения системы вычтем третье:
Приравняем правые части равенств b=-2a+10 и b=3a-20:
Подставим в первое уравнение системы a=6 и b=-2:
a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности
Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин.
Нахождение радиуса описанной вокруг треугольника окружности
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около произвольного (любого), прямоугольного или равностороннего треугольника. Также разберем примеры решения задач для закрепления представленного теоретического материала.
Формулы вычисления радиуса описанной окружности
Произвольный треугольник
Радиус окружности, описанной вокруг любого треугольника, рассчитывается по формуле:
где a, b, c – стороны треугольника, S – его площадь.
Прямоугольный треугольник
Радиус окружности, описанной около прямоугольного треугольника, равен половине его гипотенузы или высоте, проведенной к гипотенузе.
Равносторонний треугольник
Радиус описанной около правильного треугольника окружности вычисляется по формуле:
где a – сторона треугольника.
Примеры задач
Задание 1
Дан треугольник со сторонами 4, 6 и 9 см. Найдите радиус описанной около него окружности.
Решение
Для начала нам необходимо найти площадь треугольника. Т.к. нам известны длины всех его сторон, можно применить формулу Герона:
Теперь мы можем воспользоваться первой формулой из перечисленных выше для расчета радиуса круга:
Задание 2
Дан треугольник, у которого известны две стороны из трех: 6 и 8 см. Найдите радиус описанной вокруг него окружности.
Решение
Треугольник со сторонами 6 и 8 см может быть только прямоугольным, причем известные по условиям задачи стороны являются его катетами. Таким образом, мы можем найти гипотенузу фигуры, воспользовавшись теоремой Пифагора:
Как мы знаем, радиус круга, описанного вокруг прямоугольного треугольника, равняется половине его гипотенузы, следовательно: R = 10 : 2 = 5.
Окружность, описанная около треугольника.
Треугольник, вписанный в окружность. Теорема синусов
Серединный перпендикуляр к отрезку
Определение 1 . Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).
Теорема 1 . Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.
Доказательство . Рассмотрим произвольную точку D , лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.
Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB . Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1) . Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.
Доказательство . Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D .
Докажем, что отрезок AE длиннее отрезка EB . Действительно,
Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.
Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE . Действительно,
Полученное противоречие и завершает доказательство теоремы 2
Окружность, описанная около треугольника
Определение 2 . Окружностью, описанной около треугольника , называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником .
Свойства описанной около треугольника окружности. Теорема синусов
Для любого треугольника справедливы равенства (теорема синусов):

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.
Для любого треугольника справедливо равенство:
где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.
Для любого треугольника справедливо равенство:
где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.
| Фигура | Рисунок | Свойство |
| Серединные перпендикуляры к сторонам треугольника |
 |
Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство |
| Окружность, описанная около треугольника |  |
Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство |
| Центр описанной около остроугольного треугольника окружности | Центр описанной около остроугольного треугольника окружности лежит внутри треугольника. | |
| Центр описанной около прямоугольного треугольника окружности |  |
Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство |
| Центр описанной около тупоугольного треугольника окружности |  |
Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. |
| Теорема синусов |  |
|
| Площадь треугольника |  |
|
| Радиус описанной окружности |  |
| Серединные перпендикуляры к сторонам треугольника |
 |
Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.
Окружность, описанная около треугольника
Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Центр описанной около остроугольного треугольника окружности
Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.
Центр описанной около прямоугольного треугольника окружности
Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.
Центр описанной около тупоугольного треугольника окружности
Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Теорема синусов
Для любого треугольника справедливы равенства (теорема синусов):

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.
Площадь треугольника
Для любого треугольника справедливо равенство:
где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.
Радиус описанной окружности
Для любого треугольника справедливо равенство:
где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.
Доказательства теорем о свойствах описанной около треугольника окружности
Теорема 3 . Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.
Доказательство . Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC , и обозначим точку их пересечения буквой O (рис. 6).
Поскольку точка O лежит на серединном перпендикуляре к отрезку AC , то в силу теоремы 1 справедливо равенство:
Поскольку точка O лежит на серединном перпендикуляре к отрезку AB , то в силу теоремы 1 справедливо равенство:
Следовательно, справедливо равенство:
откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.
Следствие . Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Доказательство . Рассмотрим точку O , в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).
При доказательстве теоремы 3 было получено равенство:
из которого вытекает, что окружность с центром в точке O и радиусами OA , OB , OC проходит через все три вершины треугольника ABC , что и требовалось доказать.
Теорема 4 (теорема синусов) . Для любого треугольника (рис. 7)

Доказательство . Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R , на которую опирается вписанный угол величины φ , вычисляется по формуле:
Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).
Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.
Формула (1) доказана.
Из формулы (1) для вписанного треугольника ABC получаем (рис.7):
http://www.resolventa.ru/spr/planimetry/otcircle.htm
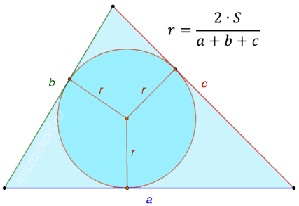
Центр вписанной в треугольник окружности является точкой пересечения биссектрис этого треугольника. Радиус окружности, вписанной в любой треугольник, равняется удвоенной площади треугольника, деленной на его периметр.
.
Центр и радиус вписанной окружности в треугольник через координаты его вершин
Центр и радиус вписанной окружности в треугольник
Известны координаты вершин треугольника и известный координаты точки. Нужно установить принадлежность точки треугольнику.
Существует несколько способов определения. лежит-ли точка внутри треугольника или снаружи:
1. Метод сравнения площадей — по формуле Герона находятся площади 3-х треугольников которые образует точка с каждой стороной треугольника, далее находится площадь самого треугольника и сравнивается с суммой трех предыдущих треугольников, если суммы равны то значит точка принадлежит треугольнику.
2. Метод относительности — выбирается ориентация движения по вершинам треугольника, например по часовой стрелке. По данной ориентации проходим все стороны треугольника, рассматривая их как прямые, и рассчитываем по какую сторону от текущей прямой лежит наша точка. Если точка для всех прямых, лежит с правой стороны, то значит точка принадлежит треугольнику, если хоть для какой-то прямой она лежит с левой стороны, то значит условие принадлежности не выполняется.
3. Метод геометрического луча — из точки пускается луч по какой-либо оси в каком-либо направлении. Вычисляется количество пересечений со сторонами, если кол-во нечётное, то значит точка лежит внутри многоугольника.
Примечание: дробные числа записывайте
через точку, а не запятую.
Округлять до -го знака после запятой.
Как найти координаты центра окружности, описанной около треугольника, знаякоординаты его вершин. Построение этой окружности
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
ТЕМА: КАК НАЙТИ КООРДИНАТЫ ЦЕНТРА ОКРУЖНОСТИ, ОПИСАННОЙ ОКОЛО ТРЕУГОЛЬНИКА, ЗНАЯКООРДИНАТЫ ЕГО ВЕРШИН. ПОСТРОЕНИЕ ЭТОЙ ОКРУЖНОСТИ.
Работу выполнила ученица 9 класса
МОУ «Лицей №1 пос. Львовский»
математики Габова Ю.В.
История появления координатной плоскости.
Координаты середины отрезка.
Расстояние между точками.
Окружность, описанная около треугольника.
Окружность вписанная в треугольник.
Доказательство тождества tg (90 0 + a )=- ctga .
Как найти координаты центра окружности, описанной около треугольника, зная координаты его вершин. Построение этой окружности.
Список используемой литературы.
Данная работа носит исследовательский характер.
Выведенные формулы с доказательством позволяют решать новые, еще не встречавшиеся задачи. Школьная программа не включает в себя решение наиболее сложных задач, связанных с координатной плоскостью, и мы предлагаем расширить круг знаний в этой области. Задачи, связанные с этими формулами, можно использовать как олимпиадные задачи, а также они будут интересны учащимся, изучающим курс математики, выходящий за рамки школьного курса.
Здесь предложена одна из задач на выбранную нами тему. Она связана с описанной окружностью, но можно составить задачи и на вписанную окружность, и на нахождение точки пересечения медиан, высот, биссектрис на координатной плоскости.
Данная работа направлена на расширение круга знаний ученика.
История появления координатной плоскости.
Более чем 100 лет до н.э. греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести хорошо теперь известные географические координаты: широту и долготу – и обозначить их числами.
В 14 веке французский математик Н. Оресм ввел, по аналогии с географическими, координаты на плоскости. Он предложил покрыть плоскость прямоугольной сеткой и назвать широтой и долготой то, что мы теперь называем абсциссой и ординатой.
Это нововведение оказалось чрезвычайно продуктивным. На его основе возник метод координат, связавший геометрию с алгеброй. Основная заслуга в создании метода координат принадлежит французскому математику Р. Декарту. Такую систему координат стали называть декартовой. Точку О пересечения прямых называют началом координат, а сами направленные прямые – осями, ось Ох – осью абсцисс, а ось Оу – осью ординат. Числа х, у называют декартовыми координатами точки (х; у). точка плоскости – геометрический объект – заменяется парой чисел (х;у), т.е. алгебраическим объектом. Принадлежность точки заданной кривой теперь соответствует тому, что числа х и у удовлетворяют некоторому уравнению. Так, координаты точки окружности с центром в заданной точке (а;в) удовлетворяют уравнению (х-а) 2 +(у-в) 2 =R 2 .
Координатная плоскость состоит из двух перпендикулярных прямых X и Y , которые пересекаются в начале отсчета – точке О и на них обозначен единичный отрезок (смотри рис.). эти прямые называют системой координат на плоскости, а точку О – началом координат. Плоскость, на которой выбрана система координат, называют координатной плоскостью.
Пусть А – некоторая точка плоскости. Проведем через нее прямую M А , перпендикулярно координатной прямой Х , и прямую LA , перпендикулярную координатной прямой Y . Т.к. точка М имеет координату 5, а точка L координату 4, то положение точки А определяется парой чисел (5;4). Эту пару чисел называют координатами точки А. Число 5 называют абсциссой точки А, а число 4 называют ординатой точки А. К оординатную прямую Х называют осью абсцисс, а координатную прямую Y — осью ординат. Точку А с абсциссой 5 и ординатой 4 обозначают так: А (5;4 ). При этом всегда на первом месте пишут абсциссу точки, а на втором месте её ординату. Если переставить местами координаты, то получится другая точка N (4;5), которая показана на рисунке.
Каждой точке А на координатной плоскости соответствует пара чисел: ее абсцисса и ордината. Наоборот, каждой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.
КООРДИНАТЫ СЕРЕДИНЫ ОТРЕЗКА.
где А (х 1 ;у 1 ) и В(х 2 ;у 2 ) – концы отрезка.
А (х 1 ;у 1 ) и В(х 2 ;у 2 ) – произвольные точки плоскости Оху.







О А х С х В х х
Пусть АВ не параллелен оси Оу, т.е. х 1 ≠х 2. проведем через точки А,В,С прямые, параллельные оси Оу. Они пересекут ось Ох в точках А(х 1 ;0), В(х 2 ;0), С(х;0). По теореме Фалеса точка С х – середина отрезка [А х В х ], то есть А х С х = С х В х или отсюда либо х-х 1 =х-х 2 , либо х-х 1 =-(х-х 2 ). Первое равенство невозможно, т.к. х 1 ≠х 2, а второе дает . Если х 1 =х 2, то х=х 1 =х 2 и равенство остается верным. Ордината точки С находится аналогичными построениями и рассуждениями.
Следовательно, теорема доказана.
РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ.
Если А 1 (х 1 ;у 1 ) и А 2 (х 2 ;у 2 ) две произвольные точки плоскости Оху, а d –расстояние между ними, то d вычисляется из соотношения .
Утверждение теоремы следует из определения проекции отрезка и теоремы Пифагора.
Уравнение вида называется общим уравнением прямой.
Угол α, определяемый, как показано на рисунке, называется углом наклона прямой к оси Ох. Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой; его обычно обозначают буквой k: k=tgα




Уравнение y=kx+b называется уравнением прямой с угловым коэффициентом; k – угловой коэффициент, b – величина отрезка, который отсекает прямая на оси Оу, считая от начала координат.
Уравнение вида ax+by+c=0 при условии, что a и b одновременно не равны нулю, задает прямую в плоскости Оху, и наоборот, уравнение произвольной прямой может быть записано в указанном виде.
Пусть b≠0. Тогда уравнение прямой можно переписать в виде y=kx+b.
Число k называется угловым коэффициентом прямой и равно тангенсу угла между положительной полуосью абсцисс и лучом прямой, лежащей в одной с положительной полуосью ординат полуплоскости относительно оси абсцисс.
Уравнение окружности ω(А;R) имеет вид
, где а и b- координаты центра А окружности ω(А;R).
Пусть дана окружность ω(А;R) на плоскости Оху, где А, центр окружности – имеет координаты а и b, по определению окружности для любой точки В(х;у), лежащей на окружности ω(А;R), верно АВ=R. Но в соответствии с теоремой: Если А 1 (х 1 ;у 1 ) и А 2 (х 2 ;у 2 ) две произвольные точки плоскости Оху, а d –расстояние между ними, то d вычисляется из соотношения .
АВ 2 . Таким образом, координаты х и у любой точки окружности ω(А;R) удовлетворяет уравнению
Обратно: любая точка В(х;у), координаты которой удовлетворяют уравнению, принадлежит окружности, т.к. расстояние от нее до точки А(a;b) равно R. Отсюда по определению данное уравнение – уравнение окружности ω(А;R).
ОКРУЖНОСТЬ, ОПИСАННАЯ ОКОЛО ТРЕУГОЛЬНИКА.
Окружность называется описанной около треугольника, если она проходит через все его вершины.
Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к сторонам треугольника, проведенных через середины этих сторон.
Пусть АВС – данный треугольник и О – центр окружности описанной около данного треугольника. ΔАОВ – равнобедренный (АО=ОВ как радиусы). Медиана ОD – этого треугольника одновременно является его высотой. Поэтому центр окружности лежит на прямой, перпендикулярной стороне АС и проходящей через ее середину. Так же доказывается, что цент окружности лежит на перпендикулярах к другим сторонам треугольника. Теорема доказана.
ОКРУЖНОСТЬ, ВПИСАННАЯ В ТРЕУГОЛЬНИК.
Окружность называется вписанной в треугольник, если она касается всех его сторон.
Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.
Пусть АВС — данный треугольник, О – центр вписанной в него окружности, D, E, F – точки касания окружности со сторонами. ΔAEO=ΔAOD по гипотенузе и катету (EO=OD – как радиус, АО – общая). Из равенства треугольников следует, что
КАК НАЙТИ КООРДИНАТЫ ЦЕНТРА ОКРУЖНОСТИ, ОПИСАННОЙ ОКОЛО ТРЕУГОЛЬНИКА, ЗНАЯ КООРДИНАТЫ ЕГО ВЕРШИН. ПОСТРОЕНИЕ ЭТОЙ ОКРУЖНОСТИ.
Теперь выясним, как найти координаты центра окружности, описанной около треугольника, зная координаты его вершин. Чтобы найти центр этой окружности, нужно найти точку пересечения серединных перпендикуляров, проведенных к сторонам этого треугольника.
Для начала найдем середину каждой стороны треугольника.








Выражая k из первого уравнения и подставляя во второе, найдем значение L 1 . Подставляя значение L 1 в одно из уравнений, найдем значение k 1 . Зная k 1 и L 1 , получим уравнение прямой АВ: у=k 1 x+L 1.
Рассмотрим отдельно прямую АВ. Серединный перпендикуляр включает в себя сразу два понятия: медиану и высоту. Точки на сторонах треугольника для прохождения медиан найдены. Теперь через одну из этих точек проведем высоту.
Угол пересечения прямой АВ с осью Ох обозначим α (альфа). Тогда острый угол, образованный прямой DY и осью Ох будет равен: 180 0 -(90 0 +α)=90 0 -α. А угол, смежный с ним: 180 0 -(90 0 -α)=90 0 +α.
В уравнении прямой АВ у=k 1 x+L 1 k 1 — угловой коэффициент, он равен tgα.
Если k 1 =tgα, то k 2 в уравнении у=k 2 x+L 2 для прямой DY равно tg(90 0 +α)=-сtgα.









Мы знаем уравнение прямой АВ: у=k 1 x+L 1 и знаем, как k 1 связан с k 2 . Тогда уравнение прямой DY примет вид : у=-1:k 1* x+L 2 ; зная координаты точки D, принадлежащей этой прямой, и подставляя их в это уравнение, найдем L 2.
Аналогично пишем уравнения другим серединным перпендикулярам треугольника и ( с помощью систем уравнений) находим точку их пересечения – это и есть центр описанной окружности.
Чтобы найти радиус, надо соединить центр окружности с одной из вершин треугольника и найти длину этого отрезка.
Теперь, зная центр и радиус описанной около треугольника окружности, можно ее построить.
Доказательство тождества tg(90 0 +α)=-сtgα.
Возьмем окружность радиусом 1 и центром в точке начала координат. Из начала координат проведем вектор Р, образующий с осью Ох угол α, а затем повернем этот вектор на 90 0 и проведем прямые, параллельные оси Оу и проходящие через точки А и В.
Пусть точка А(х а ;у а ), а точка В(х 90+α ; у 90+α ).
Рассмотрим ΔОАД. Он прямоугольный и следует, sinα=AD:OA=y a :1=y a . A cosα=OD:OA=x 1 :1=x 1 . Значит координаты точки А можно записать так A (cosα; sinα).
Аналогично точке А, координаты точки В можно записать: В(cos(90 0 +α); sin(90 0 +α)).
Треугольники ОВЕ и АОД равны по одной стороне и двум , прилежащим к ней углам. Из этого следует равенство:
ВЕ=ОД, sin(90 0 +α)=cosα и ОЕ=АД, cos (90 0 +α)=-sinα (т.к. ОЕ принимает отрицательное значение)
Из нашей исследовательской работы следует, что произведение коэффициентов перпендикулярных прямых равно -1. Этот результат работы можно использовать при решении других задач на координатной плоскости. Например, при нахождении точки пересечения высот треугольника. Попутно мы пришли к выводу, что tg(90+α)=-ctgα. Это тождество поможет успешно изучать тригонометрию. Мы предлагаем расширить круг задач в школьном курсе геометрии по теме «Координатная плоскость»
Список использованной литературы.
Энциклопедический словарь юного математика. Савин А.П. Москва. «Педагогика», 1989г.
Большой справочник математика для школьников и поступающих в вузы. Д.И. Аверьянов. «Дрофа», 1998г.
Энциклопедический словарь юного математика. Савин А.П. Москва. «Педагогика», 1985г.
источники:
http://mathhelpplanet.com/static.php?p=onlain-reshit-treugolnik
http://gigabaza.ru/doc/61563.html
Решить треугольник Онлайн по координатам
Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

![Rendered by QuickLaTeX.com [ left{ begin{array}{l} (2 - a)^2 + (1 - b)^2 = R^2 , \ (6 - a)^2 + (3 - b)^2 = R^2 , \ (9 - a)^2 + (2 - b)^2 = R^2 . \ end{array} right. ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-82dd95fa041ab9c8ca35f00eaea5d2ba_l3.png)