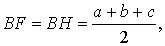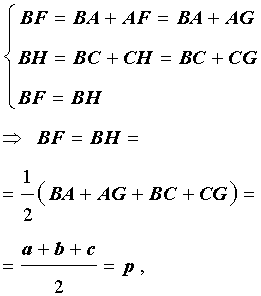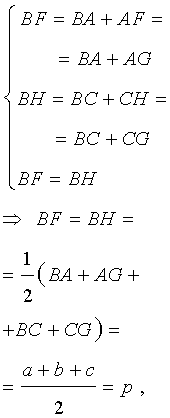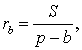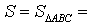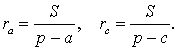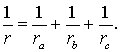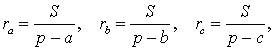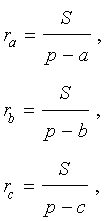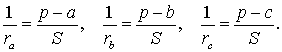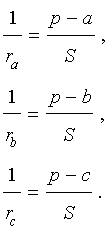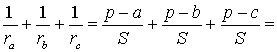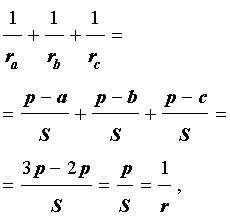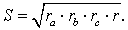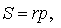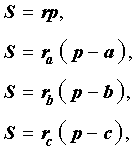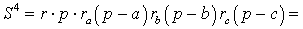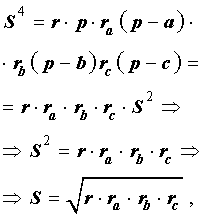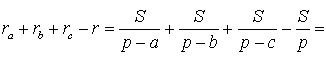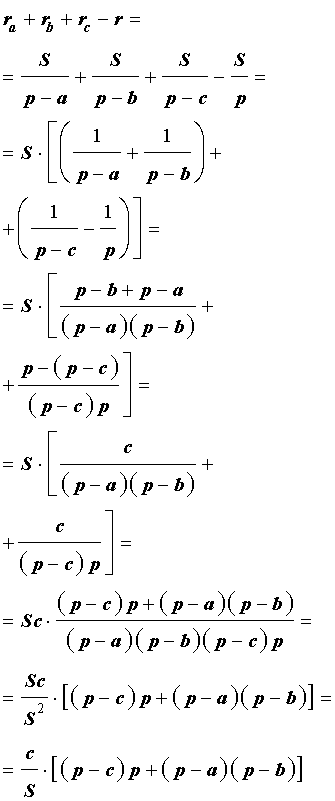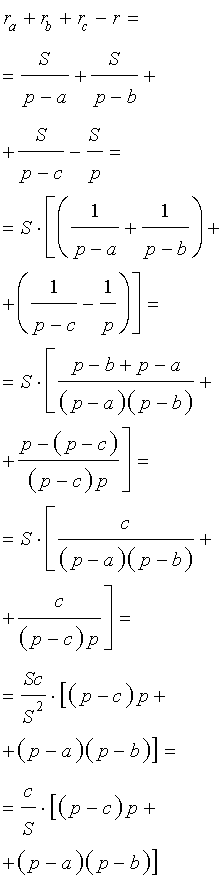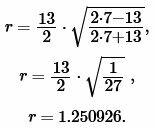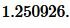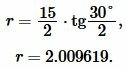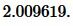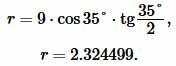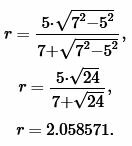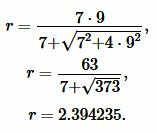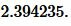Как найти радиус вневписанной окружности равнобедренного треугольника

Вневписанные окружности

Теорема 1 . В любом треугольнике биссектрисы двух внешних углов и биссектриса внутреннего угла, не смежного с ними, пересекаются в одной точке.

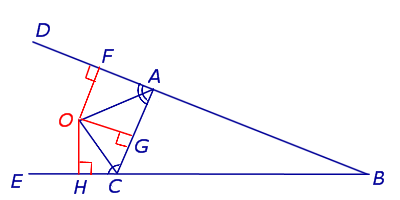
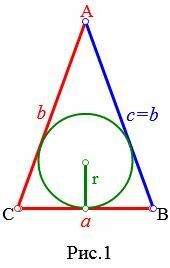
Доказательство . Рассмотрим произвольный треугольник ABC и продолжим, например, стороны BA и BC за точки A и C соответственно (рис.1).

Проведём биссектрисы углов DAC и ECA , которые являются внешними углами треугольника ABC . Обозначим точку пересечения этих биссектрис буквой O . Докажем, что точка O лежит на биссектрисе угла ABC , который является внутренним углом треугольника ABC , не смежным с внешними углами DAC и ECA . С этой целью опустим из точки O перпендикуляры OF , OG и OH на прямые AB , AC и BC соответственно. Поскольку AO – биссектриса угла DAC , то справедливо равенство:

Следовательно, справедливо равенство

Замечание 1 . В ходе доказательства теоремы 1 мы установили, что справедливы равенства

откуда вытекает, что точки F , G и H лежат на одной окружности с центром в точке O .

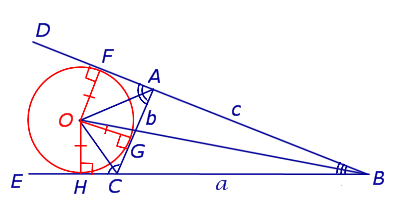
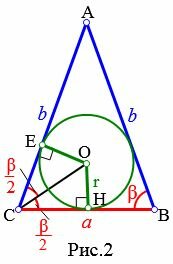
Определение . Окружность называют окружностью, вневписанной в треугольник , или вневписанной окружностью, если она касается касается одной стороны треугольника и продолжений двух других сторон (рис.2).

Замечание 2 . У каждого треугольника существуют три вневписанных окружности. На рисунке 2 изображена одна из них.

Замечание 3 . Центр вневписанной окружности, изображенной на рисунке 2, лежит на биссектрисе угла B , а окружность касается стороны b . Для удобства обозначений и терминологии будем называть эту окружность вневписанной окружностью, касающейся стороны b , и обозначать её радиус символом rb .

Теорема 2 . Пусть вневписанная окружность касается стороны AC треугольника ABC . Тогда отрезки касательных касательных от вершины B до точек касания с вневписанной окружностью равны полупериметру треугольника.

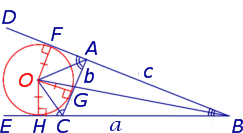
Доказательство . Снова рассмотрим рисунок 2 и докажем, что выполнено равенство

где a, b, c – стороны треугольника ABC . Действительно, отрезки AG и AF равны, как отрезки касательных к окружности, выходящих из точки A . Отрезки CG и CH равны, как отрезки касательных к окружности, выходящих из точки C . Отрезки BF и BH равны, как отрезки касательных к окружности, выходящих из точки B . Отсюда получаем:

где буквой p обозначен полупериметр треугольника ABC . Теорема 2 доказана.

Теорема 3 . Радиус вневписанной окружности , касающейся стороны b , вычисляется по формуле

где буквой S обозначена площадь треугольника ABC , а буквой p обозначен полупериметр треугольника ABC .

Доказательство . Снова рассмотрим рисунок 2 и заметим, что выполнены равенства

Следовательно, справедливо равенство

что и требовалось доказать.

Следствие . Радиусы двух других вневписанных в треугольник ABC окружностей вычисляются по формулам:

Теорема 4 . Если обозначить буквой r радиус вписанной в треугольник ABC окружности, то будет справедлива формула:

Складывая эти формулы и воспользовавшись формулой для радиуса вписанной окружности

,

что и требовалось доказать.

Теорема 5 . Площадь треугольника можно вычислить по формуле

Доказательство . Перемножим формулы

что и требовалось доказать.

Теорема 6 . Если обозначить буквой R радиус описанной около треугольника ABC окружности, то будет справедлива формула:

Доказательство . Воспользовавшись формулами для радиусов вписанной и вневписанных окружностей, а также формулой Герона, получим

Преобразуем выражение, стоящее в квадратной скобке:

Радиус вписанной окружности в равнобедренный треугольник онлайн

С помощю этого онлайн калькулятора можно найти радиус вписанной в треугольник окружности, в том числе радиус вписанной в равнобедренный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Открыть онлайн калькулятор

1. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона

Пусть известны известны основание a и боковая сторона b равнобедренного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной окружности через основание и боковую сторону.

Радиус вписанной в треугольник окружности через три стороны a, b, c вычисляется из следующей формулы:

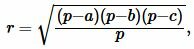(1)

где полупериметр p вычисляется из формулы:

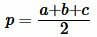. (2)

Учитывая, что у равнобедренного треугольника боковые стороны равны (( small b=c )), имеем:

( small p=frac<large a+b+c> <large 2>) ( small =frac<large 2b+a><large 2>, ) (3)
( small p-a=frac<large 2b+a><large 2>-a ) ( small =frac<large 2b-a><large 2>, ) (4)
( small p-b=p-c=frac<large 2b+a><large 2>-b ) ( small =frac<large a><large 2>. ) (5)

Подставляя (3)-(5) в (1), получим формулу вычисления радиуса вписанной в равнобедренный треугольник окружности:

,

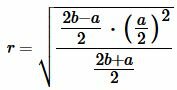
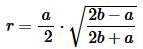. (6)

Пример 1. Известны основание a=13 и боковая сторона b=7 равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.

Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (6). Подставим значения ( small a,; b ) в (6):

Ответ:

2. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и угол при основании

Пусть известны основание a и прилежащий к ней угол β равнобедренного треугольника (Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.

Из центра вписанной окружности проведем перпендикуляры OH и OE к сторонам a=BC и b=AC, соответственно (r=OH=OE). Соединим точки C и O. Полученные прямоугольные треугольники OCE и OCH равны по гипотенузе и катету (см. статью Прямоугольный треугольник. Тогда ( small angle OCE=angle OCH=frac<large beta><large 2>. ) Для прямоугольного треугольника OCH можно записать:

( small frac<large OH><large HC>=frac<large r><large frac<2>>=mathrmfrac<large beta> <large 2>.)

Откуда получим формулу радиуса вписанной в треугольник окружности:

( small r=frac<large a> <large 2>cdot mathrmfrac<large beta> <large 2>.) (8)
( small r=frac<large a> <large 2>cdot frac<large sin beta> <large 1+cos beta>.) (9)

Пример 2. Известны основание ( small a=15 ) и ( small beta=30° ) равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.

Решение. Для нахождения радиуса окружности вписанный в треугольник воспользуемся формулой (8) (или (9)). Подставим значения ( small a=15, ; beta=30° ) в (8):

Ответ:

3. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и угол при основании

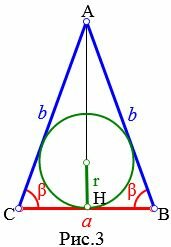
Пусть известны боковая сторона b и угол при основании β равнобедренного треугольника (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.

Высота равнобедренного треугольника AH делит равнобедренный треугольник ABC на две равные части. Тогда для треугольника AHC справедливо равенство:

( small frac<large CH><large AC>=frac<large frac<2>><large b>= cos beta .)

( small a=2b cdot cos beta .) (10)

Подставляя (10) в (8), получим формулу вписанной в равнобедренный треугольник окружности:

( small r=frac<large a> <large 2>cdot mathrmfrac<large beta><large 2>=frac<large 2b cdot cos beta> <large 2>cdot mathrmfrac<large beta> <large 2>) ( small =b cos beta cdot mathrmfrac<large beta> <large 2>)
( small r=b cdot cos beta cdot mathrmfrac<large beta> <large 2>) (11)

Учитывая формулы половинного угла тригонометрических функций, формулу (11) можно записать и так:

( small r=b cdot frac<large sin beta cdot cos beta> <large 1+ cos beta>) (12)

Пример 3. Известны боковая сторона равнобедренного треугольника: ( small b=9 ) и угол при основании β=35°. Найти радиус окружности вписанной в треугольник.

Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11) (или (12)).

Подставим значения ( small b=9 ,; beta=35° ) в (11):

Ответ:

4. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и высота

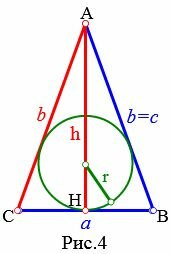
Пусть известны боковая сторона b и высота h равнобедренного треугольника (Рис.4). Найдем формулу радиуса вписанной в треугольник окружности.

Формула радиуса вписанной окружности через площадь и полупериметр имеет следующий вид (см. статью на странице Радиус вписанной в треугольник окружности онлайн) :

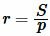, (13)
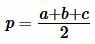(14)

Так как треугольник AHC прямоугольный, то из Теоремы Пифагора имеем:

( small left( frac<large a><large 2>right)^2=b^2-h^2 )

( small a=2 cdot sqrt ) (15)

Площадь равнобедренного треугольника по основанию и высоте вычисляется из формулы:

( small S=frac<large 1> <large 2>cdot a cdot h. ) (16)

Подставим (15) в (16):

( small S=h cdot sqrt ) (17)

Учитывая, что для равнобедренного треугольника b=c, а также равенство (15), получим:

( small p=frac<large a+b+c> <large 2>) ( small =frac<large a+2b> <large 2>) ( small =frac<large a><large 2>+b )( small =b+ sqrt ) (18)

Подставляя, наконец, (17) и (18) в (13), получим формулу радиуса вписанной в равнобедренный треугольник окружности:

( small r=frac<large S> <large p>) ( small =frac<large h cdot sqrt><large b+ sqrt> ) (19)

Пример 4. Боковая сторона и высота равнобедренного треугольника равны ( small b=7 ,) ( small h=5, ) соответственно. Найти радиус окружности вписанной в треугольник.

Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (19). Подставим значения ( small b=7 ,) ( small h=5 ) в (19):

Ответ:

5. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и высота

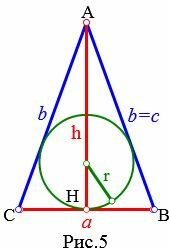
Пусть известны основание a и высота h равнобедренного треугольника (Рис.5). Найдем формулу радиуса вписанной в равнобедренный треугольник окружности.

Из формулы (15) найдем b:

( small b^2-h^2=left( frac<large a> <large 2>right)^2 )

( small b^2= frac<large a^2> <large 4>+h^2 )

( small b= frac<large 1> <large 2>cdot sqrt< a^2+ 4h^2 >) (20)

Подставляя (20) в (19), получим формулу радиуса вписанной окружности в равнобедренный треугольник:

( small r=frac<large h cdot sqrt><large b+ sqrt>) ( small =frac<large h cdot sqrt<frac<large a^2><large 4>+h^2-h^2>><large frac<large 1> <large 2>cdot sqrt< a^2+ 4h^2 >+ sqrt<frac<large a^2><large 4>+h^2-h^2>>) ( small = large frac< h cdot frac< a>< 2>>< frac< 1> < 2>cdot sqrt< a^2+ 4h^2 >+frac< a> < 2>>)
( small r=large frac< a cdot h >>) (21)

Пример 5. Основание и высота равнобедренного треугольника равны ( small a=7 ,) ( small h=9, ) соответственно. Найти радиус окружности вписанной в треугольник.

Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (21). Подставим значения ( small a=7 ,) ( small h=9 ) в (21):

Ответ:

Все формулы для радиуса вписанной окружности

Радиус вписанной окружности в треугольник

a , b , c — стороны треугольника

p — полупериметр, p=( a + b + c )/2

Формула радиуса вписанной окружности в треугольник ( r ):

Радиус вписанной окружности в равносторонний треугольник

a — сторона треугольника

r — радиус вписанной окружности

Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):

Радиус вписанной окружности равнобедренный треугольник

1. Формулы радиуса вписанной окружности если известны: стороны и угол

a — равные стороны равнобедренного треугольника

b — сторона ( основание)

α — угол при основании

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :

2. Формулы радиуса вписанной окружности если известны: сторона и высота

a — равные стороны равнобедренного треугольника

b — сторона ( основание)

h — высота

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :

источники:

http://matworld.ru/geometry/radius-vpisannoj-okruzhnosti-v-ravnobedrennyj-treugolnik.php

http://www-formula.ru/2011-09-24-00-40-48

Источник

Слайд 1ВНЕВПИСАННАЯ ОКРУЖНОСТЬ ТРЕУГОЛЬНИКА

ВНЕВПИСАННАЯ ОКРУЖНОСТЬ ТРЕУГОЛЬНИКА

Слайд 2Вневписанной окружностью треугольника называется окружность, к которой являются касательными одна из

сторон треугольника и продолжения двух других сторон.

Вневписанной окружностью треугольника называется окружность, к которой являются касательными одна из сторон треугольника и продолжения двух других

Слайд 3Соотношение между длинами отрезков касательных
Теорема 1: Расстояние от вершины треугольника до

точки касания вневписанной окружности с продолжением стороны, содержащей ее, за вершину противолежащей стороны равно полупериметру треугольника.

Доказательство. Обозначим через В₁, С₁, и Та – точки касания вневписанной окружности с прямыми АС, АВ и ВС соответственно. Тогда СВ₁ = СТа, ВС₁ = ВТа и периметр треугольника АВС: P = AC + СТа + ВТа + АВ = АС + СВ₁ + ВС₁ + АВ = АВ₁ + АС₁. Т.к. АВ₁ = АС₁, то расстояния АВ₁ и АС₁ равны полупериметру треугольника АВС.

Соотношение между длинами отрезков касательныхТеорема 1: Расстояние от вершины треугольника до точки касания вневписанной окружности с продолжением

Слайд 4Следствие 1: Прямая, проведенная через вершину треугольника и точку, в которой

вневписанная окружность касается противоположной стороны, делит периметр треугольника пополам.
Примечание: В треугольнике расстояние от вершины треугольника до точки касания вписанной окружности со стороной треугольника, выходящей из данной вершины, есть разность полупериметра треугольника и стороны, противолежащей данной вершине. То же соблюдается и для вневписанной окружности.
AN = AK = p – a,
BM = BK = p – b,
CN = CM = p – c.

Следствие 1: Прямая, проведенная через вершину треугольника и точку, в которой вневписанная окружность касается противоположной стороны, делит

Слайд 5Следствие 2: Для отрезков касательных, связанных с вневписанными окружностями треугольника, выполняются

равенства:
ВТс = ВА1 = СТb = CA2 = p-a,
ATc = AB2 = CTa = CB1 = p-b,
BTa = BC1 = ATb = AC2 = p-c.
Следствие 3: Верны следующие равенства:
B2Tb = C2Tc = ATc + ATb = a,
C1Tc = A1Ta = BTc + BTa = b,
B1Tb = A2Ta = CTb + CTa = c.
Следствие 4: Расстояния между точками касаний вневписанных окружностей продолжений сторон за вершины треугольника равны:
C1C2 = a +b,
B1B2 = a + c,
A1A2 = b + c.

Из следствия 1

Получаются при попарном сложении равенств из следствия 2

Получаются при попарном сложении равенств из следствия 3

Следствие 2: Для отрезков касательных, связанных с вневписанными окружностями треугольника, выполняются равенства: ВТс = ВА1 =

Слайд 6Формулы для вычисления радиусов вневписанных окружностей
Теорема 2: Радиус вневписанной окружности, касающейся

стороны ВС треугольника АВС, вычисляется по формуле ra =

Доказательство. Выполняются следующие равенства:
SABC = SOCA + SOBA — SOCB = 0,5rab + 0,5rac – 0,5raa = ra(p -a).
Аналогично получаются формулы:
rb = и rc =

Формулы для вычисления радиусов вневписанных окружностейТеорема 2: Радиус вневписанной окружности, касающейся стороны ВС треугольника АВС, вычисляется по

Слайд 7Следствие 1: Большей стороне треугольника соответствует касающаяся её вневписанная окружность большего

радиуса и наоборот.
Следствие 2: Радиус вневписанной окружности треугольника больше радиуса окружности, вписанной в тот же треугольник.
Следствие 3: Площадь треугольника АВС может быть вычислена по формулам:
S = ra(p — a), S = rb(p — b), S = rc(p — c).

Следствие 1: Большей стороне треугольника соответствует касающаяся её вневписанная окружность большего радиуса и наоборот.Следствие 2: Радиус вневписанной

Слайд 8Следствие 4: Для отношения радиусов вписанной и вневписанных окружностей имеют место

равенства:
r/ra = , ra/rb = , ra/rc = .
Следствие 5: Используя формулу Герона, получим формулы для вычисления длин радиусов через стороны треугольника:

ra =

rb =

rc =

Следствие 4: Для отношения радиусов вписанной и вневписанных окружностей имеют место равенства: r/ra =

Слайд 9Теорема 3: Радиус вневписанной окружности, касающейся боковой стороны равнобедренного треугольника, равен

высоте треугольника, опущенной на основание.

Доказательство. Пусть Oa, Ob и Oc – центры вневписанных окружностей треугольника АВС, Ca, Cb и Tc – точки касания этих окружностей с прямой АВ.
Т.к. треугольник АВС – равнобедренный (АС = ВС), то высота, опущенная из вершины С, лежит на биссектрисе СОс угла С, и поэтому СОс ⊥ АВ. С другой стороны радиус ОсТс ⊥ АВ, следовательно, точка Тс лежит на биссектрисе угла С. Отсюда ОТс ⊥ АВ и СТс является высотой треугольника АВС. Заметим, что СОс ⊥ COb как биссектрисы внутреннего и внешнего угла треугольника при вершине С, СОс ⊥ АВ и ObCb ⊥ АВ. Следовательно, четырехугольник TcCObCb – прямоугольник. Значит, rb = ObCb = CTc.

Теорема 3: Радиус вневписанной окружности, касающейся боковой стороны равнобедренного треугольника, равен высоте треугольника, опущенной на основание.Доказательство. Пусть

Слайд 10Следствие: В равнобедренном треугольнике расстояние от вершины, лежащей напротив основания, до

центра вневписанной окружности, касающееся боковой стороны, равно боковой стороне.
Доказательство. Т.к. BCb = p = b + 0,5c, то получаем COb = TcCb = p – 0,5c = b.

Следствие: В равнобедренном треугольнике расстояние от вершины, лежащей напротив основания, до центра вневписанной окружности, касающееся боковой стороны,

Слайд 11Теорема 4: Радиусы вневписанных окружностей выражаются через стороны равнобедренного треугольника формулами:

ra = rb = и rc = 0,5c *

Доказательство. Из доказательства теоремы 3 следует, что CTc ⊥ AB и BTc = ATc = 0,5c. Из прямоугольного треугольника
TcCA rb = CTc =
Прямоугольные треугольники ОсТсА и ObCbA подобны по двум углам. Тогда
= = = . Отсюда = или rc =0,5c *
Следствие. Для равностороннего треугольника ra = rb = rc = =3r, где а – сторона треугольника и r – радиус вписанной окружности.

Теорема 4: Радиусы вневписанных окружностей выражаются через стороны равнобедренного треугольника формулами: ra = rb =

Слайд 12Теорема 5: Радиус вневписанной окружности, касающейся гипотенузы прямоугольного треугольника, равен полупериметру

этого треугольника, т.е. rc = p.

Доказательство. Пусть вневписанная окружность с центром в Ос касается продолжений катетов СВ и СА в точках А3 и В3 соответственно.
Радиусы, проведенные в точки касания, перпендикулярны прямым СВ и СА. Из теоремы 1 отрезки СА3 = СВ3 = p. Т.к. четырехугольник СВ3ОсА3 – квадрат, то rc = ОсА3 = СА3 = p.

Теорема 5: Радиус вневписанной окружности, касающейся гипотенузы прямоугольного треугольника, равен полупериметру этого треугольника, т.е. rc = p.Доказательство.

Слайд 13Следствие: Т.к. для прямоугольного треугольника имеют место формулы p = 2R

+r = c + r, то получаем еще равенства rc = 2R + r = c + r.

Следствие: Т.к. для прямоугольного треугольника имеют место формулы p = 2R +r = c + r, то

Слайд 14Теорема 6: Гипотенуза прямоугольного треугольника равна сумме радиусов вневписанных окружностей, касающихся

катетов, т.е. c = ra + rb .

Доказательство. Т.к. четырехугольники СТаОаВ1 и СА1ОbTb – квадраты, то CTa = ra, CTb = rb. Из следствия 3 теоремы 1 имеем ra + rb = CT­a + CT­b = c.

Теорема 6: Гипотенуза прямоугольного треугольника равна сумме радиусов вневписанных окружностей, касающихся катетов, т.е. c = ra +

Слайд 15Следствие: Т.к. rc = c + r, то получаем rc =

Следствие: Т.к. rc = c + r, то получаем rc = r + ra + rb.

Слайд 16Теорема 7: Доказать, что катеты прямоугольного треугольника АВС с прямым углом

в вершине С могут быть найдены через радиусы rc , ra, rb вневписанных окружностей по формулам:
а) a = rc – rb и b = rc – ra;
б) a = 2rarc / ra + rc и b = 2rbrc/ rb + rc .

Доказательство. а) По следствию 2 теоремы 1 имеем rb = CTb = p – a. Т.к. по теореме 5 rc = p, то получаем a = rc – rb. Вторая формула доказывается аналогично.
б) Т.к. центры вневписанных окружностей Oa и Ос лежат на биссектрисе внешнего угла В треугольника АВС, то прямоугольные треугольники ОаТаВ и ОсА3В подобны по двум углам. Тогда из равенства отношения сторон, лежащих против равных углов, ОаТа/ОсА3 = ТаВ/ВА3, получаем ra/rc = a – ra/rc – a. Отсюда a = 2rarc / ra + rc.

Следствие. Из первых двух формул теоремы 7 получаем |a – b| = |ra – rb|.

Теорема 7: Доказать, что катеты прямоугольного треугольника АВС с прямым углом в вершине С могут быть найдены

Слайд 17Расстояния до центров вневписанных окружностей

Расстояния до центров вневписанных окружностей

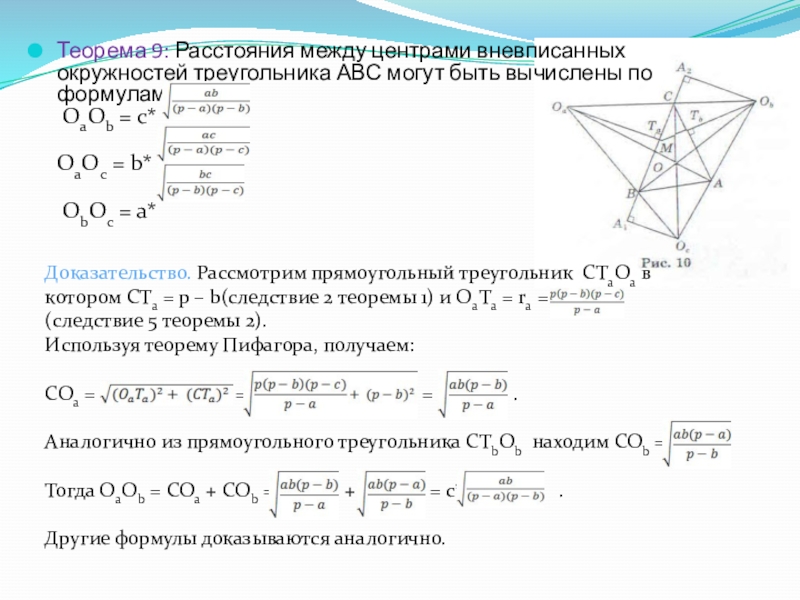
Слайд 18Теорема 9: Расстояния между центрами вневписанных окружностей треугольника АВС могут быть

вычислены по формулам:
OaOb = c*

OaOc = b*

ObOc = a*

Доказательство. Рассмотрим прямоугольный треугольник CTaOa в котором CTa = p – b(следствие 2 теоремы 1) и OaTa = ra = (следствие 5 теоремы 2).
Используя теорему Пифагора, получаем:

СОа = = = .

Аналогично из прямоугольного треугольника CTbOb находим COb =

Тогда OaOb = COa + COb = + = c* .

Другие формулы доказываются аналогично.

Теорема 9: Расстояния между центрами вневписанных окружностей треугольника АВС могут быть вычислены по формулам: OaOb =

Слайд 19Следствие. Расстояния от вершины С треугольника АВС до центров Oa и

Ob вневписанных окружностей соответственно равны:
СOa = и COb =

Замечание. Из прямоугольного треугольника СОсА1 можно найти расстояние от вершины С треугольника АВС до центра Ос вневписанной окружности:
СОс = =

Следствие. Расстояния от вершины С треугольника АВС до центров Oa и Ob вневписанных окружностей соответственно равны:

Слайд 20Соотношения между величинами углов
Теорема 10: Сторона ВС треугольника АВС видна из

центра Oa вневписанной окружности, касающейся стороны С, под углом 90 — .

Доказательство. Т.к. BOa и COa – биссектрисы внешних углов треугольника АВС при вершинах В и С, то СВОа = 90 — и ВСОа = 90 — .

Отсюда получаем ВОаС = 180 — СВОа — ВСОа = 180 — (90 — + 90 — ) = 90 —

Соотношения между величинами угловТеорема 10: Сторона ВС треугольника АВС видна из центра Oa вневписанной окружности, касающейся стороны

Источник

2021-11-23   comment

Вневписанная окружность равнобедренного треугольника касается его боковой стороны.
а) Докажите, что радиус этой окружности равен высоте треугольника, опущенной на основание.
б) Известно, что радиус этой окружности в пять раз больше радиуса вписанной окружности треугольника. В каком отношении точка касания вписанной окружности с боковой стороной треугольника делит эту сторону?

Решение:



а) Пусть вписанная окружность с центром $O$ касается боковой стороны $AB$ и основания $BC$ равнобедренного треугольника $ABC$ в точках $M$ и $H$ (рис.1), а окружность с центром $O_{1}$ касается боковой стороны $AB$, продолжения основания $BC$ в точке $D$ и продолжения боковой стороны $AC$ в точке $E$. Тогда $AH$ — высота треугольника $ABC$.
Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому $AO_{1}$ — биссектриса угла $BAE$. В четырёхугольнике $AHDO_{1}$ угол $HAO_{1}$ — прямой как угол между биссектрисами смежных углов $BAC$ и $BAE$, а т.к. $angle HDO_{1}=angle AHD=90^{circ}$, то $AHDO_{1}$ — прямоугольник, поэтому $O_{1}D=AH$.
б) Пусть радиус окружности с центром $O$ равен $r$ (рис.2). Тогда радиус окружности с центром $O_{1}$ равен $5r$.

$AH=O_{1}D=5r,~OA=AH-OH=5r-r=4r.$

Из прямоугольного треугольника $AOM$ находим, что

$AM=sqrt{AO^{2}-OM^{2}}=sqrt{16r^{2}-r^{2}}=rsqrt{15}.$

Прямоугольные треугольники $AOM$ и $ABH$ подобны по двум углам, поэтому $frac{AM}{OM}=frac{AH}{BH}$, откуда

$BH=frac{OMcdot AH}{AM}=frac{rcdot5r}{rsqrt{15}}=frac{rsqrt{15}}{3}.$

По теореме об отрезках касательных, проведённых к окружности из одной точки $BM=BH=frac{rsqrt{15}}{3}$. Следовательно,

$frac{BM}{AM}=frac{frac{rsqrt{15}}{3}}{rsqrt{15}}=frac{1}{3}.$

Источник

Скачать материал

ВНЕВПИСАННАЯ ОКРУЖНОСТЬ ТРЕУГОЛЬНИКА

Скачать материал

  • Сейчас обучается 967 человек из 80 регионов

  • Сейчас обучается 49 человек из 26 регионов

  • Сейчас обучается 139 человек из 43 регионов

Описание презентации по отдельным слайдам:

  • ВНЕВПИСАННАЯ ОКРУЖНОСТЬ ТРЕУГОЛЬНИКА

    1 слайд

    ВНЕВПИСАННАЯ ОКРУЖНОСТЬ ТРЕУГОЛЬНИКА

  • Вневписанной окружностью треугольника называется окружность, к которой являют...

    2 слайд

    Вневписанной окружностью треугольника называется окружность, к которой являются касательными одна из сторон треугольника и продолжения двух других сторон.

  • Соотношение между длинами отрезков касательныхТеорема 1: Расстояние от вершин...

    3 слайд

    Соотношение между длинами отрезков касательных
    Теорема 1: Расстояние от вершины треугольника до точки касания вневписанной окружности с продолжением стороны, содержащей ее, за вершину противолежащей стороны равно полупериметру треугольника.

    Доказательство. Обозначим через В₁, С₁, и Та – точки касания вневписанной окружности с прямыми АС, АВ и ВС соответственно. Тогда СВ₁ = СТа, ВС₁ = ВТа и периметр треугольника АВС: P = AC + СТа + ВТа + АВ = АС + СВ₁ + ВС₁ + АВ = АВ₁ + АС₁. Т.к. АВ₁ = АС₁, то расстояния АВ₁ и АС₁ равны полупериметру треугольника АВС.

  • Следствие 1: Прямая, проведенная через вершину треугольника и точку, в которо...

    4 слайд

    Следствие 1: Прямая, проведенная через вершину треугольника и точку, в которой вневписанная окружность касается противоположной стороны, делит периметр треугольника пополам.
    Примечание: В треугольнике расстояние от вершины треугольника до точки касания вписанной окружности со стороной треугольника, выходящей из данной вершины, есть разность полупериметра треугольника и стороны, противолежащей данной вершине. То же соблюдается и для вневписанной окружности.
    AN = AK = p – a,
    BM = BK = p – b,
    CN = CM = p – c.

  • Следствие 2: Для отрезков касательных, связанных с вневписанными окружностями...

    5 слайд

    Следствие 2: Для отрезков касательных, связанных с вневписанными окружностями треугольника, выполняются равенства:
    ВТс = ВА1 = СТb = CA2 = p-a,
    ATc = AB2 = CTa = CB1 = p-b,
    BTa = BC1 = ATb = AC2 = p-c.
    Следствие 3: Верны следующие равенства:
    B2Tb = C2Tc = ATc + ATb = a,
    C1Tc = A1Ta = BTc + BTa = b,
    B1Tb = A2Ta = CTb + CTa = c.
    Следствие 4: Расстояния между точками касаний вневписанных окружностей продолжений сторон за вершины треугольника равны:
    C1C2 = a +b,
    B1B2 = a + c,
    A1A2 = b + c.

    Из следствия 1
    Получаются при попарном сложении равенств из следствия 2
    Получаются при попарном сложении равенств из следствия 3

  • Формулы для вычисления радиусов вневписанных окружностейТеорема 2: Радиус вне...

    6 слайд

    Формулы для вычисления радиусов вневписанных окружностей
    Теорема 2: Радиус вневписанной окружности, касающейся стороны ВС треугольника АВС, вычисляется по формуле ra =

    Доказательство. Выполняются следующие равенства:
    SABC = SOCA + SOBA — SOCB = 0,5rab + 0,5rac – 0,5raa = ra(p -a).
    Аналогично получаются формулы:
    rb = и rc =

  • Следствие 1: Большей стороне треугольника соответствует касающаяся её вневпис...

    7 слайд

    Следствие 1: Большей стороне треугольника соответствует касающаяся её вневписанная окружность большего радиуса и наоборот.
    Следствие 2: Радиус вневписанной окружности треугольника больше радиуса окружности, вписанной в тот же треугольник.
    Следствие 3: Площадь треугольника АВС может быть вычислена по формулам:
    S = ra(p — a), S = rb(p — b), S = rc(p — c).

  • Следствие 4: Для отношения радиусов вписанной и вневписанных окружностей имею...

    8 слайд

    Следствие 4: Для отношения радиусов вписанной и вневписанных окружностей имеют место равенства:
    r/ra = , ra/rb = , ra/rc = .
    Следствие 5: Используя формулу Герона, получим формулы для вычисления длин радиусов через стороны треугольника:

    ra =

    rb =

    rc =

  • Теорема 3: Радиус вневписанной окружности, касающейся боковой стороны равнобе...

    9 слайд

    Теорема 3: Радиус вневписанной окружности, касающейся боковой стороны равнобедренного треугольника, равен высоте треугольника, опущенной на основание.
    Доказательство. Пусть Oa, Ob и Oc – центры вневписанных окружностей треугольника АВС, Ca, Cb и Tc – точки касания этих окружностей с прямой АВ.
    Т.к. треугольник АВС – равнобедренный (АС = ВС), то высота, опущенная из вершины С, лежит на биссектрисе СОс угла С, и поэтому СОс ⊥ АВ. С другой стороны радиус ОсТс ⊥ АВ, следовательно, точка Тс лежит на биссектрисе угла С. Отсюда ОТс ⊥ АВ и СТс является высотой треугольника АВС. Заметим, что СОс ⊥ COb как биссектрисы внутреннего и внешнего угла треугольника при вершине С, СОс ⊥ АВ и ObCb ⊥ АВ. Следовательно, четырехугольник TcCObCb – прямоугольник. Значит, rb = ObCb = CTc.

  • Следствие: В равнобедренном треугольнике расстояние от вершины, лежащей напро...

    10 слайд

    Следствие: В равнобедренном треугольнике расстояние от вершины, лежащей напротив основания, до центра вневписанной окружности, касающееся боковой стороны, равно боковой стороне.
    Доказательство. Т.к. BCb = p = b + 0,5c, то получаем COb = TcCb = p – 0,5c = b.

  • Теорема 4: Радиусы вневписанных окружностей выражаются через стороны равнобед...

    11 слайд

    Теорема 4: Радиусы вневписанных окружностей выражаются через стороны равнобедренного треугольника формулами:
    ra = rb = и rc = 0,5c *
    Доказательство. Из доказательства теоремы 3 следует, что CTc ⊥ AB и BTc = ATc = 0,5c. Из прямоугольного треугольника
    TcCA rb = CTc =
    Прямоугольные треугольники ОсТсА и ObCbA подобны по двум углам. Тогда
    = = = . Отсюда = или rc =0,5c *
    Следствие. Для равностороннего треугольника ra = rb = rc = =3r, где а – сторона треугольника и r – радиус вписанной окружности.

  • Теорема 5: Радиус вневписанной окружности, касающейся гипотенузы прямоугольно...

    12 слайд

    Теорема 5: Радиус вневписанной окружности, касающейся гипотенузы прямоугольного треугольника, равен полупериметру этого треугольника, т.е. rc = p.
    Доказательство. Пусть вневписанная окружность с центром в Ос касается продолжений катетов СВ и СА в точках А3 и В3 соответственно.
    Радиусы, проведенные в точки касания, перпендикулярны прямым СВ и СА. Из теоремы 1 отрезки СА3 = СВ3 = p. Т.к. четырехугольник СВ3ОсА3 – квадрат, то rc = ОсА3 = СА3 = p.

  • Следствие: Т.к. для прямоугольного треугольника имеют место формулы p = 2R +r...

    13 слайд

    Следствие: Т.к. для прямоугольного треугольника имеют место формулы p = 2R +r = c + r, то получаем еще равенства rc = 2R + r = c + r.

  • Теорема 6: Гипотенуза прямоугольного треугольника равна сумме радиусов вневпи...

    14 слайд

    Теорема 6: Гипотенуза прямоугольного треугольника равна сумме радиусов вневписанных окружностей, касающихся катетов, т.е. c = ra + rb .
    Доказательство. Т.к. четырехугольники СТаОаВ1 и СА1ОbTb – квадраты, то CTa = ra, CTb = rb. Из следствия 3 теоремы 1 имеем ra + rb = CT­a + CT­b = c.

  • Следствие: Т.к. rc = c + r, то получаем rc = r + ra + rb.

    15 слайд

    Следствие: Т.к. rc = c + r, то получаем rc = r + ra + rb.

  • Теорема 7: Доказать, что катеты прямоугольного треугольника АВС с прямым угло...

    16 слайд

    Теорема 7: Доказать, что катеты прямоугольного треугольника АВС с прямым углом в вершине С могут быть найдены через радиусы rc , ra, rb вневписанных окружностей по формулам:
    а) a = rc – rb и b = rc – ra;
    б) a = 2rarc / ra + rc и b = 2rbrc/ rb + rc .
    Доказательство. а) По следствию 2 теоремы 1 имеем rb = CTb = p – a. Т.к. по теореме 5 rc = p, то получаем a = rc – rb. Вторая формула доказывается аналогично.
    б) Т.к. центры вневписанных окружностей Oa и Ос лежат на биссектрисе внешнего угла В треугольника АВС, то прямоугольные треугольники ОаТаВ и ОсА3В подобны по двум углам. Тогда из равенства отношения сторон, лежащих против равных углов, ОаТа/ОсА3 = ТаВ/ВА3, получаем ra/rc = a – ra/rc – a. Отсюда a = 2rarc / ra + rc.

    Следствие. Из первых двух формул теоремы 7 получаем |a – b| = |ra – rb|.

  • Расстояния до центров вневписанных окружностей

    17 слайд

    Расстояния до центров вневписанных окружностей

  • Теорема 9: Расстояния между центрами вневписанных окружностей треугольника АВ...

    18 слайд

    Теорема 9: Расстояния между центрами вневписанных окружностей треугольника АВС могут быть вычислены по формулам:
    OaOb = c*

    OaOc = b*

    ObOc = a*

    Доказательство. Рассмотрим прямоугольный треугольник CTaOa в котором CTa = p – b(следствие 2 теоремы 1) и OaTa = ra = (следствие 5 теоремы 2).
    Используя теорему Пифагора, получаем:

    СОа = = = .

    Аналогично из прямоугольного треугольника CTbOb находим COb =

    Тогда OaOb = COa + COb = + = c* .

    Другие формулы доказываются аналогично.

  • Следствие. Расстояния от вершины С треугольника АВС до центров Oa и Ob вневпи...

    19 слайд

    Следствие. Расстояния от вершины С треугольника АВС до центров Oa и Ob вневписанных окружностей соответственно равны:
    СOa = и COb =

    Замечание. Из прямоугольного треугольника СОсА1 можно найти расстояние от вершины С треугольника АВС до центра Ос вневписанной окружности:
    СОс = =

  • Соотношения между величинами угловТеорема 10: Сторона ВС треугольника АВС вид...

    20 слайд

    Соотношения между величинами углов
    Теорема 10: Сторона ВС треугольника АВС видна из центра Oa вневписанной окружности, касающейся стороны С, под углом 90 — .

    Доказательство. Т.к. BOa и COa – биссектрисы внешних углов треугольника АВС при вершинах В и С, то СВОа = 90 — и ВСОа = 90 — .

    Отсюда получаем ВОаС = 180 — СВОа — ВСОа = 180 — (90 — + 90 — ) = 90 —

Краткое описание документа:

Материал предназначен для профильных классов и лицеев. Детей средней и низкой подготовленности лучше не пугать данным материалом, иначе математику они точно любить не будут

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 266 078 материалов в базе

  • Выберите категорию:

  • Выберите учебник и тему

  • Выберите класс:

  • Тип материала:

    • Все материалы

    • Статьи

    • Научные работы

    • Видеоуроки

    • Презентации

    • Конспекты

    • Тесты

    • Рабочие программы

    • Другие методич. материалы

Найти материалы

Другие материалы

  • 21.04.2015
  • 876
  • 8
  • 21.04.2015
  • 1642
  • 1
  • 21.04.2015
  • 2278
  • 73
  • 21.04.2015
  • 1048
  • 1
  • 21.04.2015
  • 992
  • 0
  • 21.04.2015
  • 3951
  • 7
  • 21.04.2015
  • 1256
  • 5
Источник

Вневписанная окружность равнобедренного треугольника касается его боковой стороны.

а)  Докажите, что радиус этой окружности равен высоте треугольника, опущенной на его основание.

б)  Известно, что радиус этой окружности в 4 раза больше радиуса вписанной окружности треугольника. В каком отношении точка касания вписанной окружности с боковой стороной треугольника делит эту сторону?

Решение.

а)  Пусть b  — боковая сторона треугольника, c  — его основание, h  —  высота, опущенная на основание треугольника.

Радиус вневписанной окружности вычисляется по формуле R= дробь: числитель: S, знаменатель: p минус a конец дроби , где p  —  полупериметр треугольника, a  —  сторона, которой касается окружность. Таким образом,

R= дробь: числитель: дробь: числитель: hc, знаменатель: 2 конец дроби , знаменатель: дробь: числитель: c, знаменатель: 2 конец дроби плюс b минус b конец дроби =h.

б)  Пусть O2  — центр вписанной окружности. Проведем радиус в точку касания H. Трегольники AMC и CHO2 подобны по двум углам, поэтому дробь: числитель: CA, знаменатель: CO_2 конец дроби = дробь: числитель: CM, знаменатель: CH конец дроби .

Так как R=h, то r= дробь: числитель: 1, знаменатель: 4 конец дроби умножить на h. Тогда CO_2=3r. Найдем CH по теореме Пифагора. Получим, что CH=2 корень из 2 r

Тогда

CA= дробь: числитель: CM умножить на CO_2, знаменатель: CH конец дроби = дробь: числитель: 4r умножить на 3r, знаменатель: 2 корень из 2 r конец дроби =3 корень из 2 r.

Откуда получаем

дробь: числитель: CH, знаменатель: HA конец дроби = дробь: числитель: 2 корень из 2 r, знаменатель: CA минус CH конец дроби = дробь: числитель: 2, знаменатель: 1 конец дроби .

Ответ: б)2:1.

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти угол альфа на графике
  • Найти как восстановить пароль в одноклассниках
  • Как найти объединенные ячейки в google sheets
  • Как исправить raw диск без форматирования
  • Как найти стоящего мужчину