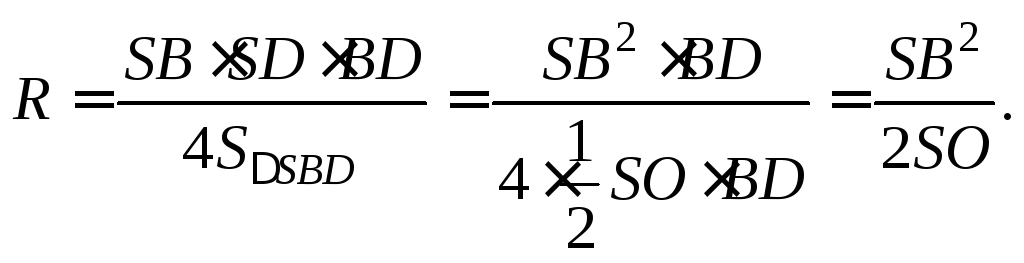Как найти радиус вписанного шара в параллелепипеде - Исправление недочетов и поиск решений вместе с Examum.ru

Ответы

Автор ответа: mugalim13

Ответ:

3,5 см.

Пошаговое объяснение:

Используем формулу теоремы Пифагора для прямоугольного треугольника:

a ^ 2 + b ^ 2 = c ^ 2.

Диагональ фигуры в квадрате:

2 ^ 2 + 3 ^ 2 + 6 ^ 2 = 4 + 9 + 36 = 13 + 36 = 49.

Тогда диагональ прямоугольного параллелепипеда равна:

= 7 (см).

Зная, что длина диагонали прямоугольного параллелепипеда равна диаметру описанного шара / сферы, имеем:

D = 7 (см).

Из формулы:

D = 2 * R,

найдём радиус:

R = D / 2.

Подставим вычисленное значение диаметра в формулу:

R = 7 / 2 = 3,5 (см) — радиус описанного около прямоугольного параллелепипеда шара.

Интересные вопросы

Помогите пожалуйста.
Найдите число, которое нужно поставить вместо знака ?, чтобы равенство стало верным: Напишите сразу ответ. Переписывать пример НЕ ОБЯЗАТЕЛЬНО!!
0,1*?=10
9,8+?=10
17:?=10
?*0,2=10
5,6+?=10
100*?=10
0,25*?=10
7.8:?=10
?:0,1=10
4*?=10
?+1,5=10
?:1,2=10
6,5+?=10
?*1,25=10
?-0,02=10
2,1-?=0,5
5*?=0,5
?:2=0,5
0,15+?=0,5
?*0,1=0,5
0,3+?=0,5

?:10=0,5
0,8-?=0,5
?*25=0,5
2:?=10
3,7-?=0,5
?+0,05=0,5
10*?=0,5
?:0,01=0,5
0,04+?=0,5

Источник

Скачать материал

Сейчас обучается 268 человек из 65 регионов

Сейчас обучается 389 человек из 62 регионов

Описание презентации по отдельным слайдам:

1 слайд

Реферат
на тему «Вписанные и описанные многогранники»
(Математика)
Выполнили:
ученицы 11 класса Б
гимназии № 12
Злова Виктория и
Обедина Екатерина

Проверила:
Третьякова Н. А.
2 слайд

Цель работы состоит в том, чтобы узнать весь теоретический материал по теме «Вписанные и описанные многогранники» и научиться применять его на практике.
Цель реферата
3 слайд

Правильные многогранники
Тетраэдр
Куб
Октаэдр
Додекаэдр
Икосаэдр
4 слайд

Многогранники, вписанные в шар
Выпуклый многогранник называется вписанным, если все его вершины лежат на некоторой сфере. Эта сфера называется описанной для данного многогранника. Центр этой сферы является точкой, равноудаленной от вершин многогранника. Она является точкой пересечения плоскостей, каждая из которых проходит через середину ребра многогранника перпендикулярно ему.
5 слайд

Пирамида, вписанная в шар
Теорема:
Около пирамиды можно описать сферу тогда и только тогда, когда около основания пирамиды можно описать окружность.
6 слайд

Формула для нахождения радиуса описанной сферы
Пусть SABC — пирамида с равными боковыми ребрами, h — ее высота, R — радиус окружности, описанной около основания. Найдем радиус описанной сферы.
Заметим подобие прямоугольных треугольников SKO1 и SAO.
Тогда
SO1/SA = KS/SO;
R1 = KS · SA/SO
Но KS = SA/2.
Тогда
R1 = SA2/(2SO);
R1 = (h2 +R2)/(2h);
R1 = b2/(2h), где b — боковое ребро.
7 слайд

Призма, вписанная в шар
Теорема:
Около призмы можно описать шар только в том случае, если призма является прямой и около ее основания можно описать окружность.
8 слайд

Параллелепипед, вписанный в шар
Теорема:
Сфера может быть описана около параллелепипеда тогда и только тогда, когда параллелепипед прямоугольный, так как в данном случае он является прямым и около его основания — параллелограмма — может быть описана окружность (т. к. основание — прямоугольник).
9 слайд

Конус и цилиндр, вписанные в шар
Теорема:
Около всякого конуса можно описать сферу.
Теорема:
Около любого цилиндра можно описать сферу.
10 слайд

Задача 1
Найти радиус шара, описанного около правильного тетраэдра с ребром а.
Решение:
SO1 = SA2/(2SO);
SO =
SO =
=
= a
SO1 = a2/(2 a
) = a
/4.
Ответ:
SO1 = a
/4.
Предварительно построим на изображении правильного тетраэдра SABC изображение центра описанного шара. Проведем апофемы SD и AD (SD = AD). В равнобедренном треугольнике ASD каждая точка медианы DN равноудалена от концов отрезка AS. Поэтому точка O1 есть пересечение высоты SO и отрезка DN.
Используя формулу из R1 = b2/(2h), получим:
11 слайд

Задача 2
Решение:
По формуле R1=b2/(2h) для нахождения радиуса описанного шара найдем SC и SO.
SC = a/(2sin(α/2));
SO2 = (a/(2sin(α/2))2 – (a
/2)2 =
= a2/(4sin2(α/2)) – 2a2/4 =
= a2/(4sin2(α/2)) · (1 – 2sin2(α/2)) =
= a2/(4sin2(α/2)) · cosα
В правильной четырехугольной пирамиде сторона основания равна а, а плоский угол при вершине равен α. Найти радиус описанного шара.
R1 = a2/(4sin2(α/2)) · 1/(2a
/(2sin(α/2))) =
a/(4sin(α/2) ·
).
Ответ:
R1 = a/(4sin(α/2) ·
).
12 слайд

Многогранники, описанные около шара
Выпуклый многогранник называется описанным, если все его грани касаются некоторой сферы. Эта сфера называется вписанной для данного многогранника. Центром вписанной сферы является точка, равноудаленная от всех граней многогранника.
13 слайд

Положение центра вписанной сферы
Понятие биссекторной плоскости двугранного угла.
Биссекторной называется плоскость, делящая двугранный угол на два равных двугранных угла.
Каждая точка этой плоскости равноудалена от граней двугранного угла.
В общем случае центр вписанной в многогранник сферы является точкой пересечения биссекторных плоскостей всех двугранных углов многогранника. Он всегда лежит внутри многогранника.
14 слайд

Пирамида, описанная около шара
Шар, называется вписанным в (произвольную) пирамиду, если он касается всех граней пирамиды (как боковых, так и основания).
Теорема:
Если боковые грани одинаково наклонены к основанию, то в такую пирамиду можно вписать шар.

Так как двугранные углы при основании равны, то их половинки тоже равны  биссектрисы пересекаются в одной точке на высоте пирамиды. Эта точка принадлежит всем биссекторным плоскостям при основании пирамиды и  равноудалена от всех граней пирамиды – центр вписанного шара.
15 слайд

Формула для нахождения радиуса вписанной сферы
Пусть SABC — пирамида с равными боковыми ребрами, h — ее высота, r — радиус вписанной окружности. Найдем радиус описанной сферы.
Пусть SO = h, OH = r, O1O = r1.
Тогда по свойству биссектрисы внутреннего угла треугольника
O1O/OH = O1S/SH;
r1/r = (h – r1)/ ;
r1 · = rh – rr1;
r1 · ( + r) = rh;
r1 = rh/( + r).
Ответ: r1 = rh/( + r).
16 слайд

Призма, описанная около шара
Теорема:
Сферу можно вписать в призму тогда и только тогда, когда призма прямая и в основание можно вписать окружность, диаметр которой равен высоте призмы.
17 слайд

Параллелепипед и куб, описанные около шара
Теорема:
В параллелепипед можно вписать сферу тогда и только тогда, когда параллелепипед прямой и его основание — ромб, причем высота этого ромба есть диаметр вписанной сферы, который, в свою очередь, равен высоте параллелепипеда. (Из всех параллелограммов только в ромб можно вписать окружность)
Теорема:
В куб всегда можно вписать сферу. Центр этой сферы — точка пересечения диагоналей куба, а радиус равен половине длины ребра куба.
18 слайд

Цилиндр и конус, описанные около шара
Теорема:
Сферу можно вписать лишь в такой цилиндр, высота которого равна диаметру основания.
Теорема:
Во всякий конус можно вписать сферу.
19 слайд

Комбинации фигур
Вписанная и описанная призмы
Призма, описанная около цилиндра – призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а боковые грани касаются цилиндра.
Призма, вписанная в цилиндр – призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а боковыми ребрами – образующие цилиндра.
Касательная плоскость к цилиндру – плоскость, проходящая через образующую цилиндра и перпендикулярная плоскости осевого сечения, содержащей эту образующую.
20 слайд

Вписанная и описанная пирамиды
Пирамида, вписанная в конус – пирамида, основание которой есть многоугольник, вписанный в окружность основания конуса, а вершиной является вершина конуса.
Боковые ребра пирамиды, вписанной в конус – образующие конуса.
Пирамида, описанная около конуса – пирамида, у которой основанием служит многоугольник, описанный около основания конуса, а вершина совпадает с вершиной конуса.
Плоскости боковых граней описанной пирамиды – касательные плоскости конуса.
Касательная плоскость к конусу – плоскость, проходящая через образующую и перпендикулярная плоскости осевого сечения, содержащей эту образующую.
21 слайд

Другие виды конфигураций
Цилиндр вписан в пирамиду, если окружность одного его основания касается всех боковых граней пирамиды, а другое его основание лежит на основании пирамиды.
Конус вписан в призму, если его вершина лежит на верхнем основании призмы, а его основание – круг, вписанный в многоугольник – нижнее основание призмы.
Призма вписана в конус, если все вершины верхнего основания призмы лежат на боковой поверхности конуса, а нижнее основание призмы лежит на основании конуса.
22 слайд

Задача 1
В правильной четырехугольной пирамиде сторона основания равна а, а плоский угол при вершине равен α. Найдите радиус вписанного в пирамиду шара.
Решение:
Выразим стороны ∆SOK через а и α.
OK = a/2.
SK = KC · ctg(α/2);
SK = (a · ctg(α/2))/2.
SO =
SO =
= (a/2)
Использую формулу r1 = rh/(
+ r), найдем радиус вписанного шара:
r1 = OK · SO/(SK + OK);
r1 = (a/2) · (a/2)
/((a/2) · ctg(α/2) + (a/2)) =
= (a/2)
/(ctg(α/2) + 1) =
(a/2)
=
= (a/2)
Ответ: r1 = (a/2)
23 слайд

Вывод
Тема «Многогранники» изучается учениками в 10 и 11 классах, но в учебной программе очень мало материала на тему «Вписанные и описанные многогранники», хотя она вызывает очень большой интерес у учащихся, так как изучение свойств многогранников способствует развитию абстрактного и логического мышления, что впоследствии пригодится нам в учебе, работе, жизни.
Работая над данным рефератом, мы изучили весь теоретический материал на тему «Вписанные и описанные многогранники», рассмотрели возможные комбинации фигур и научились применять весь изученный материал на практике.
Задачи на комбинацию тел – наиболее трудный вопрос курса стереометрии 11 класса. Но теперь мы с уверенностью можем сказать, что у нас не возникнет проблем при решении подобных задач, так как в ходе нашей исследовательской работы мы установили и доказали свойства вписанных и описанных многогранников. Очень часто у учащихся возникают трудности при построении чертежа к задаче на данную тему. Но, узнав, что для решения задач на комбинацию шара с многогранником изображение шара бывает излишним и достаточно указать его центр и радиус, мы можем быть уверены, что данных трудностей у нас не возникнет.
Благодаря данному реферату мы смогли разобраться в этой трудной, но очень увлекательной теме. Мы надеемся, что теперь у нас не возникнет трудностей при применении изученного материала на практике.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 264 310 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

13.12.2020
142
1

07.12.2020
284
4

07.12.2020
234
1

23.11.2020
480
1

08.10.2020
186
1

27.09.2020
154
0

26.09.2020
232
0

08.09.2020
142
0

Вам будут интересны эти курсы:

Курс профессиональной переподготовки «Маркетинг: теория и методика обучения в образовательной организации»
Курс повышения квалификации «Организация научно-исследовательской работы студентов в соответствии с требованиями ФГОС»
Курс повышения квалификации «Экономика предприятия: оценка эффективности деятельности»
Курс профессиональной переподготовки «Клиническая психология: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Основы построения коммуникаций в организации»
Курс профессиональной переподготовки «Организация деятельности по подбору и оценке персонала (рекрутинг)»
Курс повышения квалификации «Основы менеджмента в туризме»
Курс повышения квалификации «Использование активных методов обучения в вузе в условиях реализации ФГОС»
Курс профессиональной переподготовки «Управление ресурсами информационных технологий»
Курс профессиональной переподготовки «Организация технической поддержки клиентов при установке и эксплуатации информационно-коммуникационных систем»
Курс профессиональной переподготовки «Корпоративная культура как фактор эффективности современной организации»
Курс профессиональной переподготовки «Управление информационной средой на основе инноваций»
Курс профессиональной переподготовки «Политология: взаимодействие с органами государственной власти и управления, негосударственными и международными организациями»
Курс профессиональной переподготовки «Организация маркетинговой деятельности»

Источник

Нахождение радиуса описанной вокруг правильного многоугольника окружности

В публикации представлена формула, с помощью которой можно найти радиус окружности, описанной около правильного многоугольника, а также приведен пример решения задачи для лучшего понимания представленного материала.

Формула расчета радиуса окружности

На рисунке изображен правильный шестиугольник с описанной вокруг него окружностью, но формула ниже подходит для любого правильного n-угольника.

где a – длина стороны.

Примечание: зная радиус описанного круга можно найти сторону равностороннего n-угольника (формула выводится из представленной выше):

Пример задачи

Дан правильный пятиугольник с длиной стороны 8 см. Вычислите радиус описанной около данной фигуры окружности.

Решение:
Применим соответствующую формулу, подставив в нее известное нам значение.

Прямоугольный параллелепипед

Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.

На рисунке изображен прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Его основаниями являются прямоугольники $ABCD$ и $A_1B_1C_1D_1$, а боковые ребра $AA_1, BB_1, CC_1$ и $DD_1$ перпендикулярны к основаниям.

Свойства прямоугольного параллелепипеда:

В прямоугольном параллелепипеде $6$ граней и все они являются прямоугольниками.
Противоположные грани попарно равны и параллельны.
Все двугранные углы прямоугольного параллелепипеда – прямые.
Диагонали прямоугольного параллелепипеда равны.
Прямоугольный параллелепипед имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
Любая грань прямоугольного параллелепипеда может быть принята за основание.
Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.

Чтобы были понятны формулы, введем обозначения:

$с$ — высота(она же боковое ребро);

$P_<осн>$ — периметр основания;

$S_<осн>$ — площадь основания;

$S_<бок>$ — площадь боковой поверхности;

$S_<п.п>$ — площадь полной поверхности;

$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.

$S_<бок>=P_<осн>·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.

Дополнительные сведения, которые пригодятся для решения задач:

$а$ — длина стороны.

$d=a√3$ – диагональ равна длине стороны, умноженной на $√3$.

Пирамида

Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) — треугольники, имеющие общую вершину.

Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.

Объем любой пирамиды равен трети произведения основания и высоты.

В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.

В основании лежит треугольник.

$S=/<2>$, где $h_a$ — высота, проведенная к стороне $а$.
$S=/<2>$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
Формула Герона $S=√$, где $р$ — это полупериметр $p=/<2>$.
$S=p·r$, где $r$ — радиус вписанной окружности.
$S=/<4R>$, где $R$ — радиус описанной окружности.
Для прямоугольного треугольника $S=/<2>$, где $а$ и $b$ — катеты прямоугольного треугольника.
Для равностороннего треугольника $S=/<4>$, где $а$ — длина стороны.

В основании лежит четырехугольник.

Прямоугольник.
$S=a·b$, где $а$ и $b$ — смежные стороны.
Ромб.
$S=/<2>$, где $d_1$ и $d_2$ — диагонали ромба.
$S=a^2·sin⁡α$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
Трапеция.
$S=<(a+b)·h>/<2>$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
Квадрат.
$S=a^2$, где $а$ — сторона квадрата.

Найдите объём многогранника, вершинами которого являются точки $C, A_1, B_1, C_1, D_1$ параллелепипеда $ABCDA_1B_1C_1D_1$, у которого $AB=8, AD=12, AA_1=4$.

Изобразим прямоугольный параллелепипед и на нем отметим вершины многогранника $C, A_1, B_1, C_1, D_1$, получим в итоге четырехугольную пирамиду. В основании пирамиды лежит прямоугольник, так основание пирамиды и прямоугольного параллелепипеда совпадают.

Объем пирамиды, в основании которой лежит прямоугольник

Для нашего рисунка стороны прямоугольника – это $А_1В_1$ и $A_1D_1$.

В прямоугольном параллелепипеде противоположные ребра равны и параллельны, следовательно, $AB=А_1В_1=8; AD=A_1D_1=12$.

Высотой в пирамиде $CA_1B_1C_1D_1$ будет являться ребро $СС_1$, так как оно перпендикулярно основанию (из прямоугольного параллелепипеда).

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Окружность описана около параллелепипеда

Прямоугольный параллелепипед. Что это такое?

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Определение параллелепипеда

Начнем с того, что узнаем, что такое параллелепипед.

Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.

На рисунке два параллелограмма АВСD и A₁B₁C₁D₁. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA₁, ВB₁, CC₁, DD₁ параллельны друг другу. Образовавшаяся фигура — параллелепипед.

Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.

Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.

Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.

Параллелепипед — это:

Свойства параллелепипеда

Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.

Вот 4 свойства параллелепипеда, которые необходимо запомнить:

Противолежащие грани параллелепипеда равны и параллельны друг другу.
Все 4 диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Параллелепипед симметричен относительно середины его диагонали.
Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Подготовка к ЕГЭ по математике онлайн в школе Skysmart — отличный способ освежить знания и снять стресс перед экзаменом.

Прямой параллелепипед

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.

Свойства прямого параллелепипеда:

Основания прямого параллелепипеда — одинаковые параллелограммы, лежащие в параллельных плоскостях.
Боковые ребра прямого параллелепипеда равны, параллельны и перпендикулярны плоскостям оснований.
Высота прямого параллелепипеда равна длине бокового ребра.
Противолежащие боковые грани прямого параллелепипеда — равные прямоугольники.
Диагонали прямого параллелепипеда точкой пересечения делятся пополам.

На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.

Формулы прямого параллелепипеда:

Площадь боковой поверхности прямого параллелепипеда
Sб = Ро*h
Ро — периметр основания
h — высота
Площадь полной поверхности прямого параллелепипеда
Sп = Sб+2Sо
Sо — площадь основания
Объем прямого параллелепипеда
V = Sо*h

Прямоугольный параллелепипед

Определение прямоугольного параллелепипеда:

Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.

Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.

Свойства прямоугольного параллелепипеда

Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.

Прямоугольный параллелепипед содержит 6 граней. Все грани прямоугольного параллелепипеда — прямоугольники.
Противолежащие грани параллелепипеда попарно параллельны и равны.
Все углы прямоугольного параллелепипеда, состоящие из двух граней — 90°.
Диагонали прямоугольного параллелепипеда равны.
В прямоугольный параллелепипеде четыре диагонали, которые пересекаются в одной точке и делятся этой точкой пополам.
Любая грань прямоугольного параллелепипеда может быть принята за основание.
Если все ребра прямоугольного параллелепипеда равны, то такой параллелепипед является кубом.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

Формулы прямоугольного параллелепипеда:

Объем прямоугольного параллелепипеда
V = a · b · h
a — длина, b — ширина, h — высота
Площадь боковой поверхности
Sбок = Pосн·c=2(a+b)·c
Pосн — периметр основания, с — боковое ребро
Площадь поверхности
Sп.п = 2(ab+bc+ac)

Диагонали прямоугольного параллелепипеда: теорема

Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.

Если есть теорема, нужно ее доказать. (с) Пифагор

Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.

Дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Доказать теорему.

Доказательство теоремы:

Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.

Все грани прямоугольного параллелепипеда — прямоугольники.

ΔABD: ∠BAD = 90°, по теореме Пифагора

ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора

d² = d₁² + c² = a² + b² + c²

d² = a² + b² + c²

Доказанная теорема — пространственная теорема Пифагора.

Куб: определение, свойства и формулы

Кубом называется прямоугольный параллелепипед, все три измерения которого равны.

Каждая грань куба — это квадрат.

Свойства куба:

В кубе 6 граней, каждая грань куба — квадрат.
Противолежащие грани параллельны друг другу.
Все углы куба, образованные двумя гранями, равны 90°.
У куба четыре диагонали, которые пересекаются в центре куба и делятся пополам.
Диагонали куба равны.
Диагональ куба в √3 раз больше его ребра.
Диагональ грани куба в √2 раза больше длины ребра.

Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.

Формулы куба:

Объем куба через длину ребра a
V = a3
Площадь поверхности куба
S = 6a2
Периметр куба
P = 12a

Решение задач

Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.

Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.

Для наглядного решения обозначим измерения прямоугольного параллелепипеда: a — длина, b — ширина, c — высота. Тогда a = 10, b = 5, c = 8.

Так как в прямоугольном параллелепипеде всего по 4 — высота, ширина и длина, и все измерения равны между собой, то:
1) 4 * 10 = 40 (см) — сумма длин параллелепипеда;
2) 4 * 5 = 20 (см) — суммарное значение ширины параллелепипеда;
3) 4 * 8 = 32 (см) — сумма высот параллелепипеда;
4) 40 + 20 + 32 = 92 (см) — сумма длин всех ребер прямоугольного параллелепипеда.

Отсюда можно вывести формулу по нахождению суммы длин всех сторон ПП:
X = 4a + 4b + 4c (где X — сумма длин ребер).

Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.

Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Нужно найти длину ребра A₁B₁.

В фокусе внимания треугольник BDD1.
Угол D = 90°.

По теореме Пифагора:
BD₁ 2 = DD₁ 2 + BD 2
BD 2 = BD₁ 2 – DD₁ 2
BD 2 = 26 – 9 = 17
BD = √17
В треугольнике ADB угол А = 90°.
BD 2 = AD 2 + AB 2
AB 2 = BD 2 — AD 2 = (√17)2 — 4 2 = 1
A₁B₁ = AB = 1.

Задачка 3. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

AB = 4
AD = 6
AA₁= 5
Нужно найти отрезок BD₁.

В треугольнике ADB угол A = 90°.

По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD₁ угол D = 90°.
BD₁ 2 = 52 + 25 = 77
BD₁ = √77.

Самопроверка

Теперь потренируйтесь самостоятельно — мы верим, что все получится!

Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.

Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.

Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Вычислите длину ребра AA₁.

Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:

прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию;
параллелепипед называется прямоугольным, когда его боковые ребра перпендикулярны к основанию;
основание прямоугольного параллелепипеда — прямоугольник;
три измерения прямоугольного параллелепипеда: длина, ширина, высота;
диагональ параллелепипеда равна сумме квадратов его измерений.

Окружность описана около параллелепипеда

Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.

Радиусы шара и основания цилиндра равны. Площадь поверхности цилиндра, с радиусом основания r и высотой 2r равна

Площадь поверхности шара радиуса r равна то есть в 1,5 раза меньше площади поверхности цилиндра. Следовательно, площадь поверхности шара равна 12.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 4, а объем параллелепипеда равен

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому сторона основания равна 8, а площадь основания равна 64. Тогда высота цилиндра равна

Почему получилось 64? Что-то не понятно:(

Длина диаметра цилиндра равна длине стороны квадрата в основании.

Площадь квадрата

В куб вписан шар радиуса 1. Найдите объем куба.

Ребро куба равно диаметру вписанного в него шара, а объем куба равен кубу его ребра. Отсюда имеем:

В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.

По теореме Пифагора длина гипотенузы треугольника в основании Поскольку гипотенуза является диаметром основания описанного цилиндра, его объем

Прямоугольный параллелепипед

Свойства прямоугольного параллелепипеда:

В прямоугольном параллелепипеде $6$ граней и все они являются прямоугольниками.
Противоположные грани попарно равны и параллельны.
Все двугранные углы прямоугольного параллелепипеда – прямые.
Диагонали прямоугольного параллелепипеда равны.
Прямоугольный параллелепипед имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
Любая грань прямоугольного параллелепипеда может быть принята за основание.
Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.

Чтобы были понятны формулы, введем обозначения:

$с$ — высота(она же боковое ребро);

$P_ $ — периметр основания;

$S_ $ — площадь основания;

$S_ $ — площадь боковой поверхности;

$S_ $ — площадь полной поверхности;

$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.

$S_ =P_ ·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.

Дополнительные сведения, которые пригодятся для решения задач:

$а$ — длина стороны.

$d=a√3$ – диагональ равна длине стороны, умноженной на $√3$.

Пирамида

Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.

Объем любой пирамиды равен трети произведения основания и высоты.

В основании лежит треугольник.

В основании лежит четырехугольник.

Прямоугольник.
$S=a·b$, где $а$ и $b$ — смежные стороны.
Ромб.
$S= / $, где $d_1$ и $d_2$ — диагонали ромба.
$S=a^2·sin⁡α$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
Трапеция.
$S= / $, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
Квадрат.
$S=a^2$, где $а$ — сторона квадрата.

Объем пирамиды, в основании которой лежит прямоугольник

Для нашего рисунка стороны прямоугольника – это $А_1В_1$ и $A_1D_1$.

В прямоугольном параллелепипеде противоположные ребра равны и параллельны, следовательно, $AB=А_1В_1=8; AD=A_1D_1=12$.

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

источники:

http://examer.ru/ege_po_matematike/teoriya/pryamiugolnyi_parallelepiped

http://b4.cooksy.ru/articles/okruzhnost-opisana-okolo-parallelepipeda

Источник

Сфера
называется вписанной
в многогранник,
если она касается всех граней многогранника.

Многогранник
соответственно называется описанным
около сферы.

Теоремы:

Сферу можно вписать
в призму, если призма прямая и ее высота
равна диаметру окружности, вписанной
в основание призмы.
Сферу
можно вписать в пирамиду, если в основание
можно вписать окружность, а вершина
пирамиды ортогонально проектируется
в центр этой окружности.
Сферу можно вписать
в любую правильную пирамиду.

Сфера
называется вписанной
в цилиндр,
если она касается оснований и боковой
поверхности цилиндра. Цилиндр
соответственно называется описанным
около сферы.

Теорема.
Для того чтобы сферу можно было вписать
в цилиндр, необходимо и достаточно,
чтобы высота цилиндра равнялась диаметру
его основания.

Сфера
называется вписанной
в конус,
если она касается основания и боковой
поверхности конуса. Конус соответственно
называется описанным
около сферы.

Теорема.
Сферу можно вписать в любой конус.

Сфера
называется вписанной
в усеченный конус,
если она касается оснований и боковой
поверхности конуса. Усеченный конус
соответственно называется описанным
около сферы.

Теорема.
Для того чтобы сферу можно было вписать
в усеченный конус, необходимо и достаточно,
чтобы образующая усеченного конуса
равнялась сумме радиусов оснований.

Теорема.
Сферу можно вписать в тело вращения,
если в осевое сечение можно вписать
окружность.

Сфера,
описанная около многогранника

или
тела вращения

Сфера
называется описанной
около многогранника,
если все вершины многогранника лежат
на сфере. Многогранник соответственно
называется вписанным
в сферу.

Теоремы:

1. Для
того чтобы сферу можно было описать
около призмы, необходимо и достаточно,
чтобы призма была прямая и около основания
можно было описать окружность.

2. Для
того чтобы сферу можно было описать
около пирамиды, необходимо и достаточно,
чтобы около основания можно было описать
окружность.

3.
Сферу можно описать около любой правильной
пирамиды.

Сфера
называется описанной
около цилиндра,
если окружности оснований цилиндра
лежат на сфере. Цилиндр соответственно
называется вписанным
в сферу.

Теорема.
Сферу можно описать около любого
цилиндра.

Сфера
называется описанной
около конуса,
если окружность основания и вершина
конуса лежат на сфере. Конус соответственно
называется вписанным
в сферу.

Теорема.
Сферу можно описать около любого конуса.

Сфера
называется описанной
около усеченного конуса,
если окружности оснований конуса лежат
на сфере. Усеченный конус соответственно
называется вписанным
в сферу.

Теорема.
Сферу можно описать около любого
усеченного конуса.

Многогранники и тела вращения

Цилиндр
называется описанным
около призмы,
если окружности оснований цилиндра
описаны около оснований призмы, а боковые
ребра призмы являются образующими
цилиндра. Призма соответственно
называется вписанной
в цилиндр.

Теорема.
Для того чтобы около призмы можно было
описать цилиндр, необходимо и достаточно,
чтобы призма была прямая и около ее
основания можно было описать окружность.

Цилиндр
называется вписанным
в призму,
если окружности его оснований вписаны
в основания призмы, а боковая поверхность
касается боковых граней призмы.

Теорема.
Для того чтобы в призму можно было
вписать цилиндр, необходимо и достаточно,
чтобы призма была прямая и в ее основание
можно было вписать окружность.

Конус
называется описанным
около пирамиды,
если окружность основания конуса описана
около основания пирамиды, а боковые
ребра пирамиды являются образующими
конуса. Пирамида соответственно
называется вписанной
в конус.

Теорема.
Для того чтобы около пирамиды можно
было описать конус, необходимо и
достаточно, чтобы боковые ребра пирамиды
были равны.

Конус
называется вписанным
в пирамиду,
если окружность его основания вписана
в основание пирамиды, а боковая поверхность
касается боковых граней пирамиды.
Пирамида соответственно называется
описанной
около конуса.

Теорема.
Для того чтобы в пирамиду можно было
вписать конус, необходимо и достаточно,
чтобы в основание пирамиды можно было
вписать окружность, а вершина пирамиды
ортогонально проектировалась в центр
этой окружности.

Пример 1.
Шар вписан в прямую призму, основанием
которой является прямоугольный
треугольник с катетом a
и противолежащим ему острым углом α.
Найти объем призмы.

Решение. Сделаем
рисунок (рис. 12.48). Шар вписан в прямую
призму, значит, высота призмы равна
диаметру шара, а в треугольник основания
вписана окружность, радиус которой
равен радиусу шара. Рассмотрим
прямоугольный треугольник ABC,
у которого катет BC
= a,
противолежащий ему BAC =
α. Найдем катет AC
и гипотенузу AB:

Рис. 12.48

Площадь треугольника ABC
равна:

Вычислим радиус окружности, вписанной
в треугольник:

Вычисляем объем призмы по
формуле

Получаем ответ:

Пример 2.
Боковое ребро правильной четырехугольной
пирамиды равно a.
Двугранный угол, образованный смежными
боковыми гранями, равен β.
Найти радиус шара, описанного около
этой пирамиды.

Решение.
Сделаем рисунок (рис. 12.49): ABCD
– квадрат, SO
– высота пирамиды, AEC
= 
– двугранный угол.

Рассмотрим диагональное
сечение пирамиды – треугольник SBD
(SB = SD).
Радиусом шара, описанного около данной
пирамиды, будет радиус окружности,
описанной около треугольника SBD.
Найдем его по формуле

Рис. 12.49

Из подобия треугольников
(SOB = SEO
= 90,
BSO = OSE)
следует пропорциональность сторон:
SB/SO
= BO/OE.

Из треугольника
найдемТак какАО = ВО,
то
Следовательно,

Вычисляем радиус окружности:

Получаем ответ:

Пример 3. В
усеченный конус вписан шар радиуса R.
Образующая конуса наклонена к плоскости
основания под углом .
Найти объем усеченного конуса.

Решение.Рассмотрим осевое
сечение конуса (рис. 12.50).

Рис. 12.50

Введем обозначения: R₁
– радиус нижнего основания конуса, R₂
– радиус верхнего основания. Высота
данного усеченного конуса будет равна
диаметру вписанного в него шара 2R.
Рассмотрим прямоугольный треугольник
ABC:
B = 90,
A = ,
BC = 2R.
Найдем катет BA
и гипотенузу AC:
BA = BC  ctg,
Так как в усеченный конус вписан шар,
то образующая этого конуса равна сумме
радиусов его оснований. Получим равенство:

Заметим, что

Решив систему

найдем

Вычисляем объем усеченного конуса по
формуле (12.8).

Получаем ответ:

Пример 4. В
шар радиуса R
вписан конус, образующая которого
составляет с плоскостью основания угол
φ. Найти
площадь полной поверхности конуса.

Решение.
Для вычисления площади полной поверхности
конуса необходимо знать радиус основания
и образующую конуса. Рассмотрим осевое
сечение данного конуса – равнобедренный
треугольник SAB:
SA = SB
– образующие, SD
– высота, DB
– радиус основания конуса (рис. 12.51).

Рис. 12.51

По условию задачи SAD = φ,
следовательно,
ТреугольникAOS
– равнобедренный (AO = OS = R),
поэтому

Внешний угол этого треугольника при
вершине О
равен: AOD = SAO + ASO = 
– 2.

Из
треугольника AOD
(D = 90,
AO = R,
AOD = 
– 2)
выразим AD:

Из треугольника ASD
(D = 90,
AD = Rsin
2)
выразим SA:

Подставив найденные выражения
в формулу для вычисления площади полной
поверхности конуса, получим:

Таким образом,

Пример 5. В
прямой параллелепипед вписан цилиндр,
объем которого в m
раз меньше объема параллелепипеда.
Найти двугранные углы при боковых ребрах
параллелепипеда.

Решение.Двугранными углами при
боковых ребрах данного параллелепипеда
являются углы параллелограмма, лежащего
в его основании. В параллелепипед вписан
цилиндр, значит, в параллелограмм
основания вписана окружность. Если в
четырехугольник вписана окружность,
то суммы длин противолежащих сторон
четырехугольника равны. Таким образом,
основанием параллелепипеда является
ромб. Сделаем рисунок (рис. 12.52).

Рис. 12.52

Обозначим искомый угол .
Из треугольника ABC
(C = 90,
A = )
найдем сторону ромба AB
и его высоту BC:

Так как высоты цилиндра и
параллелепипеда равны, то площадь
основания цилиндра будет в m
раз меньше площади основания
параллелепипеда. Запишем равенство:
и выразим из негодалее

Двугранные
углы при боковых ребрах параллелепипеда
будут равны:

Задания

Соседние файлы в папке Часть 2

Источник

В данной публикации мы рассмотрим, как можно найти радиус вписанного в куб шара (сферы), если известна длина ребра куба или его диагональ.

Примечание: Напомним, что в любой куб можно вписать шар.

Для начала выполним чертеж.

шар касается всех 6 граней куба (на рисунке показаны только 4 точки касания);
центр шара – точка O, которая также является центром куба.

Радиус шара (R), вписанного в куб, равняется половине его ребра, т.е.:

R = a/2, где “a” – ребро куба (является стороной его грани).

Чтобы было понятнее, выполним сечение, параллельное одной из граней куба и проходящее через точки касания шара двух других параллельных друг другу граней. Это сечение, в том числе, проходит через середины соответствующих сторон.

Таким образом, мы получим квадрат со вписанной окружностью, радиус которой равняется половине его стороны, которая в свою очередь равна ребру куба.

Радиус вписанного шара через диагональ куба

Если известна длина диагонали куба (примем ее за “d”), радиус вписанного в него шара (R) можно вычислить так:

Источник