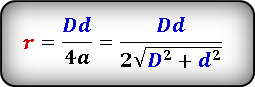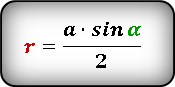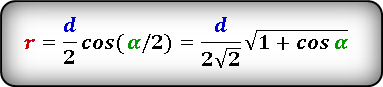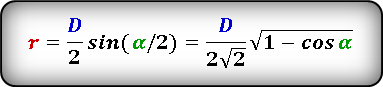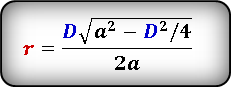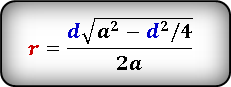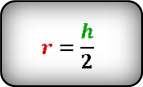Как найти радиус вписанной окружности в параллелограмм

В параллелограмм вписана окружность

Если в условии задачи сказано, что в параллелограмм вписана окружность, то что сразу можно сказать об этом параллелограмме?

Для этого надо вспомнить, когда в четырехугольник можно вписать окружность. Это можно сделать лишь в том случае, если суммы противолежащих сторон четырехугольника равны.

Это условие выполняется только для тех параллелограммов, у которых все стороны равны, то есть только для ромба (и квадрата, как частного случая ромба).

Следовательно, если известно, что в параллелограмм можно вписать окружность, сразу можно сделать вывод, что все его стороны равны, и для него справедливы все свойства ромба. Если же дополнительно сказано, что хотя бы один из углов этого параллелограмма прямой, то такой параллелограмм — квадрат.

Радиус вписанной в ромб окружности можно найти по формуле

где S — площадь ромба, p — его полупериметр;

или как половину высоты ромба

1) В параллелограмм вписана окружность. Найти периметр параллелограмма, если одна из его сторон равна 10 см.

Из всех параллелограммов вписать окружность можно только в ромб (и квадрат). У ромба все стороны равны.

2) В параллелограмм вписана окружность. Найти её радиус, если высота параллелограмма равна 12 см.

Из параллелограммов вписать окружность можно в ромб (и квадрат). Радиус вписанной в ромб (и квадрат) окружности равен половине его высоты:

3) В параллелограмм вписана окружность. Найти её радиус, если диагонали параллелограмма равны 6 см и 8 см.

Из всех параллелограммов окружность можно вписать в ромб (и квадрат. У квадрата диагонали равны, следовательно, в задаче речь идёт о ромбе).

Пусть ABCD — ромб, AC=6 см, BD=8 см.

Рассмотрим треугольник AOB.

По теореме Пифагора

полупериметр — p=2a=2∙AB=25=10 см.

Следовательно, радиус вписанной окружности равен

Все формулы для радиуса вписанной окружности

Радиус вписанной окружности в треугольник

a , b , c — стороны треугольника

p — полупериметр, p=( a + b + c )/2

Формула радиуса вписанной окружности в треугольник ( r ):

Радиус вписанной окружности в равносторонний треугольник

a — сторона треугольника

r — радиус вписанной окружности

Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):

Радиус вписанной окружности равнобедренный треугольник

1. Формулы радиуса вписанной окружности если известны: стороны и угол

a — равные стороны равнобедренного треугольника

b — сторона ( основание)

α — угол при основании

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :

2. Формулы радиуса вписанной окружности если известны: сторона и высота

a — равные стороны равнобедренного треугольника

b — сторона ( основание)

h — высота

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :

Вписанная окружность

Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.

Окружность, точно можно вписать в такие геометрические фигуры, как:

  • Треугольник
  • Выпуклый, правильный многоугольник
  • Квадрат
  • Равнобедренная трапеция
  • Ромб

В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.

Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.

Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.

Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.

Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.

Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.

Свойства вписанной окружности

В треугольник

  1. В любой треугольник может быть вписана окружность, причем только один раз.
  2. Центр вписанной окружности — точка пересечения биссектрис треугольника.
  3. Вписанная окружность касается всех сторон треугольника.
  4. Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac<1><2>(a+b+c) cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

  • Центр окружности вписанной в треугольник равноудален от всех сторон.
  • Точка касания — это точка, в которой соприкасается
    окружность и любая из сторон треугольника.
  • От центра вписанной окружности можно провести
    перпендикуляры к любой точке касания.
  • Вписанная в треугольник окружность делит стороны
    треугольника на 3 пары равных отрезков.
  • Вписанная и описанная около треугольника окружность тесно взаимосвязаны.
    Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:

    с — расстояние между центрами вписанной и описанной окружностей треугольника.
    R — радиус описанной около треугольника.
    r — радиус вписанной окружности треугольника.

    В четырехугольник

    1. Не во всякий четырехугольник можно вписать окружность.
    2. Если у четырехугольника суммы длин его противолежащих
      сторон равны, то окружность, может быть, вписана (Теорема Пито).
    3. Центр вписанной окружности и середины двух
      диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона).
    4. Точка пересечения биссектрис — это центр вписанной окружности.
    5. Точка касания — это точка, в которой соприкасается
      окружность и любая из сторон четырехугольника.
    6. Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:

    [ S = frac<1><2>(a+b+c+d)cdot r = pr ]

    p — полупериметр четырехугольника.
    r — радиус вписанной окружности четырехугольника.

  • Точка касания вписанной окружности, которая лежит на любой из сторон,
    равноудалены от этой конца и начала этой стороны, то есть от его вершин.

    • Примеры вписанной окружности

    Примеры описанного четырехугольника:
    равнобедренная трапеция, ромб, квадрат.

    Примеры описанного треугольника:
    равносторонний    , равнобедренный,
    прямоугольный треугольники.

    Верные и неверные утверждения

    1. Радиус вписанной окружности в треугольник и радиус вписанной
      в четырехугольник вычисляется по одной и той же формуле. Верное утверждение.
    2. Любой параллелограмм можно вписать в окружность. Неверное утверждение.
    3. В любой четырехугольник можно вписать окружность. Неверное утверждение.
    4. В любой ромб можно вписать окружность. Верное утверждение.
    5. Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
    6. Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
    7. Угол вписанный в окружность равен соответствующему центральному
      углу опирающемуся на ту же дугу. Неверное утверждение.
    8. Радиус вписанной окружности в прямоугольный треугольник равен
      половине разности суммы катетов и гипотенузы. Верное утверждение.
    9. Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
    10. Вписанная окружность в треугольник имеет в общем
      три общие точки со всеми сторонами треугольника. Верное утверждение.

    Окружность вписанная в угол

    Окружность вписанная в угол — это окружность, которая
    лежит внутри этого угла и касается его сторон.

    Центр окружности, которая вписана в угол,
    расположен на биссектрисе этого угла.

    К центру окружности вписанной в угол, можно провести,
    в общей сложности два перпендикуляра со смежных сторон.

    Длина диаметра, радиуса, хорды, дуги вписанной окружности
    измеряется в км, м, см, мм и других единицах измерения.

    источники:

    http://www-formula.ru/2011-09-24-00-40-48

    http://colibrus.ru/vpisannaya-okruzhnost/

    Источник

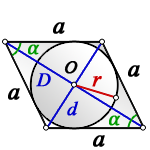
    1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол

    Радиус вписанной окружности в ромб

    a — сторона ромба

    D — большая диагональ

    d — меньшая диагональ

    α — острый угол

    О — центр вписанной окружности

    r — радиус вписанной окружности

    Формула радиуса вписанной окружности в ромб через диагонали ( r ) :

    Формула 1 радиуса вписанной окружности в ромб

    Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :

    Формула 2 радиуса вписанной окружности в ромб

    Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :

    Формула 3 радиуса вписанной окружности в ромб

    Формула 4 радиуса вписанной окружности в ромб

    Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :

    Формула 5 радиуса вписанной окружности в ромб

    Формула 6 радиуса вписанной окружности в ромб

    2. Радиус вписанной окружности ромба, равен половине его высоты

    Радиус вписанной окружности в ромб

    a — сторона ромба

    h — высота

    О — центр вписанной окружности

    r — радиус вписанной окружности

    Формула радиуса вписанной окружности в ромб ( r ) :

    Формула 7 радиуса вписанной окружности в ромб

    Источник

    Можно ли вписать окружность в параллелограмм и наоборот

    Содержание:

    • Параллелограмм, вписанный в окружность

      • Свойство радиуса окружности, описанной около прямоугольника
      • Пример решения задачи. Параллелограмм и описанная окружность
    • Параллелограмм, описанный около окружности

      • Радиус окружности, вписанной в ромб
      • Задачи. Параллелограмм и вписанная окружность.

    Параллелограмм, вписанный в окружность

    Параллелограмм — это четырехугольник с попарно параллельными и равными противолежащими сторонами.

    Все четыре стороны этой фигуры принадлежат одной плоскости.

    параллелограмм

    Четырехугольник можно вписать в окружность, если сумма его противоположных углов равна 180°. Если сумма противоположных углов параллелограмма равна 180°, то такой параллелограмм — прямоугольник.

    Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

    вписанный параллелограмм

    Точка пересечения диагоналей прямоугольника является центром описанной окружности.

    вписанный параллелограмм центр окружности

    Свойство радиуса окружности, описанной около прямоугольника

    Радиус описанной окружности равен половине диагонали прямоугольника.

    Пример решения задачи. Параллелограмм и описанная окружность

    Задача 1

    Дано: прямоугольник со сторонами 8 см и 6 см.

    Найти: радиус описанной окружности.

    Решение: диагональ прямоугольника равна (sqrt{8^2+6^2}=10 (см)); следовательно, радиус описанной окружности равен 10÷2=5 (см).

    Ответ: 5 см.

    Параллелограмм, описанный около окружности

    Когда параллелограмм можно описать около окружности? Другими словами — при каком условии можно вписать окружность или круг в параллелограмм?

    Так как параллелограмм — это частный случай четырехугольника, будет действовать то же правило, что и для любого другого четырехугольника. Окружность можно вписать в параллелограмм, только если суммы его противоположных сторон равны.

    Это условие выполняется только для тех параллелограммов, у которых все стороны равны, то есть только для ромба (и квадрата, как частного случая ромба).

    Если в задаче дано, что в параллелограмм вписана окружность, то из этого условия можно сделать вывод, что все его стороны равны, и данный параллелограмм является ромбом. Если по условию один из углов этого параллелограмма прямой, то такой параллелограмм — квадрат.

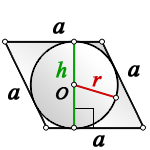
    Радиус окружности, вписанной в ромб

    Радиус вписанной в ромб окружности можно найти несколькими способами.

    окружность вписана в ромб

    Если известны диагонали и сторона

    Формула 1

    (r=frac{Dd}{4a}), где:

    • r — радиус вписанной окружности;
    • а — сторона ромба;
    • D — большая диагональ;
    • d — меньшая диагональ.

    Если известны диагонали

    Формула 2

    (r=frac{Dd}{2sqrt{D^2+d^2}}), где:

    • r — радиус вписанной окружности;
    • D — большая диагональ;
    • d — меньшая диагональ.

    Если известны сторона и угол

    Формула 3

    (r=frac{a·sinalpha}2), где:

    • r — радиус вписанной окружности;
    • а — сторона ромба;
    • α — острый угол.

    Если известны диагонали и угол

    Формула 4

    (r=frac d2cosalpha/2=frac d{2sqrt2}sqrt{1+cosalpha})

    Формула 5

    (r=frac D2sin;alpha/2=frac D{2sqrt2}sqrt{1-cosalpha}), где:

    • r — радиус вписанной окружности;
    • D — большая диагональ;
    • d — меньшая диагональ;
    • α — острый угол.

    Если известны диагонали и сторона

    Формула 6

    (r=frac{Dsqrt{a^2-D^2/4}}{2a})

    Формула 7

    (r=frac{dsqrt{a^2-d^2/4}}{2a}), где:

    • r — радиус вписанной окружности;
    • D — большая диагональ;
    • d — меньшая диагональ;
    • а — сторона ромба.

    Если известна высота ромба

    Формула 8

    (r=frac h2), где:

    • r — радиус вписанной окружности;
    • h — высота ромба.

    Если известны площадь и полупериметр

    Формула 9

    (r=frac Sp), где:

    • r — радиус вписанной окружности;
    • S — площадь ромба;
    • p — полупериметр ромба.

    Задачи. Параллелограмм и вписанная окружность.

    Задача 2

    Дано: параллелограмм со вписанной окружностью. Одна из сторон параллелограмма равна 5 см.

    Найти: периметр параллелограмма.

    Решение: в параллелограмм можно вписать окружность только если это ромб. Четыре стороны ромба равны. Следовательно, периметр данного параллелограмма равен 5·4=20 (см).

    Ответ: 20 см.

    Задача 3

    Дано: параллелограмм MNKP с диагоналями 12 см и 16 см. В MNKP вписана окружность.

    Найти: радиус вписанной окружности.

    Решение:

    задача параллелограмм

    Из того, что в параллелограмм MNKP вписана окружность, делаем вывод, что MNKP — ромб.

    Параллелограмм MNKP не является квадратом, так как его диагонали не равны. MK=16 см, NP=12 см.

    ΔMOP прямоугольный, (∠MOP=90°. MO=8 см, OP=6 см. S_{MОР}=(8·6)÷2=24 (см^2)).

    (S_{MNKP}=24·4=96 (см^2)).

    По теореме Пифагора ( MP=sqrt{MО^2+ОР^2}=sqrt{8^2+6^2}=10 (см)).

    Полупериметр MNKP равен 20 см.

    Следовательно, радиус вписанной окружности равен

     (r=frac Sp=96÷10=9,6 (см)).

    Ответ: 9,6 см.

    Насколько полезной была для вас статья?

    У этой статьи пока нет оценок.

    Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

    Текст с ошибкой:

    Расскажите, что не так

    Поиск по содержимому

    Источник

    Если в условии задачи сказано, что в параллелограмм вписана окружность, то что сразу можно сказать об этом параллелограмме?

    Для этого надо вспомнить, когда в четырехугольник можно вписать окружность. Это можно сделать лишь в том случае, если суммы противолежащих сторон четырехугольника равны.

    Это условие выполняется только для  тех параллелограммов, у которых все стороны равны, то есть только для ромба (и квадрата, как частного случая ромба).

    Следовательно, если известно, что в параллелограмм можно вписать окружность, сразу можно сделать вывод, что все его стороны равны, и для него справедливы все свойства ромба. Если же дополнительно сказано, что хотя бы один из углов этого параллелограмма прямой, то такой параллелограмм — квадрат.

    Радиус вписанной в ромб окружности можно найти по формуле

        [r = frac{S}{p},]

    где S — площадь ромба, p — его полупериметр;

    или как половину высоты ромба

        [r = frac{1}{2}h]

    Задачи.

    1) В параллелограмм вписана окружность. Найти периметр параллелограмма, если одна из его сторон равна 10 см.

    Решение:

    Из всех параллелограммов вписать окружность можно только в ромб (и квадрат). У ромба все стороны равны.

    Периметр ромба

        [P = 4a = 4 cdot 10 = 40(cm).]

    Ответ: 40 см.

    2) В параллелограмм вписана окружность. Найти её радиус, если высота параллелограмма равна 12 см.

    Решение:

    Из параллелограммов вписать окружность можно в ромб (и квадрат). Радиус вписанной в ромб (и квадрат) окружности равен половине его высоты:

        [r = frac{1}{2}h = frac{1}{2} cdot 12 = 6cm.]

    Ответ: 6 см.

    3) В параллелограмм вписана окружность. Найти её радиус, если диагонали параллелограмма равны 6 см и 8 см.

    Решение:

    v-parallelogramm-vpisana-okruzhnostИз всех параллелограммов окружность можно вписать в ромб (и квадрат. У квадрата диагонали равны, следовательно, в задаче речь идёт о ромбе).

    Пусть ABCD — ромб, AC=6 см, BD=8 см.

    Рассмотрим треугольник AOB.

    По свойствам ромба, ∠AOB=90,

        [AO = frac{1}{2}AC = 3cm,]

        [BO = frac{1}{2}BD = 4cm.]

    По теореме Пифагора 

        [AB = sqrt {A{O^2} + B{O^2}} ]

        [AB = sqrt {{3^2} + {4^2}} = sqrt {25} = 5cm.]

    Площадь ромба равна

        [S = frac{1}{2}{d_1} cdot {d_2}]

        [{S_{ABCD}} = frac{1}{2}AC cdot BD = frac{1}{2} cdot 6 cdot 8 = 24c{m^2}]

    полупериметр — p=2a=2∙AB=25=10 см.

    Следовательно, радиус вписанной окружности равен

        [r = frac{S}{p} = frac{{24}}{{10}} = 2,4cm.]

    Ответ: 2,4 см.

    Источник

    Вписанная окружность — это окружность, которая вписана
    в геометрическую фигуру и касается всех его сторон.

    Окружность, точно можно вписать в такие геометрические фигуры, как:

    • Треугольник
    • Выпуклый, правильный многоугольник
    • Квадрат
    • Равнобедренная трапеция
    • Ромб

    В четырехугольник, можно вписать окружность,
    только при условии, что суммы длин
    противоположных сторон равны.

    Во все вышеперечисленные фигуры
    окружность, может быть вписана, только один раз.

    Окружность невозможно вписать в прямоугольник
    и параллелограмм, так как окружность не будет
    соприкасаться со всеми сторонам этих фигур.

    Геометрические фигуры, в которые вписана окружность,
    называются описанными около окружности.

    Описанный треугольник — это треугольник, который описан
    около окружности и все три его стороны соприкасаются с окружностью.

    Описанный четырехугольник — это четырехугольник, который описан
    около окружности и все четыре его стороны соприкасаются с окружностью.

    Содержание

    1. Свойства вписанной окружности
    2. В треугольник
    3. В четырехугольник
    4. Примеры вписанной окружности
    5. Верные и неверные утверждения
    6. Окружность вписанная в угол

    Свойства вписанной окружности

    В треугольник

    1.  В любой треугольник может быть вписана окружность, причем только один раз.
    2.  Центр вписанной окружности — точка пересечения биссектрис треугольника.
    3.  Вписанная окружность касается всех сторон треугольника.
    4.  Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:

      [ S = frac{1}{2}(a+b+c) cdot r = pr ]

      p —  полупериметр четырехугольника.
      r — радиус вписанной окружности четырехугольника.

    5.  Центр окружности вписанной в треугольник равноудален от всех сторон.
    6.  Точка касания — это точка, в которой соприкасается
      окружность и любая из сторон треугольника.
    7.  От центра вписанной окружности можно провести
      перпендикуляры к любой точке касания.
    8.  Вписанная в треугольник окружность делит стороны
      треугольника на 3 пары равных отрезков.
    9.  Вписанная и описанная около треугольника окружность тесно взаимосвязаны.
      Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:

      [ с = sqrt{R^2 — 2Rr} ]

      с — расстояние между центрами вписанной и описанной окружностей треугольника.
      R — радиус описанной около треугольника.
      r — радиус вписанной окружности треугольника.

    В четырехугольник

    1. Не во всякий четырехугольник можно вписать окружность.
    2. Если у четырехугольника суммы длин его противолежащих
      сторон равны, то окружность, может быть, вписана (Теорема Пито).
    3. Центр вписанной окружности и середины двух
      диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона).
    4. Точка пересечения биссектрис — это центр вписанной окружности.
    5. Точка касания — это точка, в которой соприкасается
      окружность и любая из сторон четырехугольника.
    6. Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:

      [ S = frac{1}{2}(a+b+c+d)cdot r = pr ]

      p —  полупериметр четырехугольника.
      r — радиус вписанной окружности четырехугольника.

    7. Точка касания вписанной окружности, которая лежит на любой из сторон,
      равноудалены от этой конца и начала этой стороны, то есть от его вершин.

    Примеры вписанной окружности

    Примеры описанного четырехугольника:
    равнобедренная трапеция, ромб, квадрат.

    Примеры описанного треугольника:
    равносторонний    , равнобедренный,
    прямоугольный треугольники.

    Верные и неверные утверждения

    1. Радиус вписанной окружности в треугольник и радиус вписанной
      в четырехугольник вычисляется по одной и той же формуле. Верное утверждение.
    2. Любой параллелограмм можно вписать в окружность. Неверное утверждение.
    3. В любой четырехугольник можно вписать окружность. Неверное утверждение.
    4. В любой ромб можно вписать окружность. Верное утверждение.
    5. Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
    6. Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
    7. Угол вписанный в окружность равен соответствующему центральному
      углу опирающемуся на ту же дугу. Неверное утверждение.
    8. Радиус вписанной окружности в прямоугольный треугольник равен
      половине разности суммы катетов и гипотенузы. Верное утверждение.
    9. Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
    10. Вписанная окружность в треугольник имеет в общем
      три общие точки со всеми сторонами треугольника. Верное утверждение.

    Окружность вписанная в угол

    Окружность вписанная в угол — это окружность, которая
    лежит внутри этого угла и касается его сторон.

    Центр окружности, которая вписана в угол,
    расположен на биссектрисе этого угла.

    К центру окружности вписанной в угол, можно провести,
    в общей сложности два перпендикуляра со смежных сторон.

    Центральный угол вписанной окружности – это угол, вершина
    которого лежит в центре вписанной окружности.

    Вписанный угол вписанной окружности – это угол,
    вершина которого лежит на вписанной окружности.

    Длина диаметра, радиуса, хорды, дуги вписанной окружности
    измеряется в км, м, см, мм и других единицах измерения.

    Так-же читайте статью про треугольник вписанный в окружность.

    Источник

    Понравилась статья? Поделить с друзьями:
  • Как найти свою очередь на землю
  • Как найти ссылку на контакт в телеграмме
  • Ошибка 0x80240035 как исправить
  • Ошибка при запуске приложения 0xc000012d windows 10 как исправить ошибку
  • Как найти рекламу на ютубе которую смотрел