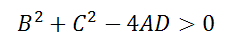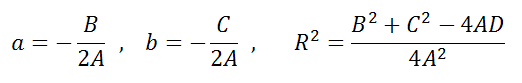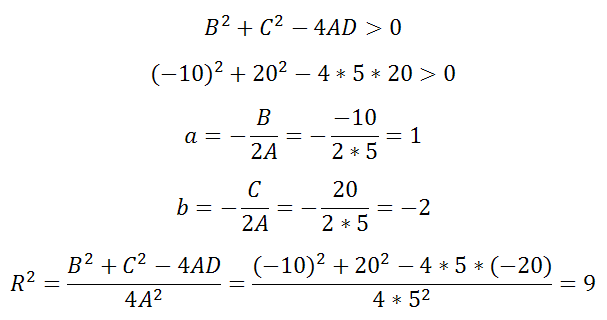Как найти радиус зная координаты диаметра - Исправление недочетов и поиск решений вместе с Examum.ru

Найти центр и радиус окружности

Если окружность задана уравнением вида

найти центр (a;b) и радиус R такой окружности несложно.

Определить по уравнению окружности координаты её центра и радиуса:

Таким образом, центр данной окружности — точка (3;7), радиус R=2.

a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.

Центр окружности — (0;-3), радиус R=3.

Центр — в точке (6;0), радиус R=√5.

Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.

Чтобы найти центр и радиус окружности, заданной уравнением вида

нужно дополнить его до полных квадратов, чтобы привести к привычному виду.

Для этого сначала сгруппируем слагаемые

затем прибавим и вычтем квадрат второго слагаемого из формулы квадрата разности (2ax- удвоенное произведение первого слагаемого на второе. Первое — x, второе — a)

При a²+b²-c>0 это уравнение задаёт окружность с радиусом

При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).

При a²+b²-c

Выделяем в уравнении полные квадраты. В первых скобках удвоенное слагаемое 10x представляем как 10x=2·a·5 (чтобы получить 2ab для формулы a²+2ab+b²=(a+b)²). Получается, что b=5. Если прибавить и вычесть b², результат не изменится:

Центром этой окружности является точка (-5;3), радиус R=7.

Центр окружности — точка (2,5;0), радиус R=1,5.

Как найти радиус окружности по координатам

Окружность на координатной плоскости

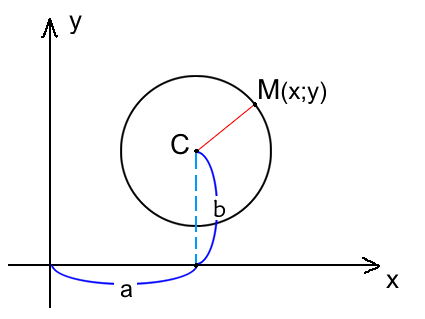
Окружность на плоскости — это множество точек на плоскости равноудаленных от точки центра. На рисунке данная точка обозначена C.

Окружность радиуса R с центром в начале координат представляется уравнением:

Окружность радиуса R с центром в точке C(a;b) представляется уравнением:

Расстояние от центра окружности С(a;b) до точки M(x;y) называется радиусом окружности R (на рисунке красная линия ).
Это уравнение можно записать в виде:

Если уравнение помножить на любое число A, то получим

Примечание
Окружность относится к линии второго порядка, так как представляется уравнением второй степени.

Необходимые условия для этого:
1. Отсутствие в уравнение второй степени члена с произведением xy;
2. Коэффициенты при x 2 и y 2 были равны в уравнение вида:

3. Если выполняется неравенство

Как найти радиус и центр окружности

Уравнение Ax 2 +Bx+Ay 2 +Cy+D=0 если оно удовлетворяет примечаниям (1, 2 и 3), то тогда (a;b) и радиус R окружности можно найти по формулам:

Пример 1
Уравнение 5x 2 -10x+5y 2 +20y-20=0
Здесь
A=5, B=-10, C=20, D=-20
Оно удовлетворяет примечаниям 1, 2 и выполняется неравенство

Решая, получаем что центр есть (1;-2), а радиус R=3

Анимационный график окружности

Пример 2
Уравнение второй степени x 2 +4xy+y 2 =1 не является окружностью, так как в нём есть член 4xy.

Пример 3
Уравнение второй степени 4x 2 +9y 2 =36 не представляет окружность, так как в нём коэффициенты при x 2 и y 2 не равны.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.3 / 5. Количество оценок: 4

Найти центр и радиус окружности

Если окружность задана уравнением вида

найти центр (a;b) и радиус R такой окружности несложно.

Определить по уравнению окружности координаты её центра и радиуса:

Таким образом, центр данной окружности — точка (3;7), радиус R=2.

a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.

Центр окружности — (0;-3), радиус R=3.

Центр — в точке (6;0), радиус R=√5.

Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.

Чтобы найти центр и радиус окружности, заданной уравнением вида

нужно дополнить его до полных квадратов, чтобы привести к привычному виду.

Для этого сначала сгруппируем слагаемые

При a²+b²-c>0 это уравнение задаёт окружность с радиусом

При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).

При a²+b²-c

Центром этой окружности является точка (-5;3), радиус R=7.

Центр окружности — точка (2,5;0), радиус R=1,5.

Нахождение центра и радиуса окружности по общему уравнению окружности

Этот калькулятор проверяет, является ли введенное уравнение общим уравнением окружности, и вычисляет координаты центра и радиуса окружности, если это возможно. Описание способа решения подобных задач находится под калькулятором

Нахождение центра и радиуса окружности по общему уравнению окружности

Уравнение НЕ является общим уравнением окружности

Приведение общего уравнения окружности к стандартному виду

Калькулятор выше можно применять для решения задач на уравнение окружности. Чаще всего вы имеете дело с уравнением окружности, выраженном в так называемом стандартном виде

Из этого уравнения достаточно легко найти центр окружности — это будет точка с координатами (a,b), и радиус окружности — это будет квадратный корень из правой части уравнения.

Однако, если возвести в квадрат выражения в скобках и перенести правую часть налево, то уравнение станет выглядеть примерно так:

Это — уравнение окружности в общем виде. Здесь радиус и центр окружности уже не выделены явно, и в задачах обычно просят их найти именно по общему виду уравнения окружности.

Способ решения такого рода задач следующий:

Перегруппируем слагаемые уравнения

Для каждой скобки применим метод выделения полного квадрата (подробнее смотри тут — Метод выделения полного квадрата), то есть заменим выражение вида на выражение вида . С учетом того, что коэффициенты при квадратах равны единице, а свободный член можно принять за ноль, формула для вычисления h и k упрощаются.

Как видим, выражение в конце это уравнение окружности в стандартном виде, из которого уже легко получить и координаты центра окружности и ее радиус. Если же справа получилось отрицательное число — значит заданное вначале уравнение не является уравнением окружности (бывают задачи и на такую проверку). Калькулятор тоже проверяет это условие.

Для решения обратной задачи — нахождения общего уравнения окружности по координатам центра и радиусу — можно использовать калькулятор Уравнение окружности по заданному центру и радиусу в различных формах

Окружность на координатной плоскости

Окружность радиуса R с центром в начале координат представляется уравнением:

Окружность радиуса R с центром в точке C(a;b) представляется уравнением:

Если уравнение помножить на любое число A, то получим

Примечание
Окружность относится к линии второго порядка, так как представляется уравнением второй степени.

3. Если выполняется неравенство

Как найти радиус и центр окружности

Решая, получаем что центр есть (1;-2), а радиус R=3

Анимационный график окружности

Пример 2
Уравнение второй степени x 2 +4xy+y 2 =1 не является окружностью, так как в нём есть член 4xy.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.3 / 5. Количество оценок: 4

источники:

http://b4.cooksy.ru/articles/kak-nayti-radius-okruzhnosti-po-koordinatam

Окружность на координатной плоскости

Источник

Нахождение центра и радиуса окружности по общему уравнению окружности

Коэффициенты a, b, c, d, e уравнения

Введите коэффициенты a, b, c, d, e в указанном порядке ax² + by² + cx + dy + e = 0

Точность вычисления

Знаков после запятой: 2

Уравнение после выделения полного квадрата

Уравнение НЕ является общим уравнением окружности

Приведение общего уравнения окружности к стандартному виду

Калькулятор выше можно применять для решения задач на уравнение окружности. Чаще всего вы имеете дело с уравнением окружности, выраженном в так называемом стандартном виде

Из этого уравнения достаточно легко найти центр окружности — это будет точка с координатами (a,b), и радиус окружности — это будет квадратный корень из правой части уравнения.

Однако, если возвести в квадрат выражения в скобках и перенести правую часть налево, то уравнение станет выглядеть примерно так:

Это — уравнение окружности в общем виде. Здесь радиус и центр окружности уже не выделены явно, и в задачах обычно просят их найти именно по общему виду уравнения окружности.

Способ решения такого рода задач следующий:

Перегруппируем слагаемые уравнения
Для каждой скобки применим метод выделения полного квадрата (подробнее смотри тут — Метод выделения полного квадрата), то есть заменим выражение вида на выражение вида . С учетом того, что коэффициенты при квадратах равны единице, а свободный член можно принять за ноль, формула для вычисления h и k упрощаются.

Для x^2+cx :
$h_x=-frac{c}{2}\k_x=-frac{c^2}{4}$

Для y^2+dy :
$h_y=-frac{d}{2}\k_y=-frac{d^2}{4}$

Тогда
$(x^2+cx) + (y^2+dy)+e=0 \ to (x-h_x)^2+k_x + (y-h_y)^2+k_y + e=0 \ to (x-h_x)^2 + (y-h_y)^2=-e - k_x - k_y$

Источник

Как найти радиус круга

2 методика:Вычисление радиуса по основным величинамВычисление радиуса по трем точкам на окружности

Радиус круга — отрезок, соединяющий центр круга с любой точкой на его окружности. Значение радиуса используется для вычисления длины окружности, площади круга, диаметра окружности, а также при нахождении объема трехмерных фигур, например, объема цилиндра. Радиус круга равен d/2, где d – диаметр круга; C/2π, где C – длина окружности; √(A/π), где A – площадь круга.

Шаги

Метод 1 из 2: Вычисление радиуса по основным величинам

Определение основных величин

1
Радиус можно найти по известным значениям основных величин круга/окружности. К таким величинам относятся:
- Длина окружности (C).
- Диаметр (D) (отрезок, соединяющей две точки на окружности и проходящий через центр круга).
- Радиус (R) (отрезок, соединяющий центр круга с любой точкой на окружности).
- Площадь (A) (пространство, ограниченное окружностью).
- Число Пи (π) (математическая постоянная, представляющая отношение длины окружности к ее диаметру; это число применяется при вычислении всех основных величин круга и обычно округляется до 3,14).
2
Ниже приведены формулы для вычисления диаметра, длины окружности и площади круга; каждая из них включает радиус. Запомните: обособив радиус на одной стороне формулы, вы сможете найти его по известным значениям основных величин круга/окружности.
- D = 2r. Диаметр вдвое больше радиуса.
- С = πD = 2πr. Длина окружности равна произведению π на ее диаметр. Так как диаметр в два раза больше радиуса, то длина окружности равна произведению π на двойку и на радиус этой окружности.
- A = πr^2. Площадь круга равна произведению квадрата его радиуса на π.

Вычисление радиуса по формулам

1
Если вам дан диаметр, разделите его пополам (на 2) и получите радиус. Так как D = 2r, то r =D/2.
- Например, если диаметр круга равен 10 м, то радиус круга равен 10/2 = 5 м.
2
Если вам дана длина окружности, разделите ее на 2π и получите радиус. Так как C = 2πr, то r = C/2π.
- Например, если длина окружности равна 10 см, то сначала разделите это значение на π: 10/π = 3,14 см. Теперь разделите полученное значение на 2, чтобы вычислить радиус: 3,14/2 = 1,59 см.
3
Если вам дана площадь круга, разделите ее на π и из полученного значения извлеките квадратный корень, чтобы найти радиус. Так как А = πr2, то r = √(A/π).
- Например, площадь круга равна 10 м2. Сначала разделите это значение на π: 10/π = 3,14. Теперь из полученного значения извлеките квадратный корень, чтобы найти радиус: √3,14 = 1,78 м.

Метод 2 из 2: Вычисление радиуса по трем точкам на окружности

1
Если вам не даны значения диаметра, длины окружности или площади круга, вы можете вычислить радиус круга по координатам трех точек на окружности (назовем их P1, P2 и P3). Это делается при помощи одной из двух формул, приведенных ниже.
- Формулы для нахождения радиуса круга по трем точкам, лежащем на окружности:
  - (abc)/(√(a + b + c)(b + c — a)(c + a — b)(a + b — c)), где a, b, c – стороны треугольника с вершинами в точках P1, P2, P3.[1]
  - a/(2sin(θ)), где a –сторона треугольника с вершинами в точках P1, P2, P3; θ – противолежащий угол.
- Во второй формуле вам нужно знать только координаты двух точек и угол; если угол не дан, вам понадобятся координаты всех трех точек.
2
Найдите расстояние между каждыми двумя точками, чтобы определить значения сторон треугольника. Для этого подставьте известные вам координаты в формулу: Расстояние = √((x2 — x1)2 + (y2 — y1)2), где x1,y1 — координаты первой точки; x2,y2 — координаты второй точки.
- Пример. На окружности круга лежат точки с координатами (3,0), (3,8) и (-1, 4). Найдите расстояние между точками (3,8) и (-1,4) по следующей формуле (то есть вы находите сторону треугольника):
  - √((x2 — x1)2 + (y2 — y1)2)
  - √((-1 — 3)2 + (4 — 8)2)
  - √((-4)2 + (-4)2)
  - √(16 + 16) = √(32) = 5,66
3
Найдите расстояние между двумя другими парами точек (то есть найдите две другие стороны треугольника) при помощи процесса, описанного в предыдущем шаге. Подставьте известные вам координаты в ту же формулу: Расстояние = √((x2 — x1)2 + (y2 — y1)2).
- В нашем примере вам необходимо найти расстояние между точками (3,0) и (3,8) и между точками (3,0) и (-1, 4). В первой паре меняется только координата «у», поэтому расстояние равно 8. Расстояние между второй парой точек вычислите следующим образом:
  - √((x2 — x1)2 + (y2 — y1)2)
  - √((-1 — 3)2 + (4 — 0)2)
  - √((-4)2 + (4)2)
  - √(16 + 16) = √(32) = 5,66. Таким образом, стороны треугольника равны 5,66; 8; 5,66.
4
Воспользуйтесь формулой (abc)/(√(a + b + c)(b + c — a)(c + a — b)(a + b — c)) для вычисления радиуса круга (a, b, c – стороны треугольника). Для этого подставьте в эту формулу найденные вами стороны треугольника.
- В нашем примере а = 5,66; b = 8; с = 5,66.
  - (abc)/(√(a + b + c)(b + c — a)(c + a — b)(a + b — c))
  - ((5,66)(8)(5,66))/(√(5,66 + 8 + 5,66)(8 + 5,66 – 5,66)(5,66 + 5,66 — 8)(5,66 + 8 – 5,66))
  - (256,28)/(√(19,32)(8)(3,32)(8))
  - (256,28)/(√(4105,11))
  - (256,28)/(64,07) = 4. Радиус нашего круга равен 4. Этот ответ верный, потому что сторона треугольника, равная 8, проходит через центр круга, то есть это его диаметр. Так как радиус равен половине диаметра, то 8/2 = 4.
5
Теперь найдем угол, противолежащий найденной стороне треугольника, по формуле (теорема косинусов): c2 = a2 + b2 — 2abCos(θ), где a, b, c – стороны треугольника, θ — угол между сторонами а и b, противолежащий стороне с. Найдя противолежащий угол, вы можете вычислить радиус по формуле: a/(2sin(θ))).
- В нашем примере а = 5,66; b = 8; с = 5,66. Найдем угол, противолежащий первой стороне.
  - c2 = a2 + b2 — 2abCos(θ)
  - 5,662 = 5,662 + 82 — 2(5,66)(8)Cos(θ)
  - 32,04 = 32,04 + 64 – 90,56Cos(θ)
  - -64 = — 90,56Cos(θ)
  - 0.707 = Cos(θ)
  - θ = 45o (для нахождения угла необходимо вычислить arcos).
6
Подставьте известные вам значения стороны треугольника и противолежащего угла в формулу а/(2sin(θ)), чтобы найти радиус круга. Эта формула выведена из теоремы синусов, которая гласит, что отношение стороны треугольника к ее противолежащему углу равно удвоенному радиусу (или диаметру) окружности, описанной вокруг треугольника, то есть а/sin(θ) = 2r.[2]
- В нашем примере сторона равна 5,66, а противолежащий угол равен 45o. Подставьте эти значения в формулу.
  - a/(2sin(θ))
  - 5,66/(2sin(45o))
  - 5,66/ 2(0,707)
  - 5,66/1,414 = 4. Обратите внимание, что вы получили такое же значение радиуса, как и при использовании формулы ((abc)/(√(a + b + c)(b + c — a)(c + a — b)(a + b — c))).

Советы

Пользуйтесь калькулятором для проверки ответа.
Для получения более точных результатов на калькуляторе используйте клавишу π.

Источник

Если окружность задана уравнением вида

$[{(x - a)^2} + {(y - b)^2} = {R^2},]$

найти центр (a;b) и радиус R такой окружности несложно.

Примеры.

Определить по уравнению окружности координаты её центра и радиуса:

$[1){(x - 3)^2} + {(y - 7)^2} = 4;]$

$[2){(x + 2)^2} + {(y - 5)^2} = 1;]$

$[3){x^2} + {(y + 3)^2} = 9;]$

$[4){(x - 6)^2} + {y^2} = 5;]$

$[5){x^2} + {y^2} = 11.]$

Решение:

$[1){(x - 3)^2} + {(y - 7)^2} = 4;]$

a=3, b=7, R²=4.

Таким образом, центр данной окружности — точка (3;7), радиус R=2.

$[2){(x + 2)^2} + {(y - 5)^2} = 1;]$

a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.

$[3){x^2} + {(y + 3)^2} = 9;]$

a=0, b=-3, R²=9.

Центр окружности — (0;-3), радиус R=3.

$[4){(x - 6)^2} + {y^2} = 5;]$

a=6, b=0, R²=5.

Центр — в точке (6;0), радиус R=√5.

$[5){x^2} + {y^2} = 11.]$

Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.

Чтобы найти центр и радиус окружности, заданной уравнением вида

$[{x^2} + {y^2} - 2ax - 2by + c = 0,]$

нужно дополнить его до полных квадратов, чтобы привести к привычному виду.

Для этого сначала сгруппируем слагаемые

$[({x^2} - 2ax) + ({y^2} - 2by) + c = 0,]$

$[({x^2} - 2ax + {a^2}) - {a^2} + ({y^2} - 2by + {b^2}) - {b^2} + c = 0.]$

Отсюда

$[{(x - a)^2} + {(y - b)^2} + c - {a^2} - {b^2} = 0,]$

$[{(x - a)^2} + {(y - b)^2} = {a^2} + {b^2} - c.]$

При a²+b²-c>0 это уравнение задаёт окружность с радиусом

$[R = sqrt {{a^2} + {b^2} - c} .]$

При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).

При a²+b²-c<0 нет ни одной точки, удовлетворяющей этому уравнению.

Примеры.

Найти координаты центра и радиус окружности:

$[1){x^2} + {y^2} + 10x - 6y - 15 = 0;]$

$[2){x^2} + {y^2} - 5x + 4 = 0;]$

$[3)3{x^2} + 3{y^2} - 4x - 9y + 4 = 0.]$

Решение:

$[1){x^2} + {y^2} + 10x - 6y - 15 = 0]$

Группируем слагаемые

$[({x^2} + 10x) + ({y^2} - 6y) - 15 = 0]$

$[{x^2} + 10x = ({x^2} + 2 cdot x cdot 5 + {5^2}) - {5^2}.]$

Аналогично

$[{y^2} - 6y = ({y^2} - 2 cdot y cdot 3 + {3^2}) - {3^2}.]$

Таким образом,

$[({x^2} + 2 cdot x cdot 5 + {5^2}) - {5^2} + ({y^2} - 2 cdot y cdot 3 + {3^2}) - {3^2} - 15 = 0]$

$[{(x + 5)^2} + {(y - 3)^2} - 25 - 9 - 15 = 0]$

$[{(x + 5)^2} + {(y - 3)^2} = 49]$

Центром этой окружности является точка (-5;3), радиус R=7.

$[2){x^2} + {y^2} - 5x + 4 = 0]$

$[({x^2} - 5x) + {y^2} + 4 = 0]$

$[({x^2} - 2 cdot x cdot 2,5 + {2,5^2}) - {2,5^2} + {y^2} + 4 = 0]$

$[{(x - 2,5)^2} + {y^2} + 4 - 6,25 = 0]$

$[{(x - 2,5)^2} + {y^2} = 2,25]$

Центр окружности — точка (2,5;0), радиус R=1,5.

$[3)3{x^2} + 3{y^2} - 4x - 9y + 4 = 0]$

Разделим обе части уравнения на 3:

$[{x^2} + {y^2} - frac{4}{3}x - 3y + frac{4}{3} = 0]$

Далее — аналогично

$[({x^2} - frac{4}{3}x) + ({y^2} - 3y) + frac{4}{3} = 0]$

$[({x^2} - 2 cdot x cdot frac{2}{3} + {(frac{2}{3})^2}) - {(frac{2}{3})^2} + ({y^2} - 2 cdot y cdot frac{3}{2} + {(frac{3}{2})^2}) - ]$

$[ - {(frac{3}{2})^2} + frac{4}{3} = 0]$

$[{(x - frac{2}{3})^2} + {(y - frac{3}{2})^2} - frac{{{4^{backslash 4}}}}{9} - frac{{{9^{backslash 9}}}}{4} + frac{{{4^{backslash 12}}}}{3} = 0]$

$[{(x - frac{2}{3})^2} + {(y - frac{3}{2})^2} = frac{{49}}{{36}}]$

Центр этой окружности лежит в точке

$[(frac{2}{3};frac{3}{2}),R = frac{7}{6}.]$

Источник

Как найти радиус и центр окружности

Окружность радиуса R с центром в начале координат представляется уравнением:

Окружность радиуса R с центром в точке C(a;b) представляется уравнением:

Расстояние от центра окружности С(a;b) до точки M(x;y) называется радиусом окружности R (на рисунке красная линия).
Это уравнение можно записать в виде:

Если уравнение помножить на любое число A, то получим

Примечание
Окружность относится к линии второго порядка, так как представляется уравнением второй степени.

Необходимые условия для этого:
1. Отсутствие в уравнение второй степени члена с произведением xy;
2. Коэффициенты при x² и y² были равны в уравнение вида:

3. Если выполняется неравенство

Как найти радиус и центр окружности

Уравнение Ax²+Bx+Ay²+Cy+D=0 если оно удовлетворяет примечаниям (1, 2 и 3), то тогда (a;b) и радиус R окружности можно найти по формулам:

Пример 1
Уравнение 5x²-10x+5y²+20y-20=0
Здесь
A=5, B=-10, C=20, D=-20
Оно удовлетворяет примечаниям 1, 2 и выполняется неравенство

Решая, получаем что центр есть (1;-2), а радиус R=3

Анимационный график окружности

Пример 2
Уравнение второй степени x²+4xy+y²=1 не является окружностью, так как в нём есть член 4xy.

Пример 3
Уравнение второй степени 4x²+9y²=36 не представляет окружность, так как в нём коэффициенты при x² и y² не равны.

8030

Источник