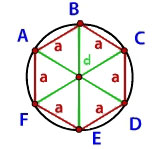
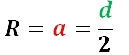Как из площади вписанного в окружность правильного шестиугольника найти радиус??
-
- 0
-
-
- 0
-
Надеюсь то.
Сторона правильного шестиугольника равна радиусу Описанной около него окружности. Соединим концы стороны шестиугольника с центром окружности. Получим правильный треугольник. Площадь правильного треугольника равна S=(√3/4)*R². Таких треугольников 6.
В нашем случае S=6√3дм².
Или:
Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне. Высота правильного треугольника по Пифагору равна √(а²-а²/4)=а√3/2.
Тогда его площадь равна S=(1/2)*a*a√3/2 или S=a²√3/4. Вот мы и вывели формулу. далее, как уже было сказано: площадь шести таких треугольников равна а²√3*3/2. а=2дм. S=6√3дм²
Ответ: S=6√3 дм²
-
Комментариев (0)
Ваш ответ
Радиус окружности шестиугольника с учетом площади Калькулятор
| Search | ||
| Дом | математика ↺ | |
| математика | Геометрия ↺ | |
| Геометрия | 2D геометрия ↺ | |
| 2D геометрия | Шестиугольник ↺ | |
| Шестиугольник | Радиус шестиугольника ↺ | |
| Радиус шестиугольника | Круговой радиус шестиугольника ↺ |
|
✖Площадь шестиугольника — это общее количество плоскостей, заключенных между граничными линиями шестиугольника.ⓘ Площадь шестиугольника [A] |
+10% -10% |
|
✖Радиус окружности шестиугольника — это радиус описанной окружности шестиугольника или окружности, содержащей шестиугольник со всеми вершинами, лежащими на этой окружности.ⓘ Радиус окружности шестиугольника с учетом площади [rc] |
⎘ копия |
Радиус окружности шестиугольника с учетом площади Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Площадь шестиугольника: 95 Квадратный метр —> 95 Квадратный метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
6.04694278529872 метр —> Конверсия не требуется
9 Круговой радиус шестиугольника Калькуляторы
Радиус окружности шестиугольника с учетом площади формула
Окружность шестиугольника = sqrt((2/(3*sqrt(3)))*Площадь шестиугольника)
rc = sqrt((2/(3*sqrt(3)))*A)
Что такое шестиугольник?
Правильный шестиугольник определяется как равносторонний и равноугольный шестиугольник. Просто это шестисторонний правильный многоугольник. Он бицентрический, что означает, что он одновременно циклический (имеет описанную окружность) и тангенциальный (имеет вписанную окружность). Общая длина сторон равна радиусу описанной окружности или описанной окружности, которая равна 2/sqrt(3), умноженной на апофему (радиус вписанной окружности). Все внутренние углы равны 120 градусов. Правильный шестиугольник имеет шесть вращательных симметрий.
Радиус описанной окружности шестиугольника
Если у шестиугольника как углы, так и стороны равны, соответственно, это — правильный многоугольник, вокруг которого можно описать лишь одну окружность. Все вершины шестиугольника лежат на описанной вокруг него окружности. У правильного шестиугольника центр расположен на равном расстоянии от его вершин. Центр шестиугольника и центр описанной окружности совпадают. Линия, которая соединяет центр с вершинами, считается радиусом как многоугольника, так и описанной окружности. В правильном шестиугольнике сторона и радиус равны. Отсюда, R описанной окружности равняется его стороне или диагонали, поделенной пополам:
В данном выражении:
а — величина стороны шестиугольника;
R — величина радиуса;
d — диагональ.
Онлайн калькулятор поможет быстро и правильно найти величину радиуса, для этого вам нужно лишь занести исходные данные.
Правильный шестиугольник: свойства, формулы, площадь
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны.
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
, где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне.
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
Ты нашел то, что искал? Поделись с друзьями!
. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Радиус такой окружности равен .
. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Правильный шестиугольник и его свойства
Определение
Выпуклый многоугольник называется правильным, если все его стороны равны и все его углы равны.
Замечание
Т.к. сумма всех углов (n) –угольника равна (180^circ(n-2)) , то каждый угол правильного (n) –угольника равен [alpha_n=dfracn cdot 180^circ]
Пример
Каждый угол правильного четырехугольника (т.е. квадрата) равен (dfrac <4-2>4cdot 180^circ=90^circ) ;
каждый угол правильного шестиугольника равен (dfrac<6-2>6cdot 180^circ=120^circ) .
Теоремы
1. Около любого правильного многоугольника можно описать окружность, и притом только одну.
2. В любой правильный многоугольник можно вписать окружность, и притом только одну.
Следствия
1. Окружность, вписанная в правильный многоугольник, касается всех его сторон в серединах.
2. Центры вписанной и описанной окружности у правильного многоугольника совпадают.
Теорема
Если (a) – сторона правильного (n) –угольника, (R) и (r) – радиусы описанной и вписанной окружностей соответственно, то верны следующие формулы: [begin S&=dfrac n2ar\ a&=2Rcdot sindfrac<180^circ>n\ r&=Rcdot cosdfrac<180^circ>n end]
Свойства правильного шестиугольника
1. Сторона равна радиусу описанной окружности: (a=R) .
2. Радиус описанной окружности является биссектрисой угла правильного шестиугольника.
3. Все углы правильного шестиугольника равны (120^circ) .
4. Площадь правильного шестиугольника со стороной (a) равна (dfrac<3sqrt<3>><2>a^2) .
5. Диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу (r) вписанной в правильный шестиугольник окружности.
6. Инвариантен относительно поворота плоскости на угол, кратный (60^circ) относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями).
Замечание
В общем случае правильный (n) -угольник инвариантен относительно поворота на угол (dfrac<360^circ>) .
http://ege-study.ru/ru/ege/materialy/matematika/pravilnyj-shestiugolnik-i-ego-ploshhad/
http://shkolkovo.net/theory/77
В публикации представлена формула, с помощью которой можно найти радиус окружности, описанной около правильного многоугольника, а также приведен пример решения задачи для лучшего понимания представленного материала.
- Формула расчета радиуса окружности
- Пример задачи
Формула расчета радиуса окружности
На рисунке изображен правильный шестиугольник с описанной вокруг него окружностью, но формула ниже подходит для любого правильного n-угольника.
где a – длина стороны.
Примечание: зная радиус описанного круга можно найти сторону равностороннего n-угольника (формула выводится из представленной выше):
Пример задачи
Дан правильный пятиугольник с длиной стороны 8 см. Вычислите радиус описанной около данной фигуры окружности.
Решение:
Применим соответствующую формулу, подставив в нее известное нам значение.
Радиус окружности, описанной около правильного шестиугольника
Содержание:
- Что такое окружность, описанная около правильного шестиугольника
- Как найти радиус, формула
- Свойства окружности, описанной около шестиугольника
- Площадь круга, ограниченного описанной окружностью
- Пример расчета радиуса окружности, описанной около шестиугольника
Что такое окружность, описанная около правильного шестиугольника
Правильный шестиугольник — выпуклый шестиугольник, у которого все стороны и углы равны.
Описанная около многоугольника окружность — это окружность, которая содержит все вершины выпуклого многоугольника. Ее центром является точка пересечения срединных перпендикуляров к сторонам многоугольника, обычно её обозначают прописной буквой О.
Как найти радиус, формула
Для расчетов используем формулу радиуса окружности, описанной около правильного многоугольника.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Формула 1
(R=frac a{2sinleft(frac{360^0}{2n}right)})
где R — радиус описанной окружности правильного многоугольника,
а — длина стороны многоугольника,
n — количество сторон (или вершин) многоугольника.
Подставим в формулу значение n=6.
(R=frac a{2sinleft(frac{360^0}{2n}right)}=R=frac a{2sinleft(frac{360^0}{2·6}right)}=frac a{2sinleft(frac{360^0}{12}right)}=frac a{2sin30^0}.)
Так как (sin30^0=frac12), то (R=frac a{2sin30^0}=frac a{2·frac12}=frac a1). Получаем формулу радиуса окружности, описанной около правильного шестиугольника:
Формула 2
R=a
где R — радиус описанной окружности,
а — сторона правильного шестиугольника.
Примечание 1
Эту же формулу модно найти и другим способом. Биссектрисы углов правильного шестиугольника разбивают его на шесть равных равносторонних треугольников. Точка пересечения биссектрис у правильного шестиугольника совпадает с точкой пересечения срединных перпендикуляров и является центром описанной окружности. Расстояние между центром окружности и вершиной шестиугольника равно радиусу описанной окружности и стороне равностороннего треугольника. Этот отрезок также равен стороне шестиугольника.
Свойства окружности, описанной около шестиугольника
- У правильного шестиугольника центры вписанной и описанной окружностей совпадают.
- Диаметр описанной окружности совпадает с большей диагональю правильного шестиугольника и равен его удвоенной стороне.
Площадь круга, ограниченного описанной окружностью
Чтобы вычислить площадь круга, ограниченного описанной окружностью правильного шестиугольника, используем стандартную формулу площади круга.
Формула 3
(S=π·r^2)
где S — площадь круга,
π — коэффициент, число π,
r — радиус круга.
Так как радиус круга равен стороне правильного шестиугольника, около которого описана окружность, получаем формулу:
Формула 4
(S=π·а^2)
где S — площадь круга,
π — коэффициент, число π,
а — сторона правильного шестиугольника.
Пример расчета радиуса окружности, описанной около шестиугольника
Задача
Дано: около правильного шестиугольника описана окружность. Меньшая диагональ правильного шестиугольника равна (5sqrt3 см.)
Найти: радиус описанной окружности.
Решение: Обозначим сторону правильного шестиугольника как а. Тогда его меньшая диагональ будет (аsqrt3 см). Следовательно, а=5 см. Радиус окружности, описанной около правильного шестиугольника равен его стороне. R=5 см.
Ответ: 5 см.
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 1)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так