По теореме синусов
Правило
Теорема синусов
|
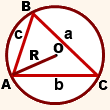
В треугольнике (displaystyle ABC) (displaystyle frac{color {blue}{BC}}{sin angle color {blue}{A}}=frac{color {#339900}{CA}}{sin angle color {#339900}{B}}=frac{red{AB}}{sin angle red{C}}=2R{small ,}) где (displaystyle R) – радиус описанной окружности. |
(displaystyle frac{AB}{sin angle C}=2R small.)
По условию задачи, (displaystyle AB=13sqrt{2} small,) (displaystyle angle C=135^circ small.) Значит,
(displaystyle frac{13sqrt{2}}{sin 135^{circ}}=2R small,)
(displaystyle R=frac{13sqrt{2}}{2sin 135^{circ}} small .)
Так как (displaystyle sin 135^{circ} =frac{sqrt{2}}{2}{small ,})
(displaystyle R=frac{13sqrt{2}}{2cdot frac{sqrt{2}}{2}} small ,)
(displaystyle R=frac{13}{1}=13 small.)
Ответ: (displaystyle 13 {small .})
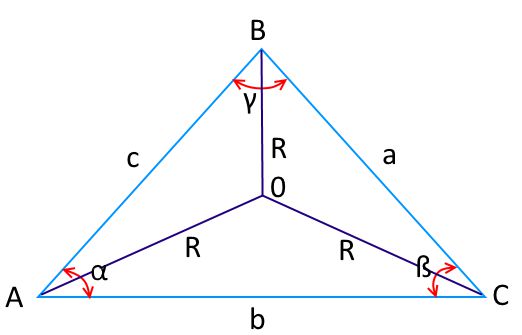
Теорема синусов
begin{align}
& text{Во всяком треугольнике отношение любой стороны к синусу
противолежащего ей угла}\
& text{постоянно и равно диаметру описанной вокруг треугольника
окружности.}\
& frac{a}{sin{alpha}}=frac{b}{sin{beta}}=frac{c}{sin{gamma}}=2R\
& angle{BAC}=alpha, angle{ABC}=beta, angle{ACB}=gamma, R-радиус
описанной окружности\
end{align}
Пример 1
begin{align}
& text{Даны сторона a=16, угол } alpha = 60°, text{ сторона b=8, найти угол }
beta. \
& text{Воспользуемся теоремой синусов, получим } frac{a}{sin{alpha}} =
frac{b}{sin{beta}}\
& text{подставим заданные значения } frac{16}{sin{60°}} = frac{8}{sin{beta}}\
& sin{beta} = frac{8sin{60°}}{16}=frac{8sqrt{3}}{16 * 2}==frac{sqrt{3}}{4}\
& beta approx 25.66 \
end{align}
Даны сторона a, угол α, противолежащий стороне, сторона b.
Найти значение
противолежащего стороне b угла β.
сторона a
Пример 2
begin{align}
& text{Даны сторона a=16, угол } alpha = 60°, text{ угол } beta=45° text{,
найти сторону b } \
& text{Воспользуемся теоремой синусов, получим } frac{a}{sin{alpha}} =
frac{b}{sin{beta}}\
& text{подставим заданные значения } frac{16}{sin{60°}} = frac{b}{sin{45°}}\
& b = frac{16 sin{45°}}{sin{60°}}=frac{16sqrt{2}}{sqrt{3}}\
& b approx 13.06 \
end{align}
Даны сторона a, угол α, противолежащий стороне, угол β.
Найти значение стороне b,
противолежащей углу β.
сторона a
Пример 2
begin{align}
& text{Даны сторона a=16, угол } alpha = 60°. text{ Найти радиус описанной
окружности R } \
& text{Воспользуемся теоремой синусов, получим } frac{a}{sin{alpha}} =2R\
& text{подставим заданные значения } frac{16}{sin{60°}} = 2R\
& R = frac{8}{sin{60°}}=frac{16}{sqrt{3}}\
& b approx 18.47 \
end{align}
Даны сторона a, угол α, противолежащий стороне.
Найти радиус описанной окружности R.
сторона a
Copyright calcs.su © 2021
Казалось бы, синус — это что-то про тригонометрию, но на самом деле совсем не только. Планиметрия может с этим смело поспорить, и теорема синусов явный аргумент в этом воображаемом споре. Если коротко, теорема синусов — это формула связи угла с противолежащей ему стороной в треугольнике.
✅ Отношение любой стороны треугольника к синусу противолежащего угла строго равно диаметру или двум радиусам описанной окружности. Формулу можно использовать в задачах несколькими способами.
💁🏻♂️ Во-первых, можно быстро найти радиус описанной окружности по известной стороне и противолежащему ей углу.
💁🏻♂️ Во-вторых, если треугольник не прямоугольный, то в нем можно просто найти синус угла по известным стороне и радиусу описанной окружности. Ну и в конце концов можно использовать отношение двух любых сторон и углов. Формула синусов в ЕГЭ используется нечасто, но иметь ее в своем арсенале полезно и обязательно. 😌
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
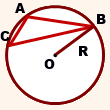
Радиус описанной около треугольника окружности можно найти по одной из двух общих формул.
Кроме того, для правильного и прямоугольного треугольников существуют дополнительные формулы.
Радиус описанной около произвольного треугольника окружности
Формула I (следствие из теоремы синусов)
То есть радиус описанной окружности равен отношению длины стороны треугольника к удвоенному синусу противолежащего этой стороне угла.
В общем виде эту формулу записывают так:
Формула II.
в общем виде —
То есть чтобы найти радиус описанной около треугольника окружности, надо произведения длин сторон треугольника разделить на четыре площади треугольника.
Если площадь треугольника находить по формуле Герона
где p — полупериметр,
то получим формулу радиуса описанной около треугольника окружности через длины сторон:
Обе эти формулы можно применить к треугольнику любого вида. Следует только учесть положение центра.
Центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы.
Центр описанной около тупоугольного треугольника окружности лежит вне треугольника, напротив тупого угла.
Радиус окружности, описанной около прямоугольного треугольника

То есть в прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы.
Обычно гипотенузу обозначают через c (AB=c) и формулу записывают так:
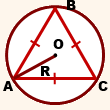
Радиус окружности, описанной около правильного треугольника
Формула:
Если без иррациональности в знаменателе, то
В равностороннем треугольнике радиус описанной окружности в два раза больше радиуса вписанной окружности:
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Определение окружности
Окружность – геометрическое место точек, равноудаленных от данной точки.
Эта точка называется центром окружности.
Отрезки в окружности
Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.
Хорда a – отрезок, соединяющий две точки на окружности.
Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).
O A – радиус, D E – хорда, B C – диаметр.
Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.
Касательная к окружности – прямая, имеющая с окружностью одну общую точку.
Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.
Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).
Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.
Дуга в окружности
Часть окружности, заключенная между двумя точками, называется дугой окружности.
Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .
Теорема 4:
Равные хорды стягивают равные дуги.
Если A B = C D , то ∪ A B = ∪ C D
Углы в окружности
В окружности существует два типа углов: центральные и вписанные.
Центральный угол – угол, вершина которого лежит в центре окружности.
∠ A O B – центральный.
Центральный угол равен градусной мере дуги, на которую он опирается. ∪ A B = ∠ A O B = α
Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.
Градусная мара всей окружности равна 360 ° .
Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.
∠ A C B – вписанный.
Вписанный угол равен половине градусной меры дуги, на которую он опирается. ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α
Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2
Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .
M N – диаметр.
∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °
Длина окружности, длина дуги
Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .
Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .
∪ A B = ∪ C D = α
Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.
Длина окружности находится по формуле:
l = 2 π R
Длина дуги окружности, на которую опирается центральный угол α равна:
l α = π R 180 ∘ ⋅ α
Площадь круга и его частей
Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.
Круг – часть пространства, которая находится внутри окружности.
Иными словами, окружность – это граница, а круг – это то, что внутри.
Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.
Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.
Площадь круга находится по формуле: S = π R 2
Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Примеры сектора в реальной жизни: кусок пиццы, веер.
Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α
Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.
Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.
Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.
S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α
Теорема синусов
Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с окружностями.