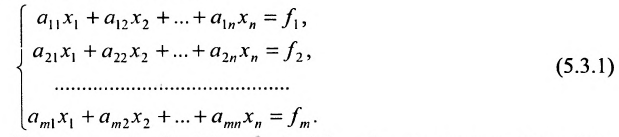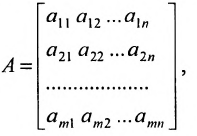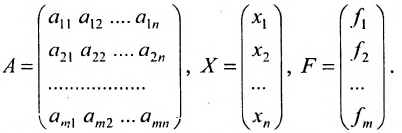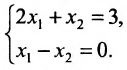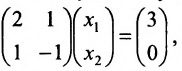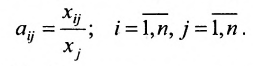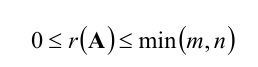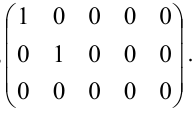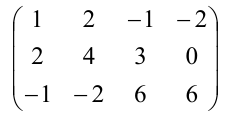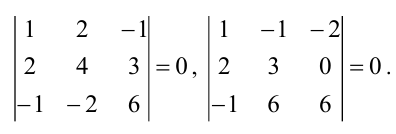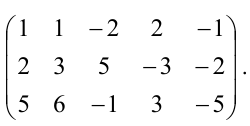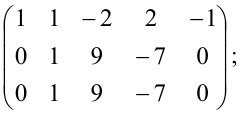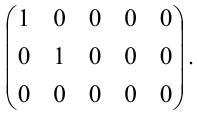Вычисление ранга матрицы методом окаймляющих миноров.
В данной теме нам понадобятся такие понятия как минор матрицы и окаймляющий минор. В теме «Алгебраические дополнения и миноры. Виды миноров и алгебраических дополнений» есть подробное пояснение этих понятий.
В предыдущей теме было рассмотрено понятие ранга матрицы, а также на примерах показано, как находить ранг по определению. Конечно, находить ранг матрицы таким образом несколько затруднительно, – в первую очередь из-за объёма вычислений. Однако количество вычисляемых миноров можно существенно уменьшить, если использовать так называемый метод окаймляющих миноров.
Суть метода окаймляющих миноров выражается парой пунктов простого алгоритма:
- Пусть некий минор $M$ k-го порядка не равен нулю.
- Если окаймляющие миноры для минора $M$ (это уже будут миноры (k+1)-го порядка), составить невозможно (т.е. матрица содержит k строк или k столбцов), то ранг равен k. Если окаймляющие миноры существуют и все равны нулю, то ранг равен k. Если среди окаймляющих миноров есть хотя бы один, отличный от нуля, то повторяем для него пункт №1, приняв k+1 вместо k.
Наглядно всё вышеизложенное можно выразить следующей схемой:
Поясню эту схему более подробно. Станем рассуждать с самого начала, т.е. с миноров первого порядка. Если все миноры первого порядка некоей матрицы $A$ (миноры первого порядка – это элементы матрицы) равны нулю, то $rang A=0$. Если в матрице есть минор первого порядка $M_1neq 0$, то $rang A≥ 1$.
Проверяем окаймляющие миноры для минора $M_1$. Это уже будут миноры второго порядка. Если все миноры, окаймляющие $M_1$, равны нулю, то $rang A=1$. Если среди миноров второго порядка, окаймляющих $M_1$, есть хоть один минор $M_2 neq 0$, то $rang A≥ 2$.
Проверяем окаймляющие миноры для минора $M_2$. Это будут миноры третьего порядка. Если все миноры третьего порядка, окаймляющие $M_2$, равны нулю, то $rang A=2$. Если среди миноров третьего порядка, окаймляющих $M_2$, есть хоть один минор $M_3neq 0$, то $rang A≥ 3$.
Проверяем окаймляющие миноры для минора $M_3$. Если все миноры четвёртого порядка, окаймляющие $M_3$, равны нулю, то $rang A=3$. Если среди миноров четвёртого порядка, окаймляющих $M_3$, есть хоть один минор $M_4neq 0$, то $rang A≥ 4$.
Проверяем все окаймляющие миноры для минора $M_4$, и так далее. В конце концов возможны два случая: либо на каком-то шаге окажется, что все окаймляющие миноры равны нулю, либо окаймляющий минор составить просто не получится, так как в матрице «закончатся» строки или столбцы. Порядок последнего составленного ненулевого минора и будет равен рангу матрицы.
Пример №1
Найти ранг матрицы $A=left(begin{array}{cccc}
-1 & 2 & 1 & 3 \
-3 & 0 & 5 & 4 \
-5 & 4 & 7 & 10
end{array} right)$ методом окаймляющих миноров.
Решение
Можно, конечно, начать с миноров первого порядка, которые представляют собой просто элементы данной матрицы. Но лучше сразу выбрать какой-либо не равный нулю минор второго порядка, тем паче что такой выбор большой сложности не представляет. Например, на пересечении строк №1, №2 и столбцов №1, №2 расположены элементы минора $left|begin{array}{cc}
-1 & 2 \
-3 & 0
end{array} right|$, который несложно вычислить, используя формулу №1 из темы про вычисление определителей второго и третьего порядков:
$$
left|begin{array}{cc}
-1 & 2 \
-3 & 0
end{array} right|=-1cdot 0-2cdot (-3)=6.
$$
Итак, существует минор второго порядка, не равный нулю, из чего следует, что $rang A≥ 2$. Рассмотрим миноры третьего порядка, окаймляющие данный минор второго порядка. Как составить окаймляющий минор? Для этого к набору строк и столбцов, на пересечении которых лежат элементы минора второго порядка, нужно добавить ещё одну строку и ещё один столбец. Вспоминаем, что элементы записанного нами минора второго порядка расположены на пересечении строк №1, №2 и столбцов №1, №2. Добавим к строкам ещё строку №3, а к столбцам – столбец №3. Мы получим минор третьего порядка, элементы которого (они для наглядности показаны в матрице синим цветом) лежат на пересечении строк №1, №2, №3 и столбцов №1, №2, №3. Найдём значение этого минора, используя формулу №2 из темы про вычисление определителей второго и третьего порядков:
$$
left(begin{array}{cccc}
normblue{-1} & normblue{2} & normblue{1} & 3 \
normblue{-3} & normblue{0} & normblue{5} & 4 \
normblue{-5} & normblue{4} & normblue{7} & 10
end{array} right);;
left|begin{array}{ccc}
-1 & 2 & 1 \
-3 & 0 & 5 \
-5 & 4 & 7
end{array} right|
=0.
$$
Окаймляющий минор равен нулю. О чём это говорит? Это говорит о том, что нам нужно продолжить нахождение окаймляющих миноров. Либо они все равны нулю (и тогда ранг будет равен 2), либо среди них найдётся хотя бы один, отличный от нуля.
Элементы второго окаймляющего минора лежат на пересечении строк №1, №2, №3 и столбцов №1, №2, №4. В матрице для наглядности элементы этого минора показаны зелёным цветом. Сразу вычислим данный минор, используя всё ту же формулу №2 из темы про вычисление определителей второго и третьего порядков:
$$
left(begin{array}{cccc}
normgreen{-1} & normgreen{2} & 1 & normgreen{3} \
normgreen{-3} & normgreen{0} & 5 & normgreen{4} \
normgreen{-5} & normgreen{4} & 7 & normgreen{10}
end{array} right);;
left|begin{array}{ccc}
-1 & 2 & 3 \
-3 & 0 & 4 \
-5 & 4 & 10
end{array} right|=0.
$$
И этот окаймляющий минор равен нулю. Иных окаймляющих миноров нет. Следовательно, все окаймляющие миноры равны нулю. Порядок последнего составленного ненулевого минора равен 2. Вывод: ранг равен 2, т.е. $rang A=2$.
Ответ: $rang A=2$.
Пример №2
Найти ранг матрицы $A=left(begin{array}{ccccc}
1 & 2 & 0 & 4 & 5\
3 & 6 & -2 & -1 & -3\
-2 & -4 & 2 & 5 & 7\
-1 & -2 & 2 & 9 & 11
end{array} right)$ методом окаймляющих миноров.
Решение
Вновь, как и в предыдущем примере, начнём решение с выбора минора второго порядка, не равного нулю. Например, на пересечении строк №1, №2 и столбцов №1, №2 расположены элементы минора $left|begin{array}{cc}
1 & 2 \
3 & 6
end{array} right|$, который несложно вычислить, используя формулу №1 из темы про вычисление определителей второго и третьего порядков:
$$
left|begin{array}{cc}
1 & 2 \
3 & 6
end{array} right|=1cdot 6-2cdot 3=0.
$$
Данный минор второго порядка равен нулю, т.е. выбор неудачен. Возьмём иной минор второго порядка. Например, тот, элементы которого расположены на пересечении строк №1, №2 и столбцов №2, №3:
$$
left|begin{array}{cc}
2 & 0 \
6 & -2
end{array} right|=-4.
$$
Итак, ненулевой минор второго порядка существует, поэтому $rang A≥ 2$. Обозначим этот минор как $M_2$ и станем окаймлять его минорами третьего порядка. Например, добавим к строкам и столбцам, на которых расположены элементы $M_2$, ещё строку №3 и столбец №1. Т.е. найдём минор третьего порядка, элементы которого находятся на пересечении строк №1, №2, №3 и столбцов №1, №2, №3. Используем для этого формулу №2 из темы про вычисление определителей второго и третьего порядков. Подробные вычисления я приводить не стану, запишем лишь ответ:
$$
left|begin{array}{ccc}
1 & 2 & 0 \
3 & 6 & -2 \
-2 & -4 & 2
end{array} right|=0.
$$
Этот минор равен нулю, значит нужно переходить к иному окаймляющему минору. Либо все миноры третьего порядка, окаймляющие $M_2$, равны нулю, либо среди них всё-таки найдётся хоть один, отличный от нуля.
Рассмотрим минор третьего порядка, элементы которого лежат на пересечении строк №1, №2, №3 и столбцов №2, №3, №4. Этот минор тоже окаймляет $M_2$:
$$
left|begin{array}{ccc}
2 & 0 & 4 \
6 & -2 & -1 \
-4 & 2 & 5
end{array} right|=0.
$$
И вновь минор третьего порядка, окаймляющий $M_2$, равен нулю. Значит, переходим к иному минору третьего порядка. Возьмём минор третьего порядка, элементы которого лежат на пересечении строк №1, №2, №3 и столбцов №2, №3, №5. Этот минор тоже окаймляет $M_2$:
$$
left|begin{array}{ccc}
2 & 0 & 5 \
6 & -2 & -3 \
-4 & 2 & 7
end{array} right|=4.
$$
Итак, среди миноров третьего порядка, окаймляющих $M_2$, есть минор, не равный нулю, откуда следует $rang A≥ 3$. Обозначим этот ненулевой минор как $M_3$. Элементы минора $M_3$ лежат на пересечении строк №1, №2, №3 и столбцов №2, №3, №5. Станем окаймлять минор $M_3$ минорами четвёртого порядка. Для начала возьмём минор четвёртого порядка, элементы которого лежат на пересечении строк №1, №2, №3, №4 и столбцов №1, №2, №3, №5. Этот минор окаймляет $M_3$. Его значение найти несложно, если использовать, например, разложение по строке или по столбцу:
$$
left|begin{array}{cccc}
1 & 2 & 0 & 5\
3 & 6 & -2 & -3\
-2 & -4 & 2 & 7\
-1 & -2 & 2 & 11
end{array} right|=0.
$$
Аналогично, рассматривая минор четвёртого порядка, элементы которого расположены на пересечении строк №1, №2, №3, №4 и столбцов №2, №3, №4, №5, получим:
$$
left|begin{array}{cccc}
2 & 0 & 4 & 5\
6 & -2 & -1 & -3\
-4 & 2 & 5 & 7\
-2 & 2 & 9 & 11
end{array} right|=0.$$
Иных окаймляющих миноров для минора $M_3$ нет. Все миноры четвёртого порядка, окаймляющие $M_3$, равны нулю. Последний ненулевой минор, т.е. $M_3$, был третьего порядка. Вывод: ранг равен 3, т.е. $rang A=3$.
Ответ: $rang A=3$.
Пример №3
Найти ранг матрицы $A=left(begin{array}{ccccc}
-1 & 3 & 2 & 4 & 1\
0 & -2 & 5 & 0 & -3\
1 & -5 & 3 & 7 & 6
end{array} right)$ методом окаймляющих миноров.
Решение
Снова начинаем решение с выбора минора второго порядка, не равного нулю. Например, на пересечении строк №1, №2 и столбцов №1, №2 расположены элементы минора $left|begin{array}{cc}
-1 & 3 \
0 & -2
end{array} right|$, который вычисляем, используя формулу №1 из темы про вычисление определителей второго и третьего порядков:
$$
left|begin{array}{cc}
-1 & 3 \
0 & -2
end{array} right|=2.
$$
Данный минор (обозначим его $M_2$) не равен нулю, посему именно его мы и станем окаймлять минорами третьего порядка. Например, добавим к строкам и столбцам, на которых расположены элементы $M_2$, ещё строку №3 и столбец №3. Т.е. найдём минор третьего порядка, элементы которого расположены на пересечении строк №1, №2, №3 и столбцов №1, №2, №3. Используем для этого формулу №2 из темы про вычисление определителей второго и третьего порядков:
$$
left|begin{array}{ccc}
-1 & 3 & 2 \
0 & -2 & 5 \
1 & -5 & 3
end{array} right|=0.
$$
Этот минор равен нулю, значит нужно переходить к иному окаймляющему минору. Либо все миноры третьего порядка, окаймляющие $M_2$, равны нулю, либо среди них всё-таки найдётся хоть один, отличный от нуля.
Рассмотрим минор третьего порядка, элементы которого лежат на пересечении строк №1, №2, №3 и столбцов №1, №2, №4. Этот минор тоже окаймляет $M_2$:
$$
left|begin{array}{ccc}
-1 & 3 & 4 \
0 & -2 & 0 \
1 & -5 & 7
end{array} right|=22.
$$
Итак, среди миноров третьего порядка, окаймляющих $M_2$, есть хоть один, не равный нулю. Миноры четвёртого порядка мы образовать уже не можем, так как для них потребуется 4 строки, а в матрице $A$ всего 3 строки. Посему, так как последний ненулевой минор был третьего порядка, то ранг равен 3, т.е. $rang A=3$.
Ответ: $rang A=3$.
Перед тем как начать знакомство с темой, необходимо повторить правила нахождения определителей второго, третьего и высших порядков. Также необходимо знать, что детерминант 1-го порядка — число. Рассмотрим 2 метода вычисления ранга матриц.
Онлайн-калькулятор
Метод окаймляющих миноров
Для нахождения ранга матрицы данным методом требуется уметь находить миноры матриц.
Рангом матрицы QQ называется наивысший порядок миноров, среди которых есть хотя бы один отличный от 00.
При этом ранг матрицы не может превышать порядка матрицы: 0⩽rang Qm×n⩽min(m,n)0leqslant rang Q_{mtimes n}leqslant min (m, n).
Обозначить ранг матрицы QQ можно следующим образом: rang Qrang Q или r(Q)r(Q).
Если ранг матрицы QQ равен rr, то это означает, что в матрице QQ имеется отличный от нуля минор порядка rr. При этом всякий минор порядка больше, чем rr равен нулю.
Исходя из определения ранга матрицы, следует, что если все миноры первого порядка (т. е. элементы матрицы QQ) равны 00, то rang Q=0rang Q=0. Если один из миноров первого порядка отличен от 00, а все миноры второго порядка равны 00, то rang Q=1rang Q=1. Если все миноры kk-го порядка равны 00, или миноров kk-го порядка не существует, то rang Q=k−1rang Q=k-1.
Рассмотрим примеры нахождения ранга матриц данным методом.
Пример 1
Найти ранг матрицы методом окаймляющих миноров
F=(03−1210−2−10)F=begin{pmatrix}0&3&-1\2&1&0\-2&-1&0end{pmatrix}.
Данная матрица имеет размер 3×33times3, поэтому ее ранг не может быть больше 33, т.е. rang F⩽3rang Fleqslant3.
Перейдем к вычислению ранга матрицы.
Среди миноров 1-го порядка (т.е. элементов определителя) есть хотя бы один, не равный 00, поэтому rang F≥1rang Fgeq1.
Перейдем к проверке миноров 2-го порядка. Например, на пересечении строк №1 и №2 и столбцов №1 и №2 получим минор: ∣0321∣=0⋅1−2⋅3=0−6=−6begin{vmatrix}0&3\2&1end{vmatrix}=0cdot1-2cdot3=0-6=-6. Значит, среди миноров 2-го порядка есть хотя бы один, не равный 00 и поэтому rang F≥2rang Fgeq2.
Перейдем к проверке миноров 3-го порядка. Минор 3-го порядка — определитель матрицы FF, поскольку она состоит из 3 строк и 3 столбцов: ∣03−1210−2−10∣=0begin{vmatrix}0&3&-1\2&1&0\-2&-1&0end{vmatrix}=0. Значит, ранг матрицы FF равен 22, или rang F=2rang F=2.
Пример 2
Найти ранг матрицы методом окаймляющих миноров
K=(21−23−121213−15−2−21243−31)K=begin{pmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}.
Данная матрица имеет размер 5×45times4. Из чисел 55 и 44 минимальным является 44, поэтому ее ранг не может быть больше 44, а значит rang K⩽4rang Kleqslant4.
Перейдем к вычислению ранга матрицы.
Среди миноров 1-го порядка (т.е. элементов определителя) есть хотя бы один, не равный 00, поэтому rang K≥1rang Kgeq1.
Перейдем к проверке миноров 2-го порядка. Например, на пересечении строк №1 и №2 и столбцов №1 и №2 получим минор: ∣21−12∣=2⋅2−(−1)⋅1=4+1=5begin{vmatrix}2&1\-1&2end{vmatrix}=2cdot2-(-1)cdot1=4+1=5. Значит, среди миноров 2-го порядка есть хотя бы один, не равный 00 и поэтому rang K≥2rang Kgeq2.
Перейдем к проверке миноров 3-го порядка. Например, на пересечении строк №1, №3 и №5 и столбцов №2, №3 и №4 получим минор:
∣1−233−153−31∣=1⋅(−1)⋅1+(−2)⋅5⋅3+3⋅(−3)⋅3−3⋅(−1)⋅3−(−2)⋅1⋅3−1⋅5⋅(−3)=−1−30−27+9+6+15=−28begin{vmatrix}1&-2&3\3&-1&5\3&-3&1end{vmatrix}=1cdot(-1)cdot1+(-2)cdot5cdot3+3cdot(-3)cdot3-3cdot(-1)cdot3-(-2)cdot1cdot3-1cdot5cdot(-3)=-1-30-27+9+6+15=-28.
Значит, среди миноров 3-го порядка есть хотя бы один, не равный 00 и поэтому rang K≥3rang Kgeq3.
Перейдем к проверке миноров 4-го порядка. Например, на пересечении строк №1, №2, №3 и №4 и столбцов №1, №2, №3 и №4 получим минор:
∣21−23−121213−15−2−212∣=2(−1)1+1∣2123−15−212∣−(−1)2+1∣1−233−15−212∣+(−1)3+1∣1−23212−212∣−2(−1)4+1∣1−232123−15∣=2(−1)2∣2123−15−212∣−(−1)3∣1−233−15−212∣+(−1)4∣1−23212−212∣−2(−1)5∣1−232123−15∣=2∣2123−15−212∣+∣1−233−15−212∣+∣1−23212−212∣+2∣1−232123−15∣=2(−4+6−10−4−10−6)−2+9+20−6−5+12+2+6+8+6−2+8+2(5−6−12−9+2+20)=−56+56+0=0begin{vmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\-2&-2&1&2end{vmatrix}=2(-1)^{1+1}begin{vmatrix}2&1&2\3&-1&5\-2&1&2end{vmatrix}-(-1)^{2+1}begin{vmatrix}1&-2&3\3&-1&5\-2&1&2end{vmatrix}+(-1)^{3+1}begin{vmatrix}1&-2&3\2&1&2\-2&1&2end{vmatrix}-2(-1)^{4+1}begin{vmatrix}1&-2&3\2&1&2\3&-1&5end{vmatrix}=2(-1)^{2}begin{vmatrix}2&1&2\3&-1&5\-2&1&2end{vmatrix}-(-1)^{3}begin{vmatrix}1&-2&3\3&-1&5\-2&1&2end{vmatrix}+(-1)^{4}begin{vmatrix}1&-2&3\2&1&2\-2&1&2end{vmatrix}-2(-1)^{5}begin{vmatrix}1&-2&3\2&1&2\3&-1&5end{vmatrix}=2begin{vmatrix}2&1&2\3&-1&5\-2&1&2end{vmatrix}+begin{vmatrix}1&-2&3\3&-1&5\-2&1&2end{vmatrix}+begin{vmatrix}1&-2&3\2&1&2\-2&1&2end{vmatrix}+2begin{vmatrix}1&-2&3\2&1&2\3&-1&5end{vmatrix}=2(-4+6-10-4-10-6)-2+9+20-6-5+12+2+6+8+6-2+8+2(5-6-12-9+2+20)=-56+56+0=0.
Остальные миноры 4-го порядка также равны нулю:
∣21−23−121213−1543−31∣=0begin{vmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\4&3&-3&1end{vmatrix}=0,
∣21−23−1212−2−21243−31∣=0begin{vmatrix}2&1&-2&3\-1&2&1&2\-2&-2&1&2\4&3&-3&1end{vmatrix}=0,
∣21−2313−15−2−21243−31∣=0begin{vmatrix}2&1&-2&3\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{vmatrix}=0,
∣−121213−15−2−21243−31∣=0begin{vmatrix}-1&2&1&2\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{vmatrix}=0.
Значит, ранг матрицы KK равен 33, или rang K=3rang K=3.
Данный метод не всегда удобен, поскольку связан с вычислением большого количества определителей. Рассмотрим метод нахождения ранга матриц, который наиболее часто применяется на практике.
Метод Гаусса (метод элементарных преобразований)
Метод основан на элементарных преобразованиях матриц, под которыми будем понимать такие преобразования, в результате которых сохраняется эквивалентность матриц:
- перестановка местами любых двух рядов (строк или столбцов) матрицы;
- умножение любого ряда матрицы (строки или столбца) на некоторое число, отличное от нуля;
- прибавление к любому ряду (строке или столбцу) матрицы другого ряда (строки или столбца), умноженного на некоторое число, отличное от нуля.
Рангом матрицы называется количество ненулевых строк матрицы после ее приведения к ступенчатому виду при помощи элементарных преобразований над строками и столбцами.
Рассмотрим суть данного метода на примерах.
Пример 1
Найти ранг матрицы методом Гаусса F=(03−1210−2−10)F=begin{pmatrix}0&3&-1\2&1&0\-2&-1&0end{pmatrix}.
Приведем матрицу FF с помощью элементарных преобразований к ступенчатому виду.
Поменяем местами строки №1 и №2:
(03−1210−2−10)∼(21003−1−2−10)begin{pmatrix}0&3&-1\2&1&0\-2&-1&0end{pmatrix}sim begin{pmatrix}2&1&0\0&3&-1\-2&-1&0end{pmatrix}.
Прибавим к строке №3 строку №1, умноженную на 1:
(21003−1−2−10)∼(21003−1000)begin{pmatrix}2&1&0\0&3&-1\-2&-1&0end{pmatrix}simbegin{pmatrix}2&1&0\0&3&-1\0&0&0end{pmatrix}.
С помощью элементарных преобразований мы привели матрицу FF к ступенчатому виду. В ней остались 2 ненулевые строки, следовательно, rang F=2rang F=2.
Пример 2
Найти ранг матрицы методом Гаусса
K=(21−23−121213−15−2−21243−31)K=begin{pmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}.
Приведем матрицу KK с помощью элементарных преобразований к ступенчатому виду.
Поменяем местами строки №1 и №2:
(21−23−121213−15−2−21243−31)∼(−121221−2313−15−2−21243−31)begin{pmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}sim begin{pmatrix}-1&2&1&2\2&1&-2&3\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}.
Поменяем местами строки №2 и №4:
(−121221−2313−15−2−21243−31)∼(−1212−2−21213−1521−2343−31)begin{pmatrix}-1&2&1&2\2&1&-2&3\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}sim begin{pmatrix}-1&2&1&2\-2&-2&1&2\1&3&-1&5\2&1&-2&3\4&3&-3&1end{pmatrix}.
Поменяем местами строки №3 и №4:
(−1212−2−21213−1521−2343−31)∼(−1212−2−21221−2313−1543−31)begin{pmatrix}-1&2&1&2\-2&-2&1&2\1&3&-1&5\2&1&-2&3\4&3&-3&1end{pmatrix}sim begin{pmatrix}-1&2&1&2\-2&-2&1&2\2&1&-2&3\1&3&-1&5\4&3&-3&1end{pmatrix}.
Поменяем местами строки №4 и №5:
(−1212−2−21221−2313−1543−31)∼(−1212−2−21221−2343−3113−15)begin{pmatrix}-1&2&1&2\-2&-2&1&2\2&1&-2&3\1&3&-1&5\4&3&-3&1end{pmatrix}sim begin{pmatrix}-1&2&1&2\-2&-2&1&2\2&1&-2&3\4&3&-3&1\1&3&-1&5end{pmatrix}.
Прибавим к строке №2 строку №1, умноженную на -2:
(−1212−2−21221−2343−3113−15)∼(−12120−6−1−221−2343−3113−15)begin{pmatrix}-1&2&1&2\-2&-2&1&2\2&1&-2&3\4&3&-3&1\1&3&-1&5end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-6&-1&-2\2&1&-2&3\4&3&-3&1\1&3&-1&5end{pmatrix}.
Прибавим к строке №3 строку №1, умноженную на 2:
(−12120−6−1−221−2343−3113−15)∼(−12120−6−1−2050743−3113−15)begin{pmatrix}-1&2&1&2\0&-6&-1&-2\2&1&-2&3\4&3&-3&1\1&3&-1&5end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\4&3&-3&1\1&3&-1&5end{pmatrix}.
Прибавим к строке №4 строку №1, умноженную на 4:
(−12120−6−1−2050743−3113−15)∼(−12120−6−1−205070111913−15)begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\4&3&-3&1\1&3&-1&5end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\0&11&1&9\1&3&-1&5end{pmatrix}.
Прибавим к строке №5 строку №1, умноженную на 1:
(−12120−6−1−205070111913−15)∼(−12120−6−1−20507011190507)begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\0&11&1&9\1&3&-1&5end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\0&11&1&9\0&5&0&7end{pmatrix}.
Прибавим к строке №2 строку №3, умноженную на 1:
(−12120−6−1−20507011190507)∼(−12120−1−150507011190507)begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\0&11&1&9\0&5&0&7end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&5&0&7\0&11&1&9\0&5&0&7end{pmatrix}.
Прибавим к строке №5 строку №3, умноженную на -1:
(−12120−1−150507011190507)∼(−12120−1−150507011190000)begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&5&0&7\0&11&1&9\0&5&0&7end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&5&0&7\0&11&1&9\0&0&0&0end{pmatrix}.
Прибавим к строке №3 строку №2, умноженную на 5:
(−12120−1−150507011190000)∼(−12120−1−1500−532011190000)begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&5&0&7\0&11&1&9\0&0&0&0end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&11&1&9\0&0&0&0end{pmatrix}.
Прибавим к строке №4 строку №2, умноженную на 11:
(−12120−1−1500−532011190000)∼(−12120−1−1500−53200−10640000)begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&11&1&9\0&0&0&0end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&0&-10&64\0&0&0&0end{pmatrix}.
Прибавим к строке №4 строку №3, умноженную на -2:
(−12120−1−1500−53200−10640000)∼(−12120−1−1500−53200000000)begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&0&-10&64\0&0&0&0end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&0&0&0\0&0&0&0end{pmatrix}.
С помощью элементарных преобразований мы привели матрицу KK к ступенчатому виду. В ней остались 3 ненулевые строки, следовательно, rang K=3rang K=3.
Любым из рассмотренных методов можно найти ранг матрицы.
Наши эксперты готовы оказать вам помощь с решением задачи онлайн по самым низким ценам!
Тест по теме «Ранг матрицы»
В данной публикации мы рассмотрим определение ранга матрицы, а также методы, с помощью которых его можно найти. Также разберем примеры для демонстрации применения теории на практике.
- Определение ранга матрицы
-
Нахождение ранга матрицы
- Метод окаймляющих миноров
- Приведение матрицы к ступенчатому виду
Определение ранга матрицы
Ранг матрицы – ранг ее системы строк или столбцов. В любой матрице есть ее строчный и столбцовый ранги, которые равны между собой.
Ранг системы строк – это максимальное количество линейно-независимых строк. Аналогичным образом определяется ранг системы столбцов.
Примечания:
- Ранг нулевой матрицы (обозначается символом “θ“) любого размера равняется нулю.
- Ранг любого ненулевого вектора-строки или вектора-столбца равняется единице.
- Если в матрице любых размеров присутствует хотя бы один элемент, не равный нулю, значит ее ранг не меньше единицы.
- Ранг матрицы не больше её минимальной размерности.
- Элементарные преобразования, выполненные над матрицей, не меняют её ранга.
Нахождение ранга матрицы
Метод окаймляющих миноров
Ранг матрицы равняется максимальному порядку ненулевого минора.
Алгоритм следующий: находим миноры от низших порядков к высоким. Если минор n-го порядка не равняется нулю, а все последующие (n+1) равны 0, значит ранг матрицы равен n.
Пример
Чтобы было понятнее, давайте разберем практический пример и найдем ранг матрицы A ниже, пользуясь методом окаймляющих миноров.
Решение
Мы имеем дело с матрицей 4×4, следовательно, ее ранг не может быть выше 4. Также в матрице присутствуют ненулевые элементы, значит, ее ранг не меньше единицы. Итак, приступим:
1. Начинаем проверять миноры второго порядка. Для начала берем две строки первого и второго столбцов.
Минор равняется нулю.
Следовательно переходим к следующему минору (первый столбец остается, а вместо второго берем третий).
Минор равен 54≠0, следовательно ранг матрицы не меньше двух.
Примечание: Если бы и этот минор оказался равным нулю, мы бы дальше проверили следующие комбинации:
Если требуется, перебор можно аналогичным образом продолжить со строками:
- 1 и 3;
- 1 и 4;
- 2 и 3;
- 2 и 4;
- 3 и 4.
Если бы все миноры второго порядка оказались равными нулю, то ранг матрицы равнялся бы одному.
2. Нам удалось почти сразу найти минор, который нам подходит. Поэтому переходим к минорам третьего порядка.
К найденному минору второго порядка, который дал отличный от нуля результат, добавляем одну строку и один из столбцов, выделенных зеленым цветом (начнем со второго).
Минор оказался равным нулю.
Следовательно меняем второй столбец на четвертый. И со второй попытки нам удается найти минор, не равный нулю, значит ранг матрицы не может быть меньше 3.
Примечание: если бы результат снова оказался равным нулю, вместо второй строки мы бы дальше взяли четвертую и продолжили бы поиски “хорошего” минора.
3. Теперь остается определить миноры четвертого порядка с учетом найденного ранее. В данном случае он один, который совпадает с определителем матрицы.
Минор равняется 144≠0. А это значит, что ранг матрицы A равняется 4.
Приведение матрицы к ступенчатому виду
Ранг ступенчатой матрицы равняется количеству её ненулевых строк. То есть все, что нам нужно сделать – это привести матрицу к соответствующему виду, например, с помощью элементарных преобразований, которые, как мы уже упомянули выше, не меняют ее ранг.
Пример
Найдем ранг матрицы B ниже. Мы не берем слишком сложный пример, т.к. наша основная цель – это просто продемонстрировать применение метода на практике.
Решение
1. Сначала вычтем из второй строки удвоенную первую.
2. Теперь отнимем из третьей строки первую, умноженную на четыре.
Таким образом, мы получили ступенчатую матрицу, в которой количество ненулевых строк равняется двум, следовательно ее ранг, также, равен 2.
Содержание:
- Ранг системы строк и столбцов матрицы
- Ранг матрицы
- Метод окаймления миноров
Ранг системы строк и столбцов матрицы
В каждой матрице можно связать два ранга: строчный ранг (ранг системы строк) и столбцовый ранг (ранг системы столбцов).
Теорема
Строчный ранг матрицы равен её столбцовому рангу.
Ранг матрицы
Определение
Рангом матрицы $A$ называется ранг её системы
строк или столбцов.
Обозначается $operatorname{rang} A$
На практике для нахождения ранга матрицы используют следующее утверждение:
ранг матрицы равен количеству ненулевых строк после приведения матрицы к ступенчатому виду.
Элементарные преобразования
над строками (столбцами) матрицы не меняют её ранга.
Ранг ступенчатой матрицы равен
количеству её ненулевых строк.
Пример
Задание. Найти ранг матрицы $ A=left( begin{array}{cccc}{0} & {4} & {10} & {1} \ {4} & {8} & {18} & {7} \ {10} & {18} & {40} & {17} \ {1} & {7} & {17} & {3}end{array}right) $
Решение. С помощью элементарных преобразований над ее строками приведем матрицу $A$ к
ступенчатому виду. Для этого вначале от третьей строки отнимем две вторых:
$$ A sim left( begin{array}{cccc}{0} & {4} & {10} & {1} \ {4} & {8} & {18} & {7} \ {2} & {2} & {4} & {3} \ {1} & {7} & {17} & {3}end{array}right) $$
От второй строки отнимаем четвертую строку, умноженную на 4; от третьей — две четвертых:
$$ A sim left( begin{array}{rrrr}{0} & {4} & {10} & {1} \ {0} & {-20} & {-50} & {-5} \ {0} & {-12} & {-30} & {-3} \ {1} & {7} & {17} & {3}end{array}right) $$
Ко второй строке прибавим пять первых, к третьей — три третьих:
$$ A sim left( begin{array}{cccc}{0} & {4} & {10} & {1} \ {0} & {0} & {0} & {0} \ {0} & {0} & {0} & {0} \ {1} & {7} & {17} & {3}end{array}right) $$
Меняем местами первую и вторую строчки:
$$ A sim left( begin{array}{cccc}{0} & {0} & {0} & {0} \ {0} & {4} & {10} & {1} \ {0} & {0} & {0} & {0} \ {1} & {7} & {17} & {3}end{array}right) $$
Далее четвертую и первую строки:
$$ A sim left( begin{array}{cccc}{1} & {7} & {17} & {3} \ {0} & {4} & {10} & {1} \ {0} & {0} & {0} & {0} \ {0} & {0} & {0} & {0}end{array}right) Rightarrow operatorname{rang} A=2 $$
Ответ. $ operatorname{rang} A=2 $
Метод окаймления миноров
Теорема
Ранг матрицы равен наибольшему порядку отличного от нуля
минору.
На этой теореме базируется еще один метод нахождения ранга матрицы — метод окаймления миноров. Суть этого
метода заключается в нахождении миноров, начиная с низших порядков и двигаясь к более высоким. Если минор
$n$-го порядка не равен нулю, а все миноры $n+1$-го равны нулю, то ранг матрицы будет равен $n$ .

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти ранг матрицы $ A=left( begin{array}{rrrr}{1} & {2} & {-1} & {-2} \ {2} & {4} & {3} & {0} \ {-1} & {-2} & {6} & {6}end{array}right) $ ,
используя метод окаймления миноров.
Решение. Минорами минимального порядка являются миноры первого порядка, которые равны элементам
матрицы $A$ . Рассмотрим, например, минор $ M_{1}=1 neq 0 $ . расположенный в первой строке и первом
столбце. Окаймляем его с помощью второй строки и второго столбца, получаем минор
$ M_{2}^{1}=left| begin{array}{ll}{1} & {2} \ {2} & {4}end{array}right|=0 $ ; рассмотрим еще один минор второго
порядка, для этого минор $M_1$ окаймляем при
помощи второй строки и третьего столбца, тогда имеем минор
$ M_{2}^{2}=left| begin{array}{rr}{1} & {-1} \ {2} & {3}end{array}right|=5 neq 0 $ ,
то есть ранг матрицы не меньше двух. Далее рассматриваем миноры третьего порядка, которые окаймляют минор
$ M_{2}^{2} $ . Таких миноров два: комбинация
третьей строки со вторым столбцом или с четвертым столбцом. Вычисляем эти миноры:
$$ M_{3}^{1}=left| begin{array}{rrr}{1} & {2} & {-1} \ {2} & {4} & {3} \ {-1} & {-2} & {6}end{array}right|=0 $$
так как содержит два пропорциональных столбца (первый и второй); второй минор
$$ M_{3}^{2}=left| begin{array}{rrr}{1} & {-1} & {-2} \ {2} & {3} & {0} \ {-1} & {6} & {6}end{array}right| $$
преобразуем следующим образом: к первой строке прибавим третью, а ко второй две третьих:
$$ M_{3}^{2}=left| begin{array}{rrr}{0} & {5} & {4} \ {0} & {15} & {12} \ {-1} & {6} & {6}end{array}right|=0 $$
И так как первая и вторая строки пропорциональны, то минор равен нулю.
Таким образом, все окаймляющие миноры третьего порядка равны нулю. А, значит, ранг матрицы $A$
равен двум: $ operatorname{rang} A=2 $
Ответ. $ operatorname{rang} A=2 $
Читать дальше: примеры решения задач с матрицами.
Содержание:
Элементарные преобразования матриц:
Рассмотрим прямоугольную матрицу:
состоящую из m строк и n столбцов. В п.3.2 отмсчалось, что каждую строку матрицы можно рассматривать как n-мсрный вектор, а каждый столбец — как m-мерный вектор. Тогда матрицу А можно записать в виде:
и, следовательно, данную матрицу можно рассматривать как систему вектор строк или вектор столбцов. Б указанных системах вектор-строк и вектор-столбцов можно выделять линейно независимые (зависимые) векторы. Тогда будем говорить, что строки (столбцы) матрицы линейно независимы (зависимы), если соответствующие им векторы независимы (зависимы).
Определения
Определение: Рангом системы строк (соответственно столбцов) матрицы А называется наибольшее число линейно независимых среди них.
Поскольку легко доказать, что ранг системы строк матрицы равен рангу системы её столбцов, то справедливо следующее
Определение: Рангом матрицы, обозначаемым r(А), называется максимальное число линейно независимых строк (столбцов) матрицы.
При транспонировании матрицы ранг её не изменяется.
Другой метод определения ранга матрицы связан с понятием определителя.
Выделим в матрице А любые k строк и k столбцов. Элементы, стоящие на их пересечении, образуют квадратную матрицу, определитель которой называется минором k-го порядка матрицы А. Ясно, что величина к должна удовлетворять двум условиям: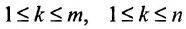
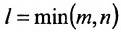
Определение: Рангом матрицы, обозначаемым r(А), называется порядок самого старшего минора этой матрицы, не равного нулю.
Из определения следует, что если ранг матрицы А равен l, то среди всех её миноров существует хотя бы один минор l-го порядка, отличный от нуля, но все миноры (l+1)-го порядков либо равны нулю, либо не могут быть составлены.
Вычисление ранга матрицы путём перебора всех её миноров весьма трудоёмко. Существует, однако, более простой способ вычисления ранга матрицы, основанный на упрощении структуры матрицы с помощью элементарных преобразований. Элементариыми преобразованиями матрицы называют следующие преобразования:
- обмен местами двух строк или двух столбцов матрицы;
- умножение всех элементов строки или столбца матрицы на произвольное число
, не равное нулю;
- прибавление ко всем элементам строки (столбца) матрицы соответствующих элементов другой строки (столбца), предварительно умноженных на одно и то же число;
- исключение из матрицы строки или столбца, состоящего из нулей.
Матрицы называются эквивалентными, если от одной из них к другой можно перейти путём конечного числа элементарных преобразований.
Ступенчатой матрицей называется матрица, удовлетворяющая тому свойству, что если в какой-либо из сё строк первый отличный от нуля элемент стоит на l-м месте, то во всех следующих строках на первых l местах стоят нули:
где элементы 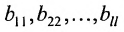
Для вычисления ранга матрицы приводят её с помощью цепочки элементарных преобразований к ступенчатому виду. Тогда ранг матрицы совпадает с числом её ненулевых диагональных элементов.
Теоремы о ранге матриц. Свойства ранга матриц
Относительно ранга матриц можно сформулировать следующие теоремы:
Теорема: Если матрица имеет минор порядка r, отличный от нуля, для которого все содержащие его миноры порядка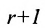
Вычисление ранга матрицы при помощи метода окаймления нужно вести от низших порядков к высшим. Сначала ищем минор первого порядка (т.е. элемент матрицы) или сразу второго порядка, отличный от нуля. Затем вычисляем окаймляющие его миноры следующего порядка, пока не найдём среди них отличного от нуля и т.д., пока не найдем минор порядка l, отличный от нуля, для которого либо все окаймляющие его миноры порядка l+1 равны нулю, либо такие миноры не могут быть составлены.
Теорема: Элементарные преобразования не меняют ранга матрицы.
Доказательство теоремы следует из определения ранга матрицы и свойств определителей.
Пример:
Найти ранг матрицы:
Решение:
Минор первого порядка в левом верхнем углу равен 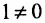
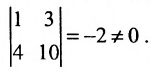
Значит ранг матрицы равен 2.
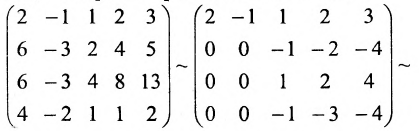
Пример:
Найти ранг матрицы:
Решение:
При помощи элементарных преобразований приведём данную матрицу к ступенчатому виду. На первом шаге умножим последовательно первую строку на 3, 3, 2 и вычтем из второй, третьей, четвёртой строк соответственно:
В эквивалентной матрице прибавим к третьей строке вторую и вычтем вторую из четвёртой строки:
(поменяем местами третью и четвертую строки)
(поменяем местами третий, четвёртый и пятый столбцы со вторым и опустим строки, состоящие из нулей) 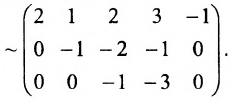
Отмстим некоторые свойства ранга матриц.
- Ранг суммы двух (или нескольких) матриц не больше суммы их рангов.
- Любую матрицу ранга r можно представить в виде суммы r матриц ранга 1, но нельзя представить в виде суммы менее чем r таких матриц.
- Любую матрицу С ранга r можно представить в виде произведения
, где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.
- Ранг произведения матриц порядка n удовлетворяет неравенству
.
Определение системы m линейных уравнений с n неизвестными
Системой m линейных уравнений с n неизвестными 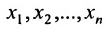
Числа 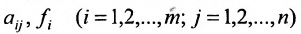
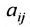
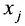
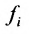
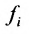
С помощью знака суммирования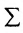
Матрица
составленная из коэффициентов системы 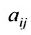
системы. Если к этой матрице добавить столбец свободных членов, то получим расширенную матрицу системы: 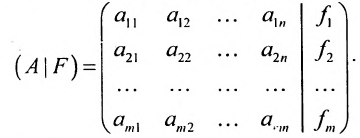
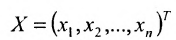
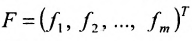

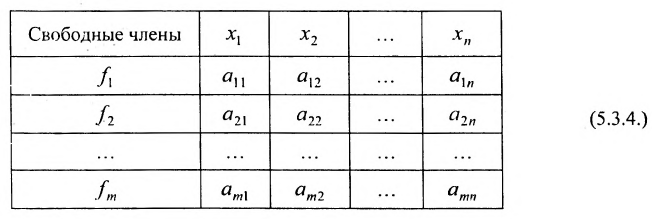
Используется также табличная форма записи системы (5.3.1):
Отметим, что (5.3.1), (5.3.2), (5.3.3), (5.3.4)- различные виды записи одной и той же системы линейных уравнений.
Решением системы (5.3.1) называется любой упорядоченный набор действительных чисел 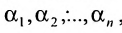
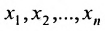
Система уравнений (5.3.1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Две системы уравнений с одинаковыми наборами неизвестных 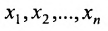
Отмстим, что для любой системы (5.3.1) возможны только три случая:
- система (5.3.1) имеет единственное решение;
- система (5.3.1) имеет бесчисленное множество решений;
- система (5.3.1) несовместна.
Множество всех решений системы (5.3.1) называется ее общим решением.
Решить систему (5.3.1) — значит найти ее общее решение.
Пример:
Пусть задана система
Тогда эту систему можно записать в матричном виде:
или в виде таблицы:
Система определенная, так как она имеет единственное решение 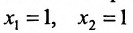
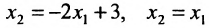
Экономические задачи, приводящие к системе линейных уравнений
Предположим, что производственные мощности для изготовления n различных видов продукции установлены в т цехах. Пусть 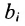
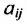
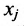
Широкий круг задач экономики приводит к составлению системы уравнений. Так в примере 4.3.2 составлялась система линейных уравнений (4.3.1) балансовой модели для трёх отраслей. В общем случае под балансовой моделью понимается система уравнений, каэ/сдое из которых выражает требование баланса между производимым количеством продукции и совокупной потребностью в этой продукции.
При построении балансовых моделей используется понятие чистой (или технологической) отрасли, т.е. условной отрасли, объединяющей всё производство данного продукта независимо от ведомственной (административной) подчинённости и форм собственности предприятий и фирм. Всё народное хозяйство представляется в виде совокупности п отраслей, каждая из которых рассматривается как производящая и как потребляющая.
Если обозначить через:
то систему уравнений баланса можно записать в виде:
или в матричной форме:
где Х- вектор-столбец валовой продукции; Y- вектор-столбец конечной продукции; А — матрица коэффициентов прямых затрат.
Основу экономико-математической модели межотраслевого баланса составляет технологическая матрица А, содержащая коэффициенты прямых затрат на производство единицы продукции:
Коэффициент!,! прямых затрат являются довольно стабильной величиной во времени.
Переписав матричное уравнение (5.4.2) в виде EX-AX = Y или (E-A)X = Y, (5.4.3) получим стандартную форму записи системы уравнений.
Определение ранга матрицы
Рассмотрим прямоугольную матрицу (4.1). Если в этой матрице выделить произвольно 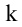
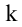
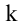
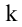
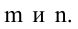
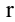
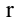
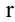
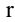
Очевидно, что выполняется соотношение
Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D 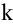
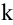
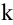
Элементарными называются следующие преобразования матрицы:
- перестановка двух любых строк (или столбцов),
- умножение строки (или столбца) на отличное от нуля число,
- прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.
Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.
Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: А ~ В.
Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы
равны нулю, например,
При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.
- Заказать решение задач по высшей математике
Пример:
Найти методом окаймления миноров ранг матрицы
Решение:
Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) 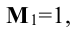
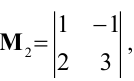
Переходим теперь к минорам 3-го порядка, окаймляющим 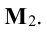
Таким образом, асе окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум.
Пример:
Найти ранг матрицы 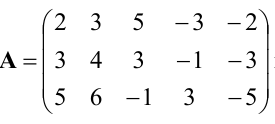
Решение:
Из второй строки вычтем первую и переставим эти строки:
Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:
из третьей строки вычтем первую; получим матрицу 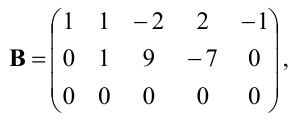
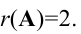
Вычисление ранга матрицы
Для исследования разрешимости систем линейных уравнений важную роль играет понятие ранга матрицы. Рассмотрим прямоугольную матрицу А
Выделим k произвольных строк и k произвольных столбцов этой матрицы. Определитель k-го порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называется минором k-го порядка матрицы А.
Рангом матрицы А называется наибольший порядок ее миноров, отличных от нуля. Обозначение: rank А,
Базисным минором матрицы называется всякий отличный от нуля ее минор, порядок которого равен рангу матрицы.
Рассмотрим некоторые методы вычисления ранга матрицы.
Метод окаймляющих миноров
Минор порядка k+1, содержащий в себе минор порядка k, называется окаймляющим минором.
Вычисляя ранг матрицы, удобнее переходить от миноров меньших порядков к минорам больших порядков. Если найден минор k-го порядка, отличный от нуля, а все окаймляющие его миноры порядка k+1 равны нулю, то ранг матрицы равен k.
- Определители второго и третьего порядков и их свойства
- Метод Гаусса — определение и вычисление
- Прямая линия на плоскости и в пространстве
- Плоскость в трехмерном пространстве
- Кратный интеграл
- Ряды в математике
- Дифференциальные уравнения с примерами
- Обратная матрица — определение и нахождение



















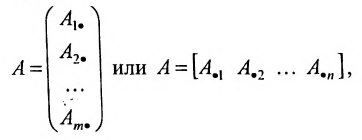
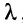 , не равное нулю;
, не равное нулю;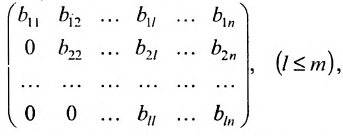
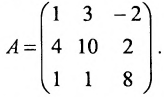
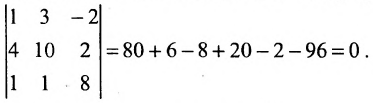



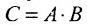 , где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.
, где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.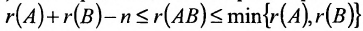 .
.