Глава
4
Системы
линейных уравнений
§
4.1. Ранг матрицы. Однородные системы.
Фундаментальная
система
решений
Рангом
матрицы
(обозначается
)
называется наивысший порядок
отличных
от нуля миноров этой матрицы.
Ранг
нулевой матрицы полагается равным нулю
по определению.
Для
любой прямоугольной матрицы ранги ее
систем векторов- строк и векторов-
столбцов совпадают и равны рангу матрицы.
Система
уравнений
называется
однородной.
Однородная система всегда совместна,
так как одним из ее частных решений
является нулевое решение.
Для
того, чтобы однородная система имела
ненулевое решение, необходимо и
достаточно, чтобы ранг матрицы системы
был меньше числа неизвестных.
Множество
решений однородной системы линейных
уравнений
образует линейное пространство
размерности
,
где
—
ранг матрицы системы. Любой базис
пространства решений однородной системы
называется фундаментальной
системой решений
этой системы.
Пример
1.
Найдите ранг матрицы в зависимости от
значения параметра
Решение.
При помощи элементарных преобразований,
не изменяющих ранг, приведем матрицу к
ступенчатому виду. Прибавив ко второй
строке первую, к третьей- первую,
умноженную на
,
к четвертой- первую, получим:
Если
,
то
Рассмотрим
теперь случай, когда
:
Очевидно,
что если
,
то
.
Пример
2.
Найдите размерность пространства
решений однородной системы линейных
уравнений с матрицей системы из примера
1.
Решение.
Размерность пространства решений равна
Пример
3.
Найдите общее решение и фундаментальную
систему решений однородной системы
линейных уравнений из примера 1.
Решение.
Если
система имеет только нулевое решение.
Пусть
.
Тогда, как было показано в примере 1,
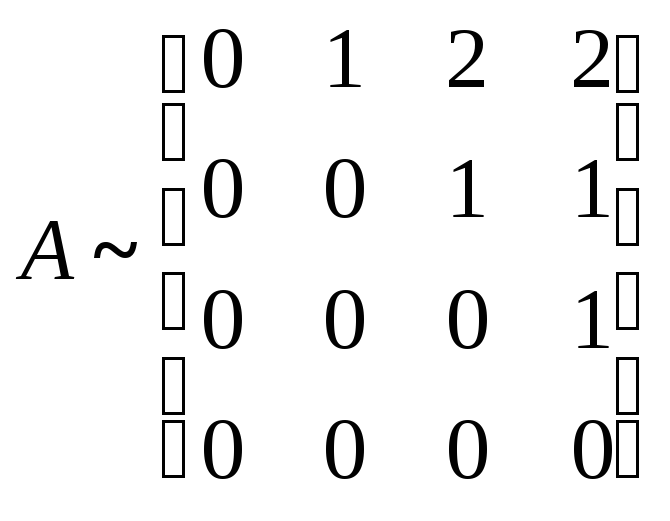
Пространство
решений одномерное и фундаментальная
система решений состоит из одного
вектора. Из
находим:
—
свободная переменная.
Общее
решение имеет вид:.
Фундаментальная система решений:.
Пусть
теперь
.
В этом случае
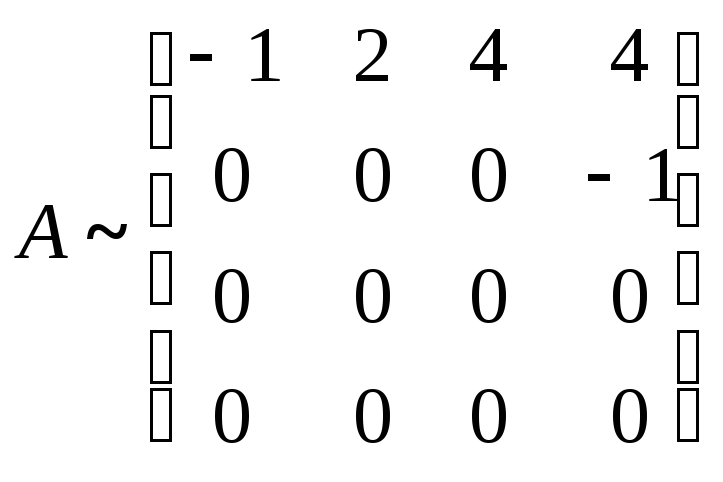
пространство
решений двумерное и фундаментальная
система решений состоит из двух векторов.
Из
получаем:
—
свободные переменные;
.
Общее
решение имеет вид:
.
Выбирая
значения свободных переменных в
соответствии с таблицей,
|
i |
|
|
|
1 |
1 |
0 |
|
2 |
0 |
1 |
записываем
фундаментальную систему решений:
и
.
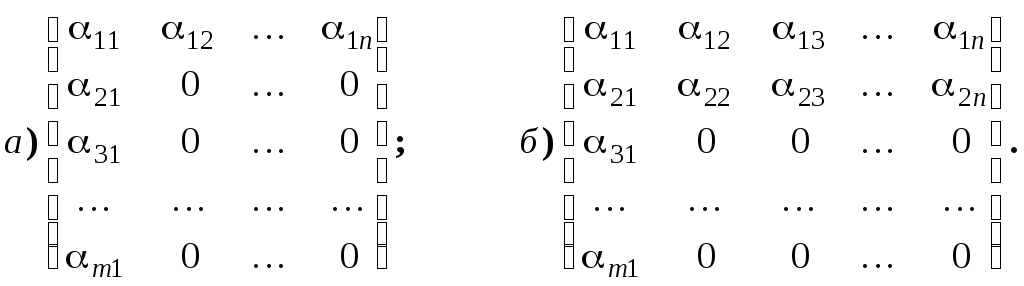
4.1.1.
Укажите всевозможные значения ранга
матриц вида:
4.1.2.Как
может измениться ранг матрицы, если
изменить значение одного ее элемента?
4.1.3.
Как может изменится ранг матрицы, при
изменении элементов лишь одной строки?
строк?
4.1.4.
Докажите, что ранг квазидиагональной
матрицы
равен сумме рангов матриц
и
.
4.1.5.
Верно ли следующее утверждение:
ранг квазитреугольной
матрицы
всегда равен сумме рангов матриц
и
?
-
Докажите,
что ранг суммы двух матриц не больше
суммы их рангов.
4.1.7.
Вычислите ранг матриц:
4.1.8.
Найдите ранг матриц в зависимости от
значений параметров:
4.1.9.
Найдите общее решение и фундаментальную
систему решений для систем уравнений:
4.1.10.
Образуют ли строки каждой из матриц
фундаментальную
систему решений для системы уравнений
§
4.2. Неоднородные системы. Теорема
Кронекера- Капелли
Согласно
теореме
Кронекера- Капелли неоднородная система
линейных уравнений
совместна
тогда и только тогда, когда ранг матрицы
этой системы
равен
рангу ее расширенной матрицы
т.е.
когда
.
Общее
решение
неоднородной системы представимо в
виде суммы общего решения
соответствующей однородной системы и
какого- либо частного решения
неоднородной системы.
Пример
1.
Исследуйте совместность и запишите
общее решение неоднородной системы
уравнений
в
виде суммы частного решения этой системы
и линейной комбинации базисных решений
соответствующей однородной системы.
Решение.
Запишем систему уравнений в матричном
виде. Используя элементарные преобразования
над строками полученной матрицы, приведем
ее к ступенчатому виду и проверим
выполнимость условия
:
т.е.
по теореме Кронекера- Капелли система
уравнений совместна. Запишем ее общее
решение. Поскольку
будем иметь две свободные переменные.
—
свободная переменная,
—
свободная переменная,
Таким
образом,
.
Заметим,
что
,
а векторы
и
образуют фундаментальную систему
решений соответствующей однородной
системы уравнений.
Пример
2.
Подберите
так, чтобы система уравнений
имела
решение.
Решение.
Нужно найти такое значение параметра
,
при котором выполняется условие
.
По
теореме Кронекера- Капелли система
уравнений совместна при
4.2.1.
Исследуйте совместность и найдите общее
решение систем уравнений

4.2.2.
Исследуйте систему и найдите общее
решение в зависимости от значения
параметра
:
4.2.3.
Исследуйте совместность и запишите
общее решение неоднородной системы
уравнений в виде суммы одного решения
этой системы и линейной комбинации
базисных решений соответствующей
однородной системы:
8
Соседние файлы в папке Задачник-1
- #
- #
- #
- #
- #
- #
- #
- #
- #
Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность. Вторая часть.
В первой части мы рассматривали системы линейных алгебраических уравнений (СЛАУ), все коэффициенты которых были известны. В этой же части разберём СЛАУ, среди коэффициентов которых есть некий параметр. Для исследования СЛАУ на совместность станем использовать теорему Кронекера-Капелли. В процессе решения примеров на данной странице будем применять метод Гаусса или же метод Крамера. Сформулируем теорему и следствие из неё ещё раз:
Теорема Кронекера-Капелли
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е. $rang A=rangwidetilde{A}$.
Следствие из теоремы Кронекера-Капелли
- Если $rang Aneqrangwidetilde{A}$, то СЛАУ несовместна (не имеет решений).
- Если $rang A=rangwidetilde{A} < n$, то СЛАУ является неопределённой (имеет бесконечное количество решений).
- Если $rang A=rangwidetilde{A} = n$, то СЛАУ является определённой (имеет ровно одно решение).
Параметр $n$, использованный выше, равен количеству переменных рассматриваемой СЛАУ.
Пример №1
Исследовать СЛАУ $
left {begin{aligned}
& kx_1+2x_2+x_3=8;\
& -x_1+x_2+2x_3=7;\
& x_2+kx_3=5.end{aligned}right.$ на совместность и найти решение системы в зависимости от значений параметра $k$.
Решение
Чтобы исследовать заданную систему на совместность, нам нужно найти ранг матрицы системы $A$ и ранг расширенной матрицы системы $widetilde{A}$. Сделать это можно несколькими путями. Стоит учесть, что в данном примере нам требуется не только исследовать систему на совместность, но и указать её решения. Мне кажется наиболее удобным в таких задачах применять метод Гаусса, однако это вовсе не является обязательным. Для разнообразия данный пример решим методом Гаусса, а следующий – методом Крамера. Итак, запишем и начнём преобразовывать расширенную матрицу системы. При записи расширенной матрицы системы поменяем местами первую и вторую строки. Это нужно для того, чтобы первым элементом первой строки стало число -1.
$$
left(begin{array}{ccc|c}
-1 & 1 &2 &7 \ k & 2 & 1 & 8\ 0 & 1 & k & 5
end{array} right)
begin{array} {l} phantom{0} \ r_2+kcdot{r_1}\ phantom{0}end{array}rightarrow
left(begin{array}{ccc|c}
-1 & 1 &2 &7 \ 0 & 2+k & 1+2k & 8+7k\ 0 & 1 & k & 5
end{array} right)rightarrowleft|begin{aligned}&text{меняем местами}\&text{вторую и третью строки}end{aligned}right|rightarrow \
rightarrow
left(begin{array}{ccc|c}
-1 & 1 &2 &7 \0 & 1 & k & 5 \ 0 & 2+k & 1+2k & 8+7k
end{array} right)
begin{array} {l}phantom{0}\phantom{0}\r_3-(2+k)cdot{r_2}end{array}
rightarrow
left(begin{array}{ccc|c}
-1 & 1 &2 &7 \0 & 1 & k & 5 \ 0 & 0 & 1-k^2 & 2k-2
end{array} right)
$$
Мы привели расширенную матрицу системы к ступенчатому виду. Напомню, что до черты расположена преобразованная матрица матрица системы: $left(begin{array}{ccc}-1 & 1 &2\0 & 1 & k\ 0 & 0 & 1-k^2end{array} right)$.
Каким бы ни было значение параметра $k$, полученная нами после преобразований матрица будет содержать не менее двух ненулевых строк (первая и вторая строки точно останутся ненулевыми). Вопрос о количестве решений зависит лишь от третьей строки.
В следствии из теоремы Кронекера-Капелли указаны три случая, и в данном примере легко рассмотреть каждый из них. Начнём с варианта $rang Aneqrangwidetilde{A}$, при котором система не имеет решений, т.е. несовместна.
$rang Aneqrangwidetilde{A}$
Ранги будут не равны друг другу лишь в одном случае: когда $1-k^2=0$, при этом $2k-2neq{0}$. В этом случае преобразованная матрица системы будет содержать две ненулевых строки (т.е. $rang A=2$), а преобразованная расширенная матрица системы будет содержать три ненулевых строки (т.е. $rang widetilde{A}=3$). Иными словами, нам требуется решить систему уравнений:
$$
left{begin{aligned}
& 1-k^2=0;\
& 2k-2neq{0}.
end{aligned}right.
Rightarrow
left{begin{aligned}
& k^2=1;\
& kneq{1}.
end{aligned}right.
$$
Из первого уравнения имеем: $k=1$ или $k=-1$, однако $kneq{1}$, поэтому остаётся лишь один случай: $k=-1$. Следовательно, при $k=-1$ система не имеет решений.
$rang A=rangwidetilde{A}<3$
Рассмотрим второй пункт следствия из теоремы Кронекера-Капелли – ранги равны между собой, но меньше, чем количество переменных (т.е. меньше 3). Это возможно лишь в том случае, если последняя строка преобразованной расширенной матрицы системы полностью станет нулевой, т.е.
$$
left{begin{aligned}
& 1-k^2=0;\
& 2k-2=0.
end{aligned}right.
$$
Из данной системы имеем: $k=1$. Именно при $k=1$ третья строка преобразованной расширенной матрицы системы станет нулевой, поэтому $rang{A}=rangwidetilde{A}=2$. При этом, повторюсь, у нас всего три переменных, т.е. имеем случай $rang A=rangwidetilde{A}=2<3$.
Система имеет бесконечное количество решений. Найдём эти решения. Подставим $k=1$ в преобразованную матрицу и продолжим операции метода Гаусса. Третью строку (она станет нулевой) просто вычеркнем:
$$
left(begin{array}{ccc|c}
-1 & 1 &2 &7 \0 & 1 & k & 5 \ 0 & 0 & 1-k^2 & 2k-2
end{array} right)rightarrow|k=1|rightarrow
left(begin{array}{ccc|c}
-1 & 1 &2 &7 \0 & 1 & 1 & 5 end{array} right)
rightarrowleft|begin{aligned}&text{переносим третий столбец}\&text{за черту}end{aligned}right|rightarrow \
rightarrowleft(begin{array}{cc|ccc}-1 & 1 &-2 &7\0 & 1 & -1 & 5end{array}right)
begin{array} {l}r_1-r_2\phantom{0}end{array}
rightarrowleft(begin{array}{cc|ccc}-1 & 0 &-1 &2\0 & 1 & -1 & 5end{array}right)
begin{array} {l}-1cdot{r_1}\phantom{0}end{array}
rightarrowleft(begin{array}{cc|ccc}1 & 0 &1 &-2\0 & 1 & -1 & 5end{array}right)
$$
Из последней матрицы имеем: $left{begin{aligned}& x_1=x_3-2;\& x_2=-x_3+5.end{aligned}right.$
$rang A=rangwidetilde{A}=3$
Рассмотрим третий пункт следствия из теоремы Кронекера-Капелли – ранги равны между собой и равны количеству переменных. Это возможно лишь в том случае, если $1-k^2neq{0}$, т.е. $kneq{-1}$ и $kneq{1}$. Продолжаем решение методом Гаусса:
$$
left(begin{array}{ccc|c}
-1 & 1 &2 &7 \0 & 1 & k & 5 \ 0 & 0 & 1-k^2 & 2k-2
end{array}right)rightarrow
left(begin{array}{ccc|c}
-1 & 1 &2 &7 \0 & 1 & k & 5 \ 0 & 0 & (1-k)(1+k) & -2(1-k)
end{array}right)
begin{array} {l}phantom{0}\phantom{0}\r_3:((1-k)(1+k))end{array}
rightarrow\
rightarrowleft(begin{array}{ccc|c}
-1 & 1 &2 &7 \0 & 1 & k & 5 \ 0 & 0 & 1 & -2/(1+k)
end{array}right)
begin{array} {l}r_1-2r_3\r_2-kcdot{r_3}\phantom{0}end{array}
rightarrow
left(begin{array}{ccc|c}
-1 & 1 &0 &(7k+11)/(k+1) \0 & 1 & 0 & (7k+5)/(k+1) \ 0 & 0 & 1 & -2/(1+k)
end{array}right)
begin{array} {l}r_1-r_2\phantom{0}\phantom{0}end{array}rightarrow\
rightarrow
left(begin{array}{ccc|c}
-1 & 0 &0 &6/(k+1)\0 & 1 & 0 & (7k+5)/(k+1) \ 0 & 0 & 1 & -2/(1+k)
end{array}right)
begin{array} {l}-1cdot{r_1}\phantom{0}\phantom{0}end{array}rightarrow
left(begin{array}{ccc|c}
1 & 0 &0 &-6/(k+1)\0 & 1 & 0 & (7k+5)/(k+1) \ 0 & 0 & 1 & -2/(1+k)
end{array}right)
$$
Из последней матрицы имеем: $left{begin{aligned}& x_1=-frac{6}{k+1};\& x_2=frac{7k+5}{k+1}\&x_3=-frac{2}{k+1}.end{aligned}right.$
Ответ:
- При $k=-1$ система несовместна.
- При $k=1$ система является неопределённой. Общее решение системы: $left{begin{aligned}& x_1=x_3-2;\& x_2=-x_3+5;\&x_3in{R}.end{aligned}right.$
- При $kneq{-1}$ и $kneq{1}$ система является определённой. Решение системы: $left{begin{aligned}& x_1=-frac{6}{k+1};\& x_2=frac{7k+5}{k+1}\&x_3=-frac{2}{k+1}.end{aligned}right.$
Пример №2
Исследовать СЛАУ $left{begin{aligned}
& 2kx_1+x_2+x_3=0;\
& x_1-x_2+kx_3=1;\
& (k-6)x_1+2x_2-4x_3=-3.end{aligned}right.$ на совместность и найти решение системы при тех значениях параметра, при которых она совместна.
Решение
Вновь, как и в предыдущем примере, для того, чтобы исследовать заданную систему на совместность, нам нужно найти ранг матрицы системы $A$ и ранг расширенной матрицы системы $widetilde{A}$. Чтобы исследовать систему на совместность и указать количество решений применим метод Крамера. Можно было бы решить и методом Гаусса, однако в предыдущем примере мы его уже использовали, поэтому для разнообразия решим задачу с помощью метода Крамера. Начнём с вычисления определителя матрицы системы. Этот определитель мы получим с помощью готовой формулы.
$$Delta{A}=left|begin{array}{ccc}
2k & 1 & 1\ 1 & -1 & k\ k-6 & 2 & -4end{array} right|=3k-3k^2=3k(1-k).$$
Если $Delta{A}neq{0}$, то ранги матрицы системы и расширенной матрицы системы согласно определению ранга равны 3. Так как ранги равны между собой и равны количеству неизвестных, т.е. $rang A=rangwidetilde{A}=3$, то система будет иметь единственное решение. Найдём это решение (случай $Delta{A}={0}$ рассмотрим позже).
$$
begin{aligned}
& Delta_{x_1}=left|begin{array}{ccc}
0 & 1 & 1\ 1 & -1 & k\ -3 & 2 & -4end{array} right|=3-3k=3(1-k);\
& Delta_{x_2}=left|begin{array}{ccc}
2k & 0 & 1\ 1 & 1 & k\ k-6 & -3 & -4end{array} right|=6k^2-9k+3=3(2k-1)(k-1);\
& Delta_{x_3}=left|begin{array}{ccc}
2k & 1 & 0\ 1 & -1 & 1\ k-6 & 2 & -3end{array} right|=3k-3=3(k-1).
end{aligned}
$$
Значения переменных $x_1$, $x_2$, $x_3$ будут такими:
$$x_1=frac{3(1-k)}{3k(1-k)}=frac{1}{k};;x_2=frac{3(2k-1)(k-1)}{3k(1-k)}=frac{1-2k}{k};;x_3=frac{3(k-1)}{3k(1-k)}=-frac{1}{k}.$$
Нам остаётся исследовать совместность системы при условии $Delta{A}=0$. Это равенство возможно при $k=0$ или $k=1$.
Случай $k=0$
Если $k=0$, то $Delta{A}=0$, при этом $Delta_{x_1}=3(1-0)=3$. Так как $Delta{A}=0$, то согласно определению ранга имеем: $rang{A}≤2$. Так как $Delta_{x_1}neq{0}$, то $rang{widetilde{A}}=3$. Следовательно, $rang{A}neqrangwidetilde{A}$, поэтому система несовместна, т.е. не имеет решений.
Нам остаётся рассмотреть последний случай: $k=1$.
Случай $k=1$
Для наглядности я запишу здесь матрицу системы $A$ и расширенную матрицу системы $widetilde{A}$, подставив $k=1$:
$$
A=left(begin{array}{ccc}
2 & 1 & 1\ 1 & -1 & 1\ -5 & 2 & -4end{array} right);;
widetilde{A}=left(begin{array}{ccc|c}
2 & 1 & 1 & 0\ 1 & -1 & 1 & 1\ -5 & 2 & -4 & -3end{array} right).$$
Если $k=1$, то $Delta{A}=0$. Это значит, что $rang{A}≤2$. Рассмотрим миноры второго порядка матрицы $A$. Например, возьмём минор, образованный на пересечении строк №1, №2 и столбцов №1, №2: $M=left|begin{array}{cc}2 & 1\ 1 & -1end{array}right|=-3$. Так как $Mneq{0}$, то ранг матрицы $A$ равен 2.
Найдём ранг расширенной матрицы системы. При $k=1$ имеем: $Delta{A}=Delta_{x_1}=Delta_{x_2}=Delta_{x_3}=0$. Все миноры третьего порядка матрицы $widetilde{A}$ либо совпадают с минорами $Delta{A}$, $Delta_{x_1}$, $Delta_{x_2}$, $Delta_{x_3}$, либо получаются из данных миноров перестановкой столбцов. Следовательно, все миноры третьего порядка матрицы $widetilde{A}$ равны нулю. Отсюда имеем вывод: $rang{widetilde{A}}≤2$. Минор $M$, записанный ранее, является также минором второго порядка матрицы $widetilde{A}$. Отсюда имеем вывод: $rang{widetilde{A}}=2$. Так как $rang{A}=rangwidetilde{A}=2<3$, то система явлется неопределённой, т.е. имеет бесконечное количество решений.
Найдём указанные решения, вновь применяя метод Крамера. Так как $rang{A}=2$, то система имеет два линейно независимых уравнения. Учитывая $Mneq{0}$, делаем вывод: первые два уравнения линейно независимы, – их и выберем. Дальнейшее решение будет таким же, как и решение примера №3 в разделе «Метод Крамера».
$$
left{begin{aligned}
& 2x_1+x_2+x_3=0;\
& x_1-x_2+x_3=1.end{aligned}right.
Rightarrow
left{begin{aligned}
& 2x_1+x_2=-x_3;\
& x_1-x_2=-x_3+1.end{aligned}right.$$
$$
begin{aligned}
& Delta = -3;;Delta_{x_1}=2x_3-1;;Delta_{x_2}=-x_3+2;\
& x_1=frac{-2x_3+1}{3};;x_2=frac{x_3-2}{3}.
end{aligned}
$$
Задача решена, осталось лишь записать ответ.
Ответ:
- При $k=0$ система несовместна.
- При $k=1$ система является неопределённой. Общее решение системы: $left{begin{aligned}& x_1=frac{-2x_3+1}{3};\& x_2=frac{x_3-2}{3};\&x_3in{R}.end{aligned}right.$
- При $kneq{0}$ и $kneq{1}$ система является определённой. Решение системы: $left{begin{aligned}& x_1=frac{1}{k};\& x_2=frac{1-2k}{k}\&x_3=-frac{1}{k}.end{aligned}right.$
Разберём ещё один пример, в котором рассмотрим СЛАУ с четырьмя уравнениями.
Пример №3
Исследовать СЛАУ $
left {begin{aligned}
& kx_1+x_2+x_3+x_4=1;\
& x_1+kx_2+x_3+x_4=1;\
& x_1+x_2+kx_3+x_4=1;\
& x_1+x_2+x_3+kx_4=1.end{aligned}right.$ на совместность и найти решение системы в зависимости от значений параметра $k$.
Решение
Применим метод Гаусса. При записи расширенной матрицы системы поместим первую строку вниз, на место четвёртой строки. А дальше начнём стандартные операции метода Гаусса.
$$
left(begin{array}{cccсc|c}
1 & k &1 &1&1 \
1 & 1 &k &1&1 \
1 & 1 &1 &k&1 \
k & 1 &1 &1&1 end{array} right)
begin{array} {l}phantom{0}\r_2-r_1\r_3-r_1\r_4-kcdot{r_1}end{array}rightarrow
left(begin{array}{ccccс|c}
1 & k &1 &1&1\
0 & 1-k &k-1 &0&0\
0 & 1-k &0&k-1&0\
0 & 1-k^2 &1-k &1-k&1-kend{array} right)
$$
Здесь можно было бы остановиться и рассмотреть случаи $k=1$ и $kneq{1}$ отдельно. Цель таких действий: разделить вторую, третью и четвёртую строки на $k-1$ при условии $k-1neq{0}$. Однако пока что полученная нами матрица содержит не столь уж громоздкие элементы, поэтому сейчас отвлекаться на частности я не вижу смысла. Продолжим преобразования в общем виде:
$$
left(begin{array}{ccccс|c}
1 & k &1 &1&1\
0 & 1-k &k-1 &0&0\
0 & 1-k &0&k-1&0\
0 & 1-k^2 &1-k &1-k&1-kend{array} right)
begin{array} {l}phantom{0}\phantom{0}\r_3-r_2\r_4-(k+1)r_2end{array}rightarrow \
rightarrow
left(begin{array}{ccccс|c}
1 & k &1 &1&1\
0 & 1-k &k-1 &0&0\
0 & 0 &1-k&k-1&0\
0 & 0 &(1-k)(k+2) &1-k&1-kend{array} right)
begin{array} {l}phantom{0}\phantom{0}\phantom{0}\r_4-(k+2)r_3end{array}rightarrow \
rightarrow
left(begin{array}{ccccс|c}
1 & k &1 &1&1\
0 & 1-k &k-1 &0&0\
0 & 0 &1-k&k-1&0\
0 & 0 &0&(1-k)(k+3)&1-kend{array} right)
$$
Мы привели расширенную матрицу системы к ступенчатому виду. До черты расположена преобразованная матрица системы. Ранги матриц $A$ и $widetilde{A}$ зависят от значения параметра $k$. Рассмотрим три случая: $k=1$, $k=-3$ и случай $kneq{1}$, $kneq{-3}$.
Случай $k=-3$
Если $k=-3$, то преобразованная матрица станет такой: $left(begin{array}{ccccс|c}
1 & -3 &1 &1&1\
0 & 4 &-4 &0&0\
0 & 0 &4&-4&0\
0 & 0 &0&0&4end{array}right)$. Так как $rang{A}=3$ и $rang{widetilde{A}}=4$, то $rang{A}neqrang{widetilde{A}}$, следовательно, система несовместна.
Случай $k=1$
Если $k=1$, то преобразованная матрица станет такой: $left(begin{array}{ccccс|c}
1 & 1 &1 &1&1\
0 & 0 &0 &0&0\
0 & 0 &0&0&0\
0 & 0 &0&0&0end{array}right)$. Ранги матрицы системы и расширенной матрицы системы равны между собой (и равны 1), но меньше, чем количество переменных, т.е. $rang{A}=rang{widetilde{A}}=1<4$. Вывод: система является неопределённой. Общее решение системы непосредственно получим из первой строки записанной матрицы:
$$x_1+x_2+x_3+x_4=1; Rightarrow ; x_1=-x_2-x_3-x_4+1.$$
Случай $kneq{1}$ и $neq{-3}$
Продолжим решение методом Гаусса. Так как $kneq{1}$ и $neq{-3}$, то $(1-k)(k+3)neq{0}$. Следовательно, мы можем разделить вторую и третью строки на $1-k$, четвёртую строку – на выражение $(1-k)(k+3)$. С полученной после этого матрицей продолжим операции обратного хода метода Гаусса:
$$
left(begin{array}{ccccс|c}
1 & k &1 &1&1\
0 & 1 &-1 &0&0\
0 & 0 &1&-1&0\
0 & 0 &0&1&frac{1}{k+3}end{array} right)
begin{array} {l}r_1-r_4\phantom{0}\phantom{0}\r_3+r_4end{array}rightarrow
left(begin{array}{ccccс|c}
1 & k &1 &0&frac{k+2}{k+3}\
0 & 1 &-1 &0&0\
0 & 0 &1&0&frac{1}{k+3}\
0 & 0 &0&1&frac{1}{k+3}end{array}right)
begin{array} {l}r_1-r_3\r_2+r_3\phantom{0}\phantom{0}end{array}rightarrow\
rightarrowleft(begin{array}{ccccс|c}
1 & k &0 &0&frac{k+1}{k+3}\
0 & 1 &0 &0&frac{1}{k+3}\
0 & 0 &1&0&frac{1}{k+3}\
0 & 0 &0&1&frac{1}{k+3}end{array}right)
begin{array} {l}r_1-kcdot{r_2}\phantom{0}\phantom{0}\phantom{0}end{array}rightarrow
left(begin{array}{ccccс|c}
1 & 0 &0 &0&frac{1}{k+3}\
0 & 1 &0 &0&frac{1}{k+3}\
0 & 0 &1&0&frac{1}{k+3}\
0 & 0 &0&1&frac{1}{k+3}end{array}right)
$$
Из последней матрицы имеем: $x_1=x_2=x_3=x_4=frac{1}{k+3}$.
Ответ:
- При $k=-3$ система несовместна.
- При $k=1$ система является неопределённой. Общее решение системы: $left{begin{aligned}& x_1=-x_2-x_3-x_4+1;\&x_2in{R},;x_3in{R},;x_4in{R}. end{aligned}right.$
- При $kneq{-3}$ и $kneq{1}$ система является определённой. Решение системы: $x_1=x_2=x_3=x_4=frac{1}{k+3}$.
Ранг матрицы — определение и вычисление с примерами решения
Содержание:
Элементарные преобразования матриц:
Рассмотрим прямоугольную матрицу:
состоящую из m строк и n столбцов. В п.3.2 отмсчалось, что каждую строку матрицы можно рассматривать как n-мсрный вектор, а каждый столбец — как m-мерный вектор. Тогда матрицу А можно записать в виде:
и, следовательно, данную матрицу можно рассматривать как систему вектор строк или вектор столбцов. Б указанных системах вектор-строк и вектор-столбцов можно выделять линейно независимые (зависимые) векторы. Тогда будем говорить, что строки (столбцы) матрицы линейно независимы (зависимы), если соответствующие им векторы независимы (зависимы).
Определения
Определение: Рангом системы строк (соответственно столбцов) матрицы А называется наибольшее число линейно независимых среди них.
Поскольку легко доказать, что ранг системы строк матрицы равен рангу системы её столбцов, то справедливо следующее
Определение: Рангом матрицы, обозначаемым r(А), называется максимальное число линейно независимых строк (столбцов) матрицы.
При транспонировании матрицы ранг её не изменяется.
Другой метод определения ранга матрицы связан с понятием определителя.
Выделим в матрице А любые k строк и k столбцов. Элементы, стоящие на их пересечении, образуют квадратную матрицу, определитель которой называется минором k-го порядка матрицы А. Ясно, что величина к должна удовлетворять двум условиям: 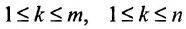
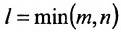
Определение: Рангом матрицы, обозначаемым r(А), называется порядок самого старшего минора этой матрицы, не равного нулю.
Из определения следует, что если ранг матрицы А равен l, то среди всех её миноров существует хотя бы один минор l-го порядка, отличный от нуля, но все миноры (l+1)-го порядков либо равны нулю, либо не могут быть составлены.
Вычисление ранга матрицы путём перебора всех её миноров весьма трудоёмко. Существует, однако, более простой способ вычисления ранга матрицы, основанный на упрощении структуры матрицы с помощью элементарных преобразований. Элементариыми преобразованиями матрицы называют следующие преобразования:
- обмен местами двух строк или двух столбцов матрицы;
- умножение всех элементов строки или столбца матрицы на произвольное число
, не равное нулю;
- прибавление ко всем элементам строки (столбца) матрицы соответствующих элементов другой строки (столбца), предварительно умноженных на одно и то же число;
- исключение из матрицы строки или столбца, состоящего из нулей.
Матрицы называются эквивалентными, если от одной из них к другой можно перейти путём конечного числа элементарных преобразований.
Ступенчатой матрицей называется матрица, удовлетворяющая тому свойству, что если в какой-либо из сё строк первый отличный от нуля элемент стоит на l-м месте, то во всех следующих строках на первых l местах стоят нули:
где элементы 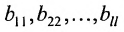
Для вычисления ранга матрицы приводят её с помощью цепочки элементарных преобразований к ступенчатому виду. Тогда ранг матрицы совпадает с числом её ненулевых диагональных элементов.
Теоремы о ранге матриц. Свойства ранга матриц
Относительно ранга матриц можно сформулировать следующие теоремы:
Теорема: Если матрица имеет минор порядка r, отличный от нуля, для которого все содержащие его миноры порядка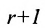
Вычисление ранга матрицы при помощи метода окаймления нужно вести от низших порядков к высшим. Сначала ищем минор первого порядка (т.е. элемент матрицы) или сразу второго порядка, отличный от нуля. Затем вычисляем окаймляющие его миноры следующего порядка, пока не найдём среди них отличного от нуля и т.д., пока не найдем минор порядка l, отличный от нуля, для которого либо все окаймляющие его миноры порядка l+1 равны нулю, либо такие миноры не могут быть составлены.
Теорема: Элементарные преобразования не меняют ранга матрицы.
Доказательство теоремы следует из определения ранга матрицы и свойств определителей.
Пример:
Найти ранг матрицы:
Решение:
Минор первого порядка в левом верхнем углу равен 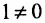
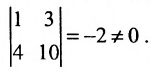
Значит ранг матрицы равен 2.
Пример:
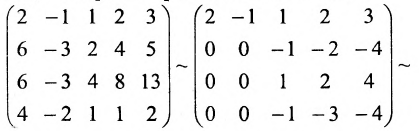
Найти ранг матрицы:
Решение:
При помощи элементарных преобразований приведём данную матрицу к ступенчатому виду. На первом шаге умножим последовательно первую строку на 3, 3, 2 и вычтем из второй, третьей, четвёртой строк соответственно:
В эквивалентной матрице прибавим к третьей строке вторую и вычтем вторую из четвёртой строки:
(поменяем местами третью и четвертую строки)
(поменяем местами третий, четвёртый и пятый столбцы со вторым и опустим строки, состоящие из нулей) 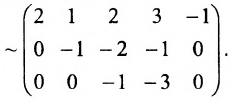
Отмстим некоторые свойства ранга матриц.
- Ранг суммы двух (или нескольких) матриц не больше суммы их рангов.
- Любую матрицу ранга r можно представить в виде суммы r матриц ранга 1, но нельзя представить в виде суммы менее чем r таких матриц.
- Любую матрицу С ранга r можно представить в виде произведения
, где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.
- Ранг произведения матриц порядка n удовлетворяет неравенству
.
Определение системы m линейных уравнений с n неизвестными
Системой m линейных уравнений с n неизвестными 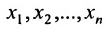
Числа 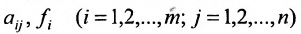
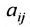
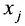
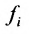
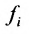
С помощью знака суммирования 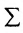
составленная из коэффициентов системы 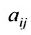
системы. Если к этой матрице добавить столбец свободных членов, то получим расширенную матрицу системы: 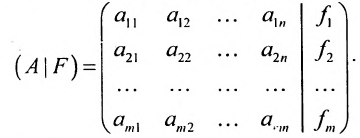
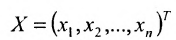
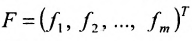

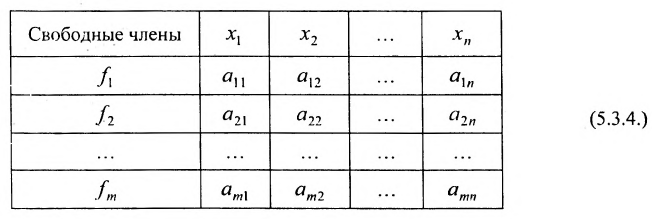
Используется также табличная форма записи системы (5.3.1):
Отметим, что (5.3.1), (5.3.2), (5.3.3), (5.3.4)- различные виды записи одной и той же системы линейных уравнений.
Решением системы (5.3.1) называется любой упорядоченный набор действительных чисел 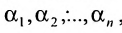
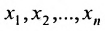
Система уравнений (5.3.1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Две системы уравнений с одинаковыми наборами неизвестных 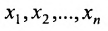
Отмстим, что для любой системы (5.3.1) возможны только три случая:
- система (5.3.1) имеет единственное решение;
- система (5.3.1) имеет бесчисленное множество решений;
- система (5.3.1) несовместна.
Множество всех решений системы (5.3.1) называется ее общим решением.
Решить систему (5.3.1) — значит найти ее общее решение.
Пример:
Пусть задана система
Тогда эту систему можно записать в матричном виде:
или в виде таблицы:
Система определенная, так как она имеет единственное решение 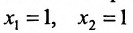
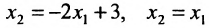
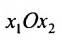
Экономические задачи, приводящие к системе линейных уравнений
Предположим, что производственные мощности для изготовления n различных видов продукции установлены в т цехах. Пусть 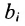
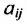
Широкий круг задач экономики приводит к составлению системы уравнений. Так в примере 4.3.2 составлялась система линейных уравнений (4.3.1) балансовой модели для трёх отраслей. В общем случае под балансовой моделью понимается система уравнений, каэ/сдое из которых выражает требование баланса между производимым количеством продукции и совокупной потребностью в этой продукции.
При построении балансовых моделей используется понятие чистой (или технологической) отрасли, т.е. условной отрасли, объединяющей всё производство данного продукта независимо от ведомственной (административной) подчинённости и форм собственности предприятий и фирм. Всё народное хозяйство представляется в виде совокупности п отраслей, каждая из которых рассматривается как производящая и как потребляющая.
Если обозначить через:
то систему уравнений баланса можно записать в виде:
или в матричной форме:
где Х- вектор-столбец валовой продукции; Y- вектор-столбец конечной продукции; А — матрица коэффициентов прямых затрат.
Основу экономико-математической модели межотраслевого баланса составляет технологическая матрица А, содержащая коэффициенты прямых затрат на производство единицы продукции:
Коэффициент. прямых затрат являются довольно стабильной величиной во времени.
Переписав матричное уравнение (5.4.2) в виде EX-AX = Y или (E-A)X = Y, (5.4.3) получим стандартную форму записи системы уравнений.
Определение ранга матрицы
Рассмотрим прямоугольную матрицу (4.1). Если в этой матрице выделить произвольно 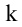
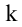
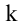
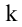
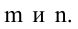
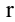
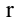
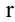
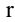
Очевидно, что выполняется соотношение
Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D 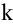
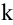
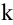
Элементарными называются следующие преобразования матрицы:
- перестановка двух любых строк (или столбцов),
- умножение строки (или столбца) на отличное от нуля число,
- прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.
Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.
Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: А
Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы
равны нулю, например,
При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.
Пример:
Найти методом окаймления миноров ранг матрицы
Решение:
Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) 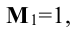
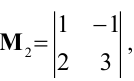
Переходим теперь к минорам 3-го порядка, окаймляющим 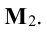
Таким образом, асе окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум.
Пример:
Найти ранг матрицы 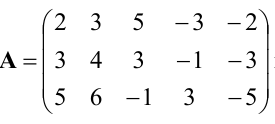
Решение:
Из второй строки вычтем первую и переставим эти строки:
Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:
из третьей строки вычтем первую; получим матрицу 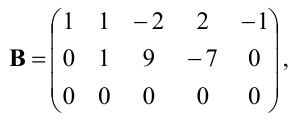
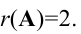
Вычисление ранга матрицы
Для исследования разрешимости систем линейных уравнений важную роль играет понятие ранга матрицы. Рассмотрим прямоугольную матрицу А
Выделим k произвольных строк и k произвольных столбцов этой матрицы. Определитель k-го порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называется минором k-го порядка матрицы А.
Рангом матрицы А называется наибольший порядок ее миноров, отличных от нуля. Обозначение: rank А,
Базисным минором матрицы называется всякий отличный от нуля ее минор, порядок которого равен рангу матрицы.
Рассмотрим некоторые методы вычисления ранга матрицы.
Метод окаймляющих миноров
Минор порядка k+1, содержащий в себе минор порядка k, называется окаймляющим минором.
Вычисляя ранг матрицы, удобнее переходить от миноров меньших порядков к минорам больших порядков. Если найден минор k-го порядка, отличный от нуля, а все окаймляющие его миноры порядка k+1 равны нулю, то ранг матрицы равен k.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Определители второго и третьего порядков и их свойства
- Метод Гаусса — определение и вычисление
- Прямая линия на плоскости и в пространстве
- Плоскость в трехмерном пространстве
- Кратный интеграл
- Ряды в математике
- Дифференциальные уравнения с примерами
- Обратная матрица — определение и нахождение
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
20. Решение системы линейных уравнений с помощью ранга матрицы
Пусть дана система линейных уравнений (25), коэффициенты которых принадлежат данному полю Р.
Пусть А = (26) матрица этой системы и А1 = (27) расширенная матрица. Если система (25) имеет хотя бы одно решение, то её называют Совместной, в противном случае система Несовместная. Если все слагаемые, содержащие неизвестные, стоят в левых частях уравнений, а свободные члены – в правых частях, то система называется Приведённой. Если в системе (25) хотя бы один свободный член отличен от нуля, то эта система называется Неоднородной. Если же все свободные члены равны нулю, то имеем систему Линейных однородных уравнений.
Теорема 26 (теорема Кронекера – Капелли). Система линейных уравнений совместна тогда и только тогда, когда ранг её матрицы равен рангу расширенной матрицы.
Доказательство. Þ Пусть система (25) совместна. Следовательно, существуют такие элементы A1, A2, … , AN , что
Записав эти равенства в векторной форме, получим, что В = A1×А1 + A2×А2 + … + AN×АN , где А1, а2, … , АN –векторы-столбцы матрицы А, В – вектор-столбец свободных членов. Из последнего равенства следует, что системы векторов А1, а2, … , АN и А1, а2, … , АN , В эквивалентны, поэтому их ранги равны. Итак, rang A = rang A1.
Ü Пусть rang A = rang A1 = К. Не нарушая общности, можно считать, что отличный от нуля минор К-го порядка в матрице А Стоит в левом верхнем углу. Векторы-столбцы обозначим А1, а2, … , Ак, ак+1, … , АN, В (*). Система А1, а2, … , Ак Будет максимальной линейно независимой подсистемой в системе (*), следовательно, найдутся такие коэффициенты Х10, х20, … , хк0, Что В = Х10 А1 + Х20 А2 + … + Хк0 Ак. Это равенство равносильно равенству В = Х10 А1 + Х20 А2 + … + Хк0 Ак + … + 0×Ак+1 + … + 0×АN. Перейдя к координатам, получим:
(28)
Отсюда следует, что (Х10, х20, … , хк0, 0,… ,0) – решение системы (25), т. е. эта система совместна.
Из теоремы Кронекера – Капелли следуют правила решения системы линейных уравнений.
Для решения системы линейных уравнений достаточно
1. Найти ранги основной и расширенной матриц ( А и А1 ). Если rang A ¹ rang A1, То система не имеет решения.
2. Если rang A = rang A1 = К, то для решения достаточно оставить К Уравнений, коэффициенты которых стоят на тех строчках матрицы А, На которых стоит базисный минор, и в этих уравнениях оставить в их левых частях те неизвестные, коэффициенты которых входят в базисный минор. Остальные неизвестные нужно перенести в правые части уравнений. Они могут принимать все возможные значения из поля Р. Эти неизвестные называются Свободными. (Не нарушая общности, можно считать, что оставлены первые К уравнений и первые К неизвестных, система (29)).
(29)
Определитель левой части системы (29) отличен от нуля, число уравнений равно числу неизвестных, поэтому (по теореме Крамера) эта система при всевозможных Хк+1, … , хN имеет единственное решение.
Условие совместности системы линейных уравнений. Теорема Кронекера-Капелли
Установить, совместна ли система линейных уравнений, с помощью теоремы Кронекера-Капелли часто можно быстрее, чем с помощью метода Гаусса, когда требуется последовательно исключать неизвестные. Основана эта теорема на использовании ранга матрицы.
Теорема Кронекера-Капелли о совместности системы. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы этой системы равен рангу её расширенной матрицы, то есть чтобы .
Здесь матрица A (матрица системы) — это матрица, составленная из коэффициентов при неизвестных:
В свою очередь матрица В (расширенная матрица) — это матрица, полученная присоединением к матрице системы столбца из свободных членов:
Ранги этих матриц связаны неравенством , при этом ранг матрицы В может быть лишь на одну единицу больше ранга матрицы A.
Следствие из теоремы Кронекера-Капелли о числе решений. Пусть для системы m линейных уравнений с n неизвестными выполнено условие совместности, то есть ранг матрицы из коэффициентов системы равен рангу её расширенной матрицы. Тогда верно следующее.
- Если ранг матрицы равен числу неизвестных (), то система имеет единственное решение.
- Если ранг матрицы системы меньше числа неизвестных (), то система имеет бесконечно много решений, а именно: некоторым n — r неизвестным можно придавать произвольные значения, тогда оставшиеся r неизвестных определятся уже единственным образом.
Если ранг матрицы системы линейных уравнений равен числу уравнений, то есть , то система совместна при любых свободных членах. В этом случае ранг расширенной матрицы также равен m, так как ранг матрицы не может быть больше числа её строчек.
В ходе доказательства теоремы Кронекера-Капелли были получены явные формулы для решений системы (в случае её совместности). Если уже известно, что система совместна, то, чтобы найти её решения, необходимо:
1) отыскать в матрице системы A ранга отличный от нуля минор порядка, равного рангу матрицы системы, то есть ранга r;
2) отбросить те уравнения, которые соответствуют строкам матрицы A, не входящим в минор ;
3) члены с коэффициентами, не входящими в , перенести в правую часть, а затем, придавая неизвестным, находящимся в правой части, произвольные значения, определить по формулам Крамера оставшиеся r неизвестных из системы r уравнений с отличным от нуля определителем .
Пример 1. Следуя теореме Кронекера-Капелли, установить, совместна ли система уравнений
Если система совместна, то решить её.
Решение. Вычисляем ранг матрицы этой системы и ранг расширенной матрицы. В обоих случаях он равен 3. Следовательно, система линейных уравнений совместна. Так как ранг матрицы системы меньше числа неизвестных, то система имеет бесконечно много решений: одно неизвестное может быть взято произвольно. Минор
отличен от нуля, поэтому последнее уравнение отбрасываем и неизвестному придаём произвольное значение .
Оставшиеся неизвестные определяются из системы
Решая последнюю систему по формулам Крамера или иным способом, находим
,
,
.
Присоединяя сюда , получаем все решения данной системы линейных уравнений.
Пример 2. Следуя теореме Кронекера-Капелли, установить, совместна ли система уравнений
Если система совместна, то решить её.
Решение. Вычисляем ранг матрицы этой системы:
.
Следовательно, ранг системы равен 3. Определим ранг расширенной матрицы:
.
Это означает, что ранг расширенной матрицы также равен 3. Следовательно, система совместна, а так как число неизвестных равно рангу матрицы системы, то она имеет единственное решение. Для решения можем использовать первые три уравнения:
Решая последнюю систему по формулам Крамера, находим
,
,
.
http://matica.org.ua/metodichki-i-knigi-po-matematike/lineinaia-algebra-uchebnoe-posobie-z-i-andreeva/20-reshenie-sistemy-lineinykh-uravnenii-s-pomoshchiu-ranga-matritcy
http://function-x.ru/systems_kroneker_kapelli.html
Задача 1.
Определить ранг матрицы
Указание
Единственным минором максимального (3-го) порядка для матрицы А является ее определитель. Если ΔА не равен нулю, R(A) = 3; если ΔА = 0, R(A) < 3.
Решение
Единственным минором максимального (3-го) порядка для матрицы А явля-ется ее определитель. Если ΔА не равен нулю, R(A) = 3; если ΔА = 0, R(A) < 3.
Найдем ΔА разложением по первой строке:
Следовательно, R(A) < 3. Поскольку матрица А содержит ненулевые элементы, R(A) > 0. Значит, R(A) = 1 или R(A) = 2. Если найдется минор 2-го порядка, не равный нулю, то R(A) = 2.
Вычислим минор из элементов, стоящих на пересечении двух первых строк и двух первых столбцов:
Ответ: R(A) = 2.
Если найден минор K-го порядка, не равный нулю, то можно утверждать, что R(A) ≥ K. Если же выбранный минор K-го порядка равен нулю, то из этого еще не следует, что R(A) < K, так как могут найтись миноры того же порядка, не равные нулю.
Задача 2.
Определить ранг матрицы
Указание
Используя элементарные преобразования, приведите матрицу А к треугольному виду.
Решение
У матрицы А существуют миноры до 4-го порядка включительно, поэтому
R(A) ≤ 4. Разумеется, непосредственное вычисление всех миноров 4-го, 3-го и т. д. порядка потребовало бы слишком много времени. Поэтому, используя элементарные преобразования, приведем матрицу А к треугольному виду. Поменяем местами 1-ю и 2-ю строки, чтобы элемент А11 стал равным 1:
Прибавим к третьей строке первую, ко второй – удвоенную первую, к четвертой – первую, умноженную на 3. Тогда все элементы 1-го столбца, кроме А11, окажутся равными нулю:
Вычтем вторую строку полученной матрицы из третьей и четвертой строк:
И вычеркнем нулевые строки:

Итак, ранг матрицы А равен рангу полученной матрицы размера , т. е.
R(A) < 2. Минор
Следовательно, R(A) = 2.
Ответ: R(A) = 2.
Задача 3.
Определить ранг матрицы
Указание
Используя элементарные преобразования, приведите матрицу А к треугольному виду.
Решение
Отметим, что минор, составленный из элементов матрицы, стоящих на пересечении первых трех строк и первых трех столбцов, не равен нулю:
Поэтому ранг данной матрицы не меньше трех.
Приведем матрицу к треугольному виду:
Вычеркивание нулевых строк приводит к тому, что
Размер полученной матрицы , поэтому ее ранг не более трех. Поскольку минор 3-го порядка, не равный нулю, существует, ранг исходной матрицы равен 3.
Ответ: R(A) = 3.
Задача 4.
Найти значения L, при которых матрица
Имеет наименьший ранг.
Указание
Приведите матрицу А к треугольному виду и найдите значения L, при которых с помощью элементарных преобразований вторую строку можно сделать нулевой.
Решение
Переставим столбцы матрицы А:
И приведем ее к треугольному виду с помощью элементарных преобразований:
Теперь видно, что при L = 0 вторая строка матрицы становится нулевой, и после ее вычеркивания получаем:
Минор 
Если L ≠ 0, то минор, составленный из последних трех столбцов, имеет вид:
Значит, при L ≠ 0 R(A) = 3.
Итак, наименьший ранг, равный 2, матрица А имеет при L= 0.
Ответ: L = 0.
| < Предыдущая | Следующая > |
|---|
Содержание
Ранг матрицы
Метод окаймляющих миноров
Задача 1. Найти ранг матрицы

методом окаймляющих миноров.
Решение. Метод окаймляющих миноров позволяет найти минорный ранг матрицы.
-
Выберем ненулевой минор
порядка 1, построенный на первой строке и первом столбце матрицы.
-
Чтобы найти окаймляющий минор для
, нужно к нему добавить по одной строке и одному столбцу. То есть минор второго порядка
, окаймляющий
должен содержать первую строку и первый столбец матрицы. Таких миноров несколько, выберем любой из них, не равный нулю. Например,
, построенный на 1-й и 2-й строках, 1-м и 4-м столбцах.
-
Далее ищем ненулевой минор третьего порядка
, окаймляющий
. Добавим к 1-й и 2-й строкам 4-ю строку, а к 1-му и 4-му столбцам — 2-й столбец. Получим
.
-
Пытаемся найти ненулевой окаймляющий минор для
. Для этого перебираем окаймляющие миноры 4-го порядка:
-
на 1-й, 2-й, 3-й, 4-й строках и 1-м, 2-м, 3-м, 4-м столбцах:
,
-
на 1-й, 2-й, 3-й, 4-й строках и 1-м, 2-м, 4-м, 5-м столбцах:
.
-
Получается, что все окаймляющие миноры четвертого порядка равны нулю, а минор третьего порядка 
Задача 2. Определить ранг матрицы

при различных значениях 
Решение. Решим задачу с помощью метода окаймляющих миноров.
-
Выберем минор порядка 1, стоящий на 1-й строке в 1-м столбце, то есть левый верхний.
.
-
Выберем минор порядка 2, окаймляющий
, добавив 2-ю строку и 4-й столбец.
. Он отличен от нуля, поэтому ранг
. Заметим, что ранг не может быть больше трех, так как матрица содержит три строки. Таким образом, возможны два варианта:
или
.
-
Предположим, что
, тогда окаймляющие миноры третьего порядка для
должны быть равны нулю, то есть мы
требуем, чтобы-
;
-
.
-
По правилу треугольника получаем, что 

Таким образом, 

Очевидно, что единственным решением этой системы является 
-
ранг
при
и
-
при
.
Метод элементарных преобразований
Какие преобразования матриц называются элементарными, можно прочитать в определении 3.
Задача 3. Найти ранг матрицы

методом элементарных преобразований.
Решение. Приведем матрицу к ступенчатому виду.
-
Прибавив ко второй строке первую, умноженную на -1, получим матрицу
.
-
Прибавив к третьей строке первую, умноженную на -2, получим матрицу
.
-
Прибавив к четвертой строке первую, умноженную на -2, получим матрицу
.
-
Прибавляя к третьей строке вторую, умноженную на 3, получим
.
-
Прибавляя к четвертой строке вторую, умноженную на 4, получим
.
-
Переставляя две последние строки, получаем матрицу ступенчатого вида
.
-
Горизонтальный ранг этой матрицы равен 3 — числу ненулевых строк. Так как элементарные преобразования не меняют ранга матрицы (предложение 1), то ранг исходной матрицы равен 3.
Наверх

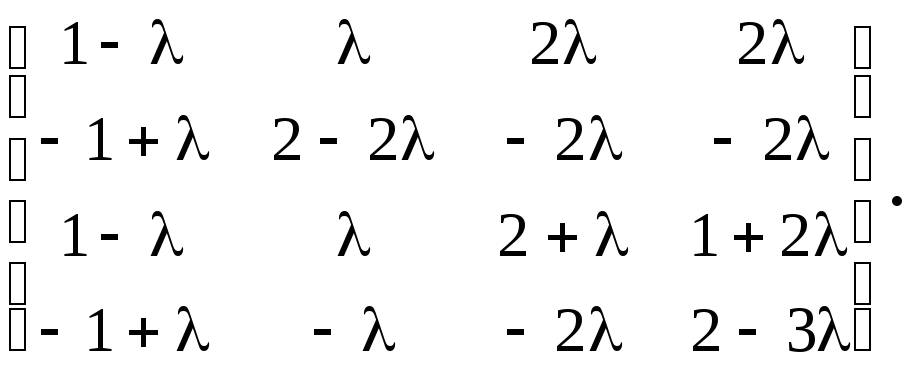
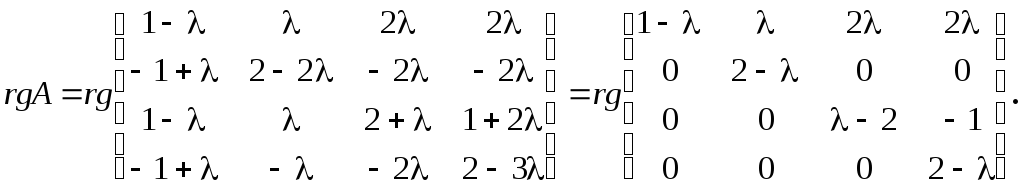
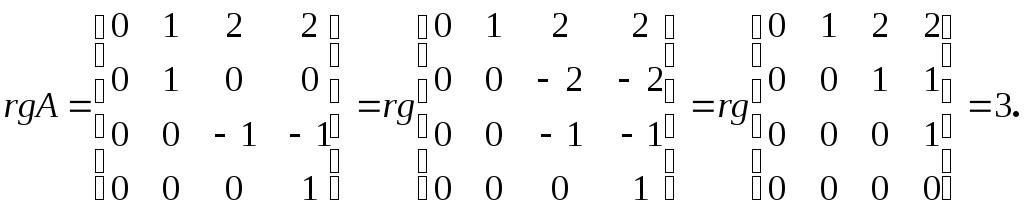
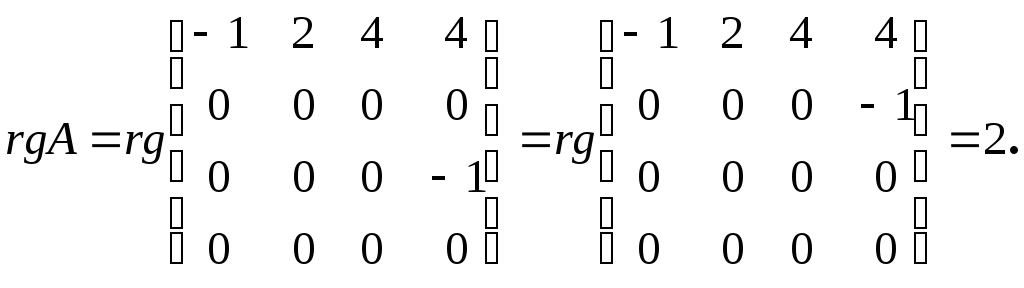
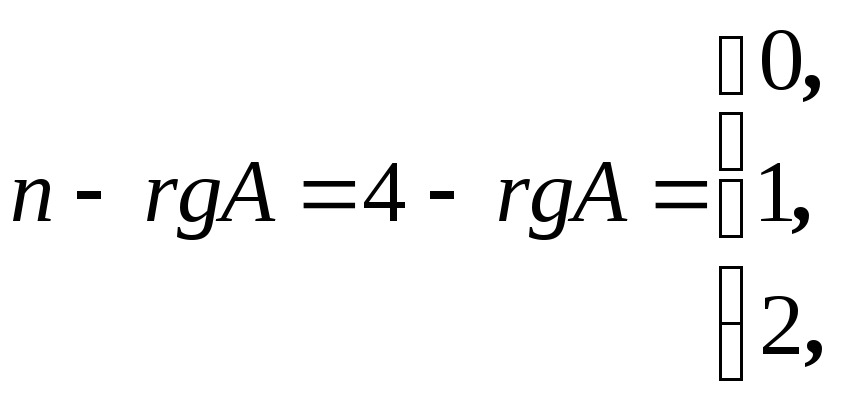
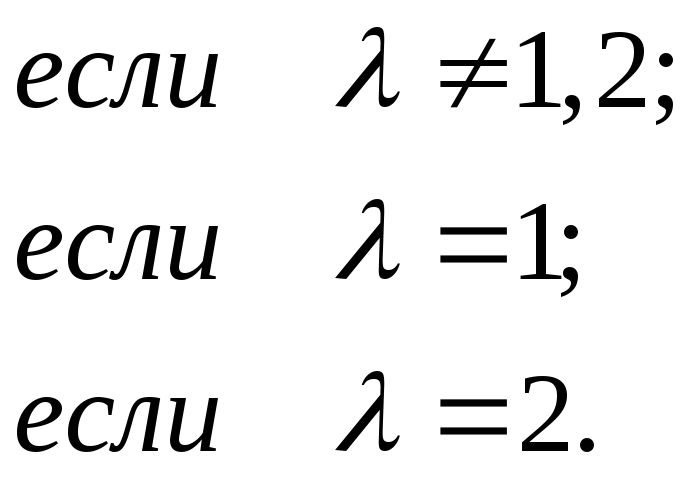
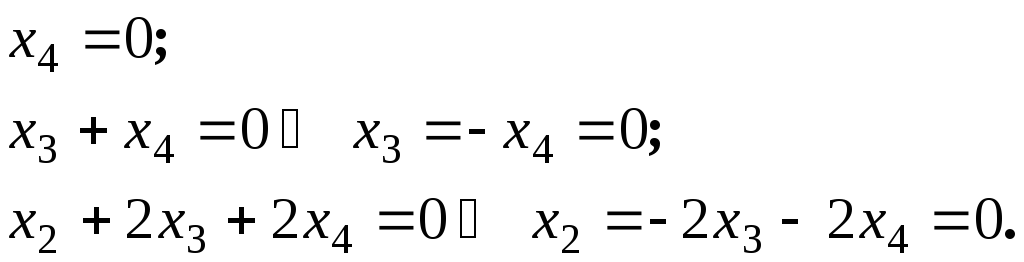
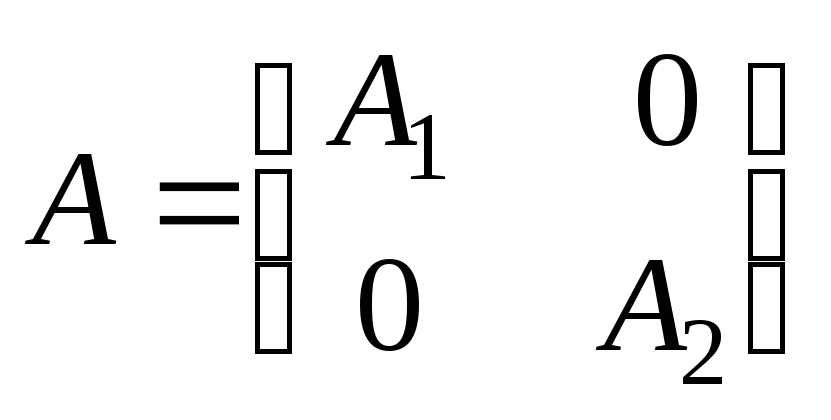
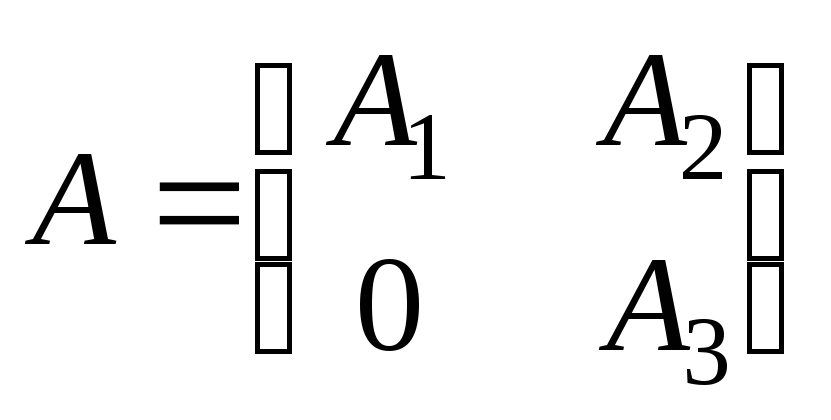
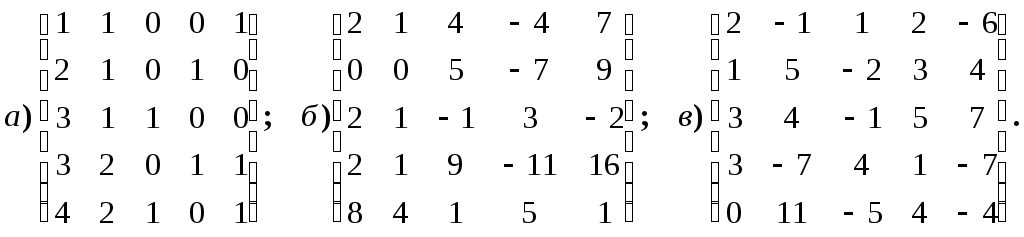
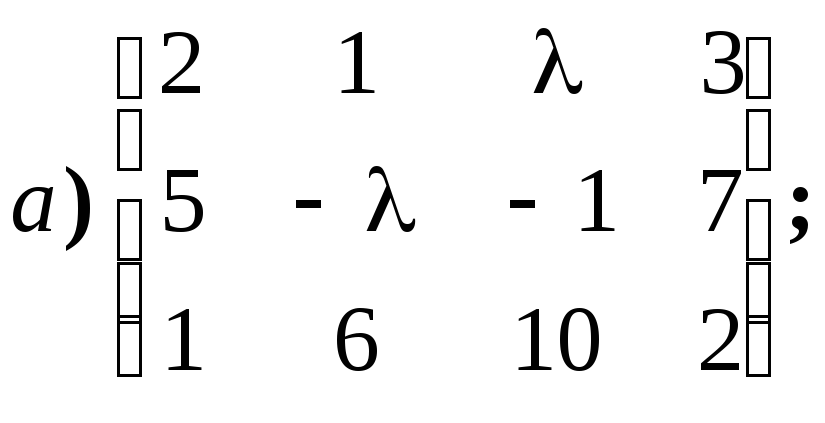
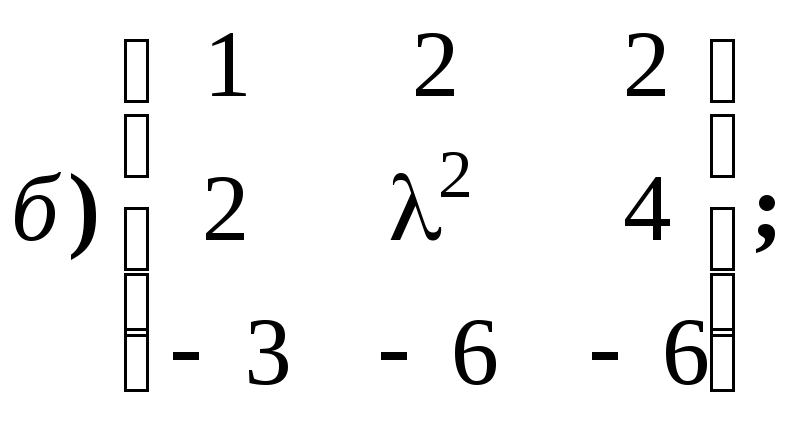
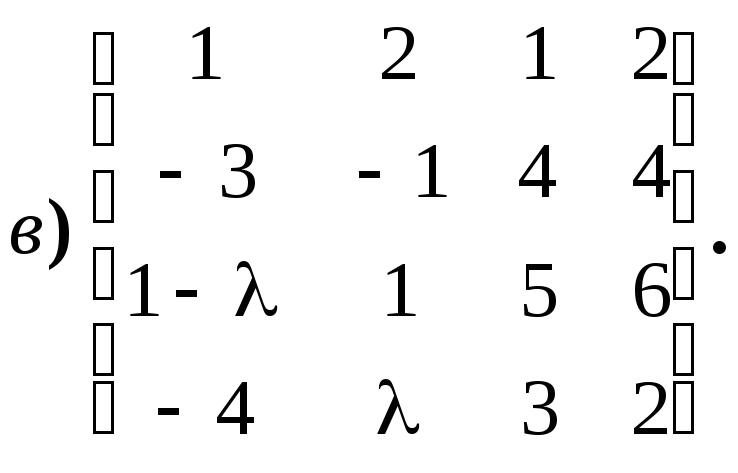
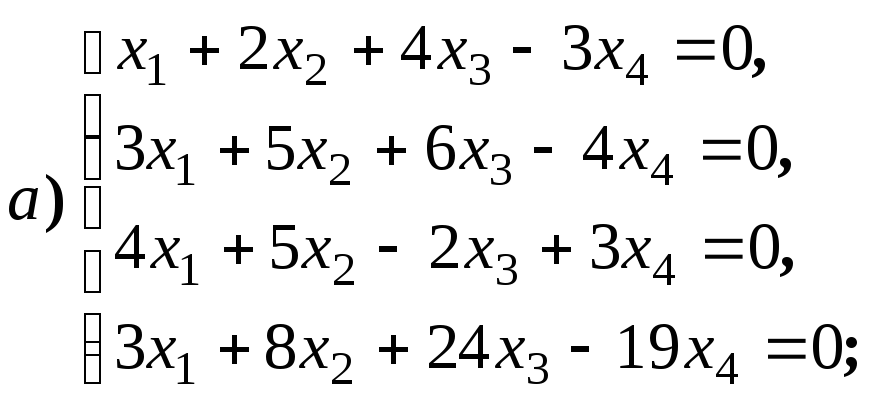
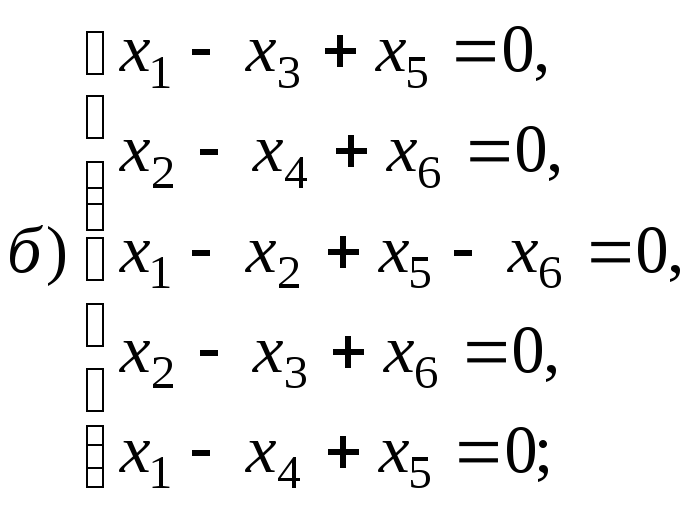
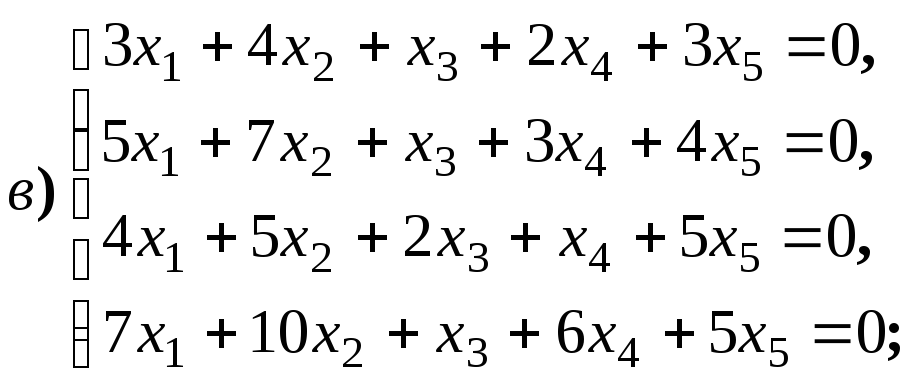
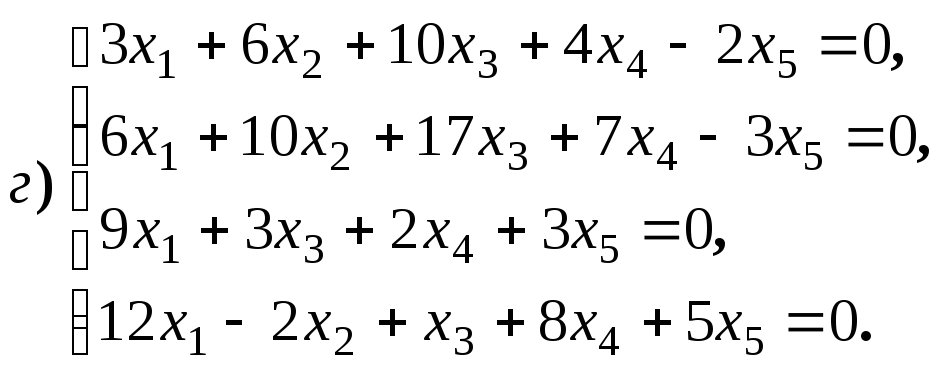

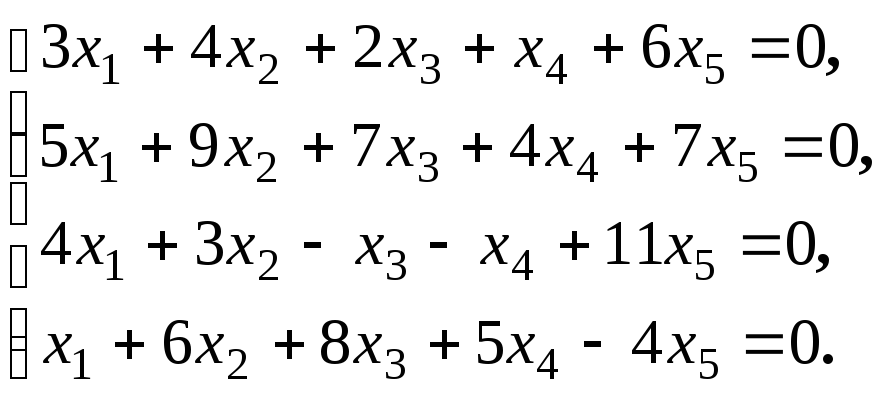
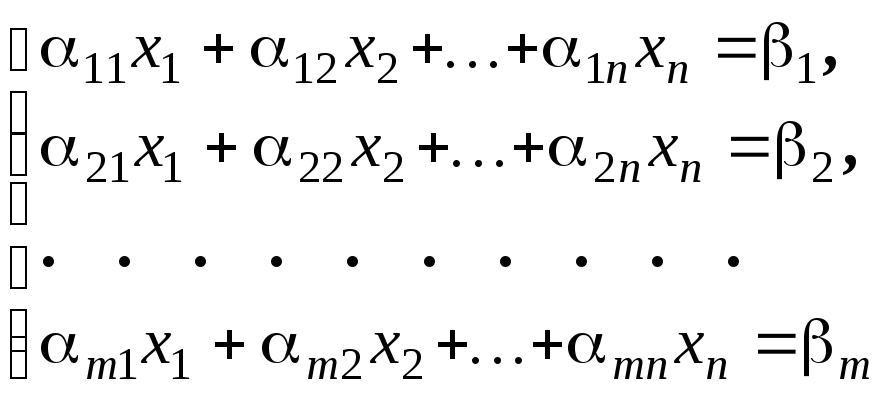


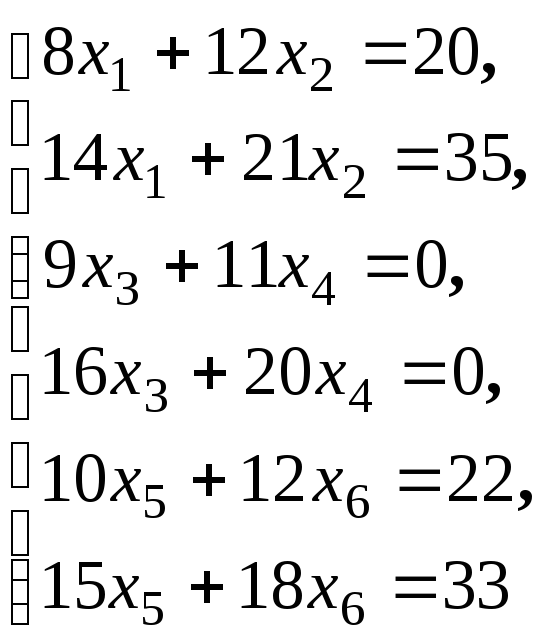

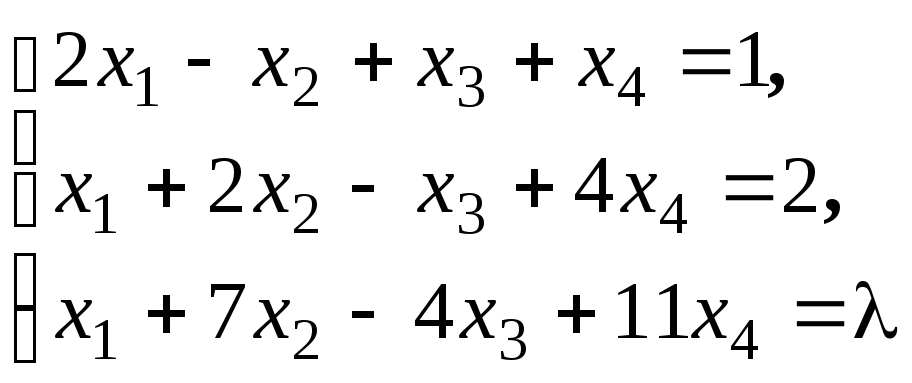

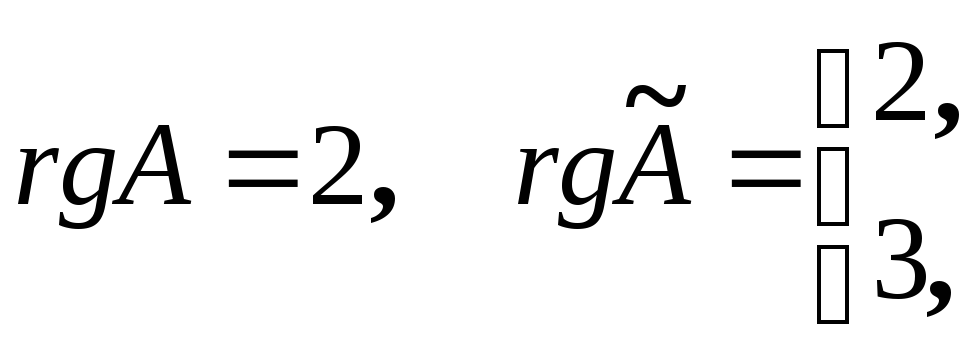
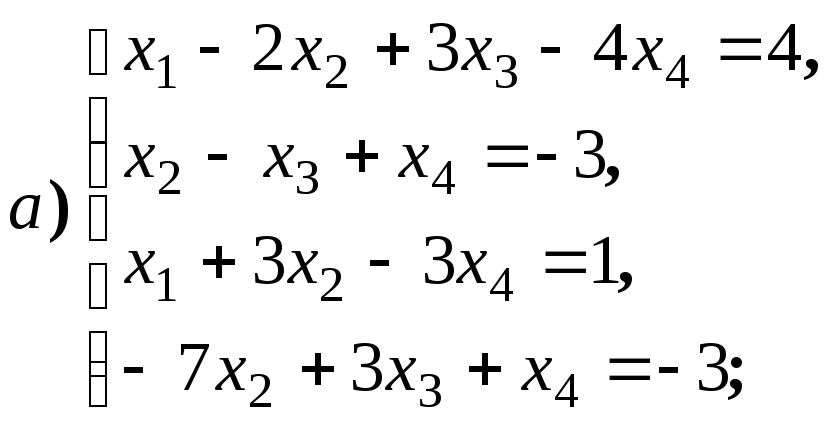

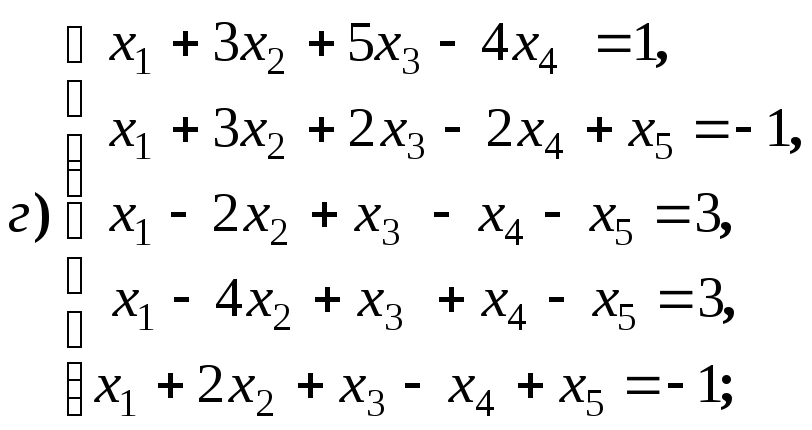
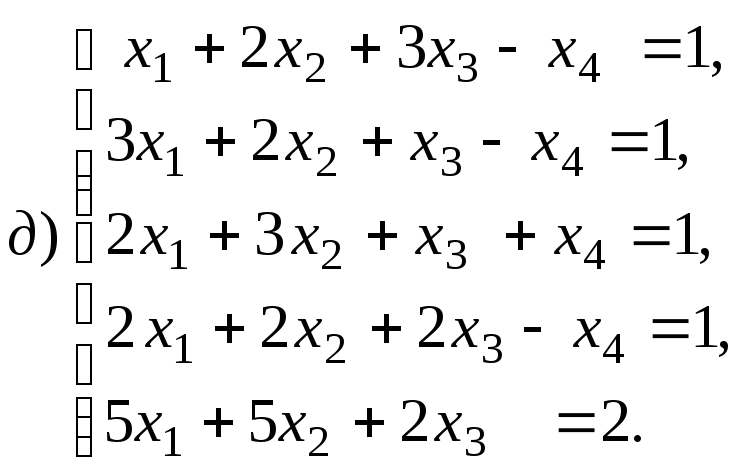
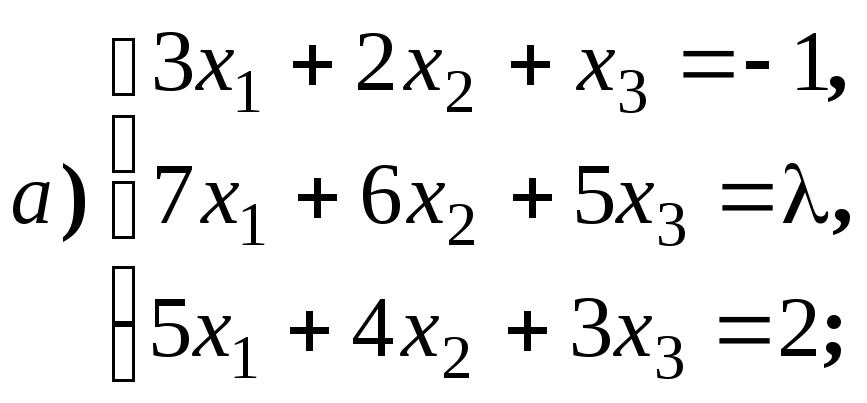
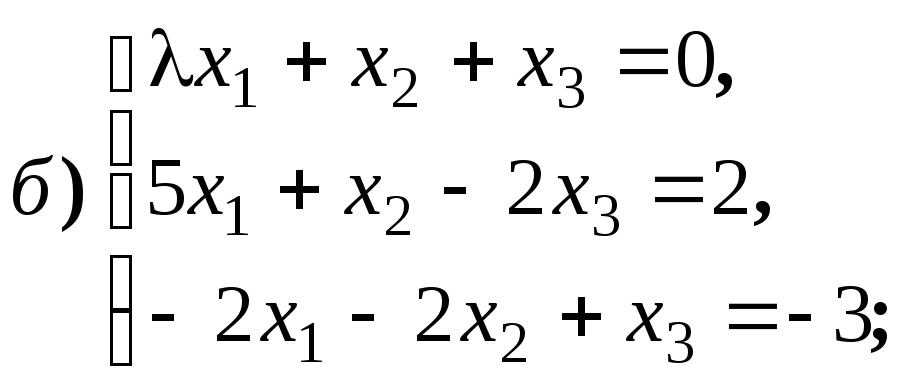
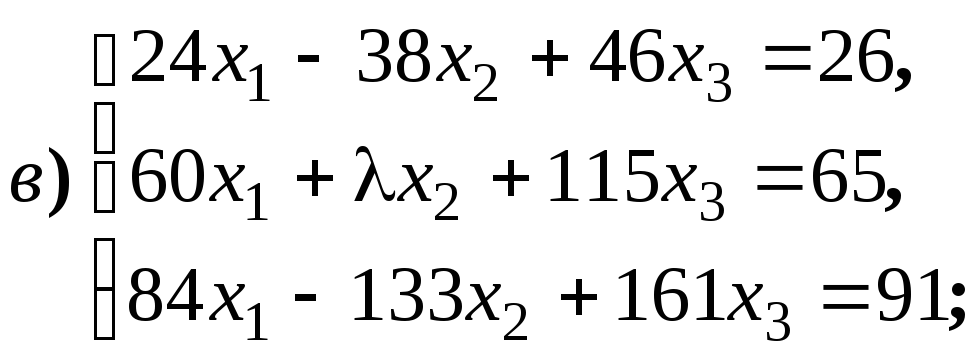
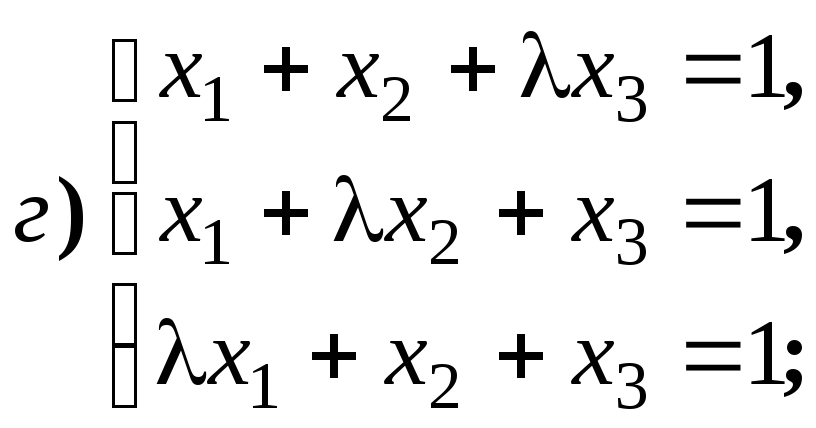
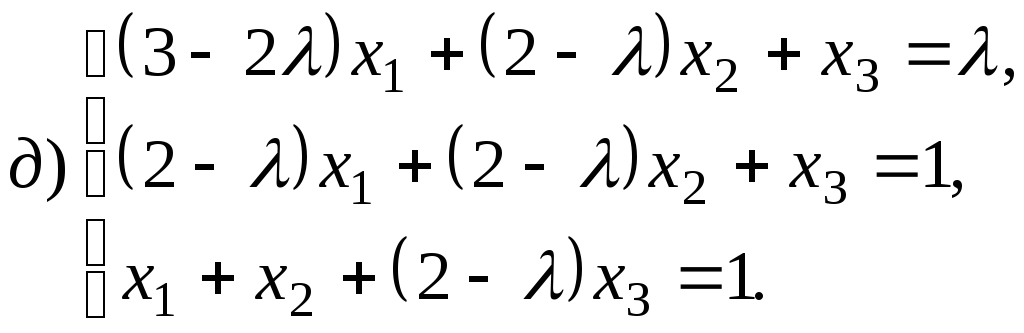
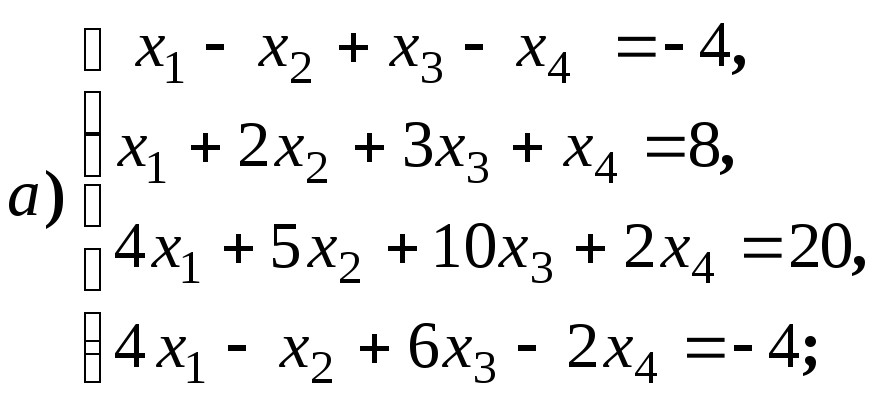
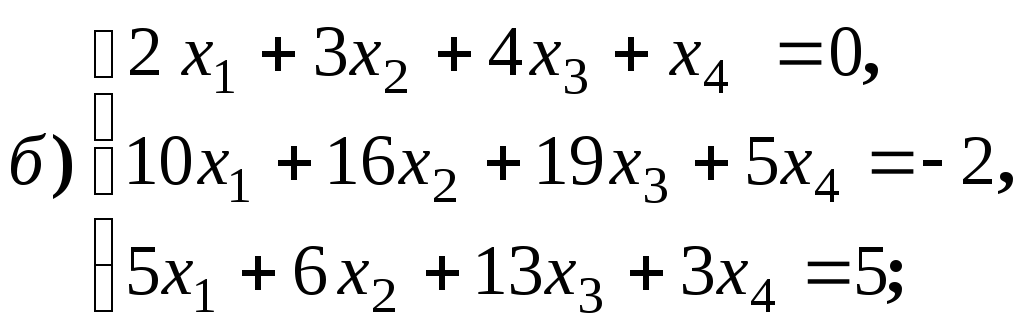
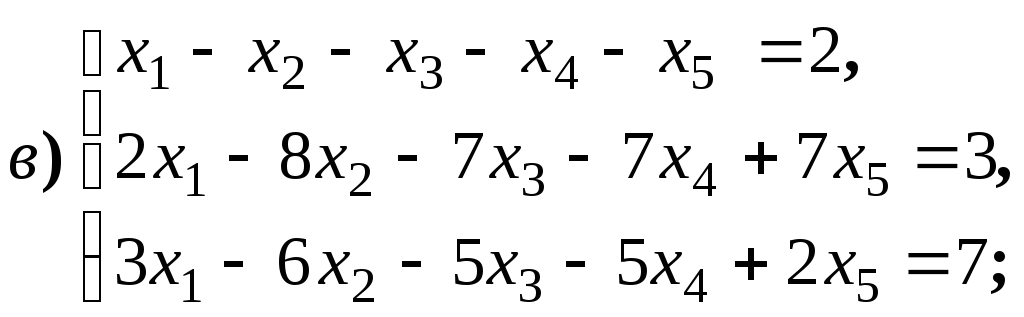
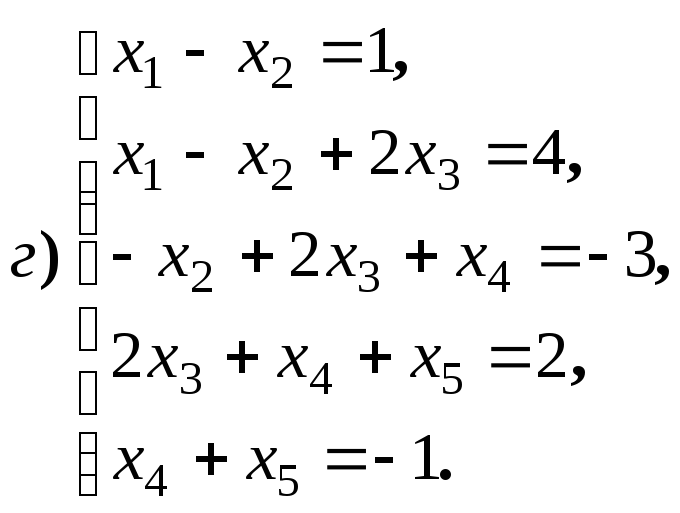

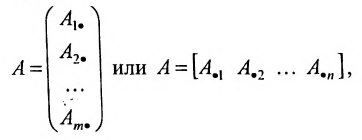
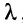 , не равное нулю;
, не равное нулю;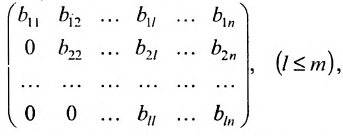
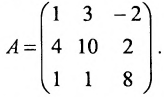
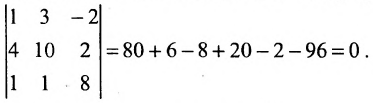



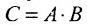 , где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.
, где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.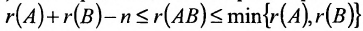 .
.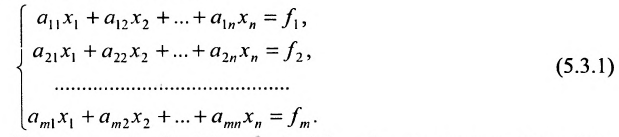

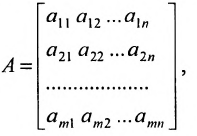
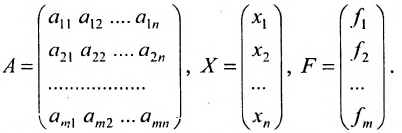
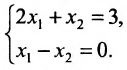
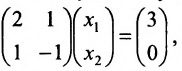



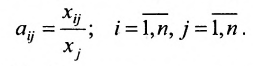
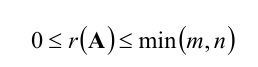
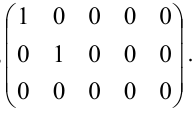
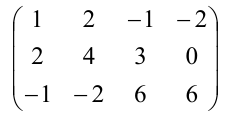
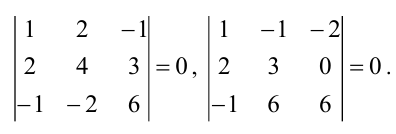
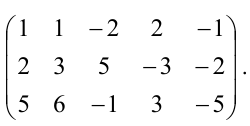
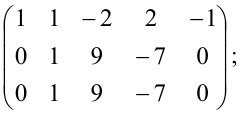
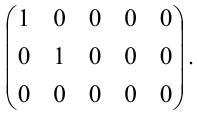

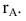


















 порядка 1, построенный на первой строке и первом столбце матрицы.
порядка 1, построенный на первой строке и первом столбце матрицы. , нужно к нему добавить по одной строке и одному столбцу. То есть минор второго порядка
, нужно к нему добавить по одной строке и одному столбцу. То есть минор второго порядка  , окаймляющий
, окаймляющий  , построенный на 1-й и 2-й строках, 1-м и 4-м столбцах.
, построенный на 1-й и 2-й строках, 1-м и 4-м столбцах. .
. ,
, .
. . Он отличен от нуля, поэтому ранг
. Он отличен от нуля, поэтому ранг  . Заметим, что ранг не может быть больше трех, так как матрица содержит три строки. Таким образом, возможны два варианта:
. Заметим, что ранг не может быть больше трех, так как матрица содержит три строки. Таким образом, возможны два варианта:  .
. ;
; .
.
 .
. .
. .
. .
. .
. .
. .
.