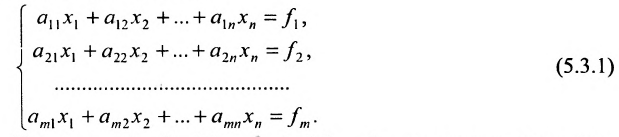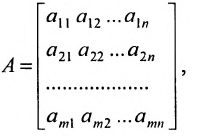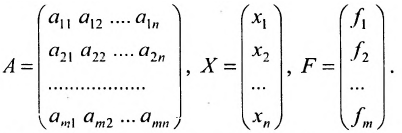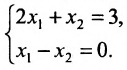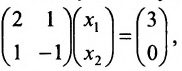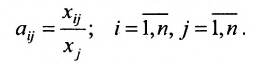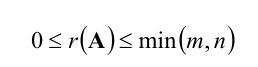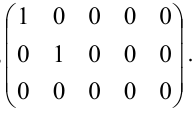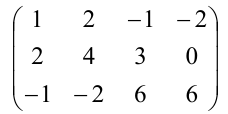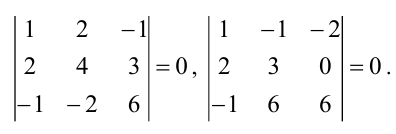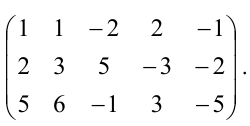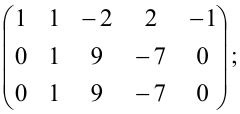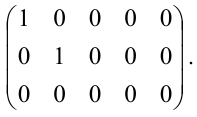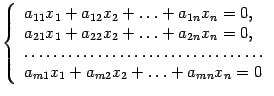Ранг матрицы — определение и вычисление с примерами решения
Содержание:
Элементарные преобразования матриц:
Рассмотрим прямоугольную матрицу:
состоящую из m строк и n столбцов. В п.3.2 отмсчалось, что каждую строку матрицы можно рассматривать как n-мсрный вектор, а каждый столбец — как m-мерный вектор. Тогда матрицу А можно записать в виде:
и, следовательно, данную матрицу можно рассматривать как систему вектор строк или вектор столбцов. Б указанных системах вектор-строк и вектор-столбцов можно выделять линейно независимые (зависимые) векторы. Тогда будем говорить, что строки (столбцы) матрицы линейно независимы (зависимы), если соответствующие им векторы независимы (зависимы).
Определения
Определение: Рангом системы строк (соответственно столбцов) матрицы А называется наибольшее число линейно независимых среди них.
Поскольку легко доказать, что ранг системы строк матрицы равен рангу системы её столбцов, то справедливо следующее
Определение: Рангом матрицы, обозначаемым r(А), называется максимальное число линейно независимых строк (столбцов) матрицы.
При транспонировании матрицы ранг её не изменяется.
Другой метод определения ранга матрицы связан с понятием определителя.
Выделим в матрице А любые k строк и k столбцов. Элементы, стоящие на их пересечении, образуют квадратную матрицу, определитель которой называется минором k-го порядка матрицы А. Ясно, что величина к должна удовлетворять двум условиям: 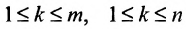
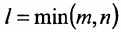
Определение: Рангом матрицы, обозначаемым r(А), называется порядок самого старшего минора этой матрицы, не равного нулю.
Из определения следует, что если ранг матрицы А равен l, то среди всех её миноров существует хотя бы один минор l-го порядка, отличный от нуля, но все миноры (l+1)-го порядков либо равны нулю, либо не могут быть составлены.
Вычисление ранга матрицы путём перебора всех её миноров весьма трудоёмко. Существует, однако, более простой способ вычисления ранга матрицы, основанный на упрощении структуры матрицы с помощью элементарных преобразований. Элементариыми преобразованиями матрицы называют следующие преобразования:
- обмен местами двух строк или двух столбцов матрицы;
- умножение всех элементов строки или столбца матрицы на произвольное число
, не равное нулю;
- прибавление ко всем элементам строки (столбца) матрицы соответствующих элементов другой строки (столбца), предварительно умноженных на одно и то же число;
- исключение из матрицы строки или столбца, состоящего из нулей.
Матрицы называются эквивалентными, если от одной из них к другой можно перейти путём конечного числа элементарных преобразований.
Ступенчатой матрицей называется матрица, удовлетворяющая тому свойству, что если в какой-либо из сё строк первый отличный от нуля элемент стоит на l-м месте, то во всех следующих строках на первых l местах стоят нули:
где элементы 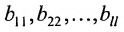
Для вычисления ранга матрицы приводят её с помощью цепочки элементарных преобразований к ступенчатому виду. Тогда ранг матрицы совпадает с числом её ненулевых диагональных элементов.
Теоремы о ранге матриц. Свойства ранга матриц
Относительно ранга матриц можно сформулировать следующие теоремы:
Теорема: Если матрица имеет минор порядка r, отличный от нуля, для которого все содержащие его миноры порядка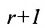
Вычисление ранга матрицы при помощи метода окаймления нужно вести от низших порядков к высшим. Сначала ищем минор первого порядка (т.е. элемент матрицы) или сразу второго порядка, отличный от нуля. Затем вычисляем окаймляющие его миноры следующего порядка, пока не найдём среди них отличного от нуля и т.д., пока не найдем минор порядка l, отличный от нуля, для которого либо все окаймляющие его миноры порядка l+1 равны нулю, либо такие миноры не могут быть составлены.
Теорема: Элементарные преобразования не меняют ранга матрицы.
Доказательство теоремы следует из определения ранга матрицы и свойств определителей.
Пример:
Найти ранг матрицы:
Решение:
Минор первого порядка в левом верхнем углу равен 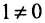
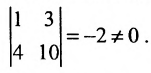
Значит ранг матрицы равен 2.
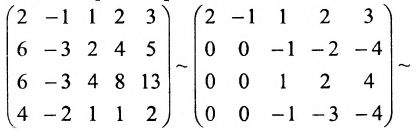
Пример:
Найти ранг матрицы:
Решение:
При помощи элементарных преобразований приведём данную матрицу к ступенчатому виду. На первом шаге умножим последовательно первую строку на 3, 3, 2 и вычтем из второй, третьей, четвёртой строк соответственно:
В эквивалентной матрице прибавим к третьей строке вторую и вычтем вторую из четвёртой строки:
(поменяем местами третью и четвертую строки)
(поменяем местами третий, четвёртый и пятый столбцы со вторым и опустим строки, состоящие из нулей) 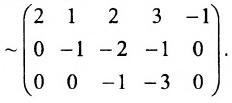
Отмстим некоторые свойства ранга матриц.
- Ранг суммы двух (или нескольких) матриц не больше суммы их рангов.
- Любую матрицу ранга r можно представить в виде суммы r матриц ранга 1, но нельзя представить в виде суммы менее чем r таких матриц.
- Любую матрицу С ранга r можно представить в виде произведения
, где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.
- Ранг произведения матриц порядка n удовлетворяет неравенству
.
Определение системы m линейных уравнений с n неизвестными
Системой m линейных уравнений с n неизвестными 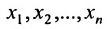
Числа 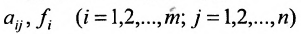
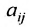
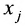
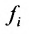
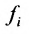
С помощью знака суммирования 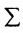
составленная из коэффициентов системы 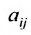
системы. Если к этой матрице добавить столбец свободных членов, то получим расширенную матрицу системы: 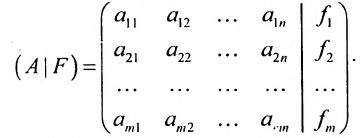
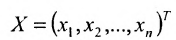
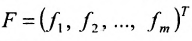

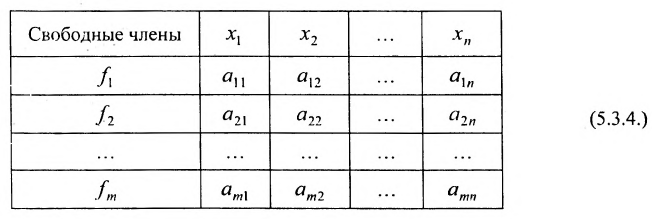
Используется также табличная форма записи системы (5.3.1):
Отметим, что (5.3.1), (5.3.2), (5.3.3), (5.3.4)- различные виды записи одной и той же системы линейных уравнений.
Решением системы (5.3.1) называется любой упорядоченный набор действительных чисел 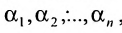
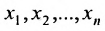
Система уравнений (5.3.1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Две системы уравнений с одинаковыми наборами неизвестных 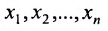
Отмстим, что для любой системы (5.3.1) возможны только три случая:
- система (5.3.1) имеет единственное решение;
- система (5.3.1) имеет бесчисленное множество решений;
- система (5.3.1) несовместна.
Множество всех решений системы (5.3.1) называется ее общим решением.
Решить систему (5.3.1) — значит найти ее общее решение.
Пример:
Пусть задана система
Тогда эту систему можно записать в матричном виде:
или в виде таблицы:
Система определенная, так как она имеет единственное решение 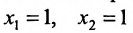
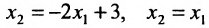
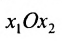
Экономические задачи, приводящие к системе линейных уравнений
Предположим, что производственные мощности для изготовления n различных видов продукции установлены в т цехах. Пусть 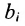
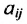
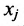
Широкий круг задач экономики приводит к составлению системы уравнений. Так в примере 4.3.2 составлялась система линейных уравнений (4.3.1) балансовой модели для трёх отраслей. В общем случае под балансовой моделью понимается система уравнений, каэ/сдое из которых выражает требование баланса между производимым количеством продукции и совокупной потребностью в этой продукции.
При построении балансовых моделей используется понятие чистой (или технологической) отрасли, т.е. условной отрасли, объединяющей всё производство данного продукта независимо от ведомственной (административной) подчинённости и форм собственности предприятий и фирм. Всё народное хозяйство представляется в виде совокупности п отраслей, каждая из которых рассматривается как производящая и как потребляющая.
Если обозначить через:
то систему уравнений баланса можно записать в виде:
или в матричной форме:
где Х- вектор-столбец валовой продукции; Y- вектор-столбец конечной продукции; А — матрица коэффициентов прямых затрат.
Основу экономико-математической модели межотраслевого баланса составляет технологическая матрица А, содержащая коэффициенты прямых затрат на производство единицы продукции:
Коэффициент. прямых затрат являются довольно стабильной величиной во времени.
Переписав матричное уравнение (5.4.2) в виде EX-AX = Y или (E-A)X = Y, (5.4.3) получим стандартную форму записи системы уравнений.
Определение ранга матрицы
Рассмотрим прямоугольную матрицу (4.1). Если в этой матрице выделить произвольно 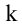
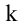
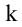
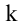
Очевидно, что выполняется соотношение
Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D 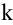
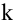
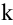
Элементарными называются следующие преобразования матрицы:
- перестановка двух любых строк (или столбцов),
- умножение строки (или столбца) на отличное от нуля число,
- прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.
Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.
Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: А
Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы
равны нулю, например,
При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.
Пример:
Найти методом окаймления миноров ранг матрицы
Решение:
Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) 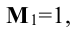
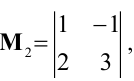
Переходим теперь к минорам 3-го порядка, окаймляющим 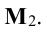
Таким образом, асе окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум.
Пример:
Найти ранг матрицы 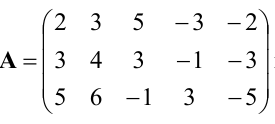
Решение:
Из второй строки вычтем первую и переставим эти строки:
Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:
из третьей строки вычтем первую; получим матрицу 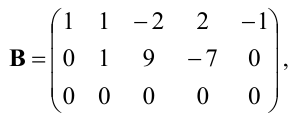
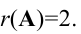
Вычисление ранга матрицы
Для исследования разрешимости систем линейных уравнений важную роль играет понятие ранга матрицы. Рассмотрим прямоугольную матрицу А
Выделим k произвольных строк и k произвольных столбцов этой матрицы. Определитель k-го порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называется минором k-го порядка матрицы А.
Рангом матрицы А называется наибольший порядок ее миноров, отличных от нуля. Обозначение: rank А,
Базисным минором матрицы называется всякий отличный от нуля ее минор, порядок которого равен рангу матрицы.
Рассмотрим некоторые методы вычисления ранга матрицы.
Метод окаймляющих миноров
Минор порядка k+1, содержащий в себе минор порядка k, называется окаймляющим минором.
Вычисляя ранг матрицы, удобнее переходить от миноров меньших порядков к минорам больших порядков. Если найден минор k-го порядка, отличный от нуля, а все окаймляющие его миноры порядка k+1 равны нулю, то ранг матрицы равен k.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Определители второго и третьего порядков и их свойства
- Метод Гаусса — определение и вычисление
- Прямая линия на плоскости и в пространстве
- Плоскость в трехмерном пространстве
- Кратный интеграл
- Ряды в математике
- Дифференциальные уравнения с примерами
- Обратная матрица — определение и нахождение
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
20. Решение системы линейных уравнений с помощью ранга матрицы
Пусть дана система линейных уравнений (25), коэффициенты которых принадлежат данному полю Р.
Пусть А = (26) матрица этой системы и А1 = (27) расширенная матрица. Если система (25) имеет хотя бы одно решение, то её называют Совместной, в противном случае система Несовместная. Если все слагаемые, содержащие неизвестные, стоят в левых частях уравнений, а свободные члены – в правых частях, то система называется Приведённой. Если в системе (25) хотя бы один свободный член отличен от нуля, то эта система называется Неоднородной. Если же все свободные члены равны нулю, то имеем систему Линейных однородных уравнений.
Теорема 26 (теорема Кронекера – Капелли). Система линейных уравнений совместна тогда и только тогда, когда ранг её матрицы равен рангу расширенной матрицы.
Доказательство. Þ Пусть система (25) совместна. Следовательно, существуют такие элементы A1, A2, … , AN , что
Записав эти равенства в векторной форме, получим, что В = A1×А1 + A2×А2 + … + AN×АN , где А1, а2, … , АN –векторы-столбцы матрицы А, В – вектор-столбец свободных членов. Из последнего равенства следует, что системы векторов А1, а2, … , АN и А1, а2, … , АN , В эквивалентны, поэтому их ранги равны. Итак, rang A = rang A1.
Ü Пусть rang A = rang A1 = К. Не нарушая общности, можно считать, что отличный от нуля минор К-го порядка в матрице А Стоит в левом верхнем углу. Векторы-столбцы обозначим А1, а2, … , Ак, ак+1, … , АN, В (*). Система А1, а2, … , Ак Будет максимальной линейно независимой подсистемой в системе (*), следовательно, найдутся такие коэффициенты Х10, х20, … , хк0, Что В = Х10 А1 + Х20 А2 + … + Хк0 Ак. Это равенство равносильно равенству В = Х10 А1 + Х20 А2 + … + Хк0 Ак + … + 0×Ак+1 + … + 0×АN. Перейдя к координатам, получим:
(28)
Отсюда следует, что (Х10, х20, … , хк0, 0,… ,0) – решение системы (25), т. е. эта система совместна.
Из теоремы Кронекера – Капелли следуют правила решения системы линейных уравнений.
Для решения системы линейных уравнений достаточно
1. Найти ранги основной и расширенной матриц ( А и А1 ). Если rang A ¹ rang A1, То система не имеет решения.
2. Если rang A = rang A1 = К, то для решения достаточно оставить К Уравнений, коэффициенты которых стоят на тех строчках матрицы А, На которых стоит базисный минор, и в этих уравнениях оставить в их левых частях те неизвестные, коэффициенты которых входят в базисный минор. Остальные неизвестные нужно перенести в правые части уравнений. Они могут принимать все возможные значения из поля Р. Эти неизвестные называются Свободными. (Не нарушая общности, можно считать, что оставлены первые К уравнений и первые К неизвестных, система (29)).
(29)
Определитель левой части системы (29) отличен от нуля, число уравнений равно числу неизвестных, поэтому (по теореме Крамера) эта система при всевозможных Хк+1, … , хN имеет единственное решение.
Условие совместности системы линейных уравнений. Теорема Кронекера-Капелли
Установить, совместна ли система линейных уравнений, с помощью теоремы Кронекера-Капелли часто можно быстрее, чем с помощью метода Гаусса, когда требуется последовательно исключать неизвестные. Основана эта теорема на использовании ранга матрицы.
Теорема Кронекера-Капелли о совместности системы. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы этой системы равен рангу её расширенной матрицы, то есть чтобы .
Здесь матрица A (матрица системы) — это матрица, составленная из коэффициентов при неизвестных:
В свою очередь матрица В (расширенная матрица) — это матрица, полученная присоединением к матрице системы столбца из свободных членов:
Ранги этих матриц связаны неравенством , при этом ранг матрицы В может быть лишь на одну единицу больше ранга матрицы A.
Следствие из теоремы Кронекера-Капелли о числе решений. Пусть для системы m линейных уравнений с n неизвестными выполнено условие совместности, то есть ранг матрицы из коэффициентов системы равен рангу её расширенной матрицы. Тогда верно следующее.
- Если ранг матрицы равен числу неизвестных (), то система имеет единственное решение.
- Если ранг матрицы системы меньше числа неизвестных (), то система имеет бесконечно много решений, а именно: некоторым n — r неизвестным можно придавать произвольные значения, тогда оставшиеся r неизвестных определятся уже единственным образом.
Если ранг матрицы системы линейных уравнений равен числу уравнений, то есть , то система совместна при любых свободных членах. В этом случае ранг расширенной матрицы также равен m, так как ранг матрицы не может быть больше числа её строчек.
В ходе доказательства теоремы Кронекера-Капелли были получены явные формулы для решений системы (в случае её совместности). Если уже известно, что система совместна, то, чтобы найти её решения, необходимо:
1) отыскать в матрице системы A ранга отличный от нуля минор порядка, равного рангу матрицы системы, то есть ранга r;
2) отбросить те уравнения, которые соответствуют строкам матрицы A, не входящим в минор ;
3) члены с коэффициентами, не входящими в , перенести в правую часть, а затем, придавая неизвестным, находящимся в правой части, произвольные значения, определить по формулам Крамера оставшиеся r неизвестных из системы r уравнений с отличным от нуля определителем .
Пример 1. Следуя теореме Кронекера-Капелли, установить, совместна ли система уравнений
Если система совместна, то решить её.
Решение. Вычисляем ранг матрицы этой системы и ранг расширенной матрицы. В обоих случаях он равен 3. Следовательно, система линейных уравнений совместна. Так как ранг матрицы системы меньше числа неизвестных, то система имеет бесконечно много решений: одно неизвестное может быть взято произвольно. Минор
отличен от нуля, поэтому последнее уравнение отбрасываем и неизвестному придаём произвольное значение .
Оставшиеся неизвестные определяются из системы
Решая последнюю систему по формулам Крамера или иным способом, находим
,
,
.
Присоединяя сюда , получаем все решения данной системы линейных уравнений.
Пример 2. Следуя теореме Кронекера-Капелли, установить, совместна ли система уравнений
Если система совместна, то решить её.
Решение. Вычисляем ранг матрицы этой системы:
.
Следовательно, ранг системы равен 3. Определим ранг расширенной матрицы:
.
Это означает, что ранг расширенной матрицы также равен 3. Следовательно, система совместна, а так как число неизвестных равно рангу матрицы системы, то она имеет единственное решение. Для решения можем использовать первые три уравнения:
Решая последнюю систему по формулам Крамера, находим
,
,
.
http://matica.org.ua/metodichki-i-knigi-po-matematike/lineinaia-algebra-uchebnoe-posobie-z-i-andreeva/20-reshenie-sistemy-lineinykh-uravnenii-s-pomoshchiu-ranga-matritcy
http://function-x.ru/systems_kroneker_kapelli.html
В примерах выше мы говорили об уникальности столбцов и строк. Ту же самую уникальность в математике обозначают еще одним термином — линейная независимость.
Сопоставим уже знакомый термин с новым понятием:
-
Когда мы говорили, что строка уникальна — мы имели в виду, что она линейно независима
-
Когда мы говорили, что строка не уникальна — мы имели в виду, что она линейно зависима. Например, если мы умножаем первую строку на
и получаем вторую строку, то вторая строка линейно зависима от первой
Другими словами, при линейной зависимости значения зависят друг от друга — из значений первой строки мы можем получить значения второй.
Все эти принципы будут работать, даже если мы представим матрицу как набор точек на графике.
Возьмем такой пример:

Опишем векторы так:
Здесь мы видим, что вектор
линейно зависит от
и
.
Также обратите внимание, что:
-
Векторы
и
линейно независимы — мы не можем представить
в виде
или наоборот
-
То же самое верно для
и
-
То же самое верно для
и
-
При этом
,
и
вместе линейно зависимы
Используя только векторы
и
, мы можем достичь любого места на плоскости. Когда векторы линейно независимы и охватывают все пространство, их называют базисом этого пространства.
В нашем случае векторы
и
— это базис плоскости, потому что двумерное пространство часто называют плоскостью. Именно поэтому
и
так же полезны, как и оси
. То же самое можно сказать о любых двух линейно независимых векторах в двумерной плоскости.
Самая простая пара линейно независимых векторов — это
и
. Вместе они образуют матрицу
:
По сути, они образуют привычные оси
:

А теперь посмотрим на самые простые линейно независимые векторы в трехмерном пространстве. Матрица будет выглядеть так:
А так выглядит сам график:

Показать четырехмерное пространство на картинке не получится, но сама матрица выглядит так:
Вычисление ранга матрицы с помощью элементарных преобразований
Элементарными называются
следующие преобразования матрицы:
1) перестановка
двух любых строк (или столбцов),
2) умножение строки
(или столбца) на отличное от нуля число,
3) прибавление к
одной строке (или столбцу) другой строки
(или столбца), умноженной на некоторое
число.
Две
матрицы называются эквивалентными,
если одна из них получается из другой
с помощью конечного множества элементарных
преобразований.
Эквивалентные
матрицы не являются, вообще говоря,
равными, но их ранги равны. Если матрицы
А и В эквивалентны, то это записывается
так: A ~ B.
Канонической матрицей
называется матрица, у которой в начале
главной диагонали стоят подряд несколько
единиц (число которых может равняться
нулю), а все остальные элементы равны
нулю, например,

При помощи
элементарных преобразований строк и
столбцов любую матрицу можно привести
к канонической. Ранг канонической
матрицы равен числу единиц на ее главной
диагонали.
Пример
2 Найти
ранг матрицы
А= 
и привести ее к
каноническому виду.
Решение. Из
второй строки вычтем первую и переставим
эти строки:
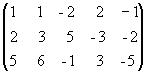
Теперь из второй
и третьей строк вычтем первую, умноженную
соответственно на 2 и 5:

из третьей строки
вычтем первую; получим матрицу
В = 
которая эквивалентна
матрице А, так как получена из нее с
помощью конечного множества элементарных
преобразований. Очевидно, что ранг
матрицы В равен 2, а следовательно, и
r(A)=2. Матрицу В легко привести к
канонической. Вычитая первый столбец,
умноженный на подходящие числа, из всех
последующих, обратим в нуль все элементы
первой строки, кроме первого, причем
элементы остальных строк не изменяются.
Затем, вычитая второй столбец, умноженный
на подходящие числа, из всех последующих,
обратим в нуль все элементы второй
строки, кроме второго, и получим
каноническую матрицу:

№19
Теоре́ма
Кро́некера — Капе́лли —
критерий совместности системы линейных
алгебраических уравнений:
-
Система
линейных алгебраических
уравнений совместна тогда
и только тогда, когда ранг её
основной матрицы равен рангу её
расширенной матрицы, причём система
имеет единственное решение, если
ранг равен числу неизвестных, и
бесконечное множество решений, если
ранг меньше числа неизвестных.
Для
того чтобы линейная система являлась
совместной, необходимо и достаточно,
что бы ранг расширенной матрицы этой
системы был равен рангу ее основной
матрицы.
Доказательство (условия совместности системы)
Необходимость
Пусть система совместна.
Тогда существуют числа такие,
что .
Следовательно, столбец является
линейной комбинацией столбцов матрицы
.
Из того, что ранг матрицы не изменится,
если из системы его строк (столбцов)
вычеркнуть или приписать строку
(столбец), которая является линейной
комбинацией других строк (столбцов)
следует, что .
Достаточность
Пусть .
Возьмем в матрице какой-нибудь
базисный минор. Так как ,
то он же и будет базисным минором и
матрицы .
Тогда, согласно теореме о базисном миноре,
последний столбец матрицы будет
линейной комбинацией базисных столбцов,
то есть столбцов матрицы .
Следовательно, столбец свободных членов
системы является линейной комбинацией
столбцов матрицы .
Следствия
-
Количество
главных переменных системы равно
рангу системы. -
Совместная система будет
определена (её решение единственно),
если ранг системы равен числу всех её
переменных.
№20
Однородная система уравнений
Предложение 15.2 Однородная
система уравнений
|
|
(15.7) |
всегда является
совместной.
Доказательство. Для
этой системы набор чисел ,
,
,
является
решением.
В
этом разделе мы будем использовать
матричную запись системы: .
Предложение 15.3 Сумма
решений однородной системы линейных
уравнений является решением этой
системы. Решение, умноженное на число,
тоже является решением.
Доказательство.
Пусть и
служат
решениями системы .
Тогда и
.
Пусть .
Тогда
Так
как ,
то —
решение.
Пусть —
произвольное число, .
Тогда
Так
как ,
то —
решение.
Следствие 15.1 Если
однородная система линейных уравнений
имеет ненулевое решение, то она имеет
бесконечно много различных решений.
Действительно,
умножая ненулевое решение на различные
числа, будем получать различные
решения.
Определение 15.5
Будем говорить, что
решения системы
образуют фундаментальную
систему решений,
если столбцы образуют
линейно независимую систему и любое
решение системы является линейной
комбинацией этих столбцов.
Определение 15.6
Пусть —
фундаментальная система решений
однородной системы .
Тогда выражение
где —
произвольные числа, будем называть общим
решением системы .
Из
определения фундаментальной системы
решений следует, что любое решение
однородной системы может быть получено
из общего решения при некоторых
значениях .
И наоборот, при любых фиксированных
числовых значениях из
общего решения получим решение однородной
системы.
Как
находить фундаментальную систему
решений мы увидим позже, в разделе «Алгоритм
нахождения решений произвольной системы
линейных уравнений (метод Гаусса)».
Теорема 15.3 Пусть —
фундаментальная система решений
однородной системы .
Тогда ,
где —
число неизвестных в системе.
Теорема
(о линейном решении однородных
систем).
Пусть —
решения однородной системы (1), —
произвольные константы. Тогда также
является решением рассматриваемой
системы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
09.06.201514.68 Mб41P.N.Bibilo_Osnovy_yazika_VHDL(2007)1.djvu
- #
- #
- #
Базисные (основные) и свободные (неосновные) переменные. Общее и базисное решения системы линейных алгебраических уравнений. Первая часть.
В теме «Теорема Кронекера-Капелли» было указано, что если ранг расширеной матрицы системы $widetilde{A}$ и ранг матрицы системы $A$ равны между собой, то заданная система линейных алгебраических уравнений (СЛАУ) совместна, т.е. имеет решение. Вопрос о количестве этих решений разрешим с помощью следствия из теоремы Кронекера. Согласно ему, если $rang A=rangwidetilde{A} = n$ ($n$ – количество неизвестных), то СЛАУ имеет единственное решение. Если же $rang A=rangwidetilde{A} < n$, то количество решений заданной СЛАУ бесконечно.
Особый интерес представляет именно случай $rang A=rangwidetilde{A} < n$, которым и займёмся в этой теме. Так как $rang A=rangwidetilde{A}$, то обозначим эти ранги просто буквой $r$, т.е. $rang A=rangwidetilde{A}=r$. Итак, $r < n$ и система неопределена, т.е. имеет бесконечное количество решений.
Что означает фраза «ранг матрицы равен $r$»? Она означает, что есть хотя бы один минор $r$-го порядка, который не равен нулю. Напомню, что такой минор называется базисным. Базисных миноров может быть несколько. При этом все миноры, порядок которых выше $r$, равны нулю или не существуют.
Если коэффициенты при $r$ переменных совместной СЛАУ образуют базисный минор матрицы системы $A$, то эти $r$ переменных называют базисными или основными. Остальные $n-r$ переменных именуют свободными или неосновными.
Выбрать $r$ базисных переменных в общем случае можно различными способами. В примерах я покажу наиболее часто используемый способ выбора.
Решение СЛАУ, в котором все свободные переменные равны нулю, называется базисным.
Во всех изложенных ниже примерах матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы – буквой $widetilde{A}$.
Пример №1
Решить СЛАУ $
left { begin{aligned}
& 3x_1-6x_2+9x_3+13x_4=9\
& -x_1+2x_2+x_3+x_4=-11;\
& x_1-2x_2+2x_3+3x_4=5.
end{aligned} right.$. Если система является неопределённой, указать базисное решение.
Решение
Итак, мы имеем СЛАУ, у которой 3 уравнения и 4 переменных: $x_1$, $x_2$, $x_3$, $x_4$. Так как количество переменных больше количества уравнений, то такая система не может иметь единственное решение (чуть позже мы строго докажем это предложение на основе теоремы Кронекера-Капелли). Найдём решения СЛАУ, используя метод Гаусса:
$$
left( begin{array} {cccc|c}
3 & -6 & 9 & 13 & 9 \
-1 & 2 & 1 & 1 & -11 \
1 & -2 & 2 & 3 & 5 end{array} right) rightarrow
left|begin{aligned}
& text{поменяем местами первую и третью}\
& text{строки, чтобы первым элементом}\
& text{первой строки стала единица.}
end{aligned}right| rightarrow \
rightarrowleft( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
-1 & 2 & 1 & 1 & -11 \
3 & -6 & 9 & 13 & 9
end{array} right)
begin{array} {l} phantom{0} \ r_2+r_1\ r_3-3r_1 end{array} rightarrow
left( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
0 & 0 & 3 & 4 & -6 \
0 & 0 & 3 & 4 & -6
end{array}right)
begin{array} {l} phantom{0} \ phantom{0}\r_3-r_2end{array} rightarrow \
rightarrowleft( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
0 & 0 & 3 & 4 & -6 \
0 & 0 & 0 & 0 & 0
end{array}right)
$$
Мы завершили прямой ход метода Гаусса, приведя расширенную матрицу системы к ступенчатому виду. Слева от черты расположены элементы преобразованной матрицы системы, которую мы также привели к ступенчатому виду. Напомню, что если некая матрица приведена к ступенчатому виду, то её ранг равен количеству ненулевых строк.
И матрица системы, и расширенная матрица системы после эквивалентных преобразований приведены к ступенчатому виду; они содержат по две ненулевых строки. Вывод: $rang A=rangwidetilde{A} = 2$.
Итак, заданная СЛАУ содержит 4 переменных (обозначим их количество как $n$, т.е. $n=4$). Кроме того, ранги матрицы системы и расширенной матрицы системы равны между собой и равны числу $r=2$. Так как $r < n$, то согласно следствию из теоремы Кронекера-Капелли СЛАУ является неопределённой (имеет бесконечное количество решений).
Найдём эти решения. Для начала выберем базисные переменные. Их количество должно равняться $r$, т.е. в нашем случае имеем две базисные переменные. Какие именно переменные (ведь у нас их 4 штуки) принять в качестве базисных? Обычно в качестве базисных переменных берут те переменные, которые расположены на первых местах в ненулевых строках преобразованной матрицы системы, т.е. на «ступеньках». Что это за «ступеньки» показано на рисунке:
На «ступеньках» стоят числа из столбцов №1 и №3. Первый столбец соответствует переменной $x_1$, а третий столбец соответствует переменной $x_3$. Именно переменные $x_1$ и $x_3$ примем в качестве базисных.
В принципе, если вас интересует именно методика решения таких систем, то можно пропускать нижеследующее примечание и читать далее. Если вы хотите выяснить, почему можно в качестве базисных взять именно эти переменные, и нельзя ли выбрать иные – прошу раскрыть примечание.
Примечание. показатьскрыть
Базисные переменные выбраны: это $x_1$ и $x_3$. Остальные $n-r=2$ переменных (т.е. $x_2$ и $x_4$) являются свободными. Нам нужно выразить базисные переменные через свободные.
Я предпочитаю работать с системой в матричной форме записи. Для начала очистим полученную матрицу $left( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
0 & 0 & 3 & 4 & -6 \
0 & 0 & 0 & 0 & 0
end{array}right)$ от нулевой строки:
$$
left( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
0 & 0 & 3 & 4 & -6
end{array}right)
$$
Свободным переменным, т.е. $x_2$ и $x_4$, соответствуют столбцы №2 и №4. Перенесём эти столбцы за черту. Знак всех элементов переносимых столбцов изменится на противоположный:
Почему меняются знаки? Что вообще значит это перенесение столбцов? показатьскрыть
А теперь продолжим решение обычным методом Гаусса. Наша цель: сделать матрицу до черты единичной. Для начала разделим вторую строку на 3, а потом продолжим преобразования обратного хода метода Гаусса:
$$
left( begin{array} {cc|ccc}
1 & 2 & 5 & 2 & -3\
0 & 3 & -6 & 0 & -4
end{array}right)
begin{array} {l} phantom{0} \ 1/3cdot{r_2} end{array} rightarrow
left( begin{array} {cc|ccc}
1 & 2 & 5 & 2 & -3\
0 & 1 & -2 & 0 & -4/3
end{array}right)
begin{array} {l} r_1-2r_2 \ phantom{0} end{array} rightarrow \
rightarrow left(begin{array} {cc|ccc}
1 & 0 & 9 & 2 & -1/3\
0 & 1 & -2 & 0 & -4/3
end{array}right).
$$
Матрица до черты стала единичной, метод Гаусса завершён. Общее решение найдено, осталось лишь записать его. Если вспомнить, что четвёртый столбец соответствует переменной $x_2$, а пятый столбец – переменной $x_4$, то получим:
$$
left{begin{aligned}
& x_1=9+2x_2-frac{1}{3}x_4;\
& x_2in R;\
& x_3=-2-frac{4}{3}x_4;\
& x_4 in R.
end{aligned}right.
$$
Нами получено общее решение заданной СЛАУ. Чтобы найти базисное решение, нужно все свободные переменные приравнять к нулю. Т.е. полагая $x_2=0$ и $x_4=0$, будем иметь:
$$
left{begin{aligned}
& x_1=9;\
& x_2=0;\
& x_3=-2;\
& x_4=0.
end{aligned}right.
$$
Решение $x_1=9$, $x_2=0$, $x_3=-2$, $x_4=0$ и является базисным решением данной СЛАУ. В принципе, задавая свободным переменным иные значения, можно получить иные частные решения данной системы. Таких частных решений бесконечное количество. Например, принимая $x_2=-4$ и $x_4=1$, получим такое частное решение: $left{begin{aligned}
& x_1=frac{2}{3};\
& x_2=-4;\
& x_3=-frac{10}{3};\
& x_4=1.
end{aligned}right.$. Базисное решение, которые мы нашли ранее – лишь одно из бесконечного множества частных решений заданной СЛАУ.
Если есть желание, то полученное решение можно проверить. Например, подставляя $x_1=9+2x_2-frac{1}{3}x_4$ и $x_3=-2-frac{4}{3}x_4$ в левую часть первого уравнения, получим:
$$
3x_1-6x_2+9x_3+13x_4=3cdot left(9+2x_2-frac{1}{3}x_4right)-6x_2+9cdot left(-2-frac{4}{3}x_4right)+13x_4=9.
$$
Проверка первого уравнения увенчалась успехом; точно так же можно проверить второе и третье уравнения.
Ответ: Общее решение: $left{begin{aligned}
& x_1=9+2x_2-frac{1}{3}x_4;\
& x_2in R;\
& x_3=-2-frac{4}{3}x_4;\
& x_4 in R.
end{aligned}right.$, базисное решение: $
left{begin{aligned}
& x_1=9;\
& x_2=0;\
& x_3=-2;\
& x_4=0.
end{aligned}right.$.
Пример №2
Решить СЛАУ
$$left{begin{aligned}
& x_1-2x_2+4x_3+2x_5=0;\
& 4x_1-11x_2+21x_3-2x_4+3x_5=-1; \
& -3x_1+5x_2-13x_3-4x_4+x_5=-2.
end{aligned}right.$$
Если система является неопределённой, указать базисное решение.
Решение
Похожий пример уже был решен в теме «метод Крамера» (пример №4). Переменные $x_4$ и $x_5$ были перенесены в правые части, а дальше применялись стандартные операции метода Крамера. Однако такой метод решения не гарантирует достижения результата. Например, мы переносим некие переменные в правую часть, а оставшийся определитель оказывается равным нулю, – что тогда? Решать перебором? 
$$
left( begin{array} {ccccc|c}
1 & -2 & 4 & 0 & 2 & 0\
4 & -11 & 21 & -2 & 3 & -1\
-3 & 5 & -13 & -4 & 1 & -2
end{array} right)
begin{array} {l} phantom{0} \r_2-4r_1\r_3+3r_1end{array} rightarrow
left( begin{array} {ccccc|c}
1 & -2 & 4 & 0 & 2 & 0\
0 & -3 & 5 & -2 & -5 & -1\
0 & -1 & -1 & -4 & 7 & -2
end{array} right) rightarrow \
rightarrow left|begin{aligned}
& text{поменяем местами вторую и третью}\
& text{строки, чтобы диагональным элементом}\
& text{второй строки стало число (-1).}
end{aligned}right|rightarrow
left( begin{array} {ccccc|c}
1 & -2 & 4 & 0 & 2 & 0\
0 & -1 & -1 & -4 & 7 & -2\
0 & -3 & 5 & -2 & -5 & -1
end{array} right)
begin{array} {l} phantom{0} \ phantom{0}\r_3-3r_1end{array} rightarrow \
rightarrow left( begin{array} {ccccc|c}
1 & -2 & 4 & 0 & 2 & 0\
0 & -1 & -1 & -4 & 7 & -2\
0 & 0 & 8 & 10 & -26 & 5
end{array} right).
$$
Матрица системы и расширенная матрица системы приведены к трапециевидной форме. Ранги этих матриц равны между собой и равны числу 3, т.е. $rang A=rangwidetilde{A} = 3$. Так как ранги равны между собой и меньше, чем количество переменных, то согласно следствию из теоремы Кронекера-Капелли данная система имеет бесконечное количество решений.
Количество неизвестных $n=5$, ранги обеих матриц $r=3$, поэтому нужно выбрать три базисных переменных и $n-r=2$ свободных переменных. Применяя тот же метод «ступенек», что и в предыдущем примере, выберем в качестве базисных переменных $x_1$, $x_2$, $x_3$, а в качестве свободных переменных – $x_4$ и $x_5$.
Столбцы №4 и №5, которые соответствуют свободным переменным, перенесём за черту. После этого разделим третью строку на 8 и продолжим решение методом Гаусса:
$$
left( begin{array} {ccc|ccc}
1 & -2 & 4 & 0 & 0 & -2\
0 & -1 & -1 & -2 & 4 & -7\
0 & 0 & 8 & 5 & -10 & 26
end{array} right)
begin{array} {l} phantom{0} \ phantom{0}\1/8cdot{r_3}end{array} rightarrow
left( begin{array} {ccc|ccc}
1 & -2 & 4 & 0 & 0 & -2\
0 & -1 & -1 & -2 & 4 & -7\
0 & 0 & 1 & 5/8 & -5/4 & 13/4
end{array} right)
begin{array} {l}r_1-4r_3 \r_2+r_3\ phantom{0}end{array} rightarrow \
left( begin{array} {ccc|ccc}
1 & -2 & 0 & -5/2 & 5 & -15\
0 & -1 & 0 & -11/8 & 11/4 & -15/4\
0 & 0 & 1 & 5/8 & -5/4 & 13/4
end{array} right)
begin{array} {l} phantom{0} \ -1cdot{r_2}\ phantom{0}end{array} rightarrow
left( begin{array} {ccc|ccc}
1 & -2 & 0 & -5/2 & 5 & -15\
0 & 1 & 0 & 11/8 & -11/4 & 15/4\
0 & 0 & 1 & 5/8 & -5/4 & 13/4
end{array} right)
begin{array} {l}r_1+2r_2 \ phantom{0}\ phantom{0}end{array} rightarrow\
rightarrowleft( begin{array} {ccc|ccc}
1 & 0 & 0 & 1/4 & -1/2 & -15/2\
0 & 1 & 0 & 11/8 & -11/4 & 15/4\
0 & 0 & 1 & 5/8 & -5/4 & 13/4
end{array} right)
$$
Из последней матрицы имеем общее решение заданной СЛАУ: $left{begin{aligned}
& x_1=frac{1}{4}-frac{1}{2}x_4-frac{15}{2}x_5;\
& x_2=frac{11}{8}-frac{11}{4}x_4+frac{15}{4}x_5;\
& x_3=frac{5}{8}-frac{5}{4}x_4+frac{13}{4}x_5;\
& x_4 in R;\
& x_5 in R.
end{aligned}right.$. Базисное решение получим, если приравняем свободные переменные к нулю, т.е. $x_4=0$, $x_5=0$:
$$
left{begin{aligned}
& x_1=frac{1}{4};\
& x_2=frac{11}{8};\
& x_3=frac{5}{8};\
& x_4=0;\
& x_5=0.
end{aligned}right.
$$
Ответ: Общее решение: $left{begin{aligned}
& x_1=frac{1}{4}-frac{1}{2}x_4-frac{15}{2}x_5;\
& x_2=frac{11}{8}-frac{11}{4}x_4+frac{15}{4}x_5;\
& x_3=frac{5}{8}-frac{5}{4}x_4+frac{13}{4}x_5;\
& x_4 in R;\
& x_5 in R.
end{aligned}right.$, базисное решение: $left{begin{aligned}
& x_1=frac{1}{4};\
& x_2=frac{11}{8};\
& x_3=frac{5}{8};\
& x_4=0;\
& x_5=0.
end{aligned}right.$.
Продолжение этой темы рассмотрим во второй части, где разберём ещё два примера с нахождением общего решения.
Модератор
5148 / 2328 / 339
Регистрация: 20.02.2013
Сообщений: 5,720
Записей в блоге: 20
12.09.2014, 17:30
7
Вот предварительно:
| C++ | ||
|
Добавлено через 1 час 18 минут
Во, прошаренный алгоритм.
Добавлено через 12 минут
А вот и готовая функция.
Добавлено через 36 минут
В общем, вот, но чё-то не работает. Короче, доработать напильником )))
| C++ | ||
|
0


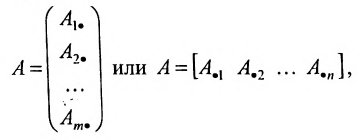
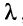 , не равное нулю;
, не равное нулю;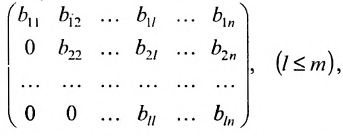
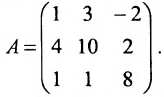
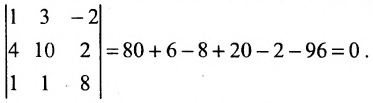



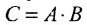 , где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.
, где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.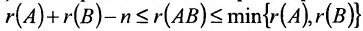 .
.