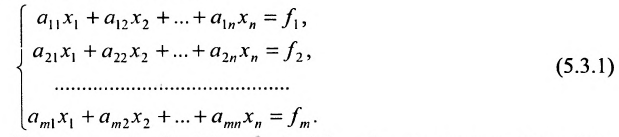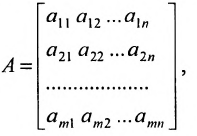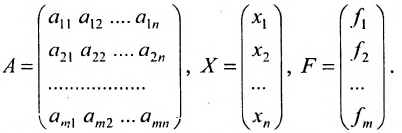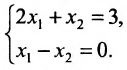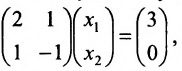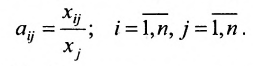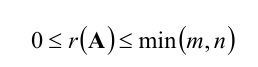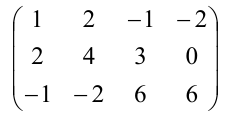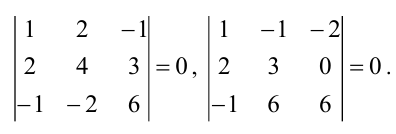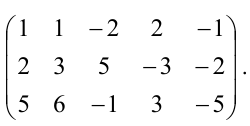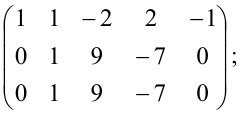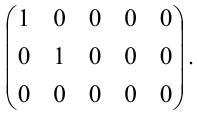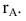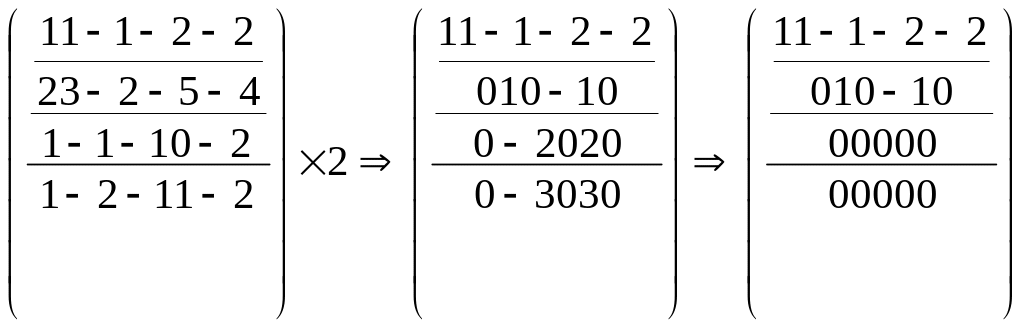Перед тем как начать знакомство с темой, необходимо повторить правила нахождения определителей второго, третьего и высших порядков. Также необходимо знать, что детерминант 1-го порядка — число. Рассмотрим 2 метода вычисления ранга матриц.
Онлайн-калькулятор
Метод окаймляющих миноров
Для нахождения ранга матрицы данным методом требуется уметь находить миноры матриц.
Рангом матрицы QQ называется наивысший порядок миноров, среди которых есть хотя бы один отличный от 00.
При этом ранг матрицы не может превышать порядка матрицы: 0⩽rang Qm×n⩽min(m,n)0leqslant rang Q_{mtimes n}leqslant min (m, n).
Обозначить ранг матрицы QQ можно следующим образом: rang Qrang Q или r(Q)r(Q).
Если ранг матрицы QQ равен rr, то это означает, что в матрице QQ имеется отличный от нуля минор порядка rr. При этом всякий минор порядка больше, чем rr равен нулю.
Исходя из определения ранга матрицы, следует, что если все миноры первого порядка (т. е. элементы матрицы QQ) равны 00, то rang Q=0rang Q=0. Если один из миноров первого порядка отличен от 00, а все миноры второго порядка равны 00, то rang Q=1rang Q=1. Если все миноры kk-го порядка равны 00, или миноров kk-го порядка не существует, то rang Q=k−1rang Q=k-1.
Рассмотрим примеры нахождения ранга матриц данным методом.
Пример 1
Найти ранг матрицы методом окаймляющих миноров
F=(03−1210−2−10)F=begin{pmatrix}0&3&-1\2&1&0\-2&-1&0end{pmatrix}.
Данная матрица имеет размер 3×33times3, поэтому ее ранг не может быть больше 33, т.е. rang F⩽3rang Fleqslant3.
Перейдем к вычислению ранга матрицы.
Среди миноров 1-го порядка (т.е. элементов определителя) есть хотя бы один, не равный 00, поэтому rang F≥1rang Fgeq1.
Перейдем к проверке миноров 2-го порядка. Например, на пересечении строк №1 и №2 и столбцов №1 и №2 получим минор: ∣0321∣=0⋅1−2⋅3=0−6=−6begin{vmatrix}0&3\2&1end{vmatrix}=0cdot1-2cdot3=0-6=-6. Значит, среди миноров 2-го порядка есть хотя бы один, не равный 00 и поэтому rang F≥2rang Fgeq2.
Перейдем к проверке миноров 3-го порядка. Минор 3-го порядка — определитель матрицы FF, поскольку она состоит из 3 строк и 3 столбцов: ∣03−1210−2−10∣=0begin{vmatrix}0&3&-1\2&1&0\-2&-1&0end{vmatrix}=0. Значит, ранг матрицы FF равен 22, или rang F=2rang F=2.
Пример 2
Найти ранг матрицы методом окаймляющих миноров
K=(21−23−121213−15−2−21243−31)K=begin{pmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}.
Данная матрица имеет размер 5×45times4. Из чисел 55 и 44 минимальным является 44, поэтому ее ранг не может быть больше 44, а значит rang K⩽4rang Kleqslant4.
Перейдем к вычислению ранга матрицы.
Среди миноров 1-го порядка (т.е. элементов определителя) есть хотя бы один, не равный 00, поэтому rang K≥1rang Kgeq1.
Перейдем к проверке миноров 2-го порядка. Например, на пересечении строк №1 и №2 и столбцов №1 и №2 получим минор: ∣21−12∣=2⋅2−(−1)⋅1=4+1=5begin{vmatrix}2&1\-1&2end{vmatrix}=2cdot2-(-1)cdot1=4+1=5. Значит, среди миноров 2-го порядка есть хотя бы один, не равный 00 и поэтому rang K≥2rang Kgeq2.
Перейдем к проверке миноров 3-го порядка. Например, на пересечении строк №1, №3 и №5 и столбцов №2, №3 и №4 получим минор:
∣1−233−153−31∣=1⋅(−1)⋅1+(−2)⋅5⋅3+3⋅(−3)⋅3−3⋅(−1)⋅3−(−2)⋅1⋅3−1⋅5⋅(−3)=−1−30−27+9+6+15=−28begin{vmatrix}1&-2&3\3&-1&5\3&-3&1end{vmatrix}=1cdot(-1)cdot1+(-2)cdot5cdot3+3cdot(-3)cdot3-3cdot(-1)cdot3-(-2)cdot1cdot3-1cdot5cdot(-3)=-1-30-27+9+6+15=-28.
Значит, среди миноров 3-го порядка есть хотя бы один, не равный 00 и поэтому rang K≥3rang Kgeq3.
Перейдем к проверке миноров 4-го порядка. Например, на пересечении строк №1, №2, №3 и №4 и столбцов №1, №2, №3 и №4 получим минор:
∣21−23−121213−15−2−212∣=2(−1)1+1∣2123−15−212∣−(−1)2+1∣1−233−15−212∣+(−1)3+1∣1−23212−212∣−2(−1)4+1∣1−232123−15∣=2(−1)2∣2123−15−212∣−(−1)3∣1−233−15−212∣+(−1)4∣1−23212−212∣−2(−1)5∣1−232123−15∣=2∣2123−15−212∣+∣1−233−15−212∣+∣1−23212−212∣+2∣1−232123−15∣=2(−4+6−10−4−10−6)−2+9+20−6−5+12+2+6+8+6−2+8+2(5−6−12−9+2+20)=−56+56+0=0begin{vmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\-2&-2&1&2end{vmatrix}=2(-1)^{1+1}begin{vmatrix}2&1&2\3&-1&5\-2&1&2end{vmatrix}-(-1)^{2+1}begin{vmatrix}1&-2&3\3&-1&5\-2&1&2end{vmatrix}+(-1)^{3+1}begin{vmatrix}1&-2&3\2&1&2\-2&1&2end{vmatrix}-2(-1)^{4+1}begin{vmatrix}1&-2&3\2&1&2\3&-1&5end{vmatrix}=2(-1)^{2}begin{vmatrix}2&1&2\3&-1&5\-2&1&2end{vmatrix}-(-1)^{3}begin{vmatrix}1&-2&3\3&-1&5\-2&1&2end{vmatrix}+(-1)^{4}begin{vmatrix}1&-2&3\2&1&2\-2&1&2end{vmatrix}-2(-1)^{5}begin{vmatrix}1&-2&3\2&1&2\3&-1&5end{vmatrix}=2begin{vmatrix}2&1&2\3&-1&5\-2&1&2end{vmatrix}+begin{vmatrix}1&-2&3\3&-1&5\-2&1&2end{vmatrix}+begin{vmatrix}1&-2&3\2&1&2\-2&1&2end{vmatrix}+2begin{vmatrix}1&-2&3\2&1&2\3&-1&5end{vmatrix}=2(-4+6-10-4-10-6)-2+9+20-6-5+12+2+6+8+6-2+8+2(5-6-12-9+2+20)=-56+56+0=0.
Остальные миноры 4-го порядка также равны нулю:
∣21−23−121213−1543−31∣=0begin{vmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\4&3&-3&1end{vmatrix}=0,
∣21−23−1212−2−21243−31∣=0begin{vmatrix}2&1&-2&3\-1&2&1&2\-2&-2&1&2\4&3&-3&1end{vmatrix}=0,
∣21−2313−15−2−21243−31∣=0begin{vmatrix}2&1&-2&3\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{vmatrix}=0,
∣−121213−15−2−21243−31∣=0begin{vmatrix}-1&2&1&2\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{vmatrix}=0.
Значит, ранг матрицы KK равен 33, или rang K=3rang K=3.
Данный метод не всегда удобен, поскольку связан с вычислением большого количества определителей. Рассмотрим метод нахождения ранга матриц, который наиболее часто применяется на практике.
Метод Гаусса (метод элементарных преобразований)
Метод основан на элементарных преобразованиях матриц, под которыми будем понимать такие преобразования, в результате которых сохраняется эквивалентность матриц:
- перестановка местами любых двух рядов (строк или столбцов) матрицы;
- умножение любого ряда матрицы (строки или столбца) на некоторое число, отличное от нуля;
- прибавление к любому ряду (строке или столбцу) матрицы другого ряда (строки или столбца), умноженного на некоторое число, отличное от нуля.
Рангом матрицы называется количество ненулевых строк матрицы после ее приведения к ступенчатому виду при помощи элементарных преобразований над строками и столбцами.
Рассмотрим суть данного метода на примерах.
Пример 1
Найти ранг матрицы методом Гаусса F=(03−1210−2−10)F=begin{pmatrix}0&3&-1\2&1&0\-2&-1&0end{pmatrix}.
Приведем матрицу FF с помощью элементарных преобразований к ступенчатому виду.
Поменяем местами строки №1 и №2:
(03−1210−2−10)∼(21003−1−2−10)begin{pmatrix}0&3&-1\2&1&0\-2&-1&0end{pmatrix}sim begin{pmatrix}2&1&0\0&3&-1\-2&-1&0end{pmatrix}.
Прибавим к строке №3 строку №1, умноженную на 1:
(21003−1−2−10)∼(21003−1000)begin{pmatrix}2&1&0\0&3&-1\-2&-1&0end{pmatrix}simbegin{pmatrix}2&1&0\0&3&-1\0&0&0end{pmatrix}.
С помощью элементарных преобразований мы привели матрицу FF к ступенчатому виду. В ней остались 2 ненулевые строки, следовательно, rang F=2rang F=2.
Пример 2
Найти ранг матрицы методом Гаусса
K=(21−23−121213−15−2−21243−31)K=begin{pmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}.
Приведем матрицу KK с помощью элементарных преобразований к ступенчатому виду.
Поменяем местами строки №1 и №2:
(21−23−121213−15−2−21243−31)∼(−121221−2313−15−2−21243−31)begin{pmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}sim begin{pmatrix}-1&2&1&2\2&1&-2&3\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}.
Поменяем местами строки №2 и №4:
(−121221−2313−15−2−21243−31)∼(−1212−2−21213−1521−2343−31)begin{pmatrix}-1&2&1&2\2&1&-2&3\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}sim begin{pmatrix}-1&2&1&2\-2&-2&1&2\1&3&-1&5\2&1&-2&3\4&3&-3&1end{pmatrix}.
Поменяем местами строки №3 и №4:
(−1212−2−21213−1521−2343−31)∼(−1212−2−21221−2313−1543−31)begin{pmatrix}-1&2&1&2\-2&-2&1&2\1&3&-1&5\2&1&-2&3\4&3&-3&1end{pmatrix}sim begin{pmatrix}-1&2&1&2\-2&-2&1&2\2&1&-2&3\1&3&-1&5\4&3&-3&1end{pmatrix}.
Поменяем местами строки №4 и №5:
(−1212−2−21221−2313−1543−31)∼(−1212−2−21221−2343−3113−15)begin{pmatrix}-1&2&1&2\-2&-2&1&2\2&1&-2&3\1&3&-1&5\4&3&-3&1end{pmatrix}sim begin{pmatrix}-1&2&1&2\-2&-2&1&2\2&1&-2&3\4&3&-3&1\1&3&-1&5end{pmatrix}.
Прибавим к строке №2 строку №1, умноженную на -2:
(−1212−2−21221−2343−3113−15)∼(−12120−6−1−221−2343−3113−15)begin{pmatrix}-1&2&1&2\-2&-2&1&2\2&1&-2&3\4&3&-3&1\1&3&-1&5end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-6&-1&-2\2&1&-2&3\4&3&-3&1\1&3&-1&5end{pmatrix}.
Прибавим к строке №3 строку №1, умноженную на 2:
(−12120−6−1−221−2343−3113−15)∼(−12120−6−1−2050743−3113−15)begin{pmatrix}-1&2&1&2\0&-6&-1&-2\2&1&-2&3\4&3&-3&1\1&3&-1&5end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\4&3&-3&1\1&3&-1&5end{pmatrix}.
Прибавим к строке №4 строку №1, умноженную на 4:
(−12120−6−1−2050743−3113−15)∼(−12120−6−1−205070111913−15)begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\4&3&-3&1\1&3&-1&5end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\0&11&1&9\1&3&-1&5end{pmatrix}.
Прибавим к строке №5 строку №1, умноженную на 1:
(−12120−6−1−205070111913−15)∼(−12120−6−1−20507011190507)begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\0&11&1&9\1&3&-1&5end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\0&11&1&9\0&5&0&7end{pmatrix}.
Прибавим к строке №2 строку №3, умноженную на 1:
(−12120−6−1−20507011190507)∼(−12120−1−150507011190507)begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\0&11&1&9\0&5&0&7end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&5&0&7\0&11&1&9\0&5&0&7end{pmatrix}.
Прибавим к строке №5 строку №3, умноженную на -1:
(−12120−1−150507011190507)∼(−12120−1−150507011190000)begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&5&0&7\0&11&1&9\0&5&0&7end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&5&0&7\0&11&1&9\0&0&0&0end{pmatrix}.
Прибавим к строке №3 строку №2, умноженную на 5:
(−12120−1−150507011190000)∼(−12120−1−1500−532011190000)begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&5&0&7\0&11&1&9\0&0&0&0end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&11&1&9\0&0&0&0end{pmatrix}.
Прибавим к строке №4 строку №2, умноженную на 11:
(−12120−1−1500−532011190000)∼(−12120−1−1500−53200−10640000)begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&11&1&9\0&0&0&0end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&0&-10&64\0&0&0&0end{pmatrix}.
Прибавим к строке №4 строку №3, умноженную на -2:
(−12120−1−1500−53200−10640000)∼(−12120−1−1500−53200000000)begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&0&-10&64\0&0&0&0end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&0&0&0\0&0&0&0end{pmatrix}.
С помощью элементарных преобразований мы привели матрицу KK к ступенчатому виду. В ней остались 3 ненулевые строки, следовательно, rang K=3rang K=3.
Любым из рассмотренных методов можно найти ранг матрицы.
Наши эксперты готовы оказать вам помощь с решением задачи онлайн по самым низким ценам!
Тест по теме «Ранг матрицы»
Содержание:
Элементарные преобразования матриц:
Рассмотрим прямоугольную матрицу:
состоящую из m строк и n столбцов. В п.3.2 отмсчалось, что каждую строку матрицы можно рассматривать как n-мсрный вектор, а каждый столбец — как m-мерный вектор. Тогда матрицу А можно записать в виде:
и, следовательно, данную матрицу можно рассматривать как систему вектор строк или вектор столбцов. Б указанных системах вектор-строк и вектор-столбцов можно выделять линейно независимые (зависимые) векторы. Тогда будем говорить, что строки (столбцы) матрицы линейно независимы (зависимы), если соответствующие им векторы независимы (зависимы).
Определения
Определение: Рангом системы строк (соответственно столбцов) матрицы А называется наибольшее число линейно независимых среди них.
Поскольку легко доказать, что ранг системы строк матрицы равен рангу системы её столбцов, то справедливо следующее
Определение: Рангом матрицы, обозначаемым r(А), называется максимальное число линейно независимых строк (столбцов) матрицы.
При транспонировании матрицы ранг её не изменяется.
Другой метод определения ранга матрицы связан с понятием определителя.
Выделим в матрице А любые k строк и k столбцов. Элементы, стоящие на их пересечении, образуют квадратную матрицу, определитель которой называется минором k-го порядка матрицы А. Ясно, что величина к должна удовлетворять двум условиям: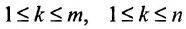
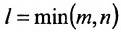
Определение: Рангом матрицы, обозначаемым r(А), называется порядок самого старшего минора этой матрицы, не равного нулю.
Из определения следует, что если ранг матрицы А равен l, то среди всех её миноров существует хотя бы один минор l-го порядка, отличный от нуля, но все миноры (l+1)-го порядков либо равны нулю, либо не могут быть составлены.
Вычисление ранга матрицы путём перебора всех её миноров весьма трудоёмко. Существует, однако, более простой способ вычисления ранга матрицы, основанный на упрощении структуры матрицы с помощью элементарных преобразований. Элементариыми преобразованиями матрицы называют следующие преобразования:
- обмен местами двух строк или двух столбцов матрицы;
- умножение всех элементов строки или столбца матрицы на произвольное число
, не равное нулю;
- прибавление ко всем элементам строки (столбца) матрицы соответствующих элементов другой строки (столбца), предварительно умноженных на одно и то же число;
- исключение из матрицы строки или столбца, состоящего из нулей.
Матрицы называются эквивалентными, если от одной из них к другой можно перейти путём конечного числа элементарных преобразований.
Ступенчатой матрицей называется матрица, удовлетворяющая тому свойству, что если в какой-либо из сё строк первый отличный от нуля элемент стоит на l-м месте, то во всех следующих строках на первых l местах стоят нули:
где элементы 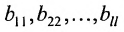
Для вычисления ранга матрицы приводят её с помощью цепочки элементарных преобразований к ступенчатому виду. Тогда ранг матрицы совпадает с числом её ненулевых диагональных элементов.
Теоремы о ранге матриц. Свойства ранга матриц
Относительно ранга матриц можно сформулировать следующие теоремы:
Теорема: Если матрица имеет минор порядка r, отличный от нуля, для которого все содержащие его миноры порядка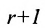
Вычисление ранга матрицы при помощи метода окаймления нужно вести от низших порядков к высшим. Сначала ищем минор первого порядка (т.е. элемент матрицы) или сразу второго порядка, отличный от нуля. Затем вычисляем окаймляющие его миноры следующего порядка, пока не найдём среди них отличного от нуля и т.д., пока не найдем минор порядка l, отличный от нуля, для которого либо все окаймляющие его миноры порядка l+1 равны нулю, либо такие миноры не могут быть составлены.
Теорема: Элементарные преобразования не меняют ранга матрицы.
Доказательство теоремы следует из определения ранга матрицы и свойств определителей.
Пример:
Найти ранг матрицы:
Решение:
Минор первого порядка в левом верхнем углу равен 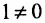
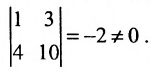
Значит ранг матрицы равен 2.
Пример:
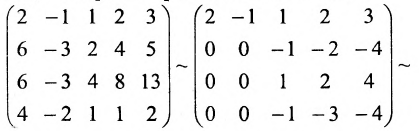
Найти ранг матрицы:
Решение:
При помощи элементарных преобразований приведём данную матрицу к ступенчатому виду. На первом шаге умножим последовательно первую строку на 3, 3, 2 и вычтем из второй, третьей, четвёртой строк соответственно:
В эквивалентной матрице прибавим к третьей строке вторую и вычтем вторую из четвёртой строки:
(поменяем местами третью и четвертую строки)
(поменяем местами третий, четвёртый и пятый столбцы со вторым и опустим строки, состоящие из нулей) 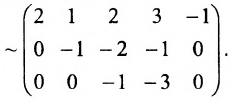
Отмстим некоторые свойства ранга матриц.
- Ранг суммы двух (или нескольких) матриц не больше суммы их рангов.
- Любую матрицу ранга r можно представить в виде суммы r матриц ранга 1, но нельзя представить в виде суммы менее чем r таких матриц.
- Любую матрицу С ранга r можно представить в виде произведения
, где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.
- Ранг произведения матриц порядка n удовлетворяет неравенству
.
Определение системы m линейных уравнений с n неизвестными
Системой m линейных уравнений с n неизвестными 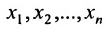
Числа 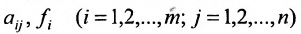
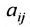
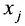
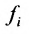
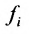
С помощью знака суммирования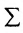
Матрица
составленная из коэффициентов системы 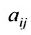
системы. Если к этой матрице добавить столбец свободных членов, то получим расширенную матрицу системы: 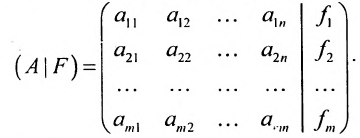
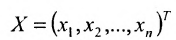
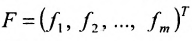

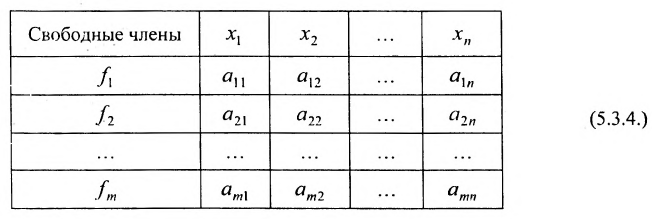
Используется также табличная форма записи системы (5.3.1):
Отметим, что (5.3.1), (5.3.2), (5.3.3), (5.3.4)- различные виды записи одной и той же системы линейных уравнений.
Решением системы (5.3.1) называется любой упорядоченный набор действительных чисел 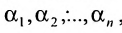
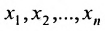
Система уравнений (5.3.1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Две системы уравнений с одинаковыми наборами неизвестных 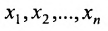
Отмстим, что для любой системы (5.3.1) возможны только три случая:
- система (5.3.1) имеет единственное решение;
- система (5.3.1) имеет бесчисленное множество решений;
- система (5.3.1) несовместна.
Множество всех решений системы (5.3.1) называется ее общим решением.
Решить систему (5.3.1) — значит найти ее общее решение.
Пример:
Пусть задана система
Тогда эту систему можно записать в матричном виде:
или в виде таблицы:
Система определенная, так как она имеет единственное решение 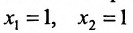
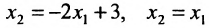
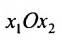
Экономические задачи, приводящие к системе линейных уравнений
Предположим, что производственные мощности для изготовления n различных видов продукции установлены в т цехах. Пусть 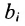
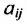
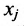
Широкий круг задач экономики приводит к составлению системы уравнений. Так в примере 4.3.2 составлялась система линейных уравнений (4.3.1) балансовой модели для трёх отраслей. В общем случае под балансовой моделью понимается система уравнений, каэ/сдое из которых выражает требование баланса между производимым количеством продукции и совокупной потребностью в этой продукции.
При построении балансовых моделей используется понятие чистой (или технологической) отрасли, т.е. условной отрасли, объединяющей всё производство данного продукта независимо от ведомственной (административной) подчинённости и форм собственности предприятий и фирм. Всё народное хозяйство представляется в виде совокупности п отраслей, каждая из которых рассматривается как производящая и как потребляющая.
Если обозначить через:
то систему уравнений баланса можно записать в виде:
или в матричной форме:
где Х- вектор-столбец валовой продукции; Y- вектор-столбец конечной продукции; А — матрица коэффициентов прямых затрат.
Основу экономико-математической модели межотраслевого баланса составляет технологическая матрица А, содержащая коэффициенты прямых затрат на производство единицы продукции:
Коэффициент!,! прямых затрат являются довольно стабильной величиной во времени.
Переписав матричное уравнение (5.4.2) в виде EX-AX = Y или (E-A)X = Y, (5.4.3) получим стандартную форму записи системы уравнений.
Определение ранга матрицы
Рассмотрим прямоугольную матрицу (4.1). Если в этой матрице выделить произвольно 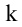
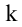
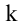
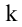
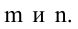
Очевидно, что выполняется соотношение
Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D 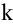
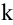
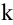
Элементарными называются следующие преобразования матрицы:
- перестановка двух любых строк (или столбцов),
- умножение строки (или столбца) на отличное от нуля число,
- прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.
Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.
Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: А ~ В.
Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы
равны нулю, например,
При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.
- Заказать решение задач по высшей математике
Пример:
Найти методом окаймления миноров ранг матрицы
Решение:
Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) 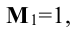
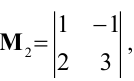
Переходим теперь к минорам 3-го порядка, окаймляющим 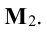
Таким образом, асе окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум.
Пример:
Найти ранг матрицы 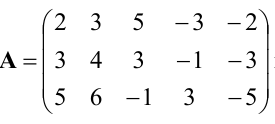
Решение:
Из второй строки вычтем первую и переставим эти строки:
Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:
из третьей строки вычтем первую; получим матрицу 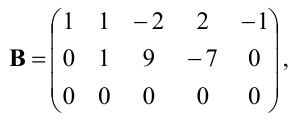
Вычисление ранга матрицы
Для исследования разрешимости систем линейных уравнений важную роль играет понятие ранга матрицы. Рассмотрим прямоугольную матрицу А
Выделим k произвольных строк и k произвольных столбцов этой матрицы. Определитель k-го порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называется минором k-го порядка матрицы А.
Рангом матрицы А называется наибольший порядок ее миноров, отличных от нуля. Обозначение: rank А,
Базисным минором матрицы называется всякий отличный от нуля ее минор, порядок которого равен рангу матрицы.
Рассмотрим некоторые методы вычисления ранга матрицы.
Метод окаймляющих миноров
Минор порядка k+1, содержащий в себе минор порядка k, называется окаймляющим минором.
Вычисляя ранг матрицы, удобнее переходить от миноров меньших порядков к минорам больших порядков. Если найден минор k-го порядка, отличный от нуля, а все окаймляющие его миноры порядка k+1 равны нулю, то ранг матрицы равен k.
- Определители второго и третьего порядков и их свойства
- Метод Гаусса — определение и вычисление
- Прямая линия на плоскости и в пространстве
- Плоскость в трехмерном пространстве
- Кратный интеграл
- Ряды в математике
- Дифференциальные уравнения с примерами
- Обратная матрица — определение и нахождение
Нахождение ранга матрицы — примеры решения
Содержание:
- Что такое ранг матрицы — понятие, для чего используется
-
Как определить ранг матрицы, примеры
- Нахождение ранга матрицы по определению
- Нахождение ранга матрицы методом окаймляющих миноров
- Отыскание ранга матрицы способом элементарных преобразований (методом Гаусса)
Что такое ранг матрицы — понятие, для чего используется
Возьмем случайную матрицу (underset{mtimes n}A) и натуральное число k, меньшее или равное числам m и n. Вычеркивая в ней произвольным образом (m — k) строк и (n — k) столбцов, мы получим квадратные подматрицы меньше размера исходной, k-го порядка. Определители таких подматриц будут минорами k-го порядка матрицы (underset{mtimes n}A.)
Минор k-го порядка матрицы A — это определитель k-го порядка с элементами, которые расположены на пересечении любых k строк и любых k столбцов.
Всего из матрицы (underset{mtimes n}A) получится выделить (C_m^kC_n^k) миноров k-го порядка.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Например, из (underset{3times 4}A) мы получим 12 миноров 1-го порядка, 18 — 2-го и 4 — 3-го.
Если среди матричных элементов (a_{ij}) (i = 1, 2 … m; j = 1, 2 … n) есть отличные от нуля, то существует натуральное число r, которое обладает следующими свойствами:
- У матрицы А есть ненулевой минор r-го порядка.
- Любой из миноров этой матрицы порядка r + 1 или выше будет нулевым.
Число r с такими характеристиками — ранг матрицы A.
Ранг матрицы — это наивысший порядок ее ненулевых миноров.
Устоявшегося обозначения ранга не существует, чаще всего его записывают как (r (A)) или rang A, где А — обозначение матрицы. Понятие ранга обычно используют в ситуациях, когда необходима проверка совместимости системы линейных уравнений.
В случае, когда базисный минор матрицы (underset{3times 4}A) имеет порядок r < m, то как минимум одна ее строка будет не базисной. Согласно теореме о базисном миноре, в таком случае строки рассматриваемой матрицы (underset{3times 4}A) линейно зависимы. В случае, когда r = m, все строки являются базисными и линейно независимыми.
Из этого можно сделать следующие выводы:
- Когда ранг матрицы A меньше числа ее строк, они линейно зависимы. В случае, когда он равен числу строк, все они линейно независимы.
- Всякие r + 1 строк матрицы A ранга r линейно зависимы.
- Ранг любой матрицы равняется максимальному числу ее линейно независимых строк.
Теорема 1
Максимальное число линейно независимых столбцов матрицы равно максимальному количеству ее линейно независимых строк и равно ее рангу.
Следствие
Ранг не меняется при транспонировании.
Как определить ранг матрицы, примеры
Нахождение ранга матрицы по определению
Определить ранг можно, перебрав все миноры.
Теорема 2
Если из элементов матрицы можно составить ненулевой минор n-го порядка, то ранг равен n.
С учетом данной теоремы перебор производится по следующему алгоритму:
- Перебрать миноры 1-го порядка. Если наличествует хоть один ненулевой минор 1-го порядка, ранг как минимум равен 1.
- Перебрать миноры 2-го порядка. Если все они нулевые, ранг — единичный. В противном случае переходим к пункту 3.
- Перебрать миноры 3-го порядка. Если все они нулевые, ранг — два. В противном случае переходим к минорам 4-го, 5-го порядков и т. д.
Нахождение ранга матрицы методом окаймляющих миноров
Этот метод дает возможность сократить вычисления.
Окаймляющий минор — минор (n+1)-го порядка матрицы А. Он окаймляет минор n-го порядка, если матрица, соответствующая минору (n+1)-го порядка, содержит матрицу, которая соответствует упомянутому минору n-го порядка. Таким образом, чтобы получить окаймляемый минор, надо взять окаймляющий его и вычеркнуть одну строку и один столбец.
Пример № 1
Вычислить ранг матрицы
(begin{pmatrix}2&3&7&11\1&2&4&7\5&0&10&5end{pmatrix}.)
Решение:
В матрице есть элементы, отличные от нуля, значит, ее ранг больше единицы.
(М_2;=;begin{pmatrix}2&3\1&2end{pmatrix};=;4;-;3;=;1; neq 0. )
Раз ранг больше двух, нужно рассмотреть миноры 3-го порядка, содержащие вышеприведенный минор (М_2.)
(М_3;=;begin{pmatrix}2&3&7\1&2&4\5&0&10end{pmatrix};=;5;times;begin{pmatrix}3&7\2&4end{pmatrix};+;10;times;begin{pmatrix}2&3\1&2end{pmatrix}=;5;times;(12;-;14);+;10;times;(4;-;3);=;-;10;+;10;=;0.)
(М_3;=;begin{pmatrix}2&3&11\1&2&7\5&0&5end{pmatrix};=;5;times;begin{pmatrix}3&11\2&7end{pmatrix};+;5;times;begin{pmatrix}2&3\1&2end{pmatrix}=;5;times;(21;-;22);+;5;times;(4;-;3);=;-;5;+;5;=;0.)
Как мы видим, все миноры 3-го порядка нулевые, значит, наибольший ненулевой минор относится ко 2-му порядку.
Ответ: 2.
Отыскание ранга матрицы способом элементарных преобразований (методом Гаусса)
В большинстве случаев нахождение ранга перебором миноров требует долгих вычислений. Более простой способ решения этой задачи базируется на элементарных преобразованиях по методу Гаусса, сохраняющих ранг исходной матрицы A и приводящих ее к ступенчатому виду. К таким преобразованиям относятся:
- Вычеркивание нулевой строки или столбца. Нулевая строка не может быть базисной строкой, ведь в таком случае базисные строки были бы линейно зависимы, а это противоречит теореме о базисном миноре.
- Перестановка двух строк между собой. Другие строки в этом случае не меняются. Это утверждение непосредственно следует из теоремы о базисном миноре, согласно которой ранг равняется максимальному числу линейно независимых строк.
- Умножение любой строки на число( lambda neq 0).
- Вычеркивание строки, которая является линейной комбинацией других строк.
- Прибавление к одной строке другой строки, умноженной на число (lambda neq 0).
- Транспонирование.
Проведем подробный разбор пункта 5. Представим, что к q-й строке прибавлена p-я строка, умноженная на (lambda neq 0). В итоге появится новая матрица A′. Если q-я и p-я строки — базисные, это преобразование не изменит значения базисного минора. В случае, когда только p-я строка — базисная, q-я строка является их линейной комбинацией. Умножение на (lambda) это не изменит, и такую строку допустимо удалить при преобразовании.
Если q-я строка — базисная, а p-я — нет, то после преобразования (r_{q} rightarrow r_{q} + lambda r_{p}) базисный минор (triangle_{r}) перейдет в минор (triangle’_{r}) матрицы A′, который отличается от (triangle_{r}) тем, что вместо элементов строки (r_{q}) содержит элементы строки( r_{q} + lambda r_{p}). Согласно теореме о линейности, (triangle’_r=triangle_r+lambda;triangle_r^{(1)}.)
Определитель r-го порядка (triangle_r^{(1)}) в этом выражении отличается от (triangle_r) тем, что вместо элементов q-й строки содержит соответствующие элементы строки( r_{p}.)
Так как p-я строка — не базисная, она может быть представлена в виде линейной комбинации r базисных строк, то (triangle_r^{(1)} = 0) и (triangle_r^{(1)} = triangle_r.)
Как мы видим, при преобразовании( r_{q} rightarrow r_{q} + lambda r_{p}) базисный минор ни при каких условиях не изменяется. Из этого делаем вывод, что r (A) = r (A′).
Примечание
Матрицы A и B эквивалентны по рангу и обозначаются A ∼ B в том случае, когда B можно получить из A путем элементарных преобразований, перечисленных выше.
Пример № 2
Вычислить ранг матрицы
(В;=;begin{pmatrix}4&0&-1\0&2&4\4&4&1end{pmatrix}.)
Решение:
Прибавим первую строку матрицы B, умноженную на -1, к ее третьей строке. После произведения необходимых расчетов получим:
(В;sim;begin{pmatrix}4&0&-1\0&2&4\0&4&2end{pmatrix}.)
Умножим вторую строку получившейся матрицы на -2 и прибавим результат умножения к третьей строке:
(В;sim;begin{pmatrix}4&0&-1\0&2&4\0&0&-6end{pmatrix}.)
Итак, исходная матрица 3-го порядка является невырожденной, поскольку ее определитель равен
(4 times 2 times (-6) = -48 neq 0.)
Ответ: 3.
В данной публикации мы рассмотрим определение ранга матрицы, а также методы, с помощью которых его можно найти. Также разберем примеры для демонстрации применения теории на практике.
- Определение ранга матрицы
-
Нахождение ранга матрицы
- Метод окаймляющих миноров
- Приведение матрицы к ступенчатому виду
Определение ранга матрицы
Ранг матрицы – ранг ее системы строк или столбцов. В любой матрице есть ее строчный и столбцовый ранги, которые равны между собой.
Ранг системы строк – это максимальное количество линейно-независимых строк. Аналогичным образом определяется ранг системы столбцов.
Примечания:
- Ранг нулевой матрицы (обозначается символом “θ“) любого размера равняется нулю.
- Ранг любого ненулевого вектора-строки или вектора-столбца равняется единице.
- Если в матрице любых размеров присутствует хотя бы один элемент, не равный нулю, значит ее ранг не меньше единицы.
- Ранг матрицы не больше её минимальной размерности.
- Элементарные преобразования, выполненные над матрицей, не меняют её ранга.
Нахождение ранга матрицы
Метод окаймляющих миноров
Ранг матрицы равняется максимальному порядку ненулевого минора.
Алгоритм следующий: находим миноры от низших порядков к высоким. Если минор n-го порядка не равняется нулю, а все последующие (n+1) равны 0, значит ранг матрицы равен n.
Пример
Чтобы было понятнее, давайте разберем практический пример и найдем ранг матрицы A ниже, пользуясь методом окаймляющих миноров.
Решение
Мы имеем дело с матрицей 4×4, следовательно, ее ранг не может быть выше 4. Также в матрице присутствуют ненулевые элементы, значит, ее ранг не меньше единицы. Итак, приступим:
1. Начинаем проверять миноры второго порядка. Для начала берем две строки первого и второго столбцов.
Минор равняется нулю.
Следовательно переходим к следующему минору (первый столбец остается, а вместо второго берем третий).
Минор равен 54≠0, следовательно ранг матрицы не меньше двух.
Примечание: Если бы и этот минор оказался равным нулю, мы бы дальше проверили следующие комбинации:
Если требуется, перебор можно аналогичным образом продолжить со строками:
- 1 и 3;
- 1 и 4;
- 2 и 3;
- 2 и 4;
- 3 и 4.
Если бы все миноры второго порядка оказались равными нулю, то ранг матрицы равнялся бы одному.
2. Нам удалось почти сразу найти минор, который нам подходит. Поэтому переходим к минорам третьего порядка.
К найденному минору второго порядка, который дал отличный от нуля результат, добавляем одну строку и один из столбцов, выделенных зеленым цветом (начнем со второго).
Минор оказался равным нулю.
Следовательно меняем второй столбец на четвертый. И со второй попытки нам удается найти минор, не равный нулю, значит ранг матрицы не может быть меньше 3.
Примечание: если бы результат снова оказался равным нулю, вместо второй строки мы бы дальше взяли четвертую и продолжили бы поиски “хорошего” минора.
3. Теперь остается определить миноры четвертого порядка с учетом найденного ранее. В данном случае он один, который совпадает с определителем матрицы.
Минор равняется 144≠0. А это значит, что ранг матрицы A равняется 4.
Приведение матрицы к ступенчатому виду
Ранг ступенчатой матрицы равняется количеству её ненулевых строк. То есть все, что нам нужно сделать – это привести матрицу к соответствующему виду, например, с помощью элементарных преобразований, которые, как мы уже упомянули выше, не меняют ее ранг.
Пример
Найдем ранг матрицы B ниже. Мы не берем слишком сложный пример, т.к. наша основная цель – это просто продемонстрировать применение метода на практике.
Решение
1. Сначала вычтем из второй строки удвоенную первую.
2. Теперь отнимем из третьей строки первую, умноженную на четыре.
Таким образом, мы получили ступенчатую матрицу, в которой количество ненулевых строк равняется двум, следовательно ее ранг, также, равен 2.
Максимальное число
линейно-зависимых строк матрицы A
наз. рангом
матрицы и обознач r(a).
Наибольшее из порядков миноров данной
матрицы отличных от 0 наз рангом
матрицы.
Свойства:
1)при транспонировании
rang=const.
2)если вычеркнуть
нулевой ряд, то rang=const;
3)rang=cost,
при элементарных преобразованиях.
3)для вычисл ранга
с помощью элементар преобраз матрица
A
преобраз в матриц B,
ранг которой легко находится.
4)ранг треуг
матрицы=числу ненулевых элем, располож
на глав. диагоналях.
Методы нахождения
ранга матрицы:
-
метод
окаймляющих миноров -
метод
элементарных преобразований
метод
окаймляющих миноров:
метод
окаймляющих миноров позволяет
алгоритмизировать процесс нахождения
ранг-матрицы и позволяет свести к
минимуму количество вычисления миноров.
-
если
в матрице все нулевые элементы, то ранг
= 0 -
если
есть хоть один ненулевой элемент =>
r(a)>0
теперь
будем окаймлять минор М1, т.е. будем
строить всевозможные миноры 2-ого
порядка, ктр. содержат в себе i-тую
строку и j-тый
столбец, до тех пор, пока не найдем
ненулевой минор 2-ого порядка.
М2
(i,
i1,
j.j1)
Дальше
аналогично строим миноры 3-го порядка,
окаймляющие М2 (минор), до тех пор, пока
не получим минор, отличный от нуля.
Процесс
будет продолжаться до одного из
событий:
1. размер минора достигнет
числа к.
-
на
каком-то этапе все окаймленные миноры
окажутся = 0.
В
обоих случаях величина ранга-матрицы
будет равна порядку большего отличного
от нуля минора.
Метод
элементарных преобразований:
как
известно, понятие треугольной матрицы
определяется только для квадратных
матриц. Для прямоугольных матриц
аналогом является понятие трапецивидной
матрицы.
Например:
ранг
= 2.
7. Невырожденные системы слау. Способы решения.
СЛАУ
принято записывать в матричной форме,
когда сами неизвестные не указываются,
а указывается только матрица системы
А и столбец свободных членов В.
Решение
невырожденных СЛАУ методом Крамера:
Х=А-1*В
А-1=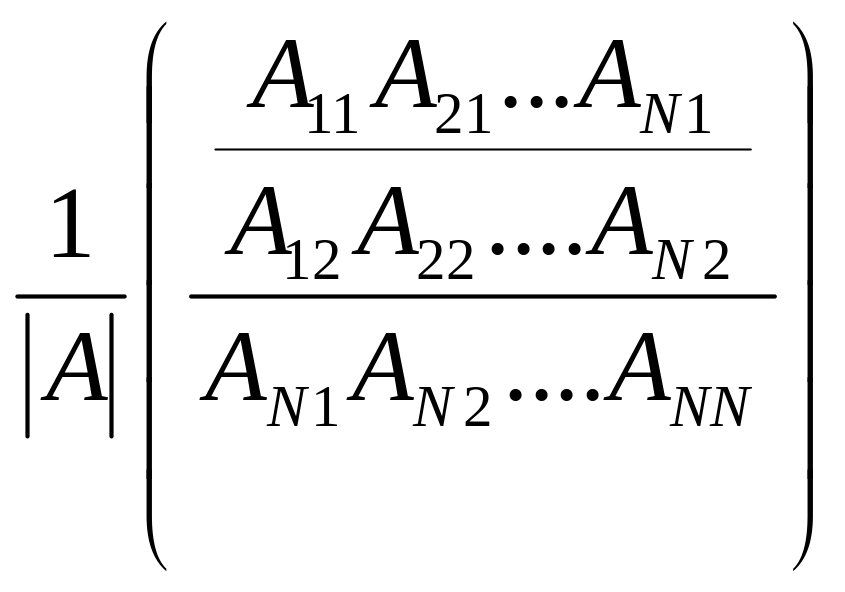
X1=
(A11b1
+ A21b2
+ …+An1bn)
Теорема:
(Крамера):
решение
невырожденных уравнений АХ=В,
можно
записать так:
,
Ак получается из А путем замены к-го
столбца на столбец свободного члена
В.
8. Метод Гаусса. Произвольные слау. Теорема Кронекера-Капелли.
Система уравнений
(СУ), содерж m-уравнений
и n-неизвестных
наз. системой
вида
a11x1+a12x2+…+a1nxn=b1
… aM1x1+aM2x2+…+aMnxn=bm,
где aij
– коэф системы и изменяется от 1 до n.
Расширенной
матрицей
наз матрица, сост из исходной матрицы
А и свободных .
Решением системы
наз n
значений неизвестных x1=c1
… xn=cn,
при подстановке которых все ур-ия
системы обращаются в верное равенство.
Система уравнений
наз. совместной,
если имеет хотя бы одно решение, иначе
она несовместна. Совместная система
наз. определённой,
если она имеет единственное решение.
Системы наз.
равносильными,
если они имеют одно и то же решение.
Замечание:
эквивалентные системы получаются при
элементарных преобразованиях при
условии, что преобраз вып только под
строками.
СЛАУ наз однородной,
если все свободные члены=0.
Теорема
Кронекера-Капелли:
система лин алг ур-ий совместна, когда
rangA=rang
(волнистая).
Теорема:
если rang
совместной системы= числу неизвестных,
то система имеет одно решение. Теорема:
если ранг совмест сист < числа
неизвестных, то система имеет бесконеч
решений.
Правило решения
СУ.
1)найти ранг основной
и расширенной матрицы (если rA
не =rA
с крыш, то система несовместна.
2) если rA=rA
с крыш и =r,
то система совместна и надо найти
базисный минор порядка r.
3)Берём r
ур-ий из коэф которых составлен базисн
минор. Остальные ур-ия отбрасываем.
Неизвестные, коэф которых входят в
минор наз главными. Из оставл слева, а
остальные (n-r)
– справа.
4)Найти выражения
главных неизв через свободные. Получено
общее решение системы
5)Придавая свободным
низвестным произвольное значение,
получим соотв значения главн неизв,
т.е. найдём частные решения.


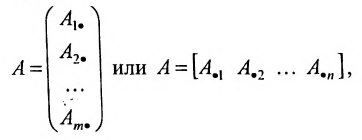
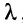 , не равное нулю;
, не равное нулю;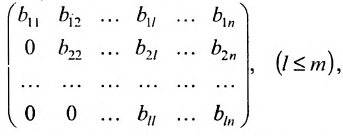
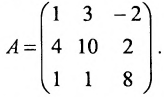
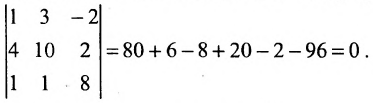



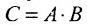 , где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.
, где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.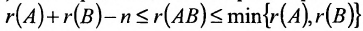 .
.