Как найти range функции

Did this article help you?

There are different ways to Find the Range of a Function Algebraically. But before that, we take a short overview of the Range of a Function.

In the first chapter What is a Function? we have learned that a function is expressed as

y=f(x),

where x is the input and y is the output.

For every input x (where the function f(x) is defined) there is a unique output.

The set of all outputs of a function is the Range of a Function.

The Range of a Function is the set of all y values or outputs i.e., the set of all f(x) when it is defined.

We suggest you read this article “9 Ways to Find the Domain of a Function Algebraically” first. This will help you to understand the concepts of finding the Range of a Function better.

In this article, you will learn

1. 5 Steps to Find the Range of a Function,

and in the end you will be able to

1. Find the Range of 10 different types of functions

Suppose we have to find the range of the function f(x)=x+2.

We can find the range of a function by using the following steps:

#1. First label the function as y=f(x)

y=x+2

#2. Express x as a function of y

Here x=y-2

#3. Find all possible values of y for which f(y) is defined

See that x=y-2 is defined for all real values of y.

#4. Element values of y by looking at the initial function f(x)

Our initial function y=x+2 is defined for all real values of x i.e., xepsilon mathbb{R}.

So here we do not need to eliminate any value of y i.e., yepsilon mathbb{R}.

#5. Write the Range of the function f(x)

Therefore the Range of the function y=x+2 is {yepsilon mathbb{R}}.

Maybe you are getting confused and don’t understand all the steps now.

But believe me, you will get a clear concept in the next examples.

---

How to Find the Range of a Function Algebraically

There are different types of functions. Here you will learn 10 ways to find the range for each type of function.

#1. Find the range of a Rational function

Example 1: Find the range

f(x)=frac{x-2}{3-x},xneq3

Solution:

Step 1: First we equate the function with y

y=frac{x-2}{3-x}

Step 2: Then express x as a function of y

y=frac{x-2}{3-x}

or, y(3-x)=x-2

or, 3y-xy=x-2

or, x+xy=3y+2

or, x(1+y)=3y+2

or, x=frac{3y+2}{y+1}

Step 3: Find possible values of y for which x=f(y) is defined

x=frac{3y+2}{y+1} is defined when y+1 can not be equal to 0,

i.e., y+1neq0

i.e., yneq-1

i.e., yepsilon mathbb{R}-{-1}

Step 4: Eliminate the values of y

See that f(x)=frac{x-2}{3-x} is defined on mathbb{R}-{3} and we do not need to eliminate any value of y from yepsilon mathbb{R}-{-1}.

Step 5: Write the Range

therefore the range of f(x)=frac{x-2}{3-x} is {xepsilon mathbb{R}:xneq-1}.

---

Example 2: Find the range

f(x)=frac{3}{2-x^{2}}

Solution:

Step 1:

y=frac{3}{2-x^{2}}

Step 2:

y=frac{3}{2-x^{2}}

or, 2y-xy^{2}=3

or, 2y-3=x^{2y}

or, x^{2}=frac{2y-3}{y}

Step 3:

The function x^{2}=frac{2y-3}{y} is defined when yneq 0 …(1)

Also since x^{2}geq 0,

therefore

frac{2y-3}{y}geq 0

or, frac{2y-3}{y}times {color{Magenta} frac{y}{y}}geq 0

or, frac{y(2y-3)}{y^{2}}geq 0

or, y(2y-3)geq 0 (because y^{2}geq 0)

or, (y-0){color{Magenta} 2}(y-frac{3}{{color{Magenta} 2}})

or, (y-0)(y-frac{3}{2})geq 0

Next we find the values of y for which (y-0)(y-frac{3}{2})geq 0 i.e., y(2y-3)geq 0 is satisfied.

Now see the table:

Value of y	Sign of (y-0)	Sign of (2y-3)	Sign of y(2y-3)	y(2y-3)geq 0 satisfied or not
y=-1<0 i.e., yepsilon (-infty,0)	-ve	-ve	+ve i.e., >0	✅
y=0	0	-ve	=0	✅
y=1 i.e., yepsilon (0,frac{3}{2})	+ve	-ve	-ve i.e., <0	❌
y=frac{3}{2}	+ve	0	=0	✅
y=2>frac{3}{2} i.e., yepsilon (frac{3}{2},infty)	+ve	+ve	+ve i.e., >0	✅

Therefore from the above table and using (1) we get,

yepsilon (-infty,0)cup [frac{3}{2},infty) (because yneq 0)

Step 4:

y=frac{3}{2-x^{2}} is not a square function,

therefore we do not need to eliminate any value of y except 0 because if y be zero then the function y=frac{3}{2-x^{2}} will be undefined.

Step 5:

Therefore the range of the function f(x)=frac{3}{2-x^{2}} is

(-infty,0)cup [frac{3}{2},infty).

---

Example 3: Find the range of a rational equation using inverse

f(x)=frac{2x-1}{x+4}

Solution:

---

#2. Find the range of a function with square root

Example 4: Find the range

f(x)=sqrt{4-x^{2}}

Solution:

Step 1: First we equate the function with y

y=sqrt{4-x^{2}}

Step 2: Then express x as a function of y

y=sqrt{4-x^{2}}

or, y^{2}=4-x^{2}

or, x^{2}=4-y^{2}

Step 3: Find possible values of y for which x=f(y) is defined

Since x^{2}geq 0,

therefore 4-y^{2}geq 0

or, (2-y)(2+y)geq 0

or, (y-2)(y+2)leq 0

Now we find possible values for which (y-2)(y+2)leq 0

Value of y	Sign of (y-2)	Sign of (y+2)	Sign of (y-2)(y+2)	(y-2)(y+2)leq 0 is satisfied or not
y=-3<-2 i.e., yepsilon (-infty,-2)	-ve	-ve	+ve i.e., >0	❌
y=-2	-ve	0	=0	✅
y=0 i.e., -2<y<2 i.e., yepsilon (-2,2)	-ve	+ve	-ve i.e., <0	✅
y=2	0	+ve	=0	✅
y=3>2 i.e., yepsilon (2,infty)	+ve	+ve	+ve i.e., >0	❌

i.e., y=-2, yepsilon (-2,2) and y=2

i.e., yepsilon [-2,2]

Step 4: Eliminate the values of y

As y=sqrt{4-x^{2}}, a square root function,

so y can not take any negative value i.e., ygeq 0

Therefore yepsilon [0,2].

Step 5: Write the range

The range of the function f(x)=sqrt{4-x^{2}} is [0,2] in interval notation.

We can also write the range of the function f(x)=sqrt{4-x^{2}} as R(f)={xepsilon mathbb{R}:0leq y leq 2}

---

Example 5: Find the range of a function f(x) =sqrt{x^{2}-4}.

Solution:

Step 1: First we equate the function with y

y=sqrt{x^{2}-4}

Step 2: Then express x as a function of y

y=sqrt{x^{2}-4}

or, y^{2}=x^{2}-4

or, x^{2}=y^{2}+4

Step 3: Find possible values of y for which x=f(y) is defined

Since x^{2}geq 0,

therefore y^{2}+4geq 0

i.e., y^{2}geq -4

i.e., ygeq sqrt{-4}

i.e, ygeq isqrt{2}, a complex number

therefore y^{2}+4geq 0 for all yepsilon mathbb{R}

Step 4: Eliminate the values of y

Since y=sqrt{x^{2}-4} is a square root function,

therefore y can not take any negative value i.e., ygeq 0

Step 5: Write the Range

The range of f(x) =sqrt{x^{2}-4} is (0,infty).

---

Example 6: Find the range for the square root function

f(x)=3-sqrt{x}

Solution:

---

#3. Find the range of a function with a square root in the denominator

Example 7: Find the range

f(x)=frac{1}{sqrt{x-3}}

Solution:

Step 1:

y=frac{1}{sqrt{x-3}}

Step 2:

y=frac{1}{sqrt{x-3}}

or, y=frac{1}{sqrt{x-3}}

or, y^{2}=frac{1}{x-3}

or, y^{2}(x-3)=1

or, xy^{2}-3y^{2}=1

or, xy^{2}=1+3y^{2}

or, x=frac{1+3y^{2}}{y^{2}}

Step 3:

For x=frac{1+3y^{2}}{y^{2}} to be defined,

y^{2}neq 0

i.e., yneq 0

Step 4:

As f(x)=frac{1}{sqrt{x-3}}, so y can not be negative (-ve).

Step 5:

The range of f(x)=frac{1}{sqrt{x-3}} is (0,infty).

---

Example 8: Find the range

f(x)=frac{1}{sqrt{4-x^{2}}}

Solution:

Step 1:

y=frac{1}{sqrt{4-x^{2}}}

Step 2:

y=frac{1}{sqrt{4-x^{2}}}

or, y=frac{1}{sqrt{4-x^{2}}}

or, y^{2}=frac{1}{4-x^{2}}

or, 4y^{2}-x^{2}y^{2}=1

or, x^{2}y^{2}=4y^{2}-1

or, x^{2}=frac{4y^{2}-1}{y^{2}}

Step 3:

For x^{2}=frac{4y^{2}-1}{y^{2}} to be defined, y can not be equal to zero

i.e., yneq 0

Also since x^{2}geq 0,

therefore frac{4y^{2}-1}{y^{2}}geq 0

or, 4y^{2}-1geq 0 (because y^{2}geq 0)

or, (2y-1)(2y+1)geq 0

or, 4(y-frac{1}{2})(y+frac{1}{2})geq 0

Value of y	Sign of (2y-1)	Sign of (2y+1)	Sign of (2y-1)(2y+1)	(2y-1)(2y+1)geq 0 is satisfied or not
y=-1<-frac{1}{2} i.e., yepsilon left ( -infty,-frac{1}{2} right )	-ve	-ve	+ve i.e., >0	✅
y=-frac{1}{2}	-ve	0	0	✅
y=0 i.e., yepsilon left (-frac{1}{2},frac{1}{2} right )	-ve	+ve	-ve i.e., <0	❌
y=frac{1}{2}	0	+ve	+ve i.e., >0	✅
y=1>frac{1}{2} i.e., yepsilon left (frac{1}{2},infty right )	+ve	+ve	+ve i.e., >0	✅

The above table implies that

yepsilon left ( -infty,-frac{1}{2} right )cup left (frac{1}{2},infty right ) …..(1)

Step 4:

Since y=frac{1}{sqrt{4-x^{2}}} is a square root function,

therefore y can not be negative (-ve).

i.e., ygeq 0 …..(2)

Now from (1) and (2), we get

yepsilon ( frac{1}{2},infty )

Step 5:

Therefore the range of the function f(x)=frac{1}{sqrt{4-x^{2}}} is [ frac{1}{2},infty )

---

Example 9: Find the range of the function

f(x)=sqrt{frac{(x-3)(x+2)}{x-1}}

Solution:

---

#4. Find the range of modulus function or absolute value function

Example 10: Find the range of the absolute value function

f(x)=left | x right |

Solution:

We can find the range of the absolute value function f(x)=left | x right | on a graph.

If we draw the graph then we get

Here you can see that the y value starts at y=0 and extended to infinity.

therefore the range of the absolute value function f(x)=left | x right | is [0,infty).

---

Example 11: Find the range of the absolute value function

f(x)=-left | x-1 right |

Solution:

The graph of f(x)=-left | x-1 right | is

From the graph, it is clear that the y value starts from y=0 and extended to -infty.

Therefore the range of f(x)=-left | x-1 right | is (-infty,0].

---

---

We can also find the range of the absolute value functions f(x)=left | x right | and f(x)=-left | x-1 right | using the above short cut trick:

The function f(x)=left | x right | can be written as f(x)=+left | x-0 right |

Now using trick 1 we can say, the range of f(x)=left | x right | is [0,infty)

Also using trick 2 we can say, the range of f(x)=-left | x-1 right | is (-infty,0].

---

Example 12: Find the range of the following absolute value functions

1. f(x)=left | x right |+6,
2. f(x)=left | x+4 right |

Solution:

---

#5. Find the range of a Step function

Example 13: Find the range of the step function f(x)=[x],xepsilon mathbb{R}.

Solution:

The step function f(x)=[x],xepsilon mathbb{R} is expressed as

f(x)=0, 0leq x<1

=1, 1leq x<2

=2,2leq x<3

………

=-1,-1leq x<0

=-2,-2leq x<-1

………

You can verify this result from the graph of f(x)=[x],xepsilon mathbb{R}

i.e., yepsilon {…,-2,-1,0,1,2,…}

i.e., yepsilon mathbb{Z}, the set of all integers.

therefore the range of the step function f(x)=[x],xepsilon mathbb{R} is mathbb{Z}, the set of all integers.

---

Example 14: Find the range of the step function f(x)=[x-3],xepsilon mathbb{R}.

Solution:

By using the definition of step function, we can express f(x)=[x-3],xepsilon mathbb{R} as

f(x)=1,3leq x<4

=2,4leq x<5

=3,5leq x<6

………

=0,2leq x<3

=-1,1leq x<2

=-2, 0leq x<1

=-3, -1leq x<0

………

You can verify this result from the graph of f(x)=[x-3],xepsilon mathbb{R}

i.e., yepsilon {…,-3,-2,-1,0,1,2,3,…}

i.e., yepsilon mathbb{Z}, the set of all integers.

therefore the range of the step function f(x)=[x-3],xepsilon mathbb{R} is mathbb{Z}, the set of all integers.

---

Example 15: Find the range of the step function f(x)=left [ frac{1}{4x} right ],xepsilon mathbb{R}.

Solution:

---

#6. Find the range of an Exponential function

Example 16: Find the range of the exponential function f(x)=2^{x}.

Solution:

The graph of the function f(x)=2^{x} is

Here y=0 is an asymptote of f(x)=2^{x} i.e., the graph is going very close and close to the y=0 straight line but it will never touch y=0.

Also, you can see on the graph that the function is extended to +infty.

So we can say y>0.

therefore the range of the exponential function f(x)=2^{x} is (0,infty).

---

Example 17: Find the range of the exponential function

f(x)=-3^{x+1}+2.

Solution:

The graph of the exponential function f(x)=-3^{x+1}+2 is

From the graph of f(x)=-3^{x+1}+2 you can see that y=2 is an asymptote of f(x)=-3^{x+1}+2 i.e., on the graph f(x)=-3^{x+1}+2 is going very close and close to y=2 towards -ve x-axis but it will never touch the straight line y=2 and extended to -infty towards +ve x-axis.

i.e., y<2

therefore the range of the exponential function f(x)=-3^{x+1}+2 is (-infty,2).

There is a shortcut trick to find the range of any exponential function. This trick will help you find the range of any exponential function in just 2 seconds.

---

---

Now we try to find the range of the exponential functions f(x)=2^{x} and f(x)=-3^{x+1}+2 with the above shortcut trick:

We can write f(x)=2^{x} as f(x)=1times 2^{x}+0, 1>0 and comparing this result with trick 1 we directly say

The range of f(x)=2^{x} is (0,infty).

Also f(x)=-3^{x+1}+2 can be written as f(x)=-1times 3^{x+1}+2, -1<0 and comparing with trick 2 we get

The range of f(x)=-3^{x+1}+2 is (-infty,2).

---

Example 18: Find the range of the exponential functions given below

f(x)=-2^{x+1}+3

Solution:

---

#7. Find the range of a Logarithmic function

The range of any logarithmic function is (-infty,infty).

We can verify this fact from the graph.

f(x)=log_{2}x^{3} is a logarithmic function and the graph of this function is

Here you can see that the y value starts from -infty and extended to +infty,

i.e., the range of f(x)=log_{2}x^{3} is (-infty,infty).

---

Example 19: Find the range of the logarithmic function

f(x)=log_{2}(x+4)+3

Solution:

---

#8. Find the range of a function relation of ordered pairs

A relation is the set of ordered pairs i.e., the set of (x,y) where the set of all x values is called the domain and the set of all y values is called the range of the relation.

In the previous chapter, we have learned how to find the domain of a function using relation.

Now we learn how to find the range of a function using relation.

For that we have to remember 2 rules which are given below:

Rules:

1. Before finding the range of a function first we check the given relation (i.e., the set of ordered pairs) is a function or not
2. Find all the y values and form a set. This set is the range of the relation.

Now see the examples given below to understand this concept:

---

Example 20: Find the range of the relation

{(1,3), (5,9), (8,23), (12,14)}

Solution:

In the relation {(1,3), (5,9), (8,23), (12,14)}, the set of x coordinates is {1, 5, 8, 12} and the set of y coordinates is {3, 9, 14, 23}.

If we draw the diagram of the given relation it will look like this

Here we can clearly see that each element of the set {1, 5, 8, 12} is related to a unique element of the set {3, 9, 14, 23}.

Therefore the given relation is a Function.

Also, we know that the range of a function relation is the set of y coordinates.

Therefore the range of the relation {(1,3), (5,9), (8,23), (12,14)} is the set {3, 9, 14, 23}.

---

Example 21: Find the range of the set of ordered pairs

{(5,2), (7,6), (9,4), (9,13), (12,19)}.

Solution:

The diagram of the given relation is

Here we can see that element 9 is related to two different elements and they are 4 and 13 i.e., 9 is not related to a unique element and this goes against the definition of the function.

Therefore the relation {(5,2), (7,6), (9,4), (9,13), (12,19)} is not a Function.

---

Example 22: Determine the range of the relation described by the table

x	y
-1	3
3	-2
3	2
4	8
6	-1

Solution:

---

#9. Find the range of a Discrete function

A Discrete Function is a collection of some points on the Cartesian plane and the range of a discrete function is the set of y-coordinates of the points.

Example 23: How do you find the range of the discrete function from the graph

Solution:

From the graph, we can see that there are five points on the discrete function and they are A (2,2), B (4,4), C (6,6), D (8,8), and E (10,10).

The set of the y-coordinates of the points A, B, C, D, and E is {2,4,6, 8, 10}.

therefore the range of the discrete function is {2,4,6,8,10}.

---

Example 24: Find the range of the discrete function from the graph

Solution:

The discrete function is made of the five points A (-3,2), B (-2,4), C (2,3), D (3,1), and E (5,5).

The set of the y coordinates of the discrete function is {2,4,3,1,5} = {1,2,3,4,5}.

therefore the range of the discrete function is {1,2,3,4,5}.

---

#10. Find the range of a trigonometric function

Trigonometric Function	Expresion	Range
Sine function	sin x	[-1,1]
Cosine function	cos x	[-1,1]
Tangent function	tan x	(-infty,+infty)
CSC function (Cosecant function)	csc x	(-infty,-1]cup[1,+infty)
Secant function	sec x	(-infty,-1]cup[1,+infty)
Cotangent function	sec x	(-infty,+infty)

---

#11. Find the range of an inverse trigonometric function

Inverse trigonometric function	Expression	Range
Arc Sine function / Inverse Sine function	arcsin x or, sin^{-1}x	[-frac{pi}{2},+frac{pi}{2}]
Arc Cosine function / Inverse Cosine function	arccos x or, cos^{-1}x	[0,pi]
Arc Tangent function / Inverse Tangent function	arctan x or, tan^{-1}x	(-frac{pi}{2},+frac{pi}{2})
Arc CSC function / Inverse CSC function	textrm{arccsc}x or, csc^{-1}x	[-frac{pi}{2},0)cup(0,frac{pi}{2}]
Arc Secant function / Inverse Secant function	textrm{arcsec}x or, sec^{-1}x	[0,frac{pi}{2})cup(frac{pi}{2},pi]
Arc Cotangent function / Inverse Cotangent function	textrm{arccot}x or, cot^{-1}x	(0,pi)

---

#12. Find the range of a hyperbolic function

Hyperbolic function	Expression	Range
Hyperbolic Sine function	sinh x=frac{e^{x}-e^{-x}}{2}	(-infty,+infty)
Hyperbolic Cosine function	cosh x=frac{e^{x}+e^{-x}}{2}	[1,infty)
Hyperbolic Tangent function	tanh x=frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}	(-1,+1)
Hyperbolic CSC function	csch x=frac{2}{e^{x}-e^{-x}}	(-infty,0)cup(0,infty)
Hyperbolic Secant function	sech x=frac{2}{e^{x}+e^{-x}}	(0,1)
Hyperbolic Cotangent function	tanh x=frac{e^{x}+e^{-x}}{e^{x}-e^{-x}}	(-infty,-1)cup(1,infty)

---

#13. Find the range of an inverse hyperbolic function

Inverse hyperbolic function	Expression	Range
Inverse hyperbolic sine function	sinh^{-1}x=ln(x+sqrt{x^{2}+1})	(-infty,infty)
Inverse hyperbolic cosine function	cosh^{-1}x=ln(x+sqrt{x^{2}-1})	[0,infty)
Inverse hyperbolic tangent function	tanh^{-1}x=frac{1}{2}lnleft (frac{1+x}{1-x}right )	(-infty,infty)
Inverse hyperbolic CSC function	csch^{-1}x=ln left ( frac{1+sqrt{1+x^{2}}}{x} right )	(-infty,0)cup(0,infty)
Inverse hyperbolic Secant function	sech^{-1}x=ln left ( frac{1+sqrt{1-x^{2}}}{x} right )	[0,infty)
Inverse hyperbolic Cotangent function	coth^{-1}x=frac{1}{2}lnleft (frac{x+1}{x-1}right )	(-infty,0)cup(0,infty)

---

#14. Find the range of a piecewise function

Example 25: Find the range of the piecewise function

Solution:

The piecewise function consists of two function:

1. f(x)=x-3 when xleq -1,
2. f(x)=x+1 when x>1.

If we plot these two functions on the graph then we get,

This is the graph of the piecewise function.

From the graph, we can see that

1. the range of the function f(x)=x-3 is (-infty,-2] when xleq -1,
2. the range of the function f(x)=x+1 is (2,infty) when x>1,

Therefore from the above results we can say that

The range of the piecewise function f(x) is

(-infty,-2]cup (2,infty).

---

Example 26: Find the range of a piecewise function given below

Solution:

If you notice the piecewise function then you can see there are functions:

1. f(x)=x defined when xleq -1,
2. f(x)=2 defined when -1<x<1),
3. f(x)=sqrt{x} defined when xgeq 1.

Now if we draw the graph of these three functions we get,

This is the graph of the piecewise function.

Here you can see that

The function f(x)=x starts y=-1 and extended to -infty when xleq -1.

So the range of the function f(x)=x,xleq -1 is (-infty,-1]……..(1)

The functional value of the function f(x)=2, -1<x<1 is 2.

The range of the function f(x)=x is {2}……..(2)

The function f(x)=sqrt{x} starts at y=1 and extended to infty when xgeq 1.

The range of the function f(x)=sqrt{x} is [1,infty) when xgeq 1……..(3)

From (1), (2), and (3), we get,

the range of the piecewise function is

(-infty,-1]cup {2}cup [1,infty)

= (-infty,-1]cup [1,infty)

---

#15. Find the range of a composite function

Example 27: Let f(x)=2x-6 and g(x)=sqrt{x} be two functions.

Find the range of the following composite functions:

Solution of (a)

Solution of (b):

---

Example 28: Let f(x)=3x-12 and g(x)=sqrt{x} be two functions.

Find the range of the following composite functions

1. fcirc g(x),
2. gcirc f(x)

Solution:

Also read:

• How to Find the Domain of a Function Algebraically – Best 9 Ways
• 3 ways to find the zeros of a function
• How to find the zeros of a quadratic function?
• 13 ways to find the limit of a function
• How to use the Squeeze theorem to find a limit?

Изучение того, как найти диапазон функции, может оказаться очень важным в алгебре и исчислении, потому что это дает вам возможность оценить, какие значения достигаются функцией. Или, другими словами, позволяет найти набор всех изображений с помощью функции

Задача поиска точек, которые могут быть достигнуты функцией, очень полезна. Например, у вас может быть производственная функция (q(x)), которая дает вам объем вывода, полученный для (x) единиц ввода.

Мы хотели бы знать, сколько единиц ввода необходимо для производства (b) единиц вывода. Другими словами, нам нужно найти (x), чтобы (q(x) = b), что является еще одним способом узнать, находится ли (b) в диапазоне функции (q(x)).

В этом уроке мы больше сконцентрируемся на механике нахождения диапазона. Для более концептуального подхода к домену и диапазону вы можете

проверьте этот учебник

.

---

Алгебраический способ определения диапазона функции

Так же, как когда мы узнали, как вычислить домен, не существует единого рецепта для нахождения диапазона, это действительно зависит от структуры функции (f(x)).

Тем не менее, всегда будет использоваться один алгебраический прием. ТАКИМ способом вы найдете диапазон. Обращать внимание:

Скажем, нам нужно получить диапазон заданной функции (f(x)). Затем мы рассмотрим типичное действительное число (y) и попытаемся решить для (x) следующее уравнение:

[f(x) = y]

Нам нужно определить, для каких значений (y) приведенное выше уравнение может быть решено для (x). Вот и все. Конечно, это может быть сложно сделать, в зависимости от структуры функции (f(x)), но это то, что вам нужно сделать.

Итак, это алгебраический способ, способ найти диапазон функции без построения графиков.

ПРИМЕР 1

Найдите диапазон функции (displaystyle f(x) = frac{x+1}{x-3}):

ОТВЕЧАТЬ:

Мы продолжаем использовать алгебраический способ: пусть (y) будет числом, и мы решим для (x) в следующем уравнении: (f(x) = y). Значение (y) находится в диапазоне, если (f(x) = y) может быть решено для (x).

В этом случае мы имеем:

[large f(x) = y Leftrightarrow frac{x+1}{x-3} = y]
[Rightarrow ,,,x+1 = yleft( x-3 right)]
[Rightarrow ,,,x+1 = yx-3y]
[Rightarrow ,,,x-yx=-1-3y]
[Rightarrow ,,,xleft( 1-y right)=-1-3y]
[Rightarrow ,,,x=frac{3y+1}{y-1}]

Следовательно, когда будет четко определено (x)? Почти для всех (y), кроме случая (y = 1), потому что в этом случае у нас есть деление на (0). Следовательно, диапазон (f) в этом случае — это вся вещественная линия, кроме 1.

Если мы используем обозначение интервалов, мы можем написать (Range(f) = (-infty, 1) cup (1, +infty)).

ПРИМЕР 2

Найдите диапазон функции (f(x) = x^2 — 4x + 3):

ОТВЕЧАТЬ:

Опять же, мы продолжаем использовать алгебраический способ, поэтому вы знаете, что упражнение: Пусть (y) будет числом, и мы решим для (x) в следующем уравнении: (f(x) = y). Значение (y) находится в диапазоне, если (f(x) = y) может быть решено для (x).

В этом случае мы имеем:

[large f(x) = y Leftrightarrow x^2 — 4x + 3 = y]
[Rightarrow ,,, x^2 — 4x + 3 — y = 0 text{ (This is a quadratic equation in x)}]
[Rightarrow displaystyle ,,, x = frac{-b pm sqrt{b^2 — 4ac}}{2a}]
[Rightarrow displaystyle ,,, x = frac{-(-4) pm sqrt{(-4)^2 — 4(1)(3-y)}}{2(1)}]
[Rightarrow displaystyle ,,, x = frac{4 pm sqrt{16 — 4(3-y)}}{2}]
[Rightarrow displaystyle ,,, x = frac{4 pm sqrt{16 — 12 + 4y}}{2}]
[Rightarrow displaystyle ,,, x = frac{4 pm sqrt{4 + 4y}}{2}]
[Rightarrow displaystyle ,,, x = 2 pm sqrt{1+y}]

Теперь, видя это последнее выражение, когда будет хорошо определено (x)? Нам нужно, чтобы аргумент квадратного корня был неотрицательным, поэтому нам нужно:

[1+y ge 0]

что означает, что (y ge -1). Если мы используем обозначение интервалов, мы можем написать (Range(f) = [-1, +infty)).

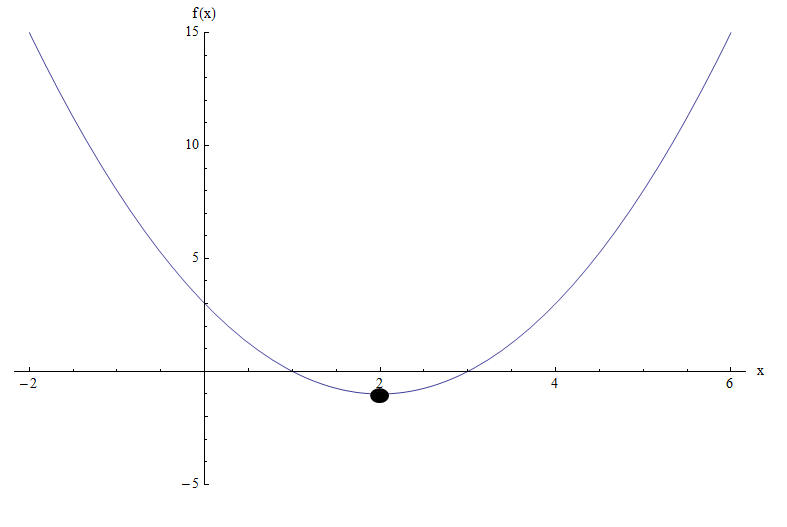
В этом примере мы могли бы решить эту проблему, используя тот факт, что (f(x) = x^2 — 4x + 3) является квадратичной функцией, а ее график представляет собой параболу, которая открывается вверх.

Точка минимума этой параболы достигается в вершине. Координата x вершины:

[displaystyle x_V = frac{-b}{2a} =frac{-(-4)}{2(1)} =frac{4}{2} = 2]

Теперь координата y вершины просто определяется путем вставки значения (x_V = 2) в квадратичную функцию:

[y_V = f(x_V) = 2^2 — 4(2) + 3 = -1]

Поскольку минимальное значение, достигаемое параболой, равно (-1), мы заключаем, что диапазон равен ([-1, +infty)), что является тем же выводом, что и найденный алгебраически.

График функции (f(x) = x^2 — 4x + 3) делает это еще более понятным:

Мы можем видеть, что на основе графика минимум достигается в (x = 2), что в точности соответствует координате x вершины.

Риск использования графика для определения диапазона заключается в том, что вы потенциально можете неправильно прочитать критические точки на графике и дать неточную оценку того, где функция достигает своего максимума или минимума.

---

Другие стратегии поиска диапазона функции

Как мы видели в предыдущем примере, иногда мы можем найти диапазон функции, просто взглянув на ее график.

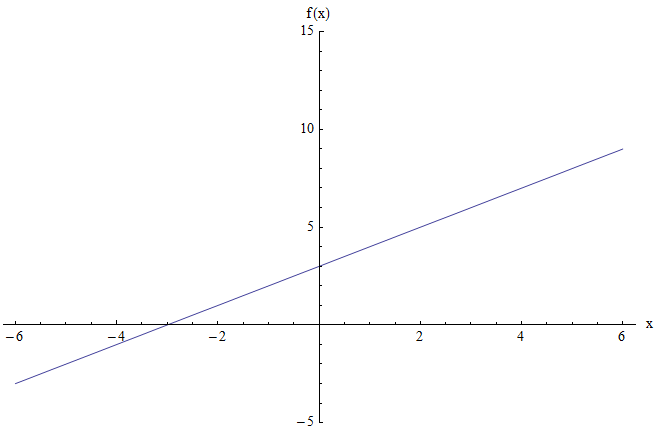
Например, вы хотите найти диапазон функции (f(x) = x + 3). График показан ниже:

На графике выше не показаны минимальные или максимальные точки. Более того, когда (x) большое и положительное значение, значение функции также большое и положительное. И аналогично, когда (x) очень отрицательно, значение функции также очень отрицательное.

Интуиция подсказывает, что функция может принимать любые отрицательные и положительные значения, выбирая достаточно большие (положительные или отрицательные) значения (x). И тогда можно сделать вывод, что диапазон — это вся реальная линия, которая равна ((-infty, +infty)) с использованием обозначения интервала.

Такой анализ верен с точки зрения результата, но ненадежен с точки зрения аргументации. У «графического метода» поиска диапазона есть та же проблема: он привлекателен с интуитивной точки зрения, но довольно скуден с точки зрения содержания.

Обычно, если возможно, мы должны предпочесть аналитический / алгебраический путь. В этом примере нам нужно найти (x):

[x + 3 = y]

[Rightarrow ,, x = y — 3]

Итак, есть ли какие-либо ограничения на (y) для правильного определения (x)? Вовсе нет, поэтому нет никаких ограничений на (y), и можно сделать вывод, что диапазон — это вся реальная линия.

Вы можете проверить эту статью, если хотите

знать, как найти домен функции

вместо.

Есть много веских алгебраических причин для нахождения диапазона, одна из них состоит в том, что он является частью процессов для

найти обратную функцию

.

Описание изображения

Вид на пустую аудиторию колледжа с задней стороны.

Для любого человека, заинтересованного в карьере математика или человека, который использует математику, например, в бизнесе, важно уметь четко объяснять формулы и решения. В случае нахождения диапазона функции, вы можете найти это значение несколькими способами. Умение объяснить эти методы может оказаться полезным по мере развития ваших математических и коммуникативных навыков.

В этой статье мы дадим определение математического диапазона, области и функции, а затем расскажем, как найти диапазон функции с помощью формулы, графика и отношения.

Основные выводы:

• В математике функция представляет собой определенную связь между независимой переменной (x) и зависимой переменной (y).

• Диапазон функции относится ко всем возможным значениям y.

• Формула для нахождения диапазона функции: y = f(x). Отношение является функцией только в том случае, если каждому значению x соответствует только одно значение y.

Что такое функция?

Функция — это прикладной математический термин, используемый для описания взаимосвязи между двумя переменными. В формуле вы можете представить функцию в виде:

y = f(x)

В этой формуле y является функцией x, то есть при изменении значения x изменяется и значение y (или диапазон, или зависимая переменная). Например:

Если x равен 2 в уравнении y = x -1, то значение y равно 1: y = 2-1

Но если x имеет значение 10, то y также изменится — до 9, или y=10-1

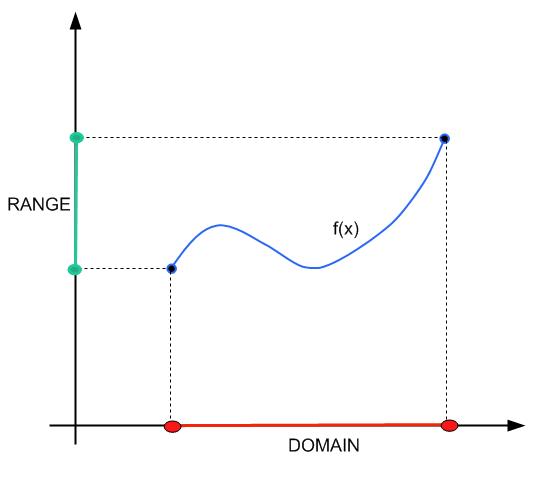
Что такое диапазон функции?

Значения переменных меняются, что можно представить в виде набора значений, называемых областью и диапазоном функции:

• Домен: Область функции — это набор чисел, представляющих все значения, которые может иметь x.

• Диапазон: Диапазон — это набор чисел, которые представляют все потенциальные значения, которые y может иметь на основе функции.

3 способа найти диапазон функции

Для x в упорядоченной паре (x, y) может соответствовать только одно значение y. Для y, однако, существует больше возможностей. Нахождение диапазона функции означает нахождение всех возможных значений, которые может иметь y в зависимости от x. Вы можете найти диапазон функции тремя способами: формула, график или зависимость.

1. Нахождение диапазона функции с помощью формулы

Формула может представлять, как переменная x взаимодействует с переменной y. Эти формулы могут выглядеть по-разному в зависимости от того, какое взаимодействие имеют значения. Ниже приведены шаги, которые можно использовать для алгебраического нахождения диапазона функции:

1. Запишите формулу

Запись формулы — где y = f(x)- может помочь вам определить некоторые аспекты связи между двумя переменными.

Пример: Если вы продаете журналы по 10 долларов за штуку, то ваш общий объем продаж, f(x), равен количеству проданных журналов, x, умноженному на 10. Итак, формула f(x) = 10(x). Если вы продаете ноль, 2, 4 или 10 журналов, то ваши общие продажи составляют $0, $20, $40 и $100.

2. Найдите другие пары координат

Если применить формулу y = f(x), то она показывает положительную зависимость между x и y для всех журналов продаж. Чтобы перепроверить эту информацию, вы можете нарисовать переменные в виде упорядоченных пар на графике. Полученный график является линейным и имеет тенденцию к росту. Это подтверждает вывод о том, что функция положительна.

3. Напишите диапазон

Зная, что вы не можете продавать отрицательные журналы, вы можете определить, что диапазон функции никогда не бывает меньше нуля. Поскольку вы всегда можете продать больше журналов, вы знаете, что диапазон может постоянно увеличиваться на интервалы в 10 раз. Таким образом, вы можете записать диапазон функции в виде эквивалентности.

В данном примере диапазон f(x) = все кратные 10 ? 0.

2. Нахождение диапазона функции с помощью графика

График может обеспечить визуальное представление формы, которую принимает функция, позволяя увидеть, как координаты y взаимодействуют с координатами x. Вот шаги для нахождения диапазона функции с помощью графика:

1. Нарисуйте функцию на графике

Чтобы найти диапазон функции на графике, отметьте (или постройте) координаты области (x) и диапазона (y) на листе бумаги с помощью маленьких точек. Это поможет вам увидеть форму функции. Вы можете увидеть прямую линию, изогнутую линию в форме u или n или что-то похожее на волны.

При построении графика перемещайтесь влево или вправо по оси x, в зависимости от того, отрицательна или положительна координата x. Затем вы двигаетесь вверх или вниз по оси y, в зависимости от того, положительна или отрицательна координата y.

После завершения работы проследите за формой графика. Например, если вы нарисуете координаты {(2, 1), (3, 2), (4, 3)}, то они образуют прямую линию, которая идет вверх (1, 2, 3).

2. Найдите минимум функции

Как только вы получите функцию в виде графика, вы сможете увидеть важные особенности, например, минимум. Это самая низкая точка, которую функция достигает визуально. Минимум может быть бесконечным, то есть график неограниченно расширяется вниз. Если это так, то нижний конец диапазона может быть представлен символом бесконечности (?).

3. Найдите максимум функции

Максимум — это наивысшая точка, которую функция достигает визуально. Как и минимум, это число может быть бесконечным. Это также может быть конкретное место на графике, которое можно записать в виде упорядоченной пары. Например, если максимум находится при 3 на оси x и 10 на оси y, то его координаты будут (3, 10).

4. Запишите диапазон в виде эквивалентности

Иногда невозможно написать каждую y-координату функции. Здесь вы можете указать диапазон как эквивалентность, используя символ меньше, чем (<), символ больше чем (>), меньше или равно символу (?) или символ больше или равно (?).

Пример: Для диапазона {-1, 1, 2, 3} вы можете использовать утверждение как:

-1 ? f(x) ? 3

Если ваш диапазон функции имеет бесконечную составляющую, например {-?, 10}, вы можете записать эквивалентность как:

f(x) ? 10

3. Нахождение диапазона функции с помощью отношения

Третий способ найти диапазон функции — записать ее в виде отношения. Отношение — это набор упорядоченных пар, представляющих координаты на графике. Вы можете записать пары отношения в форме (x, y). Ниже описаны шаги, которые можно использовать для нахождения диапазона функции, записанной в виде отношения:

1. Напишите отношение

Когда вы видите набор упорядоченных пар (x, y), вам может быть проще работать с отношением после того, как вы запишете пары на бумаге. Запишите весь набор в фигурных скобках. Например:

{(2, 1), (4, 5), (9, 21) (7, 14), (5, 14)}

2. Составьте список y-координат отношения

Вы можете перечислить y-координаты отношения, взяв второе число из каждой пары координат и записав их в фигурных скобках. Это поможет вам легче представить диапазон значений y.

Это также поможет вам сократить объем информации, с которой вы работаете при нахождении диапазона, или y. Используя приведенный выше пример, вы бы записали y-координаты как:

{1, 5, 21, 14, 14}

3. Удалите все дублирующиеся числа

В этом наборе отношений число 14 встречается дважды. Для нахождения диапазона функции второе 14 не имеет значения, поэтому его можно убрать. Вы можете записать новый список y-координат в виде:

{1, 5, 21, 14}

4. Напишите диапазон от наименьшего до наибольшего

Поскольку числа расположены не по порядку, трудно определить диапазон. Вы можете изменить порядок чисел, чтобы облегчить определение диапазона. Упорядоченный от наименьшего к наибольшему, набор y-координат отношения является таковым:

{1, 5, 14, 21}

Как только вы измените порядок чисел, вы получите диапазон функции с помощью отношения. Итак, для набора отношений:

{(2, 1), (4, 5), (9, 21) (7, 14), (5, 14)}

Диапазон после вычитания:

{1, 5, 14, 21}

5. Убедитесь, что отношение является функцией

Проверив, что каждое значение x дает одно и то же число y, вы можете подтвердить, что отношение является функцией. Отношение является функцией, только если каждому значению x соответствует только одно значение y.

Пример: Если вы вводите x как 2 и получаете на выходе 4, но в следующий раз, когда вы вводите x как 2, вы получаете на выходе 7, то это отношение не является функцией. Если вы каждый раз получаете одно и то же число, то отношение является функцией.

Для примера набора отношений {(2, 1), (4, 5), (9, 21) (7, 14), (5, 14)}, значения x 2, 4, 9, 7 и 5 имеют только одно связанное выходное число каждое, и поэтому это функция, а найденный диапазон функции проверяется.

From Wikipedia, the free encyclopedia

In mathematics, the range of a function may refer to either of two closely related concepts:

• The codomain of the function
• The image of the function

Given two sets X and Y, a binary relation f between X and Y is a (total) function (from X to Y) if for every x in X there is exactly one y in Y such that f relates x to y. The sets X and Y are called domain and codomain of f, respectively. The image of f is then the subset of Y consisting of only those elements y of Y such that there is at least one x in X with f(x) = y.

Terminology[edit]

As the term «range» can have different meanings, it is considered a good practice to define it the first time it is used in a textbook or article. Older books, when they use the word «range», tend to use it to mean what is now called the codomain.^[1][2] More modern books, if they use the word «range» at all, generally use it to mean what is now called the image.^[3] To avoid any confusion, a number of modern books don’t use the word «range» at all.^[4]

Elaboration and example[edit]

Given a function

with domain , the range of , sometimes denoted or ,^[5] may refer to the codomain or target set (i.e., the set into which all of the output of is constrained to fall), or to , the image of the domain of under (i.e., the subset of consisting of all actual outputs of ). The image of a function is always a subset of the codomain of the function.^[6]

As an example of the two different usages, consider the function as it is used in real analysis (that is, as a function that inputs a real number and outputs its square). In this case, its codomain is the set of real numbers , but its image is the set of non-negative real numbers , since is never negative if is real. For this function, if we use «range» to mean codomain, it refers to ; if we use «range» to mean image, it refers to .

In many cases, the image and the codomain can coincide. For example, consider the function , which inputs a real number and outputs its double. For this function, the codomain and the image are the same (both being the set of real numbers), so the word range is unambiguous.

See also[edit]

• Bijection, injection and surjection
• Essential range

Notes and References[edit]

Bibliography[edit]

• Childs (2009). A Concrete Introduction to Higher Algebra. Undergraduate Texts in Mathematics (3rd ed.). Springer. ISBN 978-0-387-74527-5. OCLC 173498962.
• Dummit, David S.; Foote, Richard M. (2004). Abstract Algebra (3rd ed.). Wiley. ISBN 978-0-471-43334-7. OCLC 52559229.
• Hungerford, Thomas W. (1974). Algebra. Graduate Texts in Mathematics. Vol. 73. Springer. ISBN 0-387-90518-9. OCLC 703268.
• Rudin, Walter (1991). Functional Analysis (2nd ed.). McGraw Hill. ISBN 0-07-054236-8.