Вычислить несобственный интеграл или показать его расходимость.
Пример 1:
Найти значение несобственного интеграла или установить его расходимость.
Решение от преподавателя:
Пример 2:
Вычислить несобственные интегралы или доказать их расходимость.
Решение от преподавателя:
Пример 3:
Вычислить несобственный интеграл или указать его расходимость:
Решение от преподавателя:
Пример 4:
Вычислить несобственный интеграл или доказать его расходимость.
Решение от преподавателя:
Пример 5:
Вычислить несобственный интеграл (или доказать его расходимость):
Решение от преподавателя:
Пример 6:
Вычислить несобственный интеграл или доказать его расходимость:
Решение от преподавателя:
Пример 7:
Вычислить несобственный интеграл (или доказать его расходимость):
Решение от преподавателя:
Пример 8:
Вычислить несобственный интеграл или доказать его расходимость
Решение от преподавателя:
Пример 9:
Вычислить несобственный интеграл с помощью вычетов:
Решение от преподавателя:
Пример 10:
Вычислить несобственные интегралы или доказать их расходимость.
Решение от преподавателя:
Пример 11:
Вычислить несобственный интеграл или показать его расходимость.
Решение от преподавателя:
Пример 12:
Вычислить несобственный интеграл или установить его расходимость.
Решение от преподавателя:
Пример 13:
Вычислить несобственный интеграл или показать его расходимость.
Решение от преподавателя:
Пример 14:
Вычислить несобственный интеграл или доказать его расходимость
Решение от преподавателя:
Пример 15:
Вычислить несобственный интеграл или доказать его расходимость.
Решение от преподавателя:
Пример 16:
Вычислить несобственный интеграл или показать его расходимость.
Решение от преподавателя:
Пример 17:
Вычислить несобственный интеграл или показать его расходимость.
Решение от преподавателя:
Пример 18:
Вычислить несобственный интеграл или показать его расходимость.
Решение от преподавателя:
Пример 19:
Вычислить несобственный интеграл или показать его расходимость.
Решение от преподавателя:
Пример 20:
Вычислить определённый интеграл. Для несобственных интегралов решить вопрос об их сходимости или расходимости:
Решение от преподавателя:
Пример 21:
Вычислить определённый интеграл. Для несобственных интегралов решить вопрос об их сходимости или расходимости:
Решение от преподавателя:
Пример 22:
Вычислить определённый интеграл. Для несобственных интегралов решить вопрос об их сходимости или расходимости:
Решение от преподавателя:
Пример 23:
Вычислить определённый интеграл. Для несобственных интегралов решить вопрос об их сходимости или расходимости:
Решение от преподавателя:
Работа вам нужна срочно. Не волнуйтесь, уложимся!
Заполните, пожалуйста, данные для автора:
- 22423 авторов готовы помочь тебе.
- 2402 онлайн
Содержание:
- Несобственный интеграл — Основные понятия и теоремы
- Свойства несобственного интеграла
- Несобственные интегралы
- Интегралы с бесконечными пределами интегрирования (несобственные интегралы І типа)
- Интегралы от неограниченных функций (несобственные интегралы II типа)
Несобственный интеграл — Основные понятия и теоремы
Пусть функция 




то его называют несобственным интегралом от функции 


Символ (1.2) также называется несобственным интегралом. Если предел (1.1) существует, то несобственный интеграл называется сходящимся, в противном случае — расходящимся.
Аналогично определяется несобственный интеграл с бесконечным нижним пределом:

Интегралы (1.2) и (1.3) называются несобственными интегралами по неограниченному множеству.
Пусть функция 





называют несобственным интегралом от неограниченной функции и по определению полагают

По этой ссылке вы найдёте полный курс лекций по высшей математике:
Если предел (1.5) существует, то несобственный интеграл (1.4) называется сходящимся, в противном случае — расходящимся.
Аналогично определяется несобственный интеграл по промежутку 
Обозначим через 

Пусть функция 



то его называют несобственным интегралом от функции 


Несобственный интеграл по промежутку 




Несобственные интегралы возникают в задачах на геометрические приложения интегрального исчисления: при вычислении площадей неограниченных фигур; объемов тел и площадей поверхностей вращения, если вращающаяся фигура неограничена.
Пусть функция 


которую назовем неограниченной криволинейной трапецией.
Если несобственный интеграл


Возможно вам будут полезны данные страницы:
Объем тела, образованного вращением фигуры 


Площадь поверхности, полученной вращением непрерывной кривой
вокруг оси 

Формулы (1.10), (1.11), как и формула (1.9), применимы при условии сходимости соответствующих несобственных интегралов.
При решении геометрических задач используются и несобственные интегралы от неограниченных функций.
Свойства несобственного интеграла
1
2.
3. При любом
Свойства 1 и 2 называют линейными, а свойство 3 — аддитивностью.
Теорема 1.1 (о замене переменной в несобственном интеграле). Пусть выполнены следующие условия:
1) непрерывно дифференцируемая и строго монотонная функция 




2) функция 

либо оба сходятся, либо оба расходятся. В случае сходимости справедливо равенство

Теорема 1.2 (об интегрировании по частям в несобственном интеграле). Пусть функции 



Тогда интегралы
либо оба сходятся, либо оба расходятся. В случае сходимости справедливо равенство

где
Определенный интеграл считается неуместным, если выполнено хотя бы одно из следующих условий: Поля интеграции бесконечны. Например, бесконечный разрыв. Функция не ограничена вблизи некоторых точек области интегрирования.
Примеры с решением
Вычислить несобственный интеграл или установить его расходимость.
Пример 1.
Решение:
Вычислим несобственный интеграл по определению:
Следовательно, данный интеграл интеграл сходится.
Пример 2.
Решение: По определению несобственного интеграла с бесконечным верхним пределом имеем
Следовательно, данный интеграл интеграл расходится.
Пример 3.
Решение:
По определению несобственного интеграла с бесконечным нижним пределом имеем
Итак, интеграл сходится и равен 1.
Пример 4.
Решение:
Интеграл является несобственным, поскольку верхний предел бесконечен. Рассмотрим два случая.
1). Пусть 
2). Пусть 



Пример 5.
Решение:
Данный интеграл является несобственным, поскольку подынтегральная функция 



Пример 6.
Решение:
Подынтегральная функция
1). Пусть
2). Пусть
Итак, интеграл 

Пример 7.
Решение:
Применим к данному интегралу формулу интегрирования по частям: 
Данный интеграл является несобственным, поскольку
подынтегральная функция 



Заметим, что в результате замены переменной несобственный интеграл преобразовался в определенный интеграл от непрерывной функции по отрезку.
Пример 8.
Найти площадь фигуры, ограниченной графиком функции

Решение:
Функция 

Для вычисления интеграла применим формулу (1.13) интегрирования по частям. Положим 




По формуле (1.13) имеем
Пример 9.
Найти объем тела, образованного вращением вокруг оси 

Решение: Функция 

Итак,
Несобственные интегралы
Понятие «несобственные интегралы» связано с нарушением условий теоремы 23.1 о существовании определенного интеграла. В зависимости от того, какая именно условие существования нарушена, рассматривают несобственные интегралы I и II типов.
Различают следующие случаи:
1) вместо конечного отрезка 


2) вместо подынтегральной функции, которая является непрерывной или ограниченной на отрезке интегрирования и имеет конечное число точек разрыва первого рода, рассматривают функцию, имеет на этом отрезке бесконечный разрыв, то есть разрыв второго рода.
Интегралы с бесконечными пределами интегрирования (несобственные интегралы І типа)
Пусть функция 






то есть 
Несобственным интегралом I типа функции 



Если граница 
С учетом формулы Ньютона-Лейбница соотношение (25.1) можно записать так:
где применяется обозначения:
Аналогично определяется несобственный интеграл I типа для случая, когда вместо отрезка интегрирования 
Пусть функция 


Несобственным интегралом I типа функции 


где применяется обозначение
Пусть функция 


Если в соотношении (25.4) обе границы существуют, то несобственный интеграл I типа с бесконечными пределами совпадает.
С учетом формулы Ньютона-Лейбница несобственный интеграл на промежутке
Общий порядок нахождения несобственного интеграла I типа состоит из двух шагов:
1) вычисляем определенный интеграл от 



2) находим границу определенного интеграла при
Под исследованием несобственных интегралов на сходимость понимают установления факта его сходимости или разногласия. Для этого во многих случаях бывает достаточна не вычислять самый интеграл (а он может быть таким, что и «не берется»), а сравнить его с несобственным интегралом, сходимость (или расхождение) которого известна.
Приведем признаки сравнения несобственных интегралов (которые примем без доказательства).
Теорема 25.1. Если функции 





Теорема 25.2. Если функции 




Несобственный интеграл от функции 

В предыдущих теоремах рассматривались несобственные интегралы от неотъемлемых функций. Для знакопеременной функции 
Теорема 25.3. Если несобственный интеграл от модуля заданной функции 
В этом случае несобственный интеграл от 

Рассмотрим некоторые примеры несобственных интегралов I типа. Одним из таких интегралов является интеграл Эйлера-Пуассона:
Этот интеграл нельзя представить в виде конечного числа элементарных функций, поэтому по общему алгоритму проблему вычисления интеграла Эйлера — Пуассона решить невозможно. Докажем, что этот интеграл совпадает, применив теорему 25.1.
Как эталонную функцию выберем функцию φ () x e x = -. Учтем также парность подынтегральной функции Как эталонную функцию выберем функцию φ () x e x = -. Учтем также парность подынтегральной функции 
Рис. 25.1
Сравним функции 





Следовательно, применить теорему 25.1 можно только на промежутке
Исследуем на сходимость интеграл от эталонной функции на
Эталонный интеграл совпадает на промежутке 




В главе 26 будет доказано, что:
При исследовании вопроса о сходимости несобственных интегралов I типа часто в роли эталонного интеграла принимают интеграл вида:
Свойства этого интеграла зависят от значений параметра
Интеграл (25.8) при 
Следовательно, несобственный интеграл от степенной функции 

Исследовать на сходимость несобственный интеграл I типа:
По определению:
Мы доказали, что несобственный интеграл совпадает, поскольку соответствующая граница равна конечном числу.
Исследовать на сходимость несобственный интеграл I типа:
По определению имеем:
Эта граница не существует, поскольку не существует 
Исследовать на сходимость несобственный интеграл I типа:
По определению:
то есть данный интеграл расходится.
Интегралы от неограниченных функций (несобственные интегралы II типа)
Пусть 





Рис. 25.2
Выберем некоторое положительное число 

Несобственным интегралом II типа от функции 




Аналогично определяют несобственные интегралы II типа для случая, когда особой точкой является верхняя граница отрезка интегрирования:
а также для случая, когда особая точка является внутренней точкой отрезка интегрирования:
Несобственный интеграл II типа называется сходящимся, если существуют конечные границы в правых частях формул (25.10) — (25.12). В противном случае их называют расходящимися.
Порядок исчисления несобственных интегралов II типа принципиально ничем не отличается от порядка определения несобственных интегралов I типа: вычисляют определенный интеграл на конечном отрезке и находят его границу при условии, что 


где
Для первого и второго эталонных интегралов особой точкой является нижняя граница отрезка интегрирования, а для третьего — верхний предел.
Проведем исследование на сходимость первого интеграла с (25.13):
Если 
Следовательно, несобственный интеграл II типа 

Определим, совпадает ли несобственный интеграл
Его подынтегральная функция имеет разрыв второго рода в точке 
Заданный интеграл совпадает, потому соответствующая граница равна конечном числу.
Исследуем на сходимость несобственный интеграл
Подынтегральная функция непрерывна на промежутке 

Если каждый интеграл в правой части совпадает, то выходной интеграл тоже будет совпадать.
Рассмотрим первый интеграл:
Поскольку первый интеграл расходится, то нет необходимости вычислять второй. Окончательно делаем вывод, что заданный несобственный интеграл расходится.
Лекции:
- Определенный интеграл и объем фигур вращения
- Уравнение гиперболы
- Уравнение эллипса
- Степенные ряды
- Случайные события и вероятность
- Свойства пределов функции
- Решение пределов со степенями
- Теория сплайнов примеры решения
- Жорданова форма матрицы
- Скрещивающиеся прямые
Несобственные интегралы
Сегодня я подготовил для вас подробную статью о несобственных интегралах.
Определенные интегралы , для которых отрезок [a; b] конечен, а функция f(x) – непрерывна на этом отрезке, называют собственными.
С целью обобщения понятия интеграла рассмотрим:
1) определенные интегралы от непрерывных функций, но с бесконечными пределами интегрирования;
2) определенные интегралы с конечными пределами интегрирования, но от функций, имеющих бесконечный разрыв на промежутке интегрирования. Такие определенные интегралы называют несобственными.
1. Интегралы с бесконечными пределами.
Пусть функция f(x) определена на промежутке [a; +∞) и пусть f(x) интегрирована на любом отрезке [a; b] (b> a– произвольные действительные числа).
Определение 1.1. Предел интеграла при b→+∞ называется несобственными интегралом функции f(x) от а до +∞ и обозначается символом:
Если предел (1.1) есть конечное число, то несобственный интеграл называют сходящимся. Если предел (1.1) не существует или равен бесконечности, то несобственный интеграл называют расходящимся.
Пример 1.1. Исследовать на сходимость интеграл
Решение. Вычислим определенный интеграл
Имеем
Следовательно, заданный интеграл сходится и он равен
Из рассмотренного следует, что вопрос о сходимости (расходимости) несобственных интегралов решается с помощью первоначальной функции для подынтегральной функции. Это обстоятельство сильно сужает круг практического использования понятия несобственного интеграла. В отдельных случаях вопрос о сходимости (расхождении) несобственного интеграла можно решить, не находя первообразной для подынтегральной функции. При этом пользуются так называемыми
признаками сходимости несобственных интегралов. Простейшим признаком сходимости является признак сравнения.
Теорема 1.1. Пусть для всех x ≥ a функции f(x) и g(x) определены и выполняются неравенства 0 ≤ f(x) ≤ g(x). Тогда:
Для функции f(x), непрерывной на бесконечном промежутке -∞ < x ≤ b, определяется несобственный интеграл
Для функции f(x), непрерывной на всей числовой оси, несобственный интеграл определяется равенством:
где с – произвольное действительное число.
2. Интегралы от неограниченных функций.
Пусть функция f(x) такая, что для произвольного малого ɛ>0 она определена, ограничена и интегрирована на отрезке [a+ɛ; b] и неограниченна на (a; b].
Определение 1.2. Предел определенного интеграла при ɛ→0 называется несобственным интегралом функции f(x) на отрезке [a; b] и обозначается символом
Аналогично для функции f(x), определенной, непрерывной и интегрированной на отрезке [a; b- ɛ] и неограниченной на [a; b) обозначается несобственный интеграл:
Если пределы (1.4), (1.5) есть конечные числа, то несобственные интегралы называются сходящимися, а если эти пределы не существуют, то несобственные интегралы называются
расходящимися.
В конце отметим, что для функции f(x), которая имеет на промежутке (a; b) точку с, в окрестности которой f(x) неограниченная, но является ограниченной и интегрированной на каждом из отрезков [a; c- ɛ] и [ñ + ɛ; b], интеграл определяется равенством.
Аналогично обозначается несобственный интеграл на отрезке [a; b] от функции, которая непрерывна на нем всюду, кроме конечного числа точек, и неограниченной вблизи этих точек.
Пример 1.2.Исследовать сходимость интегралов. Для сходящихся интегралов найти их значение:
Решение.
а) функция
ограничена и непрерывна, а потому и интегрируемая. Предельное значение
существует; таким образом,
ограничена и непрерывна, но
расходится.
Пример 1.3. Исследовать сходимость интегралов. Для сходящихся интегралов найти их значение
Решение.
если α > 0, интеграл сходится; если α ≤ 0, то интеграл расходится;
если α > 1; если 0 < α ≤ 1, интеграл расходится как и при α = 1:
так и при 0 < α < 1:
Пример 1.4. Найти несобственный интеграл
Решение. Функция непрерывна при 0 ≤ x < 2 и имеет бесконечный разрыв в точке x=2, поэтому имеем
Поэтому данный интеграл сходится и равен 2√2.
Пример 1.5. Исследовать сходимость интегралы. Для сходящихся интегралов найти их значение:
Решение.
то есть, несобственный интеграл расходится
то есть, несобственный интеграл I2 сходится и равен .
Пример 1.5. Исследовать на сходимость интегралы:
Решение.
Если у Вас есть ко мне вопросы, или нужна помощь, консультация по решению несобственных интегралов, записывайтесь на мои занятия. Буду рад Вам помочь.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Сходимость интегралов, формулы и примеры
Теорема (Признак сравнения). Пусть на промежутке функции и непрерывны, а в правом конце указанного промежутка, то есть в точке , терпят разрыв второго рода. Пусть для указанных функций справедливо следующее неравенство: . Тогда из сходимости интеграла следует сходимость интеграла , а из расходимости интеграла следует расходимость интеграла .
ru.solverbook.com
3.3 Признаки сходимости несобственных интегралов
Рассмотрим
достаточные признаки сходимости
несобственных интегралов (признаки
сравнения), позволяющие выяснить вопрос
о сходимости несобственного интеграла
без знания первообразной его подынтегральной
функции.
Признак
сравнения 1 (без доказательства).
Пусть
на промежутке
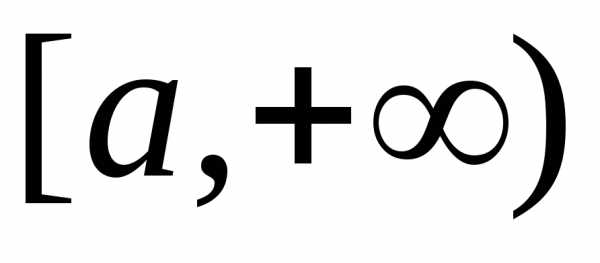
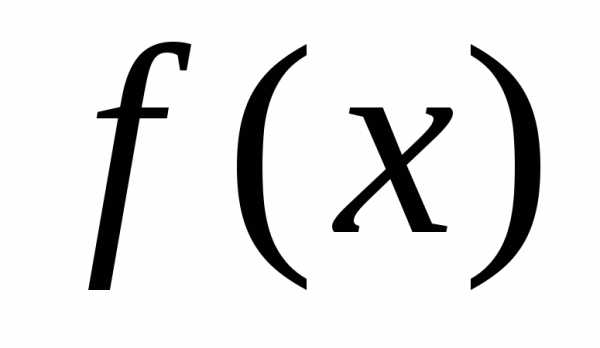
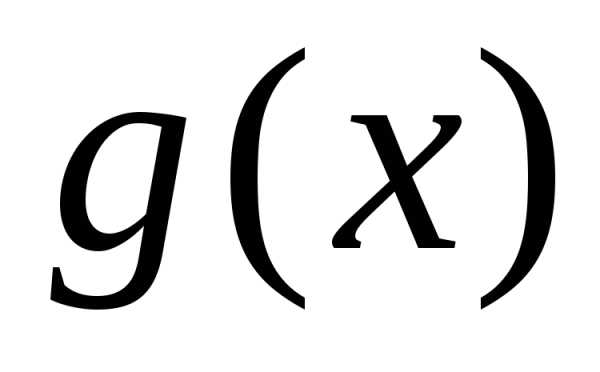
Тогда:
1) если интеграл

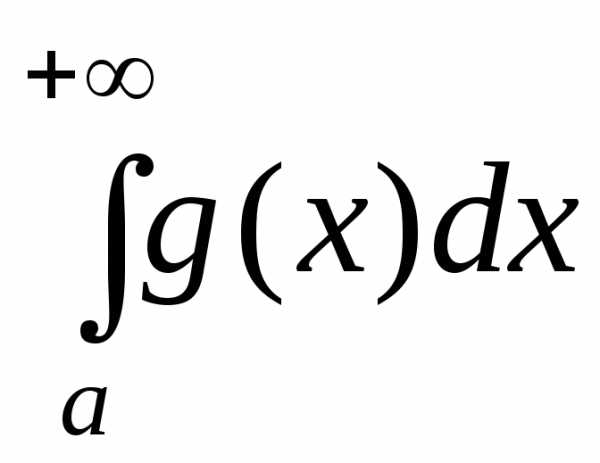
2) если интеграл
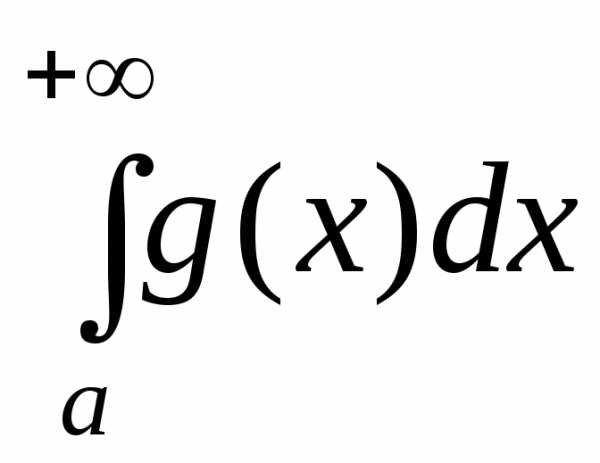
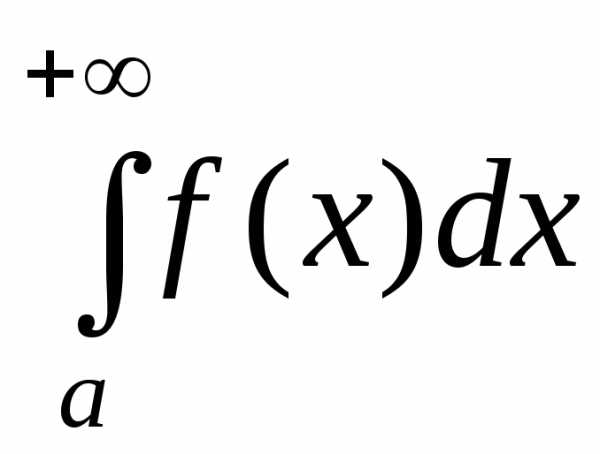
Признак
сравнения 2 (без доказательства).
Пусть
на промежутке
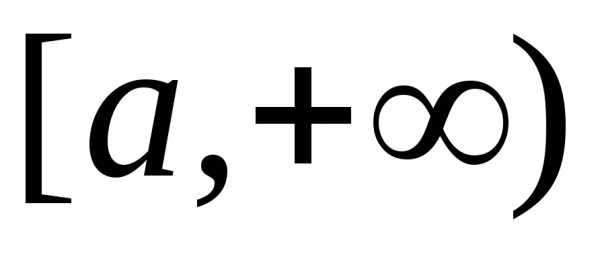
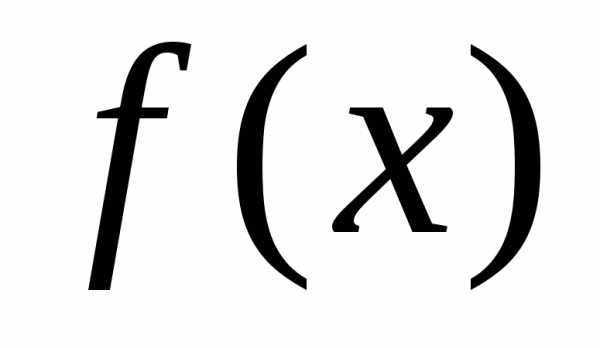
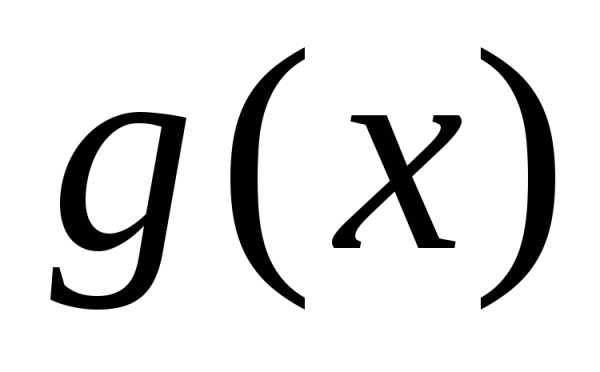
Тогда, если существует конечный и
отличный от нуля предел
,
то несобственные
интегралы
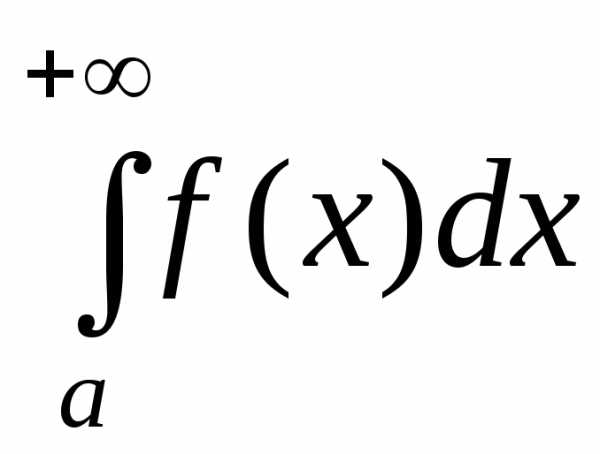

Замечание
1. Аналогичные
признаки сравнения справедливы и для
других видов несобственного интеграла
первого рода, а также для несобственных
интегралов второго рода.
Замечание
2. При
применении признаков сравнения требуется
знать несобственные интегралы,
относительно которых заранее известно,
сходятся они или расходятся. В качестве
таких «эталонных» интегралов на практике
часто используются следующие несобственные
интегралы:
1) несобственный
интеграл первого рода
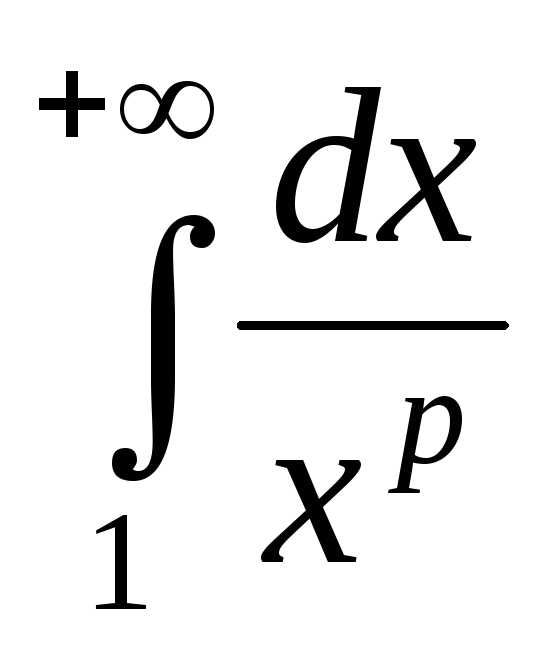
который сходится
при
и расходится при
2) несобственный
интеграл второго рода
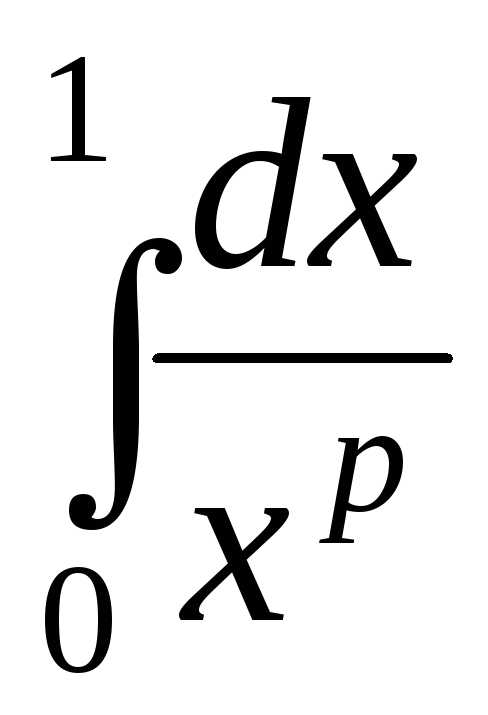
который сходится
при
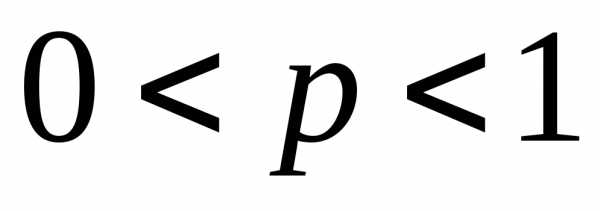

Пример.
Исследуем
на сходимость несобственный интеграл
первого рода
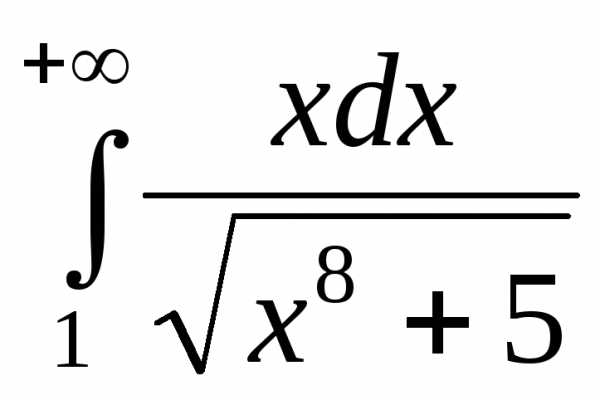
Так как на промежутке

а интеграл

то по признаку сравнения 1 исходный
интеграл также сходится.
3.4 Абсолютная и условная сходимости
Определение.
Несобственный
интеграл называется абсолютно
сходящимся,
если сходится несобственный интеграл
от абсолютной величины подынтегральной
функции.
Несобственный
интеграл называется условно
сходящимся,
если он сходится, а несобственный
интеграл от абсолютной величины
подынтегральной функции расходится.
Теорема
3.1 (без доказательства). Абсолютно
сходящийся интеграл сходится.
Используя понятие
абсолютной сходимости и данную теорему,
можно исследовать сходимость несобственных
интегралов от знакопеременных функций,
применяя признаки сравнения.
Пример.
Исследуем
на сходимость несобственный интеграл
первого рода
от знакопеременной
функции

Так как на промежутке
,
и интеграл
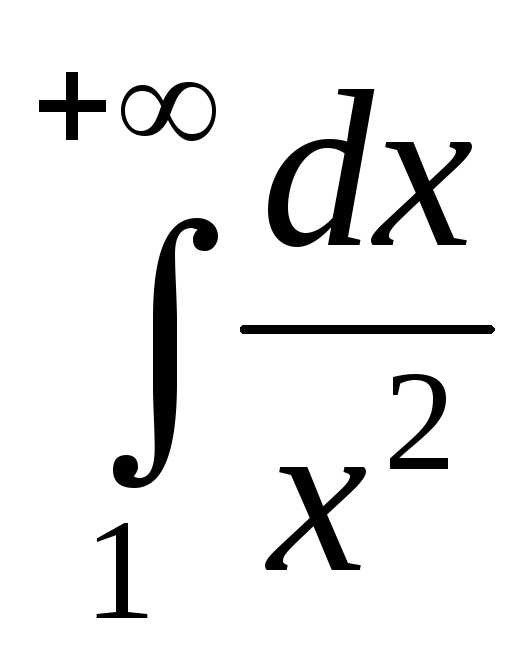
то по признаку сравнения 1 исходный
интеграл также сходится (абсолютно).
4 Обыкновенные дифференциальные уравнения
4.1 Общие понятия
Определение.
Дифференциальным
уравнением называется
уравнение, содержащее производные или
дифференциалы неизвестной функции.
Если неизвестная
функция зависит только от одного
аргумента, то дифференциальное уравнение
называется обыкновенным.
Если же неизвестная
функция зависит от двух или большего
числа независимых переменных, то
дифференциальное уравнение называется
уравнением
в частных производных.
Определение.
Порядком
n
дифференциального
уравнения называется порядок наивысшей
производной или наивысшего дифференциала,
входящих в уравнение.
В данном разделе
будем изучать только обыкновенные
дифференциальные уравнения, как правило,
относительно неизвестной функции
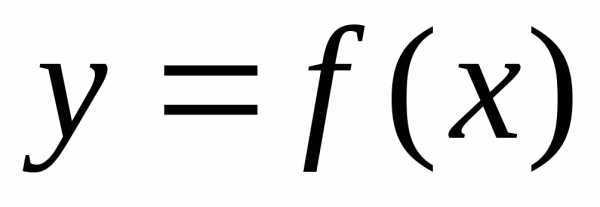
Примеры
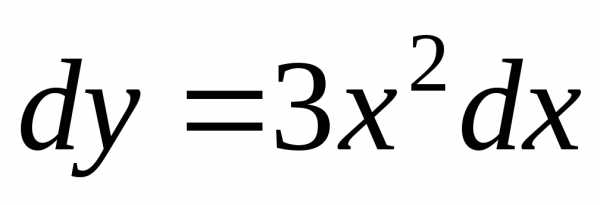
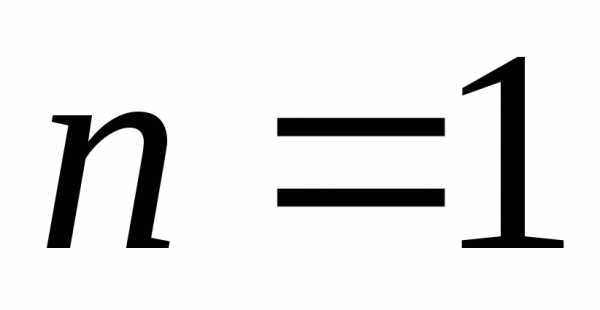
уравнение 1-го порядка;
,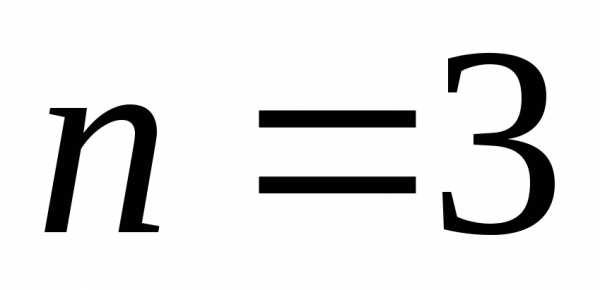
уравнение 3-го порядка;
,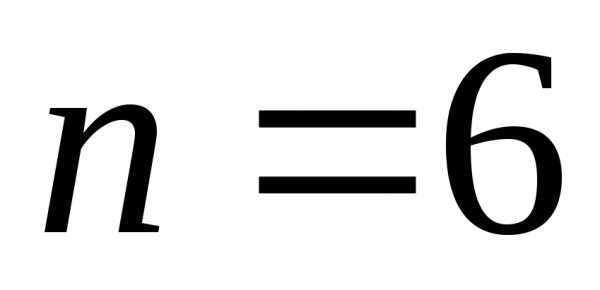
уравнение 6-го порядка.
Определение.
Решением
дифференциального
уравнения называется функция

которая при подстановке в дифференциальное
уравнение обращает его в верное равенство
(тождество).
Процесс нахождения
решений дифференциального уравнения
называется интегрированием
дифференциального уравнения,
а действие интегрирования функций
называется квадратурой.
При этом под
квадратурой
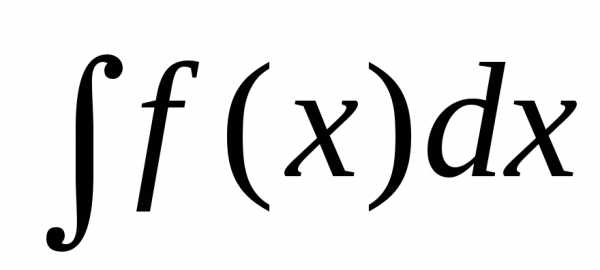
первообразную.
Однако не всегда
решение дифференциального уравнения
может быть получено в виде явно заданной
функции
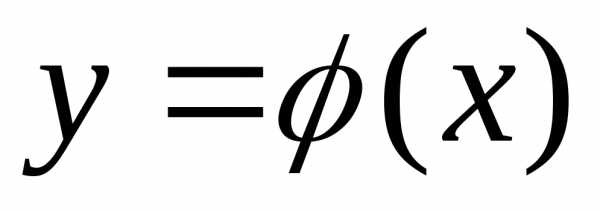
Пример
;
;
.
Обозначим
.
Определение.
Уравнение
,которое
определяет решение
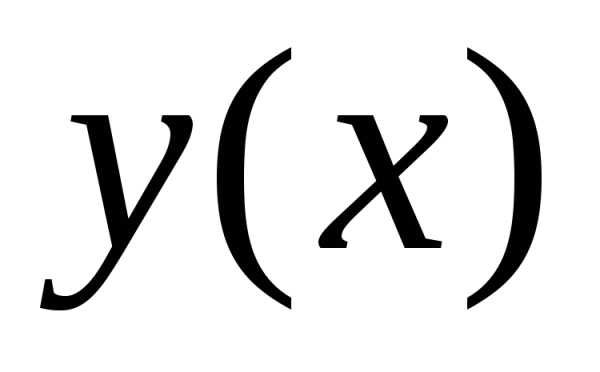
функциюx,
называется интегралом
рассматриваемого
дифференциального уравнения.
studfiles.net
Определение определенного интеграла. Основные свойства определенного интеграла. Приложения определенного интеграла, страница 7
7. Несобственные интегралы
Рассмотрим так называемые несобственные интегралы,
т.е. определенный интеграл от непрерывной функции, но с бесконечным
промежутком интегрирования (несобственный интеграл I
рода), или определенный интеграл с конечным промежутком интегрирования, но от
функции, имеющей на нем бесконечный разрыв (несобственный
интеграл II рода).
Рассмотрим, как вычисляются несобственные интегралы I
рода. Здесь возможны три варианта:
1) Пусть функция непрерывна
на промежутке , тогда
|
|
. Если |
2) Если функция непрерывна
на промежутке , тогда
|
|
. Сходимость |
Несобственный интеграл с двумя бесконечными пределами
интегрирования определяется формулой
,
где
с – произвольное число.
|
|
Интеграл, |
Вычислить несобственные интегралы или установить их
расходимость :
1. данный интеграл
сходится.
2. т. к. при не существует, данный интеграл расходится.
следовательно,
данный интеграл сходится.
В некоторых задачах нет необходимости вычислять
интеграл, достаточно лишь знать, сходится он или нет.
Сформулируем признак сходимости:
Интеграл : 1) сходится, если и ;
2) расходится, если и
, где М, m — постоянные.
Пример.
Установить, сходится или расходится интеграл ,
используя признак сходимости.
Решение. Так как , то , т.е. подынтегральная функция
удовлетворяет условию (1) при , данный интеграл сходится.
Теперь рассмотрим, как вычисляются несобственные
интегралы II рода.
Если функция терпит бесконечный
разрыв в точках , или ,
или , то интеграл называется
несобственным интегралом II рода.
Таким образом, при вычислении таких интегралов также возможны
три варианта:
Если хотя бы один из пределов не существует или
равен бесконечности, несобственный интеграл II рода расходится.
В противном случае – сходится.
Вычислить несобственные интегралы или установить их
расходимость:
1.
,
следовательно,
данный интеграл сходится.
2.
так
как этот предел не существует, следовательно, данный интеграл расходится.
3.
следовательно,
данный интеграл расходится .
Задания для самостоятельной работы
Вычислить несобственные интегралы или установить их
расходимость:
Ответы:
|
1. |
. |
|
2. |
1. |
|
3. |
Расходится. |
|
4. |
6. |
|
5. |
1. |
|
6. |
. |
vunivere.ru
2. Несобственные интегралы
Несобственный
интеграл
Определенный
интеграл как предел интегральной суммы
может
существовать (т.е. иметь определенное
конечное значение) лишь при выполнении
условий
-
отрезок
интегрирования [a;
b]
конечный; -
подынтегральная
функция
непрерывная (или хотя бы кусочно-непрерывная)
и, следовательно, ограниченная на этом
отрезке.
Если
хотя бы одно из этих условий нарушено,
то определение теряет смысл. Действительно,
в случае бесконечного отрезка, например
[a;
)
его нельзя разбить на п
частей конечной длины
,
которая к тому же с увеличением количества
отрезков стремилась бы к нулю. В случае
же неограниченной в некоторой точкес[a;
b]
нарушается требование произвольного
выбора точки
на частичных отрезках – нельзя выбрать=с,
поскольку значение функции в этой точке
не определено. Однако и для этих случаев
можно обобщить понятие определенного
интеграла, введя еще один предельный
переход. Интегралы по бесконечным
промежуткам и от разрывных (неограниченных)
функций называют несобственными.
Определение.
Пусть
функция
определена на промежутке [a;
)
и интегрируема на любом конечном отрезке
[a;
b],
т.е. существует
для любого b
> a.
Предел вида
называютнесобственным
интегралом
первого
рода (или
несобственным интегралом по бесконечному
промежутку) и обозначают
.
Таким
образом, по определению,
=.
Если
предел справа существует и конечен, то
несобственный интеграл
называютсходящимся.
Если этот предел бесконечен, или не
существует вообще, то говорят, что
несобственный интеграл расходится.
Аналогично
можно ввести понятие несобственного
интеграла от функции
по промежутку (–;
b]:
=.
А
несобственный интеграл от функции
по промежутку (–;
+)
определяется как сумма введенных выше
интегралов:
=+,
где
а
– произвольная точка. Этот интеграл
сходится, если сходятся оба слагаемых,
и расходится, если расходится хотя бы
одно из слагаемых.
С
геометрической точки зрения, интеграл,,
определяет численное значение площади
бесконечной криволинейной трапеции,
ограниченной сверху графиком функции,
слева – прямой,
снизу – осью ОХ. Сходимость интеграла
означает существование конечной площади
такой трапеции и равенство ее пределу
площади криволинейной трапеции с
подвижной правой стенкой.
На
случай интеграла с бесконечным пределом
можно обобщить и формулу
Ньютона-Лейбница:
=
=F(+)
– F(a),
где
F(+)
=
.
Если этот предел существует, то интеграл
сходится, в противном случае – расходится.
Мы
рассмотрели обобщение понятия
определенного интеграла на случай
бесконечного промежутка.
Рассмотрим теперь
обобщение для случая неограниченной
функции.
Определение
Пусть
функция
определена на промежутке [a;
b),
неограниченна в некоторой окрестности
точки b,
и непрерывна на любом отрезке
,
где>0
(и, следовательно, интегрируема на этом
отрезке, т.е.
существует). Предел виданазываетсянесобственным
интегралом второго рода
(или несобственным интегралом от
неограниченной функции) и обозначается
.
Таким
образом, несобственный интеграл от
неограниченной в точке b
функции есть по определению
=.
Если
предел справа существует и конечен, то
интеграл называется сходящимся.
Если конечного предела не существует,
то несобственный интеграл называется
расходящимся.
Аналогично
можно определить несобственный интеграл
от функции
имеющей бесконечный разрыв в точкеа:
=.
Если
функция
имеет бесконечный разрыв во внутренней
точкес,
то несобственный интеграл определяется
следующим образом
=+
=
+.
Этот интеграл
сходится, если сходятся оба слагаемых,
и расходится, если расходится хотя бы
одно слагаемое.
С
геометрической точки зрения, несобственный
интеграл от неограниченной функции
также характеризует площадь неограниченной
криволинейной трапеции:
Поскольку
несобственный интеграл выводится путем
предельного перехода из определенного
интеграла, то все свойства определенного
интеграла могут быть перенесены (с
соответствующими уточнениями) на
несобственные интеграла первого и
второго рода.
Во
многих задачах, приводящих к несобственным
интегралам, не обязательно знать, чему
равен этот интеграл, достаточно лишь
убедиться в его сходимости или
расходимости. Для этого используют
признаки
сходимости.
Признаки
сходимости несобственных интегралов:
1)
Признак
сравнения.
Пусть
для всех х.
Тогда, еслисходится, то сходится и,
причем.
Еслирасходится, то расходится и.
2)
Если сходится
,
то сходится и(последний интеграл в этом случае
называетсяабсолютно
сходящимся).
Признаки
сходимости и расходимости несобственных
интегралов от неограниченных функций
аналогичны сформулированным выше.
Примеры
решения задач.
Пример
1.
Вычислить
несобственный интеграл или установить
его расходимость:
а)
;
б);
в)
г)
; д).
Решение.
а)
По определению
имеем:
,
Следовательно,
данный интеграл сходится и равен
.
б)
Аналогично
.
Следовательно,
данный интеграл сходится и равен
.
в)
По определению
=+,
причем,а
– произвольное число. Положим в нашем
случае
,
тогда получим:
.
Данный
интеграл сходится.
г)
Значит, данный
интеграл расходится.
д)
Рассмотрим.
Чтобы найти первообразную подынтегральной
функции, необходимо применить метод
интегрирования по частям. Тогда получим:
Поскольку
ни
,
нине существуют, то не существует и
.
Следовательно,
данный интеграл расходится.
Пример
2.
Исследовать
сходимость интеграла
в зависимости от п.
Решение.
При
имеем:
.
Если
,
тои.
Следовательно, интеграл расходится.
Если
,
то,
а,
тогда
,
=,
Следовательно,
интеграл сходится.
Если
,
то
,
следовательно,
интеграл расходится.
Таким
образом,
Пример
3.
Вычислить
несобственный интеграл или установить
его расходимость:
а)
;
б);
в)
.
Решение.
а)
Интегралявляется несобственным интегралом
второго рода, поскольку подынтегральная
функцияне ограничена в точке.
Тогда, по определению,
.
Интеграл сходится и равен
.
б)
Рассмотрим.
Здесь также подынтегральная функция
не ограничена в точке.
Поэтому, данный интеграл – несобственный
второго рода и по определению,
.
Следовательно,
интеграл расходится.
в)
Рассмотрим.
Подынтегральная функциятерпит бесконечный разрыв в двух точках:и,
первая из которых принадлежит промежутку
интегрирования.
Следовательно, данный интеграл –
несобственный второго рода. Тогда, по
определению
==
.
Следовательно,
интеграл сходится и равен
.
studfiles.net
Примеры исследования несобственных интегралов на сходимость
Примеры исследования несобственных интегралов на сходимость
Пример 1 Исследовать на сходимость . Вычислим интеграл по определению: .
Таким образом, данный интеграл сходится при a>1 и расходится при a£1.
Пример 2 Исследовать на сходимость . Вычислим интеграл по определению: .
Таким образом, данный интеграл сходится при a<1 и расходится при a³1.
Пример 3 Исследовать на сходимость .
Подынтегральная функция может быть бесконечно большой ( если m<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два
.
Сходимость первого интеграла I1 исследуем с помощью эквивалентной функции: ( т. к. n>0), а интеграл сходится при m>-1 (пример 2). Аналогично, для интеграла I2 :
, а интеграл сходится при m+n<-1 (пример2). Следовательно, исходный интеграл сходится при выполнении одновременно двух условий m>-1 и m+n<-1, и будет расходится при нарушении хотя бы одного из них.
Пример 4 Исследовать на сходимость .
Подынтегральная функция может быть бесконечно большой ( если m<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два:
.
Так как arctgx »x при x®0, то интеграл I1 эквивалентен интегралу , который сходится при m+1>-1 т. е. при m>-2 (пример1).
Для подынтегральная функции в несобственном интеграле первого рода I2 подберем эквивалентную:
т. к. arctgx » p/2 при x® ¥. Следовательно, по второму признаку сравнения интеграл I2 будет сходится при m+n<-1, и расходится в противном случае.
Объединяя условия сходимости интегралов I1 и I2 получим условия сходимости исходного интеграла: m>-2 и m+n<-1 одновременно.
Замечание. В примерах 2-4 использовался 2 признак сравнения, который обеспечивает необходимые и достаточные условия сходимости, что позволяет, установив сходимость при некотором условии на значения параметров, не доказывать расходимость интеграла при нарушении полученных условий сходимости.
Пример 5 Исследовать на сходимость .
Данный интеграл содержит особую точку 0, в которой подынтегральная функция может обращается в бесконечность при p<0, поэтому снова разобьем исходный интеграл на два:
.
Интеграл I1 является несобственным интегралом второго рода, и подынтегральная функция эквивалентна при x®0 функции xp (e-x ®1 при x®0), т. е. I1 сходится при p>-1 (пример 1).
Интеграл I2 является несобственным интегралом первого рода. Подобрать функцию, эквивалентную подынтегральной функции, такую, чтобы она не содержала показательной функции, не удается. Поэтому использовать признак сравнения 2, как в предыдущих примерах, нельзя. Применим первый признак сравнения, для чего используем следующий известный факт:
При a>0 и любом p. Из этого, и того, что функция xpe-ax непрерывна, следует, что эта функция ограничена, т. е. существует такая константа M>0, что xpe-ax < M. Возьмем, например, a=1/2, и оценим интеграл I2 сверху:
,
Т. е. интеграл I2 сходится при любом p.
Таким образом, исходный интеграл сходится при p>-1.
Пример 6 Исследовать на сходимость .
Проведем замену переменной: t = lnx, и получим
.
Разбиение интеграла на два произведено аналогично примеру 5. Интеграл I1 полностью эквивалентен интегралу I1 из примера 5 и, следовательно, сходится при q<1.
Рассмотрим интеграл I2 . При условии 1-p<0 этот интеграл полностью эквивалентен интегралу I2 в примере 5 (доказательство сходимости аналогично, а условие 1-p<0 нужно для выполнения и a=(1-p)/2. ).
Итак, I2 сходится при p>1. Однако, на этом исследование сходимости этого интеграла не закончено, так как использованный признак сходимости дает только достаточные условия сходимости. Поэтому нужно исследование сходимости при 1-p£0.
Рассмотрим случай p=1. Тогда интеграл I2 эквивалентен , который сходится при q>1 (заметим, что в этом случае интеграл I1 расходится) и расходится в противном случае.
При p<1 оценим интеграл I2 и покажем его расходимость. Для этого вспомним, что При 1-p>0, и, следовательно, начиная с некоторого А>1 выполнено T—QE(1-P)T ³ M=const>0. Тогда для интеграла I2 справедлива оценка
,
Где интеграл в правой части расходится, что и доказывает расходимость интеграла I2 .
Суммируя полученные результаты, получаем что исходный интеграл сходится при q<1 и p>1, в противном случае интеграл расходится.
Пример 6 Исследовать на абсолютную и условную сходимость .
Разобьем исходный интеграл на два:
.
Сходимость. Интеграл I1 эквивалентен , т. е. сходится при p<2 (пример 1) , причем абсолютно, так как подынтегральная функция положительна на отрезке интегрирования.
Интеграл I2 сходится про признаку Дирихле-Абеля при p>0 т. к. первообразная sin(x) ограничена, а функция 1/xp монотонно стремится к нулю при x стремящемся к бесконечности.
Покажем, что при p£0 интеграл расходится. Воспользуемся для этого критерием Коши, а точнее его отрицанием
.
Возьмем в качестве R1и R2 следующие величины: R1=2pk и R2=2pk+p/2, тогда
, при p>0.
Таким образом, интеграл сходится при 0<p<1.
Абсолютная сходимость Абсолютная сходимость интеграла I1 уже установлена, рассмотрим абсолютную сходимость I2 . Оценим интеграл сверху:
, т. е. интеграл сходится при p>1.
Для доказательства расходимости при p£1 оценим интеграл снизу
.
Разобьем последний интеграл от разности функций на разность интегралов
.
Если оба интеграла сходятся, то и интеграл от разности сходится, если один из интегралов расходится, а другой сходится — то интеграл от разности расходится. В случае расходимости обоих интегралов сходимость интеграла от разности подлежит дальнейшему исследованию. Нас интересует второй из описанных случаев.
расходится (пример 1) при p<1. сходится по признаку Дирихле-Абеля при 1>p>0 (см. Сходимость), следовательно интеграл оценивается снизу расходящимся интегралом, т. е. расходится.
Случай p³1 нас не интересует, т. к. при этих значениях параметра интеграл расходится.
Таким образом, исходный интеграл сходится абсолютно при 0<p<1, сходится условно при 1£p<2.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
§1. Несобственные интегралы 1-го рода
– 68–
Тема
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
В
теме «Определенный интеграл» было
рассмотрено понятие определенного
интеграла
обобщением этого понятия для случаев
бесконечного промежутка и неограниченной
функции. Необходимость такого обобщения
показывают, например, такие ситуации.
1.
Если, используя формулу для длины дуги,
попытаться вычислить длину четверти
окружности
,,
то придем к интегралу от неограниченной
функции:
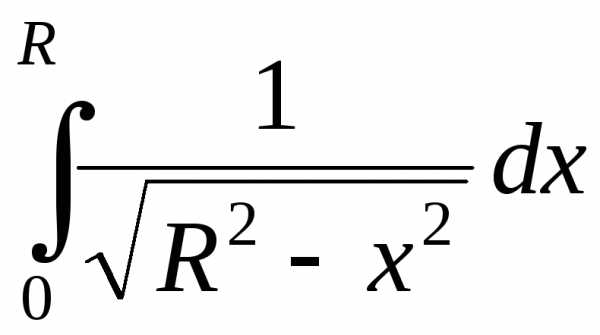
где
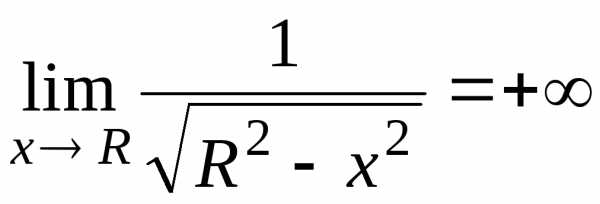
2.
Пусть тело массой
по инерции в среде с силой сопротивления
,
где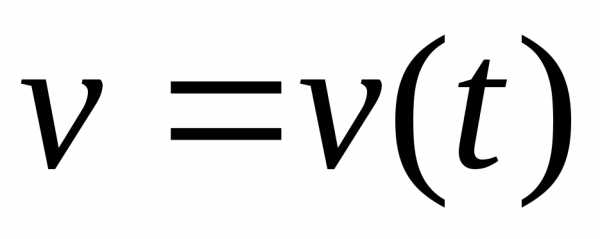
Ньютона (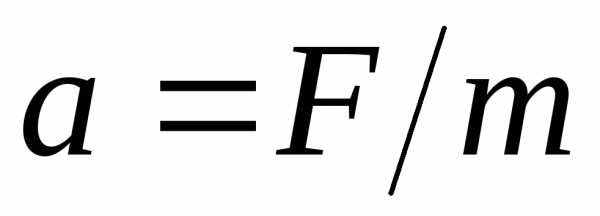
где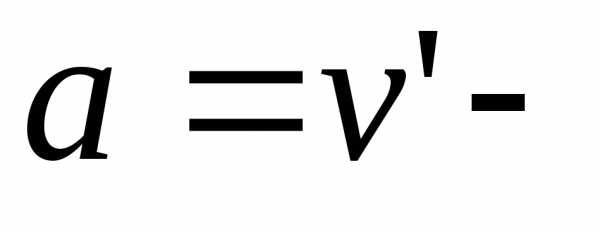
получим уравнение:,
где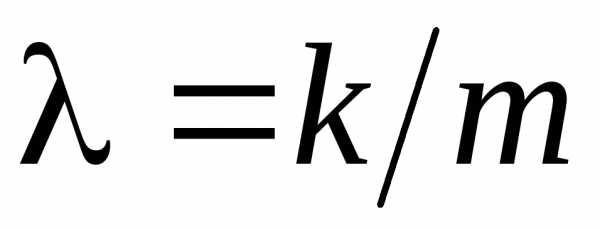
Нетрудно показать, что решением этого
(дифференциального!) уравнения является
функцияЕсли
нам потребуется вычислить путь, пройденный
телом до полной остановки, т.е. до момента,
когда

то придем к интегралу по бесконечному
промежутку:
I Определение
Пусть
функция
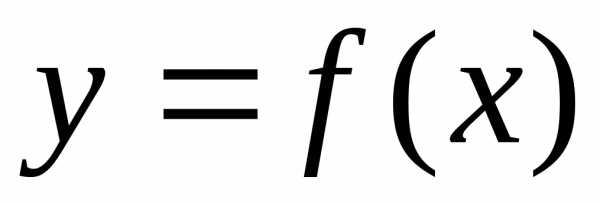
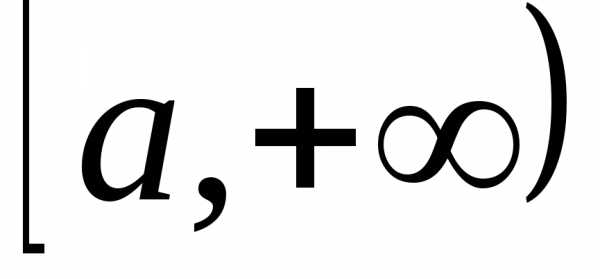
Тогда для любого
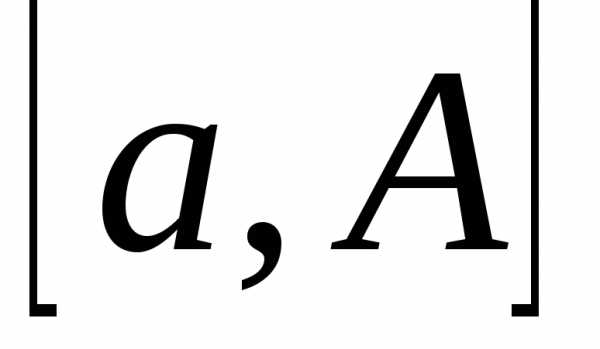
то есть существует интеграл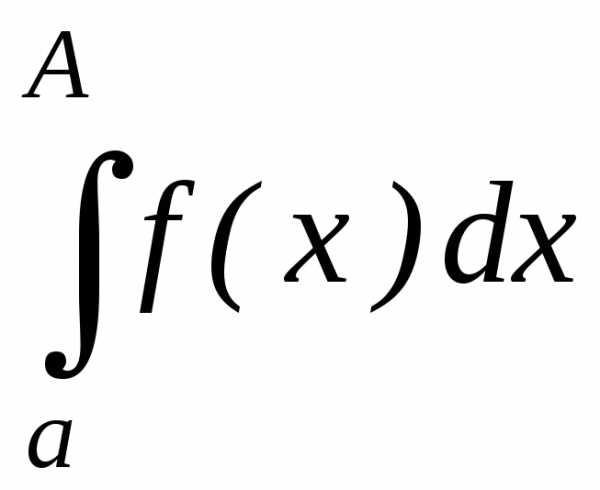
Определение
1.
Конечный или бесконечный предел этого
интеграла при
называют несобственным интегралом 1-го
рода от функции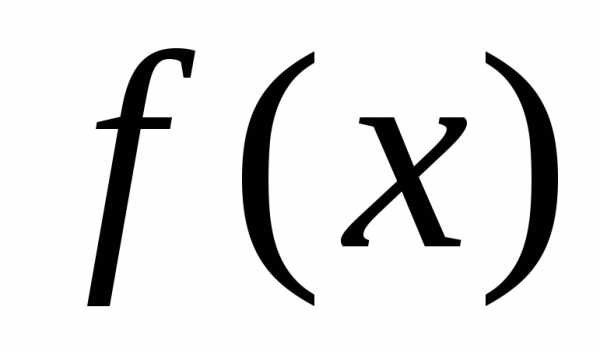
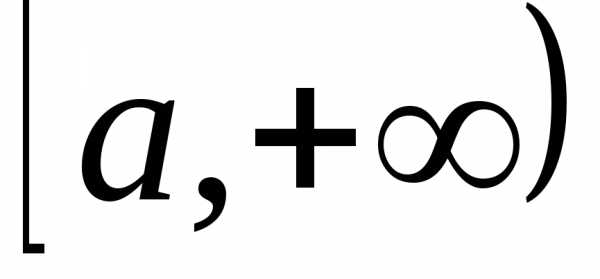

При этом, если указанный предел конечен,
то несобственный интеграл называют
сходящимся, в противном случае (или не существует ) – расходящимся.
Итак,
по определению
|
(1) |
Примеры
1..
2..
3.– не существует.
Несобственный
интеграл из примера 1 сходится, в примерах
2 и 3 интегралы расходятся.
II Формула Ньютона – Лейбница для несобственного интеграла первого рода
Пусть
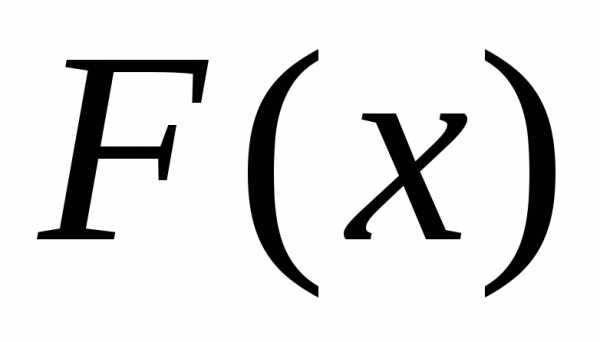
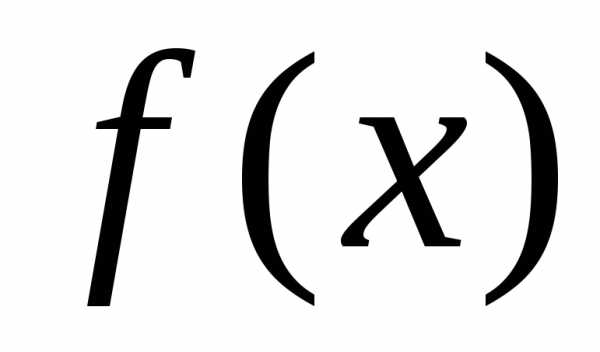
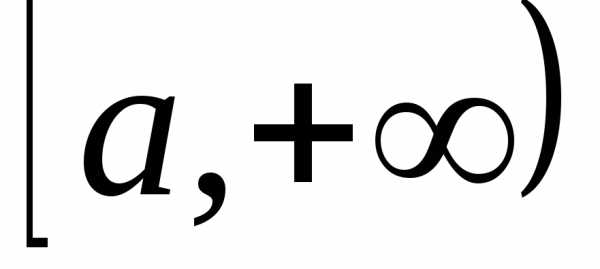
т.к.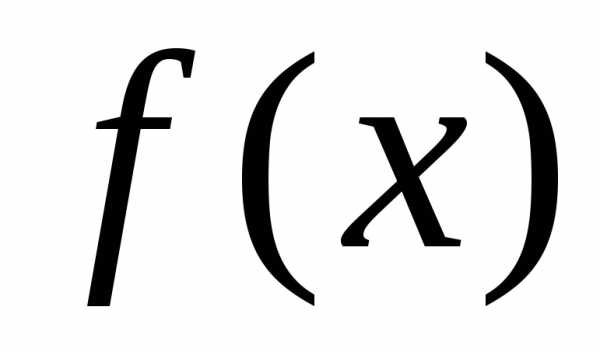
Отсюда
ясно, что сходимость несобственного
интеграла (1) равносильна существованию
конечного предела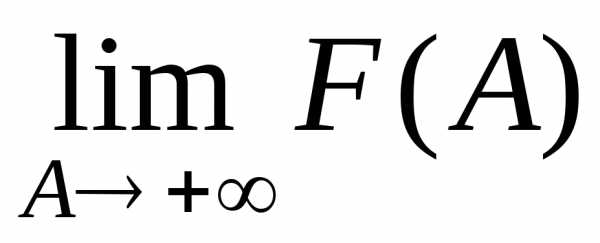
Если этот предел обозначить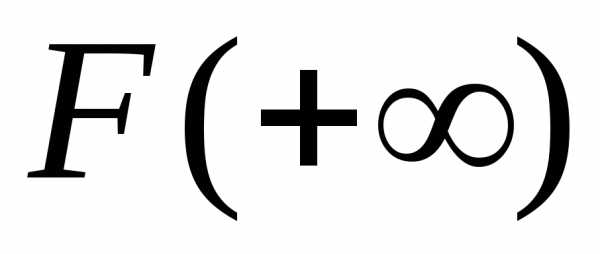
то можно написать для интеграла (1)
формулу Ньютона-Лейбница:
,
где
.
Примеры.
4.
.
5.
.
6.
Более сложный пример:
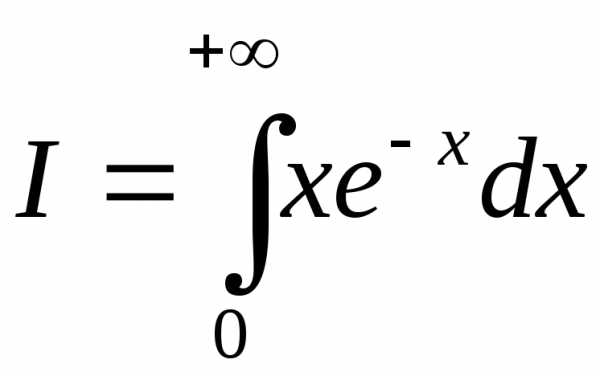
Сначала найдем первообразную:
Теперь
можем найти интеграл
учитывая,
что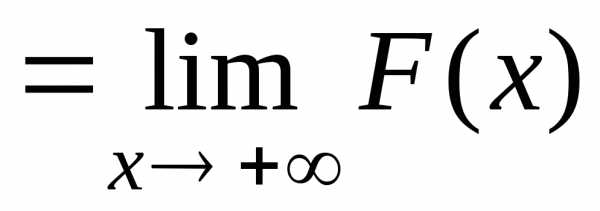
.
III
Свойства
Приведем
ряд свойств несобственного интеграла
(1), которые вытекают из общих свойств
пределов и определенного интеграла:
-
интегралы
и
сходятся или расходятся одновременно;
-
если
,
то интегралыи
сходятся или рас-ходятся одновременно;
-
если
интеграл
сходится, то
.
IV
Другие определения
Определение
2.
Если
на

то
.
Определение
3.
Если
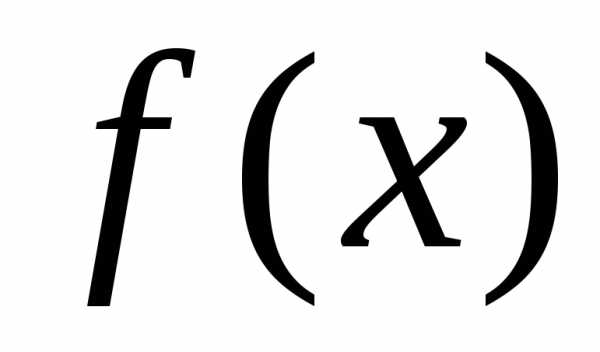
на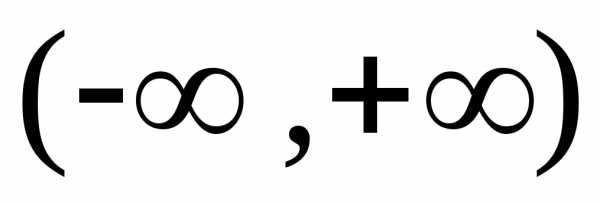
то принимают по определению
(
произвольное),
причем
несобственный интеграл в левой части
сходится, если только оба ин-теграла в
правой части сходятся.
Для
этих интегралов, как и для интеграла
(1) можно написать соответствующие
формулы Ньютона – Лейбница.
Пример
7.
§2.
Признаки сходимости несобственного
интеграла 1-го рода
Чаще
всего несобственный интеграл вычислить
по определению не-возможно, поэтому
используют приближенное равенство
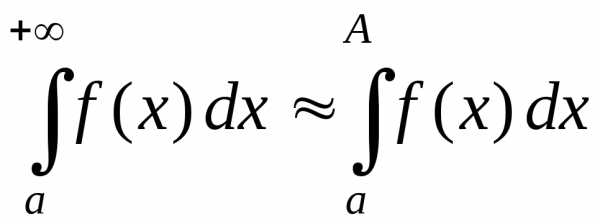
больших

Однако,
это соотношение имеет смысл лишь для
сходящихся интегралов. Необходимо иметь
методы выяснения поведения интеграла
минуя определение.
I
Интегралы от положительных функций
Пусть
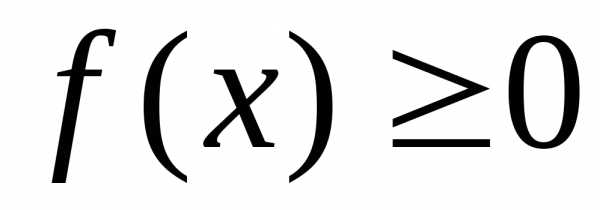
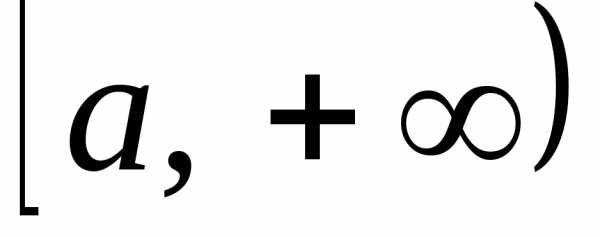
Тогда определенный интеграл
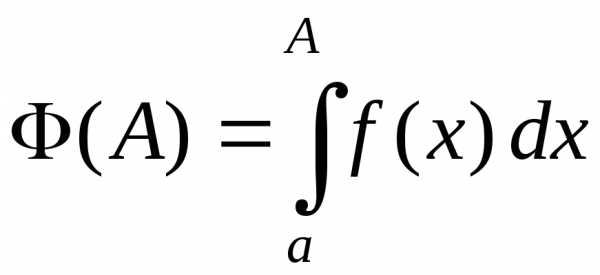
функция возрастаю-щая (это следует из
общих свойств определенного интеграла).
Теорема
1.
Несобственный интеграл 1го
рода от неотрицательной функ-ции сходится
тогда и только тогда, когда функция

ограниченной при увеличении
Эта
теорема – следствие общих свойств
монотонных функций. Практического
смысла теорема почти не имеет, но
позволяет получить т.н. признаки
сходимости.
Теорема
2
(1-й признак сравнения). Пусть функции


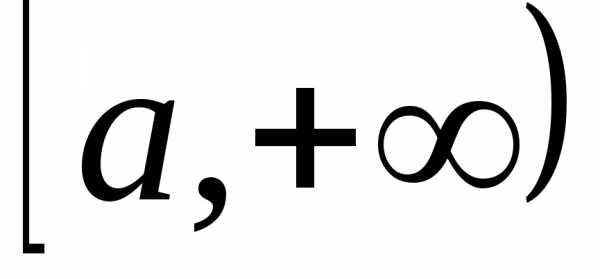
Тогда:
1)
если интеграл
сходится, то и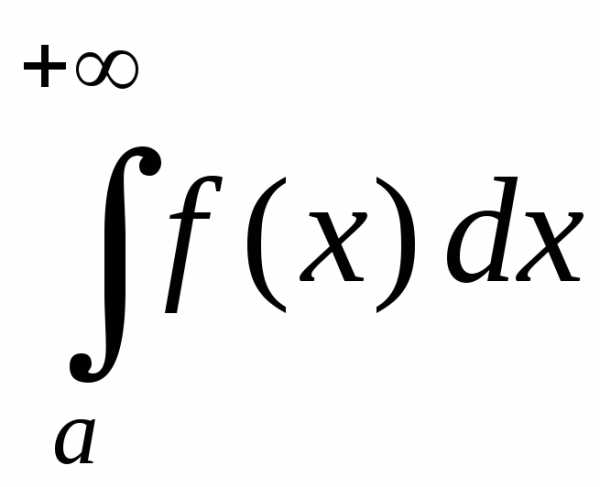
2)
если интеграл
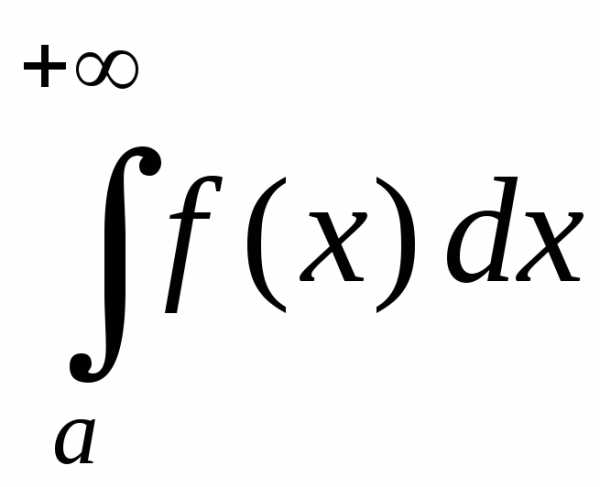

Доказательство.
Обозначим:

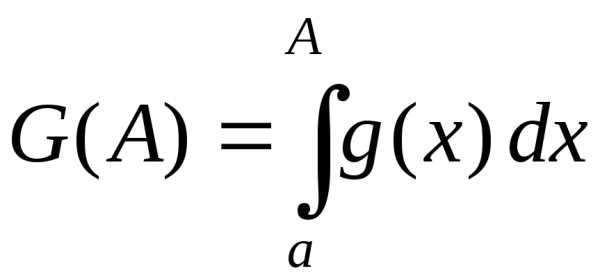
Так как,
то.
Пусть интеграл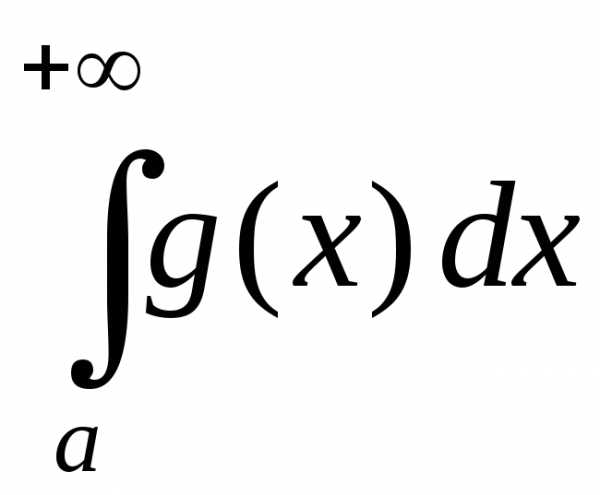

а значит, интеграл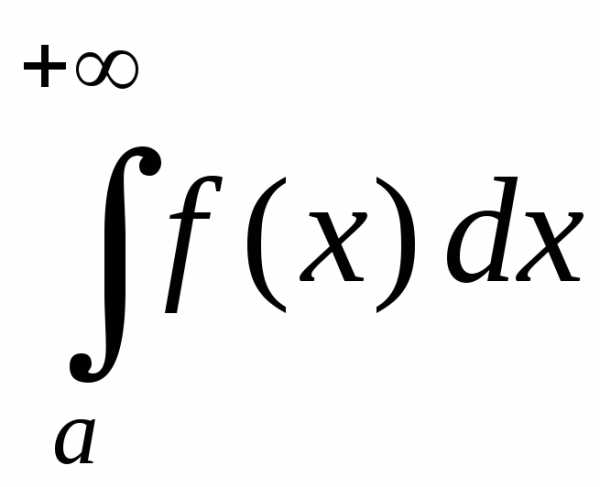
и вторая часть теоремы.
Этот
признак не применим в случае расходимости
интеграла от
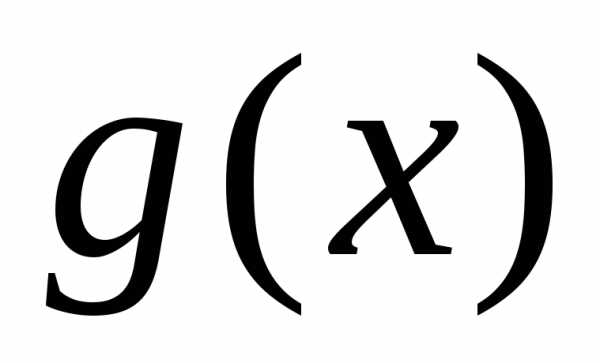
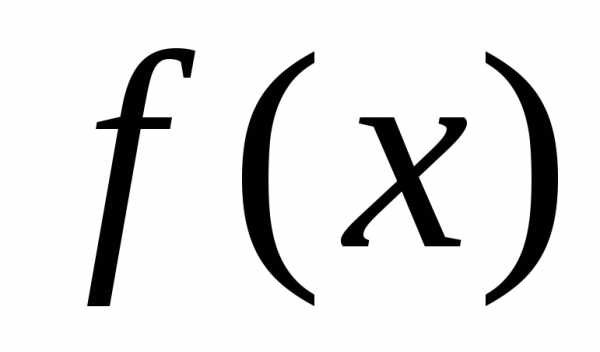
Этот недостаток отсутствует у 2-го
признака сравнения.
Теорема
3
(2-й признак сравнения). Пусть функции
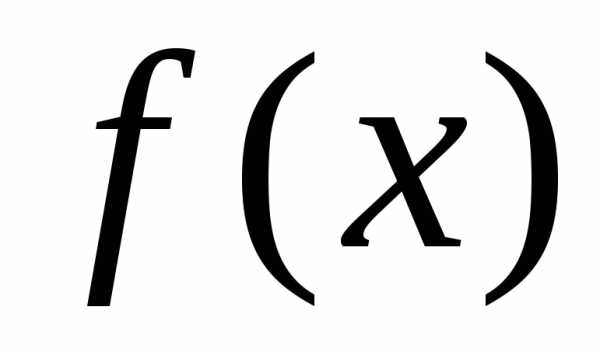
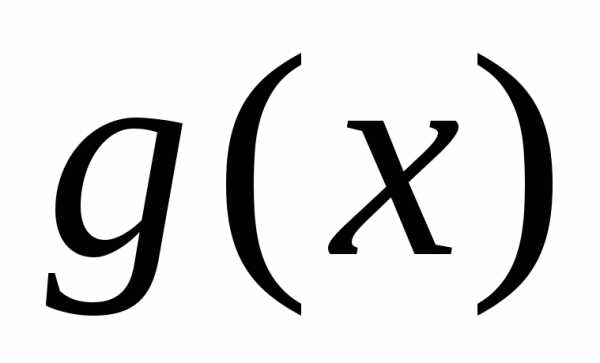
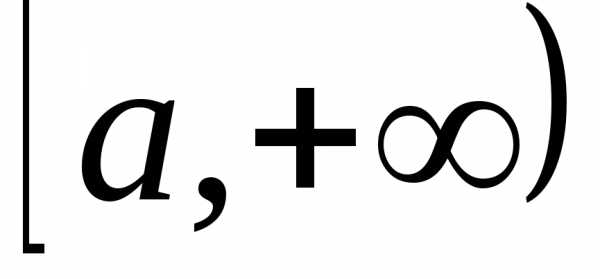
Тогда, еслипри,
то несобственные интегралы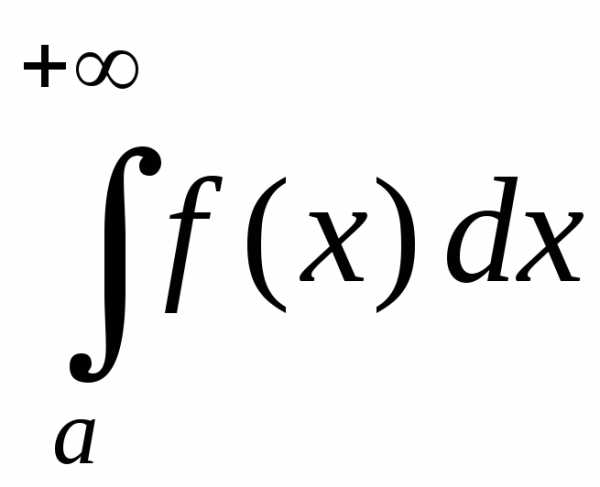
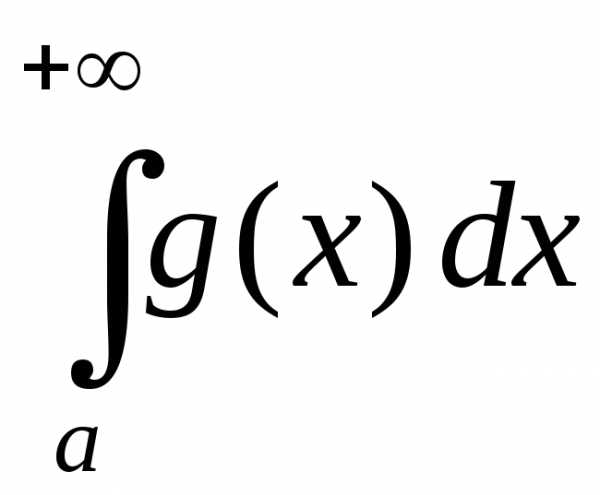
Доказательство.
Из условия теоремы получим такую цепочку
равно-сильных утверждений:
,
,
.
Пусть,
например,
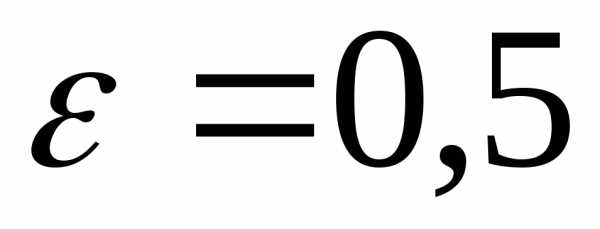
Тогда:
.
Применим
теорему 2 и свойство 1) из §1 и получим
утверждение теоремы 3.
В
качестве эталонной функции, с которой
сравнивают данную, высту-пает степенная
функция
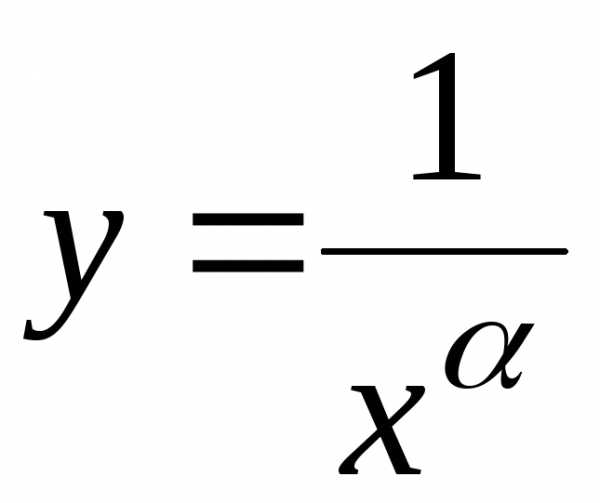
Предлагаем студентам самим доказать,
что интеграл
сходится
при


Примеры.
1.

Рассмотрим
подынтегральную функцию на промежутке
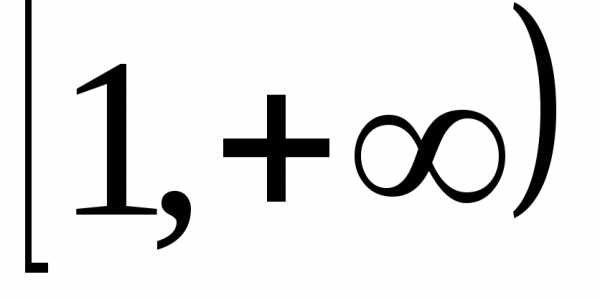
,
.
Интеграл

По 2-му признаку сравнения сходится и
интеграл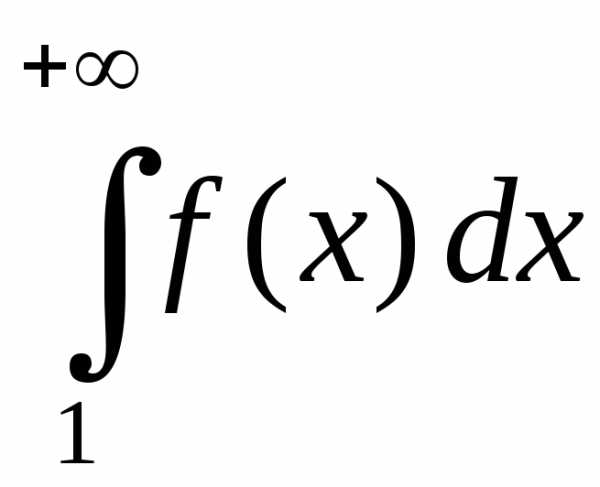
а в силу свойства 2) из §1 сходится и
исход-ный интеграл.
2.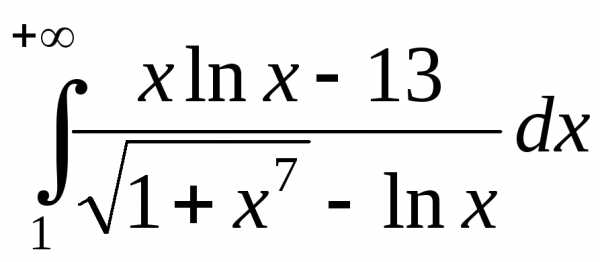
Так
как
,
тоcуществует

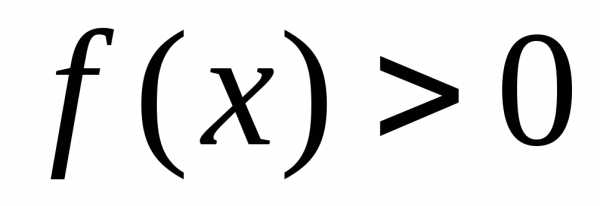
Для таких значений переменной:
.
Известно,
что логарифмическая функция растет
медленнее степенной, т.е.

а
значит, начиная с некоторого значения
переменной, эта дробь меньше 1. Поэтому
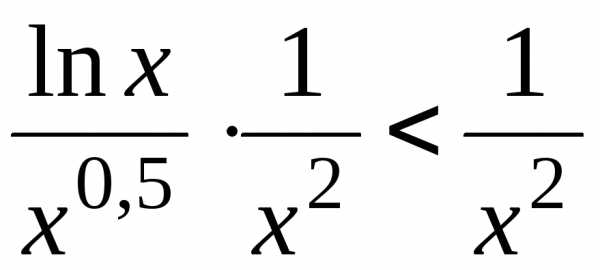
Интеграл
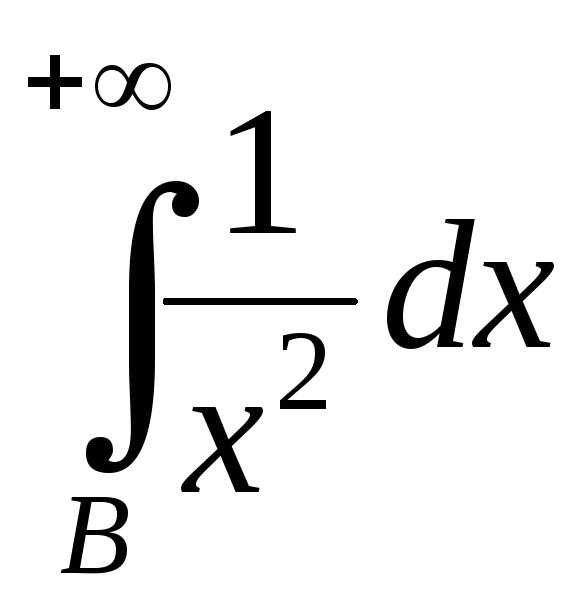
признака сравнения сходится и
Применяя 2-й признак, получим, что и
интеграл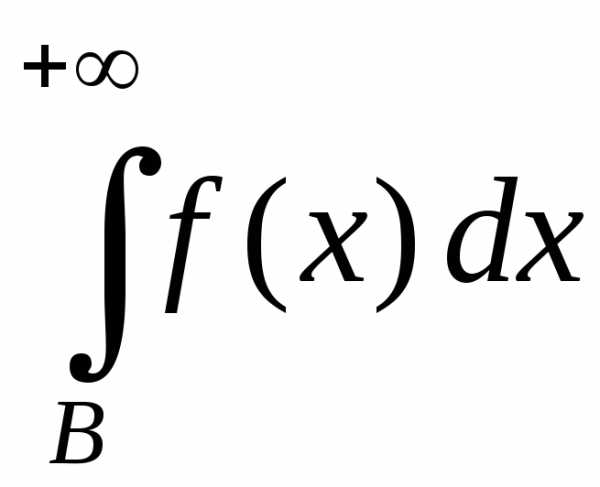
доказывает сходимость исходного
интеграла.
studfiles.net
Сегодня я подготовил для вас подробную статью о несобственных интегралах.
Определенные интегралы 
С целью обобщения понятия интеграла рассмотрим:
1) определенные интегралы от непрерывных функций, но с бесконечными пределами интегрирования;
2) определенные интегралы с конечными пределами интегрирования, но от функций, имеющих бесконечный разрыв на промежутке интегрирования. Такие определенные интегралы называют несобственными.
1. Интегралы с бесконечными пределами.
Пусть функция f(x) определена на промежутке [a; +∞) и пусть f(x) интегрирована на любом отрезке [a; b] (b> a– произвольные действительные числа).
Определение 1.1. Предел 
Если предел (1.1) есть конечное число, то несобственный интеграл 

Пример 1.1. Исследовать на сходимость интеграл
Решение. Вычислим определенный интеграл
Имеем
Следовательно, заданный интеграл сходится и он равен
Из рассмотренного следует, что вопрос о сходимости (расходимости) несобственных интегралов решается с помощью первоначальной функции для подынтегральной функции. Это обстоятельство сильно сужает круг практического использования понятия несобственного интеграла. В отдельных случаях вопрос о сходимости (расхождении) несобственного интеграла можно решить, не находя первообразной для подынтегральной функции. При этом пользуются так называемыми признаками сходимости несобственных интегралов. Простейшим признаком сходимости является признак сравнения.
Теорема 1.1. Пусть для всех x ≥ a функции f(x) и g(x) определены и выполняются неравенства 0 ≤ f(x) ≤ g(x). Тогда:
Для функции f(x), непрерывной на бесконечном промежутке -∞ < x ≤ b, определяется несобственный интеграл
Для функции f(x), непрерывной на всей числовой оси, несобственный интеграл 
где с – произвольное действительное число.
2. Интегралы от неограниченных функций.
Пусть функция f(x) такая, что для произвольного малого ɛ>0 она определена, ограничена и интегрирована на отрезке [a+ɛ; b] и неограниченна на (a; b].
Определение 1.2. Предел определенного интеграла 
Аналогично для функции f(x), определенной, непрерывной и интегрированной на отрезке [a; b- ɛ] и неограниченной на [a; b) обозначается несобственный интеграл:
Если пределы (1.4), (1.5) есть конечные числа, то несобственные интегралы называются сходящимися, а если эти пределы не существуют, то несобственные интегралы называются расходящимися.
В конце отметим, что для функции f(x), которая имеет на промежутке (a; b) точку с, в окрестности которой f(x) неограниченная, но является ограниченной и интегрированной на каждом из отрезков [a; c- ɛ] и [ñ + ɛ; b], интеграл определяется равенством.
Аналогично обозначается несобственный интеграл на отрезке [a; b] от функции, которая непрерывна на нем всюду, кроме конечного числа точек, и неограниченной вблизи этих точек.
Пример 1.2.Исследовать сходимость интегралов. Для сходящихся интегралов найти их значение:
Решение.
а) функция 
ограничена и непрерывна, а потому и интегрируемая. Предельное значение
существует; таким образом,
ограничена и непрерывна, но

Пример 1.3. Исследовать сходимость интегралов. Для сходящихся интегралов найти их значение
Решение.
если α > 0, интеграл сходится; если α ≤ 0, то интеграл расходится;

если α > 1; если 0 < α ≤ 1, интеграл расходится как и при α = 1:
так и при 0 < α < 1:
Пример 1.4. Найти несобственный интеграл
Решение. Функция 
Поэтому данный интеграл сходится и равен 2√2.
Пример 1.5. Исследовать сходимость интегралы. Для сходящихся интегралов найти их значение:
Решение.
то есть, несобственный интеграл расходится
то есть, несобственный интеграл I2 сходится и равен 
Пример 1.5. Исследовать на сходимость интегралы:
Решение.
Если у Вас есть ко мне вопросы, или нужна помощь, консультация по решению несобственных интегралов, записывайтесь на мои занятия. Буду рад Вам помочь.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
12.
Несобственные интегралы.
При
рассмотрении определённых интегралов
мы предполагали, что область интегрирования
ограничена (более конкретно, является
отрезком
); для существования определённого
интеграла
необходима ограниченность подынтегральной
функции на
.
Будем называть определённые интегралы,
для которых выполняются оба эти условия
(ограниченность и области интегрирования,
и подынтегральной функции) собственными;
интегралы, для которых нарушаются эти
требования (т.е. неограничена либо
подынтегральная функция, либо область
интегрирования, либо и то, и другое
вместе) несобственными.
В этом разделе мы изучим несобственные
интегралы.
12.1. Несобственные интегралы по
неограниченному промежутку
(несобственные интегралы первого рода).
12.1.1.
Определение несобственного интеграла
по бесконечному промежутку.
Пусть функция
определена на полуоси
и интегрируема по любому отрезку
,
принадлежащему этой полуоси. Предел
интеграла
при
называется несобственным интегралом
функции
от
до
и обозначается
.
Итак,
по определению,
.
Если этот предел существует и конечен,
интеграл
называется сходящимся; если предел не
существует или бесконечен, интеграл
называется расходящимся.
Примеры:
1.
;
этот предел не существует; следовательно,
исследуемый интеграл расходится.
2.;
следовательно,
интеграл сходится и равен
.
Аналогично
интегралу с бесконечным верхним пределом
интегрирования определяется интеграл
в пределах от
до
:
и
в пределах от
до
:
.
В последнем случае
определена на всей числовой оси,
интегрируема по любому отрезку;
— произвольная (собственная) точка
числовой оси; интеграл называется
сходящимся, если существуют и конечны
оба входящих в определение предела.
Пользуясь свойством аддитивности
определённого интеграла, можно показать,
что существование конечных пределов и
их сумма не зависят от выбора точки
.
Примеры:
3.

Интеграл сходится.
4.
следовательно,
интеграл сходится и равен
.
Очевидно
следующее утверждение, которое мы
сформулируем для интеграла с бесконечным
верхним пределом:
сходится тогда и только тогда, когда
для любого
,
удовлетворяющего неравенству
,
сходится интеграл
(док-во: так как при
по свойству аддитивности
,
и
от
не
зависит, то конечный предел при
для интеграла в левой части существует
тогда и только тогда, когда существует
конечный предел для интеграла в правой
части равенства).
12.1.2.
Формула Ньютона-Лейбница для несобственного
интеграла.
В приведённых примерах мы сначала
вычисляли с помощью первообразной
функции определённый интеграл по
конечному промежутку, а затем выполняли
предельный переход. Объединим два этих
действия в одной формуле. Символом
будем обозначать
;
символом
— соответственно,
;
тогда можно записать
,
,
,
подразумевая в каждом из этих случаев
существование и конечность соответствующих
пределов. Теперь решения примеров
выглядят более просто:
— интеграл сходится;
— интеграл расходится.
Для
несобственных интегралов применимы
формулы интегрирования по частям и
замены переменной:
;
при замене переменной несобственный
интеграл может преобразовываться в
собственный. Так, например, вычислим
интеграл:
.
Пусть
,
;
если
,
то
;
если
то
;
Поэтому
(это уже собственный интеграл) =
.
12.1.3.
Признаки сравнения для неотрицательных
функций. В
этом разделе мы будем предполагать, что
все подынтегральные функции неотрицательны
на всей области определения. До сих пор
мы определяли сходимость интеграла,
вычисляя его: если существует конечный
предел первообразной при соответствующем
стремлении (
или
),
то интеграл сходится, в противном случае
— расходится. При решении практических
задач, однако, важно в первую очередь
установить сам факт сходимости, и только
затем вычислять интеграл (к тому же
первообразная в практических задачах
часто не выражается через элементарные
функции). Сформулируем и докажем ряд
теорем, которые позволяют устанавливать
сходимость и расходимость несобственных
интегралов от неотрицательных функций,
не вычисляя их.
12.1.3.1.
Признак сравнения.
Пусть функции
и
интегрируемы по любому отрезку
и при
удовлетворяют неравенствам
.
Тогда:
если
сходится интеграл
,
то сходится интеграл
;
если
расходится интеграл
,
то расходится интеграл
(эти
утверждения имеют простой смысл: если
сходится интеграл от большей функции,
то сходится интеграл от меньшей функции;
если расходится интеграл от меньшей
функции, то расходится интеграл от
большей функции; в случаях, когда сходится
интеграл от меньшей функции или расходится
интеграл от большей функции, никаких
выводов о сходимости второго интеграла
сделать нельзя).
Док-во:
если
,
,
то функции
и
— монотонно возрастающие функции верхнего
предела
(следствие
свойств аддитивности и интегрирования
неравенств). Монотонно возрастающая
функция имеет конечный предел тогда и
только тогда, когда она ограничена
сверху. Пусть
сходится.
ограничена
,
ограничена, т.е.
сходится. Пусть
расходится
неограничена
неограничена, т.е.
расходится.
Примеры:
Исследовать на сходимость интегралы
5.
.
Функция
не имеет первообразной, выражающейся
через элементарные функции, поэтому
исследовать сходимость с помощью
предельного перехода невозможно. При
имеет место
;
интеграл
сходится
сходится
сходится.
6.
.
При
;
интеграл
расходится
расходится
расходится.
В
качестве «стандартного» интеграла,
с которым сравнивается данный, обычно
берётся интеграл типа
,
часто называемый интегралом Дирихле.
Этот интеграл сходится, если
,
и расходится, если
:
Примеры:
7.

На всём промежутке интегрирования
;
интеграл
сходится (),
поэтому исходный интеграл сходится;
8.
. Здесь
при
,
расходится (),поэтому
исходный интеграл расходится;
9.
.
Здесь сравнить подынтегральную функцию
с какой-либо степенью
невозможно, так как числитель —
неограниченная функция, поэтому
рассуждаем по-другому. При
— бесконечно большая низшего порядка
по сравнению с любой положительной
степенью
,
поэтому
ограниченная функция, поэтому
,
интеграл от большей функции сходится,
следовательно, исходный интеграл тоже
сходится;
10.
.
На всём промежутке интегрирования
(отбросив бесконечно большие низших
порядков в числителе и знаменателе, мы
увеличили числитель и уменьшили
знаменатель); интеграл
сходится, поэтому исходный интеграл
сходится.
Теперь
рассмотрим
.
Понятно, что бесконечно большие низших
порядков в числителе и знаменателе не
влияют на сходимость интеграла; в то же
время, отбросив их, мы уменьшим
подынтегральную функцию, а из сходимости
интеграла от меньшей функции не следует
сходимость интеграла от большей функции.
Можно рассуждать так: при достаточно
больших
выполняются неравенства
,
поэтому
и т.д., однако при решении таких задач
проще применить другой признак сравнения
— предельный.
12.1.3.2.
Признак сравнения в предельной форме.
Пусть неотрицательные функции
и
интегрируемы по любому отрезку
и пусть существует конечный
.
Тогда несобственные интегралы
и
сходятся или расходятся одновременно.
Док-во.
Так как функции неотрицательны, то
.
По определению предела для
существует такое значение
,
что при
выполняется
.
Дальше рассуждения простые: пусть
;
если сходится
,
то сходится
,
тогда, по теореме сравнения, сходится
сходится
сходится. Если расходится
,
то расходится
,
тогда, по теореме сравнения, расходится
расходится
расходится. Случаи, когда сходится или
расходится
,
рассмотреть самостоятельно.
Сравнение
интеграла
со «стандартным» интегралом
в предельной форме позволяет сформулировать
такое правило: если при
неотрицательная функция
— бесконечно малая порядка малости выше
первого по сравнению с
,
то
сходится; если
не является бесконечно малой или имеет
порядок малости единица или ниже, то
интеграл расходится. Примеры:
11.
.
При
эквивалентна функции
,
поэтому интеграл сходится.
12.
.
При
эквивалентна
функции
,
поэтому интеграл расходится.
13.
.
При
эквивалентна
функции
,
поэтому интеграл расходится.
14.
.
При
эквивалентна
функции
,
поэтому интеграл расходится.
12.1.4.
Абсолютная сходимость несобственных
интегралов по бесконечному промежутку.
В предыдущем разделе рассматривались
интегралы от знакоположительных
(знакопостоянных) функций; мы убедились,
что для таких несобственных интегралов
существуют хорошие методы исследования
их сходимости. Естественен вопрос:
нельзя ли свести исследование интеграла
от произвольной функции
к исследованию интеграла от положительной
функции
?
Можно показать, что если сходится
интеграл
,
то обязательно сходится интеграл
(идея доказательства: разобьем отрезок
на два множества,
и
,
т.е. к первому множеству отнесены точки,
в которых функция неотрицательна, ко
второму — в которых функция отрицательна.
Тогда


В последней сумме оба слагаемые —
монотонно возрастающие с ростом
,
ограниченные сверху, следовательно,
имеющие конечный предел при
.
Отсюда следует, что имеет конечный
предел и предыдущая сумма). Обратное
утверждение неверно, т.е. при сходимости
интеграла
интеграл
может расходиться. Введём важное понятие
абсолютной сходимости.
Опр.
12.1.4. Если
сходится интеграл
,
то интеграл
называется сходящимся абсолютно. Если
сходится интеграл
,
а интеграл
расходится, то интеграл
называется сходящимся условно.
Примеры
исследования интегралов на абсолютную
сходимость:
15.
.
;
интеграл от большей функции сходится,
следовательно,
сходится, следовательно, исходный
интеграл сходится абсолютно.
16.
.
,
первый множитель,
,
стремится к нулю при
,
следовательно, ограничен:
,
интеграл от последней функции сходится,
следовательно, исходный интеграл
сходится абсолютно.
Приведённые
примеры показывают, что переход от
к
и применение к последнему интегралу
методов исследования на сходимость
несобственных интегралов от неотрицательных
функций, в случае его сходимости,
позволяет сделать вывод и о сходимости
(притом, абсолютной) исходного интеграла.
Если же интеграл от
расходится, решение задач значительно
усложняется. Пример: исследовать на
сходимость интеграл
.
1.
Докажем, что этот интеграл сходится.
Интегрируем его по частям:
.
Для
последнего интеграла
,
т.е. он сходится абсолютно, следовательно,
исходный интеграл сходится.
2.
Докажем, что для исходного интеграла
абсолютной сходимости нет, т.е. что
расходится. Так как
,
то
,
для последнего
интеграла, по доказанному выше, существует
конечный предел при
,
для предыдущего — нет, следовательно,
расходится.
Вывод
— исходный интеграл сходится условно.
Установить
условную сходимость несобственного
интеграла по бесконечному промежутку
при отсутствии абсолютной сходимости
позволяют два следующих признака:
признак
сходимости Абеля:
пусть функции
и
определены в промежутке
,
причём 1.
интегрируема в этом промежутке, т.е.
интеграл
сходится (условно или абсолютно);
2.
монотонна и ограничена:
.
Тогда
интеграл
сходится.
признак
сходимости Дирихле:
1. пусть функция
интегрируема в любом конечном промежутке
,
и интеграл по этому промежутку ограничен
(как функция верхнего предела
):
;
2.
монотонно стремится к нулю при
:
.
Тогда
интеграл
сходится.
Применим,
например, признак Дирихле к
.
Здесь
,
,
условия признака выполнены, поэтому
интеграл сходится условно.
12.2. Несобственные интегралы от
неограниченных функций
(несобственные интегралы второго рода).
12.2.1.
Определение несобственного интеграла
от неограниченной функции.
12.2.1.1.
Особенность на левом конце промежутка
интегрирования.
Пусть функция
определена на полуинтервале
,
интегрируема по любому отрезку
,
и имеет бесконечный предел при
.
Несобственным интегралом от
по отрезку
называется предел
.
Если этот предел конечен, говорят, что
интеграл сходится; если предел не
существует или бесконечен, говорят, что
интеграл расходится. Примеры:
Соседние файлы в папке Лекции
- #
- #
- #
- #








































































































































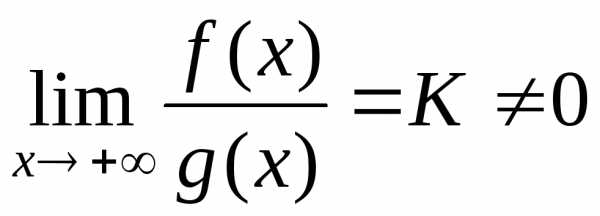
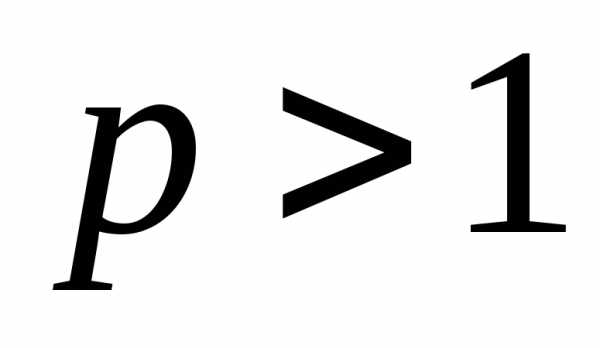

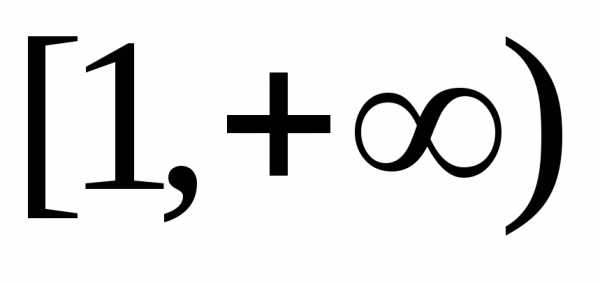
 у
у
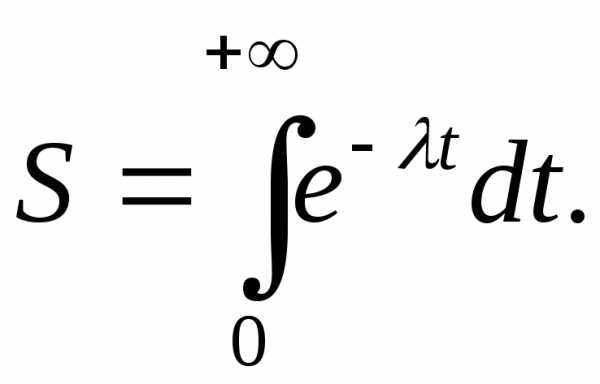
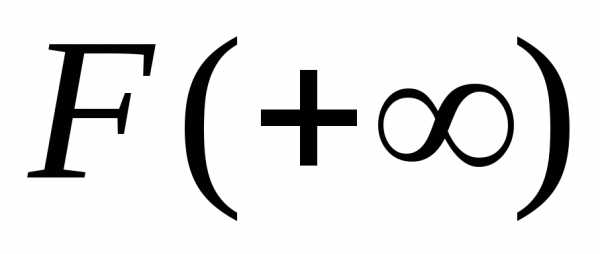
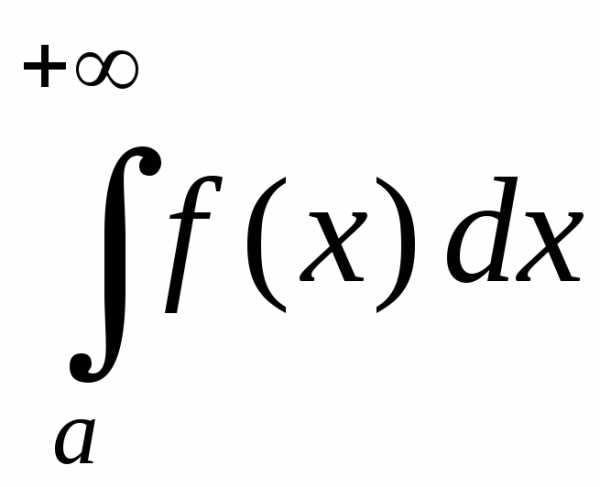 и
и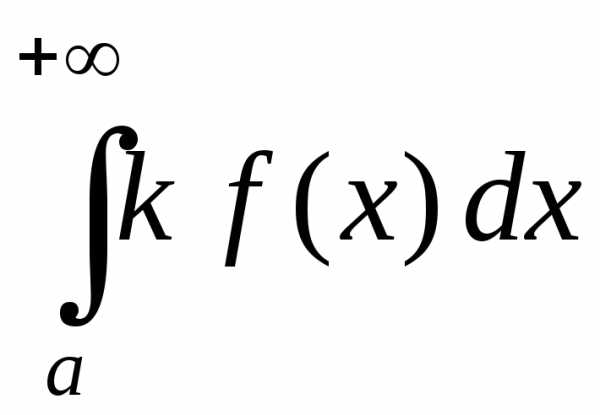
 сходятся или расходятся одновременно;
сходятся или расходятся одновременно;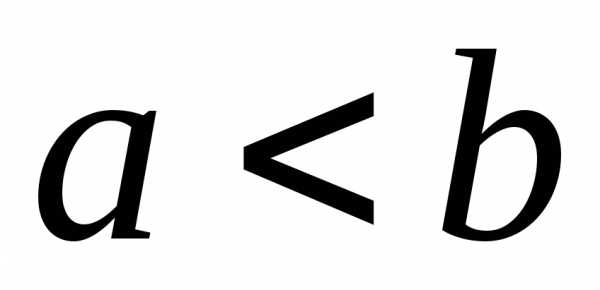 ,
,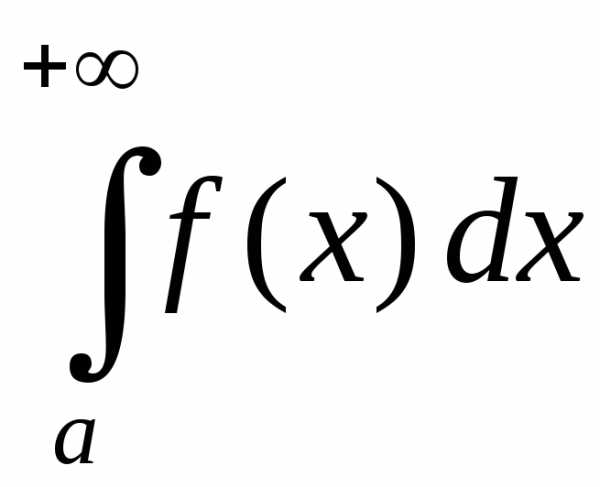 и
и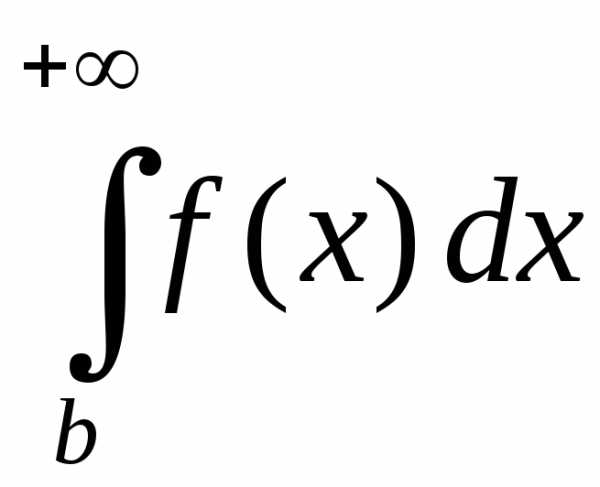 сходятся или рас-ходятся одновременно;
сходятся или рас-ходятся одновременно; сходится, то
сходится, то .
.