Как найти распределение относительных частот выборки - Исправление недочетов и поиск решений вместе с Examum.ru

Пусть из генеральной совокупности извлечена выборка объема П, в которой значение X1 некоторого исследуемого признака Х наблюдалось П1 раз, значение X2 — п2 раз, …, значение XK — Nk раз. Значения Xi называются Вариантами, а их последовательность, записанная в возрастающем порядке,— Вариационным рядом. Числа Ni называются Частотами, а их отношения к объему выборки

— Относительными частотами. При этом Ni = П. Модой Мo называется варианта, имеющая наибольшую частоту. Медианой те называется варианта, которая делит вариационный ряд на две части с одинаковым числом вариант в каждой. Если число вариант нечетно, т. е. K = 2L + 1, то Me = Xl+1; если же число вариант четно (k = 2L), То те = (Xl + Xl+1)/2. Размахом варьирования называется разность между максимальной и минимальной вариантами или длина интервала, которому принадлежат все варианты выборки:

Перечень вариант и соответствующих им частот называется Статистическим распределением выборки. Здесь имеется аналогия с законом распределения случайной величины: в теории вероятностей — это соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике — это соответствие между наблюдаемыми вариантами и их частотами (относительными частотами). Нетрудно видеть, что сумма относительных частот равна единице: Wi = 1.

Пример 2. Выборка задана в виде распределения частот:

Найти распределение относительных частот и основные характеристики вариационного ряда.

Решение. Найдем объем выборки: П = 2 + 4 + 5 + 6 + 3 = 20. Относительные частоты соответственно равны W1 = 2/20 = 0,1; W2 = 4/20 = 0,2; W3 = 5/20 = 0,25; W4 = 6/20 = 0,3; W5 = 3/20 = 0,15. Контроль: 0,1 + 0,2 + 0,25 + 0,3 + 0,15 = 1. Искомое распределение относительных частот имеет вид

Мода этого вариационного ряда равна 12. Число вариант в данном случае нечетно: K = 2 ∙ 2 + 1, поэтому медиана Me = X3 = 8. Размах варьирования, согласно формуле (18.48), R = 17 – 4 = 13.

< Предыдущая		Следующая >

Источник

Написать распределение относительных частот.

Решение. Найдем
относительные частоты, для чего разделим
частоты на объем выборки:

,

,

.

Напишем
распределение относительных частот:

х_i	2	6	12
W_i	0,15	0,5	0,35.

Контроль:
0,15 + 0,5 + 0,35 = 1.

Эмпирической
функцией распределения
(функцией
распределения выборки)
называют функцию,
определяющую для каждого значения х
относительную частоту события X
< х

,
(5.28)

где
– число вариант, меньших х,

–объем выборки.

Таким образом,
для того чтобы найти, например,,
надо число вариант, меньших ,
разделить на объем выборки

.
(5.29)

В отличие от
эмпирической функции распределения
выборки интегральную функцию
распределения генеральной совокупности
называют теоретической
функцией распределения.
Различие между эмпирической и теоретической
функциями состоит в том, что теоретическая
функция
определяет вероятность события X
< х,
а эмпирическая
– определяет относительную частоту
этого же события. Согласно теореме
Бернулли, относительная частота события
Х <
х,
т.е.
стремится по вероятности к вероятности

этого события. Другими словами, числа

и
мало отличаются друг от друга. Отсюда
следует целесообразность использования
эмпирической функции распределения
выборки для приближенного представления
теоретической (интегральной) функции
распределения генеральной совокупности.

Из определения
функции
вытекают следующие ее свойства:

значения
эмпирической функции принадлежат
отрезку [0,1];
–неубывающая
функция;
если x₁
– наименьшая варианта, то
= 0 при х

x₁;
если x_k
– наибольшая варианта, то
= 1 при х
> х_k.

Итак, эмпирическая
функция распределения выборки служит
для оценки теоретической функции
распределения генеральной совокупности.

Пример. Построить
эмпирическую функцию по данному
распределению выборки:

Варианты хi 2 6 10 частоты ni 12 18 30.

Решение. Найдем
объем выборки: 12 + 18 + 30 = 60. Наименьшая
варианта равна 2, следовательно,

= 0
при
х <
2.

Значение Х
< 6, а
именно: x₁= 2
наблюдалось 12 раз, следовательно,

при
2 < x

6.

Значения Х
< 10, а
именно: x₁= 2 и
x₂= 6
наблюдались 12 + 18 = 30 раз, следовательно,

при 6 <
x

10.

Так как х
= 10
– наибольшая варианта, то

= 1
при
х > 10.

Искомая эмпирическая
функция

График этой
функции изображен на рис. 5.5.

Рис. 5.5.

5.4.4 Полигон и гистограмма

В целях наглядности
строят различные графики статистического
распределения и, в частности, полигон
и гистограмму.

Полигоном
частот
называют ломаную, отрезки которой
соединяют точки (x₁,
n₁),
(x₂,
n₂),
…, (x_k,
n_k).
Для построения полигона частот на оси
абсцисс откладывают варианты х_i,
а на оси ординат – соответствующие им
частоты n_i.
Точки (x_i,
n_i)
соединяют отрезками прямых и получают
полигон частот.

Полигоном
относительных частот
называют ломаную, отрезки которой
соединяют точки (x₁,
W₁),
(x₂,
W₂),…,
(x_k,
W_k).
Для построения полигона относительных
частот на оси абсцисс откладывают
варианты x_i,
a на оси ординат соответствующие им
относительные частоты W_i.

Точки (x_i,
W_i)
соединяют отрезками прямых и получают
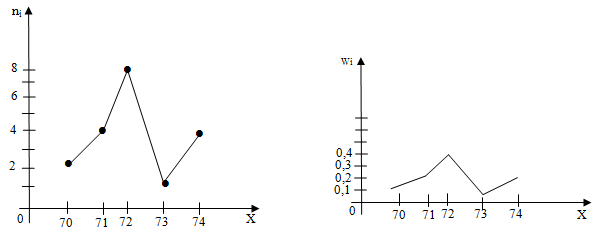
полигон относительных частот (рис. 5.6).

Рис. 5.6.

В ряде случаев,
в частности, в случае непрерывного
признака, целесообразно строить
гистограмму, для чего интервал, в котором
заключены все наблюдаемые значения
признака, разбивают на несколько
частичных интервалов длиною h
и находят для каждого частичного
интервала n_i,т.е.
сумму частот вариант, попавших в i-й
интервал.

Гистограммой
частот
называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых
служат частичные интервалы длиною h,
а высоты равны отношению
(плотность частоты).
Для
построения гистограммы частот на оси
абсцисс откладывают частичные интервалы,
а над ними проводят отрезки, параллельные
оси абсцисс на расстоянии
.
Площадь
i-гo
частичного прямоугольника равна

сумме частот вариант i-го
интервала; следовательно, площадь
гистограммы частот равна сумме всех
частот, т.е. объему выборки.

Гистограммой
относительных частот
называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых
служат частичные интервалы длиною h,
а высоты равны отношению
(плотность относительной частоты).
Для
построения гистограммы относительных
частот на оси абсцисс откладывают
частичные интервалы, а над ними проводят
отрезки, параллельные оси абсцисс на
расстоянии
(рис. 5.7). Площадьi-го
частичного прямоугольника равна
– относительной частоте вариант,
попавших вi-й
интервал. Следовательно, площадь
гистограммы относительных частот равна
сумме всех относительных частот, т.е.
единице.

Рис. 5.7.

Источник

Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость

Статистическое распределение выборки

Содержание:

Примеры использования формул и таблиц для решения практических задач
Статистический интервальный ряд распределения

Предположим случай, когда из генеральной совокупности извлекается некоторая выборка, при этом каждому значению соответствует некоторый параметр, означающий количество раз, когда появлялось данное значение. Здесь $x_1$ было зафиксировано $n_1$ раз, $x_2$ было обнаружено $n_2$$x_k$ выявлено $n_k$. При этом

$sum_{i=1}^{k}n_i=n$

Где n — объём рассматриваемой выборки.

Определение 1

Используется следующая терминология: $x_k$ носят наименование вариантов, а последовательность таких вариантов, зафиксированный по возрастанию именуется вариационным рядом. Количество наблюдений каждого из вариантов носят название частот. При этом частное частот и выборки называют относительными частотами.

Определение 2

Статистическое распределение —это название всего набора вариантов и частот, которые с ними соотносятся. Чаще всего задаётся с помощью специальной таблицы, где представлены частоты, а также интервалы им соответствующие.

$x_1$	$x_2$	…	$x_k$
$n_1$	$n_2$	…	$n_k$
$frac{n_1}{n}$	$frac{n_2}{n}$		$frac{n_k}{n}$

Здесь в первой строке представлены варианты, во второй частоты, в третьеq взяты относительные частоты.

Для определения размера интервала используется следующее выражение:

$d=frac{x_{max}- x_{min}}{1+3,332cdot lg n}$

Здесь $x_{max}$, $x_{min}$ наибольшее и наименьшее значения ряда вариантов, а n характеризуем объём выборки.

Примеры использования формул и таблиц для решения практических задач

Пример 1

В ходе проведения измерений в однородных группах, были определены следующие значения выборки: 71, 72, 74, 70, 70, 72, 71, 74, 71, 72, 71, 73, 72, 72, 72, 74, 72, 73, 72, 74. Необходимо использовать данные значения, что определить ряд распределения частот и ряд распределения относительных частот.

Решение.

1) Составим статистический ряд распределения частот:

xi	70	71	72	73	74
ni	2	4	8	2	4

2) Рассчитаем суммарный размер выборки: n=2+4+8+2+4=20. Определим относительные частоты, для этого используем формулы: ni/n=wi: wi=2/20=0.1; w2=4/20=0.2; w3=0.4; w4=4/20=0.1; w5=2/20=0.2. Теперь зафиксируем в таблице распределение относительных частот:

xi	70	71	72	73	74
wi	0.1	0.2	0.4	0.1	0.2

Контрольная сумма должна равняться единице: 0,1+0,2+0,4+0,1+0,2=1.

Полигон частот

Название «полигоном частот» применяют для обозначения ломаной линии, каждый отрезок, которой соединяют точки $(х_1,n_1),(х_2,n_2),…,(х_k,n_k)$. Для построения на графике полигона частот по оси абсцисс отмечают варианты $х_2$, при этом на оси ординат отсчитывают– соответствующие частоты $n_i$. Когда полученные точки $(х_i,n_i)$ соединяются с помощью отрезков, то автоматически получают полигон частот.

Статистический интервальный ряд распределения.

Статистическим дискретным рядом (или эмпирической функцией распределения) обычно пользуются, если число различающихся вариант в полученной выборке не слишком большое. Также применение возможно, когда дискретность имеет важное значение для экспериментатора. В тех случаях, когда важный для задачи признак генеральной совокупности Х распределяется непрерывным образом, либо его дискретность нет возможности учесть, то варианты предпочтительнее всего группировать, чтобы получить интервалы.

Статистическое распределение допустимо задавать в том числе в качестве последовательности интервалов и частот, соответствующих этим интервалам. При это за частоту какого-либо интервала принимается сумма всех частот, вошедших в данный интервал.

Особенно следует отметить ,что $h_i-h_{i-1}=h$ при всех i, т.е. группировка проводится с равным шагом h. Также в вопросе группировки можно ориентироваться на ряд полученных опытным путём рекомендацийу, касающихся таких параметров, как а, k и $h_i$:

1. $Rраз_{мах}=X_{max}-X_{min}$

2. $h=R/k$; k-число групп

3.$ kgeq 1+3.321lgn$ (формула Стерджеса)

4. $a=x_{min}, b=x_{max}$

5.$ h=a+h_i, i=0,1…k$

Определённую в ходе решения задачи группировку удобнее всего скомпоновать и перевести в вид специальной таблицы, которая также может именоваться — «статистический интервальный ряд распределения»:

Интервалы группировки	[h0;h1)	[h1;h2)	…	[hk-2;hk-1)	[hk-1;hk)
Частоты	n1	n2	…	nk-1	nk

Таблицу подобного вида можно сделать, поменяв частоты $n_i$ на относительные частоты:

Интервалы группировки	[h0;h1)	[h1;h2)	…	[hk-2;hk-1)	[hk-1;hk)
Отн. частоты	w1	w2	…	wk-1	wk

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример 2

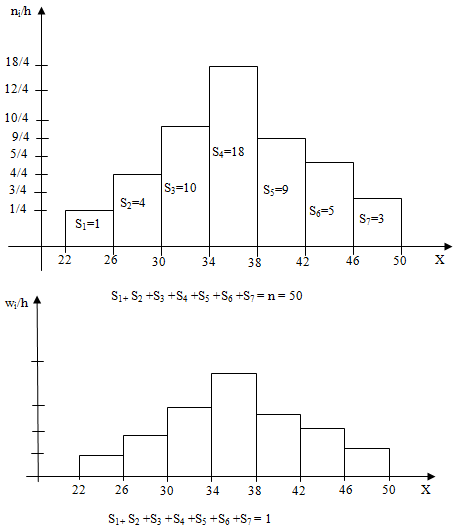
На склад пришла крупная партия деталей. Из них методом случайного отбора взято 50 экземпляров. Рассматривая изделия по одному, особенно интересующему признаку — размеру, определённому с точностью до 1 см, получим следующий вариационный ряд: 22, 47, 26, 26, 30, 28, 28, 31, 31, 31, 32, 32, 33, 33, 33, 33, 34, 34, 34, 34, 34, 35, 35, 36, 36, 36, 36, 36, 37, 37, 37, 37, 37, 37, 38, 38, 40, 40, 40, 40, 40, 41, 41, 43, 44, 44, 45, 45, 47, 50. Требуется произвести расчёт и определить статистический интервальный ряд распределения.

Решение

Найдём параметры выборки используя сведения из условия задачи.

$k geq1+3,321cdot lg50=1+3.32lg(5cdot10)=1+3.32(lg5+lg10)=6.6$

Получили a=22, k=7, h=(50-22)/7=4, hi=22+4i, i=0,1,…,7.

Интервалы группировки	22-26	26-30	30-34	34-38	38-42	42-46	46-50
Частоты	1	4	10	18	9	5	3
Отн. частоты	0.02	0.08	0.2	0.36	0.18	0.1	0.06

Десятичные логарифмы от 1 до 10

n	1	2	3	4	5	6	7	8	9	10
lnn≈	0	0.3	0.48	0.6	0.7	0.78	0.85	0.9	0.95	1

Не получается написать работу самому?

Доверь это кандидату наук!

Источник

Что такое относительное частотное распределение?

17 авг. 2022 г.
читать 2 мин

Распределение частоты описывает, как часто разные значения встречаются в наборе данных.

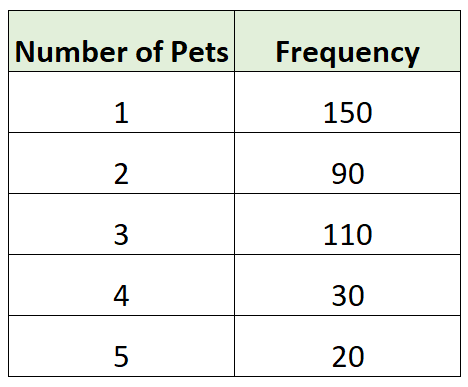
Например, предположим, что мы собираем простую случайную выборку из 400 домохозяйств в городе и записываем количество домашних животных в каждом домохозяйстве. В следующей таблице показаны результаты:

В этой таблице представлено частотное распределение.

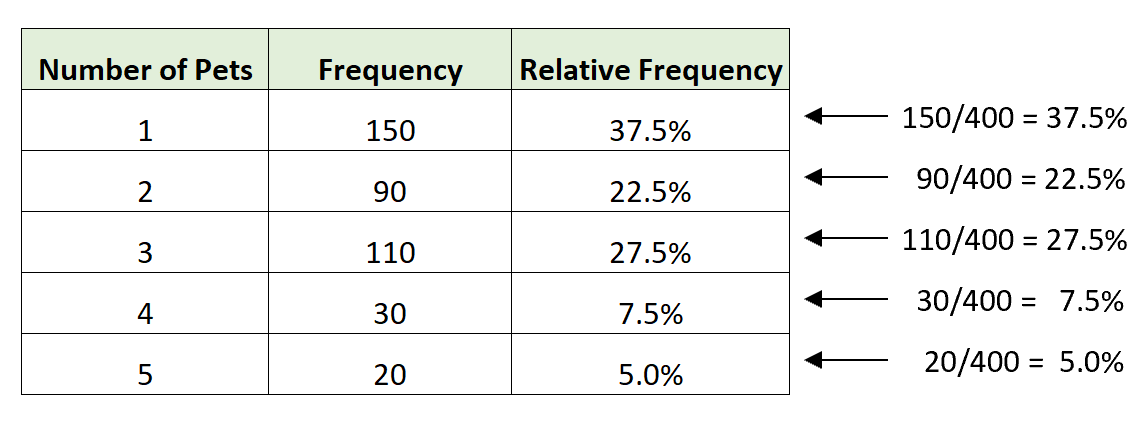
Связанное распределение известно как распределение относительной частоты , которое показывает относительную частоту каждого значения в наборе данных в процентах от всех частот.

Например, в предыдущей таблице мы видели, что всего было 400 домохозяйств. Чтобы найти относительную частоту каждого значения в распределении, мы просто делим каждую отдельную частоту на 400:

Обратите внимание, что распределения относительной частоты обладают следующими свойствами:

Каждая отдельная относительная частота находится в диапазоне от 0% до 100%.
Сумма всех отдельных относительных частот составляет 100%.

Если эти условия не выполняются, то относительное частотное распределение недействительно.

Почему относительные частотные распределения полезны

Распределения относительной частоты полезны, потому что они позволяют нам понять, насколько распространено значение в наборе данных по отношению ко всем другим значениям.

В предыдущем примере мы видели, что у 150 домохозяйств было только одно домашнее животное. Но это число само по себе не особенно полезно.

Напротив, полезнее знать, что 37,5% всех домохозяйств в выборке имели только одно домашнее животное. Это помогает нам понять, что чуть более чем в 1 из 3 домохозяйств было только одно домашнее животное, что дает нам некоторое представление о том, насколько «обычно» иметь только одного домашнего животного.

Визуализация относительного частотного распределения

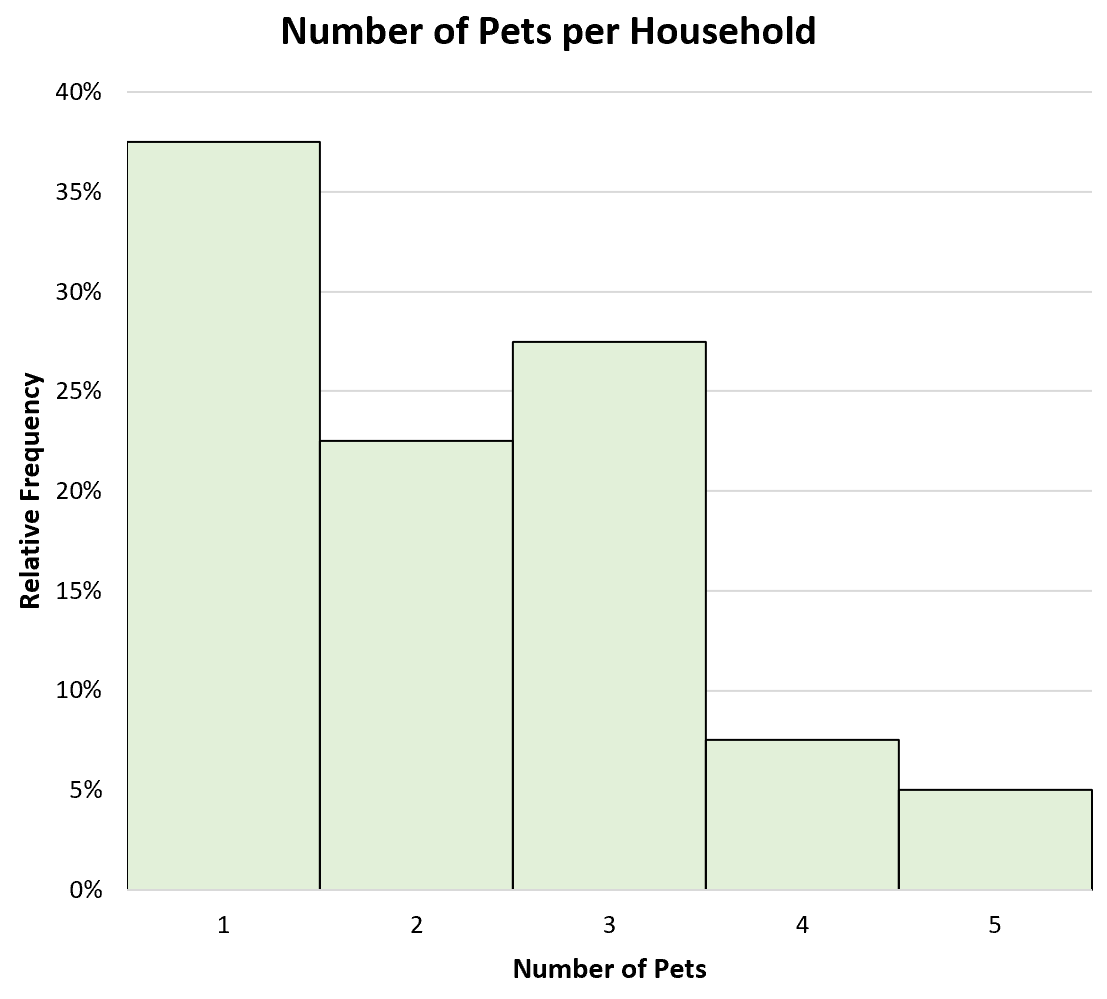
Самый распространенный способ визуализировать распределение относительной частоты — создать гистограмму относительной частоты , которая отображает отдельные значения данных по оси x графика и использует столбцы для представления относительной частоты каждого класса по оси y.

Например, вот как будет выглядеть гистограмма относительной частоты для данных из нашего предыдущего примера:

По оси X отображается количество домашних животных в домашнем хозяйстве, а по оси Y — относительная частота домашних хозяйств, в которых есть такое количество домашних животных.

Эта гистограмма помогает нам визуализировать распределение относительных частот.

Дополнительные ресурсы

Калькулятор относительной частоты
Как рассчитать относительную частоту в Excel
Как рассчитать относительную частоту в Python
Как создать гистограмму относительной частоты в R

Источник

При систематизации данных выборочных обследований используются статистические дискретные и интервальные ряды распределения.

1. Статистическое дискретное распределение. Полигон.
Пусть из генеральной совокупности извлечена выборка, причем х₁ наблюдалось n₁ раз, х₂ – n₂ раз, х_k – n_k раз и ∑n_i=n — объем выборки. Наблюдаемые значения х₁ называют вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом. Число наблюдений варианты называют частотой, а ее отношение к объему выборки — относительной частотой n_i/n=w_i

ОПРЕДЕЛЕНИЕ. Статистическим (эмпирическим) законом распределения выборки, или просто статистическим распределением выборки называют последовательность вариант х_i и соответствующих им частот n_i или относительных частот w_i.

Статистическое распределение выборки удобно представлять в форме таблицы распределения частот, называемой статистическим дискретным рядом распределения:

x₁	x₂	…	x_m
n₁	n₂	…	n_m

(сумма всех частот равна объему выборки ∑n_i=n)
или в виде таблицы распределения относительных частот:

x₁	x₂	…	x_m
w₁	w₂	…	w_m

(сумма всех относительных частот равна единице ∑w_i=1)

Пример 1. При измерениях в однородных группах обследуемых получены следующие выборки: 71, 72, 74, 70, 70, 72, 71, 74, 71, 72, 71, 73, 72, 72, 72, 74, 72, 73, 72, 74 (частота пульса). Составить по этим результатам статистический ряд распределения частот и относительных частот.

Решение. 1) Статистический ряд распределения частот:

x_i	70	71	72	73	74
n_i	2	4	8	2	4

2) Объем выборки: n=2+4+8+2+4=20. Найдем относительные частоты, для чего разделим частоты на объем выборки n_i/n=w_i: w_i=2/20=0.1; w₂=4/20=0.2; w₃=0.4; w₄=4/20=0.1; w₅=2/20=0.2. Напишем распределение относительных частот:

x_i	70	71	72	73	74
w_i	0.1	0.2	0.4	0.1	0.2

Контроль: 0,1+0,2+0,4+0,1+0,2=1.

Полигоном частот называют ломаную, отрезки, которой соединяют точки (х₁,n₁),(х₂,n₂),…,(х_k,n_k). Для построения полигона частот на оси абсцисс откладывают варианты х₂, а на оси ординат – соответствующие им частоты n_i. Точки (х_i,n_i) соединяют отрезками и получают полигон частот.

Полигоном относительных частот называют ломаную, отрезки, которой соединяют точки (х₁,w₁),(х₂,w₂),…,(х_k,w_k). Для построения полигона относительных частот на оси абсцисс откладывают варианты х_i, а на оси ординат соответствующие им частоты w_i. Точки (х_i,w_i) соединяют отрезками и получают полигон относительных частот.

Пример 2. Постройте полигон частот и относительных частот по данным примера 1.
Решение: Используя дискретный статистический ряд распределения, составленный в примере 1 построим полигон частот и полигон относительных частот:

2. Статистический интервальный ряд распределения. Гистограмма. Статистическим дискретным рядом (или эмпирической функцией распределения) обычно пользуются в том случае, когда отличных друг от друга вариант в выборке не слишком много, или тогда, когда дискретность по тем или иным причинам существенна для исследователя. Если же интересующий нас признак генеральной совокупности Х распределен непрерывно или его дискретность нецелесообразно ( или невозможно) учитывать, то варианты группируются в интервалы.

Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).

Замечание. Часто h_i-h_i-1=h при всех i, т.е. группировку осуществляют с равным шагом h. В этой ситуации можно руководствоваться следующими эмперическими рекомендациями по выборке а, k и h_i:

1. R_размах=X_max-X_min
2. h=R/k; k-число групп
3. k≥1+3.321lgn (формула Стерджеса)
4. a=x_min, b=x_max
5. h=a+ih, i=0,1…k

Полученную группировку удобно представить в форме частотной таблицы, которая носит название статистический интервальный ряд распределения:

Интервалы группировки	[h₀;h₁)	[h₁;h₂)	…	[h_k-2;h_k-1)	[h_k-1;h_k)
Частоты	n₁	n₂	…	n_k-1	n_k

Аналогическую таблицу можно образовать, заменяя частоты ni относительными частотами:

Интервалы группировки	[h₀;h₁)	[h₁;h₂)	…	[h_k-2;h_k-1)	[h_k-1;h_k)
Отн. частоты	w₁	w₂	…	w_k-1	w_k

Пример 3. Из очень большой партии деталей извлечена случайная выборка объема 50 интересующий нас признак Х-размеры деталей, измеренные с точностью до 1см, представлен следующим вариоционным рядом: 22, 47, 26, 26, 30, 28, 28, 31, 31, 31, 32, 32, 33, 33, 33, 33, 34, 34, 34, 34, 34, 35, 35, 36, 36, 36, 36, 36, 37, 37, 37, 37, 37, 37, 38, 38, 40, 40, 40, 40, 40, 41, 41, 43, 44, 44, 45, 45, 47, 50. Найти статистический интервальный ряд распределения.

Решение. Определим характеристики группировки с помощью замечания.
k≥1+3.321lg50=1+3.32lg(5•10)=1+3.32(lg5+lg10)=6.6
Имеем, a=22, k=7, h=(50-22)/7=4, h_i=22+4i, i=0,1,…,7.

Интервалы группировки	22-26	26-30	30-34	34-38	38-42	42-46	46-50
Частоты n_i	1	4	10	18	9	5	3
Отн.частоты w_i	0.02	0.08	0.2	0.36	0.18	0.1	0.06

Десятичные логарифмы от 1 до 10

n	1	2	3	4	5	6	7	8	9	10
lnn≈	0	0.3	0.48	0.6	0.7	0.78	0.85	0.9	0.95	1

Наиболее информативной графической формой частот является специальный график, называемы гистограммой частот.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению n_i/h (плотность частоты).

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии n_i/h. Площадь i-го частичного прямоугольника равна h•n_i/h=n_i — сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии w_i/h. Площадь i-го частичного прямоугольника равна h•w_i/h=w_i — относительной частоте вариант, попавших в i-й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.

Пример 4. Постройте гистограмму частот и относительных частот по данным примера 3.

Выборочная медиана – это середина вариационного ряда, значение, расположенное на одинаковом расстоянии от левой и правой границы выборки.

Выборочная мода – это наиболее вероятное, т.е. чаще всего встречающееся, значение в выборке.

Добавлять комментарии могут только зарегистрированные пользователи.

Регистрация Вход

Источник