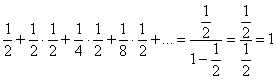Геометрическое распределение дискретной случайной величины
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Дискретная случайная величина
имеет геометрическое распределение с
параметром
,
если она принимает значения
(бесконечное, но счетное множество значений) с
вероятностями:
где
Ряд геометрического распределения случайной величины имеет вид:
Случайная величина
,
имеющая геометрическое распределение, представляет собой число
испытаний, проведенных по схеме Бернулли, с
вероятностью
наступления события в каждом испытании до
первого положительного исхода.
Вероятности
образуют собой геометрическую прогрессию с
первым членом
и знаменателем
.
Определение геометрического распределения корректно, так как сумма
ряда:
Так как
есть сумма геометрического ряда
при
.
Математическое ожидание случайной величины X, имеющей геометрическое распределение с параметром
:
Дисперсия случайной величины X, имеющей геометрическое распределение:
Для геометрического распределения асимметрия и эксцесс:
Другие законы распределения дискретных случайных величин:
Смежные темы решебника:
- Дискретная случайная величина
- Биномиальный закон распределения дискретной случайной величины
- Гипергеометрический закон распределения дискретной случайной величины
- Закон распределения Пуассона
Примеры решения задач
Пример 1
Производится ряд попыток завести двигатель, каждая попытка длительностью
10 с заканчивается запуском двигателя независимо от других с вероятностью
. Найти
распределение количества попыток запуска двигателя. Вычислите математическое
ожидание и дисперсию случайной величины.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Вероятность завести двигатель с 1-й попытки:
Вероятность завести двигатель со 2-й попытки:
Вероятность завести двигатель с 3-й попытки:
……
Вероятность завести двигатель с m-й попытки:
Получаем следующий ряд распределения количества попыток запуска
двигателя:
Общее число попыток запуска двигателя подчинено закону геометрического
распределения.
В нашем случае
Математическое ожидание в этом случае:
Дисперсия:
Пример 2
Дискретная случайная величина X распределена по геометрическому
закону с показателем p=0,6. Найти M(X2).
Решение
Математическое ожидание:
Дисперсия:
С другой стороны, дисперсию можно найти по
формуле:
Ответ:
Пример 3
Случайные величины X,Y распределены по
геометрическому закону. Найдите дисперсию D(X-Y), если их математические
ожидания равны 5, а коэффициент корреляции X и Y равен 0,3.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Искомую дисперсию можно найти по формуле:
Так как величины распределены по
геометрическому закону, то математическое ожидание:
Дисперсия случайной величины
:
Аналогично дисперсия случайной величины
:
Искомая дисперсия:
Ответ:
Пример 4
На плоскости начерчены два квадрата, стороны
которых 20 и 60 соответственно. Меньший квадрат содержится внутри большого
квадрата. В большой квадрат случайным образом бросают точки до тех пор, пока не
попадут в маленький квадрат. Пусть случайная величина X — число бросаний. Найдите
математическое ожидание M(X) и дисперсию D(X).
Решение
Вероятность попасть в маленький квадрат:
Вероятность попасть с 1-й попытки:
Вероятность попасть со 2-й попытки:
Вероятность попасть с 3-й попытки:
……
Вероятность попасть с m-й попытки:
Общее число попыток подчинено закону
геометрического распределения.
В нашем случае
Математическое ожидание в этом случае:
Дисперсия:
Ответ:
Задачи контрольных и самостоятельных работ
Задача 1
Случайная
величина ξ распределена по геометрическому закону с параметром p=0.3. Найти:
а) M(6ξ+4);
б) D(4-3ξ);
в) P(|ξ-Mξ|<σ(ξ)).
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
Производится
ряд независимых опытов, в каждом из которых может появится некоторое событие
. Вероятность появления
события
в каждом опыте равна 0,32. Опыты производятся
до первого появления события
, после чего они прекращаются.
Случайная
величина
– число произведенных опытов.
Составить
закон распределения случайной величины X, найти математическое ожидание М(X) и
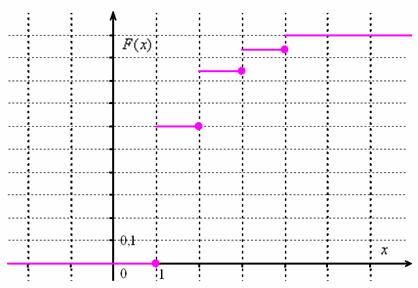
дисперсию D(X), найти функцию распределения F(X) и построить ее график.
Задача 3
Два
орудия залпом, но при независимой наводке, стреляют в цель до первого попадания
хотя бы одним орудием. Вероятность попадания в цель первым орудием при одном
выстреле равна 0,2, а вторым – 0,3.
Найти
закон распределения числа X сделанных залпов, вероятность
P(X>2)
математическое ожидание M(X) числа сделанных
залпов.
Задача 4
Охотник-любитель
стреляет из ружья по неподвижной мишени. Вероятность попасть в мишень при одном
выстреле является величиной постоянной и равной 0,65. Стрельба по мишени
ведется до первого попадания.
Определить
математическое ожидание и дисперсию числа израсходованных охотником патронов.
Задача 5
Случайная
величина X имеет геометрическое распределение с параметром p=0.2. Построить ряд
распределения случайной величины X. Построить многоугольник
распределения. Определить математическое ожидание, дисперсию, среднее
квадратическое отклонение величины X.
Задача 6
Для
поиска корабля, терпящего бедствие, совершает полеты самолет. Вероятность
обнаружения корабля в одном полете равна 0,4. Найти закон распределения
случайной величины X – числа поисковых полетов. Определить математическое
ожидание, дисперсию, среднее квадратическое отклонение величины X. Определить
вероятность того, что корабль будет обнаружен с третьей попытки.
Задача 7
Производятся
многократные испытания некоторого элемента на надежность до тех пор, пока
элемент не откажет. Вероятность отказа элемента в каждом опыте равна 0,1.
Найти:
а)
математическое ожидание дискретной случайной величины X – числа опытов, которые
надо произвести;
б)
Дисперсию D(X).
Задача 8
Вероятность
выигрыша в лотерее равна 0,1. Некто решил покупать по одному билету из каждого
тиража, пока не выиграет. Найти среднее число приобретенных билетов.
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Содержание:
- Геометрическое распределение
- Гипергеометрическое распределение
Вероятности 

В последовательности независимых испытаний Бернулли (р — вероятность успеха в каждом испытании, q — вероятность неуспеха) рассмотрим случайную величину X — номер испытания, являющегося первым успехом. По смыслу X — ДСВ, так как множество реальных значений X является счетным множеством.
Дискретная случайная величина X имеет геометрическое распределение, если она принимает значения 1, 2, 3, … с вероятностями 






так как ряд представляет собой убывающую 
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Математическое ожидание

Возможно вам будут полезны данные страницы:
Пример с решением №1
Студент подготовил из 40 экзаменационных билетов 32 и мечтает, что преподаватель разрешит ему выбрать выученный билет. Составить ряд распределений числа X возможных попыток взять билет до появления первого «знакомого» билета, если преподаватель остановил студента после четвертой попытки. Найти числовые характеристики этой случайной величины.
Решение:
Вероятность того, что студент возьмет выученный билет, равна 0,8. Случайная величина X — число испытаний до появления первого выученного билета. Составим ряд распределений, найдем функцию распределения ДСВ X, построим ее график. Найдем все числовые характеристики (ограничиться тремя-пятью испытаниями).
Обозначим через 

Так как случайная величина X — число возможных попыток до появления первого выученного билета, воспользуемся геометрической вероятностью:

дисперсия
среднеквадратическое отклонение
Почему в рассмотренной задаче не выполняется условие нормировки:
Дело в том, что в случае геометрических распределений условие нормировки выполняется при 
Геометрическое распределение
Определение. Дискретная случайная величина 


Ряд геометрического распределения случайной величины имеет вид:



Определение геометрического распределения корректно, так как сумма ряда




Случайная величина 

Так, например, число вызовов радистом корреспондента до тех пор, пока вызов не будет принят, рассматриваемое в примере 3.196, есть случайная величина, имеющая геометрическое распределение с параметром р — 0,4.
Теорема. Математическое ожидание случайной величины X, имеющей геометрическое распределение с параметром р,


Пример с решением №2
Проводится проверка большой партии деталей до обнаружения бракованной (без ограничения числа проверенных деталей). Составить закон распределения числа проверенных деталей. Найти его математическое ожидание и дисперсию, если известно, что вероятность брака для каждой детали равна 0,1.
Решение:
Случайная величина X — число проверенных деталей до обнаружения бракованной — имеет геометрическое распределение (4.11) с параметром р =0,1. Поэтому ряд распределения имеет вид

Гипергеометрическое распределение
Определение. Дискретная случайная величина X имеет гипергеометрическое распределение с параметрами 


где 
Гипергеометрическое распределение имеет случайная величина 

Так, распределение случайной величины X — числа неточных приборов среди взятых наудачу четырех, полученное в примере 3.20, есть гипергеометрическое распределение с параметрами
Теорема. Математическое ожидание случайной величины X, имеющей гипергеометрическое распределение с параметрами 

а ее дисперсия 



Можно показать, что при
функция вероятностей (4.14) гипергеометрического распределения стремится к соответствующей функции (4.1) биномиального закона.
Гипергеометрическое распределение широко используется в практике статистического приемочного контроля качества промышленной продукции, в задачах, связанных с организацией выборочных обследований, и других областях.
Пример с решением №3
В лотерее «Спортлото 6 из 45» денежные призы получают участники, угадавшие 3, 4, 5 и 6 видов спорта из отобранных случайно 6 видов из 45 (размер приза увеличивается с увеличением числа угаданных видов спорта). Найти закон распределения случайной величины X — числа угаданных видов спорта среди случайно отобранных шести. Какова вероятность получения денежного приза? Найти математическое ожидание и дисперсию случайной величины X.
Решение:
Очевидно (см. гл. 1, пример 1.14), что число угаданных видов спорта в лотерее «6 из 45» есть случайная величина, имеющая гипергеометрическое распределение с параметрами 


Таким образом, среднее число угаданных видов спорта из 6 всего 0,8, а вероятность выигрыша только 0,024. ►
Лекции:
- Замечательные пределы примеры решения
- Применение определителей
- Средняя скорость изменения, мгновенная скорость изменения
- Перпендикулярные прямые
- Найти угол между векторами: пример решения
- Найдите координаты точки пересечения прямых
- Нормальное распределение примеры решения
- Площадь поверхности цилиндра
- Найти определитель матрицы
- Как привести к общему знаменателю
Испытания Бернулли
- Схема Бернулли
- Биномиальное распределение
- Примеры
п.1. Схема Бернулли
Схема Бернулли – это последовательность независимых испытаний, в каждом из которых возможны только два исхода – «успех» и «неудача».
При этом вероятность успеха в каждом испытании постоянна и равна p ∈ (0; 1).
Вероятность неудачи в каждом испытании q = 1 – p.
Например:
Стрелок попадает в мишень с вероятностью p = 0,8.
Найдите вероятности для события X – количества попаданий в серии из 4 выстрелов.
X = {0;1;2;3;4} – возможные значения X.
q = 1 – p = 0,2 – вероятность неудачи.
Полное пространство элементарных событий («+» – попал, «–» – не попал) 
(mathrm{C_n^k=frac{n!}{(n-k)!k!}}) – или биномиальными коэффициентами (см. §36 данного справочника).
Для количества попаданий в серии из 4 выстрелов получаем:
|
Количество попаданий, X |
0 |
1 |
2 |
3 |
4 |
|
Вероятность, PX |
0,0016 |
0,0256 |
0,1536 |
0,4096 |
0,4096 |
п.2. Биномиальное распределение
Вероятность того, что событие A появится в n испытаниях Бернулли ровно k раз, выражается формулой Бернулли: $$ mathrm{ P_n(k)=C_n^kp^kq^{n-k} } $$ Распределение числа успехов (появлений события) называют биномиальным распределением.
Например:
В семье четверо детей. Определите вероятность, что двое из детей – девочки.
Вероятность рождения девочки p = 1/2. $$ mathrm{ P_4(2)=C_2^4p^2q^2=frac{4cdot 3}{1cdot 2}cdot left(frac12right)^4=frac38 } $$ (Сравните с решением примера 3(1), §37 данного справочника, где при другом подходе был получен такой же результат).
В схеме Бернулли с n испытаниями количество k* появлений события A с наибольшей вероятностью (математическое ожидание) равно $$ mathrm{ k^{*}=np } $$
Например:
Стрелок попадает в мишень с вероятностью 0,85. Найдите наиболее вероятное количество попаданий в серии из 7 выстрелов и вероятность этого события.
Наиболее вероятное количество попаданий: k* = np = 7 · 0,85 = 5,95 ≈ 6.
Вероятность: (mathrm{P_n(k^{*})=P_7(6)=C_7^6p^6q=7cdot 0,85^6 cdot 0,15 approx 0,396}).
Ответ: 6; 0,396.
п.3. Примеры
Пример 1. В урне 15 белых и 9 черных шаров. Из урны достают шар, отмечают его цвет, затем возвращают обратно в урну и все шары перемешивают.
1) Найдите вероятность того, что в 5 опытах 3 раза шары оказались белыми.
2) Постройте закон распределение для числа появления белых шаров в 5 опытах.
1) Вероятность достать белый шар из урны: (mathrm{ p=frac{15}{15+9}=frac58 }).
Вероятность достать черный шар: (mathrm{ q=1-p=frac38 }).
Искомая вероятность по формуле Бернулли: $$ mathrm{ P_5(3)=C_5^3p^3q^2=frac{5cdot 4}{1cdot 2}cdot left(frac58right)^3cdot left(frac38right)^2=1-cdotfrac{125cdot 9}{8^5}approx 0,3433 } $$ 2) Число появления белых шаров описывается биномиальным законом распределения.
| Число белых шаров, k | 0 | 1 | 2 | 3 | 4 | 5 |
| P5(k) | (mathrm{C_5^0q^5}) | (mathrm{C_5^1pq^4}) | (mathrm{C_5^2p^2q^3}) | (mathrm{C_5^3p^3q^2}) | (mathrm{C_5^4p^4q}) | (mathrm{C_5^5p^5}) |
| 0,0074 | 0,0618 | 0,2060 | 0,3433 | 0,2861 | 0,0954 |
Максимальная вероятность для k = 3 белых шаров в 5 опытах.
Действительно, математическое ожидание (mathrm{k^{*}=np=5cdot frac58=frac{25}{8}approx 3.})
Минимальная вероятность для k = 0 – не достали ни одного белого шара в 5 опытах.
Пример 2*. Вероятность того, что стрелок попадёт меньше 4 раз из 5 выстрелов, равна 0,85. Вероятность того, что он попадёт меньше 3 раз, равна 0,76. Найдите наиболее вероятное количество попаданий в серии из 5 выстрелов и вероятность этого события.
По условию: (mathrm{P_5(klt 4)=0,85, P_5(klt 3)=0,76}). Тогда
(mathrm{P_5(klt 4)-P_5(klt 3)=P_5(3)=0,85-0,76=0,009})
(mathrm{P_5(3)=C_5^3p^3q^2=10p^3(1-p)^2=0,09})
(mathrm{p^3(1-p)^2=0,009})
Решаем уравнение графически: (mathrm{(1-p)^2=frac{0,009}{p^3}})
Получаем два решения.
1) Стрелок может быть очень хорош: вероятность попадания p = 0,88
Тогда наиболее вероятное количество попаданий: (mathrm{k^{*}=np=5cdot 0,88=4,4approx 4})
Вероятность этого события: (mathrm{P_5(4)=C_5^4p^4q=5cdot 0,88^4cdot 0,12approx 0,3598})
2) Стрелок может быть также весьма плох: вероятность попадания p = 0,25
Тогда наиболее вероятное количество попаданий: (mathrm{k^{*}=np=5cdot 0,25=1,25approx 1})
Вероятность этого события: (mathrm{P_5(1)=C_5^1pq^4=5cdot 0,25cdot 0,75^4approx 0,3955})
Ответ: (mathrm{k^{*}=4, P_5(4)approx 0,2598 text{или} k^{*}=1, P_5(1)approx 0,3955}).
Пример 3. Среди выпускаемых цехом плат в среднем 0,1% брака.
1) Найдите вероятность того, что среди 50 взятых на проверку качества изделий 2 будут бракованными.
2) Какова вероятность, что хотя бы одно изделие из 50 будет бракованным?
3) Чему равно наиболее вероятное количество бракованных изделий в партии из 50 штук и чему равна вероятность этого события?
4) Какую по количеству партию изделий нужно проверять, чтобы наиболее вероятное количество бракованных изделий было равно 1?
По условию: p = 0,001, n = 50, k = 2
q = 1 – p = 0,999
1) Искомая вероятность: (mathrm{P_{50}(2)=C_{50}^2p^2q^{48}=frac{50cdot 49}{1cdot 2}cdot 0,001^2cdot 0,999^{48}approx 0,0012})
2) Найдем вероятность того, что все 50 изделий стандартные: $$ mathrm{ P_{50}(0)=q^{50}=0999^{50}approx 0,9512 } $$ Вероятность того, что хотя бы одно изделие бракованное: $$ mathrm{ P_{50}(kgeq 1)=1-P_{50}(0)=1-0,9512=0,0488 } $$ 3) Наиболее вероятное количество: (mathrm{k^{*}=np=50cdot 0,001=0,05approx 0}) – ни одного бракованного изделия. Вероятность этого события: (mathrm{P_{50}(0)approx 0,9512})
4) (mathrm{Np=1Rightarrow N=frac{1}{p}=frac{1}{0,001}=1000}) – размер партии для проверки.
Ответ: 0,0012; 0,0488; k*=0, P50(0) ≈ 0,9512; 1000.
Пример 4. Монета подбрасывается 7 раз.
1) Какова вероятность, что 7 раз подряд выпадет орел?
2) Постройте закон распределения для события «орел выпал k раз в 7 испытаниях». Сделайте выводы.
1) (mathrm{p=q=frac12, n=7, k=7})
(mathrm{P_7(7)=C_7^7p^7q^0=p^7=frac{1}{2^7}=frac{1}{128}approx 0,0078}).
2)
| Число выпадений орла, k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| (mathrm{C_7^k}) | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 |
| (mathrm{P_7(k)}) | (mathrm{frac{C_7^0}{2^7}}) | (mathrm{frac{C_7^1}{2^7}}) | (mathrm{frac{C_7^2}{2^7}}) | (mathrm{frac{C_7^3}{2^7}}) | (mathrm{frac{C_7^4}{2^7}}) | (mathrm{frac{C_7^5}{2^7}}) | (mathrm{frac{C_7^6}{2^7}}) | (mathrm{frac{C_7^7}{2^7}}) |
| 0,0078 | 0,0547 | 0,1641 | 0,2734 | 0,2734 | 0,1641 | 0,0547 | 0,0078 |
Распределение является симметричным, т.к. p = q
Максимальная вероятность 27,34% при k* = 3 и k* = 4
Минимальные вероятности 0,78% при k = 0 – выпали все решки, и k = 7 – выпали все орлы.
Что такое вероятностное распределение?
Во многих ситуациях возможны несколько исходов. При любом исходе есть вероятность, что это произойдет. Это называется распределением вероятностей. Вероятности всех возможных результатов должны составлять в сумме 1 или 100%.
Распределение вероятностей может быть дискретным или непрерывным. В дискретном распределении вероятностей существует только счетное число возможностей. В непрерывном распределении вероятностей возможно бесчисленное количество исходов. Пример дискретной вероятности — бросание кубика. Есть только шесть возможных исходов. Кроме того, количество людей, стоящих в очереди на вход, является дискретным событием. Хотя теоретически это может быть любая возможная длина, она счетна и, следовательно, дискретна. Примерами непрерывных результатов являются время, вес, длина и т. Д., Если вы не округляете результат, а берете точную сумму. Тогда есть бесчисленное множество вариантов. Даже если принять во внимание все веса от 0 до 1 кг, это бесчисленное множество вариантов. Если округлить любой вес до одного десятичного знака, он становится дискретным.
Примеры общих распределений вероятностей
Наиболее естественным распределением вероятностей является равномерное распределение. Если исходы события распределены равномерно, то любой исход одинаково вероятен — например, бросок кубика. Тогда все исходы 1, 2, 3, 4, 5 и 6 равновероятны и произойдут с вероятностью 1/6. Это пример дискретного равномерного распределения.
Равномерное распределение
Равномерное распределение также может быть непрерывным. Тогда вероятность того, что произойдет одно определенное событие, равна 0, поскольку существует бесконечно много возможных исходов. Поэтому более полезно посмотреть на вероятность того, что результат находится между некоторыми значениями. Например, когда X равномерно распределен между 0 и 1, тогда вероятность того, что X <0,5 = 1/2, а также вероятность того, что 0,25 <X <0,75 = 1/2, поскольку все исходы равновероятны. В общем, вероятность того, что X равно x, или, более формально, P (X = x) может быть вычислена как P (X = x) = 1 / n, где n — общее количество возможных результатов.
Распределение Бернулли
Другое известное распределение — это распределение Бернулли. В распределении Бернулли есть только два возможных результата: успех и отсутствие успеха. Вероятность успеха равна p, поэтому вероятность безуспешности равна 1-p. Успех обозначается 1, отсутствие успеха — 0. Классическим примером является подбрасывание монеты, при котором орел — успех, решка — не успех, или наоборот. Тогда p = 0,5. Другой пример — это бросок шестерки с помощью кубика. Тогда p = 1/6. Итак, P (X = 1) = p.
Биномиальное распределение
Биномиальное распределение учитывает повторяющиеся результаты Бернулли. Это дает вероятность того, что за n попыток вы получите k успехов и nk неудач. Следовательно, это распределение имеет три параметра: количество попыток n, количество успехов k и вероятность успеха p. Тогда вероятность P (X = x) = (n ncr x) p x (1-p) nx, где n ncr k — биномиальный коэффициент.
Геометрическое распределение
Геометрическое распределение предназначено для рассмотрения количества попыток до первого успеха в настройке Бернулли — например, количества попыток до выпадения шестерки или количества недель до того, как вы выиграете в лотерее. Р (Х = х) = р * (1-р) ^ х.
Распределение Пуассона
Распределение Пуассона подсчитывает количество событий, которые происходят в определенном фиксированном временном интервале — например, количество клиентов, которые приходят в супермаркет каждый день. У него есть один параметр, который чаще всего называется лямбда. Лямбда — это интенсивность приходов. Так что в среднем приходят лямбда-клиенты. Тогда вероятность того, что поступит x, равна P (X = x) = lambda x / x! е- лямбда
Экспоненциальное распределение
Экспоненциальное распределение — это хорошо известное непрерывное распределение. Это тесно связано с распределением Пуассона, поскольку это время между двумя вступлениями в процесс Пуассона. Здесь P (X = x) = 0, и поэтому более полезно посмотреть на функцию массы вероятности f (x) = lambda * e -lambda * x. Это производная функции плотности вероятности, которая представляет P (X <x).
Существует гораздо больше распределений вероятностей, но именно они наиболее часто встречаются на практике.
Как найти среднее значение распределения вероятностей
Среднее значение вероятностного распределения — это среднее значение. По закону больших чисел, если вы будете постоянно отбирать образцы распределения вероятностей, то среднее значение ваших выборок будет средним значением распределения вероятностей. Среднее также называется ожидаемым значением или ожиданием случайной величины X. Ожидание E случайной величины X, когда X является дискретным, можно вычислить следующим образом:
E = sum_ {x от 0 до бесконечности} x * P (X = x)
Равномерное распределение
Пусть X равномерно распределено. Тогда ожидаемое значение — это сумма всех результатов, разделенная на количество возможных результатов. В примере с кубиком мы увидели, что P (X = x) = 1/6 для всех возможных результатов. Тогда E = (1 + 2 + 3 + 4 + 5 + 6) / 6 = 3,5. Здесь вы видите, что ожидаемое значение не обязательно должно быть возможным результатом. Если вы продолжаете бросать кубик, то среднее число, которое вы бросаете, будет 3,5, но вы, конечно, никогда не выбросите 3,5.
Математическое ожидание распределения Бернулли равно p, поскольку есть два возможных исхода. Это 0 и 1. Итак:
E = 0 * P (X = 0) + 1 * P (X = 1) = p
Биномиальное распределение
Для биномиального распределения мы снова должны решить сложную сумму:
сумма x * (n ncr x) * p x * (1-p) nx
Эта сумма равна n * p. Точный расчет этой суммы выходит за рамки данной статьи.
Геометрическое распределение
Для геометрического распределения ожидаемое значение рассчитывается с использованием определения. Хотя сумму довольно сложно вычислить, результат очень прост:
E = сумма x * p * (1-p) x-1 = 1 / p
Это тоже очень интуитивно понятно. Если что-то происходит с вероятностью p, вы ожидаете, что для успеха потребуется 1 / p попыток. Например, в среднем вам нужно шесть попыток, чтобы бросить шесть кубиков. Иногда будет больше, иногда меньше, но в среднем шесть.
Распределение Пуассона
Математическое ожидание распределения Пуассона — это лямбда, поскольку лямбда определяется как интенсивность прихода. Если мы применим определение среднего, мы действительно получим следующее:
E = сумма x * лямбда x / x! * e -lambda = lambda * e -lambda * sum lambda x-1 / (x-1)! = лямбда * е- лямбда * е лямбда = лямбда
Экспоненциальное распределение
Экспоненциальное распределение является непрерывным, поэтому невозможно вычислить сумму по всем возможным исходам. Также P (X = x) = 0 для всех x. Вместо этого мы используем интеграл и функцию массы вероятности. Потом:
E = интеграл _ {- от бесконечности до бесконечности} x * f (x) dx
Экспоненциальное распределение определяется только для x, большего или равного нулю, поскольку отрицательная скорость поступления невозможна. Это означает, что нижняя граница интеграла будет равна 0 вместо минус бесконечности.
E = интеграл_ {от 0 до infty} x * лямбда * e- лямбда * x dx
Чтобы решить этот интеграл, необходимо частичное интегрирование, чтобы получить E = 1 / lambda.
Это также очень интуитивно понятно, так как лямбда — это интенсивность приходов, то есть количество прибытий за одну единицу времени. Таким образом, время до прибытия действительно будет в среднем 1 / лямбда.
Опять же, существует гораздо больше распределений вероятностей, и все они имеют свои собственные ожидания. Однако рецепт всегда будет одним и тем же. Если он дискретный, используйте сумму и P (X = x). Если это непрерывное распределение, используйте интеграл и функцию массы вероятности.
Свойства ожидаемой стоимости
Ожидание суммы двух событий — это сумма ожиданий:
E = E + E
Кроме того, умножение на скаляр внутри математического ожидания такое же, как и снаружи:
E = aE
Однако ожидание произведения двух случайных величин не равно произведению ожиданий, поэтому:
E ≠ E * E в общем
Только когда X и Y независимы, они будут равны.
Разница
Другой важной мерой вероятностных распределений является дисперсия. Он количественно оценивает разброс результатов. Распределения с низкой дисперсией имеют результаты, близкие к среднему. Если дисперсия высока, то результаты разбросаны намного больше. Если вы хотите узнать больше о дисперсии и о том, как ее вычислить, я предлагаю прочитать мою статью о дисперсии.
- Математика: как найти дисперсию распределения вероятностей
2.3.1. Геометрическое распределение вероятностей
И геометрия тут не при чём.
Пусть проводится серия испытаний, в каждом из которых случайное событие может появиться с вероятностью
; причём, испытания заканчиваются при первом же появлении данного события. Тогда случайная величина
, характеризующая количество совершённых попыток, как раз и имеет геометрическое распределение.
Рассмотрим, например, такое событие: – в результате броска монеты выпадет орёл.
Начинаем подбрасывать монету. Совершенно понятно, что вероятность появления орла в любом испытании равна , и наша задача заключается в том, чтобы проанализировать – как скоро появится первый орёл (после чего серия закончится). Составим закон распределения случайной величины
– количества проведённых бросков.
Если , то это означает, что орёл выпал в первой же попытке. Вероятность этого события равна:
Если , то в первой попытке выпала решка (вероятность
), а во второй – орёл. По теореме умножения вероятностей ЗАвисимых событий:
Если , то в первых двух испытаниях появились решки, а в третьем – орёл. По той же теореме:
Если , то первый орёл появился лишь в четвёртом испытании:
…сколько же можно подбрасывать монету? Теоретически – до бесконечности.
И перед нами пример дискретной случайной величины, которая принимает бесконечное и счётное количество значений. В общем виде её закон распределения записывается следующим образом:
Вероятности представляют собой бесконечно убывающую геометрическую прогрессию с первым членом
и основанием
. Отсюда и название – геометрическое распределение вероятностей. Как известно, сумма такой прогрессии равна:
, что полностью соответствует вероятностному смыслу задачи.
В частности, для примера с «волшебной» монетой:
сумма вероятностей составляет:
Однако жизнь такова, что всё когда-то заканчивается, и поэтому в практических задачах количество испытаний почти всегда ограничивается. На «грубую» такое распределение тоже можно считать геометрическим, и сейчас мы разберём классический пример:
Задача 96
Стрелок производит несколько выстрелов в цель до первого попадания, имея всего 4 патрона. Вероятность попадания при одном выстреле равна 0,6. Найти закон распределения случайной величины , математическое ожидание
, дисперсию
, где
– количество произведённых выстрелов. Построить многоугольник и функцию распределения данной случайной величины. Найти
.
…если что-то позабылось, то я заботливо проставлю ссылки, решаем:
По условию, вероятность попадания в каждом испытании равна . Тогда вероятность промаха:
.
Составим закон распределения случайной величины :
1)
Это означает, что стрелок попал с 1-й попытки и на этом испытания закончились:
2) – в первом испытании промах, во втором – попадание. По теореме умножения вероятностей ЗАвисимых событий:
3) – попадание с третьей попытки, мимо-мимо, попал:
И, наконец:
4)
Здесь стрелок может промахнуться или попасть, но испытания заканчиваются в любом случае. Вместе с патронами. По теоремам умножения вероятностей зависимых и сложения вероятностей несовместных событий:
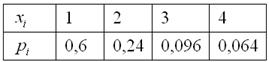
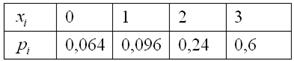
Таким образом, искомый закон распределения:
Обязательно выполняем проверку:
, что и требовалось проверить.
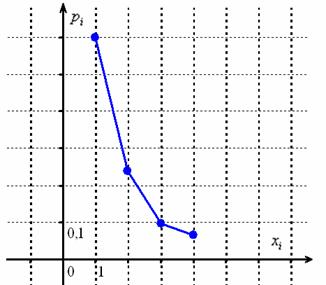
Построим многоугольник распределения:
Вычислим и
. Для геометрического распределения существуют готовые формулы нахождения математического ожидания и дисперсии:
, но нам ими воспользоваться не удастся – по той причине, что количество испытаний не бесконечно.
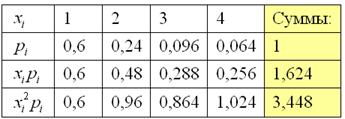
Поэтому придётся использовать общий алгоритм. Заполним расчётную таблицу:
Математическое ожидание лежит готовенькое: – это среднеожидаемое количество выстрелов (при многократном повторении таких серий из 4 выстрелов).
Дисперсию вычислим по формуле:
– это мера рассеяния количества выстрелов относительно математического ожидания.
Составим функцию распределения вероятностей:
Выполним чертёж:
Найдём – вероятность того, что значение случайной величины отклонится от математического ожидания не более чем на
.
Сначала вычислим среднее квадратическое отклонение:
затем – требуемую вероятность:
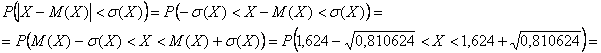
– вспоминаем, что это за интервал, и почему вероятность получилась столь большой

Готово!
Но при всей кажущейся простоте, у этого задания существуют подводные камни. Главное коварство состоит в том, условие может быть сформулировано по такому же шаблону, но случайная величина быть ДРУГОЙ. Например:
– количество промахов.
В этом случае закон распределения вероятностей примет следующий вид:
Здесь – вероятность того, что будет 3 промаха (и в 4-й попытке попадание);
– вероятность того, что стрелок совершит 4 промаха.
Естественно, что числовые характеристики и содержательные выводы этой задачи будут несколько другими, однако сам закон распределения сохранит свой «геометрический» характер.
Вот ещё одна хитрая вариация, которая мне встречалась на практике:
– количество неизрасходованных патронов.
Закон распределения этой величины таков:
Проанализируйте данный случай самостоятельно. Кстати, в примере, который мы прорешали, случайную величину можно эквивалентно сформулировать, как Количество израсходованных патронов.
Таким образом, к решению подобных задач тоже нельзя подходить формально – во избежание ошибок, ВСЕГДА ДУМАЙТЕ ГОЛОВОЙ и анализируйте реалистичность полученных результатов. И тогда полученное значение в разобранной задаче вас явно насторожит



| Оглавление |
Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин










 функция вероятностей (4.14) гипергеометрического распределения стремится к соответствующей функции (4.1) биномиального закона.
функция вероятностей (4.14) гипергеометрического распределения стремится к соответствующей функции (4.1) биномиального закона.