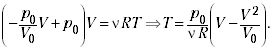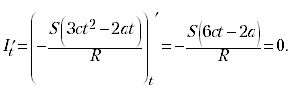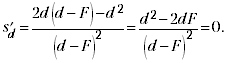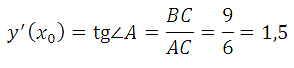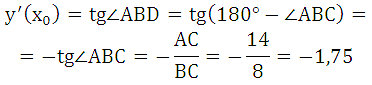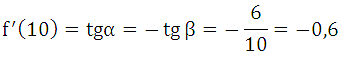Как найти расстояние через производную

15 мая 2014

Иногда в задаче 6 из ЕГЭ по математике вместо всеми любимых графиков функции или производной дается просто уравнение расстояния от точки до начала координат. Что делать в этом случае? Как по расстоянию найти скорость или ускорение.

На самом деле все просто. Скорость — это производная от расстояния, а ускорение — это производная скорости (или, что то же самое, вторая производная от расстояния). В этом коротком видео вы убедитесь, что такие задачи решаются ничуть не сложнее «классических» заданий 6.

Сегодня мы разберем две задачи на физический смысл производных из ЕГЭ по математике. Эти задания встречаются в части Bи существенно отличаются от тех, что большинство учеников привыкло видеть на пробниках и экзаменах. Все дело в том, что они требуют понимать физический смысл производной функции. В данных задачах речь пойдет о функциях, выражающих расстояния.

Если $S=xleft( t right)$, то $v$ мы можем посчитать следующим образом:

[v={S}’={x}’left( t right)]

Точно так же мы можем посчитать и ускорение:

[a={v}’={{S}’}’={{x}’}’left( t right)]

Эти три формулы – все, что вам потребуется для решения таких примеров на физический смысл производной. Просто запомните, что $v$ — это производная от расстояния, а ускорение — это производная от скорости.

Давайте посмотрим, как это работает при решении реальных задач.

Пример № 1

Материальная точка движется по закону:

[xleft( t right)=-frac{1}{5}{{t}^{5}}+{{t}^{4}}-{{t}^{3}}+5t]

где $x$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, прошедшее с начала движения. Найдите скорость точки (в м/с) в момент времени $t=2c$.

Это означает, что у нас есть функция, задающая расстояние, а нужно посчитать скорость в момент времени $t=2c$. Другими словами, нам нужно найти $v$, т.е.

[v={S}’={x}’left( 2 right)]

Вот и все, что нам нужно было выяснить из условия: во-первых, как выглядит функция, а во-вторых, что от нас требуется найти.

Давайте решать. В первую очередь, посчитаем производную:

[{x}’left( t right)=-frac{1}{5}cdot 5{{t}^{4}}+4{{t}^{3}}-3{{t}^{2}}+5]

[{x}’left( t right)=-{{t}^{4}}+4{{t}^{3}}-3{{t}^{2}}+5]

Нам требуется найти производную в точке 2. Давайте подставим:

[{x}’left( 2 right)=-{{2}^{4}}+4cdot {{2}^{3}}-3cdot {{2}^{2}}+5=]

[=-16+32-12+5=9]

Вот и все, мы нашли окончательный ответ. Итого, скорость нашей материальной точки в момент времени $t=2c$ составит 9 м/с.

Пример № 2

Материальная точка движется по закону:

[xleft( t right)=frac{1}{3}{{t}^{3}}-4{{t}^{2}}+19t-11]

где $x$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, измеренное с начала движения. В какой момент времени ее скорость была равна 3 м/с?

Взгляните, в прошлый раз от нас требовалось найти $v$ в момент времени 2 с, а в этот раз от нас требуется найти тот самый момент, когда эта скорость будет равна 3 м/с. Можно сказать, что нам известно конечное значение, а по этому конечному значению нам требуется найти исходное.

В первую очередь, вновь ищем производную:

[{x}’left( t right)=frac{1}{3}cdot 3{{t}^{2}}-4cdot 2t+19]

[{x}’left( t right)={{t}^{2}}-8t+19]

От нас просят найти, в какой момент времени скорость будет равна 3 м/с. Составляем и решаем уравнение, чтобы найти физический смысл производной:

[{{t}^{2}}-8t+19=3]

[{{t}^{2}}-8t+16=0]

[{{left( t-4 right)}^{2}}=0]

[t-4=0]

[t=4]

Полученное число означает, что в момент времени 4 с $v$ материальной точки, движущейся по выше описанному закону, как раз и будет равна 3 м/с.

Ключевые моменты

В заключении давайте еще раз пробежимся по самому главному моменту сегодняшней задачи, а именно, по правилу преобразования расстояние в скорость и ускорение. Итак, если нам в задаче прямо описан закон, прямо указывающий расстояние от материальной точки до точки отсчета, то через эту формулу мы можем найти любую мгновенную скорость (это просто производная). И более того, мы можем найти еще и ускорение. Ускорение, в свою очередь, равно производной от скорости, т.е. второй производной от расстояния. Такие задачи встречаются довольно редко, поэтому сегодня мы их не разбирали. Но если вы увидите в условии слово «ускорение», пусть оно вас не пугает, достаточно просто найти еще одну производную.

Надеюсь, этот урок поможет вам подготовиться к ЕГЭ по математике.

Смотрите также:

1. Не допускайте таких ошибок, когда видите график производной в задаче 6 из ЕГЭ по математике!
2. ЕГЭ 2022, задание 6. Касательная и квадратичная функция с параметром
3. Схема Бернулли. Примеры решения задач
4. Комбинаторика в задаче B6: средний тест
5. Как решать задачи про летающие камни?
6. B4: счетчики на электричество

Нахождение оптимального расстояния через производную

Вы можете заказать подробное решение вашей задачи здесь!!!

.

Задача. Группа соревнующихся пловцов направляется с лодки А в расположенный на берегу пункт В. Условия соревнования разрешают часть пути сделать по суше. Лодка стоит против пристани О на расстоянии ОА = a = 360 м; пункт назначения В расположен от пристани O на расстоянии ОВ = b = 420 м. Какой наилучший результат может показать участник соревнования, если он будет покрывать 90 м в минуту вплавь и 150 м в минуту бегом.

Всё схематически показано на рисунке.
Решение. Пусть пловец выходит на берег в точке М, находящейся на расстоянии ОМ = х от пристани. Достаточно рассмотреть изменение х в промежутке (0, b). Время t (в минутах), затрачиваемое на путь АМВ, равно:

Здесь а = 360, b = 420. Требуется найти наименьшее значение функции t в промежутке (0, b).
Имеем:

Решив уравнение:

найдём единственное значение переменной x:

Это значение лежит в рассматриваемом промежутке (0, b). Так как вторая производная:

в точке x=3/4a положительна, то в этой точке имеем минимум. Будучи единственным, этот минимум и даёт искомое наименьшее значение функции t:

Материалы по теме:

• Нахождение экстремумов функции
• Монотонные функции
• Промежутки выпуклости, точки перегиба…
• Возрастание, убывание, максимум и минимум функции

Загрузка…

Спецвыпуск

Решение задач с использованием производной

Решение задач с использованием производной

··· Решение задач: примеры, методы,
приёмы ···

А.Н.ДОЛГУШИН,
МОУ СОШ № 23 с УИОП,
г. Воскресенск, Московская обл.

dolgushin23fizika@yandex.ru

Решение задач с использованием
производной

В рамках авторского профильного курса
«Практикум решения физических задач»,
11-й класс.
Базовый уровень

Знать физику – значит уметь решать
задачи.

Э.Ферми

Основными целями и задачами
факультативного курса «Практикум решения
физических задач» являются: знакомство учащихся
с основными типами физических задач: расчётными,
качественными, графическими, исторического
содержания, технического содержания,
межпредметного характера, комбинированными,
задачами-оценками; формирование знаний, умений и
навыков решения физических задач, в том числе
повышенной сложности; ознакомление с разными
способами решения физических задач: логическим,
математическим (арифметическим, алгебраическим,
графическим, геометрическим) и
экспериментальным; разбор типовых заданий на
вступительных экзаменах в технические вузы (МЭИ,
МГТУ им. Н.Э.Баумана).

Подборка задач соответствует основным
темам школьного курса физики, где можно
использовать элемент математического анализа –
производную:

– «Кинематика»: если изменение
координаты задано уравнением вида x = x(t),
то производная первого порядка от координаты по
времени есть скорость, т.е. (t) = x‘(t), а производная
второго порядка от координаты по времени, или
производная первого порядка от скорости по
времени, есть ускорение, т.е. a(t) = x«(t)
= ‘ (t);

– «Импульс»: при определении импульса
по формуле p = m он определяется по скорости тела как
производной от координаты по времени.

– «Механические колебания»:
энергетический подход (метод производной)
позволяет вывести дифференциальные уравнения
второго порядка, описывающие процессы в
математическом и пружинном маятниках, затем
получить формулы для периодов колебаний, а также
рассчитать период колебаний сложных
колебательных систем;

– «Термодинамика»: использование
производной позволяет решать задачи на
нахождение экстремальных значений параметров в
циклах идеального газа;

– «Электромагнитная индукция»:
производная от магнитного потока по времени,
взятая с противоположным знаком (по правилу
Ленца), позволяет определить мгновенное значение
ЭДС, индуцируемой в замкнутом проводящем
контуре: _i
= –Ф‘ (t);

– «Постоянный ток»: производная
позволяет определить величину внешнего
сопротивления в цепи постоянного тока, при
которой полезная мощность принимает
максимальное значение;

– «Электромагнитные колебания»:
энергетический подход (метод производной)
позволяет вывести дифференциальное уравнение
второго порядка, описывающее процессы в
идеальном колебательном контуре, а затем
получить формулу Томсона;

– «Цепи переменного тока»:
производная позволяет установить разность фаз
между колебаниями электрического заряда на
обкладках конденсатора и силы тока в цепи с
ёмкостным сопротивлением;

– «Геометрическая оптика»: используя
принцип Ферма, можно вывести закон преломления
света.

Рассмотрим некоторые задачи.

Кинематика. Закон сохранения энергии

• [1]. Движение материальной точки
описывается уравнениями: x = 10 cos 3t, y
=10 sin 3t. [x] = см, [y] = см, [] = c^–1.
Определите скорость, ускорение и траекторию
точки.

Решение

– Скорость: ² = _x² + _y². Используя
механический смысл производной, после
преобразований получаем = 30 см/с.

– Ускорение: a² = a_x²
+ a_y². Используя механический смысл
производной, после преобразований получаем a =
90 см/с².

– Траектория: уравнение
траектории движущейся точки определяется
зависимостью: y = f(x), т.е. позволяет
исключить переменную t. Целесообразно обе
части исходных уравнений движения материальной
точки возвести в квадрат, а затем сложить.
Используя основное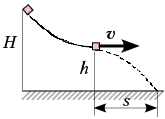 тригонометрическое
тождество cos² + sin²
= 1, после преобразований получаем x² + y²
= 100, что соответствует уравнению окружности
радиусом 10 см с центром в точке с координатами (0;
0).

• [2]. Небольшое тело соскальзывает
без начальной скорости с вершины гладкой горки
высотой H, имеющей горизонтальный трамплин
высотой h. При какой высоте h тело пролетит
наибольшее расстояние s по горизонтали? Чему
равно это расстояние?

Решение

Связываем нулевой уровень с
поверхностью Земли, используем закон сохранения
механической энергии: mgH = mgh + m²/2. С момента
отрыва тела от трамплина используем
кинематические уравнения движения тела,
брошенного горизонтально:

h = gt²/2 – по вертикали;

= s/t
– по горизонтали, т.к. g_x = 0.

Время падения по вертикали совпадает со
временем движения тела по горизонтали. В итоге
получаем выражение для скорости в момент отрыва
тела от трамплина: – которое подставляем в выражение
для закона сохранения энергии. После
преобразования получаем зависимость

Далее исследуем полученную
зависимость, находим производную по переменной h
и приравниваем её к нулю (s‘_h = 0):

т.е. расстояние s будет наибольшим
при h = H/2, когда производная обращается в нуль:
4H – 8h = 0.

Подставляя полученное выражение для
высоты трамплина h = H/2 в формулу для s,
получаем s = H.

Импульс

• [3]. Движение материальной точки в
единицах СИ описывается уравнением x = 5 – 8t +
4t². Приняв массу точки равной 2 кг,
найдите её импульс через 2 с и через 4 с от начала
отсчёта времени, а также силу, вызвавшую это
изменение импульса.

Решение

Уравнение скорости с учётом
механического смысла производной имеет вид: = –8 + 8t. Тогда
импульс через 2 с от начала отсчёта времени: p₂
= 16 кг · м/с, а импульс через 4 с: p₄ = 48 кг ·
м/с.

Сила, которая вызывает это изменение
импульса, определяется с учётом второго закона
Ньютона в импульсной форме: F = (p₄ – p₂)/t, где t = 2 с. Численно
получаем: F = 16 Н.

Механические колебания

• [1]. Материальная точка массой m движется
вдоль оси X по закону x = A sint, где A, – некоторые постоянные, t
– время. Определите модуль изменения импульса
материальной точки с момента времени t = t₁
до момента времени t = t₂.

Решение

По механическому смыслу производной
скорость определяется выражением: =Acost. Тогда модуль изменения импульса
определяется выражением:

p = mA|cost₂ – cost₁|.

• [ЕГЭ]. Тело, подвешенное на
пружине, совершает свободные гармонические
колебания частотой . С какой частотой происходит изменение
кинетической энергии тела?

Решение

Пусть координата тела изменяется по
закону x = x₀sint. Используя механический смысл
производной, находим закон изменения скорости: = x‘ = x₀cost. Тогда
кинетическая энергия тела W_k = m²/2 = (mx₀²²cos²t)/2. С учётом
тригонометрического тождества cos²t = (1 +
+ cos2t)/2,
получаем:

W_k = mx₀²²(1 + cos2t)/4,

следовательно, изменение кинетической
энергии колеблющегося тела происходит с
частотой 2.

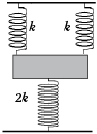
• [2]. Брусок подвешен за края к
потолку на двух одинаковых пружинах жёсткостью k
каждая и притянут к полу пружиной жёсткостью 2k.
Масса бруска m. Определите период колебаний
бруска.

Решение

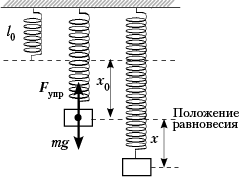
Важно отметить, что сила тяжести,
действующая на брусок, постоянна, поэтому на
период колебаний не влияет. Для доказательства
рассмотрим груз, подвешенный на вертикальной
пружине. В положении равновесия справедливо
равенство: mg = kx₀. В процессе колебаний,
для произвольного момента времени (например, при
дополнительном растяжении на величину x)
второй закон Ньютона в скалярной форме имеет вид:
–k(x₀ + x) + mg = mx«.

После преобразований получаем
уравнение, в котором исключена сила тяжести: –kx
= mx«. Далее приходим к
дифференциальному уравнению второго порядка,
описывающему колебания пружинного маятника с
вертикальной пружиной:

Полученный результат показывает, что
постоянная сила тяжести не влияет на период
колебаний.

С учётом закона сохранения
механической энергии в любой момент времени W_k
+ W_упр = const, т.е.

Далее находим производную от обеих
частей:

Термодинамика. Газовые законы

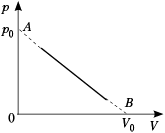
• [4]. Состояния идеального газа в
количестве =
1 моль в ходе некоторого процесса изображаются
точками, лежащими на отрезке прямой AB: V_A =
0, p_A = p₀; V_B = V₀, p_B
= 0. Найдите зависимость температуры газа от
объёма и определите максимальную температуру
газа в ходе такого процесса.

Решение

В соответствии с графиком составляем
уравнение прямой: y = –kx + b, где y = p, x = V, b =
p₀;

Заменяя переменные, получаем:

Зная уравнения Клапейрона–Менделеева
pV = RT, находим
зависимость температуры идеального газа от
объёма:

Находим производную и приравниваем её
нулю:

Решая последнее уравнение, получаем,
что температура максимальна при V = V₀/2.
Подставляя это значение в выражение для
температуры, после преобразований получаем

Электромагнитная индукция

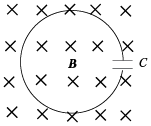
• [2]. Проводящий контур площадью S
= 400 см², в который включён конденсатор
ёмкостью C = 10 мкФ, расположен в однородном
магнитном поле перпендикулярно линиям индукции.
Магнитная индукция возрастает по закону
B = (2 + 5t)10^–2 Тл, где t – время в
секундах. Определите энергию электрического
поля конденсатора. Укажите, какая обкладка
конденсатора заряжается положительно.

Решение

Изменение магнитной индукции приводит
к появлению в цепи электрического тока (между
обкладками конденсатора – диэлектрик),
конденсатор начнёт заряжаться, следовательно,
между его обкладками возникнет электрическое
поле энергией W = CU²/2 = C_i²/2, где
_i = –Ф_t‘
= –(BScos)_t‘
– ЭДС, наводимая между обкладками
конденсатора. Площадь контура постоянна, = B^n =
0° (по условию),
cos 0° = 1, поэтому:

_i =
–S · B_t‘ = –4 · 10^–2 · 5 · 10^–2
= –2 · 10^–3 (В).

Подставляя найденное значение в
выражение для энергии электрического поля
заряженного конденсатора, получаем W = 20 ·
10^–12 Дж.

Чтобы определить, какая из обкладок
конденсатора зарядится положительно, используем
правило Ленца: т.к., по условию задачи, величина
магнитной индукции увеличивается, то вектор
магнитной индукции внешнего магнитного поля B
направлен противоположно вектору магнитной
индукции магнитного поля B_i
наведённого в контуре тока. Зная направление B_i
и правило правой руки (правого винта), определяем
направление индукционного тока: против часовой
стрелки. Поскольку за направление
электрического тока принимают упорядоченное
движение положительно заряженных частиц, то
приходим к выводу, что нижняя обкладка
конденсатора заряжается положительно.

• [5]. Рамка площадью S = 100 см²
расположена перпендикулярно однородному
магнитному полю, индукция которого изменяется по
закону B = ct³ – at², где c = 1
Тл/с², t – время в секундах, a = 3 Тл/с³.
Сопротивление рамки R = 10^–2 Ом. В какой
момент времени индукционный ток максимален? Чему
он равен?

Решение

Найдём зависимость индукционного тока
от времени: I_i = _i/R, где _i = –Ф_t‘
= –(BScos)_t‘
= –SB_t‘ = –S(ct³ – at²)_t‘
= –S(3ct² – 2at), т.е.
I_i = –S(3ct² – 2at)/R.

Исследуем полученную зависимость, т.е.
найдём производную и приравняем её нулю:

При индукционный
ток принимает максимальное значение:

Находим числовые значения: t = 1 с, I_i
max = 3 А.

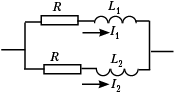
• [3]. В цепи, представленной на
рисунке, L₁ = 0,02 Гн, L₂ = 0,01 Гн.
Силы токов изменяются во времени по законам: I₁
= 0,2 + 10t, I₂ = 0,1 + 10t. Найдите
сопротивление R. Величины токов заданы в СИ.

Решение

При параллельном соединении участков
цепи:

Следовательно:

Геометрическая оптика

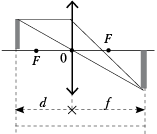
• [1]. На каком расстоянии d_min
надо поместить предмет от собирающей линзы с
фокусным расстоянием F, чтобы расстояние от
предмета до его действительного изображения
было наименьшим?

Решение

Выполним рисунок. Используем формулу
тонкой линзы с учётом правила знаков: из которой выразим
расстояние от оптического центра собирающей
линзы до предмета:

Расстояние от предмета до его действительного
изображения
Исследуем последнее выражение, для чего найдём
производную от s по d и приравняем её нулю:

Из равенства d² – 2dF = 0
следует d_min = 2F. При этом значении d
расстояние от предмета до его действительного
изображения будет наименьшим: s_min = 4 F.

Литература

1. Дмитриев С.Н., Васюков В.И., Струков
Ю.А. Физика. Сборник задач для поступающих в
вузы: Изд. 5-е, доп. – М.: Демиург-Арт, 2001.

2. Славов А.В., Спивак В.С., Цуканов
В.В. Сборник задач по физике: Учеб. пособие для
довуз. подгот.: Под ред. А.В.Славова: Изд 7-е, испр. и
доп. – М.: Издательство МЭИ, 2006.

3. Рымкевич А.П. Физика. Задачник.
10–11 кл. – М.: Дрофа, 2006.

4. Баканина Л.П., Белонучкин В.Е., Козел
С.М. Сборник задач по физике для 10–11 классов с
угл. изучением физики: Под ред. С.М.Козела. – М.:
Вербум, 2003.

5. Турчина Н.В. Физика: 3800 задач для
школьников и поступающих в вузы. – М.: Дрофа, 2000.

Ещё два примера решения задач с помощью
производной приведены в рубрике «Дополнительные
материалы» к № 12 на сайте газеты http://fiz.1september.ru

Вадим Муранов, победитель всероссийского конкурса «Учитель года», преподаватель физики с 24-летним опытом работы.

Добрый день! Рад приветствовать всех на нашем канале по физике от ЕГЭ-Студии.

Сегодня мы запускаем наш сериал! Да-да, именно сериал, не удивляйтесь. И первый сезон этого сериала называется «Производная». В первой пилотной серией нашего сезона вы узнаете производной в кинематике. В главных ролях: физика и математика, а в эпизодах – я, Муранов Вадим Александрович, учитель физики, решаю с вами задачи.

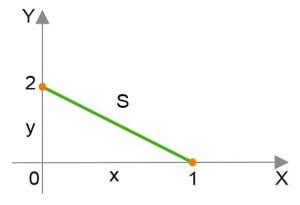
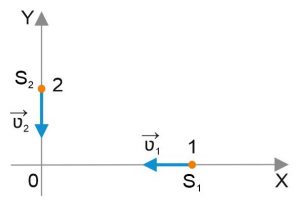
«Точки 1 и 2 движутся по осям х и у к началу координат. В момент t=0 точка 1 находится на расстоянии S₁=10 см, а точка 2 на расстоянии S₂=5 см от начала координат. Первая точка движется со скоростью V₁=2 см/с, а вторая V₂=4 см/с. Каково наименьшее расстояние между ними в процессе движения?»

Изобразим нашу ситуацию по кинематике в соответствии с условием задачи на рисунке

S1 = 10 см S2 = 5 см V1 = 2 см/с V2 = 4 см/с Smin = ?

Оси х и у, вдоль которых движутся два тела, две материальные точки

Необходимо определить в какой момент времени и каким будет минимальное расстояние между этими точками в процессе их движения. Расстояние между точками определяется следующим образом

И вы, наверное, уже догадались, что это расстояние S между точками мы будем находить по теореме Пифагора. Но главное здесь будет – это нахождение минимального расстояния между телами, то есть с помощью производной. Эта задача на нахождение минимального значения некой функции. В математике она решается довольно часто, в физике бывает реже, но тем не менее это очень важное умение. Если вы его освоите, то вы будете на шаг ближе к настоящей, реальной физике, чего мне очень бы и хотелось.

Сначала мы должны составить уравнение движения каждой точки.

Уравнением движения первой точки будет выглядеть следующим образом: движение равномерное, без ускорения, вектор скорости направлен против оси х, это значит, что проекция скорости V₁ на ось х будет отрицательной x = S₁ — V₁ × t

Запишем уравнение движения второй материальной точки. Вектор ее скорости, как вы видите, также направлен против оси у, значит, проекция скорости будет отрицательной. Ускорения нет, и это значит, что третьего слагаемого не будет в этих уравнениях y = S₂ — V₂ × t

Система уравнений движения материальных точек записана

⎰x = S₁ — V₁ × t
⎱y = S₂ — V₂ × t

Все числовые данные представлены в сантиметрах и сантиметрах в секунду, значит, нет смысла переводить эти значения в метры и метры в секунду. Оставим их в тех единица, которые нам были даны, тогда ответ мы тоже получим в сантиметрах.

В числовом виде уравнения движения будут выглядеть следующим образом

⎰x = S₁ — V₁ × t = 10 — 2 × t
⎱y = S₂ — V₂ × t = 5 — 4 × t

Как определить расстояние между точками, мы с вами уже обсудили, по теореме Пифагора

S = √ x² + y²

Вместо х и у мы подставим те уравнения движения, которые мы с вами составили

S = √ (10 — 2 × t)² + (5 — 4 × t)²

Раскроем скобки, приведем подобные слагаемые

S = √ (10 — 2 × t)² + (5 — 4 × t)² = √ 100 — 40 × t + 4 × t² + 25 — 4 × t + 16 × t² = √ 125 — 80 × t + 20 × t²

Получили выражение для расстояния между нашими точками. Это расстояние меняется и является функцией времени по сути получили с вами зависимость S(t). Но дело в том, что подкоренное выражение – это обычная квадратичная функция, и если оно будет минимальным, то и само значение S также будет минимальным, поэтому удобнее будет рассмотреть в нашей задаче не S(t), а S²(t), чтобы квадратный корень нам не очень сильно мешал в нахождении производной.

Тогда S²(t) = 125 — 80 × t + 20 × t²

Необходимо найти минимальное значение этой функции. Да, конечно, вы можете обойтись и без знаний о производной, вы можете вспомнить, что это парабола, ветвями вверх или вниз и т. д. Но мы с вами сделаем по-другому, мы найдем производную этой функции (S²)′ = — 80 + 40 × t. Приравниваем к нулю, т. к. условие экстремума ƒ′(x) = 0. Это математическая запись, в нашем случае (S²)′ = 0.

Из этого равенства — 80 + 40 × t = 0 мы находим, что минимальное значение функции S² будет при t = 2 с

(S²)′ = 0 ⇒ t = 2 с

Нам остается толь выяснить, чему будет равно S. Для этого надо 2 с подставить в уравнения движения наших тел. В итоге получаем x = 10 — 2 × 2 = 6 см, y = 5 — 4 × 2 = — 3 см.

Такие будут значения х и у, а S мы находим по теореме Пифагора и получаем S = √ 6² + 3², S ≈ 6,7 см.

Это и есть минимальное расстояние между точками в нашей задаче, которые мы нашли при помощи вычисления производной и приравнивания этой производной к нулю. Это общее правило нахождения максимального и минимального значения: вычисляем производную данной функции, приравниваем ее к нулю, находим значение переменной, при которой эта производная обращается в ноль, далее по этому значению определяем значение самой функции, оно и будет минимальным или максимальным. Вот таким образом в кинематике можно применить знание о производной и решить задачу на максимальное и минимальное значение. В данном случае мы определили, что минимальным расстояние между телами будет 6,7 см.

Итак, вы посмотрели первую нашего сериала «Производная в кинематике». Приходите к нам на наши занятия, смотрите наши трансляции, заходите на наш канал, смотрите наш сериал дальше. Во второй серии вас ожидает производная в молекулярно-кинетической теории.

Все видео по физике

Учитель математики Е.И.Акимова

«Геометрический и физический смысл производной при решении прикладных задач»

2017г.

Геометрический смысл производной

Построим произвольный график некой функции y = f (x)  на координатной плоскости, построим касательную в точке x_о, обозначим угол между прямой о осью ox как α (альфа)

Из курса алгебры известно, что уравнение прямой имеет вид:

То есть производная функции  y = f(x) в точке x₀ равна угловому коэффициенту касательной:

А угловой  коэффициент в свою очередь равен тангенсу  угла α (альфа), то есть:

Угол α (альфа) может быть меньше, больше 90 градусов или равен нулю. 

Проиллюстрируем, два случая:

1.    Угол наклона касательной больше 90 градусов (тупой угол).

2.    Угол наклона касательной равен нулю градусов (касательная параллельна оси ох).

 

То есть задачи, в которых дан график функции, касательная к этому графику в определённой точке, и требуется найти производную в точке касания, сводятся к нахождению углового коэффициента касательной (либо тангенса угла наклона касательной, что одно и тоже).

Ниже рассмотрим  решение таких задач через нахождение тангенса угла между касательной и осью абсцисс (осью ох), ещё один способ решения (нахождение производной через угловой коэффициент) рассмотрим в недалёком будущем. Также будем рассматривать задачи, где требуется знание свойств производной для чтения графика функции. Не пропустите! 

Обратите внимание, что на координатной плоскости обозначены две точки через которые проходит касательная – это очень важный момент (можно сказать ключевой в этих задачах). Что ещё потребуется — это знание формулы приведения для тангенса тупого угла.

Задача.

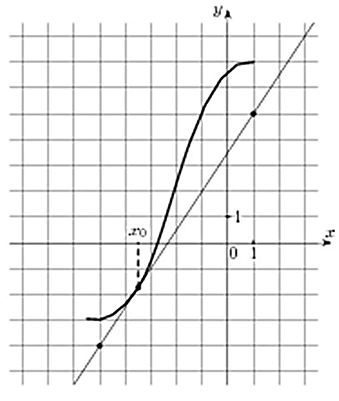
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции y = f(x)  в точке  x₀.

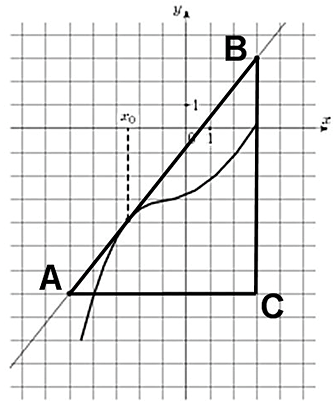
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Для того, чтобы найти тангенс этого угла, построим прямоугольный треугольник, где отрезок ограниченный двумя точками на графике, будет являться гипотенузой, а катеты параллельны осям.  В данной задаче это точки  (–5; –4), (1; 5).

Напомню: тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.

Катеты определяем по числу клеток.

Угол наклона касательной к оси абсцисс равен углу BAC, так как катет АС параллелен оси ох. Значит

Ответ: 1,5

Задача

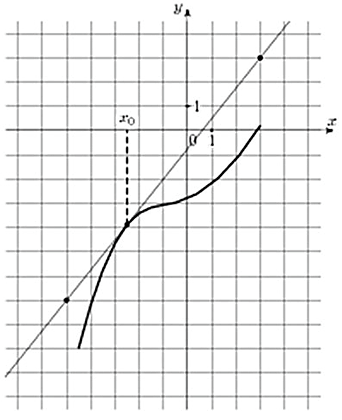
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции y = f(x)  в точке  x₀.

Задача аналогична предыдущей. Так же строим прямоугольный треугольник, где отрезок ограниченный двумя точками на графике, будет являться гипотенузой. В данной задаче это точки  (–5; –7), (3; 3).

Катеты также определяем по числу клеток.

Угол наклона касательной к оси абсцисс равен углу ВАС, так как катет АС параллелен оси ох. Значит

Ответ: 1,25

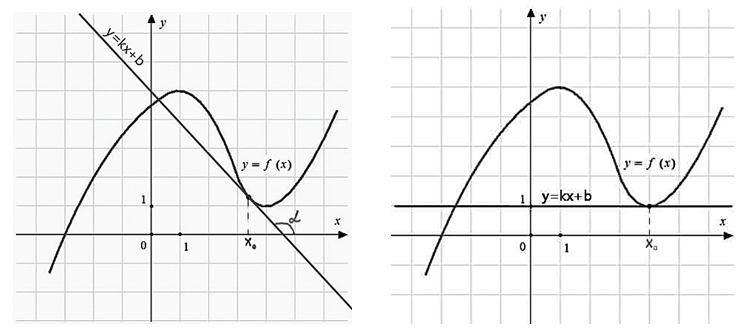
Задача.

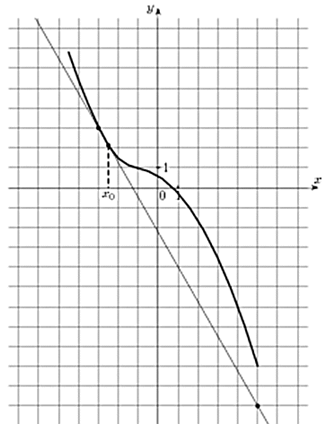
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции y = f(x)  в точке  x₀.

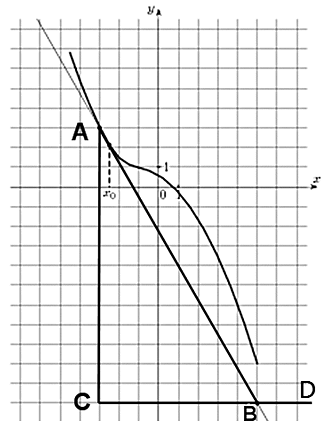
Строим прямоугольный треугольник, где отрезок ограниченный двумя точками на графике, будет являться гипотенузой. В данной задаче это точки  (–3; 3) и  (5; 11).  Из точки (5;11) построим продолжение катета так, чтобы  получился внешний угол.

Так как CD параллельна оси ох, то угол ABD равен углу наклона касательной к оси ох.  Таким образом, мы будем вычислять тангенс угла ABD. Отметим, что он больше 90 градусов, поэтому здесь необходимо воспользоваться формулой приведения для тангенса:

Значит

*Длины катетов считаем по количеству клеток.

Ответ: -1,75

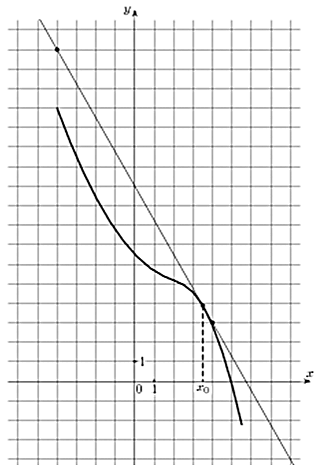
Задача.

На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции y = f(x)  в точке  x₀.

Решите задачу самостоятельно.

Ответ: -1,75

Задача.

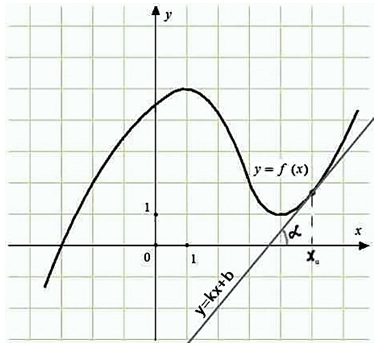
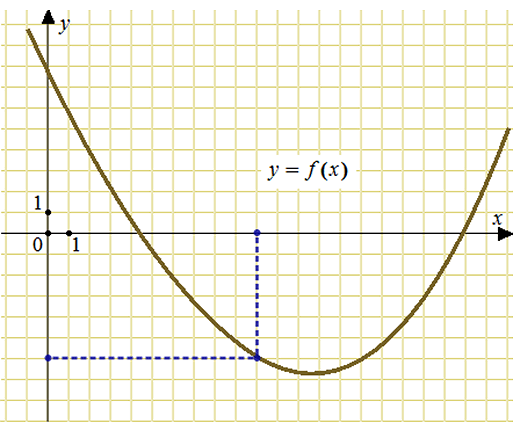
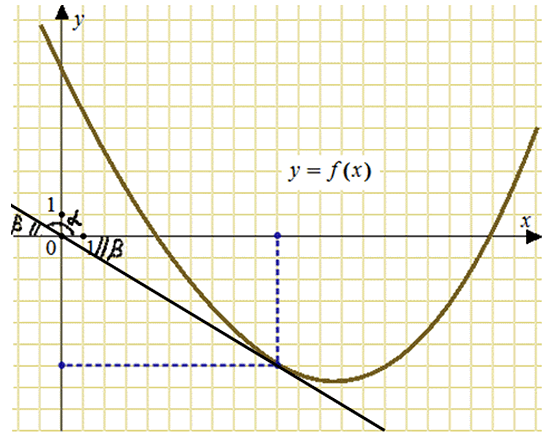
На рисунке изображен график функции y = f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 10. Найдите значение производной функции в точке х₀ = 10.

Построим касательную, проходящую через начало координат и точку графика с абсциссой равной 10. Обозначим угол наклона касательной как альфа, а смежный с ним угол как бета.

Значение производной в точке х₀ = 10 равно тангенсу угла наклона касательной к оси абсцисс. То есть, для нахождения производной достаточно вычислить тангенс  угла  альфа. Воспользуемся формулой приведения:

Тангенс угла бета можем найти из прямоугольного треугольника, катеты которого равны 6 и 10:

Ответ: — 0,6

На первый взгляд задачи, связанные с использованием производной входящие в ЕГЭ по математике, довольно разнообразны. Но на самом деле для их решения нужно изучить совсем небольшой «кусочек» теории.

Физический смысл производной при решении прикладных задач

Задача.

Материальная точка движется прямолинейно по закону

x (t) = (1/6) t² + 5t + 28

где x — расстояние от точки отсчета в метрах,  t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 6 м/с?

Найдем закон изменения скорости:

Для того, чтобы найти, в какой момент времени t скорость была равна 3 м/с,  необходимо решить уравнение:

Ответ: 3

Материальная точка движется прямолинейно по закону   x (t) = t² – 7t – 20

где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 5 c.

Физический смысл производной это скорость (скорость движения, скорость изменения процесса, скорость работы и т.д.)

Найдем закон изменения скорости:  v (t) = x′(t) = 2t – 7 м/с.

При t = 5 имеем:

Ответ: 3

Задача.

Материальная точка движется по закону:

x(t)=−15t5+t4−t3+5tx(t)=−15t5+t4−t3+5t

где xx — расстояние от точки отсчета в метрах, tt — время в секундах, прошедшее с начала движения. Найдите скорость точки (в м/с) в момент времени t=2ct=2c.

Это означает, что у нас есть функция, задающая расстояние, а нужно посчитать скорость в момент времени t=2ct=2c. Другими словами, нам нужно найти vv, т.е.

v=S′=x′(2)v=S′=x′(2)

Вот и все, что нам нужно было выяснить из условия: во-первых, как выглядит функция, а во-вторых, что от нас требуется найти.

Давайте решать. В первую очередь, посчитаем производную:

x′(t)=−15⋅5t4+4t3−3t2+5x′(t)=−15⋅5t4+4t3−3t2+5

x′(t)=−t4+4t3−3t2+5x′(t)=−t4+4t3−3t2+5

Нам требуется найти производную в точке 2. Давайте подставим:

x′(2)=−24+4⋅23−3⋅22+5=x′(2)=−24+4⋅23−3⋅22+5=

=−16+32−12+5=9=−16+32−12+5=9

Вот и все, мы нашли окончательный ответ. Итого, скорость нашей материальной точки в момент времени t=2ct=2c составит 9 м/с.

Задача.

Материальная точка движется по закону:

x(t)=13t3−4t2+19t−11x(t)=13t3−4t2+19t−11

где xx — расстояние от точки отсчета в метрах, tt — время в секундах, измеренное с начала движения. В какой момент времени ее скорость была равна 3 м/с?

Взгляните, в прошлый раз от нас требовалось найти vv в момент времени 2 с, а в этот раз от нас требуется найти тот самый момент, когда эта скорость будет равна 3 м/с. Можно сказать, что нам известно конечное значение, а по этому конечному значению нам требуется найти исходное.

В первую очередь, вновь ищем производную:

x′(t)=13⋅3t2−4⋅2t+19x′(t)=13⋅3t2−4⋅2t+19

x′(t)=t2−8t+19x′(t)=t2−8t+19

От нас просят найти, в какой момент времени скорость будет равна 3 м/с. Составляем и решаем уравнение, чтобы найти физический смысл производной:

t2−8t+19=3t2−8t+19=3

t2−8t+16=0t2−8t+16=0

(t−4)2=0(t−4)2=0

t−4=0t−4=0

t=4t=4

Полученное число означает, что в момент времени 4 с vv материальной точки, движущейся по выше описанному закону, как раз и будет равна 3 м/с.

Ключевые моменты

В заключении давайте еще раз пробежимся по самому главному моменту сегодняшней задачи, а именно, по правилу преобразования расстояние в скорость и ускорение. Итак, если нам в задаче прямо описан закон, прямо указывающий расстояние от материальной точки до точки отсчета, то через эту формулу мы можем найти любую мгновенную скорость (это просто производная). И более того, мы можем найти еще и ускорение. Ускорение, в свою очередь, равно производной от скорости, т.е. второй производной от расстояния. Такие задачи встречаются довольно редко, поэтому сегодня мы их не разбирали. Но если вы увидите в условии слово «ускорение», пусть оно вас не пугает, достаточно просто найти еще одну производную.