Как найти расстояние до линейного многообразия - Исправление недочетов и поиск решений вместе с Examum.ru

Содержание

English version

Вычисление расстояний между геометрическими объектами

Расстояние между точками $ X=(x_{1},dots,x_n) $ и $ Y=(y_{1},dots,y_n) $ из пространства $ mathbb R^{n}_{} $ понимается в стандартной евклидовой метрике:
$$ sqrt{(x_1-y_1)^2+dots+(x_n-y_n)^2} . $$
Для согласования дальнейших обозначений будем всегда считать точки пространства $ mathbb R^{n}_{} $ векторами-столбцами.

Линейные многообразия

Расстояние от точки до линейного многообразия (плоскости)

Задача. Найти расстояние от точки $ X_{0} in {mathbb R}^{n} $ до линейного многообразия (плоскости) $ mathbb M $ в $ {mathbb R}^{n} $, заданного системой уравнений
$$
left{
begin{array}{ccc}
c_{11}x_1+c_{12}x_2+dots+c_{1n}x_n &=& h_1 \
dots & & dots \
c_{m1}x_1+c_{m2}x_2+dots+c_{mn}x_n &=& h_m
end{array}
right.
$$
или, в матричном виде
$$
CX={mathcal H} quad npu quad
C=left(
begin{array}{cccc}
c_{11}& c_{12} & dots & c_{1n} \
dots & & & dots \
c_{m1}& c_{m2} & dots & c_{mn}
end{array}
right)_{mtimes n} ,
{mathcal H} =left(
begin{array}{c}
h_1 \ vdots \ h_m
end{array}
right),
X=left(
begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)
$$
При этом предполагается, что $ mle n_{} $ и что ранг матрицы $ C_{} $ равен $ m_{} $, то есть система уравнений совместна и определяемое ею многообразие в $ {mathbb R}^{n} $ является $ (n-m)_{} $-мерным.

Теорема 1. [1]. Составим квадратную матрицу порядка $ m+1_{} $:

$$
M=left(
begin{array}{cc}
Ccdot C^{top} & CX_0- {mathcal H} \
(CX_0- {mathcal H})^{top} & 0
end{array}
right)
$$
Расстояние от точки $ X_{0} $ до линейного многообразия $ mathbb M $ вычисляется по формуле
$$
d= sqrt{-frac{det M}{det(Ccdot C^{top})}} .
$$

Доказательство

☞

ЗДЕСЬ.

Расстояние от точки $ X_{0}=(x_{10},dots,x_{n0})^{top} $ до гиперплоскости (или, в случае $ n=2 $, прямой)

$$ c_1x_1+dots+c_nx_n= h $$
равно
$$ d= frac{|c_1x_{10}+dots+c_nx_{n0}-h|}{sqrt{c_1^2+dots+c_n^2}} . $$
Ближайшая к $ X_0 $ точка гиперплоскости:
$$
X_{ast}=X_0- frac{c_1x_{10}+dots+c_nx_{n0}-h}{c_1^2+dots+c_n^2} left(begin{array}{c} c_1 \ vdots \ c_n end{array} right) , .
$$

Пусть теперь линейное многообразие (плоскость) задано параметрически
$$
mathbb M= { Y_0+lambda_1 Y_1+dots+lambda_k Y_k quad mid quad
{lambda_1,dots,lambda_k} subset {mathbb R} }
$$
при фиксированных столбцах
$$ {Y_0,Y_1,dots,Y_k }subset {mathbb R}^n . $$
Предположим, что эти столбцы линейно независимы. Составим из них матрицы
$$
L=left[ Y_1|dots|Y_k right]_{ntimes k} quad u quad tilde L = left[ Y_1|dots|Y_k| X_0-Y_0 right]_{ntimes (k+1)}
$$
(здесь $ |_{} $ означает конкатенацию).

Теорема 2. Расстояние $ d_{} $ от точки $ X_{0} $ до линейного многообразия $ mathbb M $ вычисляется по формуле

$$
d=sqrt{frac{det(tilde L^{top}cdot tilde L)}{det( L^{top}cdot L)}} .
$$

Доказательство. Утверждение теоремы 2 является частным случаем общего результата о вычислении расстояния от точки до линейного многообразия в евклидовом пространстве.

♦

На основании свойств определителя Грама, матрица $ L^{top}cdot L_{} $ — при сделанном предположении о линейной независимости $ {Y_1,dots,Y_{k} } $ —
будет положительно определенной, а матрица $ tilde L^{top}cdot tilde L_{} $ при любых столбцах
$ {Y_0,Y_1,dots,Y_{k} } $ имеет неотрицательный определитель.

Теорема 3. Ближайшая к точке $ X_0 $ точка многообразия $ mathbb M_{} $ (проекция точки на многообразие) определяется по формуле

$$
X_{ast}=Y_0+ L(L^{top}cdot L_{})^{-1} L^{top} (X_0-Y_0) , .
$$

Доказательство

☞

ЗДЕСЬ.

Пример. Найти расстояние от точки $ X_{0}=(1,1,1,1)^{top} $ до плоскости

$$
left{begin{array}{rrrrc}
3x_1&+x_2&-x_3&+x_4&=1 \
x_1 & -2x_2&+x_3&+2x_4&=2.
end{array}
right.
$$

Решение. 1-й способ: применение теоремы 1. Имеем:
$$
C=left( begin{array}{rrrr}
3 & 1 & -1 & 1 \
1 & -2 & 1 & 2
end{array}
right), {mathcal H}= left( begin{array}{r} 1 \ 2 end{array} right),
$$
$$
Ccdot C^{top} =
left( begin{array}{cc}
12 & 2 \
2 & 10
end{array}
right), CX_0=left( begin{array}{r} 4 \ 2 end{array} right),
CX_0-{mathcal H}=left( begin{array}{r} 3 \ 0 end{array} right) ,
$$
$$
frac{left| begin{array}{ccc}
12 & 2 & 3 \
2 & 10 & 0 \
3 & 0 & 0
end{array}
right|}{left| begin{array}{cc}
12 & 2 \
2 & 10
end{array}
right|}=frac{-90}{116}=-frac{45}{58} .
$$

2-й способ: применение теоремы 2. Общее решение системы уравнений, задающей плоскость:
$$ x_3=frac{5}{3}x_1+frac{4}{3}x_2, x_4=1-frac{4}{3}x_1+frac{1}{3}x_2 . $$
Таким образом, плоскость может быть представлена в параметрическом виде
$$
Y_0+lambda_1 Y_1 + lambda_2 Y_2 quad npu quad Y_0 = left( begin{array}{r} 0 \ 0 \ 0 \ 1 end{array}
right), Y_1=left( begin{array}{r} 0 \ 3 \ 4 \ 1 end{array}
right), Y_2=left( begin{array}{r} 3 \ 0 \ 5 \ -4 end{array}
right) .
$$
Имеем:
$$
L=
left( begin{array}{rr}
0 & 3 \
3 & 0 \
4 & 5 \
1 & -4
end{array}
right), tilde L =left( begin{array}{rrr}
0 & 3 & 1 \
3 & 0 & 1 \
4 & 5 & 1 \
1 & -4 & 0
end{array}
right),
frac{left| begin{array}{ccc}
26 & 16 & 7 \
16 & 50 & 8 \
7 & 8 & 3
end{array}
right|}{left| begin{array}{cc}
26 & 16 \
16 & 50
end{array}
right|}=frac{810}{1044}=frac{45}{58} .
$$
Координаты ближайшей точки к $ X_{0} $:
$$
X_{ast}= left(begin{array}{c} 1 \ 1 \ 1 \ 1 end{array}right)+left( begin{array}{rr}
0 & 3 \
3 & 0 \
4 & 5 \
1 & -4
end{array}
right)left( begin{array}{ccc}
26 & 16 \
16 & 50 \
end{array}
right)^{-1}
left(begin{array}{rrrr}
0 & 3 & 4 & 1 \
3 & 0 & 5 & -4
end{array}
right)left(begin{array}{c} 1 \ 1 \ 1 \ 0 end{array}right)=frac{1}{58}
left(begin{array}{c} 16 \ 37 \ 76 \ 49 end{array}right) , .
$$

Ответ. $ d=sqrt{45/58} approx 0.8808303295 $.

Расстояние между линейными многообразиями (плоскостями)

Пусть линейные многообразия в $ {mathbb R}^{n} $ заданы параметрически
$$
mathbb M_1={ X_0+ lambda_1 X_1+dots + lambda_k X_k mid {lambda_1,dots,lambda_k } subset mathbb R } ;
$$
$$
mathbb M_2={ Y_0+mu_1Y_1+dots+mu_{ell}Y_{ell} mid {mu_1,dots,mu_{ell} } subset mathbb R }
$$
при фиксированных столбцах
$$ {X_0,X_1,dots,X_k,Y_0,Y_1,dots,Y_{ell}}subset {mathbb R}^n . $$
Составим из этих столбцов матрицы
$$
P=left[ X_1|dots|X_k| Y_1|dots | Y_{ell} right]_{ntimes (k+ell)} quad u quad tilde P = left[ X_1|dots|X_k| Y_1|dots | Y_{ell}| X_0-Y_0 right]_{ntimes (k+ell+1)}
$$
(здесь $ |_{} $ означает конкатенацию).

Теорема. Расстояние между линейными многообразиями $ mathbb M_1 $ и $ mathbb M_2 $ вычисляется по формуле

$$
d=sqrt{frac{det(tilde P^{top}cdot tilde P)}{det( P^{top}cdot P)}} .
$$

На основании свойств определителя Грама имеем:

$$
det (P^{top}cdot P) > 0 quad iff quad mbox{ столбцы } {X_1,dots,X_k,Y_1,dots,Y_{ell} } mbox{ линейно независимы};
$$
$$ det(tilde P^{top}cdot tilde P) ge 0 quad mbox{ при } forall {X_0,X_1,dots,X_k,Y_0,Y_1,dots,Y_{ell} } .
$$

Пример. [2]. Найти расстояние между плоскостями

$$
left( begin{array}{r} 89 \ 37 \ 111 \ 13 \54 end{array}
right) + lambda_1 left( begin{array}{r} 1 \ 1 \ 0 \ -1 \ -1 end{array}
right) + lambda_2 left( begin{array}{r} 1 \ -1 \ 0 \ -1 \ 1 end{array}
right) quad mbox{ и } quad
left( begin{array}{r} 42 \ -16 \ -39 \ 71 \3 end{array}
right) + mu_1 left( begin{array}{r} 1 \ 1 \ 0 \ 1 \ 1 end{array}
right) + mu_2 left( begin{array}{r} 1 \ -1 \ 0 \ 1 \ -1 end{array}
right) .
$$

Решение.
$$
P^{top}cdot P=4cdot E_{4 times 4}, quad
tilde P^{top}cdot tilde P=
left(begin{array}{ccccc}
4 & 0 & 0 & 0 & 107 \
0 & 4 & 0 & 0 & 103 \
0 & 0 & 4 & 0 & 93\
0 & 0 & 0 & 4 & -115 \
107 & 103 & 93 & -115 & 33483
end{array}
right) .
$$

Ответ. $ d=150_{} $.

Квадратичные многообразия (квадрики)

В последующих пунктах, касающихся вычисления расстояний между геометрическими объектами, хотя бы один из которых представлен квадратным уравнением, используется следующая идеология решения. Первоначальной целью ставится построение уравнения расстояний, т.е. алгебраического уравнения от одной переменной, среди корней которого находится квадрат искомого расстояния. После нахождения этого корня, координаты ближайшей точки (или пары ближайших точек) находятся в виде рациональных функций от величины квадрата расстояния. Таким образом, мы «переворачиваем» традиционную схему решения оптимизационных задач:

стационарные точки

$ rightarrow $

критические значения

Такая реверсия традиционного подхода оправдана, с одной стороны, тем, что задача сводится к одномерной — поиску корней полинома от одной переменной. Причем нас будет интересовать, как правило, единственный корень этого полинома — минимальный положительный. С другой стороны, уравнение расстояний удается построить в результате чисто алгебраической процедуры: конечного числа элементарных алгебраических операций над коэффициентами уравнений, задающих многообразия. Алгоритм основан на аппарате исключения переменных в системах нелинейных алгебраических уравнений, и ключевым объектом в нем оказывается вычисление дискриминанта полинома (от одной или двух переменных).

Расстояние от точки до квадрики

Теорема 1. Пусть квадрика в $ {mathbb R}^{n} $, задана уравнением

$$
X^{top}AX+2B^{top}X-1=0 , (A=A^{top}) .
$$
Квадрат расстояния до нее от не лежащей на ней точки
$$ X_{0} in {mathbb R}^{n}, quad ( X_0^{top}AX_0+2 B^{top}X_{0}-1ne 0 ) $$
равен минимальному положительному корню уравнения расстояний
$$
{mathcal F}(z)=0 quad npu quad {mathcal F}(z)={mathcal D}_{mu} left( Phi(mu,z) right) .
$$
Здесь
$$
Phi(mu,z)=det left( left[ begin{array}{cc} A & B \ B^{top} & -1
end{array} right]
+ mu left[ begin{array}{cc} -E & X_0 \ X_0^{top} & z-X_0^{top}X_0 end{array} right] right),
$$
$ {mathcal D}_{} $ означает дискриминант полинома $ Phi(mu,z) $, рассматриваемого относительно переменной $ mu_{} $, а $ E_{} $ — единичная матрица порядка $ n_{} $. Дополнительно предполагается, что указанный корень не является кратным.

[3]. Квадрат расстояния от начала координат $ {mathbb O} in {mathbb R}^{n} $ до квадрики в $ {mathbb R}^{n} $, заданной уравнением

$$
X^{top}AX+2,B^{top}X-1=0 ,
$$
равен минимальному положительному корню уравнения расстояний
$$
{mathcal F}(z)=0, quad npu quad {mathcal F}(z)={mathcal D}_{mu} left(
f(mu)(mu z-1)-B^{top}q(A,mu)B right) ,
$$
и при условии, что указанный корень не является кратным. Здесь $ f(mu_{})=det (A-mu E) $ — характеристический полином матрицы $ A_{} $, а $ q(A,mu)_{} $ — матрица взаимная матрице $ A-mu E_{} $.

В частном случае $ B={mathbb O}_{} $ (квадрика центрирована к началу координат), имеем:

$$
{mathcal F}(z)=left[z^nf(1/z) right]^2{mathcal D}_{mu}(f(mu)) ,
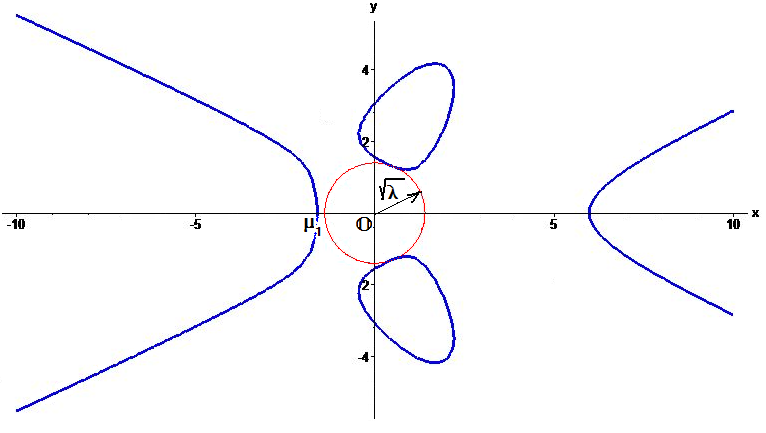
$$
и расстояние от начала координат до квадрики оказывается равным $ 1/sqrt{lambda_{max}^{}} $,
где $ lambda_{max}^{} $ — максимальное собственное число матрицы $ A_{} $.

Пример. Найти расстояние от начала координат до эллипсоида

$$ 7,x_1^2+6,x_2^2+5,x_3^2-4,x_1x_2-4,x_2x_3-3,x_1-4,x_2+5,x_3-18=0 .$$

Решение. Здесь
$$A = left(
{begin{array}{rrr}
frac{7}{18} & -frac{1}{9} & 0 \
&& \
-frac{1}{9} & frac{1}{3} & -frac{1}{9} \
&& \
0 & -frac{1}{9} & frac{5}{18}
end{array}}
right),quad
B = left(
begin{array}{r}
-frac{1}{12} \
\
-frac{1}{9} \
\
frac{5}{36}
end{array}
right) ,$$
$$
f(mu)=det (A-mu E)=-mu ^{3} + mu ^{2} — frac{11}{36} mu
+ frac {1}{36}
$$
Матрица взаимная матрице $ A-mu E_{} $:
$$
q(A, mu)= left(
begin{array}{ccc}
mu ^{2} — frac{11}{18} mu + frac{13}{162} & — frac{1}{9} mu + frac{5}{162} & frac{1}{81} \
&& \
— frac{1}{9} mu + frac{5}{162} & mu^2 -frac{2}{3}mu+frac{35}{324} & — frac{1}{9} mu +frac{7}{162} \
&& \
frac{1}{81} & — frac{1}{9} mu + frac{7}{162} &
mu ^{2} — frac{13}{18}mu+frac{19}{162}
end{array}
right) .
$$
$$
Phi(mu,z)=f(mu)(mu z-1)-B^{top}q(A,mu)B=
$$
$$
=-z mu ^{4} + (z+1) mu ^{3} +
left(-frac {11}{36} z — frac{673}{648}right) mu ^{2}
+left( frac {1}{36} z + frac {241}{729} right) mu —
frac {1621}{52488} .
$$
Воспользуемся детерминантным представлением дискриминанта:
$$
{mathcal F}(z) = {mathcal D}_{mu} (Phi(mu,z)) = frac{1}{16} times
$$
$$
times
left|
begin{array}{cccccc}
4z & — 3z-3 & frac{11}{18}z +
frac{673}{324} & — frac{1}{36} z — frac{241}{729} & 0 & 0 \
&&&&& \
0 & 4z & — 3z-3 & frac{11}{18} z + frac{673}{324} & — frac{1}{36} z
— frac{241}{729} & 0 \
&&&&& \
0 & 0 & 4z & — 3z-3 & frac{11}{18}z
+ frac{673}{324} & — frac{1}{36} z — frac{241}{729} \
&&&&& \
0 & 0 & — z — 1 & frac{11}{18}z + frac{673}{324} & — frac{1}{12} z
— frac{241}{243} & frac{1621}{13122} \
&&&&& \
0 & — z — 1 & frac{11}{18}z + frac{673}{324} & — frac{1}{12}z
— frac{241}{243} & frac{1621}{13122} & 0 \
&&&&& \
— z — 1 & frac{11}{18} z + frac{673}{324} & — frac{1}{12} z
— frac{241}{243} & frac{1621}{13122} & 0 & 0
end{array}
right| =
$$
$$
=2^{-11}3^{-24} (
38263752,z^6-966487788,z^5+9376985736,z^4-43882396481,z^3+$$
$$
+102982092872,z^2-116747905827,z+50898162294)
quad .
$$
Вещественные корни уравнения расстояний:
$$ z_1approx 1.394685, z_2 approx 5.701814, z_3 approx 7.043941, z_4 approx 7.590060 . $$

Ответ. $ d= sqrt{z_1} approx 1.180968 $.

Нахождение точки на квадрике, ближайшей к заданной точке $ X_{0} $, возможно с помощью следующего результата.

Теорема 2. При выполнении условий теоремы 1, координаты точки $ X_{ast} $ квадрики, ближайшей к точке $ X_{0} $ находятся по формуле

$$ X_{ast}=-A^{-1} B — mu_{ast} (A -mu_{ast}E)^{-1} (A^{-1} B+X_0)=(mu_{ast}E- A)^{-1} (B+mu_{ast} X_0) . $$
Здесь $ mu_{ast} $ означает кратный корень полинома $ Phi(mu,z_{ast}) $, где полином $ Phi(mu,z) $ берется из формулировки теоремы 1, а
$ z_{ast}^{} $ означает минимальный положительный корень уравнения расстояний.

Этот результат требует пояснений. Итак, поскольку дискриминант полинома $ Phi(mu,z_{ast}) $ обращается в нуль, то у этого полинома — как полинома по $ mu_{} $ — имеется кратный корень $ mu =mu_{ast} $. Можно доказать [4], что при условии простоты корня $ z=z_{ast} $ уравнения расстояний $ mathcal F(z)=0 $ кратность корня $ mu =mu_{ast} $ для полинома $ Phi(mu,z_{ast}) $ будет равна ровно $ 2_{} $, и других кратных корней этот полином не имеет. Но тогда, выражение для $ mu_{ast}^{} $ может быть найдено в виде рациональной функции коэффициентов полинома $ Phi(mu,z_{ast}) $. Последнее утверждение может быть доказано разными способами, и в качестве самого наглядного выберем тот, что основан на свойствах дискриминанта, например, на том, что изложено

☞

ЗДЕСЬ.

При выполнении условия предыдущей теоремы, координаты точки $ X_{ast}^{} $, ближайшей на квадрике к точке $ X_{0} $, являются рациональными функциями от квадрата расстояния.

Точка $ X_{ast} $ квадрики $ X^{top}AX+2,B^{top}X-1=0 $, ближайшая к началу координат $ X_0= mathbb O $, находится по формуле:

$$ X_{ast} = — frac{1}{f(mu_{ast})} q(A,mu_{ast}) B . $$
Здесь $ f(mu_{})=det (A-mu E) $ — характеристический полином матрицы $ A_{} $, $ q(A,mu)_{} $ — матрица взаимная матрице $ A-mu E_{} $, а $ mu_{ast} $ означает кратный корень уравнения
$$f(mu)(mu z_{ast}-1)-B^{top}q(A,mu)B=0 , $$
где $ z_{ast}^{} $ — величина квадрата расстояния от $ mathbb O_{} $ до квадрики.

Пример. Найти ближайшую к началу координат точку эллипсоида из предыдущего примера.

Решение. Подставляем $ z_{}=z_{ast} approx 1.394685 $ в формулу для определения кратного корня, т.е. в отношение двух конкретных миноров детерминантного представления дискриминанта:
$$
mu=-frac{left|
begin{array}{cccc}
4z & — 3z-3 & frac{11}{18} z + frac{673}{324} & 0 \
&&& \
0 & 4z & — 3z-3 & — frac{1}{36} z — frac{241}{729} \
&&& \
0 & — z — 1 & frac{11}{18}z + frac{673}{324} & frac{1621}{13122} \
&&& \
— z — 1 & frac{11}{18}z + frac{673}{324} & — frac{1}{12}z — frac{241}{243} & 0
end{array}
right|}
{left|
begin{array}{cccc}
4z & — 3z-3 & frac{11}{18} z + frac{673}{324} & — frac{1}{36} z — frac{241}{729} \
&&& \
0 & 4z & — 3z-3 & frac{11}{18}z + frac{673}{324} \
&&& \
0 & — z — 1 & frac{11}{18}z + frac{673}{324} & — frac{1}{12}z — frac{241}{243} \
&&& \
— z — 1 & frac{11}{18}z + frac{673}{324} & — frac{1}{12}z — frac{241}{243} & frac{1621}{13122}
end{array}
right|}
$$
получаем $ mu_{ast}^{} approx 0.572670 $. Подставляем это значение в формулу для определения $ X_{ast}^{} $ из последнего следствия:
$$
X_{ast}approx left(begin{array}{r}
0.071171 \ -0.867719 \ 0.797924
end{array}
right) .
$$

Проверка. Если подставить вместо $ X_{ast} $ его приближенное значение, то получим:
$$
X_{ast}^{top} X_{ast} approx mathbf{1.39468}4, X_{ast}^{top}AX_{ast}+2,B^{top}X_{ast}-1 approx 2.9cdot 10^{-5} ,
$$
и вектор $ {mathbb O}X_{ast} $ перпендикулярен эллипсоиду в точке $ X_{}=X_{ast} $:
$$
AX_{ast}+B approx left(begin{array}{r}
0.040757\ -0.496917 \ 0.456948
end{array} right)approx mu_{ast} X_{ast} .
$$

Более подробный анализ уравнения расстояний для частных случаев плоскости $ mathbb R^{2} $ и трехмерного пространства $ mathbb R^{3} $ (в частности, почему существенно условие простоты минимального положительного корня, упомянутое в теореме 1)

☞

ЗДЕСЬ.

Расстояние от линейного многообразия (плоскости) до квадрики

Задача. Найти расстояние от эллипсоида в $ {mathbb R}^{n} $, заданного уравнением
$$
X^{top}AX+2B^{top}X-1=0 , (A=A^{top})
$$
до линейного многообразия (плоскости) в $ {mathbb R}^{n} $, заданной системой уравнений
$$
left{
begin{array}{ccc}
c_{11}x_1+c_{12}x_2+dots+c_{1n}x_n &=& 0 \
dots & & dots \
c_{m1}x_1+c_{m2}x_2+dots+c_{mn}x_n &=& 0
end{array}
right. iff
CX={mathbb O} quad npu quad
C=left(
begin{array}{cccc}
c_{11}& c_{12} & dots & c_{1n} \
dots & & & dots \
c_{m1}& c_{m2} & dots & c_{mn}
end{array}
right)_{mtimes n}
$$
При этом предполагается, что $ mle n_{} $ и что ранг матрицы $ C_{} $ равен $ m_{} $, т.е.
определяемая системой плоскость в $ {mathbb R}^{n} $ является $ (n-m)_{} $-мерной.

Теорема. [3]. Необходимое и достаточное условие того, что линейное многообразие (плоскость) пересекает эллипсоид зависит от знакоопределенности матрицы $ A_{} $:

$$0 le left|
begin{array}{lrc}
A & B & C^{top}\
B^{top} & -1 & {mathbb O}\
C & {mathbb O} & mathbb{O}
end{array} right| times
left{ begin{array}{l}
(-1)^{m-1} mbox{при} A mbox{пол. определенной}, \
(-1)^n mbox{при} A mbox{отр. определенной}
end{array} right.$$

Условие равенства нулю определителя из теоремы является необходимым и достаточным для существования точки касания эллипсоида и плоскости.

Теорема. [3]. Если условие предыдущей теоремы не выполняется, то квадрат расстояния от эллипсоида
до плоскости совпадает с минимальным положительным корнем полинома

$$
{mathcal F}(z) ={mathcal D}_mu left( mu^m left|
begin{array}{ccc}
A & B & C^{top}\
B^{top} & -1 + mu z & mathbb{O}\
C & mathbb{O} & frac{1}{mu} C cdot C^{top}
end{array}
right| right),
$$
в предположении, что этот корень не является кратным. Здесь $ {mathcal D}_{} $ — дискриминант полинома, рассматриваемого относительно переменной $ mu_{} $.

Если строки матрицы $ C_{} $ ортонормированны, то преобразованием
определителя в теореме можно понизить его порядок: выражение под знаком дискриминанта
можно преобразовать в

$$left|
begin{array}{cc}
A-mu C^{top} C & B \
B^{top} & -1+mu z
end{array}
right|.$$

Пример. Найти расстояние от оси $ {mathbb O}x_{1} $ до эллипсоида

$$
7, x_1^2+6, x_2^2 +5, x_3^2 -4,x_1x_2-4,x_2x_3-37,x_1-12,x_2+3,x_3+54=0 .
$$

Решение. Здесь
$$
A=
left(
begin{array}{rrr}
-frac{7}{54} & frac{1}{27} & 0 \
&&\
frac{1}{27} & -frac{1}{9} & frac{1}{27} \
&&\
0 & frac{1}{27} & -frac{5}{54}
end{array}
right), B=left(
begin{array}{r}
frac{37}{108} \
\
frac{1}{9} \
\
-frac{1}{36}
end{array}
right)
$$
и можно взять
$$
C=
left(
begin{array}{ccc}
0 & 1 & 0 \
0 & 0 & 1
end{array}
right) .
$$
Матрица $ A_{} $ отрицательно определена, условие пересечения прямой и эллипсоида не выполняется:
$$
left|
begin{array}{ccc}
A & B & C^{top}\
B^{top} & -1 & {mathbb O}\
C & {mathbb O} & mathbb{O}
end{array} right| times (-1)^3 = — frac{143}{11664} < 0 .
$$
Имеем, на основании следствия:
$$
left|
begin{array}{cc}
A-mu C^{top} C & B \
B^{top} & -1+mu z
end{array}
right|=left|
begin{array}{cccc}
-frac{7}{54} & frac{1}{27} & 0 & frac{37}{108} \
&&&\
frac{1}{27} & -frac{1}{9}-mu & frac{1}{27} & frac{1}{9} \
&&&\
0 & frac{1}{27} & -frac{5}{54}-mu & -frac{1}{36} \
&&&\
frac{37}{108} & frac{1}{9} & -frac{1}{36} & -1 + mu z
end{array}
right| =
$$
$$
=-frac{7}{54}z mu^3+left(-frac{73}{2916}z+frac{143}{11664}right)mu^2+left(-frac{1}{972}z-frac{1069}{314928}right)mu-frac{1621}{4251528}
$$
и дискриминант полученного полинома по переменной $ mu_{} $ равен
$$
{mathcal F}(z)=2^{-16}3^{-30}
left(1331935488,z^4-38807307008,z^3+245988221152,z^2-1086769525104,z+61289436065 right)
$$
Положительные корни последнего полинома: $ z_1 approx 0.057128, z_2 approx 22.545607_{} $.

Ответ. $ d_{} = sqrt{z_1} approx 0.239015 $.

Как правило, степень полинома $ {mathcal F}(z)_{} $ равна $ 2m_{} $, т.е. удвоенному количеству линейных уравнений, задающих плоскость. В частном случае $ m=1_{} $ получаем квадратное уравнение:

Расстояния в $ {mathbb R}^{n} $ от плоскости

$$ c_1x_1+dots+c_nx_n = h iff CX=h $$
до ближайшей и до самой дальней точек эллипсоида
$$
X^{top}AX+2B^{top}X-1=0 , (A=A^{top})
$$
совпадают с модулями корней полинома:
$$
{mathcal F}(Z)=left|
begin{array}{ccc}
A & B & C^{top}/|C|\
B^{top} & -1 & Z-h/|C|\
C/|C| & Z-h/|C| & 0
end{array} right| .
$$
Здесь $ |C|=sqrt{c_1^2+dots+c_n^{2}} $ и предполагается, что поверхности не пересекаются.

Пример. Найти расстояние от прямой $ 2, x_1- x_{2}=0 $ до эллипса

$$ 7,x_1^2-4,x_1x_2 + 6, x_2^2-47, x_1 -24, x_{2} +124 = 0 .$$

Решение. Здесь
$$
{mathcal F}(Z)=left|
begin{array}{ccc}
A & B & C^{top}/|C| \
B^{top} & -1 & Z-h/|C| \
C/|C| & Z-h/|C| & 0
end{array} right| =
left|
begin{array}{cccc}
-frac{7}{124} & frac{1}{62} & frac{47}{248} & frac{2}{sqrt{5}} \
&&& \
frac{1}{62} & — frac{3}{62} & frac{3}{31} &- frac{1}{sqrt{5}} \
&&& \
frac{47}{248} & frac{3}{31} & -1 & Z \
&&& \
frac{2}{sqrt{5}} & — frac{1}{sqrt{5}} & Z & 0
end{array} right| =
$$
$$
=-frac{1}{307520}left(760,Z^2+1592sqrt{5}, Z+2383 right)
$$
и корни этого полинома:
$$ -frac{199}{190}sqrt{5}pm frac{1}{76} sqrt{13570} . $$

Ответ.
$$ d = left| -frac{199}{190}sqrt{5}+ frac{1}{76} sqrt{13570} right| approx 0.809219_{} . $$

Расстояние между квадриками

Теорема. Пусть $ X^{top} A_{1} X =1 $ и $ X^{top} A_{2} X =1 $ – квадрики в $ {mathbb R}^{n} $, причем первая является эллипсоидом. Квадрики не пересекаются тогда и только тогда, когда матрица $ A_{1}-A_2 $ является знакоопределенной.

Доказательство

☞

ЗДЕСЬ.

Теорема. [3,4]. Если выполняется условие предыдущей теоремы, то квадрат расстояния между

$$ mbox{эллипсоидом} X^{top} A_{1} X =1 mbox{и квадрикой} X^{top} A_{2} X =1 $$
совпадает с минимальным положительным корнем уравнения расстояний
$$
{mathcal F}(z)=0 quad npu quad {mathcal F}(z)={mathcal D}_{lambda} left( Phi(lambda,z) right) .
$$
Здесь
$$
Phi(lambda,z)=det (lambda A_1 +
(z- lambda) A_2 — lambda (z-lambda) A_1 A_2),
$$
$ {mathcal D}_{} $ — дискриминант полинома рассматриваемого относительно переменной $ lambda_{} $.
Дополнительно предполагается, что указанный корень не является кратным.

Пример. Найти расстояние между эллипсами

$$10,x_1^2-12,x_1x_2+8,x_2^2=1 qquad u qquad x_1^2+x_1x_2+x_2^2=1 . $$

Решение. Здесь
$$
A_1=
left(
begin{array}{rr}
10 & — 6 \
-6 & 8
end{array}
right), quad
A_2=
left(
begin{array}{rr}
1 & frac{1}{2} \
frac{1}{2} & 1
end{array}
right)
$$
и матрица $ A_{1}-A_2 $ положительно определена. Следовательно эллипсы не пересекаются.
$$
Phi(lambda,z)=det (lambda A_1 + (z- lambda) A_2 — lambda (z-lambda) A_1 A_2)=
$$
$$
=33,lambda^4+left(-66z+frac{149}{2}right)lambda^3+left(33,z^2-61,z+frac{83}{4}right)lambda^2+left(-frac{27}{2}z^2+frac{45}{2}zright)lambda+frac{3}{4},z^2
$$
и дискриминант этого полинома по переменной $ lambda_{} $ равен
$$
{mathcal F}(z)=frac{3}{16}z^2 ({scriptstyle 936086976}, z^6-{scriptstyle 10969697376},z^5+
{scriptstyle 50706209664}, z^4
-{scriptstyle 115515184664}, z^3+{scriptstyle 130176444432}, z^2
-{scriptstyle 59826725574},z+{scriptstyle 2866271785}) .
$$
Положительные корни уравнения расстояний $ {mathcal F}(z)=0 $:
$$
z_1 approx 0.053945666, z_2 approx 1.3340583883, z_3 approx 1.95921364, z_4 approx 2.8785867381 .
$$

Ответ. $ d_{}= sqrt{z_1} approx 0.23226206 $.

Как правило, степень полинома $ {mathcal F}(z)_{} $ из последней теоремы (после отбрасывания постороннего множителя $ z^{n(n-1)}_{} $) равна $ n(n+1)_{} $.

Нахождение координат ближайших точек на квадриках (обеспечивающих найденное расстояние)
возможно по алгоритму:

Если $ z=z_{ast} $ — корень полинома $ {mathcal F}(z) $, то это значит, что полином
$$ Phi(lambda, z_{ast}) = det ( lambda A_1 +(z_{ast}-lambda)A_2 — lambda (z_{ast}-lambda) A_2A_1) $$
имеет кратный корень $ lambda_{} = lambda_{ast} $. При выполнении условий теоремы, этот корень будет единственным второй кратности и его можно выразить в виде рациональной функции от $ z_{ast} $ с помощью субдискриминантов.

2.

Столбец координат $ X_{ast}^{} $ точки первой квадрики, удовлетворяет тогда однородной системе уравнений
$$ ( lambda_{ast} A_1 +(z_{ast}-lambda_{ast})A_2 — lambda_{ast} (z_{ast}-lambda_{ast}) A_2A_1) X = mathbb O , $$
которая имеет бесконечное множество решений, поскольку определитель ее матрицы равен нулю. Из этого бесконечного множества мы выделяем те решения, что удовлетворяют условию $ X^{top}A_{1}X=1 $.

При выполнении условий теоремы таких решений будет два (что соответствует симметрии задачи, см. рисунок).

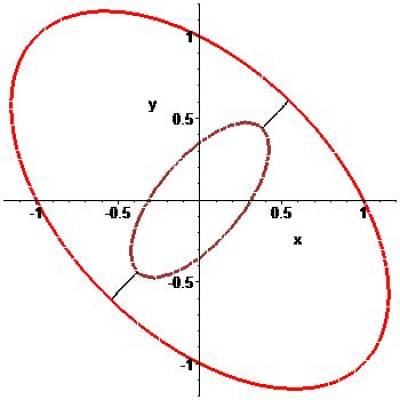
Аналогично, столбец координат $ Y_{ast}^{} $ точки на второй квадрике $ Y^{top}A_{2}Y=1_{} $ будет решением системы уравнений
$$ ( lambda_{ast} A_1 +(z_{ast}-lambda_{ast})A_2 — lambda_{ast} (z_{ast}-lambda_{ast}) A_1A_2) Y = mathbb O . $$

Заметим, что матрицы рассматриваемых линейных систем различаются лишь транспонированием.

Для нахождения решений воспользуемся одним из результатов теории систем линейных уравнений. Составим столбец из
алгебраических дополнений к элементам какой-либо строки матрицы
$$ M= lambda_{ast} A_1 +(z_{ast}-lambda_{ast})A_2 — lambda_{ast} (z_{ast}-lambda_{ast}) A_2A_1 . $$
Тогда вектор $ X_{ast}^{} $ отличается от этого столбца лишь множителем, который определится из условия $ X^{top}A_{1}X=1_{} $. Аналогично, для получения столбца координат $ Y_{ast}^{} $ возьмем столбец из алгебраических дополнений к элементам какого-либо столбца той же матрицы $ M_{} $ и домножим его на константу, чтобы обеспечить выполнение условия $ Y^{top}A_{2}Y=1_{} $.

Получившиеся пары $ X_{ast},Y_{ast}^{} $ надо согласовать: они должны подчиняться условию
$$ (X_{ast}-Y_{ast})^{top}(X_{ast}-Y_{ast})=z_{ast} . $$

Пример. Найти ближайшие точки эллипсов из предыдущего примера.

Решение. Для найденного значения $ z_{ast}=z_1 approx 0.053945666_{} $ определитель матрицы
$$
M=left(
begin{array}{cc}
7,lambda^2+(-7z+9)lambda+z & -2lambda^2+(2,z-frac{13}{2})lambda+frac{1}{2}z \
& \
-lambda^2+(z-frac{13}{2})lambda+frac{1}{2}z & 5lambda^2+(-5z+7)lambda+z
end{array}
right)
$$
как полином по $ lambda_{} $ будет иметь кратный корень. Этот корень определяем¹⁾ с помощью субдискриминантов в виде:
$$
lambda=-frac{-725274,z^5+1455894,z^4+frac{11286981}{2}z^3-frac{26486523}{2}z^2+frac{42000075}{8}z}
{17591706,z^4-109992894,z^3+frac{450450691}{2}z^2-frac{315606253}{2}z+frac{77466805}{8}} .
$$
Подстановка сюда $ z=z_{ast}^{} $ даст $ lambda_{ast} approx -0.13576051_{} $.

Далее, при найденных значениях $ z_{} $ и $ lambda_{} $ система линейных уравнений
$$ MX=mathbb O_{2times 1} $$
должна иметь бесконечное множество решений относительно вектора $ X_{2times 1}^{} $. Одно из
этих решений может быть построено (см. упражнение

☞

ЗДЕСЬ ) с помощью алгебраических дополнений к элементам, например,
второй строки матрицы $ M_{} $:
$$
left(
begin{array}{c}
2lambda^2-(2,z-frac{13}{2})lambda-frac{1}{2}z \
\
7,lambda^2+(-7z+9)lambda+z
end{array}
right)
quad
begin{array}{c}
longrightarrow \
z=z_{ast}, lambda= lambda_{ast}
end{array} quad
X=left(
begin{array}{c}
-0.8579069 \
\
-0.9876166
end{array}
right) .
$$
Любое другое решение получается домножением полученного на произвольную константу («растяжением» вектора). Воспользуемся этим, чтобы добиться выполнения условия $ X^{top}A_{1} X =1_{} $.
$$
X_{ast}=frac{1}{sqrt{X^{top}A_1 X}} X approx
left(
begin{array}{c}
-0.3838312 \
-0.4418639
end{array}
right) .
$$
Аналогично, для нахождения точки на другом эллипсе, мы решаем систему
$$ M^{top}Y=mathbb O_{2times 1} , $$
представив ее решение опять-таки с помощью алгебраических дополнений к элементам второго столбца
матрицы $ M_{} $:
$$
left(
begin{array}{c}
lambda^2-(z-frac{13}{2})lambda-frac{1}{2}z \
\
7,lambda^2+(-7z+9)lambda+z
end{array}
right)
quad
begin{array}{c}
longrightarrow \
z=z_{ast}, lambda= lambda_{ast}
end{array} quad
left(
begin{array}{c}
-0.8836615 \
\
-0.9876166
end{array}
right) quad Rightarrow quad
Y_{ast} approx
left(
begin{array}{c}
-0.5449964 \
\
-0.6091105
end{array}
right) .
$$

Ответ. $ pm (0.3838312,, 0.4418639)_{} $ и $ pm (0.5449964,, 0.6091105)_{} $ соответственно (знаки должны быть согласованы).

Проверка. Если в ответе взять знак $ +_{} $:
$$ X_{ast}-Y_{ast} =
left(
begin{array}{c}
-0.1611652 \
-0.1672466
end{array}
right)= lambda_{ast} A_1X_{ast}=(lambda_{ast}-z_{ast})A_2Y_{ast},quad (X_{ast}-Y_{ast})^{top}(X_{ast}-Y_{ast})approx mathbf{0.0539456}4 .
$$

Теорема. [3,4].Пусть

$$ X^{top} A_{1}X+2,B^{top}_1X-1=0 mbox{и} X^{top} A_{2}X+2,B^{top}_2X-1=0 $$
— квадрики в $ {mathbb R}^{n}_{} $, причем первая является эллипсоидом. Квадрики пересекаются тогда и только тогда, когда
среди вещественных корней полинома

$$
Theta (z) = {mathcal D}_lambda left( det left( left[
begin{array}{cc}
A_2 & B_2\
B_2^{top} & -1-z
end{array} right] — lambda left[
begin{array}{cc}
A_1 & B_1\
B_1^{top} & -1
end{array} right] right) right)
$$
имеются числа разных знаков или нуль. Здесь $ {mathcal D}_{} $ — дискриминант полинома рассматриваемого относительно переменной $ lambda_{} $.

Условие теоремы проверяется чисто алгебраически, т.е. без привлечения численных методов нахождения корней полинома. См. следствие к теореме Йоахимшталя

☞

ЗДЕСЬ.

Для того, чтобы существовала точка касания квадрик

$$ X^{top} A_{1}X+2,B^{top}_1X-1=0 mbox{и} X^{top} A_{2}X+2,B^{top}_2X-1=0 $$
необходимо и достаточно, чтобы было выполнено условие
$$
{mathcal D}_lambda left( det left( left[
begin{array}{cc}
A_2 & B_2\
B_2^{top} & -1
end{array} right] — lambda left[
begin{array}{cc}
A_1 & B_1\
B_1^{top} & -1
end{array} right] right) right) =0 .
$$

Теорема. [3,4]. Если не выполняется условие предыдущей теоремы, то квадрат расстояния между

$$ mbox{эллипсоидом} quad X^{top} A_{1}X+2,B^{top}_1X-1=0 quad mbox{ и квадрикой } quad X^{top} A_{2}X+2,B^{top}_2X-1=0 $$ совпадает с минимальным положительным корнем полинома
$$
{mathcal F}(z) =
$$
$$
={mathcal D}_{mu_1, mu_2} left( det left( mu_1 left[
begin{array}{cc}
A_1 & B_1\
B_1^{top} & -1
end{array} right] + mu_2 left[
begin{array}{cc}
A_2 & B_2\
B_2^{top} & -1
end{array} right] — left[
begin{array}{cc}
A_2 A_1 & A_2 B_1\
B_2^{top} A_1 & B_2^{top}B_1 — mu_1 mu_2 z
end{array} right] right) right),
$$
в предположении, что этот корень не является кратным. Здесь $ {mathcal D}_{} $ — дискриминант полинома рассматриваемого относительно переменных $ mu_{1}, mu_{2} $.

Пример. Найти расстояние между эллипсами

$$-frac{1}{2},x_1^2+frac{1}{2},x_1x_2-frac{3}{2},x_2^2+frac{5}{2},x_1+4,x_2=1 $$
и
$$-frac{1}{84},x_1^2-frac{4}{189},x_2^2-frac{1}{3}, x_1=1 . $$

Решение. Здесь
$$
A_1=
left(
begin{array}{rr}
-frac{1}{2} & frac{1}{4} \
\
frac{1}{4} & -frac{3}{2}
end{array}
right), quad
B_1=left(
begin{array}{c}
frac{5}{4} \ \ 2
end{array}
right), quad
A_2=
left(
begin{array}{cc}
-frac{1}{84} & 0 \
\
0 & -frac{4}{189}
end{array}
right),quad B_2=left(
begin{array}{r}
-frac{1}{6} \ \ 0
end{array}
right) .
$$
Проверяем сначала условия пересечения поверхностей.
$$
Theta (z) = {mathcal D}_lambda left(-begin{array}{c} frac{157}{32} end{array} lambda^3-left{ begin{array}{c} frac{4315}{3024} end{array} + begin{array}{c} frac{11}{16}z end{array} right}lambda^2+left{-begin{array}{c} frac{11}{2646} end{array} + begin{array}{c} frac{43}{1512} end{array} z right}lambda- begin{array}{c} frac{1}{3969}end{array} z + begin{array}{c} frac{4}{11907} end{array}right)=
$$
$$
=begin{array}{c}frac{1}{{scriptstyle 9219465541730304}} end{array}
({scriptstyle 505118694465},z^4-{scriptstyle 1023679248858},z^3-
{scriptstyle 7568287236783},z^2+
{scriptstyle 33720131260536},z +{scriptstyle 34005894083152}) .
$$
Полином имеет два вещественных корня, оба отрицательны. Эллипсы не пересекаются. Далее,
$$
Psi(mu_1,mu_2,z)=det left( mu_1 left[
begin{array}{cc}
A_1 & B_1\
B_1^{top} & -1
end{array} right] + mu_2 left[
begin{array}{cc}
A_2 & B_2\
B_2^{top} & -1
end{array} right] — left[
begin{array}{cc}
A_2 A_1 & A_2 B_1\
B_2^{top} A_1 & B_2^{top}B_1 — mu_1 mu_2 z
end{array} right] right) =
$$
$$
=frac{11}{16}zmu_1^3 mu_2+frac{43}{1512}zmu_1^2mu_2^2+frac{1}{3969}zmu_1mu_2^3+
frac{157}{32}mu_1^3-frac{4315}{3024}mu_1^2mu_2+
$$
$$
+frac{275}{12096}zmu_1^2mu_2+frac{11}{2646}mu_1mu_2^2+frac{2}{3969}zmu_1mu_2^2+frac{4}{11907}mu_2^3+frac{3925}{24192}mu_1^2+
$$
$$
+frac{11}{63504}zmu_1mu_2-frac{619}{31752}mu_1mu_2+frac{8}{11907}mu_2^2+frac{157}{127008}mu_1+frac{11}{47628}mu_2 .
$$
Вычисляем дискриминант этого полинома по переменным $ mu_{1} $ и $ mu_{2} $, представив соответствующий результант
$$
{mathcal R}_{mu_1,mu_2}left(frac{partial Psi}{partial mu_1}, frac{partial Psi}{partial mu_2}, Psi right)
$$
в виде определителя матрицы Безу²⁾:
$$
mathfrak B=
left(
begin{array}{cccc}
-{scriptstyle 949850},z-{scriptstyle 38319304} & -{scriptstyle 76994841},z+
{scriptstyle 29798905836} & dots & \
{scriptstyle 179712037934},z^2-{scriptstyle 6628863332080},z-{scriptstyle 18668859390944800} & & dots & \
dots &&& dots \
& & &
end{array}
right)
$$
Выражения для элементов первой и последней строк

☞

ЗДЕСЬ.
$$
{mathcal F}(z) =det (mathfrak B) equiv 3869893(20090,z+3526681)^2 times
$$
$$
times
({scriptstyle 12866891832025},z^{12}-{scriptstyle 2445505463588880},z^{11}-{scriptstyle 10867111637549652716},z^{10}-{scriptstyle 3123865087697933253136},z^9+
$$
$$
+{scriptstyle 1561852119815441835822424},z^8+{scriptstyle 1041845279230362476059640640},z^7+{scriptstyle 302844249329911871856294474624},z^6+
$$
$$
+{scriptstyle 50781476668832773753935668661952},z^5+{scriptstyle 2215513880036430404751762329796624},z^4-
$$
$$
-{scriptstyle 646131957386364232922218724008039168},z^3-{scriptstyle 99189074464451279399168578577559865856},z^2-
$$
$$
-{scriptstyle 5789019527920299026625801973715386789888},z+{scriptstyle 60730952901233749068462660878127980941312})
$$
Первый сомножитель по $ z_{} $ является «посторонним»³⁾ и отбрасывается. Положительные корни второго сомножителя:
$$
9.0183982802, 121.59673276, 582.35840496, 1031.42118655
$$

Ответ. $ d approx sqrt{9.0183982802} approx 3.00306481 $.

Нахождение ближайших точек на квадриках (обеспечивающих найденное расстояние) возможно по следующему алгоритму.

После нахождения (с необходимой точностью) минимального положительного корня $ z_{ast}^{} $ полинома $ {mathcal F}(z) $, установим соответствующие ему значения $ mu_{1}^{} $ и $ mu_{2}^{} $. Соответствие понимается в том смысле, что при $ z=z_{ast}^{} $ дискриминант полинома
$$
Psi(mu_1,mu_2,z)=det left( mu_1 left[
begin{array}{cc}
A_1 & B_1\
B_1^{top} & -1
end{array} right] + mu_2 left[
begin{array}{cc}
A_2 & B_2\
B_2^{top} & -1
end{array} right] — left[
begin{array}{cc}
A_2 A_1 & A_2 B_1\
B_2^{top} A_1 & B_2^{top}B_1 — mu_1 mu_2 z
end{array} right] right)
$$
— как полинома по переменным $ mu_{1},mu_{2} $ — обращается в нуль, то есть этот полином обладает кратным корнем, который мы обозначим $ (mu_{1ast},mu_{2ast}) $. Этот корень может быть найден в виде рациональной функции от $ z_{ast}^{} $ с помощью миноров матрицы Безу.
Если матрица Безу $ mathfrak B_{} $ порядка $ N_{} $ построена для мономиального базиса, в котором первые три монома имеют вид $ 1,mu_1, mu_{2} $, то, обозначив $ {mathfrak B}_{N1}, {mathfrak B}_{N2}, {mathfrak B}_{N3}^{} $ алгебраические дополнения элементов ее последней строки, будем иметь
$$
mu_{1ast} = frac{mathfrak B_{N2}}{mathfrak B_{N1}}; mu_{2ast} = frac{mathfrak B_{N3}}{mathfrak B_{N1}} .
$$

Составим матрицу
$$ M= mu_{1ast} A_1+mu_{2ast}A_2-A_2A_1 . $$
Тогда координатные столбцы ближайших точек на квадриках вычисляются по формулам:
$$
X_{ast}=M^{-1} (A_2B_1-mu_{1ast} B_1-mu_{2ast}B_2),
Y_{ast}=(M^{-1})^{^{top}} (A_1B_2 — mu_{1ast} B_1-mu_{2ast}B_2).
$$

Пример. Найти ближайшие точки эллипсов из предыдущего примера.

Решение. Подставляем найденное значение квадрата расстояния $ z=z_{ast}^{} $ в формулы для определения компонент кратного корня:
$$
mu_1=frac{mathfrak B_{9,2}}{mathfrak B_{9,1}}equiv -frac{2}{21} frac{p_2(z)}{p_1(z)},
mu_2=frac{mathfrak B_{9,3}}{mathfrak B_{9,1}}equiv -frac{1099}{8} frac{p_3(z)}{p_1(z)}
$$
при
$$
p_1(z)={scriptstyle 30581063813712982235616866861258531260075854083860480}+dots
+{scriptstyle 42267948346218643456100},z^{13} ,
$$
$$
p_2(z)={scriptstyle 6423295122838229007549546733287643446036432415004672}+dots +
{scriptstyle 10295520700745795900000},z^{13}
$$
и
$$
p_3(z)={scriptstyle 11528328181753695140063436659475618124233172074496}+dots
+{scriptstyle 303317089743521700},z^{13} .
$$
(Полные представления

☞

ЗДЕСЬ.)
В результате, получаем:
$$
mu_{1ast}approx 0.0420933593 ,
mu_{2ast}approx 0.5932113733 .
$$
Матрица $ M_{} $:
$$
M=mu_{1ast} A_1+mu_{2ast}A_2-A_2A_1=
left(begin{array}{rr}
-0.0340611008 & 0.0134995303 \
0.0158143451 & -0.1074408089
end{array}
right)
$$
и по указанным выше формулам получаем

Ответ.
$$ X_{ast}approx left(begin{array}{r}
-0.4824707833 \
1.1065143947
end{array}
right),
Y_{ast}approx left(
begin{array}{r}
-3.46262940675\
0.73630788509
end{array}
right) .
$$

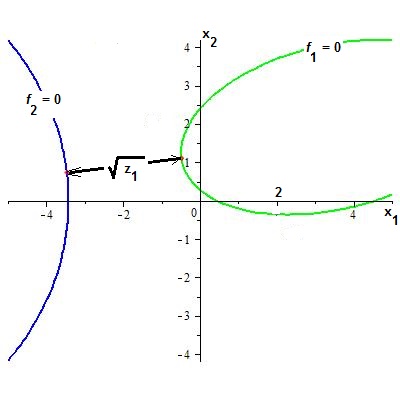
Проверка.
$$
(X_{ast}-Y_{ast})^{top}(X_{ast}-Y_{ast})approx mathbf{9.018398280}3 ,
$$
$$
X_{ast}^{top}A_1X_{ast}+2B_1^{top}X_{ast}-1 approx 1cdot 10^{-9} ,
Y_{ast}^{top}A_2Y_{ast}+2B_2^{top}Y_{ast}-1approx -3cdot 10^{-10} ,
$$
и вектор $ X_{ast}-Y_{ast}^{} $ перпендикулярен обоим эллипсам в соответствующих ближайших точках:
$$
A_1X_{ast}+B_1=
left(begin{array}{r}
1.767863990 \
0.219610712
end{array}
right)=mu_{2ast} (X_{ast}-Y_{ast}),
A_2Y_{ast}+B_2=
left(begin{array}{r}
-0.1254448880 \
-0.0155832356
end{array}
right)=-mu_{1ast} (X_{ast}-Y_{ast}) .
$$

Как правило, степень полинома $ {mathcal F}(z)_{} $ из последней теоремы (после отбрасывания постороннего множителя) равна $ 2n(n+1)_{} $. Коэффициенты этого полинома могут быть чудовищны.

Пример. Найти расстояние между эллипсоидами

$$
7,x_1^2+6,x_2^2+5,x_3^2-4,x_1x_2-4,x_2x_3-37,x_1-12,x_2+3,x_3+54=0$$
и
$$ 189,x_1^2+x_2^2+189,x_3^2+2,x_1x_3-x_2x_3-27=0 .$$

Решение. Здесь
$$
mathcal F (z)= underbrace{scriptstyle{891807829233048602 dots 129270962946048}}_{146} , z^{24} + dots +
underbrace{scriptstyle{11195843896426573542 dots 420939042193186989409}}_{189}
$$

Ответ. $ d approx sqrt{1.3537785005} approx 1.1635198754_{} $

Алгебраические кривые и многообразия

Расстояние от точки до плоской алгебраической кривой

Задача. Пусть алгебраическая кривая задана уравнением
$$ Phi(x,y)=0 . $$
Здесь $ Phi_{}(x,y) $ — отличный от константы полином от $ x_{} $ и $ y_{} $ с вещественными коэффициентами. Требуется найти расстояние до этой кривой от начала координат.

Здесь возникает проблема, которую для рассмотренных выше случаев удавалось либо обойти, либо же сравнительно дешево решить: это проблема существования решения. Дело в том, что уравнение может не иметь вещественных решений, то есть не определять никакой кривой на плоскости $ mathbb R^{2} $.

Будем решать задачу сначала для частного случая — пусть полином $ Phi_{}(x,y) $ является четным по переменной
$ y_{} $. Геометрически это означает, что кривая (если она существует) будет зеркально симметричной относительно оси $ mathbb Ox $. А с аналитической точки зрения такой полином можно представить в виде полинома
$$ F(x,Y) equiv Phi_{}(x,y) quad npu quad Y=y^2 . $$

Теорема 1 [6]. Пусть $ Phi_{}(x,y) equiv Phi_{}(x,-y) $. Уравнение $ Phi_{}(x,y)=0 $ не имеет вещественных решений если одновременно выполняются два условия:

a) уравнение $ Phi(x,0)=0 $ не имеет вещественных решений;

б) уравнение
$$ mathcal F(z)=mathcal D_x( F(x,z-x^2))=0 $$
не имеет положительных решений.

Если хотя бы одно из этих условий не выполняется, то квадрат расстояния от начала координат до кривой $ Phi(x_{},y)=0 $ равен либо квадрату минимального по модулю вещественного корня уравнения $ Phi(x,0)=0 $, либо же минимальному положительному корню уравнения $ mathcal F(z)= 0 $, при условии, что последний не является кратным. Здесь $ {mathcal D}_{} $ — дискриминант полинома, рассматриваемого относительно переменной $ x_{} $.

Пример. Найти расстояние от начала координат до кривой

$$ Phi(x,y)=x^6-5,x^4y^2-y^6-6,x^5+6,xy^4+10,y^4+25,x-45=0 . $$

Решение. Уравнение
$$ Phi(x,0)=x^6-6,x^5+25,x-45=0 $$
имеет вещественные корни $ mu_1approx -1.621919 $ и $ mu_2 approx 5.986387 $.

Далее,
$$ F(x,Y)=x^6-5,x^4Y-Y^3-6,x^5+6,xY^2+10,Y^2+25,x-45 $$
и полином
$$
mathcal F(z)=mathcal D_x (F(x,z-x^2))=
{scriptstyle 124422592},z^{15}-{scriptstyle 1996675968}z^{14}-{scriptstyle 26107738048},z^{13}+{scriptstyle 270691240064},z^{12}+
{scriptstyle 1462429768576}z^{11}
$$
$$
-{scriptstyle 31070151855680}z^{10}+
{scriptstyle 104850679100160},z^9+{scriptstyle 106422502370800},z^8-{scriptstyle 1956603249193600},z^7+{scriptstyle 1683409252901600},z^6+
$$
$$
+{scriptstyle 3565828983027500}z^5
-{scriptstyle 23058839076745500},z^4+{scriptstyle 30272455856370000},z^3+{scriptstyle 28139412928130000},z^2-{scriptstyle 97452805338000000}, z+
$$
$$
+{scriptstyle 171049864407603125}
$$
имеет минимальный положительный корень равный $ lambda approx 1.965293 $. Поскольку $ sqrt{lambda} < |mu_1| $, то получаем

Ответ. $ d approx 1.334155 $.

Понятно как решать задачу и в случае четности полинома $ Phi_{}(x,y) $ по переменной $ x_{} $.
Но как решить задачу в общем случае — когда свойства четности нет ни по одной из переменных? — Надо эту четность «сделать». Рассмотрим полином
$$ tilde F(x,Y) equiv Phi_{}(x,y) Phi_{}(x,-y) quad npu quad Y=y^2 . $$

Теорема 2 [6]. Уравнение $ Phi_{}(x,y)=0 $ не имеет вещественных решений если одновременно выполняются два условия:

a) уравнение $ Phi(x,0)=0 $ не имеет вещественных решений;

б) уравнение
$$ widetilde{mathcal F}(z)=mathcal D_x( widetilde{F} (x,z-x^2))=0 $$
не имеет положительных решений.

Если хотя бы одно из этих условий не выполняется, то квадрат расстояния от начала координат до кривой $ Phi(x_{},y)=0 $ равен либо квадрату минимального по модулю вещественного корня уравнения $ Phi(x,0)=0 $, либо же минимальному положительному корню уравнения $ widetilde{mathcal F}(z)= 0 $, при условии, что последний не является кратным. Здесь $ {mathcal D}_{} $ — дискриминант полинома, рассматриваемого относительно переменной $ x_{} $.

Пример. Найти расстояние от начала координат до кривой

$$
begin{array}{lll}
Phi(x,y) & = & 32,x^4y+64,x^2y^3+32,y^5-16,x^4-96,x^2y^2-80,y^4+
\
&& +48,x^2y+80,y^3+120,x^2-576,xy+56,y^2+160,x-118,y+71=0 .
end{array}
$$

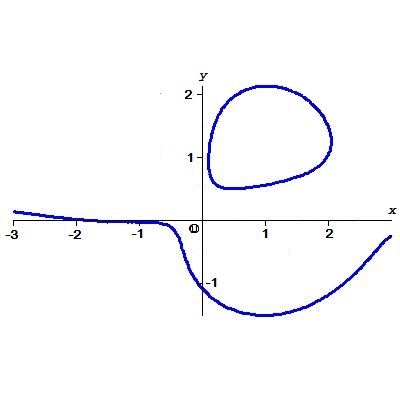
Решение. Опуская промежуточные выкладки, привожу только выражение для дискриминанта:
$$ widetilde{mathcal F}(z) equiv widetilde{mathcal F}_1(z) widetilde{mathcal F}_2^2(z) $$
при
$$
widetilde{mathcal F}_1(z) =
{scriptstyle 87241523200},z^{15}-{scriptstyle 244343373824},z^{14}+
{scriptstyle 6135125901312},z^{13}-{scriptstyle 99762334334976},z^{12}+{scriptstyle 122650759266304},z^{11}-
$$
$$
-{scriptstyle 2018722496380928},z^{10}
+{scriptstyle 36775841922285568},z^9+{scriptstyle 83476886207856640},z^8-{scriptstyle 125448251244072960},z^7-{scriptstyle 3659244138715855872},z^6-
$$
$$
-{scriptstyle 16653164114254566912},z^5-{scriptstyle 39789124482714260608},z^4+{scriptstyle 21724179049244829584},z^3-{scriptstyle 2250891598084946580},z^2+{scriptstyle 484733011031273132},z-
$$
$$
-{scriptstyle117947376101831257}
$$
и
$$
widetilde{mathcal F}_2(z) =4096,z^6+18432,z^5+18176,z^4-1501440,z^3+305136,z^2+2195912,z+709721
, .
$$
Полином $ widetilde{mathcal F}_1(z) $ имеет три вещественных корня: $ lambda_1 approx 0.208349, lambda_2 approx 0.360823, lambda_3 approx 6.480707 $. Вещественные корни $ Phi(x,0) $: $ mu_1 approx -1.835484, mu_2 approx 3.306151 $.

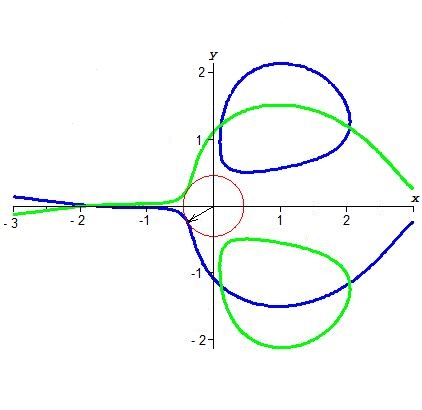
Сомножитель $ widetilde{mathcal F}_2^2(z) $ я отбросил как «посторонний», т.е. его корни — все они кратные — не сравнивал по величине с $ lambda_1 $ и $ mu_1^2 $. Откуда, собственно, этот сомножитель взялся? Будет ли он присутствовать и в общем случае, т.е. можно ли в полиноме $ widetilde{mathcal F} $ из теоремы $ 2 $ выделить сомножитель в виде квадрата некоторого другого полинома? — Для того, чтобы угадать происхождение этого множителя всё же вычислим его положительные корни: $ xi_1 approx 1.483677, xi_2 approx 5.553837 $. Теперь изобразим на последнем рисунке окружности $ x^2+y^2= xi_{1,2} $:

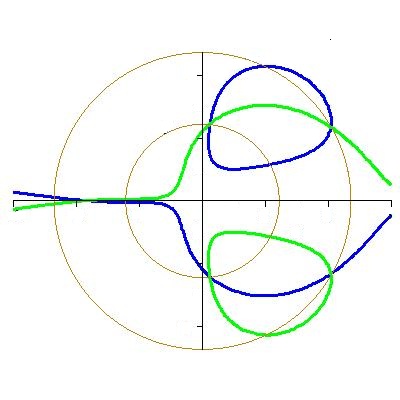
Окружности прошли через точки пересечения кривых $ Phi_{}(x,y) = 0 $ и $ Phi_{}(x,-y) =0 $.

Гипотеза. Разложим полином $ Phi_{}(x,y) $ по степеням $ y_{} $ и выделим четные и нечетные слагаемые по этой переменной:
$$ Phi_{}(x,y) equiv F_1(x,Y)+ y F_2(x,Y) qquad npu quad Y=y^2 . $$
С точностью до постоянного сомножителя, имеет место тождество
$$ widetilde{mathcal F}_2(z) equiv mathcal R_x(F_1(x,z-x^2),F_2(x,z-x^2)) . $$
Здесь $ mathcal R_{} $ — результант полиномов, рассматриваемых относительно переменной $ x_{} $.

Ответ. $ d approx 0.456453 $.

Расстояние в пространстве матриц

до некоторых критических многообразий:

до многообразия вырожденных матриц;
до многообразия матриц, имеющих собственное число на мнимой оси $ mathfrak{Re}(z)=0 $ комплексной плоскости;
до многообразия матриц, имеющих кратные собственные числа

☞

ЗДЕСЬ.

Разные задачи

Обобщенная задача Ферма-Торричелли

Задача. Пусть на плоскости заданы три точки $ P_1=(x_1,y_1),P_2=(x_2,y_2),P_3=(x_3,y_3) $, не лежащие на одной прямой.
Определить координаты точки $ P_{ast}=(x_{ast},y_{ast}) $, решающей задачу оптимизации:
$$
min_{(x,y)} F(x,y) quad mbox{ для } quad F(x,y)= sum_{j=1}^3m_j sqrt{(x-x_j)^2+(y-y_j)^2} .
$$
Здесь числа $ m_1,m_2,m_3 $ предполагаются положительными и в дальнейшем называются весами.

Задача известна под различными названиями: (обобщенная) задача Ферма-Торричелли-Штейнера,
задача Вебера, задача об оптимальном расположении (узловой) станции⁴⁾, задача о трёх заводах.

Пример. В точках $ P_{1},P_2,P_3 $ расположены источники полезных ископаемых: железной руды, угля и воды соответственно. Известно, что для производства одной тонны стали необходимо иметь $ m_{1} $ тонн руды, $ m_2 $ тонн угля и $ m_3 $ тонн воды. В предположении, что стоимость перевозки одной тонны груза не зависит от его природы, где следует расположить сталелитейное производство так, чтобы минимизировать транспортные издержки?

Подробное обсуждение этой задачи (и к ней примыкающих)

☞

ЗДЕСЬ.

Задача о точке Лемуана-Греба

Задача. Найти точку плоскости, cумма квадратов расстояний от которой до сторон треугольника, лежащего в этой же плоскости, минимальна.

В русскоязычной литературе [5] иногда называется задачей Кэзи⁵⁾, однако в других источниках атрибуция приведенной задачи Кэзи не подтверждена. См. краткое описание
истории задачи

☞

ЗДЕСЬ.

Решение. Пусть $ d_1, d_2,d_3 $ — расстояния от точки $ P_{} $ плоскости до сторон треугольника с длинами
$ D_1, D_2, D_3 $ соответственно. Воспользуемся тождеством Лагранжа:
$$ (d_1^2+ d_2^2+d_3^2)(D_1^2+ D_2^2+D_3^2)equiv $$
$$ equiv (d_1D_1+ d_2D_2+d_3D_3)^2+(d_1D_2-d_2D_1)^2+(d_2D_3-d_3D_2)^2+
(d_1D_3-d_3D_1)^2 . $$
Величина $ d_1D_1+ d_2D_2+d_3D_3 $ является постоянной, не зависящей от координат точки $ P_{} $:
$$ d_1D_1+ d_2D_2+d_3D_3 =2S , $$
где $ S_{} $ — площадь данного треугольника. Следовательно
$ min (d_1^2+d_2^2+d_3^2) $
достигается при условиях
$$ d_1D_2-d_2D_1=0, d_2D_3-d_3D_2=0, d_1D_3-d_3D_1=0 , $$
то есть когда
$$ frac{d_1}{D_1}=frac{d_2}{D_2}=frac{d_3}{D_3} . $$
Определяемая этими соотношениями точка называется точкой Лемуана⁶⁾ или точкой Греба⁷⁾; в ней пересекаются симедианы треугольника.

Интересна параллель этой задачи с решаемой в пункте

☞

РАССТОЯНИЕ ДО ПЛОСКОСТИ: в трехмерном пространстве найти ближайшую к началу координат точку плоскости $ D_1x+D_2y+D_3z=2 S $. Решением будет точка с координатами $ (d_1,d_2,d_3) $.

Еще некоторые задачи

Построение прямой на плоскости, сумма квадратов расстояний до которой от заданных точек минимальна

☞

ЗДЕСЬ

Задачи учебные

Источники

[1]. Чезаро Э. Элементарный учебник алгебраического анализа и исчисления бесконечно малых. c.360-361

[2]. Икрамов Х.Д. Задачник по линейной алгебре. М.Наука. 1975 .

[3]. Uteshev A.Yu., Yashina M.V. Distance Computation from an Ellipsoid to a Linear or a Quadric Surface in)) $ {mathbb R}^{n} $. Lect.Notes Comput. Sci. 2007. V.4770. P.392-401

[4]. Uteshev A.Yu., Yashina M.V. Metric Problems for Quadrics in Multidimensional Space. J.Symbolic Computation, 2015, Vol. 68, Part I, P. 287-315. Текст

☞

ЗДЕСЬ (pdf)

[5]. Попов Г.Н. Сборник исторических задач по элементарной математике. М.-Л.ГТТИ.1932

[6]. Uteshev A.Yu., Goncharova M.V. Metric problems for algebraic manifolds: Analytical approach. Constructive Nonsmooth Analysis and Related Topics (dedicated to the memory of V.F. Demyanov) (CNSA), 2017, IEEE, http://ieeexplore.ieee.org/document/7974027/

Источник

VMath

Инструменты сайта

Основное

Информация

Действия

Содержание

Вычисление расстояний между геометрическими объектами

Линейные многообразия

Расстояние от точки до линейного многообразия (плоскости)

Задача. Найти расстояние от точки $ X_ <0>in <mathbb R>^ $ до линейного многообразия (плоскости) $ mathbb M $ в $ <mathbb R>^ $, заданного системой уравнений $$ left< begin c_<11>x_1+c_<12>x_2+dots+c_<1n>x_n &=& h_1 \ dots & & dots \ c_x_1+c_x_2+dots+c_x_n &=& h_m end right. $$ или, в матричном виде $$ CX= <mathcal H>quad npu quad C=left( begin c_<11>& c_ <12>& dots & c_ <1n>\ dots & & & dots \ c_& c_ & dots & c_ end right)_ , <mathcal H>=left( begin h_1 \ vdots \ h_m end right), X=left( begin x_1 \ x_2 \ vdots \ x_n end right) $$ При этом предполагается, что $ mle n_<> $ и что ранг матрицы $ C_<> $ равен $ m_<> $, то есть система уравнений совместна и определяемое ею многообразие в $ <mathbb R>^ $ является $ (n-m)_<> $-мерным.

Теорема 1. [1]. Составим квадратную матрицу порядка $ m+1_<> $:

$$ M=left( begin Ccdot C^ <top>& CX_0- <mathcal H>\ (CX_0- <mathcal H>)^ <top>& 0 end right) $$ Расстояние от точки $ X_ <0>$ до линейного многообразия $ mathbb M $ вычисляется по формуле $$ d= sqrt<-frac<det M><det(Ccdot C^<top>)>> . $$

Доказательство ☞ ЗДЕСЬ.

Расстояние от точки $ X_<0>=(x_<10>,dots,x_)^ <top>$ до гиперплоскости (или, в случае $ n=2 $, прямой)

$$ c_1x_1+dots+c_nx_n= h $$ равно $$ d= frac<|c_1x_<10>+dots+c_nx_-h|><sqrt> . $$ Ближайшая к $ X_0 $ точка гиперплоскости: $$ X_<ast>=X_0- frac+dots+c_nx_-h> left(begin c_1 \ vdots \ c_n end right) , . $$

Пусть теперь линейное многообразие (плоскость) задано параметрически $$ mathbb M= < Y_0+lambda_1 Y_1+dots+lambda_k Y_k quad mid quad <lambda_1,dots,lambda_k>subset <mathbb R>> $$ при фиксированных столбцах $$ \subset <mathbb R>^n . $$ Предположим, что эти столбцы линейно независимы. Составим из них матрицы $$ L=left[ Y_1|dots|Y_k right]_ quad u quad tilde L = left[ Y_1|dots|Y_k| X_0-Y_0 right]_ $$ (здесь $ |_<> $ означает конкатенацию).

Теорема 2. Расстояние $ d_<> $ от точки $ X_ <0>$ до линейного многообразия $ mathbb M $ вычисляется по формуле

Теорема 3. Ближайшая к точке $ X_0 $ точка многообразия $ mathbb M_<> $ (проекция точки на многообразие) определяется по формуле

Доказательство ☞ ЗДЕСЬ.

Пример. Найти расстояние от точки $ X_<0>=(1,1,1,1)^ <top>$ до плоскости

Решение. 1-й способ: применение теоремы 1. Имеем: $$ C=left( begin 3 & 1 & -1 & 1 \ 1 & -2 & 1 & 2 end right), <mathcal H>= left( begin 1 \ 2 end right), $$ $$ Ccdot C^ <top>= left( begin 12 & 2 \ 2 & 10 end right), CX_0=left( begin 4 \ 2 end right), CX_0-<mathcal H>=left( begin 3 \ 0 end right) , $$ $$ frac<left| begin 12 & 2 & 3 \ 2 & 10 & 0 \ 3 & 0 & 0 end right|><left| begin 12 & 2 \ 2 & 10 end right|>=frac<-90><116>=-frac<45> <58> . $$

2-й способ: применение теоремы 2. Общее решение системы уравнений, задающей плоскость: $$ x_3=frac<5><3>x_1+frac<4><3>x_2, x_4=1-frac<4><3>x_1+frac<1><3>x_2 . $$ Таким образом, плоскость может быть представлена в параметрическом виде $$ Y_0+lambda_1 Y_1 + lambda_2 Y_2 quad npu quad Y_0 = left( begin 0 \ 0 \ 0 \ 1 end right), Y_1=left( begin 0 \ 3 \ 4 \ 1 end right), Y_2=left( begin 3 \ 0 \ 5 \ -4 end right) . $$ Имеем: $$ L= left( begin 0 & 3 \ 3 & 0 \ 4 & 5 \ 1 & -4 end right), tilde L =left( begin 0 & 3 & 1 \ 3 & 0 & 1 \ 4 & 5 & 1 \ 1 & -4 & 0 end right), frac<left| begin 26 & 16 & 7 \ 16 & 50 & 8 \ 7 & 8 & 3 end right|><left| begin 26 & 16 \ 16 & 50 end right|>=frac<810><1044>=frac<45> <58> . $$ Координаты ближайшей точки к $ X_ <0>$: $$ X_<ast>= left(begin 1 \ 1 \ 1 \ 1 endright)+left( begin 0 & 3 \ 3 & 0 \ 4 & 5 \ 1 & -4 end right)left( begin 26 & 16 \ 16 & 50 \ end right)^ <-1>left(begin 0 & 3 & 4 & 1 \ 3 & 0 & 5 & -4 end right)left(begin 1 \ 1 \ 1 \ 0 endright)=frac<1> <58>left(begin 16 \ 37 \ 76 \ 49 endright) , . $$

Ответ. $ d=sqrt <45/58>approx 0.8808303295 $.

Расстояние между линейными многообразиями (плоскостями)

Теорема. Расстояние между линейными многообразиями $ mathbb M_1 $ и $ mathbb M_2 $ вычисляется по формуле

Пример. [2]. Найти расстояние между плоскостями

$$ left( begin 89 \ 37 \ 111 \ 13 \54 end right) + lambda_1 left( begin 1 \ 1 \ 0 \ -1 \ -1 end right) + lambda_2 left( begin 1 \ -1 \ 0 \ -1 \ 1 end right) quad mbox < и >quad left( begin 42 \ -16 \ -39 \ 71 \3 end right) + mu_1 left( begin 1 \ 1 \ 0 \ 1 \ 1 end right) + mu_2 left( begin 1 \ -1 \ 0 \ 1 \ -1 end right) . $$

Решение. $$ P^<top>cdot P=4cdot E_<4 times 4>, quad tilde P^<top>cdot tilde P= left(begin 4 & 0 & 0 & 0 & 107 \ 0 & 4 & 0 & 0 & 103 \ 0 & 0 & 4 & 0 & 93\ 0 & 0 & 0 & 4 & -115 \ 107 & 103 & 93 & -115 & 33483 end right) . $$

Ответ. $ d=150_<> $.

Квадратичные многообразия (квадрики)

стационарные точки $ rightarrow $ критические значения

Расстояние от точки до квадрики

Теорема 1. Пусть квадрика в $ <mathbb R>^ $, задана уравнением

$$ X^<top>AX+2B^<top>X-1=0 , (A=A^<top>) . $$ Квадрат расстояния до нее от не лежащей на ней точки $$ X_ <0>in <mathbb R>^, quad ( X_0^<top>AX_0+2 B^<top>X_<0>-1ne 0 ) $$ равен минимальному положительному корню уравнения расстояний $$ <mathcal F>(z)=0 quad npu quad <mathcal F>(z)=<mathcal D>_ <mu>left( Phi(mu,z) right) . $$ Здесь $$ Phi(mu,z)=det left( left[ begin A & B \ B^ <top>& -1 end right] + mu left[ begin -E & X_0 \ X_0^ <top>& z-X_0^<top>X_0 end right] right), $$ $ <mathcal D>_<> $ означает дискриминант полинома $ Phi(mu,z) $, рассматриваемого относительно переменной $ mu_<> $, а $ E_<> $ — единичная матрица порядка $ n_<> $. Дополнительно предполагается, что указанный корень не является кратным.

[3]. Квадрат расстояния от начала координат $ <mathbb O>in <mathbb R>^ $ до квадрики в $ <mathbb R>^ $, заданной уравнением

$$ X^<top>AX+2,B^<top>X-1=0 , $$ равен минимальному положительному корню уравнения расстояний $$ <mathcal F>(z)=0, quad npu quad <mathcal F>(z)=<mathcal D>_ <mu>left( f(mu)(mu z-1)-B^<top>q(A,mu)B right) , $$ и при условии, что указанный корень не является кратным. Здесь $ f(mu_<>)=det (A-mu E) $ — характеристический полином матрицы $ A_<> $, а $ q(A,mu)_<> $ — матрица взаимная матрице $ A-mu E_<> $.

В частном случае $ B=<mathbb O>_<> $ (квадрика центрирована к началу координат), имеем:

$$ <mathcal F>(z)=left[z^nf(1/z) right]^2<mathcal D>_<mu>(f(mu)) , $$ и расстояние от начала координат до квадрики оказывается равным $ 1/sqrt<lambda_<max>^<>> $, где $ lambda_<max>^<> $ — максимальное собственное число матрицы $ A_<> $.

Пример. Найти расстояние от начала координат до эллипсоида

Решение. Здесь $$A = left( <begin frac<7> <18>& -frac<1> <9>& 0 \ && \ -frac<1> <9>& frac<1> <3>& -frac<1> <9>\ && \ 0 & -frac<1> <9>& frac<5> <18>end> right),quad B = left( begin -frac<1> <12>\ \ -frac<1> <9>\ \ frac<5> <36>end right) ,$$ $$ f(mu)=det (A-mu E)=-mu ^ <3>+ mu ^ <2>- frac<11> <36>mu + frac <1> <36>$$ Матрица взаимная матрице $ A-mu E_<> $: $$ q(A, mu)= left( begin mu ^ <2>- frac<11> <18>mu + frac<13> <162>& — frac<1> <9>mu + frac<5> <162>& frac<1> <81>\ && \ — frac<1> <9>mu + frac<5> <162>& mu^2 -frac<2><3>mu+frac<35> <324>& — frac<1> <9>mu +frac<7> <162>\ && \ frac<1> <81>& — frac<1> <9>mu + frac<7> <162>& mu ^ <2>- frac<13><18>mu+frac<19> <162>end right) . $$ $$ Phi(mu,z)=f(mu)(mu z-1)-B^<top>q(A,mu)B= $$ $$ =-z mu ^ <4>+ (z+1) mu ^ <3>+ left(-frac <11> <36>z — frac<673><648>right) mu ^ <2>+left( frac <1> <36>z + frac <241> <729>right) mu — frac <1621> <52488> . $$ Воспользуемся детерминантным представлением дискриминанта: $$ <mathcal F>(z) = <mathcal D>_ <mu>(Phi(mu,z)) = frac<1> <16>times $$ $$ times left| begin 4z & — 3z-3 & frac<11><18>z + frac<673> <324>& — frac<1> <36>z — frac<241> <729>& 0 & 0 \ &&&&& \ 0 & 4z & — 3z-3 & frac<11> <18>z + frac<673> <324>& — frac<1> <36>z — frac<241> <729>& 0 \ &&&&& \ 0 & 0 & 4z & — 3z-3 & frac<11><18>z + frac<673> <324>& — frac<1> <36>z — frac<241> <729>\ &&&&& \ 0 & 0 & — z — 1 & frac<11><18>z + frac<673> <324>& — frac<1> <12>z — frac<241> <243>& frac<1621> <13122>\ &&&&& \ 0 & — z — 1 & frac<11><18>z + frac<673> <324>& — frac<1><12>z — frac<241> <243>& frac<1621> <13122>& 0 \ &&&&& \ — z — 1 & frac<11> <18>z + frac<673> <324>& — frac<1> <12>z — frac<241> <243>& frac<1621> <13122>& 0 & 0 end right| = $$ $$ =2^<-11>3^ <-24>( 38263752,z^6-966487788,z^5+9376985736,z^4-43882396481,z^3+$$ $$ +102982092872,z^2-116747905827,z+50898162294) quad . $$ Вещественные корни уравнения расстояний: $$ z_1approx 1.394685, z_2 approx 5.701814, z_3 approx 7.043941, z_4 approx 7.590060 . $$

Ответ. $ d= sqrt approx 1.180968 $.

Нахождение точки на квадрике, ближайшей к заданной точке $ X_ <0>$, возможно с помощью следующего результата.

Теорема 2. При выполнении условий теоремы 1, координаты точки $ X_ <ast>$ квадрики, ближайшей к точке $ X_ <0>$ находятся по формуле

$$ X_<ast>=-A^ <-1>B — mu_ <ast>(A -mu_<ast>E)^ <-1>(A^ <-1>B+X_0)=(mu_<ast>E- A)^ <-1>(B+mu_ <ast>X_0) . $$ Здесь $ mu_ <ast>$ означает кратный корень полинома $ Phi(mu,z_<ast>) $, где полином $ Phi(mu,z) $ берется из формулировки теоремы 1, а $ z_<ast>^<> $ означает минимальный положительный корень уравнения расстояний.

Этот результат требует пояснений. Итак, поскольку дискриминант полинома $ Phi(mu,z_<ast>) $ обращается в нуль, то у этого полинома — как полинома по $ mu_<> $ — имеется кратный корень $ mu =mu_ <ast>$. Можно доказать [4], что при условии простоты корня $ z=z_ <ast>$ уравнения расстояний $ mathcal F(z)=0 $ кратность корня $ mu =mu_ <ast>$ для полинома $ Phi(mu,z_<ast>) $ будет равна ровно $ 2_<> $, и других кратных корней этот полином не имеет. Но тогда, выражение для $ mu_<ast>^<> $ может быть найдено в виде рациональной функции коэффициентов полинома $ Phi(mu,z_<ast>) $. Последнее утверждение может быть доказано разными способами, и в качестве самого наглядного выберем тот, что основан на свойствах дискриминанта, например, на том, что изложено ☞ ЗДЕСЬ.

При выполнении условия предыдущей теоремы, координаты точки $ X_<ast>^<> $, ближайшей на квадрике к точке $ X_ <0>$, являются рациональными функциями от квадрата расстояния.

Точка $ X_ <ast>$ квадрики $ X^<top>AX+2,B^<top>X-1=0 $, ближайшая к началу координат $ X_0= mathbb O $, находится по формуле:

$$ X_ <ast>= — frac<1>)> q(A,mu_<ast>) B . $$ Здесь $ f(mu_<>)=det (A-mu E) $ — характеристический полином матрицы $ A_<> $, $ q(A,mu)_<> $ — матрица взаимная матрице $ A-mu E_<> $, а $ mu_ <ast>$ означает кратный корень уравнения $$f(mu)(mu z_<ast>-1)-B^<top>q(A,mu)B=0 , $$ где $ z_<ast>^<> $ — величина квадрата расстояния от $ mathbb O_<> $ до квадрики.

Пример. Найти ближайшую к началу координат точку эллипсоида из предыдущего примера.

Решение. Подставляем $ z_<>=z_ <ast>approx 1.394685 $ в формулу для определения кратного корня, т.е. в отношение двух конкретных миноров детерминантного представления дискриминанта: $$ mu=-frac<left| begin 4z & — 3z-3 & frac<11> <18>z + frac<673> <324>& 0 \ &&& \ 0 & 4z & — 3z-3 & — frac<1> <36>z — frac<241> <729>\ &&& \ 0 & — z — 1 & frac<11><18>z + frac<673> <324>& frac<1621> <13122>\ &&& \ — z — 1 & frac<11><18>z + frac<673> <324>& — frac<1><12>z — frac<241> <243>& 0 end right|> <left| begin 4z & — 3z-3 & frac<11> <18>z + frac<673> <324>& — frac<1> <36>z — frac<241> <729>\ &&& \ 0 & 4z & — 3z-3 & frac<11><18>z + frac<673> <324>\ &&& \ 0 & — z — 1 & frac<11><18>z + frac<673> <324>& — frac<1><12>z — frac<241> <243>\ &&& \ — z — 1 & frac<11><18>z + frac<673> <324>& — frac<1><12>z — frac<241> <243>& frac<1621> <13122>end right|> $$ получаем $ mu_<ast>^<> approx 0.572670 $. Подставляем это значение в формулу для определения $ X_<ast>^<> $ из последнего следствия: $$ X_<ast>approx left(begin 0.071171 \ -0.867719 \ 0.797924 end right) . $$

Проверка. Если подставить вместо $ X_ <ast>$ его приближенное значение, то получим: $$ X_<ast>^ <top>X_ <ast>approx mathbf<1.39468>4, X_<ast>^<top>AX_<ast>+2,B^<top>X_<ast>-1 approx 2.9cdot 10^<-5> , $$ и вектор $ <mathbb O>X_ <ast>$ перпендикулярен эллипсоиду в точке $ X_<>=X_ <ast>$: $$ AX_<ast>+B approx left(begin 0.040757\ -0.496917 \ 0.456948 end right)approx mu_ <ast>X_ <ast> . $$

Расстояние от линейного многообразия (плоскости) до квадрики

Задача. Найти расстояние от эллипсоида в $ <mathbb R>^ $, заданного уравнением $$ X^<top>AX+2B^<top>X-1=0 , (A=A^<top>) $$ до линейного многообразия (плоскости) в $ <mathbb R>^ $, заданной системой уравнений $$ left< begin c_<11>x_1+c_<12>x_2+dots+c_<1n>x_n &=& 0 \ dots & & dots \ c_x_1+c_x_2+dots+c_x_n &=& 0 end right. iff CX= <mathbb O>quad npu quad C=left( begin c_<11>& c_ <12>& dots & c_ <1n>\ dots & & & dots \ c_& c_ & dots & c_ end right)_ $$ При этом предполагается, что $ mle n_<> $ и что ранг матрицы $ C_<> $ равен $ m_<> $, т.е. определяемая системой плоскость в $ <mathbb R>^ $ является $ (n-m)_<> $-мерной.

Теорема. [3]. Необходимое и достаточное условие того, что линейное многообразие (плоскость) пересекает эллипсоид зависит от знакоопределенности матрицы $ A_<> $:

Теорема. [3]. Если условие предыдущей теоремы не выполняется, то квадрат расстояния от эллипсоида до плоскости совпадает с минимальным положительным корнем полинома

$$ <mathcal F>(z) =<mathcal D>_mu left( mu^m left| begin A & B & C^<top>\ B^ <top>& -1 + mu z & mathbb\ C & mathbb & frac<1> <mu>C cdot C^ <top>end right| right), $$ в предположении, что этот корень не является кратным. Здесь $ <mathcal D>_<> $ — дискриминант полинома, рассматриваемого относительно переменной $ mu_<> $.

Если строки матрицы $ C_<> $ ортонормированны, то преобразованием определителя в теореме можно понизить его порядок: выражение под знаком дискриминанта можно преобразовать в

Пример. Найти расстояние от оси $ <mathbb O>x_ <1>$ до эллипсоида

$$ 7, x_1^2+6, x_2^2 +5, x_3^2 -4,x_1x_2-4,x_2x_3-37,x_1-12,x_2+3,x_3+54=0 . $$

Решение. Здесь $$ A= left( begin -frac<7> <54>& frac<1> <27>& 0 \ &&\ frac<1> <27>& -frac<1> <9>& frac<1> <27>\ &&\ 0 & frac<1> <27>& -frac<5> <54>end right), B=left( begin frac<37> <108>\ \ frac<1> <9>\ \ -frac<1> <36>end right) $$ и можно взять $$ C= left( begin 0 & 1 & 0 \ 0 & 0 & 1 end right) . $$ Матрица $ A_<> $ отрицательно определена, условие пересечения прямой и эллипсоида не выполняется: $$ left| begin A & B & C^<top>\ B^ <top>& -1 & <mathbb O>\ C & <mathbb O>& mathbb end right| times (-1)^3 = — frac <143>

Расстояния в $ <mathbb R>^ $ от плоскости

$$ c_1x_1+dots+c_nx_n = h iff CX=h $$ до ближайшей и до самой дальней точек эллипсоида $$ X^<top>AX+2B^<top>X-1=0 , (A=A^<top>) $$ совпадают с модулями корней полинома: $$ <mathcal F>(Z)=left| begin A & B & C^<top>/|C|\ B^ <top>& -1 & Z-h/|C|\ C/|C| & Z-h/|C| & 0 end right| . $$ Здесь $ |C|=sqrt> $ и предполагается, что поверхности не пересекаются.

Пример. Найти расстояние от прямой $ 2, x_1- x_<2>=0 $ до эллипса

$$ 7,x_1^2-4,x_1x_2 + 6, x_2^2-47, x_1 -24, x_ <2>+124 = 0 .$$

Решение. Здесь $$ <mathcal F>(Z)=left| begin A & B & C^<top>/|C| \ B^ <top>& -1 & Z-h/|C| \ C/|C| & Z-h/|C| & 0 end right| = left| begin -frac<7> <124>& frac<1> <62>& frac<47> <248>& frac<2><sqrt<5>> \ &&& \ frac<1> <62>& — frac<3> <62>& frac<3> <31>&- frac<1><sqrt<5>> \ &&& \ frac<47> <248>& frac<3> <31>& -1 & Z \ &&& \ frac<2><sqrt<5>> & — frac<1><sqrt<5>> & Z & 0 end right| = $$ $$ =-frac<1><307520>left(760,Z^2+1592sqrt<5>, Z+2383 right) $$ и корни этого полинома: $$ -frac<199><190>sqrt<5>pm frac<1> <76>sqrt <13570> . $$

Ответ. $$ d = left| -frac<199><190>sqrt<5>+ frac<1> <76>sqrt <13570>right| approx 0.809219_<> . $$

Расстояние между квадриками

Теорема. Пусть $ X^ <top>A_ <1>X =1 $ и $ X^ <top>A_ <2>X =1 $ – квадрики в $ <mathbb R>^ $, причем первая является эллипсоидом. Квадрики не пересекаются тогда и только тогда, когда матрица $ A_<1>-A_2 $ является знакоопределенной.

Доказательство ☞ ЗДЕСЬ.

Теорема. [3,4]. Если выполняется условие предыдущей теоремы, то квадрат расстояния между

$$ mbox <эллипсоидом> X^ <top>A_ <1>X =1 mbox<и квадрикой> X^ <top>A_ <2>X =1 $$ совпадает с минимальным положительным корнем уравнения расстояний $$ <mathcal F>(z)=0 quad npu quad <mathcal F>(z)=<mathcal D>_ <lambda>left( Phi(lambda,z) right) . $$ Здесь $$ Phi(lambda,z)=det (lambda A_1 + (z- lambda) A_2 — lambda (z-lambda) A_1 A_2), $$ $ <mathcal D>_<> $ — дискриминант полинома рассматриваемого относительно переменной $ lambda_<> $. Дополнительно предполагается, что указанный корень не является кратным.

Пример. Найти расстояние между эллипсами

$$10,x_1^2-12,x_1x_2+8,x_2^2=1 qquad u qquad x_1^2+x_1x_2+x_2^2=1 . $$

Решение. Здесь $$ A_1= left( begin 10 & — 6 \ -6 & 8 end right), quad A_2= left( begin 1 & frac<1> <2>\ frac<1> <2>& 1 end right) $$ и матрица $ A_<1>-A_2 $ положительно определена. Следовательно эллипсы не пересекаются. $$ Phi(lambda,z)=det (lambda A_1 + (z- lambda) A_2 — lambda (z-lambda) A_1 A_2)= $$ $$ =33,lambda^4+left(-66z+frac<149><2>right)lambda^3+left(33,z^2-61,z+frac<83><4>right)lambda^2+left(-frac<27><2>z^2+frac<45><2>zright)lambda+frac<3><4>,z^2 $$ и дискриминант этого полинома по переменной $ lambda_<> $ равен $$ <mathcal F>(z)=frac<3><16>z^2 (<scriptstyle 936086976>, z^6-<scriptstyle 10969697376>,z^5+ <scriptstyle 50706209664>, z^4 -<scriptstyle 115515184664>, z^3+<scriptstyle 130176444432>, z^2 -<scriptstyle 59826725574>,z+<scriptstyle 2866271785>) . $$ Положительные корни уравнения расстояний $ <mathcal F>(z)=0 $: $$ z_1 approx 0.053945666, z_2 approx 1.3340583883, z_3 approx 1.95921364, z_4 approx 2.8785867381 . $$

Ответ. $ d_<>= sqrt approx 0.23226206 $.

1. Если $ z=z_ <ast>$ — корень полинома $ <mathcal F>(z) $, то это значит, что полином $$ Phi(lambda, z_<ast>) = det ( lambda A_1 +(z_<ast>-lambda)A_2 — lambda (z_<ast>-lambda) A_2A_1) $$ имеет кратный корень $ lambda_<> = lambda_ <ast>$. При выполнении условий теоремы, этот корень будет единственным второй кратности и его можно выразить в виде рациональной функции от $ z_ <ast>$ с помощью субдискриминантов.

2. Столбец координат $ X_<ast>^<> $ точки первой квадрики, удовлетворяет тогда однородной системе уравнений $$ ( lambda_ <ast>A_1 +(z_<ast>-lambda_<ast>)A_2 — lambda_ <ast>(z_<ast>-lambda_<ast>) A_2A_1) X = mathbb O , $$ которая имеет бесконечное множество решений, поскольку определитель ее матрицы равен нулю. Из этого бесконечного множества мы выделяем те решения, что удовлетворяют условию $ X^<top>A_<1>X=1 $.

При выполнении условий теоремы таких решений будет два (что соответствует симметрии задачи, см. рисунок).

Аналогично, столбец координат $ Y_<ast>^<> $ точки на второй квадрике $ Y^<top>A_<2>Y=1_<> $ будет решением системы уравнений $$ ( lambda_ <ast>A_1 +(z_<ast>-lambda_<ast>)A_2 — lambda_ <ast>(z_<ast>-lambda_<ast>) A_1A_2) Y = mathbb O . $$

Для нахождения решений воспользуемся одним из результатов теории систем линейных уравнений. Составим столбец из алгебраических дополнений к элементам какой-либо строки матрицы $$ M= lambda_ <ast>A_1 +(z_<ast>-lambda_<ast>)A_2 — lambda_ <ast>(z_<ast>-lambda_<ast>) A_2A_1 . $$ Тогда вектор $ X_<ast>^<> $ отличается от этого столбца лишь множителем, который определится из условия $ X^<top>A_<1>X=1_<> $. Аналогично, для получения столбца координат $ Y_<ast>^<> $ возьмем столбец из алгебраических дополнений к элементам какого-либо столбца той же матрицы $ M_<> $ и домножим его на константу, чтобы обеспечить выполнение условия $ Y^<top>A_<2>Y=1_<> $.

3. Получившиеся пары $ X_<ast>,Y_<ast>^<> $ надо согласовать: они должны подчиняться условию $$ (X_<ast>-Y_<ast>)^<top>(X_<ast>-Y_<ast>)=z_ <ast> . $$

Пример. Найти ближайшие точки эллипсов из предыдущего примера.

Решение. Для найденного значения $ z_<ast>=z_1 approx 0.053945666_<> $ определитель матрицы $$ M=left( begin 7,lambda^2+(-7z+9)lambda+z & -2lambda^2+(2,z-frac<13><2>)lambda+frac<1><2>z \ & \ -lambda^2+(z-frac<13><2>)lambda+frac<1><2>z & 5lambda^2+(-5z+7)lambda+z end right) $$ как полином по $ lambda_<> $ будет иметь кратный корень. Этот корень определяем 1) с помощью субдискриминантов в виде: $$ lambda=-frac<-725274,z^5+1455894,z^4+frac<11286981><2>z^3-frac<26486523><2>z^2+frac<42000075><8>z> <17591706,z^4-109992894,z^3+frac<450450691><2>z^2-frac<315606253><2>z+frac<77466805><8>> . $$ Подстановка сюда $ z=z_<ast>^<> $ даст $ lambda_ <ast>approx -0.13576051_<> $.

Далее, при найденных значениях $ z_<> $ и $ lambda_<> $ система линейных уравнений $$ MX=mathbb O_ <2times 1>$$ должна иметь бесконечное множество решений относительно вектора $ X_<2times 1>^<> $. Одно из этих решений может быть построено (см. упражнение ☞ ЗДЕСЬ ) с помощью алгебраических дополнений к элементам, например, второй строки матрицы $ M_<> $: $$ left( begin 2lambda^2-(2,z-frac<13><2>)lambda-frac<1><2>z \ \ 7,lambda^2+(-7z+9)lambda+z end right) quad begin longrightarrow \ z=z_<ast>, lambda= lambda_ <ast>end quad X=left( begin -0.8579069 \ \ -0.9876166 end right) . $$ Любое другое решение получается домножением полученного на произвольную константу («растяжением» вектора). Воспользуемся этим, чтобы добиться выполнения условия $ X^<top>A_ <1>X =1_<> $. $$ X_<ast>=frac<1><sqrtA_1 X>> X approx left( begin -0.3838312 \ -0.4418639 end right) . $$ Аналогично, для нахождения точки на другом эллипсе, мы решаем систему $$ M^<top>Y=mathbb O_ <2times 1> , $$ представив ее решение опять-таки с помощью алгебраических дополнений к элементам второго столбца матрицы $ M_<> $: $$ left( begin lambda^2-(z-frac<13><2>)lambda-frac<1><2>z \ \ 7,lambda^2+(-7z+9)lambda+z end right) quad begin longrightarrow \ z=z_<ast>, lambda= lambda_ <ast>end quad left( begin -0.8836615 \ \ -0.9876166 end right) quad Rightarrow quad Y_ <ast>approx left( begin -0.5449964 \ \ -0.6091105 end right) . $$

Ответ. $ pm (0.3838312,, 0.4418639)_<> $ и $ pm (0.5449964,, 0.6091105)_<> $ соответственно (знаки должны быть согласованы).

Проверка. Если в ответе взять знак $ +_<> $: $$ X_<ast>-Y_ <ast>= left( begin -0.1611652 \ -0.1672466 end right)= lambda_ <ast>A_1X_<ast>=(lambda_<ast>-z_<ast>)A_2Y_<ast>,quad (X_<ast>-Y_<ast>)^<top>(X_<ast>-Y_<ast>)approx mathbf<0.0539456>4 . $$

Теорема. [3,4].Пусть

$$ X^ <top>A_<1>X+2,B^<top>_1X-1=0 mbox <и> X^ <top>A_<2>X+2,B^<top>_2X-1=0 $$ — квадрики в $ <mathbb R>^_<> $, причем первая является эллипсоидом. Квадрики пересекаются тогда и только тогда, когда среди вещественных корней полинома

$$ Theta (z) = <mathcal D>_lambda left( det left( left[ begin A_2 & B_2\ B_2^ <top>& -1-z end right] — lambda left[ begin A_1 & B_1\ B_1^ <top>& -1 end right] right) right) $$ имеются числа разных знаков или нуль. Здесь $ <mathcal D>_<> $ — дискриминант полинома рассматриваемого относительно переменной $ lambda_<> $.

Для того, чтобы существовала точка касания квадрик

$$ X^ <top>A_<1>X+2,B^<top>_1X-1=0 mbox <и> X^ <top>A_<2>X+2,B^<top>_2X-1=0 $$ необходимо и достаточно, чтобы было выполнено условие $$ <mathcal D>_lambda left( det left( left[ begin A_2 & B_2\ B_2^ <top>& -1 end right] — lambda left[ begin A_1 & B_1\ B_1^ <top>& -1 end right] right) right) =0 . $$

Теорема. [3,4]. Если не выполняется условие предыдущей теоремы, то квадрат расстояния между

$$ mbox <эллипсоидом>quad X^ <top>A_<1>X+2,B^<top>_1X-1=0 quad mbox < и квадрикой >quad X^ <top>A_<2>X+2,B^<top>_2X-1=0 $$ совпадает с минимальным положительным корнем полинома $$ <mathcal F>(z) = $$ $$ =<mathcal D>_ <mu_1, mu_2>left( det left( mu_1 left[ begin A_1 & B_1\ B_1^ <top>& -1 end right] + mu_2 left[ begin A_2 & B_2\ B_2^ <top>& -1 end right] — left[ begin A_2 A_1 & A_2 B_1\ B_2^ <top>A_1 & B_2^<top>B_1 — mu_1 mu_2 z end right] right) right), $$ в предположении, что этот корень не является кратным. Здесь $ <mathcal D>_<> $ — дискриминант полинома рассматриваемого относительно переменных $ mu_<1>, mu_ <2>$.

Пример. Найти расстояние между эллипсами

Ответ. $ d approx sqrt <9.0183982802>approx 3.00306481 $.

2. Составим матрицу $$ M= mu_ <1ast>A_1+mu_<2ast>A_2-A_2A_1 . $$ Тогда координатные столбцы ближайших точек на квадриках вычисляются по формулам: $$ X_<ast>=M^ <-1>(A_2B_1-mu_ <1ast>B_1-mu_<2ast>B_2), Y_<ast>=(M^<-1>)^<^<top>> (A_1B_2 — mu_ <1ast>B_1-mu_<2ast>B_2). $$

Пример. Найти ближайшие точки эллипсов из предыдущего примера.

Ответ. $$ X_<ast>approx left(begin -0.4824707833 \ 1.1065143947 end right), Y_<ast>approx left( begin -3.46262940675\ 0.73630788509 end right) . $$

Проверка. $$ (X_<ast>-Y_<ast>)^<top>(X_<ast>-Y_<ast>)approx mathbf<9.018398280>3 , $$ $$ X_<ast>^<top>A_1X_<ast>+2B_1^<top>X_<ast>-1 approx 1cdot 10^<-9> , Y_<ast>^<top>A_2Y_<ast>+2B_2^<top>Y_<ast>-1approx -3cdot 10^<-10> , $$ и вектор $ X_<ast>-Y_<ast>^<> $ перпендикулярен обоим эллипсам в соответствующих ближайших точках: $$ A_1X_<ast>+B_1= left(begin 1.767863990 \ 0.219610712 end right)=mu_ <2ast>(X_<ast>-Y_<ast>), A_2Y_<ast>+B_2= left(begin -0.1254448880 \ -0.0155832356 end right)=-mu_ <1ast>(X_<ast>-Y_<ast>) . $$

Пример. Найти расстояние между эллипсоидами

$$ 7,x_1^2+6,x_2^2+5,x_3^2-4,x_1x_2-4,x_2x_3-37,x_1-12,x_2+3,x_3+54=0$$ и $$ 189,x_1^2+x_2^2+189,x_3^2+2,x_1x_3-x_2x_3-27=0 .$$

Ответ. $ d approx sqrt <1.3537785005>approx 1.1635198754_<> $

Алгебраические кривые и многообразия

Расстояние от точки до плоской алгебраической кривой

Задача. Пусть алгебраическая кривая задана уравнением $$ Phi(x,y)=0 . $$ Здесь $ Phi_<>(x,y) $ — отличный от константы полином от $ x_<> $ и $ y_<> $ с вещественными коэффициентами. Требуется найти расстояние до этой кривой от начала координат.

Будем решать задачу сначала для частного случая — пусть полином $ Phi_<>(x,y) $ является четным по переменной $ y_<> $. Геометрически это означает, что кривая (если она существует) будет зеркально симметричной относительно оси $ mathbb Ox $. А с аналитической точки зрения такой полином можно представить в виде полинома $$ F(x,Y) equiv Phi_<>(x,y) quad npu quad Y=y^2 . $$

Теорема 1 [6]. Пусть $ Phi_<>(x,y) equiv Phi_<>(x,-y) $. Уравнение $ Phi_<>(x,y)=0 $ не имеет вещественных решений если одновременно выполняются два условия:

a) уравнение $ Phi(x,0)=0 $ не имеет вещественных решений;

б) уравнение $$ mathcal F(z)=mathcal D_x( F(x,z-x^2))=0 $$ не имеет положительных решений.

Если хотя бы одно из этих условий не выполняется, то квадрат расстояния от начала координат до кривой $ Phi(x_<>,y)=0 $ равен либо квадрату минимального по модулю вещественного корня уравнения $ Phi(x,0)=0 $, либо же минимальному положительному корню уравнения $ mathcal F(z)= 0 $, при условии, что последний не является кратным. Здесь $ <mathcal D>_<> $ — дискриминант полинома, рассматриваемого относительно переменной $ x_<> $.

Пример. Найти расстояние от начала координат до кривой

Решение. Уравнение $$ Phi(x,0)=x^6-6,x^5+25,x-45=0 $$ имеет вещественные корни $ mu_1approx -1.621919 $ и $ mu_2 approx 5.986387 $. Далее, $$ F(x,Y)=x^6-5,x^4Y-Y^3-6,x^5+6,xY^2+10,Y^2+25,x-45 $$ и полином $$ mathcal F(z)=mathcal D_x (F(x,z-x^2))= <scriptstyle 124422592>,z^<15>-<scriptstyle 1996675968>z^<14>-<scriptstyle 26107738048>,z^<13>+<scriptstyle 270691240064>,z^<12>+ <scriptstyle 1462429768576>z^ <11>$$ $$ -<scriptstyle 31070151855680>z^<10>+ <scriptstyle 104850679100160>,z^9+<scriptstyle 106422502370800>,z^8-<scriptstyle 1956603249193600>,z^7+<scriptstyle 1683409252901600>,z^6+ $$ $$ +<scriptstyle 3565828983027500>z^5 -<scriptstyle 23058839076745500>,z^4+<scriptstyle 30272455856370000>,z^3+<scriptstyle 28139412928130000>,z^2-<scriptstyle 97452805338000000>, z+ $$ $$ + <scriptstyle 171049864407603125>$$ имеет минимальный положительный корень равный $ lambda approx 1.965293 $. Поскольку $ sqrt <lambda>4) , задача о трёх заводах.

Пример. В точках $ P_<1>,P_2,P_3 $ расположены источники полезных ископаемых: железной руды, угля и воды соответственно. Известно, что для производства одной тонны стали необходимо иметь $ m_ <1>$ тонн руды, $ m_2 $ тонн угля и $ m_3 $ тонн воды. В предположении, что стоимость перевозки одной тонны груза не зависит от его природы, где следует расположить сталелитейное производство так, чтобы минимизировать транспортные издержки?

Подробное обсуждение этой задачи (и к ней примыкающих) ☞ ЗДЕСЬ.

Задача о точке Лемуана-Греба

Решение. Пусть $ d_1, d_2,d_3 $ — расстояния от точки $ P_<> $ плоскости до сторон треугольника с длинами $ D_1, D_2, D_3 $ соответственно. Воспользуемся тождеством Лагранжа: $$ (d_1^2+ d_2^2+d_3^2)(D_1^2+ D_2^2+D_3^2)equiv $$ $$ equiv (d_1D_1+ d_2D_2+d_3D_3)^2+(d_1D_2-d_2D_1)^2+(d_2D_3-d_3D_2)^2+ (d_1D_3-d_3D_1)^2 . $$ Величина $ d_1D_1+ d_2D_2+d_3D_3 $ является постоянной, не зависящей от координат точки $ P_<> $: $$ d_1D_1+ d_2D_2+d_3D_3 =2S , $$ где $ S_<> $ — площадь данного треугольника. Следовательно $ min (d_1^2+d_2^2+d_3^2) $ достигается при условиях $$ d_1D_2-d_2D_1=0, d_2D_3-d_3D_2=0, d_1D_3-d_3D_1=0 , $$ то есть когда $$ frac=frac=frac . $$ Определяемая этими соотношениями точка называется точкой Лемуана 6) или точкой Греба 7) ; в ней пересекаются симедианы треугольника.

Еще некоторые задачи

Построение прямой на плоскости, сумма квадратов расстояний до которой от заданных точек минимальна ☞ ЗДЕСЬ

§3.2 Перпендикуляр из точки на под пространство. Кратчайшее расстояние от точки до подпространства*).

Primary tabs

Forums:

Определение 2. Пусть $ R_1 -$ подпространство евклидова пространства R. Мы будем говорить, что вектор $ h in R$ ортогонален подпространству $ R_1$, если он ортогонален любому вектору x из $ R_1$.

Если вектор h ортогонален векторам $ e_1, e_2, . e_m, $ то он ортогонален любой их линейной комбинации. Действительно из равенств
$$ (h, e_i) = 0 $$
следует, что для любых чисел $ lambda_1, lambda_2, . lambda_m $
$$ (h_1, lambda_1 e_1 + lambda_2 e_2 + . + lambda_m e_m) = 0. $$
Поэтому, для того чтобы вектор h был ортогонален m-мерному подпространству $ R_1$, достаточно, чтобы он был ортогонален m линейно независимым векторам из $ R_1$ (базису в $ R_1$ **).

Упражнение. Показать, что совокупность всех векторов $ y in R,$ ортогональных к подпространству $ R_1,$ также образует подпространство пространства R. Это подпространство называется ортогональным дополнением к подпространству $ R_1$ в пространстве R.

Рассмотрим в пространстве R некоторое m-мерное подпространство $R_1$ ***) и вектор f, не принадлежащий $ R_1$. Поставим задачу: опустить перпендикуляр из точки f на $ R_1$, т. е. найти вектор $f_0$ из $R_1$ такой, чтобы вектор $ h = f — f_0$ был ортогонален $ R_1$. Вектор $f_0$ называется при этом ортогональной проекцией вектора f на подпространство $R_1$. Несколько позже мы увидим, что эта задача имеет решение, притом единственное. Сейчас мы покажем, что, как и в элементарной геометрии, перпендикуляр есть кратчайшее расстояние от точки до подпространства. Другими словами, покажем, что если $f_1$ есть отличный от $ f_0$ вектор из $ R_1,$ то
$$ |f-f_1| > |f-f_0|. $$

Действительно, вектор $ f_0 — f_1,$ как разность двух векторов из $ R_1$, принадлежит $ R_1$, и, следовательно, ортогонален вектору $ h = f — f_0.$ По теореме Пифагора имеем:
$$ |f — f_0|^2 + |f_0 — f_1|^2 = |f — f_0 + f_0 — f_1|^2 = |f — f_1|^2 $$
и, значит,
$$ | f — f_1| > |f — f_0|. $$

Покажем теперь, как фактически вычислить по f его ортогональные проекцию $ f_0$ на подпространство $ R_1$ (т. е. опустить перпендикуляр из f на $ R_1$). Пусть базис подпространства $ R_1$ состоит из векторов $ e_1, e_2, . e_m.$ Будем искать вектор $ f_0$ в виде
$$ f_0 = c_1 e_1 + c_2 e_2 + . + c_m e_m, qquad qquad (9)$$
где коэффициенты $c_k$ найдем из условия ортогональности $ f — f_0 $ к $ R_1.$ Для того чтобы эта ортогональность имела место, необходимо и достаточно, чтобы выполнялись m равенств $ (f — f_0, e_k) = 0 (k = 1, 2, . m), $ т. е.
$$ ( f_0, e_k) = (f, e_k). qquad qquad (10) $$
Подставляя сюда вместо $f_0$ его выражение (9), получаем систему m уравнений
$$ c_1 (e_1, e_k) + c_2 (e_2, e_k) + . + c_m (e_m, e_k) = (f, e_k)$$
$$ (k = 1, 2, . m) qquad qquad (11)$$
относительно чисел $ c_i$.

Рассмотрим сначала отдельно часто встречающийся случай, когда базис $ e_1, e_2, . e_m -$ ортогональный и нормированный. В этом случае задача решается особенно просто. Действительно система (11) превращается в таком базисе в систему равенств
$$ c_i = (f, e_i), qquad qquad (12) $$
сразу определяющих нудные коэффициенты.

Так как в каждом m-серном подпространстве можно выбрать Ортогональный нормированный базис, то мы доказали, таким образом, что у каждого вектора f существует, и притом только одна, ортогональная проекция $ f_0$ на подпространство $ R_1. $

Вернёмся теперь к случаю произвольного базиса. В этом случае система 11) также должна иметь единственное решение. Действительно, вектор $f_0$, по дрказанному, существует и притом только один. В базисе $ e_1, e_2, . e_m. $ вектор $ f_0$ имеет вполне определенные координаты $ c_1, c_2, . c_m.$ Так как эти числа удовлетворяют системе (11), то эта система имеет, следовательно, единственное решение. Система m уравнений с m неизвестными может иметь единственное решение, лишь если не определитель отличен от нуля. Отсюда следует, что определитель системы (11)
$$begin
(e_1, e_1) & (e_2, e_1) & cdots & (e_m, e_1) \
(e_1, e_2) & (e_2, e_2) & cdots & (e_m, e_2) \
cdots & cdots & cdots & cdots \
(e_1, e_m) & (e_2, e_m) & cdots & (e_m, e_m)\
end$$
отличен от нуля. Этот определитель называется определителем Грама векторов $ e_1, e_2, . e_m.$

Итак, пусть задано подпространство $R_1$ с базисом $ e_1, . e_m $ и произвольный вектор f пространства R. Ортогональная проекция $ f_0$ вектора f на $ R_1$ имеет вид
$$ f_0 = c_1 e_1 + . + c_m e_m. $$
При этом, если базис $ e_1, e_2, . e_m $ ортогонален, то
$$ c_i = (f, e_i).$$
Если же базис $ e_1, . e_m $ произволен, то коэффициенты $ c_i$ определяются как решение системы (11).

Пример 1. Способ наименьших квадратов. Предположим, что величина y есть линейная функция величин $ x_1, . x_m, $ т. е. что
$$ y = c_1 x_1 + . + c_m x_m, $$
где $ c_1, . c_m — $ постоянные, неизвестные нам коэффициенты. Часто коэффициенты $ c_1, . c_m $ определяются экспериментально. Для этого производится ряд измерений величин $ x_1, . x_m$ и y. Обозначим результаты k-го измерения через $ x_, . x_$ и, соответственно, $y_k.$
Коэффициенты $ c_1, . c_m $ можно было бы попытаться определить из системы уравнений
$$
left.begin
x_ <11>c_1 + x_ <21>c_2 + . + x_ c_m = y_1, \
x_ <12>c_1 + x_ <22>c_2 + . + x_ c_m = y_2, \
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . \
x_ <1n>c_1 + x_ <2n>c_2 + . + x_ c_m = y_n.
endrightrbrace qquad qquad (13)
$$
Здесь число уравнений n равно числу произведенных измерений и обычно превосходит число неизвестных $ (n>m). $ Так как измерение величин $ x_1, . x_n, y$ неизбежно связано с погрешностями, то система (13), вообще говоря, противоречива и о ее точно решении говорит бессмысленно. Поэтому уравнениям (13) можно удовлетворить лишь приближенно. Таким образом, ставится задача разыскать такие значения неизвестных $ c_1, . c_m, $ при которых левые части уравнения (13) были бы возможно более близки к соответствующим правым частям. В качестве «меры близости» берется так называемое левых частей уравнений от свободных членов, т. е. величина
$$ sum_^n (x_ <1k>c_1 + x_ <2k>c_2 + . + x_ c_m — y_k)^2. qquad qquad (14) $$
Нам нужно найти числа $ c_1, c_2, . c_m, $ при которых квадратичное уклонение имеет наименьшее значение.Эту задачу на минимум можно решить непосредственно. Однако ее решение можно сразу получить из результатов, изложенных выше.

В самом деле, рассмотрим n-мерное евклидово пространство и векторы $ e_1 = (x_<11>, x_<12>, . x_<1n>), e_2 = (_<21>, . x_<2n>, . $
$ . e_m = (_, . x_)$ и $ f=(y_1, . y_n) $ в этом пространстве. Правые части уравнений системы (13) являются компонентами вектора f, левые части — вектора
$$ c_1 e_1 + c_2 e_2 + . + c_m e_m. $$
Выражение (14) есть, следовательно, квадрат расстояния вектора $ c_1 e_1 + c_2 e_2 + . + c_m e_m $ от вектора f. Таким образом, условие, чтобы квадратичное уклонение было минимальным, равносильно следующей задаче: выбрать числа $ c_1, c_2, . c_m $ так, чтобы расстояние вектора f до вектора $ I_0 = c_1 e_1 + c_2 e_2 + . + c_m e_m $ было наименьшим. Если обозначить через $ R_1$ подпространство n-мерного пространства, состоящее из линейных комбинаций векторов $ e_1, e_2, . e_m *), $ то задача состоит в нахождении проекции вектора f на это подпространство. Как мы видели (формула (11)), числа $ c_1, c_2, . c_m, $ решающие эту задачу, находятся из системы уравнений
$$
left.begin
(e_1, e_1) c_1 + (e_2, e_1) c_2 + . + (e_m, e_1) c_m = (f, e_1), \
(e_1, e_2) c_1 + (e_2, e_2) c_2 + . + (e_m, e_2) c_m = (f, e_2), \
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . \
(e_1, e_m) c_1 + (e_2, e_m) c_2 + . +(e_m, e_m) c_m = (f, e_m),
endrightrbrace
$$
где
$$ (f, e_k) = sum_^n x_ y_j; (e_i, e_k) = sum_^n x_ x_. $$

Система (15) называется в этом случае системой нормальных уравнений . Итак, приближенное решение системы (13) состоит в замене ее нормальной системой (15) m уравнений с m неизвестными. Изложенный метод называется способом наименьших квадратов.

Упражнение. Решить по способу наименьших квадратов систему уравнений
$$ 2c = 3,
3c = 4,
4c = 5. $$
Решение. $ e_1 = (2, 3, 4), f = (3, 4, 5). $ Нормальная система сводится в этом случае к одному уравнению:
$$ (e_1, e_1) c=(e_1, f_1),$$
т. е.
$$ 29c = 40; c = <<40>over <29>>. $$

Для случая, когда система (13) есть система n уравнений с одним неизвестным
$$ x_1 c = y_1,
x_2 c = y_2,
. . . . . . . . . . . qquad qquad (13′)
x_n c = y_n, $$
решение запишется следующим образом:
$$ c= <<(x, y)>over <(x, x)>> = << sum_^n> x_k y_k over < sum_^n x_k^2>> $$
Приближенное решение системы (13′) может быть истолковано геометрически как проведение через начало координат прямой, проходящий «возможно более близко» от совокупности точек $ (x_1, y_1), (x_2, y_2), . (x_n, y_n).$ Число c представляет тогда угловой коэффициент такой прямой.

Пример 2. Приближение функций тригонометрическими многочленами. Пусть $ f(t) -$ некоторая непрерывная функция, заданная на интервале $ (0, 2π)$. Часто бывает нужно подобрать тригонометрический многочлен. $ P(t)$ данного порядка, возможно меньше отличающийся от $ f(t).$ В качестве меры отклонения $ P(t) $ от $ f_(t) $ мы возьмём квадратичное уклонение, которое задаётся формулой
$$ intlimits_0^ <2π>[f(t) — P(t)]^2 dt. qquad qquad (16)$$

Итак, точная постановка рассматриваемой задачи такова: среди всех тригонометрических многочленов порядка n
$$ P(t) = << alpha_0 over <2>> + alpha_1 cos t+b_1 sin t + . + alpha_n cos nt + b_n sin nt qquad qquad (17)
найти тот, квадратичное уклоне которого от ваданной функции $ f(t) $ минимально.

Введем в рассмотрение пространство R непрерывных функций на отрезке $ (0; 2π).$ Скалярное произведение в этом пространстве зададим, как обычно, интегралом
$$ (g, g) = intlimits_0^2π f(t) g(t) dt.$$
Длина вектора выражается тогда формулой
$$ |f| = sqrt< intlimits_0^2π [f (t)]^2 dt>, $$
и следовательно, квадратичное уклонение (16) есть в нашем пространстве просто квадрат расстояния от $ i(t) $ до $P(t).$ Тригонометрические многочлены вида (17) образуют в R подпространство $ R_1$ размерности $ 2π + 1$. Нам нужно найти элемент из $ R_1,$ находящийся на минимальном расстоянии от $ f(t). $ Эта задача снова решается опусканием перпендикуляра из точки $ f(t) $ на подпространство $R_1$.
Так функции
$$ e_0 = <<1>over < sqrt<2π>>>; e_1 = << cos t>over < sqrt<π>>>; e_2 = << sin t>over < sqrt<π>>>; . ; e_ <2n-1>= << cos nt>over < sqrt<π>>>; e_ <2n>= << sin nt>over < sqrt<π>>>; $$
образуют ортогональный и нормированный базис в этом подпространстве (см. пример 2 предыдущего пункта), то решением этой задачи служит линейная комбинация базисных векторов.
$$ P(t) = sum_^ <2π>c_k e_k, qquad qquad (18)$$
где
$$ c_k = (f, e_k), $$
т. е., вспоминая определение скалярного произведения имееим:
$$ c_0 = <<1>over < sqrt<2π>>> intlimits_0^ <2π>f(t) dt; c_ <2k-1>= <<1>over < sqrt<π>>> intlimits_0^ <2π>f(t) cos kt dt; $$
$$ c_ <2k>= <<1>over <π>> intlimits_0^ <2π>f(t) sin kt dt qquad (k=1, . n). $$
Подставляя $ c_k $ и $e_k (k=1, . n)$ в формулу (18), мы приходим, таким образом, к следующему результату: для того чтобы определить тригонометрический многочлен
$$ P(t) = <<alpha_0>over <2>> + sum_^n alpha_k cos kt + b_k sin kt, $$
квадратичное уклонение которого от заданной функции $ f(t) $ минимально, надо определить коэффициенты $ alpha_k, b_k$ по формулам
$$ alpha_0 = <<1>over <π>> intlimits_0^ <2π>f(t) dt; alpha_k = <<1>over <π>> intlimits_0^ <2π>f(t) kt dt; b_k = <<1>over <π>> intlimits_0^ <2π>f(t) sin kt dt. $$
Так определенные числа $ alpha_k, b_k$ называются коэффициентами Фурье функции f(t).

источники:

http://fkn.ktu10.com/?q=node/11476

Источник

. Расстояния. Псевдорешения. Нормальные решения. Нормальные псевдорешения.

Расстоянием
между множествами X
и Y
называется
.

Рассмотрим
задачу нахождения расстояния от точки
x
до подпространства W.
В начале рассмотрим случай, когда
подпространство задано в виде линейной
оболочки системы векторов.

Теорема 2.5.
Расстояние от точки до подпространства
достигается на перпендикуляре, опущенном
из точкиx
на подпространство.

Доказательство.
Представим
.
Расстояние от точкиx
до подпространства W
равно
.
Векторыиортогональны друг другу, и по неравенству
Бесселя,
причем равенство достигается только в
случае.
Тем самым установлено,
что и требовалось.

Пусть
и система векторовлинейно независимая. Расстояние от
точкиx
до подпространства W
можно найти как отношение объема
k+1-мерного
параллелепипеда натянутого на векторы
к объемуk-мерного
параллелепипеда натянутого на векторы
.
Таким образом, справедлива формула.
К сожалению, эта формула не позволяет
находить проекцию и ортогональную
составляющую вектора. Для нахождения
проекции можно поступать следующим
образом. Представими,
а затем умножим скалярно на векторывекторx.
Получим систему линейных уравнений
.
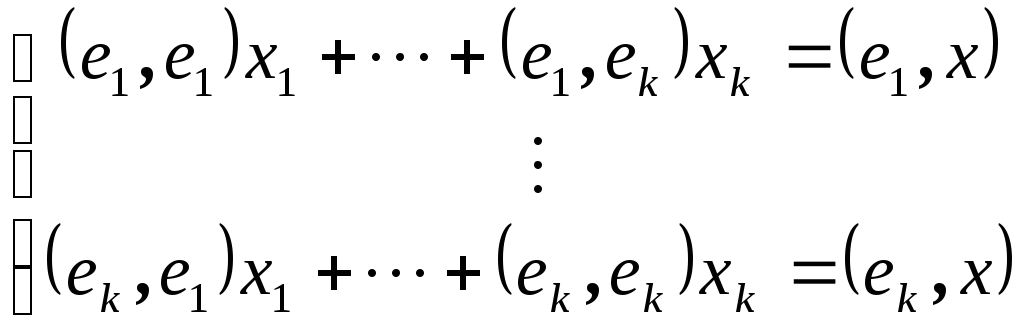
Коэффициенты при неизвестных образуют
матрицу Грама, определитель которой не
равен нулю. Следовательно, система имеет
единственное решение. Решив эту систему,
найдем проекцию вектораx,
а затем и ортогональную составляющую.

Рассмотрим
случай, когда линейное подпространство
задано системой однородных линейных
уравнений Ax=0.
Для простоты проведения рассуждений
будем считать, что строки матрицы A
линейно независимы. В ортонормированном
базисе, коэффициенты при неизвестных
в уравнении являются координатами
вектора из ортогонального дополнения
(см. п.2.4). Таким образом, по системе
линейных уравнений можно найти базис
ортогонального дополнения к пространству
W.
Обозначим базис
через.
Тогда представими,
а затем умножим скалярно на векторывекторx.
Получим систему линейных уравнений
.
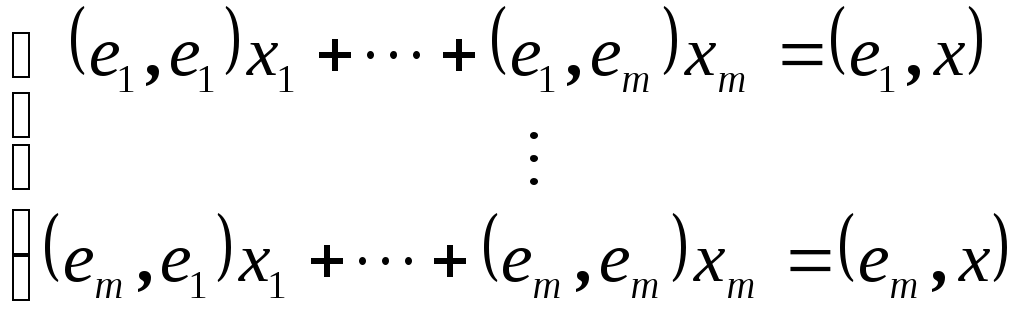
Коэффициенты при неизвестных образуют
матрицу Грама, определитель которой не
равен нулю. Следовательно, система имеет
единственное решение. Решив эту систему,
найдем ортогональную составляющую
вектораx,
а затем и проекцию.

Рассмотрим
теперь задачу нахождения расстояния
от точки x
до линейного многообразия M.
Эта задача легко сводится к аналогичной
задаче построения расстояния от точки
до подпространства. Действительно,
пусть M=z+W,
где z
– произвольная точка из M,
а W
– подпространство.
Тогда
,
то есть задача свелась к определению
расстояния от точкиx—z
до подпространства W.

Линейное
многообразие, заданное как множество
решений одного линейного уравнения
ax=b
называется гиперплоскостью. Рассмотрим
задачу отыскания расстояния от точки
y
до гиперплоскости ax=b.
Перпендикуляр, опущенный из y
на гиперплоскость равен
и.
Отсюда находим неизвестный параметр,
а затем и расстояние.

Рассмотрим
задачу определения расстояния между
двумя линейными многообразиями

и
.
Расстояние между ними равно
,
то есть задача свелась к нахождению
расстояния от точкиy—z
до подпространства
.
Заметим, что расстояние между линейными
многообразиями достигается на общем
перпендикуляре.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Сообщения без ответов | Активные темы

Автор

Сообщение

ahgel1990

Заголовок сообщения: Расстояние от точки до многообразия

Добавлено: 14 окт 2014, 00:28

Продвинутый

Зарегистрирован:
23 июл 2014, 22:48
Сообщений: 81
Cпасибо сказано: 34
Спасибо получено:
1 раз в 1 сообщении
Очков репутации: 2

найти расстояние от точки А, заданной вектором , до линейного многообразия , заданного множеством решений системы линейных неоднородных уравнений

Люди, кто разбирается в этом, подскажите, где в чем я ошиблась….просто огромные числа..может это вообще решается не так?!.ну или может есть у кого подобный пример.
Спасибо за внимание)))))))))))))))000000

Вернуться к началу

ahgel1990	Заголовок сообщения: Re: Расстояние от точки до многообразия Добавлено: 16 окт 2014, 23:19
	Prokop писал(а): Видимо условие задачи взято «с потолка», т.к. ответ неприятен. Наверно так и есть, т.к. каждому дают индивидуальные задания…Считать то их некому. Спасибо большое)))
Вернуться к началу

Похожие темы	Автор	Ответы	Просмотры	Последнее сообщение
Вычислить расстояние от точки B в форуме Аналитическая геометрия и Векторная алгебра	unknow	6	513	19 дек 2017, 18:53
Расстояние от точки до отрезка в форуме Геометрия	EvgenyAL	8	2358	15 июн 2016, 10:27
Расстояние от точки до подпространства в форуме Функциональный анализ, Топология и Дифференциальная геометрия	Susanna Gaybaryan	5	328	19 янв 2020, 00:14
Расстояние от точки до прямой в форуме Геометрия	Ladytaft24	3	428	05 фев 2018, 20:50
Расстояние от точки до прямой в форуме Геометрия	Ladytaft24	0	293	05 фев 2018, 21:51
Расстояние от точки до прямой в форуме Геометрия	Ladytaft24	2	444	05 фев 2018, 21:53
Расстояние от точки до прямой в форуме Аналитическая геометрия и Векторная алгебра	Apakalipsis	9	587	20 июн 2017, 12:40
Расстояние от точки до плоскости в форуме Геометрия	aninibas	2	613	10 июл 2014, 20:38
Расстояние от точки до прямой в форуме Геометрия	Ladytaft24	0	270	05 фев 2018, 20:48
Найти: Расстояние от точки С до прямой АВ в форуме Аналитическая геометрия и Векторная алгебра	rightgame	3	530	14 янв 2017, 16:42

Кто сейчас на конференции

Сейчас этот форум просматривают: YaCy [Bot] и гости: 9

Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете добавлять вложения

Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group

Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru

Русская поддержка phpBB

Источник

Умножать в принципе можно, только X станет столбцом. Получится $%CX^T$%.

(28 Мар ’16 11:37)
falcao

@s1mka: я не знаю, каким методом Вы решали, но точно знаю, что расстояние не может быть отрицательным!

(28 Мар ’16 19:40)
falcao

@s1mka: а я ещё одну нашёл У Вас написано, что -240/19=-4.

(28 Мар ’16 23:35)
falcao

@s1mka: а верно ли то равенство, которое Вы только что написали в комментарии? Это я так, на всякий случай.

(29 Мар ’16 16:53)
falcao

@falcao невнимательная я минус потеряла -4

(29 Мар ’16 17:02)
s1mka

Источник

Содержание

Вычисление расстояний между геометрическими объектами

Линейные многообразия

Расстояние от точки до линейного многообразия (плоскости)

Расстояние между линейными многообразиями (плоскостями)

Квадратичные многообразия (квадрики)

Расстояние от точки до квадрики

Расстояние от линейного многообразия (плоскости) до квадрики

Расстояние между квадриками

Алгебраические кривые и многообразия

Расстояние от точки до плоской алгебраической кривой

Расстояние в пространстве матриц

Разные задачи

Обобщенная задача Ферма-Торричелли

Задача о точке Лемуана-Греба

Еще некоторые задачи

Задачи учебные

Источники

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Вычисление расстояний между геометрическими объектами

Линейные многообразия

Расстояние от точки до линейного многообразия (плоскости)

Расстояние между линейными многообразиями (плоскостями)

Квадратичные многообразия (квадрики)

Расстояние от точки до квадрики

Расстояние от линейного многообразия (плоскости) до квадрики

Расстояние между квадриками

Алгебраические кривые и многообразия

Расстояние от точки до плоской алгебраической кривой

Задача о точке Лемуана-Греба

Еще некоторые задачи

§3.2 Перпендикуляр из точки на под пространство. Кратчайшее расстояние от точки до подпространства*).

Primary tabs

Forums:

. Расстояния. Псевдорешения. Нормальные решения. Нормальные псевдорешения.

Кто сейчас на конференции