Как найти расстояние до не определяемого места

МОУ «Красноборская СШ»

Исследовательская работа по теме: 

Определение
расстояния до недоступного предмета

       (геометрия
на местности)

Выполнила:

Кучина Елизавета,

ученица
8  класса

МОУ
«Красноборская СШ»

с.
Красный Бор,

ул.
Молодёжная, д.3

Руководитель:

Серова Ольга Владимировна,

                                                                                                  
учитель математики

с. Красный
Бор, 2019 г.

Актуальность
темы исследования.

Мир, в котором мы живем, наполнен геометрией домов и
улиц, гор и полей, творениями природы и человека. Геометрия зародилась в
глубокой древности. Строя жилища и храмы, украшая их орнаментами, размечая
землю, измеряя расстояния и площади, человек применял свои знания о форме,
размерах и взаимном расположении предметов, полученные из наблюдений и опытов.

Тема нашей исследовательской работы актуальна  тем,
что принцип определения расстояний до «недоступного» предмета на
земле, с одной стороны, лежит в основе определения расстояний до небесных тел,
а с другой стороны, неоценим с точки зрения приложения его в практической
жизни: на стройках, при геодезических работах, прокладке трасс, в военном деле
и т. д.

Цель исследовательской работы: Научиться
определять
расстояние до недоступного предмета геометрическими способами.

Задачи: 

1)    рассмотреть
различные способы определения расстояния до выбранного недоступного предмета;

2)    Рассмотреть
задачи по данной теме;

Объект исследования:
недоступные предметы на местности.

Предмет исследования:
определение расстояния до недоступного предмета различными способами.

Гипотеза: можно ли
определить расстояние до недоступного предмета на местности.

Практическая значимость исследования
состоит в получении знаний об измерительных работах на местности, изучении и
применении полученных знаний на уроках геометрии, в повседневной жизни.

Различные
способы определения расстояния до выбранного недоступного предмета

1
способ: (с помощью равнобедренного прямоугольного треугольника)

Ход
работы:

1)    Встать напротив недоступной точки В и зафиксировать свое положение А; 2)    Двигаясь перпендикулярно АВ вправо , найти точку С, в которой гипотенуза совпадает с точкой В с помощью транспортира и планки; 3)    Измерить расстояние АС = АВ.

Измерения:

АС
= 14,3 м

АВ
= АС = 14,3 м

2
способ: (с помощью подобия треугольников)

Ход
работы:

1)    Встать напротив недоступной точки В и зафиксировать свое положение А; 2)    Двигаясь из точки А перпендикулярно вправо определенное расстояние, зафиксировать положение точкой С; 3)    Из точки С перпендикулярно АС положить шест СD; 4)    Продолжить движение по прямой АС, зафиксировать свое положение Е и найти точку D, лежащую на прямой ВЕ 5)    Произвести вычисления по формуле

Измерения:

AC = 9,5 м; CE = 1,7 м; CD = 2,2 м

 

3
способ: (пропорциональные отрезки в прямоугольном треугольнике)

Ход
работы:

1)    Встать напротив недоступной точки В и зафиксировать свое положение А; 2)    Двигаясь из точки А перпендикулярно вправо определенное расстояние, зафиксировать положение точкой Е; 3)    Из точки Е перпендикулярно ВЕ направить планку; 4)    По направлению планки идти до нахождения точки С, лежащей на прямой ВА; 5)    Провести нужные измерения; 6)    Вычислить АВ по формуле

Измерения:

AE = 5,5 м; AC = 2,2 м; EC = 6 м;

4
способ: (с помощью равенства треугольников)

Ход
работы:

1)    Встать напротив недоступной точки В и зафиксировать свое положение А; 2)    Двигаясь из точки А перпендикулярно вправо определенное расстояние, зафиксировать положение точкой Е; 3)    Зафиксировать середину С отрезка АЕ 4)    Из точки Е перпендикулярно АЕ пройти расстояние и найти точку F, которая лежит на прямой ВС; 5)    Провести измерения и вычислить AB = EF

Измерения:

AC
= CE = 2,5 м; EF = 14,5 м; AB = EF = 14,5 м

5
способ:

Ход
работы:

1)    Стать напротив недоступной точки В и зафиксировать свое положение А; 2)    По направлению ВА пройти определенное расстояние АЕ и зафиксировать положение Е; 3)    Двигаясь из точки А перпендикулярно вправо определенное расстояние, зафиксировать положение точкой D; 4)    Отмерить FD = DE и зафиксировать точку F; 5)    Отмерить DQ = DA и зафиксировать точку Q; 6)    Из точки F по прямой FQ пройти расстояние и найти точку Н, с которой через точку D видна точка В; 7)    Провести измерения и вычислить HQ = AB

Измерения:

AD
= DQ = 2,5 м; AE = FQ = 2,2 м; ED = DF = 3,4 м

HQ = AB = 14,8 м

Метод триангуляции

   Этот метод нашел применение в астрономии. С его помощью
измерялись расстояния до небесных тел. Этот метод состоит из 3-х этапов:

1.    
Измерение углов ∠А и ∠B и
расстояния АВ.

2.    
Построение А’В’К’
с углами 1 и 2 при вершинах А’ и В’ соответственно.

3.    
Учитывая подобие треугольников АВК, А’В’К’ и равенство ,
по известным длинам отрезков АВ, А’К’ и А’В’ нетрудно найти длину отрезка
АК. 

Задача 582

(геометрия 7-9, Л.С. Атанасян)

Задачи на нахождение
расстояний в поизведениях писателей.

     Поэт Г. Лонгфелло был еще и математиком. Наверное, поэтому
яркие образы, украшающие математические понятия, которые он использовал в своем
романе “Кавана”, позволяет запечатлеть некоторые теоремы и их применение.
Читаем в романе Лонгфелло следующую задачу:

“Лилия, на одну пядь,
поднимавшаяся над поверхностью воды, под порывом свежего ветра коснулась
поверхности озера в двух локтях от прежнего места: исходя из этого требовалось
определить глубину озера”. (1 пядь равна 10 дюймам, два локтя 21 дюйму)

А
решается эта задача на основе теоремы: если две хорды одной окружности
пересекаются, то произведение длин частей одной из них равно произведению длин
частей другой.
Посмотрим на рисунок, и сразу станет ясно, как находится глубина озера (x):

21 ^. 21
= 10(x + (x +10)),
441 = 20x + 100,
x = 17,05 (дюймов).

Ответ: 17,05 дюймов.

Заключение

     В нашей работе рассмотрено несколько
способов определения расстояния до недоступной точки. Решение таких задач  имеет
значительный практический интерес, закрепляют полученные знания по геометрии и
может использоваться для практических работ. Ведь на практике картографам для составления карт, геодезистам для
того, чтобы размечать участки на местности, например, для закладки фундамента
дома, приходится использовать специальные методы.

Недоступное (неприступное) расстояние – это расстояние до объекта, находящегося в поле зрения наблюдателя, которое не может быть измерено непосредственно.

Метод определения недоступного расстояния используется в тех случаях, когда надо измерить наклонное расстояние, горизонтальное проложение и разность высот между начальной точкой и любыми другими точками без перемещения инструмента.
Последняя измеренная точка может быть задана, как начальная для последующих измерений.
Результат измерений может быть выведен как градиент (уклон в %) между двумя точками.
 

Измерение расстояний между точками

Вычисление по введенным координатам

Смена начальной точки

Последняя измеренная точка может быть задана, как начальная для последующих измерений.

1.    Наблюдайте начальную точку и отражатель в соответствии с действиями, описанными в предыдущем разделе. «Измерение расстояний между точками»
2.    После измерения визирных целей нажмите клавишу [СМЕНА], затем клавишу [ДА].
Для отмены измерения нажмите клавишу [НЕТ].

Последняя измеренная точка становится новой начальной точкой.
Выполните процедуру определения недоступного расстояния.

Если препятствие (река, обрыв, здание)
делает расстояние недоступным для
измерения лентой, то его измеряют
косвенным методом.

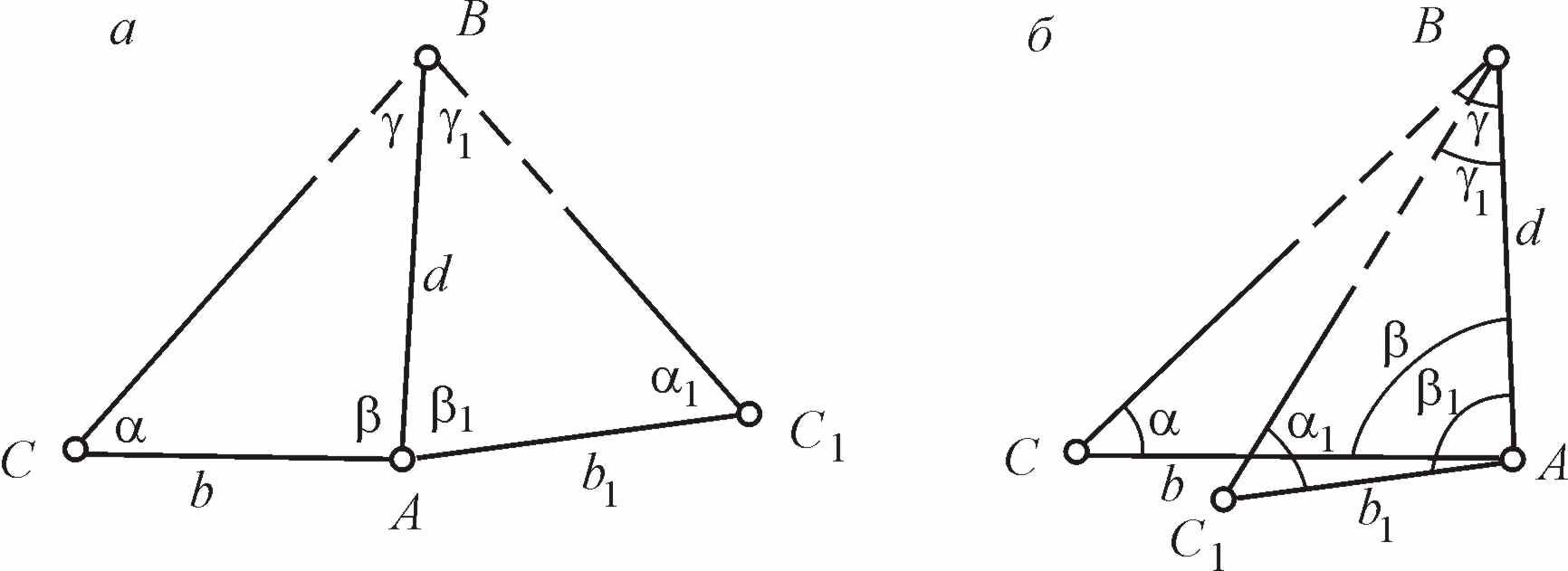
Так, для определения недоступного
расстояния dизмеряют лентой длину
базисаb(рис. 8.3, а, б) и углыи. ИзABCнаходят

d
= b sin

/ sin (
+ ),

где
учтено, что sin

= sin
(180)
= sin
(
+ ).

Рис. 8.3. Определение
недоступного расстояния

Для
контроля расстояние d
определяют ещё раз из треугольника ABC₁
и при
отсутствии недопустимых расхождений
вычисляют среднее.

8.3. Нитяный дальномер

Теория
нитяного дальномера.
Зрительные трубы многих геодезических
приборов снабжены нитяным дальномером.
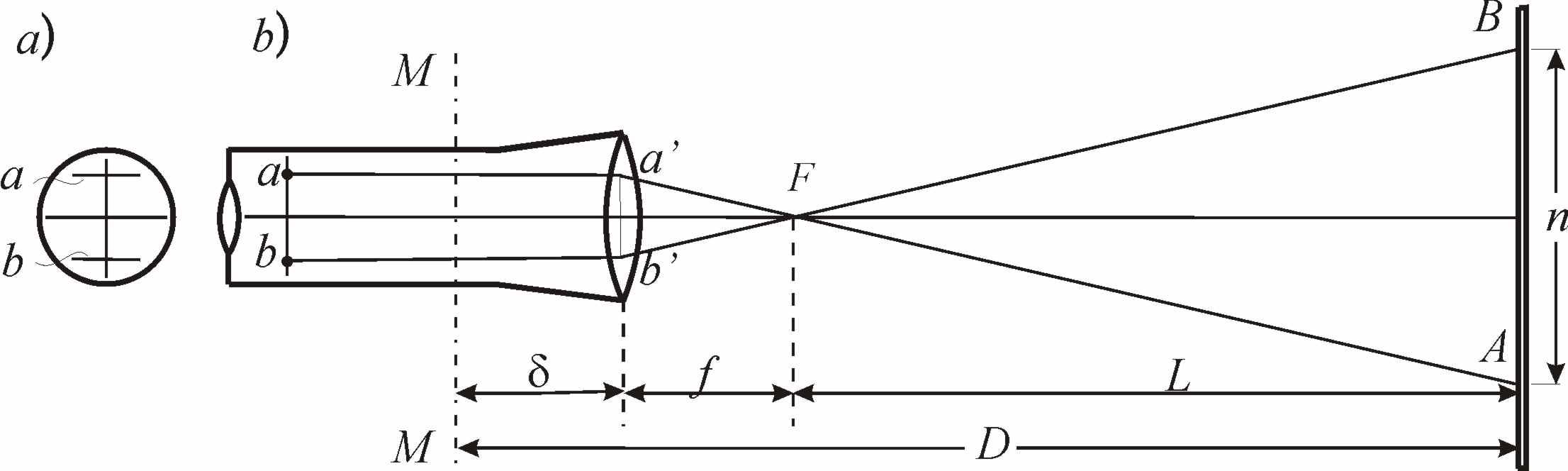
Сетка нитей зрительной трубы, кроме
основных штрихов (вертикальных и
горизонтальных), имеет дальномерные
штрихи a
и b
(рис. 8.4, а).
Расстояние D
от оси вращения прибора MM
(рис. 8.4, б)
до рейки AB
равно

D
= L
+ f
+ 
,

где
L

расстояние от фокуса объектива до рейки;
f

фокусное расстояние; 

расстояние между объективом и осью
вращения прибора.

Лучи,
идущие через дальномерные штрихи сетки
a
и b
параллельно оптической оси, преломляются
объективом, проходят через его фокус F
и проецируют изображения дальномерных
штрихов на точки A
и B,
так что дальномерный отсчёт по рейке
равен n.
Обозначив расстояние между дальномерными
штрихами p,
из подобных треугольников ABF
и abF
находим L = n
f / p. Обозначив
f / p = K
и f + 
= c , получаем

D
= K
n
+ c
,

где
K

коэффициент дальномера и
c 
постоянная дальномера.

Рис. 8.4. Нитяный
дальномер: а) – сетка нитей;б)
– схема определения расстояния

При
изготовлении прибора f
и p
подбирают такими, чтобы K=100,
а постоянная c
была близкой к нулю. Тогда D
= 100 n.

Точность
измерения расстояний нитяным дальномером

1/300.

Определение
горизонтального проложения линии,
измеренной нитяным дальномером.
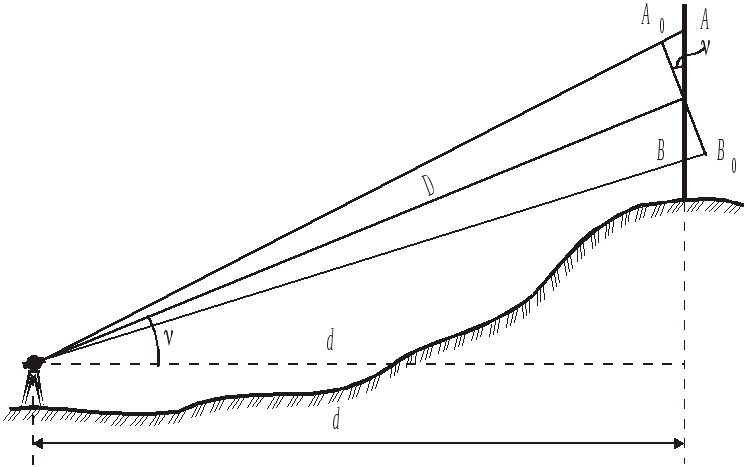
При измерении наклонной линии отсчёт
по рейке это отрезок n
= AB (рис. 8.5).
Если бы рейку наклонить на угол ,
то отсчёт был бы равен n₀
= A₀B₀
= n cos
и наклонное расстояние D=Kn₀+c
= Kncos+c.

Рис.
8.5. Измерение нитяным дальномером
наклонного расстояния

Умножив
наклонное расстояние D
на cos,
получим горизонтальное расстояние d
= K
n
cos²

+ c
cos
.

Прибавив
и отняв с
cos²,
после преобразований получим

d
= (Kn
+ с)
cos²
+ 2c
cos
sin²(2).

Вторым слагаемым по его малости пренебрежем. Получим

d
= (Kn
+ с)
cos²
.

Вычисления
упрощаются, если воспользоваться
составленными с использованием этой
формулы «Тахеометрическими таблицами».

8.4. Светодальномеры, электронные тахеометры

Светодальномер
–
прибор, измеряющий расстояние по времени
прохождения его световым сигналом.

В
комплект светодальномера входят
приёмопередатчик и отражатель.
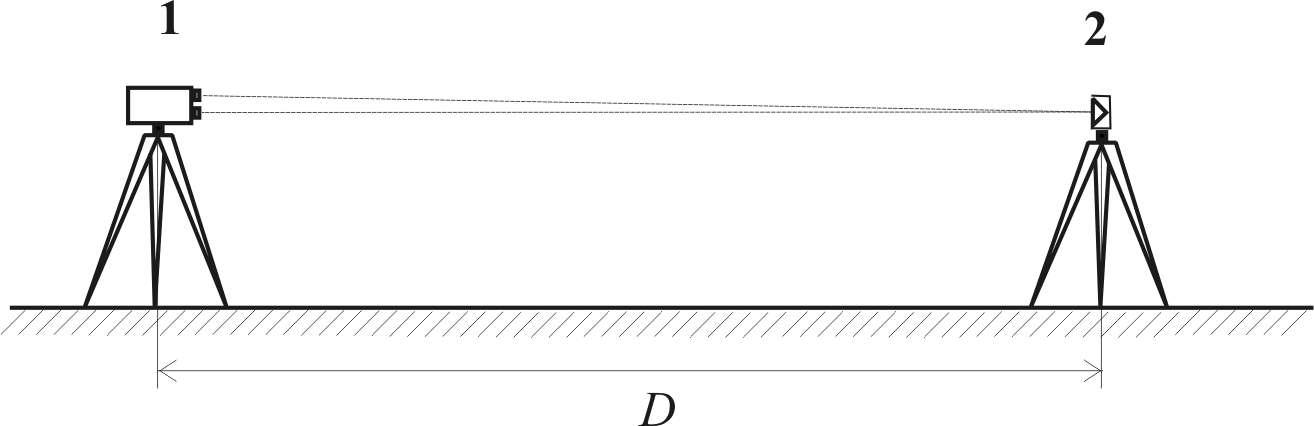
Приемопередатчик 1 (рис. 8.6) устанавливают
на штативе на одном конце измеряемой
линии, а отражатель 2 на специальной
вешке или тоже на штативе – на другом.

Рис.
8.6. Измерение расстояния
светодальномером

Приёмопередатчик
излучает световой сигнал, принимает
его после возвращения от отражателя,
измеряет время
t, прошедшее
от излучения до приёма, и вычисляет
расстояние

D
= vt/2.

Здесь
v
– скорость света (при средних условиях
v 
299710 км/с).

Время
t
необходимо измерять с высокой точностью.
Так, для точности в расстоянии 1 см время
надо знать с ошибкой не более 10^-10
с. Измерение
времени выполняется фазовым или
импульсным методом.

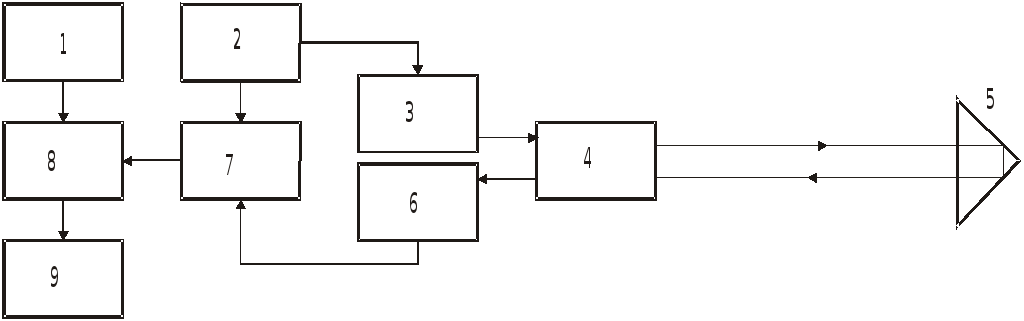
Рис. 8.7. Схема
импульсного светодальномера

В
импульсном светодальномере (рис. 8.7)
лазерный источник излучения 3 под
воздействием генератора импульсов 2
периодически посылает через объектив
4 световой импульс. Одновременно
переключатель 7 запускает счётчик 8
временных
импульсов, поступающих от высокочастотного
генератора 1. Световой импульс, отразившись
от отражателя 5, поступает на преобразователь
6, который через переключатель 7
останавливает счётчик 8. Число импульсов,
сосчитанное счётчиком 8, пропорционально
прошедшему времени и, следовательно,
измеряемому расстоянию. Для повышения
точности измерения выполняются
многократно и результаты осредняются
процессором 9. Измеренное расстояние
высвечивается на табло.

Измеренное
расстояние исправляют поправками за
атмосферное давление, температуру и
влажность воздуха, влияющие на скорость
света. Для получения горизонтального
проложения вводят поправку за наклон.

Конструктивно
приемопередатчик представляет собой
отдельный прибор, насадку на теодолит
или блок, входящий в состав электронного
тахеометра.

По
их назначению принято различать
светодальномеры для построения
государственных геодезических сетей,
светодальномеры для прикладной геодезии
и маркшейдерии и светодальномеры для
топографических съёмок.

Точность
топографических светодальномеров 2 –
3 см, а применяемых в прикладной геодезии
2 – 3 мм.

Отражатели
бывают призменные и плёночные. Основным
элементом призменного отражателя (рис.
8.8 б)
является стеклянная трипельпризма
отражающая световые лучи в тех
направлениях, откуда они пришли. Для
увеличения дальности измерений
изготавливают многопризменные отражатели.

Плёночный
отражатель представляет собой отражающую
свет пластиковую плёнку размером 11
см и больше, на которую нанесены штрихи
(например, вертикальный и горизонтальный).
Дальность измерений с пленочными
отражателями меньше, чем с призменным.
Но зато пленочный отражатель можно
закрепить там, где установить призменный
отражатель невозможно, например –
приклеить в нужном месте на сооружение.
Кроме того, пленочные отражатели гораздо
дешевле призменных. При выполнении
угловых измерений центр штрихов на
отражателе служит визирной целью.

Существуют
светодальномеры, использующие диффузное
отражение сигнала от предметов и не
требующие отражателя. Таким дальномером
является «лазерная рулетка» Disto
фирмы Leica (Швейцария). Прибор используют
без штатива, с руки. Световой луч наводят
на нужные объекты и на шкале читают
расстояния до 200 м с точностью 1,5 мм.

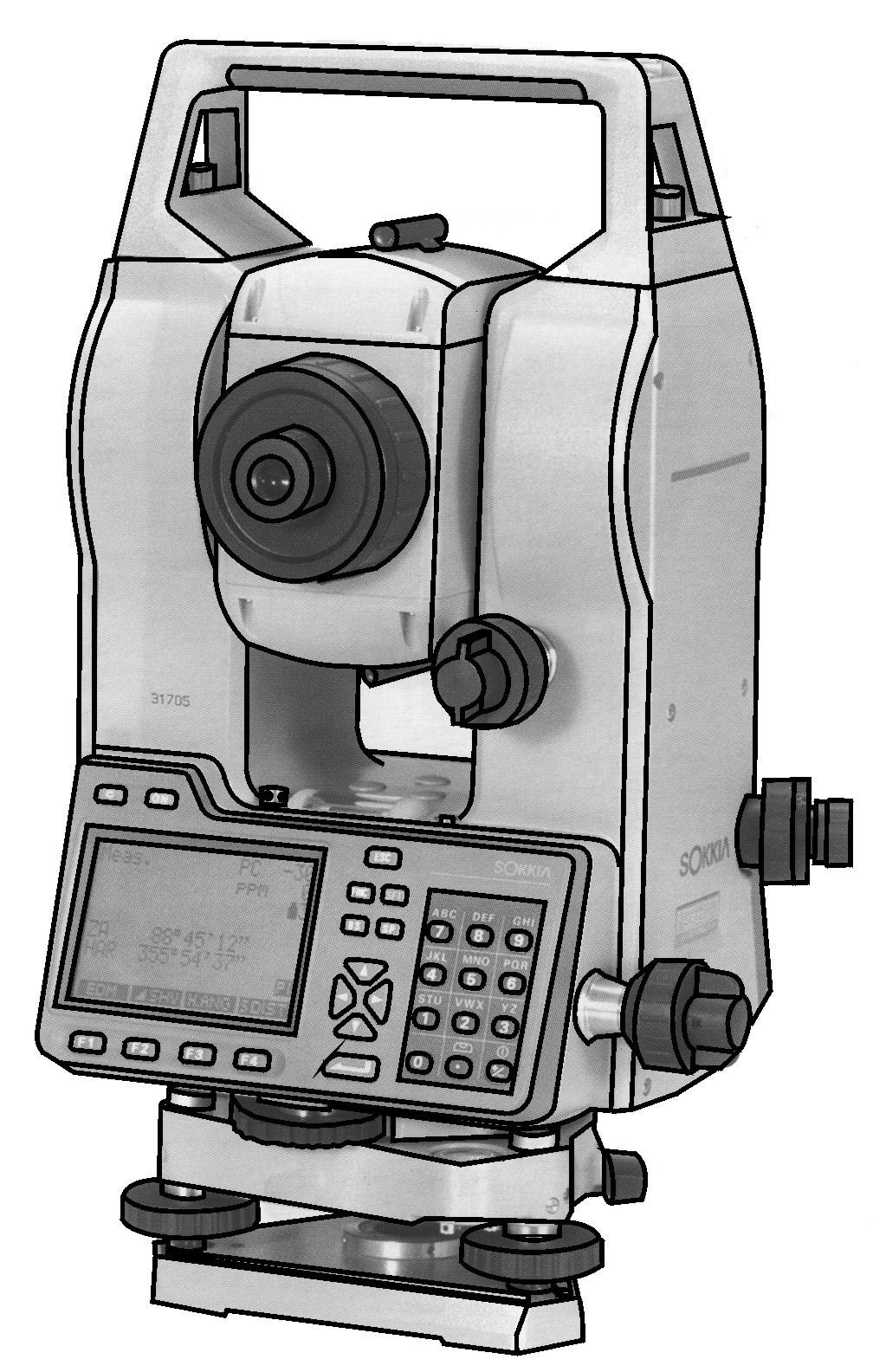
Электронные
тахеометры.
Электронным тахеометром (рис. 8.8)
называется прибор, объединяющий в себе
светодальномер, электронный теодолит
и микро-ЭВМ. Светодальномер прибора
измеряет расстояние до отражателя.
Датчики горизонтального и вертикального
кругов электронного теодолита выдают
отсчеты по кругам. Отсчеты расстояния
и углов передаются на индикацию и
регистрацию. Микро-ЭВМ обеспечивает
возможность решения целого ряда
стандартных геодезических задач, для
чего прибор снабжен набором необходимых
прикладных программ. Полученная в
результате измерений и вычислений
информация высвечивается на цифровом
табло, а также регистрируется во
внутренней памяти прибора и на флэш-картах
для последующего ввода в компьютер для
дальнейшей обработки.

Электронный
тахеометр имеет, как правило, две панели
управления, расположенные с обеих сторон
прибора. На панели управления расположены
дисплей и клавиатура для управления
процессом измерений и ввода информации
вручную. Ввод информации и управление
возможны и с дистанционного пульта
управления (контроллера). Тахеометр
может иметь световой указатель створа,
облегчающий установку вехи с отражателем
на линию, по которой направлена труба
прибора.

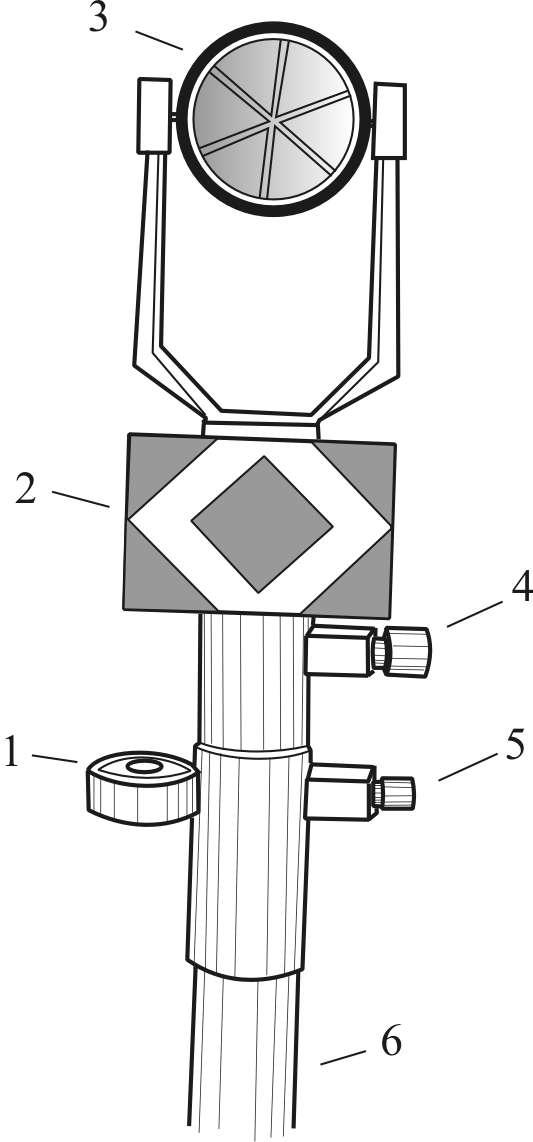
Рис. 8.8. Электронный
тахеометр: а) – основной прибор;б)однопризменный
отражатель: 1 – уровень; 2 – визирная
марка; 3 – призма; 4, 5 – закрепительные
винты; 6 — штанга.

Программное
обеспечение электронных тахеометров
поддерживает решение достаточно широкого
круга задач. Обычно бывает предусмотрен
ввод и сохранение данных о станции: ее
координат, номера точки, высоты прибора,
имени оператора, даты, времени, сведений
о погоде (ветре, температуре, давлении).
По результатам измерений выполняется
вычисление горизонтальных и вертикальных
углов, дирекционных углов линий,
горизонтальных проложений, превышений,
высот точек, где установлен отражатель,
приращений координат, плоских и
пространственных координат наблюдаемых
точек. Предусмотрена возможность
вычисления координат по результатам
засечек, вычисления расстояния до
недоступной для установки отражателя
точки и координат недоступной точки,
определения высоты недоступного объекта.
Для обеспечения разбивочных работ
служат программы вычисления угла и
расстояния для выноса точки с заданными
координатами. При решении задач
учитывается рефракция световых лучей
в атмосфере.

В
настоящее время на рынке имеется широкий
выбор электронных тахеометров, выпускаемых
разными фирмами, в числе которых Уральский
оптико-механический завод (Россия),
Sokkia
(Япония), Trimble
(США), Leica
(Швейцария) и др. Характеристики приборов
разных марок различаются. Средние
квадратические погрешности измерения
углов тахеометров лежат в пределах от
1
до 6.
Максимальные дальности измерения
расстояний на однопризменный отражатель
различаются от 1600 до 5000 м. При этом,
точность измерений в среднем характеризуется
ошибкой 2 мм + 210^-6
D,
где D
– расстояние. Многие из электронных
тахеометров позволяют измерять расстояния
без отражателя. Дальность таких измерений
меняется в разных приборах в пределах
70 – 350 м.

Использование
электронных тахеометров значительно
повышает производительность труда,
упрощает и сокращает время на обработку
результатов измерений, исключает такие
ошибки исполнителя, которые имеют место
при визуальном взятии отсчетов, при
записи результатов измерений в журналы,
в вычислениях. При работе с электронным
тахеометром отпадает необходимость
иметь калькулятор для выполнения полевых
вычислений.

Сайт «Выживание в дикой природе», рад видеть Вас. Если Вы зашли к нам, значит хотите получить полную информацию о выживании в различных экстремальных условиях, в чрезвычайных ситуациях. Человек, на протяжении всего развития, стремился сохранить и обезопасить себя от различных негативных факторов, окружающих его — холода, жары, голода, опасных животных и насекомых.

Структура сайта «Выживание в дикой природе» проста и логична, выбрав интересующий раздел, Вы получите полную информацию. Вы найдете на нашем сайте рекомендации и практические советы по выживанию, уникальные описания и фотографии животных и растений, пошаговые схемы ловушек для диких животных, тесты и обзоры туристического снаряжения, редкие книги по выживанию и дикой природе. На сайте также есть большой раздел, посвященный видео по выживанию известных профессионалов-выживальщиков по всему миру.

Основная тема сайта «Выживание в дикой природе» — это быть готовым оказаться в дикой природе и умение выживать в экстремальных условиях.

В былые времена все мужчины, в той или иной степени были обучены военному делу. Был такой момент и в моей жизни. На этот счет существует метод определения расстояния до цели.

Как было замечено другими авторами, зная расстояние от глаза до вытянутой руки и размер видимый на рулетке, можно построить прямоугольный треугольник. Зная реальный размер какого то предмета на местности (в нужном месте) можно построить треугольник подобный предыдущему. Далее из пропорции будет следовать.

Из констант мне запомнились только две. Высота столба линии электропередач 6 м, расстояние между столбами 50 м. Хотя список был по более.

Безусловно, не всегда такой ориентир найдется, да и видится он должен в реальную величину.

Можно рассчитать какому углу равен каждый миллиметр на рулетке и через тригонометрическую зависимость определить расстояние, но зная размер ориентира.

Для того чтобы не обременять себя таблицами Брадиса, военные производят вычисление в собственных угловых единицах — тысячных.

Окружность делится на 6000 частей. Поскольку длина окружности примерно равна 6R, то и единица измерения угла будет равна одной тысячной радиуса.

Провожу антропологические измерения. У меня расстояние от глаза до вытянутой руки равняется 700 мм. Следовательно одна тысячная будет равняться 0.7 мм по рулетке.

Измеряю высоту столба по рулетке. Получаю 35 мм, а значит это будет 50 тысячных (35/0.7). Высота столба 6 м, следовательно одна тысячная равна 6/50=0.12 м. Остается умножить эту величину на 1000 и получим расстояние до объекта. 0.12* 1000=120 м. Расстояние определено.

Написанное до сих пор было скорее для общего развития. А теперь попробую ответить на вопрос автора.

Попробуем определить расстояние до объекта по параллаксу.

Определим в комнате линию параллельную стене с окном. Линию и точки не обязательно чертить, их можно разметить при помощи предметов, например спичечных коробков. Размер «с» равен ширине стекла. Середину стекла можно разметить приклеив мокрый кусочек газеты.

Из подобных треугольников следует.

Отсюда х будет равен.

Если расстояние до объекта велико, то нет необходимости делить стекло пополам. Можно начертить треугольники на всю ширину стекла по границе видимости. В этом случае двоечка из расчетной формулы исчезнет.

Не знаю какова будет точность таких измерений, но делать нужно все очень быстро, пока объекту наблюдений не надоест сидеть на одном месте