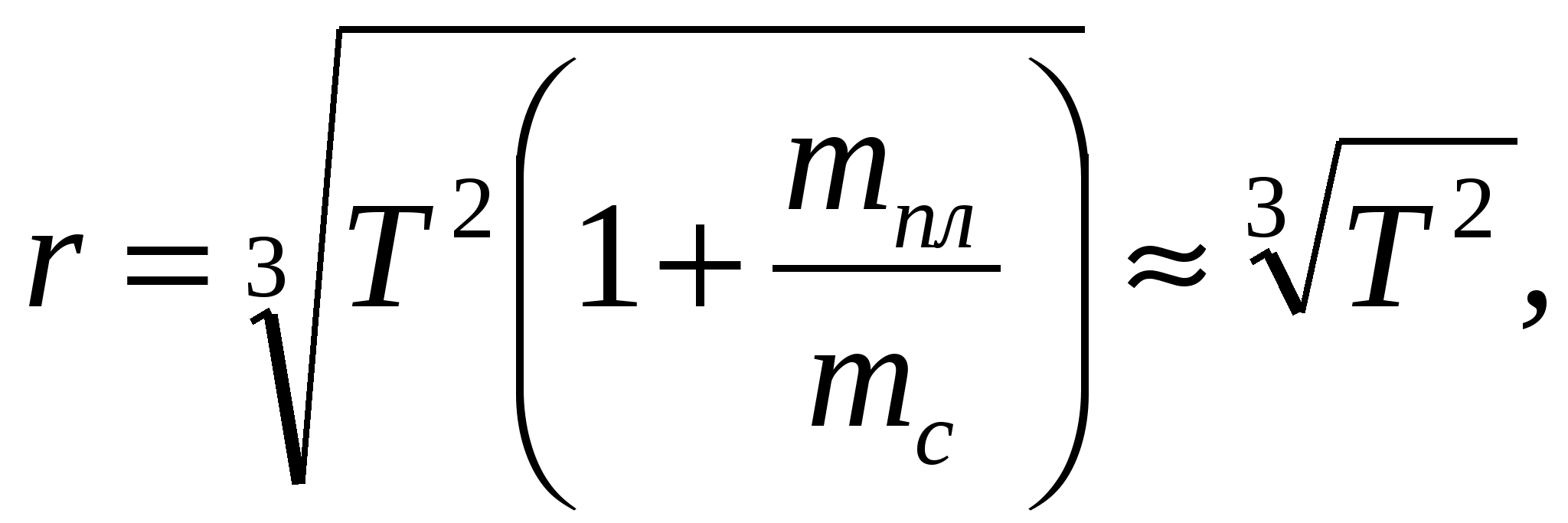Какого размера наша Солнечная система и где она кончается?
Как измерить расстояние до планеты?
В прошлом единственным методом измерения космических расстояний был метод горизонтального параллакса. Хотя этот метод достаточно точен и до сих пор применяется при расчете расстояния до очень далеких космических объектов, для измерения расстояний до планет-соседей по Солнечной системе, с середины 20-го века применяется более простой и ещё более точный способ – метод радиолокации.
В основе методики космической радиолокации лежит идея заимствованная у самой природы: достаточно просто найти на небесной сфере нужный объект (например, планету Венера), “прицелится” в неё и затем “выстрелить” радиоволнами сверхкороткого диапазона. Теперь нам остается только дождаться когда сигнал достигнет поверхности Венеры, отразится от неё и устремится обратно.
Скорость распространения радиоволн точно известна, а время между посылкой волн и их приемом также может быть измерено очень точно. Расстояние, покрытое радиоволнами за время путешествия туда и обратно, а следовательно, и расстояние до Венеры в заданный момент можно определить с несравненно большей точностью, чем методом параллаксов.
Начиная с 1961 г. года этот способ измерения близких космических расстояний стал основным. С помощью полученных данных было вычислено, что среднее расстояние от Земли до Солнца составляет 149 573 000 км.
Радиотелескопы без перерыва «сканируют» космос и ловят «эхо» своих сигналов отраженное от космических объектов
Световая секунда, световой год и другие космические единицы измерения
Используя кеплеровскую схему строения солнечной системы (Солнце в центре, планеты вращаются вокруг него), удобнее всего рассчитывать расстояния в пределах солнечной системы не от Земли, а от центра, то есть от Солнца. Но вот в каких единицах его отсчитывать?
- Во-первых, его можно выражать в миллионах километров. Километр — это наиболее распространенная единица для измерения больших расстояний.
- Во-вторых, чтобы избежать таких чисел, как миллионы километров, можно принять, что среднее расстояние от Земли до Солнца равно одной астрономической единице (сокращенно «а, е.») Тогда можно будет выражать расстояния в а, е., причем 1 а е. равна 149 500 000 км. С вполне достаточной точностью можно считать, что 1 а, е. равна 150 000 000 км.
- В-третьих, расстояние можно выразить через время, которое потребуется для того, чтобы его преодолел свет (или любое аналогичное излучение, например радиоволны). Скорость света в пустоте равна 299 776 км/сек. Число это можно для удобства округлить до 300 000 км/сек.
Таким образом, расстояние примерно в 300 000 км можно считать равным одной световой секунде (ибо это расстояние, преодолеваемое светом за одну секунду). Расстояние, в 60 раз большее, или 18 000 000 км, — это одна световая минута, а расстояние, еще в 60 раз большее, т.е. 1 080 000 000 км, — это один световой час.
Мы не слишком ошибемся, если будем считать, что световой час равен одному миллиарду километров.
Запомнив это, рассмотрим те планеты, которые были известны древним, и приведем таблицу их средних расстояний от Солнца, выраженных в каждой из трех указанных единиц.
| Планеты | Среднее расстояние от Солнца | ||
| миллионов км | астрономических единиц | световых часов | |
| Меркурий | 57,9 | 0,387 | 0,0535 |
| Венера | 108,2 | 0,723 | 0,102 |
| Земля | 149,5 | 1,000 | 0,137 |
| Марс | 227,9 | 1.524 | 0,211 |
| Юпитер | 778,3 | 5,203 | 0,722 |
| Сатурн | 1428,0 | 9,539 | 1,321 |
Уильям Гершель – в свое время раздвинул горизонты познания, открыв Уран и буквально удвоив границы Солнечной системы
Размеры Солнечной системы
В 17-м веке, когда был открыт Сатурн, астрономы считали его орбиту “границей” Солнечной системы, соответственно вся “система” умещалась в круг диаметром 3 миллиардов км.
Однако в 1781 г., когда английский астроном, немец по происхождению, Уильям Гершель (1738—1822) открыл планету Уран, диаметр Солнечной системы внезапно… удвоился!
А потом снова удвоился, когда сначала французский астроном Урбан Жозсф Леверье (1811 — 1877) открыл в 1846 г. Нептун, затем американский астроном Клайд Уильям Томбо (род. в 1906 г.) — Плутон в 1930 г.
| Планеты | Среднее расстояние от Солнца | ||
| миллионов км | астрономических единиц | световых часов | |
| Уран | 2872 | 19,182 | 2,63 |
| Нептун | 4498 | 30,058 | 4,26 |
| Плутон | 5910 | 39,518 | 5,47 |
Если мы рассмотрим орбиту Плутона, как ранее орбиту Сатурна, то увидим, что диаметр солнечной системы равен не 3, а 12 миллиардам километров. Лучу света, который преодолевает расстояние, равное окружности Земли, за 1/7 сек и пробегает от Земли до Луны за 1 1/4 сек, понадобится полдня для того, чтобы пересечь солнечную систему.
Кроме того, есть все основания считать, что вовсе не орбита Плутона отмечает границу владений Солнца. Это не значит, что мы должны предполагать существование еще не открытых более далеких планет (за исключением карликовых планет). Имеются уже известные небесные тела, которые время от времени очень легко увидеть и которые, без сомнения, уходят от Солнца гораздо дальше, чем Плутон на самой удаленной точке своей орбиты.
Где находятся границы Солнечной системы
В 1684 г. английский ученый Исаак Ньютон (1642—1727) открыл закон всемирного тяготения. Этот закон строго математически обосновал кеплеровскую схему строения солнечной системы и позволил вычислить орбиту тела, обращающегося вокруг Солнца, даже если тело наблюдалось лишь на части своей орбиты.
Это в свою очередь дало возможность приняться за кометы — небесные тела, которые время от времени появлялись на небе. В древности и в эпоху Средневековья астрономы считали, что кометы появляются без всякой правильности и что движение их не подчинено никаким естественным законам, широкие же массы были убеждены, что единственное назначение комет — предвещать несчастье.
Однако современник и друг Ньютона, английский ученый Эдмунд Галлей (1656—1742) попробовал применить к кометам закон тяготения. Он заметил, что некоторые особенно яркие кометы появлялись в небе через каждые 75—76 лет.
И вот в 1704 г. он предположил, что все эти кометы на самом деле были одним и тем же небесным телом, которое двигалось вокруг Солнца по постоянной эллиптической орбите, причем орбите настолько вытянутой, что значительная ее часть лежала на колоссальном расстоянии от Земли. Когда комета находилась вдали от Земли, она была невидима.
Но через каждые 75 или 76 лет она оказывалась на той части своей орбиты, которая расположена ближе всего к Солнцу (и к Земле), и вот тогда-то она становилась видимой.
Попытка запечатлеть реальные размеры и расстояния планет Солнечной системы от Солнца и друг от друга
Галлей вычислил орбиту этой кометы и предсказал, что она вновь вернется в 1758 г. И действительно, комета появилась в тот год (через 16 лет после смерти Галлея) и с тех пор получила название кометы Галлея.
В ближайшей к Солнцу точке своей орбиты комета Галлея оказывается от него всего лишь примерно в 90 000 000 км, заходя таким образом немного внутрь орбиты Венеры В наиболее же удаленной от Солнца части своей орбиты комета Галлея уходит от него приблизительно в 3 1/2 раза дальше, чем Сатурн.
Таким образом, к 1760 г. астрономы прекрасно знали, что солнечная система не очерчена орбитой “последней” планеты.
Более того, комета Галлея — одна из комет, относительно близких к Солнцу. Существуют кометы, которые движутся вокруг него по таким невероятно вытянутым орбитам, что возвращаются к нему только раз в несколько столетий, а то и тысячелетий. Они уходят от Солнца не на миллиарды километров, а скорее всего на сотни миллиардов.
Голландский астроном Ян Хендрик Оорт (род. в 1900 г) в 1950 г. высказал предположение, что, возможно, существует целое огромное облако комет (известное как “Облако Оорта”), которые на протяжении всей своей орбиты находятся так далеко от Солнца, что никогда не бывают видимы.
Отсюда следует, что максимальный диаметр солнечной системы может достигать 1000 миллиардов, т. е триллиона (1 000 000 000 000) километров или даже больше. Световому лучу требуется 40 суток, чтобы покрыть такое расстояние. Таким образом, можно сказать, что диаметр солнечной системы превосходит один световой месяц.
Представление о Земле как о шаре, который свободно, без всякой опоры находится в космическом пространстве, является одним из величайших достижений науки древнего мира.
Считается, что первое достаточно точное определение размеров Земли провёл греческий учёный Эратосфен (276—194 до н. э.), живший в Египте. Идея, положенная в основу измерений Эратосфена, весьма проста: измерить длину дуги земного меридиана в линейных единицах и определить, какую часть полной окружности эта дуга составляет. Получив эти данные, можно вычислить длину дуги в 1°, а затем длину окружности и величину её радиуса, т. е. радиуса земного шара. Очевидно, что длина дуги меридиана в градусной мере равна разности географических широт двух пунктов: ϕB – ϕA.
Рис. 3.8. Способ Эратосфена
Для того чтобы определить эту разность, Эратосфен сравнил полуденную высоту Солнца в один и тот же день в двух городах, находящихся на одном меридиане. Измерив высоту Солнца hB (рис. 3.8) в полдень 22 июня в Александрии, где он жил, Эратосфен установил, что Солнце отстоит от зенита на 7,2°. В этот день в полдень в городе Сиена (ныне Асуан) Солнце освещает дно самых глубоких колодцев, т. е. находится в зените (hA = 90°). Следовательно, длина дуги составляет 7,2°. Расстояние между Сиеной (A) и Александрией (B) около 5000 греческих стадий — l.
Стадией в Древней Греции считалось расстояние, которое проходит легко вооружённый греческий воин за тот промежуток времени, в течение которого Солнце, коснувшееся горизонта своим нижним краем, целиком скроется за горизонт.
Несмотря на кажущееся неудобство такой единицы и достаточную громоздкость словесного определения, её введение выглядело вполне оправданным, учитывая, что строгая периодичность небесных явлений позволяла использовать их движение для счёта времени.
Обозначив длину окружности земного шара через L, получим такое выражение:


откуда следует, что длина окружности земного шара равняется 250 тыс. стадий.
Точная величина стадии в современных единицах неизвестна, но, зная, что расстояние между Александрией и Асуаном составляет 800 км, можно полагать, что 1 стадия = 160 м. Результат, полученный Эратосфеном, практически не отличается от современных данных, согласно которым длина окружности Земли составляет 40 тыс. км.
Эратосфен ввёл в практику использование терминов «широта» и «долгота». Видимо, появление этих терминов связано с особенностями формы карт того времени: они повторяли по очертаниям побережье Средиземного моря, которое длиннее по направлению запад—восток (по долготе), чем с севера на юг (по широте).
Рис. 3.9. Параллактическое смещение
Определить географическую широту двух пунктов оказывается гораздо проще, чем измерить расстояние между ними. Зачастую непосредственное измерение кратчайшего расстояния между этими пунктами оказывается невозможным из-за различных естественных препятствий (гор, рек и т. п.). Поэтому применяется способ, основанный на явлении параллактического смещения и предусматривающий вычисление расстояния на основе измерений длины одной из сторон (базиса — BC) и двух углов B и C в треугольнике ABC (рис. 3.9).
Параллактическим смещением называется изменение направления на предмет при перемещении наблюдателя.
Чем дальше расположен предмет, тем меньше его параллактическое смещение, и чем больше перемещение наблюдателя (базис измерения), тем больше параллактическое смещение.
Рис. 3.10. Схема триангуляции
Для определения длины дуги используется система треугольников — способ триангуляции, который впервые был применён ещё в 1615 г. Пункты в вершинах этих треугольников выбираются по обе стороны дуги на расстоянии 30—40 км друг от друга так, чтобы из каждого пункта были видны по крайней мере два других. Основой для вычисления длин сторон во всех этих треугольниках является размер базиса AC (рис. 3.10). Точность измерения базиса длиной в 10 км составляет около 1 мм. Во всех пунктах устанавливают геодезические сигналы — вышки высотой в несколько десятков метров. С вершины сигнала с помощью угломерного инструмента (теодолита) измеряют углы между направлениями на два-три соседних пункта. Измерив углы в треугольнике, одной из сторон которого является базис, геодезисты получают возможность вычислить длину двух других его сторон. Проводя затем измерение углов из пунктов, расстояние между которыми вычислено, можно узнать длину двух очередных сторон в треугольнике. Зная длину сторон этих треугольников, можно определить длину дуги AB.
В какой степени форма Земли отличается от шара, выяснилось в конце XVIII в. Для уточнения формы Земли Французская академия наук снарядила сразу две экспедиции. Одна из них работала в экваториальных широтах Южной Америки в Перу, другая — вблизи Северного полярного круга на территории Финляндии и Швеции. Измерения показали, что длина одного градуса дуги меридиана на севере больше, чем вблизи экватора. Последующие исследования подтвердили, что длина дуги одного градуса меридиана увеличивается с возрастанием географической широты. Это означало, что форма Земли — не идеальный шар: она сплюснута у полюсов. Её полярный радиус на 21 км короче экваториального.
Для школьного глобуса масштаба 1 : 50 000 000 отличие этих радиусов будет всего 0,4 мм, т. е. совершенно незаметно.
Отношение разности величин экваториального и полярного радиусов Земли к величине экваториального называется сжатием. По современным данным, оно составляет 
В XX в. благодаря измерениям, точность которых составила 15 м, выяснилось, что земной экватор также нельзя считать окружностью. Сплюснутость экватора составляет всего 
В настоящее время форму Земли принято характеризовать следующими величинами:
|
сжатие эллипсоида — 1 : 298,25; |
|
средний радиус — 6371,032 км; |
|
длина окружности экватора — 40075,696 км. |
Измерить расстояние от Земли до Солнца удалось лишь во второй половине XVIII в., когда был впервые определён горизонтальный параллакс Солнца. По сути дела, при этом измеряется параллактическое смещение объекта, находящегося за пределами Земли, а базисом является её радиус.
Горизонтальным параллаксом ( p) называется угол, под которым со светила виден радиус Земли, перпендикулярный лучу зрения (рис. 3.11).
Рис. 3.11. Горизонтальный параллакс светила
Из треугольника OAS можно выразить величину — расстояние OS = D:
D = 
где R — радиус Земли. По этой формуле можно вычислить расстояние в радиусах Земли, а зная его величину, — выразить расстояние в километрах.
Очевидно, что чем дальше расположен объект, тем меньше его параллакс. Наибольшее значение имеет параллакс Луны, который меняется в связи с тем, что Луна обращается по эллиптической орбите, и в среднем составляет 57ʹ. Параллаксы планет и Солнца значительно меньше. Так, параллакс Солнца равен 8,8ʺ. Такому значению параллакса соответствует расстояние до Солнца, примерно равное 150 млн км. Это расстояние принимается за одну астрономическую единицу (1 а. е.) и используется при измерении расстояний между телами Солнечной системы.
Известно, что для малых углов sin p ≈ p, если угол p выражен в радианах. В одном радиане содержится 206 265ʺ. Тогда, заменяя sin p на p и выражая этот угол в радианной мере, получаем формулу в виде, удобном для вычислений:
D = 
или (с достаточной точностью)
D = 
Во второй половине XX в. развитие радиотехники позволило определять расстояния до тел Солнечной системы посредством радиолокации. Первым объектом среди них стала Луна. Затем радиолокационными методами были уточнены расстояния до Венеры, Меркурия, Марса и Юпитера. На основе радиолокации Венеры величина астрономической единицы определена с точностью порядка километра. Столь высокая точность определения расстояний — необходимое условие для расчётов траекторий полёта космических аппаратов, изучающих планеты и другие тела Солнечной системы. В настоящее время благодаря использованию лазеров стало возможным провести оптическую локацию Луны. При этом расстояния до лунной поверхности измеряются с точностью до сантиметров.
На каком расстоянии от Земли находится Сатурн, когда его горизонтальный параллакс равен 0,9ʺ?
|
Дано: p1 = 0,9ʺ D☉ = 1 а. е. p☉ = 8,8ʺ |
Решение: Известно, что параллакс Солнца на расстоянии в 1 а. е. равен 8,8ʺ. Тогда, написав формулы для расстояния до Солнца и до Сатурна и поделив их одна на другую, получим: |
|
D1 — ? |


Откуда
D1 = 

Ответ: D1 = 9,8 а. е.
Рис. 3.12. Угловые размеры светила
Зная расстояние до светила, можно определить его линейные размеры, если измерить его угловой радиус ρ (рис. 3.12). Формула, связывающая эти величины, аналогична формуле для определения параллакса:
D = 
Учитывая, что угловые диаметры даже Солнца и Луны составляют примерно 30ʹ, а все планеты видны невооружённым глазом как точки, можно воспользоваться соотношением: sin ρ ≈ ρ. Тогда:
D = 

Следовательно,
r = 
Если расстояние D известно, то
r = Dρ,
где величина ρ выражена в радианах.
Чему равен линейный диаметр Луны, если она видна с расстояния 400 000 км под углом примерно 30ʹ?
|
Дано: D = 400 000 км ρ = 30ʹ |
Решение: Если ρ выразить в радианах, то d = Dρ. Следовательно, |
|
d — ? |
d = 
Ответ: d = 3490 км.

Вопросы 1. Какие измерения, выполненные на Земле, свидетельствуют о её сжатии? 2. Меняется ли и по какой причине горизонтальный параллакс Солнца в течение года? 3. Каким методом определяется расстояние до ближайших планет в настоящее время?

Упражнение 11 1. Чему равен горизонтальный параллакс Юпитера, наблюдаемого с Земли в противостоянии, если Юпитер в 5 раз дальше от Солнца, чем Земля? 2. Расстояние Луны от Земли в ближайшей к Земле точке орбиты (перигее) 363 000 км, а в наиболее удалённой (апогее) — 405 000 км. Определите горизонтальный параллакс Луны в этих положениях. 3. Во сколько раз Солнце больше, чем Луна, если их угловые диаметры одинаковы, а горизонтальные параллаксы равны 8,8ʺ и 57ʹ соответственно? 4. Чему равен угловой диаметр Солнца, видимого с Нептуна?
Лекция №8. Методы
определения расстояний до космических
объектов*
План
-
Суточный параллакс.
-
Определение
расстояний до планет. -
Определение
расстояний до ближайших звезд. -
Фотометрический
метод определения расстояний. -
Определение
внегалактических расстояний. -
Определение
расстояний по красному смещению -
Единицы расстояний
в астрономии.
В астрономии нет единого универсального
способа определения расстояний. По мере
перехода от близких небесных тел к более
далеким одни методы определения
расстояний сменяют другие, служащие,
как правило, основой для последующих.
Точность оценки расстояний ограничивается
либо точностью самого грубого из методов,
либо точностью измерения астрономической
единицы длины (а.е.), величина которой
по радиолокационным измерениям известна
со среднеквадратичной погрешностью
0,9 км и равна (149597867,9 0,9) км. С учетом
различных измерений а.е. Международный
астрономический союз принял в 1976 г.
значение 1 а.е. =149597870
2 км.
-
Суточный параллакс
Координаты небесных тел, определенные
из наблюдений на поверхности Земли,
называются топоцентрическими.
Топоцентрические координаты одного
и того же светила в один и тот же момент,
вообще говоря, различны для, различных
точек поверхности Земли. Различие это
заметно лишь для тел Солнечной системы
и практически не ощутимо для звезд
(меньше 0,00004″). Из множества направлений,
по которым светило видно из разных точек
Земли, основным считается направление
из центра Земли.
Оно дает геоцентрическое
положение светила
и определяет его геоцентрические
координаты.
Угол между
направлениями, по которым светило М
было бы видно из центра Земли и
из какой-нибудь точки на ее поверхности,
называется суточным параллаксом
светила.
Рис.
1. Суточный параллакс
Иными словами, суточный параллакс есть
угол р’, под которым со светила был
бы виден радиус Земли, проведенный в
точку наблюдения (рис. 1).
Для светила, находящегося в момент
наблюдения в зените, суточный параллакс
равен нулю. Если светило М наблюдается
на горизонте, то суточный параллакс его
принимает максимальное значение и
называется горизонтальным параллаксом
р.
Из соотношения между сторонами и углами
треугольников ТОМ’ и ТОМ (рис.1)
имеем
R / Δ =
sin p/
/ sin z/
и R
/ Δ = sin p (1)
Отсюда
получаем
sin
p/=sin
p sin z/.
(2)
Горизонтальный
параллакс у всех тел Солнечной системы
— величина небольшая (у Луны в
среднем р — 57′, у Солнца р = 8,79″,
у планет меньше 1′).
Поэтому синусы углов р и р’ в последней
формуле можно заменить самими углами
и написать
p‘
= p sin
z‘. (3)
Вследствие суточного параллакса светило
кажется нам ниже над горизонтом, чем
это было бы, если бы наблюдение проводилось
из центра Земли; при этом влияние
параллакса на высоту светила пропорционально
синусу зенитного расстояния, а максимальное
его значение равно горизонтальному
параллаксу р.
Так как Земля имеет форму сфероида,
то во избежание разногласий в определении
горизонтальных параллаксов необходимо
вычислять их значения для определенного
радиуса Земли. За такой радиус принят
экваториальный радиус Земли Ro
= 6 378 км, а горизонтальные параллаксы,
вычисленные для него, называются
горизонтальными
экваториальными параллаксами ро.
Именно эти
параллаксы тел Солнечной системы
приводятся во всех справочных пособиях.
-
Определение расстояний до планет.
Другой метод определения связан с
использованием третьего (уточненного)
закона Кеплера. В этом случае среднее
расстояние r планеты от Солнца (в долях
а.е.) находят по периоду ее обращения T:
, (4)
где r выражено в а.е., а T — в земных годах.
Массой планеты
по сравнению с массой Солнца
можно пренебречь. Формула (4) следует из
3-го закона Кеплера. Расстояния до Луны
и планет с высокой точностью определены
методами радиолокации.
Определение расстояний до звезд и планет
http://monax.ru/order/ — рефераты
на заказ (более 2300 авторов в 450 городах
СНГ).
Содержание:
Вступление. 3
Определение расстояний до
космических объектов. 3
Определение
расстояний до планет. 4
Определение
расстояний до ближайших звезд. 4
Метод параллакса. 4
Фотометрический метод
определения расстояний. 6
Определение расстояния по
относительным скоростям. 7
Цефеиды. 8
Список литературы. 9
Вступление.
Наши знания о Вселенной тесно
связаны со способностью человека
определять расстояния в пространстве.
С незапамятных времен вопрос «как
далеко?» играл первостепенную роль для
астронома в его попытках познать свойства
Вселенной, в которой он живет. Но как бы
ни было велико стремление человека к
познанию, оно не могло быть осуществлено
до тех пор, пока в распоряжении людей
не оказались высокочувствительные и
совершенные инструменты. Таким образом,
хотя на протяжении веков представления
о физическом мире непрерывно развивались,
завесы, скрывавшие верстовые столбы
пространства, оставались нетронутыми.
Во все века философы и астрономы
размышляли о космических расстояниях
и усердно искали способы их измерения.
Но все было напрасно, так как необходимые
для этого инструменты не могли быть
изготовлены. И, наконец, после того как
телескопы уже в течение многих лет
использовались астрономами и первые
гении посвятили свой талант изучению
богатств, добытых этими телескопами,
настало время союза точной механики и
совершенной оптики, который позволил
создать инструмент, способный разрешить
проблему расстояний. Барьеры были
устранены, и многие астрономы объединили
свои знания, мастерство и интуицию с
целью определить те колоссальные
расстояния, которые отделяют от нас
звездные миры.
В 1838 году три астронома (в разных
частях света) успешно измерили расстояния
до некоторых звезд. Фридрих Вильгельм
Бессель в Германии определил расстояние
до звезды Лебедь 61. Выдающийся русский
астроном Василий Струве установил
расстояние до звезды Веги. На мысе Доброй
Надежды в Южной Африке Томас Гендерсон
измерил расстояние до ближайшей к Солнцу
звезды – альфа Центавра. Во всех названных
случаях астрономы измеряли невообразимо
малое угловое расстояние, чтобы определить
так называемый параллакс. Их успех был
обусловлен тем, что звезды, до которых
они измеряли расстояния, находились
относительно близко к Земле.
Определение расстояний
до космических объектов.
В астрономии нет единого
универсального способа определения
расстояний. По мере перехода от близких
небесных тел к более далеким одни методы
определения расстояний сменяют другие,
служащие, как правило, основой для
последующих. Точность оценки расстояний
ограничивается либо точностью самого
грубого из методов, либо точностью
измерения астрономической единицы
длины (а. е.), величина которой по
радиолокационным измерениям известна
со среднеквадратичной погрешностью
0,9 км. и равна 149597867,9
0,9 км. С учетом различных изменений а.
е. Международный астрономический союз
принял в 1976 году значение 1 а. е. = 149597870
2 км.
Определение
расстояний до планет.
С
реднее
расстояние r
планеты от Солнца (в долях а. е.) находят
по периоду ее обращения Т:
где
r выражено в а. е., а Т –
в земных годах. Массой планеты m
по сравнению с массой солнца m>c>
можно пренебречь. Формула следует из
третьего закона Кеплера (квадраты
периодов обращения планет вокруг Солнца
относятся как кубы их средних расстояний
от Солнца).
Расстояния до Луны и планет с
высокой точностью определены также
методами радиолокации планет.
Определение
расстояний до ближайших звезд.
Метод параллакса.
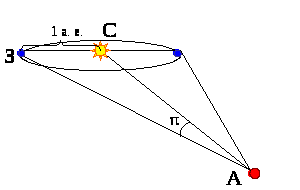
Вследствие годичного движения
Земли по орбите близкие звезды немного
перемещаются относительно далеких
«неподвижных» звезд. За год такая звезда
описывает на небесной сфере малый
эллипс, размеры которого тем меньше,
чем звезда дальше. В угловой мере большая
полуось этого эллипса приблизительно
равна величине максимального угла, под
каким со звезды видна 1 а. е. (большая
полуось земной орбиты), перпендикулярная
направлению на звезду. Этот угол (),
называемый годичным или тригонометрическим
параллаксом звезды, равный половине ее
видимого смещения за год, служит для
измерения расстояния до нее на основе
тригонометрических соотношений между
сторонами и углами треугольника ЗСА, в
котором известен угол
и базис – большая полуось земной орбиты
(см. рис. 1).
Расстояние r до звезды,
определяемое по величине ее
тригонометрического параллакса ,
равно:
r = 206265»/
(а. е.),
где
параллакс выражен
в угловых секундах.
Рисунок 1. Определение расстояния до
звезды методом параллакса (А – звезда,
З – Земля, С – Солнце).
Для удобства
определения расстояний до звезд с
помощью параллаксов в астрономии
применяют специальную единицу длины –
парсек (пс). Звезда, находящаяся на
расстоянии 1 пс, имеет параллакс, равный
1». Согласно вышеназванной формуле, 1
пс = 206265 а. е. = 3,086·1018 см.
Наряду с парсеком применяется
еще одна специальная единица расстояний
– световой год (т. е. расстояние, которое
свет проходит за 1 год), он равен 0,307 пс,
или 9,46·1017 см.
Ближайшая к Солнечной системе
звезда – красный карлик 12-й звездной
величины Проксима Центавра – имеет
параллакс 0,762, т. е. расстояние до нее
равно 1,31 пс (4,3 световых года).
Нижний предел измерения
тригонометрических параллаксов ~0,01»,
поэтому с их помощью можно измерять
расстояния, не превышающие 100 пс с
относительной погрешностью 50%. (При
расстояниях до 20 пс относительная
погрешность не превышает 10%.) Этим методом
до настоящего времени определены
расстояния до около 6000 звезд. Расстояния
до более далеких звезд в астрономии
определяют в основном фотометрическим
методом.
Таблица
1. Двадцать ближайших звезд.
|
№№ п. |
Название |
Параллакс |
Расстояние, |
Видимая |
Абсолютная |
Спек-траль-ный |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
Солнце. . . Проксима α Центавра α Центавра Звезда Лаланд 21185 . Вольф 359 . . +36˚2147 . . . Сириус . . Спутник Росс 154 . . . Росс 248 . . . Лейтен 7896 ε Эридана . Процион . Спутник 61 Лебедя . . Спутник 61 τ Кита . . . ε Индейца . |
–– 0,762 0,756 0,756 0,543 0,407 0,403 0,388 0,376 0,376 0,350 0,334 0,328 0,303 0,297 0,297 0,296 0,296 0,294 0,288 |
1/206256 1,31 1,32 1,32 1,84 2,46 2,48 2,58 2,66 2,66 2,86 2,99 3,05 3,30 3,37 3,37 3,38 3,38 3,40 3,47 |
–26,7 +11,3 +0,3 +1,7 +9,5 +10,7 +13,5 +7,5 –1,5 +8,5 +10,5 +12,2 +12,3 +3,8 +0,5 +10,8 +5,4 +6,1 +3,7 +4,7 |
+4,9 +15,7 +4,7 +6,1 +13,1 +13,7 +16,5 +10,4 +1,4 +11,4 +13,2 +14,7 +14,9 +6,2 +2,8 +13,1 +7,7 +8,4 +6,0 +7,0 |
G4 M G4 K1 M5 M2 M8 M2 A1 A5 M5 M6 M6 K2 G4 K3 K5 G5 K5 |
Фотометрический
метод определения расстояний.
Освещенности, создаваемые
одинаковыми по мощности источниками
света, обратно пропорциональны квадратам
расстояний до них. Следовательно, видимый
блеск одинаковых светил (т. е. освещенность,
создаваемая у Земли на единичной
площадке, перпендикулярной лучам света)
может служить мерой расстояния до них.
Выражение освещенностей в звездных
величинах (m – видимая звездная
величина, М – абсолютная звездная
величина) приводит к следующей основной
формуле фотометрических расстояний r>ф>
(пс):
lgr>ф> = 0,2 (m
– M) + 1.
При определении r>ф >по
вышеназванной формуле погрешность
составляет ~30%.
Для светил, у которых известны
тригонометрические параллаксы, можно,
определив М по этой же формуле, сопоставить
физические свойства с абсолютными
звездными величинами. Это сопоставление
показало, что абсолютные звездные
величины многих классов светил (звезд,
галактик и др.) можно оценивать по ряду
их физических свойств.
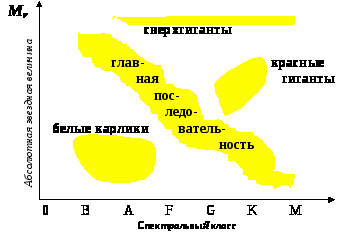
Зная расстояния до некоторого
числа звезд, вычисленные методом
параллакса, можно было вычислить
светимости и сопоставить их со спектром
тех же звезд, (см. рис. 2). Из диаграммы
видно, что каждому определенному
подклассу звезд (например A) соответствует
определенная светимость, таким образом,
достаточно точно определить спектральный
класс и можно выяснить ее светимость,
а следовательно, и расстояние.
Иногда определенному классу
соответствует другая светимость, но в
этом случае и спектр у них несколько
другой. Спектры карликов и гигантов
различаются интенсивностью определенных
линий или их пар, причем это отличие
можно выяснить, исследуя близко
находящиеся звезды. Это отличие связано
с тем, что атмосферы гигантов обширнее
и разреженнее. Точность определения
расстояния таким способом составляет
~20%.
Рисунок 2: диаграмма зависимости
спектрального класса от абс. звездной
величины (Герцшпрунга – Рессела)
Определение
расстояния по относительным скоростям.
Косвенным показателем расстояния
до звезд являются их относительные
скорости: как правило, чем ближе звезда,
тем больше смещается она по небесной
сфере. Определить таким способом
расстояние, конечно нельзя, но этот
способ дает возможность “вылавливать”
близкие звезды.
Также существует другой метод
определения расстояний по скоростям,
применимый для звездных скоплений. Он
основан на том, что все звезды, принадлежащие
одному скоплению, движутся в одном и
том же направлении по параллельным
траекториям. Измерив лучевую скорость
звезд с помощью эффекта Доплера, а также
скорость, с которой эти звезды смещаются
относительно очень удаленных, то есть
условно неподвижных звезд, можно
определить расстояние до интересующего
нас скопления.
Цефеиды.
Важный метод определения
фотометрических расстояний в Галактике
и до соседних звездных систем – галактик
– основан на характерном свойстве
переменных звезд – цефеид.
Первой из обнаруженных цефеид
была Цефея, которая
меняла свой блеск с амплитудой 1,
температуру (на 800K), размер и спектральный
класс. Цефеиды – это неустойчивые звезды
спектральных классов от F6 до G8, которые
пульсируют в результате нарушения
равновесия между силой тяжести и
внутренним давлением, причем кривая
изменения их параметров напоминает
гармонический закон. С течением времени
колебания ослабевают и затухают; к
настоящему моменту было обнаружено
постепенное прекращение переменности
у звезды RU Жирафа, обнаруженной в 1899
году. К 1966 году ее переменность полностью
прекратилась. Периоды различных цефеид
от 1,5 часов до 45 суток. Все цефеиды –
гиганты большой светимости, причем
светимость строго зависит от периода
по формуле:
M = – 0,35 – 2,08 lg
T.
Так как, в отличие от вышеприведенной
диаграммы Герцшпрунга – Ресселла (см.
рис. 2) зависимость четкая, то и расстояния
можно определять более точно. Для
долгопериодичных цефеид (периоды
колебаний от 1 до 146 суток), относящихся
к звездному населению I
типа (плоской составляющей Галактики),
установлена важная зависимость период
– светимость, согласно которой, чем
короче период колебаний блеска, тем
цефеида слабее по абсолютной величине.
Зная из наблюдений период T,
можно найди абсолютную звездную величину
M, а, зная абсолютную звездную
величину и найдя из наблюдений видимую
звездную величину m, можно найти
расстояние. Такой метод нахождения
расстояний применяется не только для
определения расстояния до самих цефеид,
но и для определения расстояний до
далеких галактик, в составе которых
удалось обнаружить цефеиды (это сделать
не очень трудно, так как цефеиды обладают
достаточно большой светимостью).
Список литературы.
-
Сюняев
Р. А. Физика космоса, 2-е изд. Москва, изд.
«Советская энциклопедия», 1986 г. -
Волынский
Б. А. Астрономия. Москва, изд. «Просвещение»,
1971 г. -
Агекян
Т. А. Звезды, галактики, Метагалактика.
Москва, изд. «Наука», 1970 г. -
Мухин
Л. М. Мир астрономии. Москва, изд. «Молодая
гвардия», 1987 г. -
Левитт
И. За пределами известного мира: от
белых карликов до квазаров. Москва,
изд. «Мир», 1978 г.