Как найти расстояние хаусдорфа

From Wikipedia, the free encyclopedia

In mathematics, the Hausdorff distance, or Hausdorff metric, also called Pompeiu–Hausdorff distance,[1][2] measures how far two subsets of a metric space are from each other. It turns the set of non-empty compact subsets of a metric space into a metric space in its own right. It is named after Felix Hausdorff and Dimitrie Pompeiu.

Informally, two sets are close in the Hausdorff distance if every point of either set is close to some point of the other set. The Hausdorff distance is the longest distance you can be forced to travel by an adversary who chooses a point in one of the two sets, from where you then must travel to the other set. In other words, it is the greatest of all the distances from a point in one set to the closest point in the other set.

This distance was first introduced by Hausdorff in his book Grundzüge der Mengenlehre, first published in 1914, although a very close relative appeared in the doctoral thesis of Maurice Fréchet in 1906, in his study of the space of all continuous curves from {displaystyle [0,1]to mathbb {R} ^{3}}.

Definition[edit]

Components of the calculation of the Hausdorff distance between the green curve X and the blue curve Y.

Let X and Y be two non-empty subsets of a metric space (M,d). We define their Hausdorff distance {displaystyle d_{mathrm {H} }(X,Y)} by

{displaystyle d_{mathrm {H} }(X,Y)=max left{,sup _{xin X}d(x,Y),,sup _{yin Y}d(X,y),right},!}

where sup represents the supremum, inf the infimum, and where {displaystyle d(a,B)=inf _{bin B}d(a,b)} quantifies the distance from a point ain X to the subset Bsubseteq X.

Equivalently,

{displaystyle d_{H}(X,Y)=inf{varepsilon geq 0,; Xsubseteq Y_{varepsilon }{text{ and }}Ysubseteq X_{varepsilon }},quad }[3]

where

{displaystyle X_{varepsilon }:=bigcup _{xin X}{zin M,; d(z,x)leq varepsilon },}

that is, the set of all points within varepsilon of the set X (sometimes called the varepsilon -fattening of X or a generalized ball of radius varepsilon around X).

Equivalently,

{displaystyle d_{H}(X,Y)=sup _{win M}left|inf _{xin X}d(w,x)-inf _{yin Y}d(w,y)right|=sup _{win Xcup Y}left|inf _{xin X}d(w,x)-inf _{yin Y}d(w,y)right|,}[1]

that is, {displaystyle d_{mathrm {H} }(X,Y)=sup _{win M}|d(w,X)-d(w,Y)|}, where {displaystyle d(w,X)} is the distance from the point w to the set X.

[edit]

It is not true for arbitrary subsets {displaystyle X,Ysubset M} that {displaystyle d_{mathrm {H} }(X,Y)=varepsilon } implies

{displaystyle Xsubseteq Y_{varepsilon } {mbox{and}} Ysubseteq X_{varepsilon }.}

For instance, consider the metric space of the real numbers mathbb {R} with the usual metric d induced by the absolute value,

{displaystyle d(x,y):=|y-x|,quad x,yin mathbb {R} .}

Take

{displaystyle X:=(0,1]quad {mbox{and}}quad Y:=[-1,0).}

Then {displaystyle d_{mathrm {H} }(X,Y)=1 }. However Xnsubseteq Y_{1} because Y_{1}=[-2,1) , but 1in X.

But it is true that {displaystyle Xsubseteq {overline {Y_{varepsilon }}}} and {displaystyle Ysubseteq {overline {X_{varepsilon }}}} ; in particular it is true if X,Y are closed.

Properties[edit]

  • In general, {displaystyle d_{mathrm {H} }(X,Y)} may be infinite. If both X and Y are bounded, then {displaystyle d_{mathrm {H} }(X,Y)} is guaranteed to be finite.
  • {displaystyle d_{mathrm {H} }(X,Y)=0} if and only if X and Y have the same closure.
  • For every point x of M and any non-empty sets Y, Z of M: d(x,Y) ≤ d(x,Z) + dH(Y,Z), where d(x,Y) is the distance between the point x and the closest point in the set Y.
  • |diameter(Y)-diameter(X)| ≤ 2 dH(X,Y).[4]
  • If the intersection X ∩ Y has a non-empty interior, then there exists a constant r > 0, such that every set X′ whose Hausdorff distance from X is less than r also intersects Y.[5]
  • On the set of all subsets of M, dH yields an extended pseudometric.
  • On the set F(M) of all non-empty compact subsets of M, dH is a metric.
    • If M is complete, then so is F(M).[6]
    • If M is compact, then so is F(M).
    • The topology of F(M) depends only on the topology of M, not on the metric d.

Motivation[edit]

The definition of the Hausdorff distance can be derived by a series of natural extensions of the distance function d(x,y) in the underlying metric space M, as follows:[7]

  • Define a distance function between any point x of M and any non-empty set Y of M by:
{displaystyle d(x,Y)=inf{d(x,y)mid yin Y}. }
For example, d(1, {3,6}) = 2 and d(7, {3,6}) = 1.
  • Define a (not-necessarily-symmetric) «distance» function between any two non-empty sets X and Y of M by:
{displaystyle d(X,Y)=sup{d(x,Y)mid xin X}. }
For example, {textstyle d({1,7},{3,6})=sup{d(1,{3,6}),d(7,{3,6})}=sup{d(1,3),d(7,6)}=2.}
  • If X and Y are compact then d(X,Y) will be finite; d(X,X)=0; and d inherits the triangle inequality property from the distance function in M. As it stands, d(X,Y) is not a metric because d(X,Y) is not always symmetric, and d(X,Y) = 0 does not imply that X = Y (It does imply that X subseteq Y). For example, d({1,3,6,7}, {3,6}) = 2, but d({3,6}, {1,3,6,7}) = 0. However, we can create a metric by defining the Hausdorff distance to be:
d_{{{mathrm H}}}(X,Y)=max{d(X,Y),d(Y,X)},.

Applications[edit]

In computer vision, the Hausdorff distance can be used to find a given template in an arbitrary target image. The template and image are often pre-processed via an edge detector giving a binary image. Next, each 1 (activated) point in the binary image of the template is treated as a point in a set, the «shape» of the template. Similarly, an area of the binary target image is treated as a set of points. The algorithm then tries to minimize the Hausdorff distance between the template and some area of the target image. The area in the target image with the minimal Hausdorff distance to the template, can be considered the best candidate for locating the template in the target.
In computer graphics the Hausdorff distance is used to measure the difference between two different representations of the same 3D object[8] particularly when generating level of detail for efficient display of complex 3D models.

If X is the surface of earth, and Y is the land-surface of earth, then by finding the point Nemo, we see {displaystyle d_{H}(X,Y)} is around 2,704.8 km.

[edit]

A measure for the dissimilarity of two shapes is given by Hausdorff distance up to isometry, denoted DH. Namely, let X and Y be two compact figures in a metric space M (usually a Euclidean space); then DH(X,Y) is the infimum of dH(I(X),Y) along all isometries I of the metric space M to itself. This distance measures how far the shapes X and Y are from being isometric.

The Gromov–Hausdorff convergence is a related idea: we measure the distance of two metric spaces M and N by taking the infimum of {displaystyle d_{mathrm {H} }(I(M),J(N))} along all isometric embeddings {displaystyle Icolon Mto L} and {displaystyle Jcolon Nto L} into some common metric space L.

See also[edit]

  • Wijsman convergence
  • Kuratowski convergence
  • Hemicontinuity
  • Fréchet distance

References[edit]

  1. ^ a b Rockafellar, R. Tyrrell; Wets, Roger J-B (2005). Variational Analysis. Springer-Verlag. p. 117. ISBN 3-540-62772-3.
  2. ^ Bîrsan, Temistocle; Tiba, Dan (2006), «One hundred years since the introduction of the set distance by Dimitrie Pompeiu», in Ceragioli, Francesca; Dontchev, Asen; Futura, Hitoshi; Marti, Kurt; Pandolfi, Luciano (eds.), System Modeling and Optimization, vol. 199, Boston: Kluwer Academic Publishers, pp. 35–39, doi:10.1007/0-387-33006-2_4, ISBN 978-0-387-32774-7, MR 2249320
  3. ^ Munkres, James (1999). Topology (2nd ed.). Prentice Hall. pp. 280–281. ISBN 0-13-181629-2.
  4. ^ Diameter and Hausdorff Distance, Math.SE
  5. ^ Hausdorff Distance and Intersection, Math.SE
  6. ^ Henrikson, Jeff (1999). «Completeness and total boundedness of the Hausdorff metric» (PDF). MIT Undergraduate Journal of Mathematics: 69–80. Archived from the original (PDF) on June 23, 2002.
  7. ^ Barnsley, Michael (1993). Fractals Everywhere. Morgan Kaufmann. pp. Ch. II.6. ISBN 0-12-079069-6.
  8. ^ Cignoni, P.; Rocchini, C.; Scopigno, R. (1998). «Metro: Measuring Error on Simplified Surfaces». Computer Graphics Forum. 17 (2): 167–174. CiteSeerX 10.1.1.95.9740. doi:10.1111/1467-8659.00236. S2CID 17783159.

External links[edit]

  • Hausdorff distance between convex polygons.
  • Using MeshLab to measure difference between two surfaces A short tutorial on how to compute and visualize the Hausdorff distance between two triangulated 3D surfaces using the open source tool MeshLab.
  • MATLAB code for Hausdorff distance: [1]
Источник

Полнота метрического пространства индуцированного расстоянием Хаусдорфа

Время на прочтение
17 мин

Количество просмотров 5.6K

Аннотация

Пусть дано метрическое пространство $(X, d)$. Тогда мы можем определить метрическое пространство с расстоянием Хаусдорфа $h$ на множестве $mathcal{K}$, которое является семейством всех непустых компактных подмножеств $X$. В этой статье будет показано, что если $(X, d)$ — полное, то метрическое пространство $(mathcal{K}, h)$ также является полным.

Содержание

  • Введение
  • Предварительные сведения
  • Конструкция Хаусдорфовой метрики
  • Примеры пространств с метрикой Хаусдорфа
  • Доказательство полноты $(mathcal{K}, h)$
  • Выводы
  • Литература

Введение

Метрика Хаусдорфа, названная в честь Феликса Хаусдорфа, измеряет расстояние между подмножествами метрического пространства. Проще говоря, метрика Хаусдорфа вычисляет наибольшее из всех возможных расстояний от каждой точки одного множества до ближайшей к ней точки второго множества. Для любого наперёд заданного метрического пространства найдём, что метрика Хаусдорфа определяет метрику на пространстве всех непустых компактных подмножеств этого метрического пространства. Найдём много интересных свойств такого метрического пространства, которое будет нашим основным средоточием внимания в этой статье. Первое свойство заключается в том, что пространство, индуцированное метрикой Хаусдорфа, полное, если исходное метрическое пространство является полным. Похожим образом, второе свойство, которое мы выясним, заключается в том, что если исходное метрическое пространство является компактом, то и пространство, индуцированное метрикой Хаусдорфа, тоже компакт.

В следующем разделе будут приведены некоторые определения и теоремы необходимые для понимания статьи. Затем, в последующем разделе, будет определено расстояние Хаусдорфа и будут проверены его свойства с помощью нескольких примеров и коротких доказательств. Найдём, что метрика Хаусдорфа удовлетворяет аксиомам метрики на пространстве непустых компактных подмножеств метрического пространства. В конечном итоге, в последнем разделе, будет доказано, что если исходное метрическое пространство полное, тогда пространство, индуцированное метрикой Хаусдорфа, также полное. Далее, будет показано, что $(mathcal{K}, h)$ — компакт, когда $(X, d)$ — компакт

Предварительные сведения

Концепции, показанные в этой статье, должны быть знакомы каждому, кто проходил курс Действительного Анализа. Здесь и далее будут использоваться терминология и обозначения из книги Гордона Действительный Анализ: Первый Курс [1]. Вследствие этого, предполагается, что читатель знаком со следующими идеями, касающимися метрических пространств и действительных чисел.

Определение 2.1 Пусть $S$ — непустое множество действительных чисел ограниченное снизу. Число $alpha$ — инфимум $S$, если $alpha$ — нижняя граница
$S$, любое число большее $alpha$ не является нижней границей $S$. Обозначение: $alpha = inf S$. Определение супремума $S$ строится аналогичным образом, и обозначается он, как $sup S$.

Аксиома полноты Каждое непустое множество действительных чисел, ограниченное снизу, имеет инфимум. Похожим образом, любое непустое множество действительных чисел, ограниченное сверху, имеет супремум.

Читателю могут быть более знакомы последующие определения при их применении к метрическому пространству $(mathbb{R}, d)$, где $d(x, y) = |x - y|$. Однако, за исключением некоторых примеров, большая часть этой статьи нацелена на работу с некоторым метрическим пространством общего вида. Таким образом, определения, которые будут даны далее, относятся к любому метрическому пространству $(X, d)$.

Определение 2.2 Метрическое пространство $(X, d)$ — это объект, который включает в себя множество $X$ и функцию $d : X times X to mathbb{R}$, которая удовлетворяет следующим четырём свойствам:
(1) $d(x, y) geq 0 ; text{для всех} ; x, y in X$
(2) $d(x, y) = 0 ; text{если и только если} ; x = y$
(3) $d(x, y) = d(y, x) ; text{для всех} ; x, y in X$
(4) $d(x, y) leq d(x, z) + d(z, y) ; text{для всех} ; x, y, z in X$
Функция $d$, вычисляющая расстояние между двумя точками в $X$, называется метрикой. Например, метрикой на множестве действительных чисел является функция $d(x, y) = |x - y|$. Легко проверить, что $d$ удовлетворяет всем четырём условиям, указанным выше.

Для следующих определений положим, что $(X, d)$ — метрическое пространство.

Определение 2.3 Пусть $v in X$ и $r > 0$. Открытым шаром с центром в точке $v$ и радиусом $r$ называется множество $B_d(v, r) = {x in X : d(x, v) < r}$.

Определение 2.4 Множество $E subseteq X$ ограничено в $(X, d)$, если существуют $x in X$ и $M > 0$, такие что $E subseteq B_d(x, M)$.

Определение 2.5 Множество $К subseteq X$ вполне ограничено, если для каждого $epsilon > 0$ найдётся конечное подмножество ${ x_i : 1 leq i leq n }$ множества $K$, такое что $K subseteq bigcuplimits_{i = 1}^n B_d(x_i, epsilon)$.

Для следующий определений положим, что ${ x_n }$ — последовательность в метрическом пространстве $(X, d)$.

Определение 2.6 Последовательность ${ x_n }$ сходится к точке $x in X$, если для любого $epsilon > 0$ существует натуральное $N$, такое что $d(x_n, x) < epsilon$ для всех $n geq N$. Мы говорим, что ${ x_n }$ сходится, если существует точка $x in X$, такая что ${ x_n }$ сходится к $x$.

Определение 2.7 Последовательность ${ x_n }$ называется фундаментальной, если для любого $epsilon > 0$ существует натуральное $N$, такое что $d(x_n, x_m) < epsilon$ для всех $m, n geq N$.

Легко проверить, что каждая сходящаяся последовательность фундаментальна.

Определение 2.8 Метрическое пространство $(X, d)$ называется полным, если каждая фундаментальная последовательность в $(X, d)$ сходится к точке в $X$.

Примером не полного метрического пространства может послужить пространство $(mathbb{Q}, d)$ рациональных чисел со стандартной метрикой $d(x, y) = |x - y|$. Как бы то ни было, пространство $mathbb{R}$ действительных чисел и пространство $mathbb{C}$ комплексных чисел являются полными с той же метрикой.

Определение 2.9 Множество $K subseteq X$ является секвенциальным компактом в $(X, d)$, если каждая последовательность в $K$ имеет подпоследовательность, сходящуюся к точке в $K$.

Заметим, что согласно Теореме 8.59 в [1], подмножество метрического пространства — компакт, если и только если оно является секвенциальным компактом. Поэтому в данной статье мы будем использовать концепции секвенциальной компактности и компактности как взаимозаменяемые понятия.

Определение 2.10 Точка $x$ называется предельной точкой множества $E$, если для каждого $r > 0$, множество $E cap B_d(x, r)$ содержит точку из $E$ помимо $x$.

Теорема 8.49 из [1] в качестве альтернативного определения утверждает, что $x$ является предельной точкой множества $E$, если и только если существует последовательность точек в $E backslash {x}$ сходящаяся к $x$. Эта теорема предоставляет возможность выбрать последовательность сходящуюся к $x$, что будет полезно при доказательстве замкнутости множества.

Определение 2.11 Множество $E$ — замкнуто в $(X, d)$, если E содержит все свои предельные точки.

Определение 2.12 Замыканием $E$, обозначается $overline{E}$, называется множество $E cup E'$, где $E'$ — множество всех предельных точек E.

Два следующих результата и лемма расположены в этом разделе, поскольку к ним позже будут обращаться в дальнейших доказательствах. В дополнение к этому, они будут служить как введение в доказательства, использующие определение сходящихся последовательностей и неравенство треугольника.

Результат 1: Пусть ${ x_n }$ и ${ y_n }$ — последовательности в метрическом пространстве $(X, d)$. Если ${ x_n }$ сходится к $x$ и ${ y_n }$ сходится к $y$, то ${ d(x_n, y_n) }$ сходится к $d(x, y)$.

Доказательство. Пусть $epsilon > 0$. Поскольку ${ x_n }$ сходится к $x$, то по определению сходимости существует натуральное $N_1$, такое что $d(x_n, x) < frac{epsilon}{2}$ для всех $n geq N_1$. Аналогично, из того, что ${ y_n }$ сходится к $y$ — существует натуральное $N_2$, такое что $d(y_n, y) < frac{epsilon}{2}$ для всех $n geq N_2$. Выберем $N = max{N_1, N_2}$. Тогда для всех $n geq N$ получим, что

$d(x_n, y_n) leq d(x_n, x) + d(x, y) + d(y, y_n) < frac{epsilon}{2} + d(x,y) + frac{epsilon}{2} = d(x, y) + epsilon$

и

$d(x, y) leq d(x, x_n) + d(x_n, y_n) + d(y_n, y) < frac{epsilon}{2} + d(x_n, y_n) + frac{epsilon}{2} = d(x_n, y_n) + epsilon$

Совмещая эти неравенства получим, что $|d(x_n, y_n) - d(x, y)| < epsilon$ для всех $n geq N$. Следовательно ${ d(x_n, y_n) }$ сходится к $d(x, y)$.

Результат 2: Если ${ z_k }$ — последовательность в метрическом пространстве $(X, d)$, которая удовлетворяет свойству $d(z_k, z_{k+1}) < 1/2^k$ для всех $k$, то эта последовательность фундаментальна.
Доказательство. Пусть $epsilon > 0$. Выберем такое натуральное $N$, что $frac{1}{2^{N - 1}} < epsilon$. Тогда для всех $n > m geq N$ найдём, что

$d(z_m, z_n) leq d(z_m, z_{m + 1}) + d(z_{m + 1}, z_{m + 2}) + ... + d(z_{n - 1}, z_n) \ < frac{1}{2^m} + frac{1}{2^{m + 1}} + ... + frac{1}{2^{n - 1}} \ < sum^{infty}_{k = m} frac{1}{2^k} = frac{1}{2^{m - 1}} leq frac{1}{2^{N - 1}} < epsilon$

Отсюда следует, что ${ z_k }$ — фундаментальная последовательность.

Лемма 1: Пусть $(X, d)$ — метрическое пространство, $A$ — замкнутое подмножество $X$. Если ${ a_n }$ сходится к $x$, и $a_n in A$ для всех $n$, то $x in A$.
Доказательство. Предположим, что ${ a_n }$ — последовательность, сходящаяся к $x$ и $a_n in A$ для всех $n$. Рассмотрим два случая.

  1. Если существует натуральное $n$ такое, что $a_n = x$, то очевидно, что $x in A$.
  2. Если не существует такого натурального числа, то $x$ — предельная точка $A$ по теореме 8.49 в [1]. Поскольку $A$ замкнуто, то $x in A$.

Конструкция Хаусдорфовой метрики

Теперь мы определим метрику Хаусдорфа на множестве всех непустых и компактных подмножеств метрического пространства. Пусть $(X, d)$ — полное метрическое пространство, $mathcal{K}$ — семейство всех непустых компактных подмножеств $X$. Заметим, что $mathcal{K}$ замкнуто относительно конечных объединений и непустых пересечений. Для $x in X$ и $A, B in mathcal{K}$, определим

$r(x, B) = inf { d(x, b) : b in B } text{ и } rho(A, B) = sup { r(a, B) : a in A }$

Подметим, что $r$ неотрицательно и определено согласно аксиоме полноты, поскольку $d(a, b) geq 0$ по определению метрического пространства. И $rho(A, B)$ и $rho(B, A)$ неотрицательны и определены, так как таковым является $r$. В дополнение определим Хаусдорфово расстояние между множествами $A$ и $B$ в $mathcal{K}$ как

$h(A, B) = max { rho(A, B), rho(B, A) }$

Перед тем, как доказать, что $h$ образует метрику на множестве $mathcal{K}$, мы рассмотрим несколько примеров, для того чтобы разобраться в том, как работают эти расстояния. В качестве следующего примера рассмотрим числовые отрезки в $(mathbb{R}, d)$, где $d(x, y) = |x - y|$.
Пример Пусть $A = [0, 20], B = [22, 31]$.
Мы получим, что $r(x, B)$ окажется инфимумом множества расстояний от каждой точки $a in A$ до ближайшей к ней точки в $B$. В качестве примера одного из таких расстояний возьмём $a = 12$. Тогда $r(12, B) = inf { d(12, B) : b in B } = d(12, 22) = 10$. Также заметим, что для каждого $a in A$ ближайшая точка в $B$, дающая наименьшее расстояние, будет всегда равна числу $b = 22$. Следовательно, получим, что $rho(A, B) = sup { d(a, 22) : a in A }$. Точка $a = 0$ в $A$ увеличивает до максимума это расстояние. Значит, $rho(A, b) = d(0, 22) = |22 - 0| = 22$.
Похожим образом, найдём, что $rho(B, A) = sup { d(b, 20) : b in B }$, вследствие того, что точка $a = 20$ даст наименьшее расстояние до любой точки в $B$. Точка $b = 31$ в $B$ максимизирует это расстояние. Таким образом, имеем $rho(B, A) = d(20, 31) = |20 - 31| = 11$.
Можно заметить, что $rho(B, A)$ и $rho(A, B)$ не всегда равны. Окончательно получим, что $h(A, B) = max { rho(A, B), rho(B, A) } = 22$.

Далее рассмотрим другой пример, в качестве которого возьмём дискретные множества в $(mathbb{R}, d)$ с метрикой $d(x, y) = |x - y|$.
Пример Пусть $A = { 5n : 0 leq n leq 19 }$ и $B = { p : p < 100, text{ p - простое } }$. Найдём, что $r(p, A)$ равняется наименьшему расстоянию от любого простого числа $p in B$ до числа кратного 5 в множестве $A$, так как мы работаем с дискретными конечными подмножествами вещественной числовой прямой. Поэтому, для любого $p in B$,

$r(p, A) = min { |p - 5n| : 0 leq n leq 19 }$

Можно заметить, что минимальное расстояние между любым простым числом и ближайшим к нему числу кратному 5 равно 2 или 1. Например, если $p = 17$, то получим, что

$r(17, A) = min { |17 - 5n| : 0 leq n leq 19 } = 2, text{ когда } n = 3$

Если $p = 71$, то

$r(71, A) = min { |71 - 5n| : 0 leq n leq 19 } = 1, text{ когда } n = 14$

Следовательно, получим, что для любой точки $a in A, rho(B, A) = max { r(b, A) : b in B } = 2$. Другими словами, $rho(B, A)$ равно максимуму среди минимальных расстояний от простого числа $p$ в множестве $B$ до чисел кратных 5 в множестве $A$.
Аналогично, найдём, что $rho(A, B)$ равно максимуму среди минимальных расстояний от каждого числа кратного 5 в множестве $A$ до набора простых чисел в множестве $B$. Таким образом, $r(a, B)$ равняется минимальному расстоянию от любого числа кратного 5 в множестве $A$ до простого числа $p in B$. Другого оптимального пути для таких вычислений, кроме полного перебора расстояний между каждой точкой в $A$ и каждой точкой $B$, не существует. Рассматривая же расстояния от каждого числа кратного 5 до простого числа, получим, что наибольшее из этих минимальных расстояний достигается между точками $50 in A$ и $47, 53 in B$. Следовательно, $h(A, B) = max { rho(A, B), rho(B, A) } = max { 3, 2} = 3$.

Теперь, в следующем примере мы рассмотрим $r, rho text{ и } h$ в полном метрическом пространстве $(mathbb{R}^2, d)$, где $d((x_1, y_1), (x_2, y_2)) = sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}$

Пример Пусть $A$ и $B$ — подмножества $mathbb{R^2}$, определённые как $A = { (x, y) : x^2 + y^2 leq 1 } text{ и } B = { (x, y) : 0 leq x leq 3, 0 leq y leq 1 }$ [см. Рисунок 1].
По определению, $r(x, A) = inf { d(x, a) : a in A }$. Таким образом $r(x, A)$ — это множество всех расстояний от каждой точки $x in B$ до «ближайшей» точки $a in A$ к $x$. Заметим, что $x$ будет упорядоченной парой, каковыми являются $a$ и $b$.
Если $b in A cap B$, то очевидно, что $r(b, A) = 0$. Если $b in B backslash A$, то $r(b, A)$ находится через отрезок из $b$ в начало координат [см. Рисунок 2]. Получим, что точка, в которой достигается наибольшее расстояние, это правая верхняя вершина прямоугольника с координатой $(3,1)$.
Следовательно, $rho(B, A)$ есть расстояние из точки $(frac{3}{sqrt{10}}, frac{1}{sqrt{10}})$ на окружности до точки $(3, 1)$.


РИСУНОК 1. График $A$ и $B$ в $(mathbb{R}^2, d)$.


РИСУНОК 2. Заштрихованная область содержит все точки, дающие инфимум расстояния $r(a, B) = 0$. Дополнительно, находим, что $rho(A, B) = 1$ и $rho(B, A) = sqrt{10} - 1$.

Таким образом,

$rho(B, A) = d bigg( bigg( frac{3}{sqrt{10}}, frac{1}{sqrt{10}} bigg) , (3, 1) bigg) = sqrt{10} - 1$

Теперь мы должны найти $rho(A, B)$. Получаем, что можно использовать любую из точек третьей четверти единичной окружности. Выберем точку $(-1, 0)$. Тогда $rho(A, B) = dbig((-1, 0), (0, 0) big) = 1$.
Следовательно, расстояние Хаусдорфа есть $h(A, B) = max { 1, sqrt{10} - 1 } = sqrt{10} - 1$.

В следующем примере также будет использовано метрическое пространство $(mathbb{R}^2, d)$ с той же метрикой $d$ из предыдущего примера. Однако, на этот раз мы рассмотрим два непересекающихся множества на плоскости.

Пример Пусть $A = { (x, y) : 0 leq x leq 1, 0 leq y leq 1 }$ и $B = { (x, y) : 3 leq x leq 5, 0 leq y leq 4 }$ [см. Рисунок 3].


Рисунок 3. Множества $A$ и $B$ в $(mathbb{R}^2, d)$.

Если $(a_1, a_2) in A$, то $r big( (a_1, a_2), B) big) = d big( (a_1, a_2), (3, a_2) big) = 3 - a_1$. Поскольку $0 leq a_1 leq 1$, получим, что $rho(A, B) = 3$.
Если $(b_1, b_2) in B$, то $r big( (b_1, b_2), A) big) = dbig( (b_1, b_2), (1, a_2) big)$, где $0 leq a_2 leq 1$, который варьируется в зависимости от выбора $(b_1, b_2)$. Получим, что точка, максимизирующая $r$, это $b = (5, 4)$, такая что $rho(B, A) = d big( (5, 4), (1, 1) big) = 5$.
Таким образом, расстояние Хаусдорфа получается равным $h(A, B) = rho(B, A) = 5$.
Теперь, обладая знаниями о том, как работают $r, rho$ и $h$ в нескольких особых случаях, докажем некоторые основные свойства $r$ и $rho$.

Теорема 1. Пусть $x in X$ и $A, B, C in mathcal{K}$.
$(1) ; r(x, A) = 0 text{ если и только если } x in A$
$(2) ; rho (A, B) = 0 text{ если и только если } A subseteq B$
$(3) text{ Существует } a_x in A text{ такое, что } r(x, A) = d(x, a_x)$
$(4) text{ Существуют } a^{*} in A text{ и } b^{*} in B text{ такие, что } rho(A, B) = d(a^{*}, b^{*})$
$(5) text{ Если } A subseteq B text{, то } r(x, B) leq r(x, A)$
$(6) text{ Если } B subseteq C text{, то } rho(A, C) leq rho(A, B)$
$(7) ; rho(A cup B, C) = max { rho(A, C), rho(B, C) }$
$(8) ; rho(A, B) leq rho(A, C) + rho(C, B)$
Доказательство. Сначала докажем свойство (1). Предположим, что $x in A$. Тогда инфимум расстояния равен $d(x, a) = 0$, где $a = x$. Теперь положим, что $r(x, A) = 0$. Тогда для любого натурального $n$ существует $a_n in A$ такое, что $d(x, a_n) < frac{1}{n}$. ${ a_n }$ сходится к $x$ по определению. Поскольку $A$ компактно, то оно замкнуто. По Лемме 1 отсюда следует, что $x in A$.
Теперь докажем свойство (2). Пусть $A subseteq B$ и $a in A$. Так как $a in B$, то по свойству (1) имеем $r(a, B) = 0$. Следовательно $rho(A, B) = sup{{0}} = 0$. Чтобы доказать в обратную сторону, положим, что $rho(A, B) = 0$. Пусть $a in A$. Тогда $0 leq r(a, B) leq rho(A, B) = 0$, и, следовательно, по свойству (1), найдём, что $a in B$. Отсюда следует, что $A subseteq B$.
Чтобы доказать свойство (3), по определению инфимума мы можем сконструировать последовательность ${ a_n }$ в $A$ таким образом, чтобы выполнялось $d(x, a_n) < r(x, A) + frac{1}{n}$. Мы знаем, что $A$ секвенциально компактно, поэтому существует подпоследовательность ${ a_{n_k} }$ в ${ a_n }$, которая сходится к элементу $a_x in A$. Тогда получим, что

$r(x, A) leq d(x, a_x) leq d(x, a_{n_k}) + d(a_{n_k}, a_x) leq r(x, A) + frac{1}{n_k} + d(a_{n_k}, a_x)$

Поскольку $lim_{k to infty}(frac{1}{n_k} + d(a_{n_k}, a_x)) = 0$, то $d(x, a_x) = r(x, A)$.
Чтобы доказать свойство (4), по определению супремума мы можем сконструировать последовательность ${ a_n }$ в $A$ таким образом, чтобы $rho(A, B)$ было пределом $r(a_n, B)$. Согласно свойству (3) существует последовательность ${ b_n }$ в $B$ такая, что $r(a_n, B) = d(a_n, b_n)$. Поскольку $A$ секвенциально компактно, то существует подпоследовательность ${ a_{n_k} }$ в ${ a_n }$, которая сходится к $a^* in A$. Поскольку $B$ секвенциально компактно, то существует подпоследовательность ${ b_{n_{k_j}} }$ в ${ b_{n_k} }$, которая сходится к $b^*$. Поскольку ${ b_{n_{k_j}} }$ сходится к $b^*$, и ${ a_{n_{k_j}} }$ сходится к $a^*$, то по Результату 1 имеем, что $d(a_{n_{k_j}}, b_{n_{k_j}})$ сходится к $d(a^*, b^*)$. Значит, отсюда следует, что

$rho(A, B) = lim_{j to infty} r (a_{n_{k_j}}, B) = lim_{j to infty} d (a_{n_{k_j}}, b_{n_{k_j}}) = d(a^*, b^*)$

Следовательно, $d(a^*, b^*) = rho(A, B)$.
Теперь докажем свойство (5). Предположим, что $A subseteq B$ ДЛи $x in X$. Пусть $a in A$. Поскольку $A$ является подмножеством $B$, найдём, что $a in B$. Это значит, что

$d(x, a) geq inf { d(x, b) : b in B } = r(x, B)$

Поскольку это истинно для всех $a in A$, то получим, что $r(x, A) = inf { d(x, a) : a in A } geq r(x, B)$.
Для доказательства свойства (6) положим, что $B subseteq C$. Тогда по свойству (5) для всех $a in A ;; r(a, C) leq r(a, B)$. Это значит, что $sup { r(a, C) : a in A } leq sup { r(a, B) : a in A }$, а значит $rho(A, C) leq rho(A, B)$.
Для доказательства свойства (7) вспомним, что по определению $r$ и $rho$ имеем

$rho(A cup B, C) = sup { r(x,C) : x in A cup B } \ = max { sup{ r(x, C) : x in A }, sup{ r(x, C) : x in B }} \ = max{ rho(A, C), rho(B, C) }$

Теперь обратимся к свойству (8). Свойство (3) гарантирует, что для каждого $a in A$ существует $c_a in C$ такой, что $r(a, C) = d(a, c_a)$. Тогда имеем

$r(a, B) = inf { d(a, b) : b in B } \ leq inf { d(a, c_a) + d(c_a, b) : b in B } \ = d(a, c_a) + inf { d(c_a, b) : b in B } \ = r(a, C) + r(c_a, B) \ leq rho(A, C) + rho(C, B) $

Поскольку $a in A$ был выбран произвольно, вычисляя супремум, получим, что

$rho(A, B) leq rho(A, C) + rho(C, B)$

На этом доказательство завершается.

Отметим, что по свойству (4) Теоремы 1 существуют точки $a_1 in A$ и $b_1 in B$ такие, что $rho(A, B) = d(a_1, b_1)$, и, аналогично, существуют точки $a_2 in A$ и $b_2 in B$ такие, что $rho(B, A) = d(a_2, b_2)$. Поскольку $h(A, B)$ есть просто максимум $rho(A, B)$ и $rho(B, A)$, то это значит, что существуют точки $a^* in A$ и $b^* in B$ такие, что $h(A, B) = d(a^*, b^*)$.

Следующая теорема показывает, что расстояние Хаусдорфа определяет метрику на $mathcal{K}$.

Теорема 2. Множество $mathcal{K}$ вместе с расстоянием Хаусдорфа $h$ формируют метрическое пространство $(mathcal{K}, h)$.
Доказательство. Чтобы доказать, что $(mathcal{K}, h)$ есть метрическое пространство, необходимо проверить выполнение следующих четырёх аксиом.
$(1) ; h(A, B) geq 0 text{ для всех } A, B in mathcal{K}$
$(2) ; h(A, B) = 0 text{ если и только если } A = B$
$(3) ; h(A, B) = h(B, A) text{ для всех } A, B in mathcal{K}$
$(4) ; h(A, B) leq h(A, C) + h(C, B) text{ для всех } A, B, C in mathcal{K}$
Чтобы проверить первую аксиому, вспомним, что $rho(A, B)$ и $rho(B, A)$ неотрицательные величины. Поэтому, очевидно, $h(A, B) geq 0$ для всех $A, B in mathcal{K}$.
Проверяя вторую аксиому, предположим, что $A = B$. Тогда $A subseteq B$ и $B subseteq A$. По свойству (2) Теоремы 1 получаем, что $rho(A, B) = 0$ и $rho(B, A) = 0$, а значит $h(A, B) = 0$. Теперь положим, что $h(A, B) = 0$. Отсюда следует, что $rho(A, B) = rho(B, A) = 0$. По свойству (2) Теоремы 1, мы видим, что $A subseteq B$ и $B subseteq A$. Это значит, что $A = B$.
Третья аксиома может быть проверена, исходя из соображений о симметричности определения, поскольку

$h(A, B) = max { rho(A, B), rho(B, A) } = max { rho(B, A), rho(A, B) } = h(B, A)$

Выполнение последней аксиомы следует из определений $rho$ и $h$ и свойства (8) Теоремы 1. Находим, что

$rho(A, B) leq rho(A, C) + rho(C, B) leq max { rho(A, C), rho(C, A) } + max { rho(C, B), rho(B, C) } \ = h(A, C) + h(C, B)$

Похожим образом,

$rho(B, A) leq rho(B, C) + rho(C, A) leq max { rho(B, C), rho(C, B) } + max { rho(C, A), rho(A, C) } \ = h(C, B) + h(A, C)$

Следовательно, $h(A, B) = max { rho(A, B), rho(B, A) } leq h(A, C) + h(C, B)$.
Теперь мы знаем, что $h$ определяет метрику на $mathcal{K}$. В следующем разделе мы рассмотрим примеры того, как могут выглядеть такие метрические пространства и приступим к доказательству полноты $(mathcal{K}, h)$ при условии полноты $(X, d)$.

Примеры пространств с метрикой Хаусдорфа

Пусть дано полное метрическое пространство $(X, d)$. Теперь имеем новое сконструированное метрическое пространство $(mathcal{K}, h)$ из непустых, компактных подмножеств $X$ с помощью метрики Хаусдорфа. Остаётся доказать, что $(mathcal{K}, h)$ также полное. Для полноты в метрическом пространстве каждая фундаментальная последовательность должна сходиться к точке из этого же пространства. Соответственно, думая о $(mathcal{K}, h)$, мы выбираем последовательности непустых, компактных множеств и показываем, что эта последовательность сходиться к некоторому непустому, компактному множеству. Чтобы лучше визуализировать абстрактную математику, которой мы тут занимаемся, рассмотрим следующие два примера, демонстрирующих метрические пространства из непустых, компактных множеств с метрикой Хаусдорфа.

Пример Пусть $(mathbb{R}, d_0)$ полное метрическое пространство, где $d_0$ дискретная метрика,

$ d_0(x, y) = begin{cases} 0, & quad text{когда } x = y\ 1, & quad text{когда } x neq y\ end{cases} $

Поскольку $mathcal{K}$ множество всех непустых компактных подмножеств $(mathbb{R}, d_0)$, получим, что $mathcal{K}$ множество всех непустых конечных подмножеств $mathbb{R}$. Бесконечные множества не лежат в $mathcal{K}$, потому что они не вполне ограниченны, а значит не компактные.
Дальше, следует заметить, что

$r(x, B) = inf { d_0(x, b) : b in B } = d_0(x, b) = begin{cases} 0, & quad text{когда } x in B\ 1, & quad text{когда } x notin B\ end{cases}$

Следовательно,

$rho(A, B) = sup { r(a, B) : a in A } = begin{cases} 0, & quad text{когда } a in B\ 1, & quad text{когда } a notin B\ end{cases}$

Поэтому отсюда следует, что

$h(A, B) = begin{cases} 0, & quad text{когда } A = B\ 1, & quad text{когда } A neq B\ end{cases}$

Следовательно данное метрическое пространство состоит из множества $mathcal{K}$ дискретных подмножеств $mathbb{R}$ c Хаусдорфовой метрикой в качестве дискретной метрики. Очень просто проверить, что это пространство не вполне ограниченное. Как бы то ни было, мы знаем, что все дискретные метрические пространства полные, поэтому $(mathcal{K}, h)$. А значит, пространство $(mathcal{K}, h)$ конечных множеств с дискретной метрикой — пример нашего индуцированного метрикой Хаусдорфа пространства.

Чтобы проиллюстрировать наши представления о полноте, вкратце рассмотрим последовательность непустых компактных множеств, сходящихся к единичной окружности в $mathbb{R}^2$. Это пример сходящейся фундаментальной последовательности в индуцированном метрикой Хаусдорфа пространстве, которая сходится к множеству, также находящимся в этом пространстве.

Пример Пусть $(mathbb{R}^2, d)$ полное метрическое пространство, где $x = (x_1, x_2), y = (y_1, y_2) implies d(x, y) = sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}$.
Пусть $mathcal{K}$ множество всех непустых компактных подмножеств $mathbb{R}^2$, или иными словами, множество всех непустых замкнутых и ограниченных множеств из $mathbb{R}^2$. Поскольку $(mathbb{R}^2, d)$ полное, то и $(mathcal{K}, h)$ полное, как мы далее докажем. Чтобы увидеть в этом пространстве пример фундаментальной последовательности, сходящейся к некоторому множеству, рассмотрим пример последовательности множеств, сходящейся к единичной окружности.
Для каждого натурального $k$ обозначим $A_k = { (r, theta) : r = 1 + frac{1}{k}cos(ktheta), 0 leq theta leq 2pi }$. Пусть $A$ — единичная окружность в $mathbb{R}^2$. Легко заметить, что все $A_k$ лежат в $mathcal{K}$. Рассматривая расстояние Хаусдорфа между множествами, можно увидеть, что $h(A_k, A) = frac{1}{k}$.
Заметим, что с увеличением $k$, множества сходятся к единичной окружности [см. Рисунки 6-8]. Следовательно, ${ A_k }$ пример фундаментальной последовательности, которая сходится к $A in mathcal{K}$.

Рисунок 4. Множество $A_5$, определённое через $r = 1 + frac{1}{5}cos(5theta)$.

Рисунок 5. Множество $A_{20}$, определённое через $r = 1 + frac{1}{20}cos(20theta)$.

Доказательство полноты $(mathcal{K}, h)$

Как ранее отмечалось, для соблюдения полноты каждая фундаментальная последовательность в $(mathcal{K}, h)$ должна сходиться к точке в $mathcal{K}$. Значит, чтобы доказать полноту $(mathcal{K}, h)$, необходимо выбрать произвольную фундаментальную последовательность ${ A_k }$ из $mathcal{K}$ и показать, что она сходится к некоторому $A in mathcal{K}$. Определим $A$, как множество всех точек $x in X$, таких, что существует некоторая последовательность ${ x_n }$, сходящаяся к $x$ и при этом $x_n in A_n$ для всех $n$.

Рисунок 6. Множество $A_{50}$, определённое через $r = 1 + frac{1}{50}cos(50theta)$.
Сразу покажем, что множество $A$ подходящий кандидат. Однако, необходимо начать с некоторых важных теорем, затрагивающих $A$.
Пусть дано множество $A in mathcal{K}$ и положительное число $epsilon$, тогда множеством $A + epsilon$ назовём конструкцию ${ x in X : r(x, A) leq epsilon }$. Нам нужно показать, что это множество закрыто независимо от выбора $A$ и $epsilon$. Чтобы это сделать, начнём с выбора произвольной предельной точки множества $A + epsilon$, затем покажем, что она лежит в множестве.

Предложение 1: $A + epsilon$ закрыто для любых $A in mathcal{K}$ и $epsilon > 0$.
Доказательство. Пусть $A in mathcal{K}$ и $epsilon > 0$. Также, пусть $x$ предельная точка $A + epsilon$. Тогда в $(A + epsilon)backslash{x}$ существует последовательность точек ${ x_n }$, сходящаяся к $x$. Поскольку $x_n in A + epsilon$ для всех $n$, то по определению $r(x_n, A) leq epsilon$ для всех $n$. Свойство (3) Теоремы 1 гарантирует существование $a_n in A : r(x_n, A) = d(x_n, a_n)$ для каждого $n$. Значит, $d(x_n, a_n) leq epsilon$ для всех $n$. Множество $A$ секвенциально компактно, поэтому из определения следует, что каждая последовательность ${ a_n }$ имеет подпоследовательность { $a_{n_k}$ }, которая сходится к точке $a in A$. Поскольку ${ x_n }$ сходится к $x$, то мы знаем, что любая подпоследовательность ${ x_n }$ сходится к $x$. А согласно Результату 1 получается, что $d(x_{n_k}, a_{n_k})$ сходится к $d(x, a)$. Отметим, что ${ x_{n_k} }$ и ${ a_{n_k} }$ являются подпоследовательностями ${ x_n }$ и ${ a_n }$ соответственно, а значит, что $d(x_{n_k}, a_{n_k}) leq epsilon$ для всех $k$. Следовательно, находим, что $d(x, a) leq epsilon$. По определению $r(x, A)$ $r(x, A) leq epsilon$, поэтому $x in A + epsilon$ согласно нашему определению $A + epsilon$. Поскольку $x$ был произвольной предельной точкой, то $A + epsilon$ замкнутое множество, так как содержит все свои предельные точки.

В качестве примера, где множество $A + epsilon$ не компактно, рассмотрим множество $mathbb{R}$ с дискретной метрикой. Пусть $A$ любое непустое конечное множество и $epsilon > 1$. Тогда множество $A + epsilon = mathbb{R}$ замкнуто, но не вполне ограниченно, а значит и не компактно.
Чтобы показать, что $(mathcal{K}, h)$ полное, нам необходимо показать, что $A in mathcal{K}$ и что ${ A_n }$ сходится к $A$. Согласно нашему определению сходимости, мы должны показать, что существует натуральное $N$ такое, что $h(A_n, A) < epsilon$ для всех $n geq N$. Впрочем, следующая теорема даёт альтернативный способ доказательства сходимости.

Теорема 3. Предположим, что $A, B in mathcal{K}$ и $epsilon > 0$. Тогда $h(A, B) leq epsilon$ если и только если $A subseteq B + epsilon$ и $B subseteq A + epsilon$.
Доказательство. Достаточно доказать, что $rho(B, A) leq epsilon$ если и только если $B subseteq A + epsilon$. Предположим, что $B subseteq A + epsilon$. По определению множества $A + epsilon$ для каждого $b in B ; ; r(b, A) leq epsilon$. Отсюда следует, что $rho(B, A) leq epsilon$. Теперь положим, что $rho(B, A) leq epsilon$. Тогда для каждого $b in B ; ; r(b, A) leq epsilon$. А это значит, что $B subseteq A + epsilon$ по определению $A + epsilon$.

Лемма о расширении: Пусть ${ A_n }$ фундаментальная последовательность в $mathcal{K}$, а ${n_k}$ возрастающая последовательность натуральных чисел. Если ${ x_{n_k} }$ фундаментальная последовательность в $X$, для которой $x_{n_k} in A_{n_k}$ для всех $k$, то существует фундаментальная последовательность ${ y_n }$ в $X$ такая, что $y_n in A_n$ для всех $n$ и $y_{n_k} = x_{n_k}$ для всех $k$.
Доказательство. Предположим, что ${ x_{n_k} }$ фундаментальная последовательность в $X$ такая, что $x_{n_k} in A_{n_k}$ для всех $k$. Определим $n_0 = 0$. Для каждого $n$, удовлетворяющего неравенству $n_{k-1} < n leq n_k$, используем Свойство 3, чтобы выбрать $y_n in A_n$ такое, что $r(x_{n_k}, A_n) = d(x_{n_k},y_n)$. Тогда получим, используя определения $rho$ и $r$, что

$d(x_{n_k}, y_n)=r(x_{n_k}, A_n) leq rho(A_{n_k}, A_n) leq h(A_{n_k}, A_n)$

Заметим, что поскольку $x_{n_k} in A_{n_k}$, то $d(x_{n_k}, y_{n_k}) = r(x_{n_k}, A_{n_k}) = 0$. Это значит, что $y_{n_k} = x_{n_k}$ для всех $k$.
Пусть $epsilon > 0$. Поскольку ${ x_{n_k} }$ — фундаментальная последовательность в $X$, существует натуральное $K$, такое что $d(x_{n_k}, x_{n_j}) < frac{epsilon}{3}$ для всех $k, j geq K$. А так как ${ A_n }$ фундаментальная последовательность в $mathcal{K}$, то по определению существует натуральное $N geq n_K$ такое, что $h(A_n, A_m) < frac{epsilon}{3}$ для всех $n, m geq N$. Предположим, что $n, m geq N$. Тогда существуют целые $j, k geq K$ такие, что $n_{k-1} < n leq n_k$ и $n_{j-1} < mleq n_j$. Тогда, находим, что

$d(y_n, y_m) leq d(y_n, x_{n_k}) + d(x_{n_k}, x_{n_j}) + d(x_{n_j}, y_m) \ = r(x_{n_k}, A_n) + d(x_{n_k}, x_{n_j}) + r(x_{n_j}, A_m) \ leq rho(A_{n_k}, A_n) + d(x_{n_k}, x_{n_j}) + rho(A_{n_j}, A_m) \ leq h(A_{n_k}, A_n) + d(x_{n_k}, x_{n_j}) + h(A_{n_j}, A_m) \ < frac{epsilon}{3} + frac{epsilon}{3} +frac{epsilon}{3} = epsilon$

Следовательно, исходя из определения и более ранней подводки, ${ y_n }$ — фундаментальная последовательность в $X$ такая, что $y_n in A_n$ для всех $n$ и $y_{n_k} = x_{n_k}$ для всех $k$. Что и требовалось доказать.

Следующая лемма гарантирует, что при использовании Леммы о расширении $A$ будет замкнуто и не пусто. Данный факт понадобится нам для доказательства того, что $A$ лежит в $mathcal{K}$, поскольку необходимо показать, что $A$ является непустым замкнутым подмножеством $mathcal{K}$. Остаётся лишь доказать, что $A$ вполне ограниченно, так как замкнутые и вполне ограниченные множества — компактны.
Лемма 2: Пусть ${ A_n }$ последовательность в $mathcal{K}$ и $A$ множество вcех точек $x in X$ таких, что существует последовательность ${ x_n }$, сходящаяся к $x$ и $x_n in A_n$ для всех $n$. Если ${ A_n }$ фундаментальная последовательность, то множество $A$ замкнуто и не пусто.
Доказательство. Начнём с доказательства того, что $A$ не пусто. Поскольку ${ A_n }$ фундаментальная последовательность, то существует целое $n_1$ такое, что $h(A_m, A_n) < frac{1}{2^1} = frac{1}{2}$ для всех $m, n geq n_1$. Аналогично, существует целое $n_2$ такое, что $h(A_m, A_n) < frac{1}{2^2} = frac{1}{4}$ для всех $m, n geq n_2$. Продолжая этот процесс, получаем возрастающую последовательность ${ n_k }$ такую, что $h(A_m, A_n) < frac{1}{2^k}$ для всех $m, n geq n_k$. Зафиксируем точку $x_{n_1}$ в $A_{n_1}$. По Свойству 2 Теоремы 2 можно выбрать $x_{n_2} in A_{n_2}$ такие, что $d(x_{n_1}, x_{n_2}) = r(x_{n_1}, A_{n_2})$. Тогда по определению $r$, $rho$ и $h$ найдём, что

$d(x_{n_1}, x_{n_2}) = r(x_{n_1}, A_{n_2}) leq rho(A_{n_1}, A_{n_2}) leq h(A_{n_1}, A_{n_2}) < frac{1}{2}$

Похожим образом можно выбрать $x_{n_3} in A_{n_3}$ так, чтобы

$d(x_{n_2}, x_{n_3}) = r(x_{n_2}, A_{n_3}) leq rho(A_{n_2}, A_{n_3}) leq h(A_{n_2}, A_{n_3}) < frac{1}{4}$

Продолжая этот процесс мы можем соорудить последовательность ${ x_{n_k} }$, где $x_{n_k} in A_{n_k}$ для всех $k$,

$d(x_{n_k}, x_{n_{k + 1}}) = r(x_{n_k}, A_{n_{k + 1}}) leq rho(A_{n_k}, A_{n_{k + 1}}) leq h(A_{n_k}, A_{n_{k + 1}}) < frac{1}{2^k}$

А согласно Результату 2 ${ x_{n_k} }$ является фундаментальной последовательностью.
Следовательно, поскольку ${ x_{n_k} }$ фундаментальна и $x_{n_k} in A_{n_k}$ для всех $k$, согласно Лемме о расширении существует фундаментальная последовательность ${ y_n }$ в $X$ такая, что $y_n in A_n$ для всех $n$ и $y_{n_k} = x_{n_k}$ для всех $k$. Поскольку $X$ полное, фундаментальная последовательность ${ y_n }$ сходится к точке $y in X$. А так как $y_n in A_n$ для всех $n$, то тогда по определению множества $y in A$. Значит $A$ не пусто.
Теперь докажем, что $A$ замкнуто. Предположим, что $a$ является предельной точкой $A$. Тогда существует последовательность $a_k in A backslash {a}$, которая сходится к $a$. Поскольку каждая точка $a_k in A$, существует последовательность ${ y_n }$ такая, что ${ y_n }$ сходится к $a_k$ и $y_n in A_n$ для каждого $n$. Как следствие, существует целое $n_1$ такое, что $x_{n_1} in A_{n_1}$ и $d(x_{n_2}, a_1) < 1$. Похожим образом, существует $n_2 > n_1$ и точка $x_{n_2} in A_{n_2}$ такая, что $d(x_{n_2}, a_2) < frac{1}{2}$. Продолжая этот процесс можно выбрать возрастающую последовательность ${n_k}$ целых чисел таких, что $d(x_{n_k}, a_k) < frac{1}{k}$ для всех $k$. Тогда отсюда следует, что

$d(x_{n_k}, a) leq d(x_{n_k}, a_k) + d(a_k, a)$

Заметим, что при устремлении $k$ к бесконечности, расстояние между ${ x_{n_k} }$ и $a$ стремится к нулю, значит ${ x_{n_k} }$ сходится к $a$. Каждая сходящаяся последовательность фундаментальна, значит, что ${ x_{n_k} }$ фундаментальная последовательность, такая, что $x_{n_k} in A_{n_k}$ для всех $k$. Лемма о расширении гарантирует, что существует фундаментальная последовательность ${ y_n }$ в $X$ такая, что $y_n in A_n$ для всех $n$ и $y_{n_k} = x_{n_k}$. Следовательно, $a in A$, таким образом $A$ замкнуто.
Вместе с предыдущей леммой, чтобы доказать, что $A in mathcal{K}$, остаётся показать, что $A$ вполне ограниченно. Следующая лемма позволит нам это сделать.
Лемма 3. Пусть ${ D_n }$ последовательность вполне ограниченных множеств в $X$ и $A$ произвольное подмножество $X$. Если для каждого $epsilon > 0$ существует натуральное $N$ такое, что $A subseteq D_N + epsilon$, то $A$ вполне ограниченно.
Доказательство. Пусть $epsilon > 0$. Выберем натуральное $N$ так, чтобы $A subseteq D_N + frac{epsilon}{4}$. Поскольку $D_N$ вполне ограниченно, то по определению можно выбрать конечное множество ${ x_i : 1 leq i leq q }$, где $x_i in D_N$, такое, что $D_N subseteq bigcuplimits_{i = 1}^q B_d(x_i, frac{epsilon}{4})$. Переупорядочивая точки $x_i$, мы можем предположить, что $B_d(x_i, frac{epsilon}{2}) cap A neq emptyset$ при $1 leq i leq q$ и $B_d(x_i, frac{epsilon}{2}) cap A = emptyset$ при $p < i$. Тогда для каждого $1 leq i leq p$, пусть $y_i in B_d(x_i, frac{epsilon}{2}) cap A$. Мы полагаем, что $A subseteq bigcuplimits_{i = 1}^p B_d(y_i, epsilon)$. Пусть $a in A$. Тогда $a in D_N + frac{epsilon}{4}$, а следовательно $r(a, D_N) leq frac{epsilon}{4}$. Тогда по Свойству 3 Теоремы 1 существует $xin D_N$ такое, что $d(a, x) = r(a, D_N)$. Тогда найдём, что

$d(a, x_i) leq d(a, x) + d(x, x_i) leq frac{epsilon}{4} + frac{epsilon}{4} = frac{epsilon}{2}$

Таким образом, $xin B_d(x_i, frac{epsilon}{2})$ для некого $1 leq i leq p$. Поэтому, мы имеем $y_i in B_d(x_i, frac{epsilon}{2}) cap A$ такое, что $d(x_i, y_i) < frac{epsilon}{2}$. Из этого следует, что

$d(a, y_i) leq d(a, x_i) + d(x_i, y_i) leq frac{epsilon}{2} + frac{epsilon}{2} = epsilon$

Следовательно, так как для каждого $a in A$ мы нашли $y_i$ при $1 leq i leq p$ такой, что $a in B_d(y_i, epsilon)$, то $A in bigcuplimits_{i=1}^p B_d(y_i, epsilon)$. Тогда по определению $A$ вполне ограниченно. Что и требовалось доказать.
Наконец, мы построили фундамент для доказательства заключительного результата. Пусть дано метрическое пространство $(X, d)$, обозначим через $(mathcal{K}, h)$ метрическое пространство из непустых компактных подмножеств $X$ вместе с Хаусдорфовой метрикой. После рассмотрения важных теорем и результатов, мы близки к достижению главной цели.
Теорема 4. Если $(X, d)$ полное, то $(mathcal{K}, h)$ полное.
Доказательство. Пусть ${ A_n }$ фундаментальная последовательность в $mathcal{K}$, $A$ множество всех точек $x in X$ таких, что существует последовательность ${ x_n }$, которая сходится к $x$ и при этом $x_n in A_n$ для всех $n$. Мы должны доказать, что $A in mathcal{K}$ и ${ A_n }$ сходится к $A$.
По Лемме 2, множество $A$ замкнуто и не пусто. Пусть $epsilon > 0$. Так как ${ A_n }$ фундаментальная последовательность, то тогда существует натуральное $N$ такое, что $h(A_n, A_m) < epsilon$ для всех $m, n geq N$. Тогда по Теореме 3 $A_m subseteq A_n + epsilon$ для всех $m > n geq N$. Пусть $a in A$. Теперь мы хотим показать, что $a in A_n + epsilon$. Зафиксируем $n geq N$. По определению множества $A$, существует последовательность ${ x_i }$ такая, что $x_i in A_i$ для всех $i$ и ${ x_i }$ сходится к $a$. Благодаря Предложению 1 нам известно, что $A_n + epsilon$ замкнуто. Поскольку $x_i in A_n + epsilon$ для каждого $i$, тогда из этого вытекает, что $a in A_n + epsilon$. Этим самым мы установили, что $A subseteq A_n + epsilon$. Согласно Лемме 3 множество $A$ вполне ограниченно. Также, мы знаем, что $A$ полное, поскольку это замкнутое подмножество полного метрического пространства. $A$ компактно, так как оно не пусто, замкнуто и вполне ограниченно, а значит $A in mathcal{K}$.
Пусть $epsilon > 0$. Чтобы показать, что ${ A_n }$ сходится к $A in mathcal{K}$, необходимо показать, что существует натуральное $N$ такое, что $h(A_n, A) < epsilon$ для всех $n geq N$. Чтобы сделать это, по Теореме 3 надо показать два условия, что $A subseteq A_n + epsilon$ и $A _n subseteq A + epsilon$. Из первой части нашего доказательства известно, что существует $N$ такое, что $A subseteq A_n + epsilon$ для всех $n geq N$.
Для доказательства того, что $A_n subseteq A + epsilon$, пусть $epsilon > 0$. Поскольку ${ A_n }$ фундаментальная последовательность, можно выбрать натуральное $N$ такое, что $h(A_m, A_n) < frac{epsilon}{2}$ для всех $m, n geq N$. В связи с тем, что ${ A_n }$ фундаментальная последовательность в $mathcal{K}$, существует строго возрастающая последовательность натуральных чисел ${ n_i }$ такая, что $n_1 > N$ и $h(A_m, A_n) < epsilon 2^{-i-1}$ для всех $m, n > n_i$. Можно использовать Свойство 3 Теоремы 1 для того, чтобы получить следующее:

$A_n subseteq A_{n_1} + frac{epsilon}{2} implies exists x_{n_1} in A_{n_1} : d(y, x_{n_1}) leq frac{epsilon}{2} \ A_{n_1} subseteq A_{n_2} + frac{epsilon}{4} implies exists x_{n_2} in A_{n_2} : d(x_{n_1}, x_{n_2}) leq frac{epsilon}{4} \ A_{n_2} subseteq A_{n_3} + frac{epsilon}{8} implies exists x_{n_3} in A_{n_3} : d(x_{n_2}, x_{n_3}) leq frac{epsilon}{8}$

Продолжая этот процесс, получим, что последовательность ${ x_{n_i} }$ такова, что для всех натуральных $i$ получается $x_{n_i} in A_{n_i}$ и $d(x_{n_i}, x_{n_{i+1}}) leq epsilon2^{-i-1}$. По Результату 2 найдём, что ${ x_{n_i} }$ фундаментальная последовательность, поэтому по Лемме о расширении предел этой последовательности $a$ лежит в $A$. Также найдём, что

$d(y, x_{n_i}) leq d(y, x_{n_1}) + d(x_{n_1}, x_{n_2}) + d(x_{n_2}, x_{n_3}) + ... + d(x_{n_{i-1}}, x_{n_i}) \ leq frac{epsilon}{2} + frac{epsilon}{4} + frac{epsilon}{8} + ... + frac{epsilon}{2^î} < epsilon$

Поскольку $d(y, x_{n_i}) leq epsilon$ для всех $i$, то из этого следует, что $d(y, a) leq epsilon$, а значит и $y in A + epsilon$. Таким образом, нам стало известно, что существует $N$ такое, что $A_n subseteq A + epsilon$, то есть $h(A_n, A) < epsilon$ для всех $n geq N$, то есть ${ A_n }$ сходится к $A in mathcal{K}$. Следовательно, если $(X, d)$ полное, то $(mathcal{K}, h)$ полное.

Теперь мы докажем, что если $X$ компактно, то $mathcal{K}$ компактно. Заметим, что метрическое пространство компактно тогда и только тогда, когда оно полное и вполне ограниченное.

Теорема 5. Если $(X, d)$ компактно, то $(mathcal{K}, h)$ компактно.
Доказательство. Из предыдущего результата нам известно, что $mathcal{K}$ полное. А так как мы знаем, что множество компактно тогда и только тогда, когда оно полное и вполне ограниченное, то нам надо доказать, что $mathcal{K}$ вполне ограниченно. Пусть $epsilon > 0$. Поскольку $X$ вполне ограниченно, то существует конечное множество ${ x_i: 1 leq i leq n }$ такое, что $X subseteq bigcuplimits_{i=1}^n B_d(x_i, frac{epsilon}{3})$ и $x_i in X$ для каждого $i$. Пусть ${ C_k: 1 leq k leq 2^p -1 }$ будет коллекцией всех возможных непустых объединений замыканий этих шаров. В связи с компактностью $X$ замыкание каждого шара является компактным множеством. Следовательно, каждое $C_k$ конечное объединение компактных множеств, а потому тоже компактное, поэтому $C_k in mathcal{K}$. Покажем, что $mathcal{K} subseteq bigcuplimits_{k=1}^{2^p - 1} B_h(C_k, epsilon)$.
Пусть $Z in mathcal{K}$. Тогда покажем, что $Z in B_h (C_k, epsilon)$ для некоторого $k$. Выберем $S_Z = { i: Z cap overline{B_d(x_i, epsilon)} neq emptyset }$. Затем выберем индекс $j$ так, чтобы $С_j = bigcuplimits_{i in S_Z} overline{B_d(x_i, frac{epsilon}{3})}$. По Свойству 2 Теоремы 1 мы знаем, что $rho(Z, C_j) = 0$, так как $Z subseteq C_j$. Пусть теперь $c$ является элементом $C_j$. Тогда существует некоторое $i in S_Z$ и $z in Z$ такое, что $c, z in overline{B_d(x_i, frac{epsilon}{3})}$. Из этого следует, что $r(c, Z) leq frac{2}{3} epsilon$. Поскольку $c$ было выбрано произвольно, то получим, что $rho(C_j, Z) leq frac{2}{3} epsilon$. Следовательно, найдём, что $h(Z, C_j) = rho(C_j, Z) < epsilon$ и, таким образом, $Z subseteq B_h(C_j, epsilon)$. Поэтому, $mathcal{K}$ вполне ограниченно. Следовательно, мы доказали, что если $(X, d)$ компактно, то $(mathcal{K}, h)$ компактно.

Выводы

Расстояние Хаусдорфа — метрика, которая определяет расстояние между множествами через некое неотрицательное действительное число. Мы исследовали её через множество примеров. Затем, мы выяснили, что расстояние Хаусдорфа определяет метрику на пространстве $mathcal{K}$ всех непустых компактных подмножеств заданного метрического пространства $(X, d)$. Также мы вывели некоторые приятные качества данной метрики. Самое главное, если $(X, d)$ полное, то $(mathcal{K}, h)$ полное. В дополнение, мы доказали, что если $(X, d)$ компакт, то $(mathcal{K}, h)$ компакт, что является поистине важным результатом.

Литература

[1]

Russ Gordon, Real Analysis: A First Course. Walla Walla, Washington, 1st Edition, 2011

Ещё я веду telegram канал StepOne, где оставляю небольшие заметки про разработку и мир IT.

Источник

В геометрии, метрика Хаусдорфа есть естественная метрика определённая на множестве всех компактных подмножеств метрического пространства. Таким образом, метрика Хаусдорфа превращает множество всех компактных подмножеств метрического пространства в метрическое пространство.

Определение

Пусть X и Y суть два компактных подмножества метрического пространства M.
Тогда расстояние по Хаусдорфу, dH (X,Y), между X и Y есть минимальное число r такое что замкнутая r-окрестность X содержит Y и также замкнутая r-окрестность Y содержит X.

Другими словами, если |xy| обозначает расстояние между точками x и y в M то

{displaystyle d_{H}(X,Y)=max left{sup _{xin X}inf _{yin Y}|xy|, sup _{yin Y}inf _{xin X}|xy|right}.}

Свойства

Пусть F(M) обозначает множество всех компактных подмножеств метрического пространства M с метрикой Хаусдорфа

  • Топология пространства F(M) полностью определяется топологией M.
  • F(M) компактно тогда и только тогда когда компактно M.
  • F(M) полно тогда и только тогда когда M полное.

Вариации

  • Иногда метрика Хаусдорфа рассматривается на множестве всех замкнутых подмножеств метрического пространства, в этом случае расстояние между некоторыми подмножествами может равняться бесконечности.
  • Иногда метрика Хаусдорфа рассматривается на множестве всех подмножеств метрического пространства, в этом случае она уже не является метрикой, так как «расстояние» между различными подмножествами может равняться нулю.
  • В евклидовой геометрии, часто применяется метрика Хаусдорфа с точностью до конгруэнтности. Пусть X и Y два компактных подмножества евклидова пространства тогда DH(X,Y) определяется как минимум dH(I(X),Y) по всем движениям евклидова пространства I. Строго говоря, эта метрика на пространстве классов конгруэнтности компактных подмножеств евклидова пространства.
  • Метрика Громова-Хаусдорфа аналогична метрике Хаусдорфа с точностью до конгруэнтности. Она превращает множество (изометрических классов) компактных метрических пространств в метрическое пространство.

Ссылки

  • В.А.Скворцов, Примеры метрических пространств, Библиотека «Математическое просвещение», выпуск 9, (2001).

bg:Хаусдорфова мярка
nl:Hausdorffmetriek
pl:Metryka Hausdorffa

Источник

Метрика Хаусдорфа есть естественная метрика, определённая на множестве всех непустых замкнутых ограниченных подмножеств пространства. Она превращает это множество в метрическое пространство. Метрику Хаусдорфа иногда также называют метрикой Помпейю- Хаусдорфа.

Содержание

  • 1 Расстояние по Хаусдорфу
    • 1.1 Предложение
    • 1.2 Переход к метрике
  • 2 Свойства
  • 3 Альтернативные способы задания расстояния
  • 4 Список литературы

Расстояние по Хаусдорфу

Пусть $$(X, rho) ~- $$ метрическое пространство. Введем понятие расстояния по Хаусдорфу между двумя непустыми ограниченными множествами. Итак, пусть $$M, N subset X ~-$$ непустые ограниченные множества. Для них положим
begin{gather*}
h(M, N) = infleft{ r > 0: O(M, r) supseteq N, O(N, r) supseteq M right},
end{gather*}

где $$O(cdot, r) ~-$$ открытая $$r$$-окрестность множества.

Число $$h(M, N)$$ называется расстоянием по Хаусдорфу между множествами $$M$$ и $$N$$. Кроме того, приведенная выше формула определяет расстояние по Хаусдорфу и для неограниченных множеств $$M$$ и $$N$$, однако при этом $$h(M, N)$$ уже может принимать значение $$+infty$$.

Предложение

Для любых $$a_1, a_2 in X$$ и $$r_1, r_2 > 0$$ справедливо неравенство
begin{gather}label{eq1}
h(B(a_1, r_1), B(a_2, r_2)) leqslant rho(a_1, a_2) + maxleft{r_1, r_2right},
end{gather}
где $$B(a, r) ~-$$ замкнутый шар метрического пространства в точке $$a$$ с радиусом $$r$$.

Доказательство

Пусть $$x_1 in B(a_1, r_1)$$. Тогда имеет место неравенство $$rho(x_1, a_2) leqslant r_1 + rho(a_1, a_2) $$, которое вытекает из следующей цепочки неравенств:
begin{gather*}
rho(x_1, a_2) leqslant rho(x_1, a_1) + rho(a_1, a_2) leqslant r_1 + rho(a_1, a_2).
end{gather*}
Таким же образом получаем, что $$rho(x_2, a_1) leqslant r_2 + rho(a_1, a_2)$$ для всех $$x_2 in B(a_2, r_2)$$. Далее из получившихся неравенств и определения расстояния по Хаусдорфу вытекает формула (ref{eq1}).

Замечание

Если дополнительно предположить, что $$X ~-$$ линейное нормированное пространство, то
begin{gather*}
h(B(a_1, r_1), B(a_2, r_2)) = |a_2 — a_1| + left|r_2 — r_1 right|.
end{gather*}

Пример 1

Данный пример показывает, что доказанное выше неравенство (ref{eq1}) может превратиться в равенство.
Рассмотрим метрическое пространство $$(X, rho)$$, в котором $$X = left{ -2, -1, 1, 2right} ~- $$ множество состоящее из точек на прямой с естественной метрикой расстояния между точками. Тогда при $$a_1 = -1, a_2 = 1, r_1 = r_2 = 1$$ имеет место
begin{gather*}
h(B(a_1, r_1), B(a_2, r_2)) = 3 = rho(a_1, a_2) + max(r_1, r_2).
end{gather*}

Пример 2

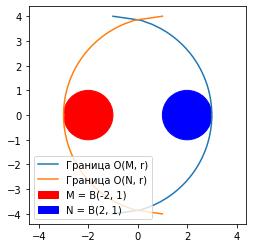
Пусть теперь возьмем на рассмотрение метрическое пространство $$(X, rho)$$, в котором $$X = mathbb{R}^2$$ с естественной метрикой расстояния между точками в пространстве $$mathbb{R}^2$$. Найдем Хаусдорфово расстояние между $$B(2,1)$$ и $$B(-2,1)$$:
begin{gather*}
h(B(-2, 1), B(2, 1)) = 4.
end{gather*}

Переход к метрике

Несложно видеть, что для замкнутых ограниченных множеств расстояние по Хаусдорфу $$h$$ удовлетворяет всем аксиомам метрики. А именно, для любых непустых замкнутых ограниченных множеств $$M, N$$ и $$E$$ имеют место соотношения
begin{gather*}
h(M, N) = 0 Leftrightarrow M = N,
end{gather*}
begin{gather*}
h(M, N) = h(N, M) geqslant 0,
end{gather*}
begin{gather*}
h(M, N) leqslant h(M, E) + h(E, N).
end{gather*}
Таким образом, функция $$h$$ превращает множество всех непустых замкнутых ограниченных подмножеств пространства $$X$$ в метрическое пространство, которое обозначается через $$H(X)$$. Метрику $$h$$ называют метрикой Хаусдорфа. Однако в общем случае расстояние Хаусдорфа метрикой не является, так как может равняться нулю между различными множествами. Например, это имеет место для отрезка $$M = left[a, bright]$$ и полуинтервала $$N = left[a, b right)$$, которые рассматриваются как подмножества числовой прямой. Действительно, для любого $$varepsilon > 0$$ выполняется, что $$M subset O(N, varepsilon)$$ и $$N subset O(M, varepsilon)$$, поэтому $$h(M, N) = 0$$.

Наряду с метрическим пространством обычно рассматривается его подпространство $$H_{c}(X)$$, которое состоит из непустых компактных подмножеств $$X$$. Стоит отметить, что если множество $$X$$ ограничено, то функция $$h$$ ограничена на множестве всех подмножеств множества $$X$$.

Свойства

Пусть $$(X, rho) ~- $$ метрическое пространство, а $$M, N ~-$$ непустые подмножества пространства $$X$$.

1. Для любых $$x in M$$ и $$varepsilon > 0$$ существует $$y in N$$ такое, что $$rho(x, y) leqslant h(M, N) + varepsilon$$.

2. $$h(M, N) = 0$$ тогда и только тогда, когда $$overline{M} = overline{N}$$.

3. Пусть $$X = mathbb{R}^n$$, а $$M, N ~-$$ выпуклые компакты. Тогда
begin{gather*}
h(M, N) = max_{|l | leqslant 1}left|s(l| M) — s(l| N) right|,
end{gather*}
где $$s(l| cdot) ~-$$ опорная функция.

4. Если пространство $$X$$ ограничено, то метрическое пространство $$H(X)$$ сепарабельно.

5. Если пространство $$X$$ полно, то метрические пространства $$H(X)$$ и $$H_{c}(X)$$ тоже полны.

Альтернативные способы задания расстояния

Наряду с расстоянием Хаусдорфа часто используют и другое расстояние между множествами, которое обозначается через dist и определяется следующим соотношением:
begin{gather*}
text{dist}(M, N) = infleft{rho(x, y), x in M, y in Nright}.
end{gather*}
Для данного расстояния, очевидно, имеет место
begin{gather*}
text{dist}(M, N) leqslant h(M, N),
end{gather*}
begin{gather*}
text{dist}(M, N) = text{dist}(N, M) geqslant 0.
end{gather*}
Также можно рассмотреть еще одну величину, которая характеризует взаимное расположение множеств $$M$$ и $$N$$, лежащих в $$X$$. Это $$~-$$ отклонение множества $$M$$ от множества $$N$$, которое определяется соотношением
begin{gather*}
h^{+}(M, N) = infleft{ varepsilon > 0: O(N, varepsilon) supset Mright}.
end{gather*}
Отклонение $$h^{+}$$ обычно называют полуметрикой Хаусдорфа. Наряду с $$h^+$$, можно ввести еще одну полуметрику $$h^-$$:
begin{gather*}
h^{-}(M, N) = h^{+}(N, M).
end{gather*}
Величину $$h^+$$ можно выразить через dist:
begin{gather*}
h^{+}(M, N) = supleft{ text{dist}(x, N), x in Mright},
end{gather*}
а расстояние по Хаусдорфу в свою очередь выражается через $$h^+$$ и $$h^-$$ по формуле
begin{gather*}
h(M, N) = maxleft{ h^{+}(M, N), h^{-}(M, N)right}.
end{gather*}
Поэтому для любых множест $$M, N$$ справедливо
begin{gather*}
text{dist}(M, N) leqslant h^{+}(M, N) leqslant h(M, N).
end{gather*}

Список литературы

1. Арутюнов А. В. «Лекции по выпуклому и многозначному анализу», М.: ФИЗМАТЛИТ, 2014.

Источник

(Оригинал: http://cgm.cs.mcgill.ca/~godfried/teaching/cg-projects/98/normand/main.html)

вперед от:http://blog.sina.com.cn/s/blog_4062094e0102vkpf.html

Расстояние Хаусдорфа

1. Введение

При обсуждении вопросов расстояния мы обычно используем кратчайшее описание: например, расстояние от точки X до многоугольника P, мы обычно ссылаемся на расстояние от точки на P, которая является ближайшей к X, до X. Та же концепция применима и к многоугольникам: если есть расстояние между многоугольником A и многоугольником B, расстояние между ними обычно понимается как кратчайшее расстояние между любыми точками на A и B. Формальное математическое описание этой концепции:

hausdorff —————— Уравнение 1

Согласно описанию компьютерной программы, это уравнение:

«Для всех точек в A найдите кратчайшее расстояние между ним и всеми точками в B; затем сохраните значение кратчайшего расстояния как расстояние между A и B».

Такое определение расстояния между многоугольниками в некоторых случаях неудовлетворительно: например, на рисунке 1 мы бы сказали, что расстояние между двумя треугольниками может быть кратчайшим расстоянием, то есть между двумя красными вершинами на рисунке. значение расстояния. Однако мы также, естественно, надеемся, что небольшое расстояние между двумя треугольниками означает, что ни одна точка на одном многоугольнике не находится далеко от другого многоугольника. Согласно последней концепции, расстояние между многоугольниками на Рисунке 1 не будет таким близким, как описано двумя красными вершинами. Синие вершины на рисунке 1 на самом деле относительно далеко друг от друга. Таким образом, концепция кратчайшего расстояния вообще не учитывает форму многоугольника.

hausdorff

Рисунок 1. Кратчайшее расстояние не учитывает форму многоугольника.

Другой пример представлен на рисунке 2. Два треугольника на рисунке такие же, как и на рисунке 1, и их кратчайшие расстояния такие же, как на рисунке 1, но их положение изменилось. Очевидно, что самое короткое расстояние такое же, но ситуация изменилась, поэтому самое короткое расстояние несет слишком мало информации.

hausdorff

Рисунок 2-Кратчайшее расстояние не учитывает положение объекта

Позже мы увидим, что, хотя расстояние Хаусдорфа кажется немного более сложным, оно может описать две упомянутые выше ситуации, которые не может дать кратчайшее расстояние.

2. Что такоерасстояние Хаусдорфа

Расстояние Хаусдорфа названо в честь Феликса Хаусдорфа (1868-1942). Расстояние Хаусдорфа относится к «максимальному значению всех расстояний от ближайшей точки в одном наборе до другого набора».

Формальное математическое описание состоит в том, что расстояние Хаусдорфа от множества A до множества B является функцией максимина, определяемой как:

hausdorff —————— Уравнение 2

Здесь a и b — точки в множестве A и множестве B соответственно, а d (a, b) — это шкала между двумя точками; для простоты мы берем d (a, b) как евклидово расстояние между a и b. Если набор A и набор B являются двумя наборами точек, исчерпывающий алгоритм может быть описан как:

Исчерпывающий алгоритм:

1. h=0

2. Для каждой точки ai в A

2.1 самый короткий = бесконечность;

2.2 Для каждой точки в B, bi

        dij = d(ai, bj)

        if dij < shortest then

             shortest = dij;

   2.3  if shortest >h then

              h = shortest

Алгоритм процесса:

hausdorff

Рисунок 3-1

hausdorff

Рисунок 3-2

hausdorff

Рисунок 3-3

hausdorff

Рисунок 3-4.

hausdorff

Рисунок 3-5

hausdorff

Рисунок 3-6

hausdorff

Рисунок 3-7

hausdorff

Рисунок 3-8

Временная сложность алгоритма показана как O (n, m), где n и m — точки в множестве A и множестве B, соответственно.

Обратите внимание, что расстояние Хаусдорфа является направленным или асимметричным. Другими словами, h (A, B) в большинстве случаев не равно h (B, A). На рис. 3 h (A, B) = d (a1, b1) и h (B, A) = d (b2, a1). Эта асимметрия является одной из характеристик функции максимина, которая отличается от симметрии функции minmin.

Более общее расстояние Хаусдорфа определяется следующим образом:

H (A, B) = max {h (A, B), h (B, A)} ———- Уравнение 3

Эта формула определяет расстояние Хаусдорфа между A и B, а уравнение 2 определяет расстояние Хаусдорфа от A до B (также называемое направленным расстоянием Хаусдорфа). h (A, B) и h (B, A) иногда называют прямым и обратным расстоянием Хаусдорфа от A до B, соответственно. Хотя иногда разные авторы будут противоречить друг другу, расстояние Хаусдорфа относится к ситуации в уравнении 3, которая встречается чаще. Поэтому, если не указано иное, когда мы будем говорить о расстоянии Хаусдорфа позже, мы будем ссылаться на уравнение 3.

Если множества A и B состоят из прямых линий или многоугольников, то есть функция H (A, B) применяется к прямым или многоугольникам, а не только к вершинам прямых линий или многоугольников. Исчерпывающий алгоритм больше не может использоваться для вычисления расстояния Хаусдорфа между этими наборами, поскольку такие наборы содержат бесконечные точки.

Итак, давайте вернемся и посмотрим на расстояние Хаусдорфа многоугольника на рисунке 1? Расстояние Хаусдорфа определяет взаимное приближение между многоугольником и другим многоугольником по максимальному расстоянию между ними. Кратчайшее расстояние учитывает только одну точку для каждого многоугольника и не учитывает другие точки.

hausdorff

Рисунок 4, расстояние Хаусдорфа, показывает, что каждый треугольник на рисунке 1 окружен предельным кругом, а радиус круга равен H (P1, P2).

Второй момент заключается в том, что по сравнению с наименьшим расстоянием, нечувствительным к положению многоугольника, расстояние Хаусдорфа имеет то преимущество, что чувствительно к положению, как показано на рисунке 5.

hausdorff

Рисунок 5, сравнение рисунка 4, два треугольника имеют одинаковое кратчайшее расстояние, но их относительное положение меняется, они имеют разные расстояния Хаусдорфа.

3.расстояние ХаусдорфаРасчет

3.1 Предположение

В следующем обсуждении мы основываемся на следующих предположениях:

A. Многоугольники A и B — простые выпуклые многоугольники;

B. Полигоны A и B не пересекаются.

3.2 Теорема

Следующий алгоритм основан на следующих трех геометрических теоремах. Для удобства описания мы определяем точки a и b как точки на многоугольниках A и B соответственно, и имеем:

d (a, b) = h (A, B)

Проще говоря, a — самая дальняя точка на A относительно B, D, а b — ближайшая точка на B к A.

Теорема 1а.: Возьмите a как вертикальную опору, а линия, перпендикулярная ab, является линией поддержки A. А А и Б находятся на одной стороне линии.

(См. Доказательство теоремы: http://cgm.cs.mcgill.ca/~godfried/teaching/cg-projects/98/normand/lemma1a.html)

Теорема 1б.: Принять б как вертикальная стопа, а прямая линия, перпендикулярная к АВАМ является поддержка линии B. А А и Б находятся по обе стороны от линии.

(См. Доказательство теоремы: http://cgm.cs.mcgill.ca/~godfried/teaching/cg-projects/98/normand/lemma1b.html)

Теорема 2.: На границе A есть точка X, расстояние от которой до B равно h (A, B)

(См .: http://cgm.cs.mcgill.ca/~godfried/teaching/cg-projects/98/normand/lemma2.html)

Теорема 3.: Пусть bi будет точкой, ближайшей к вершине a из A в B, если µ — это направление движения от bi к bi + 1 (по или против часовой стрелки). Для прохождения по очереди всех вершин в A µ меняется не более двух раз.

(См. Доказательство теоремы: http://cgm.cs.mcgill.ca/~godfried/teaching/cg-projects/98/normand/lemma3.html)

3.3 Алгоритм

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти работу рерайтера
  • Как найти расположение папки стим
  • Как найти диаметр кольца зная длину окружности
  • Как найти родственников по фамилии умершего человека
  • Дефицит азота в аквариуме как исправить