Как найти расстояние хэмминга

From Wikipedia, the free encyclopedia

Hamming distance

4-bit binary tesseract for finding Hamming distance.

Two example distances: 0100→1001 has distance 3; 0110→1110 has distance 1

Class

String similarity

Data structure

string

Worst-case performance

Best-case performance

Average performance

Worst-case space complexity

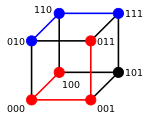
3-bit binary cube for finding Hamming distance

Two example distances: 100→011 has distance 3; 010→111 has distance 2

The minimum distance between any two vertices is the Hamming distance between the two binary strings.

In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different. In other words, it measures the minimum number of substitutions required to change one string into the other, or the minimum number of errors that could have transformed one string into the other. In a more general context, the Hamming distance is one of several string metrics for measuring the edit distance between two sequences. It is named after the American mathematician Richard Hamming.

A major application is in coding theory, more specifically to block codes, in which the equal-length strings are vectors over a finite field.

Definition[edit]

The Hamming distance between two equal-length strings of symbols is the number of positions at which the corresponding symbols are different.^[1]

Examples[edit]

The symbols may be letters, bits, or decimal digits, among other possibilities. For example, the Hamming distance between:

«karolin» and «kathrin» is 3.
«karolin» and «kerstin» is 3.
«kathrin» and «kerstin» is 4.
0000 and 1111 is 4.
2173896 and 2233796 is 3.

Properties[edit]

For a fixed length n, the Hamming distance is a metric on the set of the words of length n (also known as a Hamming space), as it fulfills the conditions of non-negativity, symmetry, the Hamming distance of two words is 0 if and only if the two words are identical, and it satisfies the triangle inequality as well:^[2] Indeed, if we fix three words a, b and c, then whenever there is a difference between the ith letter of a and the ith letter of c, then there must be a difference between the ith letter of a and ith letter of b, or between the ith letter of b and the ith letter of c. Hence the Hamming distance between a and c is not larger than the sum of the Hamming distances between a and b and between b and c. The Hamming distance between two words a and b can also be seen as the Hamming weight of a − b for an appropriate choice of the − operator, much as the difference between two integers can be seen as a distance from zero on the number line.^{[clarification needed]}

For binary strings a and b the Hamming distance is equal to the number of ones (population count) in a XOR b.^[3] The metric space of length-n binary strings, with the Hamming distance, is known as the Hamming cube; it is equivalent as a metric space to the set of distances between vertices in a hypercube graph. One can also view a binary string of length n as a vector in $mathbb {R} ^{n}$ by treating each symbol in the string as a real coordinate; with this embedding, the strings form the vertices of an n-dimensional hypercube, and the Hamming distance of the strings is equivalent to the Manhattan distance between the vertices.

Error detection and error correction[edit]

The minimum Hamming distance is used to define some essential notions in coding theory, such as error detecting and error correcting codes. In particular, a code C is said to be k error detecting if, and only if, the minimum Hamming distance between any two of its codewords is at least k+1.^[2]

For example, consider the code consisting of two codewords «000» and «111». The hamming distance between these two words is 3, and therefore it is k=2 error detecting. This means that if one bit is flipped or two bits are flipped, the error can be detected. If three bits are flipped, then «000» becomes «111» and the error can not be detected.

A code C is said to be k-error correcting if, for every word w in the underlying Hamming space H, there exists at most one codeword c (from C) such that the Hamming distance between w and c is at most k. In other words, a code is k-errors correcting if, and only if, the minimum Hamming distance between any two of its codewords is at least 2k+1. This is more easily understood geometrically as any closed balls of radius k centered on distinct codewords being disjoint.^[2] These balls are also called Hamming spheres in this context.^[4]

For example, consider the same 3 bit code consisting of two codewords «000» and «111». The Hamming space consists of 8 words 000, 001, 010, 011, 100, 101, 110 and 111. The codeword «000» and the single bit error words «001»,»010″,»100″ are all less than or equal to the Hamming distance of 1 to «000». Likewise, codeword «111» and its single bit error words «110»,»101″ and «011» are all within 1 Hamming distance of the original «111». In this code, a single bit error is always within 1 Hamming distance of the original codes, and the code can be 1-error correcting, that is k=1. The minimum Hamming distance between «000» and «111» is 3, which satisfies 2k+1 = 3.

Thus a code with minimum Hamming distance d between its codewords can detect at most d-1 errors and can correct ⌊(d-1)/2⌋ errors.^[2] The latter number is also called the packing radius or the error-correcting capability of the code.^[4]

History and applications[edit]

The Hamming distance is named after Richard Hamming, who introduced the concept in his fundamental paper on Hamming codes, Error detecting and error correcting codes, in 1950.^[5] Hamming weight analysis of bits is used in several disciplines including information theory, coding theory, and cryptography.^[6]

It is used in telecommunication to count the number of flipped bits in a fixed-length binary word as an estimate of error, and therefore is sometimes called the signal distance.^[7] For q-ary strings over an alphabet of size q ≥ 2 the Hamming distance is applied in case of the q-ary symmetric channel, while the Lee distance is used for phase-shift keying or more generally channels susceptible to synchronization errors because the Lee distance accounts for errors of ±1.^[8] If q=2 or both distances coincide because any pair of elements from or differ by 1, but the distances are different for larger .

The Hamming distance is also used in systematics as a measure of genetic distance.^[9]

However, for comparing strings of different lengths, or strings where not just substitutions but also insertions or deletions have to be expected, a more sophisticated metric like the Levenshtein distance is more appropriate.

Algorithm example[edit]

The following function, written in Python 3, returns the Hamming distance between two strings:

def hamming_distance(string1: str, string2: str) -> int:
    """Return the Hamming distance between two strings."""
    if len(string1) != len(string2):
        raise ValueException("Strings must be of equal length.")
    dist_counter = 0
    for n in range(len(string1)):
        if string1[n] != string2[n]:
            dist_counter += 1
    return dist_counter

Or, in a shorter expression:

sum(xi != yi for xi, yi in zip(x, y))

The function hamming_distance(), implemented in Python 3, computes the Hamming distance between two strings (or other iterable objects) of equal length by creating a sequence of Boolean values indicating mismatches and matches between corresponding positions in the two inputs, then summing the sequence with True and False values, interpreted as one and zero, respectively.

def hamming_distance(s1: str, s2: str) -> int:
    """Return the Hamming distance between equal-length sequences."""
    if len(s1) != len(s2):
        raise ValueError("Undefined for sequences of unequal length.")
    return sum(el1 != el2 for el1, el2 in zip(s1, s2))

where the zip() function merges two equal-length collections in pairs.

The following C function will compute the Hamming distance of two integers (considered as binary values, that is, as sequences of bits). The running time of this procedure is proportional to the Hamming distance rather than to the number of bits in the inputs. It computes the bitwise exclusive or of the two inputs, and then finds the Hamming weight of the result (the number of nonzero bits) using an algorithm of Wegner (1960) that repeatedly finds and clears the lowest-order nonzero bit. Some compilers support the __builtin_popcount function which can calculate this using specialized processor hardware where available.

int hamming_distance(unsigned x, unsigned y)
{
    int dist = 0;

    // The ^ operators sets to 1 only the bits that are different
    for (unsigned val = x ^ y; val > 0; ++dist)
    {
        // We then count the bit set to 1 using the Peter Wegner way
        val = val & (val - 1); // Set to zero val's lowest-order 1
    }

    // Return the number of differing bits
    return dist;
}

A faster alternative is to use the population count (popcount) assembly instruction. Certain compilers such as GCC and Clang make it available via an intrinsic function:

// Hamming distance for 32-bit integers
int hamming_distance32(unsigned int x, unsigned int y)
{
    return __builtin_popcount(x ^ y);
}

// Hamming distance for 64-bit integers
int hamming_distance64(unsigned long long x, unsigned long long y)
{
    return __builtin_popcountll(x ^ y);
}

References[edit]

^ Waggener, Bill (1995). Pulse Code Modulation Techniques. Springer. p. 206. ISBN 9780442014360. Retrieved 13 June 2020.
^ ^a ^b ^c ^d Robinson, Derek J. S. (2003). An Introduction to Abstract Algebra. Walter de Gruyter. pp. 255–257. ISBN 978-3-11-019816-4.
^ Warren Jr., Henry S. (2013) [2002]. Hacker’s Delight (2 ed.). Addison Wesley — Pearson Education, Inc. pp. 81–96. ISBN 978-0-321-84268-8. 0-321-84268-5.
^ ^a ^b Cohen, G.; Honkala, I.; Litsyn, S.; Lobstein, A. (1997), Covering Codes, North-Holland Mathematical Library, vol. 54, Elsevier, pp. 16–17, ISBN 9780080530079
^ Hamming, R. W. (April 1950). «Error detecting and error correcting codes» (PDF). The Bell System Technical Journal. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. ISSN 0005-8580. S2CID 61141773. Archived (PDF) from the original on 2022-10-09.
^ Jarrous, Ayman; Pinkas, Benny (2009). Abdalla, Michel; Pointcheval, David; Fouque, Pierre-Alain; Vergnaud, Damien (eds.). «Secure Hamming Distance Based Computation and Its Applications». Applied Cryptography and Network Security. Berlin, Heidelberg: Springer: 107–124. doi:10.1007/978-3-642-01957-9_7. ISBN 978-3-642-01957-9.
^ Ayala, Jose (2012). Integrated Circuit and System Design. Springer. p. 62. ISBN 978-3-642-36156-2.
^ Roth, Ron (2006). Introduction to Coding Theory. Cambridge University Press. p. 298. ISBN 978-0-521-84504-5.
^ Pilcher, Christopher D.; Wong, Joseph K.; Pillai, Satish K. (2008-03-18). «Inferring HIV Transmission Dynamics from Phylogenetic Sequence Relationships». PLOS Medicine. 5 (3): e69. doi:10.1371/journal.pmed.0050069. ISSN 1549-1676. PMC 2267810. PMID 18351799.

Подсчет расстояния Хэмминга на большом наборе данных

Время на прочтение
8 мин

Количество просмотров 46K

В данной статье речь пойдет об алгоритме HEngine и реализации решения проблемы подсчета расстояния Хэмминга на больших объемах данных.

Введение

Расстояние Хэмминга — это количество различающихся позиций для строк с одинаковой длинной. Например, HD( 100, 001 ) = 2.

Впервые проблема подсчета расстояния Хэмминга была поставлена Minsky и Papert в 1969 году [1], где задача сводилась к поиску всех строк из базы данных, которые находятся в пределах заданного расстояния Хэмминга к запрашиваемой.

Подобная задача является необычайно простой, но поиск ее эффективного решения до сих пор остается на повестке дня.

Расстояние Хэмминга уже довольно широко используется для различных задач, таких как поиск близких дубликатов, распознавание образов, классификация документов, исправление ошибок, обнаружения вирусов и т.д.

Например, Manku и сотоварищи предложили решение проблемы кластеризации дубликатов при индексации веб документов на основе подсчета расстояния Хэмминга [2].
Также Miller и друзья предложили концепцию поиска песен по заданному аудио фрагменту [3], [4].
Подобные решения были использованы и для задачи поиска изображений и распознавание сетчатки [5], [6] и т.д.

Описание проблемы

Имеется база данных бинарных строк T, размером n, где длина каждой строки m. Запрашиваемая строка a и требуемое расстояние Хэмминга k.

Задача сводится к поиску всех строк, которые находятся в пределах расстояния k.

В оригинальной концепции алгоритма рассматривается два варианта задачи: статическая и динамическая.

— В статической задачи расстояние k предопределено заранее.
— В динамической, наоборот, требуемое расстояние заранее неизвестно.

В статье описывается решение только статической задачи.

Описание алгоритма HEngine для статической задачи

Данная реализация фокусируется на поиске строк в пределах k <= 10.

Существует три решения статической задачи: линейный поиск (linear scan), расширение запроса (query expansion) и расширение базы данных (table expansion).

В данном случае под расширением запроса имеется в виду генерация всех возможных вариантов строк, которые вписываются в заданное расстояние для первоначальной строки.
Расширение базы данных подразумевает создание множества копий этой базы данных, где или также генерируются все возможные варианты, которые отвечают требованиям необходимого расстояния, либо данные обрабатываются каким-то другим способом (подробно об этом чуть дальше.).

HEngine [8] использует комбинацию этих трех методов для эффективного балансирования между памятью и временем исполнения.

Немного теории

Алгоритм базируется на небольшой теореме, которая гласит следующее:

Если для двух строк a и b расстояние HD( a, b ) <= k, то если поделить строки a и b на подстроки методом rcut используя фактор сегментации
r >= ⌊k/2⌋ + 1
обязательно найдется, по крайней мере, q= r − ⌊k/2⌋ подстрок, когда их расстояние не будет превышать единицу, HD( ai, bi ) <= 1.

Выделение подстрок из базовой строки методом rcut выполняется по следующим принципам:
Выбирается значение, названное фактором сегментации, которое удовлетворяет условию
r >= ⌊k/2⌋ + 1

Длина первых r − (m mod r) подстрок будет иметь длину ⌊m / r⌋, а последние m mod r подстроки ⌈m/r⌉. Где m — это длина строки, ⌊ — округление до ближайшего снизу, а ⌉ округление до ближайшего сверху.

Теперь тоже самое, только на примере:

Даны две бинарные строки длиной m = 8 бит: A = 11110000 и B = 11010001, расстояние между ними k = 2.
Выбираем фактор сегментации r = 2 / 2 + 1 = 2, т. е. всего будет 2 подстроки длиной m/r = 4 бита.

a1 = 1111, a2 = 0000
b1 = 1101, b2 = 0001

Если мы сейчас подсчитаем расстояние между соответствующими подстроками, то, по крайней мере, (q = 2 — 2/2 = 1) одна подстрока совпадет или их расстояние не будет превышать единицу.

Что и видим:
HD( a1, b1 ) = HD( 1111, 1101 ) = 1
и
HD( a2, b2 ) = HD( 0000, 0001 ) = 1

Подстроки базовой строки были названы сигнатурами.
Сигнатуры или подстроки a1 и b1 (a2 и b2, a3 и b3 …, ar и br) называются совместимыми с друг другом, а если их количество отличающихся битов не больше единицы, то эти сигнатуры называются совпадающими.

И главная идея алгоритма HEngine — это подготовить базу данных таким образом, чтобы найти совпадающие сигнатуры и затем выбрать те строки, которые находятся в пределах требуемого расстояния Хэмминга.

Предварительная обработка базы данных

Нам уже известно, что если правильно поделить строку на подстроки, то, по крайней мере, одна подстрока совпадет с соответствующей подстрокой либо количество отличающихся битов не будет превышать единицу (сигнатуры совпадут).

Это означает, что нам не надо проводить полный перебор по всем строкам из базы данных, а требуется сначала найти те сигнатуры, которые совпадут, т.е. подстроки будут отличаться максимум на единицу.

Но как производить поиск по подстрокам?

Метод двоичного поиска должен неплохо с этим справляться. Но он требует, чтобы список строк был отсортирован. Но у нас получается несколько подстрок из одной строки. Что бы произвести двоичный поиск по списку подстрок, надо чтобы каждый такой список был отсортирован заранее.
Поэтому здесь напрашивается метод расширения базы данных, т. е. созданию нескольких таблиц, каждая для своей подстроки или сигнатуры. (Такая таблица называется таблицей сигнатур. А совокупность таких таблиц — набор сигнатур).

В оригинальной версии алгоритма еще описывается перестановка подстрок таким образом, чтобы выбранные подстроки были на первом месте. Это делается больше для удобства реализации и для дальнейших оптимизаций алгоритма:

Имеется строка A, которая делится на 3 подстроки, a1, a2, a3, полный список перестановок будет соответственно:
a1, a2, a3
a2, a1, a3
a3, a1, a2

Затем эти таблицы сигнатур сортируются.

Реализация поиска

На этом этапе, после предварительной обработки базы данных мы имеем несколько копий отсортированных таблиц, каждая для своей подстроки.

Очевидно, что если мы хотим сперва найти подстроки, необходимо из запрашиваемой строки получить сигнатуры тем же способом, который был использован при создании таблиц сигнатур.

Так же нам известно, что необходимые подстроки отличаются максимум на один элемент. И чтобы найти их потребуется воспользоваться методом расширения запроса (query expansion).

Другими словами требуется для выбранной подстроки сгенерировать все комбинации включая саму эту подстроку, при которых различие будет максимум на один элемент. Количество таких комбинаций будет равна длине подстроки + 1.

А дальше производить двоичный поиск в соответствующей таблице сигнатур на полное совпадение.

Такие действия надо произвести для всех подстрок и для всех таблиц.

И в самом конце потребуется отфильтровать те строки, которые не вмещаются в заданный предел расстояния Хэмминга. Т.е. произвести линейный поиск по найденным строкам и оставить только те строки, которые отвечают условию HD( a, b ) <= k.

Фильтр Блума

Авторы предлагают использовать фильтр Блума [7] для уменьшения количества двоичных поисков.
Фильтр Блума может быстро определить находится ли подстрока в таблице с небольшим процентом ложных срабатываний. Что работает быстрее, чем хеш таблицы.

Если перед двоичным поиском подстроки в таблице фильтр возвращает, что эта подстрока не находится в этой таблице, то нет смысла производить поиск.

Соответственно надо создать по одному фильтру на каждую таблицу сигнатур.

Авторы также отмечают, что использование фильтра Блума таким способом снижает время обработки запросов в среднем на 57.8%.

Теперь тоже самое, только на примере

Имеется база данных бинарных строк длиной 8 бит:
11111111
10000001
00111110

Задача найти все строки, где количество отличающихся битов не превышает 2 к целевой строке 10111111.
Значит требуемое расстояние k = 2.

1. Выбираем фактор сегментации.
Исходя из формулы, выбираем фактор сегментации r = 2 и значит всего будет две подстроки из одной строки.

2. Создаем набор сигнатур.
Так как количество подстрок 2, то требуется создать только 2 таблицы:
Т1 и Т2

3. Сохраняем подстроки в соответствующих таблицах с сохранением ссылки на первоисточник.

Т1 Т2
1111 1111 => 11111111
1000 0001 => 10000001
0011 1110 => 00111110

4. Сортируем таблицы. Каждую в отдельности.
Т1
0011 => 00111110
1000 => 10000001
1111 => 11111111

Т2
0001 => 10000001
1110 => 00111110
1111=> 11111111

На этом предварительная обработка закончена. И приступаем к поиску.

1. Получаем сигнатуры запрашиваемой строки.
Искомая строка 10111110 разбивается на сигнатуры. Получается 1011 и 1100, соответственно первая для первой таблицы, а вторая для второй.

2. Генерируем все комбинации отличающихся на единицу.
Количество вариантов будет 5.

2.1 Для первой подстроки 1011:
1011
0011
1111
1001
1010

2.2 Для второй подстроки 1100:
1100
0100
1000
1110
1101

3. Двоичный поиск.

3.1 Для всех сгенерированных вариантов первой подстроки 1011 производим двоичный поиск в первой таблице на полное совпадение.

1011
0011 == 0011 => 00111110
1111 == 1111 => 11111111
1001
1010

Найдено две подстроки.

3.2 Теперь для всех вариантов второй подстроки 1100 производим двоичный поиск во второй таблице.

1100
0100
1000
1110 == 1110 => 00111110
1101

Найдена одна подстрока.

4. Объедением результаты в один список:
00111110
11111111

5. Линейно проверяем на соответствие и отфильтровываем неподходящие по условию <= 2:

HD( 10111110, 00111110 ) = 1
HD( 10111110, 11111111 ) = 2

Обе строки удовлетворяют условию различия не больше двух элементов.

Хотя на данном этапе и производится линейный поиск, но ожидается, что список строк кандидатов будет совсем не велик.
При условиях, когда число кандидатов будет велико, то предлагается использовать рекурсивный вариант HEngine.

Наглядно

На рисунке №1 показан пример работы алгоритма поиска.
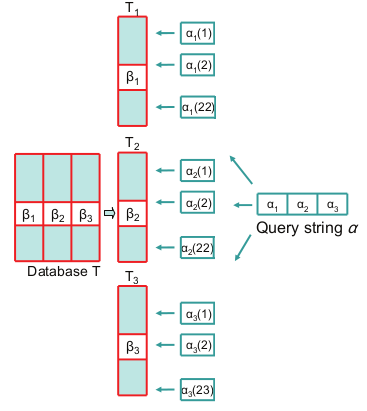
Для длины строки 64 и предел расстояния 4, фактор сегментации равен 3, соответственно только 3 подстроки на строку.
Где T1, T2 и Т3 — это таблицы сигнатур, содержащие только подстроки B1, B2, B3, длинной 21, 21 и 22 бита.

Запрашиваемая строка делится на подстроки. Далее для соответствующих подстрок генерируются диапазон сигнатур. Для первой и второй сигнатуры количество комбинаций будет 22. А последняя сигнатура дает 23 варианта. И вконце производится двоичный поиск.

Рис 1. Упращенная версия обработки запросов к таблицам сигнатур.

Результаты

Сложность подобного алгоритма в среднем случае O( P * ( log n + 1 ) ), где n — это общее число строк в базе данных, log n + 1 двоичный поиск, а P — количество двоичных поисков: считается, в нашем случае, как количество комбинаций на таблицу умнеженное на количество таблиц: P = ( 64 / r + 1 ) * r

В экстремальных случаях сложность может превышать линейную.

Отмечается, что такой подход использует в 4.65 меньше памяти и на 16 % быстрее, чем предыдущая работа описанная в [2]. И является самым быстрым способом из ныне известных, чтобы найти все строки в заданном пределе.

Реализация

Все это конечно заманчиво, но пока не потрогаешь на деле, тяжело оценить масштабы.
Был создан прототип HEngine [9] и протестирован на имеющихся реальных данных.

tests$ ./matches 7 data/db/table.txt data/query/face2.txt
Reading the dataset ........ done. 752420 db hashes and 343 query hashes.
Building with 7 hamming distance bound ....... done.

Building time: 12.964 seconds

Searching HEngine matches .......
found 100 total matches. HEngine query time: 0.1 seconds

Searching linear matches .......
found 100 total matches. Linear query time: 6.828 seconds

Результаты обрадовали, т. к. поиск 343 хешей из базы в 752420 занимает ~0.1 секунды, что в 60 раз быстрее линейного поиска.

Казалось бы тут можно было остановиться. Но уж больно хотелось попробовать это использовать как-то в реальном проекте.

В один клик до реального применения

Имеется база данных хешей изображений, и бекенд на PHP.
Задача стояла как-то связать функциональность HEngine и PHP.
Решено было использовать FastCGI [10], в этом мне сильно помогли посты habrahabr.ru/post/154187 и habrahabr.ru/post/61532.

Из PHP достаточно вызвать:

$list = file_get_contents( 'http://fcgi.local/?' . $hashes );

Что за ~0.5 секунды возвращает результат. Когда линейным поиском требуется 9 секунд, а через запросы к MySQL не меньше 20 секунд.

Спасибо всем, кто осилил.

Ссылки

[1] M. Minsky and S. Papert. Perceptrons. MIT Press, Cambridge, MA, 1969.
[2] G. S. Manku, A. Jain, and A. D. Sarma. Detecting nearduplicates for web crawling. In Proc. 16Th WWW, May 2007.
[3] M. L. Miller, M. A. Rodriguez, and I. J. Cox. Audio fingerprinting: Nearest neighbor search in high-dimensional binary space. In MMSP, 2002.
[4] M. L. Miller, M. A. Rodriguez, and I. J. Cox. Audio fingerprinting: nearest neighbor search in high dimensional binary spaces. Journal of VLSI Signal Processing, Springer, 41(3):285–291, 2005.
[5] J. Landr ́e and F. Truchetet. Image retrieval with binary hamming distance. In Proc. 2nd VISAPP, 2007.
[6] H. Yang and Y. Wang. A LBP-based face recognition method with hamming distance constraint. In Proc. Fourth ICIG, 2007.
[7] B. Bloom. Space/time trade-offs in hash coding with allowable errors. Communications of ACM, 13(7):422–426, 1970.
[8] Alex X. Liu, Ke Shen, Eric Torng. Large Scale Hamming Distance Query Processing. ICDE Conference, pages 553 — 564, 2011.
[9] github.com/valbok/HEngine Моя реализация HEngine на С++
[10] github.com/valbok/HEngine/blob/master/bin/fastcgi.cpp Пример программы обвертки для поиска хешей через FastCGI.

Источник

Расстояние Хэмминга — мера (точнее, метрика) различия объектов одинаковой размерности.

Первоначально метрика была сформулирована Ричардом Хэммингом во время его работы в Bell Labs для определения меры различия между кодовыми комбинациями (двоичными векторами) в векторном пространстве кодовых последовательностей, в этом случае расстоянием Хэмминга между двумя двоичными последовательностями (векторами) и длины называется число позиций, в которых они различны — в такой формулировке расстояние Хэмминга вошло в Словарь алгоритмов и структур данных Национального Института Стандартов США (англ. NIST Dictionary of Algorithms and Data Structures
).

Так, расстояние Хэмминга между векторами 00111 и 10101 равно 2 (красным отмечены различающиеся биты). В дальнейшем метрика была обобщена на q-ичные последовательности: для пары строк «выборы» и «забора» расстояние Хэмминга равно трём.

В общем виде расстояние Хэмминга ${displaystyle mathbf {d_{H}} }$ для объектов ${displaystyle mathbf {X_{i}} }$ и ${displaystyle mathbf {X_{j}} }$ размерности задаётся функцией:

${displaystyle d_{H}(X_{i},X_{j})=sum limits _{s=1}^{p}{rm {sign}}{left|{x_{i}^{(s)}-x_{j}^{(s)}}right|}.}$

Расстояние Хэмминга обладает свойствами метрики, удовлетворяя следующим условиям:

${displaystyle mathbf {d_{H}(X_{i},X_{j})geq 0} }$
${displaystyle mathbf {d_{H}(X_{i},X_{i})=0} }$
${displaystyle mathbf {d_{H}(X_{i},X_{j})=d_{H}(X_{j},X_{i})} }$
${displaystyle mathbf {d_{H}(X_{i},X_{k})leq d_{H}(X_{i},X_{j})+d_{H}(X_{j},X_{k})} }$

Расстояние Хэмминга в биоинформатике и геномике[]

Для нуклеиновых кислот (ДНК и РНК) возможность гибридизации двух полинуклеотидных цепей с образованием вторичной структуры — двойной спирали — зависит от степени комплементарности нуклеотидных последовательностей обеих цепей. При увеличении расстояния Хэмминга количество водородных связей, образованных комплементарными парами оснований уменьшается и, соответственно, уменьшается стабильность двойной цепи. Начиная с некоторого граничного расстояния Хэмминга гибридизация становится невозможной.дополнительно сказано об этом

При эволюционном расхождении гомологичных ДНК-последовательностей расстояние Хэмминга является мерой, по которой можно судить о времени, прошедшем с момента расхождения гомологов, например, о длительности эволюционного отрезка, разделяющего гены-гомологи и ген-предшественник.

Родственные методы[]

Расстояние Левенштейна

Литература[]

Richard W. Hamming. Error-detecting and error-correcting codes, Bell System Technical Journal 29(2):147-160, 1950.
Ричард Блейхут. Теория и практика кодов, контролирующих ошибки. М., «Мир», 1986

Ссылки[]

Ричард Хэмминг и начало теории кодирования // Виртуальный компьютерный музей

Источник

Определение:

Расстояние Хэмминга (англ. Hamming distance) — число позиций, в которых различаются соответствующие символы двух строк одинаковой длины.

В более общем случае расстояние Хэмминга применяется для строк одинаковой длины любых k-ичных алфавитов и служит метрикой различия (функцией, определяющей расстояние в метрическом пространстве) объектов одинаковой размерности.

Пример

d(1011101, 1001001)=2
d(1538124, 1523156)=4
d(hill, holl)=1

Свойства

Расстояние Хэмминга обладает свойствами метрики, так как удовлетворяет ее определению.

(Если расстояние от до равно нулю, то и совпадают ())
(Объект удален от объекта так же, как объект удален от объекта )
(Расстояние от до всегда меньше или равно расстоянию от до через точку . Это свойство обычно называют неравенством треугольника за его естественную геометрическую аналогию: сумма двух сторон треугольника всегда больше третьей стороны.)

Доказательство неравенства треугольника

Утверждение:

Пусть слова и отличаются в некоторых позициях. Тогда какое бы слово мы ни взяли, оно будет отличаться в каждой из этих позиций по крайне мере от одного из слов и . Следовательно, суммируя в правой части и , мы обязательно учтем все позиции, в которых различались слова и . Т.е. получается, что .

См. также

Избыточное кодирование, код Хэмминга

Источники информации

Расстояние Хэмминга — Википедия
Hamming distance — Wikipedia
Математические основы информатики

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 13 марта 2013;
проверки требуют 2 правки.

Расстояние Хэмминга — число позиций, в которых соответствующие символы двух слов одинаковой длины различны^[1]. В более общем случае расстояние Хэмминга применяется для строк одинаковой длины любых q-ичных алфавитов и служит метрикой различия (функцией, определяющей расстояние в метрическом пространстве) объектов одинаковой размерности.

Первоначально метрика была сформулирована Ричардом Хэммингом во время его работы в Bell Labs для определения меры различия между кодовыми комбинациями (двоичными векторами) в векторном пространстве кодовых последовательностей, в этом случае расстоянием Хэмминга d(x, y) между двумя двоичными последовательностями (векторами) и длины называется число позиций, в которых они различны — в такой формулировке расстояние Хэмминга вошло в словарь алгоритмов и структур данных национального института стандартов и технологий США (англ. NIST Dictionary of Algorithms and Data Structures). Расстояние Хэмминга является частным случаем метрики Минковского (при соответствующем определении вычитания):

$d_{ij} = sum_{k=1}^p left | x_{ik} - x_{jk} right |$ .

Примеры[править | править вики-текст]

Свойства[править | править вики-текст]

Расстояние Хэмминга обладает свойствами метрики, удовлетворяя следующим условиям:

Расстояние Хэмминга в биоинформатике и геномике[править | править вики-текст]

См. также[править | править вики-текст]

Расстояние Левенштейна
Обнаружение и исправление ошибок

Примечания[править | править вики-текст]

↑ Hamming distance: The number of digit positions in which the corresponding digits of two binary words of the same length are different (Federal Standard 1037C).

Литература[править | править вики-текст]

Блейхут Р. Теория и практика кодов, контролирующих ошибки = Theory and Practice of Error Control Codes. — М.: Мир, 1986. — 576 с.

Источник

Definition[edit]

Examples[edit]

Properties[edit]

Error detection and error correction[edit]

History and applications[edit]

Algorithm example[edit]

See also[edit]

References[edit]

Further reading[edit]

Подсчет расстояния Хэмминга на большом наборе данных

Введение

Описание проблемы

Описание алгоритма HEngine для статической задачи

Немного теории

Предварительная обработка базы данных

Реализация поиска

Фильтр Блума

Теперь тоже самое, только на примере

Наглядно

Результаты

Реализация

В один клик до реального применения

Ссылки

Расстояние Хэмминга в биоинформатике и геномике[]

Родственные методы[]

Литература[]

Ссылки[]

Пример

Свойства

Доказательство неравенства треугольника

См. также

Источники информации

Примеры[править | править вики-текст]

Свойства[править | править вики-текст]

Расстояние Хэмминга в биоинформатике и геномике[править | править вики-текст]

См. также[править | править вики-текст]

Примечания[править | править вики-текст]

Литература[править | править вики-текст]