Как найти расстояние мед

Расстояние между двумя параллельными прямыми в пространстве

Для лучшего понимания темы рассмотрим основные понятия, термины и теоремы, связанные с параллельными прямыми.

Базовые понятия и теоремы

Расстоянием есть такая величина, которая характеризует отдаленность объектов друг от друга. Это определение применимо для плоскости и для пространства. Зачастую расстояние измеряют при помощи различных измерительных приборов, таких как линейка, штангенциркуль и прочих. При передвижении на машине расстояние вычисляют с помощью спидометра. На больших расстояниях применяют различные вычисления для определения величины расстояния.

Две прямые являются параллельными в трехмерном пространстве только в том случае, если они находятся в одной плоскости и не пересекаются. Это значит, что параллельность прямых определяется двумя критериями:

• они должны находиться в одной плоскости;
• они не имеют ни одной совместной точки.

Но не нужно путать параллельные прямые со скрещивающимися, они тоже никогда не пересекаются и не имеют общих точек, но их невозможно расположить в одной плоскости.

Сложно разобраться самому?

Попробуй обратиться за помощью к преподавателям

Если рассмотреть примеры из жизни, то параллельные прямые мы можем наблюдать как противоположные края у прямоугольного или квадратного стола, железнодорожные рельсы и шпалы, провода линий электропередач, линии в тетради в полоску и прочие. Таких примеров из реального мира можно привести очень много.

Расстоянием между параллельными прямыми является перпендикулярный отрезок между этими прямыми. Он может быть проведен в любом месте между ними и везде будет одинаковым. Рассмотрим доказательство этой теоремы.

Доказательство теоремы про расстояние между параллельными прямыми

Изобразим две параллельные прямые (l) и (k) . Возьмем две случайные точки на прямой (l) , назовем их например (X) и (Y) , опустим с них перпендикуляры на прямую (k) . Совершенно не имеет значения какие именно мы возьмем точки, главное, чтобы они не совпадали, то есть между ними должно быть некоторое расстояние.

Назовем точки пересечения прямой k с перпендикулярами (A) и (B) .

Проведем отрезок (XB) , который является гипотенузой прямоугольника (XYBA) получившиеся углы (XBA) и (BXY) , находящиеся накрест друг от друга, будут равны. гипотенуза (XB) пересекает данные прямые.

Рассмотрим треугольники (XBA) и (BXY) , определим их общие элементы:

• они имеют общую сторону (XB) ;
• стороны треугольников (XY) и (AB) имеют одинаковую длину;
• величина углов (XBA) и (BXY) одинаковая, и данные углы образованы равными между собой сторонами.

Все вышесказанное указывает на то, что треугольники (XBA) и (BXY) равны, согласно первому признаку равенства треугольников, соответственно, перпендикуляры (AX) и (BY) тоже равны.

Это соотношение будет справедливым при любых случайных точках (X) и (Y) , это значит, что величины перпендикуляров между двумя параллельными прямыми, опущенных в любом месте, будут иметь одинаковое значение.

Доказательство этой теоремы справедливо как для планиметрии, так и для 3D-пространства, так как две параллельные прямые в любом случае образуют плоскость.

Примеры определения расстояния между параллельными прямыми

Рассмотрим задачу на определение расстояния меду параллельными прямыми в пространстве.

Задача 1 . Даны две параллельные прямы (l) и (k) . Определить расстояние между ними.

Решение : Согласно вышеизложенной теоремы, расстоянием между двумя параллельными прямыми является величина перпендикуляра между ними. Выберем произвольную точку на одной из прямых и опустим с нее перпендикуляр на другую прямую. длина этого перпендикулярного отрезка и будет решением этой задачи.

Практически не всегда удобно графически решать данные задачи, так как не всегда есть возможность выполнить рисунок в масштабе 1:1, поэтому их решают аналитическим путем, используя специальные уравнения.

Не нашли что искали?

Просто напиши и мы поможем

Выше мы рассматривали, что не имеет значения с какой именно точки опущен перпендикуляр, ведь все они равны между собой, поэтому решение задачи сводится, по сути, к определению расстояния между точкой, расположенной на одной из прямых, и второй прямой.

Значит, уравнение определения расстояния между прямыми (l) и (k) имеет следующий вид:

где (x_1, y_1, z_1) – координаты вектора нормали прямой (l) ;
(x_2, y_2, z_2) – координаты вектора нормали прямой (k) ;
( l, m_1, n_1) – координаты направляющего вектора прямой (l) .

Рассмотрим пример решения задачи с использованием данного уравнения.

Задача 2 . При заданных уравнениях двух параллельных прямых, что не совпадают, определить расстояние между ними.

Решение: Определим из уравнения координаты вектора нормали к прямой (l) <-1;2;-4>, к прямой (k) <3;-1;2>. Координатами направляющего вектора для прямой (l) будут <1;3;5>. Значит уравнение примет вид:

Для кого-то этот способ покажется сложным, а для кого-то простым. Всего лишь нужно уметь решать выражения матричного вида.

Рассмотрим еще один способ решения подобной задачи. Это способ алгоритма с векторным произведением.

Задача 3 . Определить расстояние между параллельными прямыми способом векторного произведения. Уравнения прямых заданы в задаче 2.

Решение : Применим формулу векторного произведения:

где (M_0 M_1) – вектор, который соединяет две случайные точки на параллельных прямых.

Вектора нормали для прямой (l) <-1;2;-4>и для прямой (k) <3;-1;2>. Координатами направляющего вектора для обоих прямых будут s=<1;3;5>, так как вектор нормали у них совпадает.

Определим разность между направляющими векторами, она и будет являться координатами вектора

Рассчитаем векторное произведение:

Теперь рассчитаем длину направляющего вектора:
(|s ̅ |= pm sqrt <1^2+3^2+5^2 >=5,916)

В итого расстояние между заданными прямыми будет равняться:
(ρ= <38,859over5,916>=6,568)

То есть мы получили по сути тот же ответ, значит оба решения правильные и могут применяться для решения задач на определение расстояния между двумя параллельными прямыми.

Не нашли нужную информацию?

Закажите подходящий материал на нашем сервисе. Разместите задание – система его автоматически разошлет в течение 59 секунд. Выберите подходящего эксперта, и он избавит вас от хлопот с учёбой.

Гарантия низких цен

Все работы выполняются без посредников, поэтому цены вас приятно удивят.

Доработки и консультации включены в стоимость

В рамках задания они бесплатны и выполняются в оговоренные сроки.

Вернем деньги за невыполненное задание

Если эксперт не справился – гарантируем 100% возврат средств.

Тех.поддержка 7 дней в неделю

Наши менеджеры работают в выходные и праздники, чтобы оперативно отвечать на ваши вопросы.

Тысячи проверенных экспертов

Мы отбираем только надёжных исполнителей – профессионалов в своей области. Все они имеют высшее образование с оценками в дипломе «хорошо» и «отлично».

Гарантия возврата денег

Эксперт получил деньги, а работу не выполнил?
Только не у нас!

Деньги хранятся на вашем балансе во время работы над заданием и гарантийного срока

Гарантия возврата денег

В случае, если что-то пойдет не так, мы гарантируем возврат полной уплаченой суммы

Отзывы студентов о нашей работе

«Всё сдал!» — безопасный онлайн-сервис с проверенными экспертами

Используя «Всё сдал!», вы принимаете пользовательское соглашение
и политику обработки персональных данных
Сайт работает по московскому времени:

Принимаем к оплате

Расстояние между двумя параллельными прямыми: определение и примеры нахождения

В материале этой статьи разберем вопрос нахождения расстояния между двумя параллельными прямыми, в частности, при помощи метода координат. Разбор типовых примеров поможет закрепить полученные теоретические знания.

Расстояние между двумя параллельными прямыми: определение

Расстояние между двумя параллельными прямыми – это расстояние от некоторой произвольной точки одной из параллельных прямых до другой прямой.

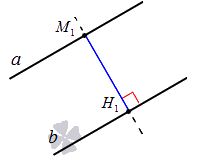
Приведем иллюстрацию для наглядности:

На чертеже изображены две параллельные прямые a и b . Точка М 1 принадлежит прямой a , из нее опущен перпендикуляр на прямую b . Полученный отрезок М 1 Н 1 и есть расстояние между двумя параллельными прямыми a и b .

Указанное определение расстояния между двумя параллельными прямыми справедливо как на плоскости, так и для прямых в трехмерном пространстве. Кроме того, данное определение взаимосвязано со следующей теоремой.

Когда две прямые параллельны, все точки одной из них равноудалены от другой прямой.

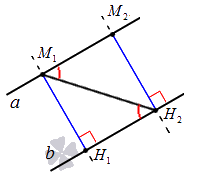
Пусть нам заданы две параллельные прямые a и b . Зададим на прямой а точки М 1 и М 2 , опустим из них перпендикуляры на прямую b , обозначив их основания соответственно как Н 1 и Н 2 . М 1 Н 1 – это расстояние между двумя параллельными прямыми по определению, и нам необходимо доказать, что | М 1 Н 1 | = | М 2 Н 2 | .

Пусть будет также существовать некоторая секущая, которая пересекает две заданные параллельные прямые. Условие параллельности прямых, рассмотренное в соответствующей статье, дает нам право утверждать, что в данном случае внутренние накрест лежащие углы, образованные при пересечении секущей заданных прямых, являются равными: ∠ M 2 M 1 H 2 = ∠ H 1 H 2 M 1 . Прямая М 2 Н 2 перпендикулярна прямой b по построению, и, конечно, перпендикулярна прямой a . Получившиеся треугольники М 1 Н 1 Н 2 и М 2 М 1 Н 2 являются прямоугольными и равными друг другу по гипотенузе и острому углу: М 1 Н 2 – общая гипотенуза, ∠ M 2 M 1 H 2 = ∠ H 1 H 2 M 1 . Опираясь на равенство треугольников, мы можем говорить о равенстве их сторон, т.е.: | М 1 Н 1 | = | М 2 Н 2 | . Теорема доказана.

Отметим, что расстояние между двумя параллельными прямыми – наименьшее из расстояний от точек одной прямой до точек другой.

Нахождение расстояния между параллельными прямыми

Мы уже выяснили, что, по сути, чтобы найти расстояние между двумя параллельными прямыми, необходимо определить длину перпендикуляра, опущенного из некой точки одной прямой на другую. Способов, как это сделать, несколько. В каких-то задачах удобно воспользоваться теоремой Пифагора; другие предполагают использование признаков равенства или подобия треугольников и т.п. В случаях, когда прямые заданы в прямоугольной системе координат, возможно вычислить расстояние между двумя параллельными прямыми, используя метод координат. Рассмотрим его подробнее.

Зададим условия. Допустим, зафиксирована прямоугольная система координат, в которой заданы две параллельные прямые a и b . Необходимо определить расстояние между заданными прямыми.

Решение задачи построим на определении расстояния между параллельными прямыми: для нахождения расстояния между двумя заданными параллельными прямыми необходимо:

— найти координаты некоторой точки М 1 , принадлежащей одной из заданных прямых;

— произвести вычисление расстояния от точки М 1 до заданной прямой, которой эта точка не принадлежит.

Опираясь на навыки работы с уравнениями прямой на плоскости или в пространстве, определить координаты точки М 1 просто. При нахождении расстояния от точки М 1 до прямой пригодится материал статьи о нахождении расстояния от точки до прямой.

Вернемся к примеру. Пусть прямая a описывается общим уравнением A x + B y + C 1 = 0 , а прямая b – уравнением A x + B y + C 2 = 0 . Тогда расстояние между двумя заданными параллельными прямыми возможно вычислить, используя формулу:

M 1 H 1 = C 2 — C 1 A 2 + B 2

Выведем эту формулу.

Используем некоторую точку М 1 ( x 1 , y 1 ) , принадлежащую прямой a . В таком случае координаты точки М 1 будут удовлетворять уравнению A x 1 + B y 1 + C 1 = 0 . Таким образом, справедливым является равенство: A x 1 + B y 1 + C 1 = 0 ; из него получим: A x 1 + B y 1 = — C 1 .

Когда С 2 0 , нормальное уравнение прямой b будет иметь вид:

A A 2 + B 2 x + B A 2 + B 2 y + C 2 A 2 + B 2 = 0

При С 2 ≥ 0 нормальное уравнение прямой b будет выглядеть так:

A A 2 + B 2 x + B A 2 + B 2 y — C 2 A 2 + B 2 = 0

И тогда для случаев, когда С 2 0 , применима формула: M 1 H 1 = A A 2 + B 2 x 1 + B A 2 + B 2 y 1 + C 2 A 2 + B 2 .

А для С 2 ≥ 0 искомое расстояние определяется по формуле M 1 H 1 = — A A 2 + B 2 x 1 — B A 2 + B 2 y 1 — C 2 A 2 + B 2 = = A A 2 + B 2 x 1 + B A 2 + B 2 y 1 + C 2 A 2 + B 2

Таким образом, при любом значении числа С 2 длина отрезка | М 1 Н 1 | (от точки М 1 до прямой b ) вычисляется по формуле: M 1 H 1 = A A 2 + B 2 x 1 + B A 2 + B 2 y 1 + C 2 A 2 + B 2

Выше мы получили: A x 1 + B y 1 = — C 1 , тогда можем преобразовать формулу: M 1 H 1 = — C 1 A 2 + B 2 + C 2 A 2 + B 2 = C 2 — C 1 A 2 + B 2 . Так мы, собственно, получили формулу, указанную в алгоритме метода координат.

Разберем теорию на примерах.

Заданы две параллельные прямые y = 2 3 x — 1 и x = 4 + 3 · λ y = — 5 + 2 · λ . Необходимо определить расстояние между ними.

Решение

Исходные параметрические уравнения дают возможность задать координаты точки, через которую проходит прямая, описываемая параметрическими уравнениями. Таким образом, получаем точку М 1 ( 4 , — 5 ) . Требуемое расстояние – это расстояние между точкой М 1 ( 4 , — 5 ) до прямой y = 2 3 x — 1 , произведем его вычисление.

Заданное уравнение прямой с угловым коэффициентом y = 2 3 x — 1 преобразуем в нормальное уравнение прямой. С этой целью сначала осуществим переход к общему уравнению прямой:

y = 2 3 x — 1 ⇔ 2 3 x — y — 1 = 0 ⇔ 2 x — 3 y — 3 = 0

Вычислим нормирующий множитель: 1 2 2 + ( — 3 ) 2 = 1 13 . Умножим на него обе части последнего уравнения и, наконец, получим возможность записать нормальное уравнение прямой: 1 13 · 2 x — 3 y — 3 = 1 13 · 0 ⇔ 2 13 x — 3 13 y — 3 13 = 0 .

При x = 4 , а y = — 5 вычислим искомое расстояние как модуль значения крайнего равенства:

2 13 · 4 — 3 13 · — 5 — 3 13 = 20 13

Ответ: 20 13 .

В фиксированной прямоугольной системе координат O x y заданы две параллельные прямые, определяемые уравнениями x — 3 = 0 и x + 5 0 = y — 1 1 . Необходимо найти расстояние между заданными параллельными прямыми.

Решение

Условиями задачи определено одно общее уравнение, задаваемое одну из исходных прямых: x-3=0. Преобразуем исходное каноническое уравнение в общее: x + 5 0 = y — 1 1 ⇔ x + 5 = 0 . При переменной x коэффициенты в обоих уравнениях равны (также равны и при y – нулю), а потому имеем возможность применить формулу для нахождения расстояния между параллельными прямыми:

M 1 H 1 = C 2 — C 1 A 2 + B 2 = 5 — ( — 3 ) 1 2 + 0 2 = 8

Ответ: 8 .

Напоследок рассмотрим задачу на нахождение расстояния между двумя параллельными прямыми в трехмерном пространстве.

В прямоугольной системе координат O x y z заданы две параллельные прямые, описываемые каноническими уравнениями прямой в пространстве: x — 3 1 = y — 1 = z + 2 4 и x + 5 1 = y — 1 — 1 = z — 2 4 . Необходимо найти расстояние между этими прямыми.

Решение

Из уравнения x — 3 1 = y — 1 = z + 2 4 легко определются координаты точки, через которую проходит прямая, описываемая этим уравнением: М 1 ( 3 , 0 , — 2 ) . Произведем вычисление расстояния | М 1 Н 1 | от точки М 1 до прямой x + 5 1 = y — 1 — 1 = z — 2 4 .

Прямая x + 5 1 = y — 1 — 1 = z — 2 4 проходит через точку М 2 ( — 5 , 1 , 2 ) . Запишем направляющий вектор прямой x + 5 1 = y — 1 — 1 = z — 2 4 как b → с координатами ( 1 , — 1 , 4 ) . Определим координаты вектора M 2 M → :

M 2 M 1 → = 3 — ( — 5 , 0 — 1 , — 2 — 2 ) ⇔ M 2 M 1 → = 8 , — 1 , — 4

Вычислим векторное произведение векторов :

b → × M 2 M 1 → = i → j → k → 1 — 1 4 8 — 1 — 4 = 8 · i → + 36 · j → + 7 · k → ⇒ b → × M 2 M 1 → = ( 8 , 36 , 7 )

Применим формулу расчета расстояния от точки до прямой в пространстве:

M 1 H 1 = b → × M 2 M 1 → b → = 8 2 + 36 2 + 7 2 1 2 + ( — 1 ) 2 + 4 2 = 1409 3 2

Расскажите, как найти расстояние между двумя параллельными прямыми. Начертите две параллельные прямые, расстояние между которыми равно 4 см.

Ваш ответ

решение вопроса

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,652
• разное 16,822

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.