Как найти расстояние между двумя линиями

Очень часто на практике необходимо найти расстояние между точкой и некой прямой линией или между двумя прямыми линиями в пространстве, например, иногда определять расстояние между двумя линиями приходится и в реальной жизни. Хорошая иллюстрация такого примера — это знак, который вешают на мосты для грузовиков, указывающий максимальную высоту грузовика, которая может проехать под данным мостом.

Расстояние от верхней грани грузовика и нижней грани в данном случае определяют как расстояние между двумя прямыми.

Расстояние между 2 прямыми в пространстве — это отрезок, соединяющий две прямые линии по наикратчайшему расстоянию между ними, то есть перпендикулярный к обеим прямым.

Чтобы было чуть проще понять, что это такое, давайте повторим определение скрещивающихся прямых:

Соответственно, для того чтобы найти расстояние между скрещивающимися прямыми в пространстве, необходимо от одной из прямых опустить перпендикуляр на плоскость, в которой лежит другая прямая.

Расстояние же между двумя параллельными прямыми в пространстве является одинаковым на протяжении всей длины параллельных прямых, то есть перпендикуляр, опущенный из одной параллельной прямой на другую, всегда будет одной и той же длины вне зависимости от того, из какой именно точки его опустили.

Метод координат для определения расстояния между скрещивающимися прямыми

Расстояние между скрещивающимися прямыми в пространстве можно найти используя метод координат, для этого необходимо:

«Расстояние между 2 прямыми в пространстве» 👇

1. Найти координаты точек $M_1$ и $M_2$, лежащих на прямых $a$ и $b$ соответственно.
2. Вычислить икс, игрек и зет направляющих векторов для прямых $a$ и $b$.
3. С помощью векторного произведения векторов $overline{a}$ и $overline{b}$ нужно найти вектор-нормаль для плоскости, в которой лежит прямая $b$. Затем необходимо записать общее уравнение плоскости: $A (x – x_0) + B(y – y_0) + C(z – z_0) = 0$, и от него перейти к нормированному виду уравнения плоскости следующего вида: $ x cdot cos α + y cdot cos β + z cdot cos{γ} – p = 0$, где $cos α, cos β$ и $cos γ$ — координаты единичного нормального вектора плоскости, а $p$ — свободный член, это число равно расстоянию от точки начала координат до плоскости.
4. Для вычисления расстояния от точки $M$ до искомой плоскости, нужно воспользоваться следующим уравнением:
   $M_1H_1 = |x_1 cdot cos α + y_1 cdot cos β + z_1 cdot cos{γ} – p|$, где $x_1, y_1, z_1$ – координаты точки $M_1$, лежащей на прямой $a$, а $H_1$ — точка, лежащая на искомой плоскости.

Here is a working translation using SymPy to calculate the distance as suggested by @user287699 (but the answer here agrees with wolframalpha.com):

def separation(l1, l2):
    """return separation of two skew lines

    Examples
    ========

    >>> from sympy import Line
    >>> a, b, c, d = (0, 0, 0), (1, 2, 3), (1, 1, 1), (2, 3, 5)
    >>> separation(Line(a, b), Line(c, d))
    sqrt(5)/5
    >>> a, b, c, d = (-1, 1, 4), (1, 1, -1), (5, 3, -3), (-2, 0, 1)
    >>> separation(Line(a, b), Line(c, d))
    sqrt(110)/55
    """
    from sympy import Matrix, Point
    n = Matrix(l1.direction.unit).cross(Matrix(l2.direction.unit))
    ps = l2.p1 - l1.p1
    return n.dot(ps)/Point(0,0,0).distance(n)

Цель
работы:
найти расстояние между двумя фигурами
на плоскости, используя оптимизационный
подход и метод неопределенных множителей
Лагранжа. Для компьютерного получения
решения и его визуализации использовать
пакет MAPLE.

1. Теоретические сведения

1. Метод
   множителей Лагранжа

Стандартная
условно-экстремальная задача формулируется
следующим образом:

найти
минимум функции (критерия) J
=
f(x₁,
…,
x_n)
при наличии ограничений

g₁(x₁,
…,
x_n)
= 0,
…, g_m(x1,
…,
x_n)
= 0,

или
коротко

Основной
аналитический метод решения связан с
введением вектора множителей Лагранжа



и построением составного критерия
(функции
Лагранжа)

L
= f(X)
+ 
g(X)

min

или
в более подробной записи

Экстремум
этой функции ищется обычным образом
путем взятия производных и приравнивания
их нулю. Тем самым исходная
условно-экстремальная задача сводится
к задаче отыскания безусловного
экстремума.

Пример
1. Вписанный прямоугольник максимального
периметра.

Эллипс
задан своим каноническим уравнением

Требуется среди всех вписанных в него
прямоугольников (рис. 1) найти прямоугольник
с максимальным периметром.

y

b

y

x

x

a

2x

2y

Рисунок
1

Решение.
Формализуем задачу, выписав критерий
и ограничения:

J
= 4x
+ 4y

max;

,
x,
y

0.

Строим
составной критерий (функцию Лагранжа):

Приравниваем
нулю производные по
x
и
y:

откуда
x
=
2a²
/ ,
y
=
2b²
/ ,
x
/y
= a²
/ b²,

Таким
образом,
стороны прямоугольника с максимальным
периметром относятся как квадраты
полуосей эллипса. Подставляя эти значения
в уравнение эллипса, находим, что ²
= 4а²
+ 4b².
Окончательно имеем

П
ример
2. Расстояние
между окружностью и параболой.

Пусть
требуется найти расстояние между
окружностью

и параболой

Решение.
Изобразим окружность и параболу на
плоскости (рис. 2). Задача сводится к
отысканию точки P₁
с координатами (x₁,
y₁),
принадлежащей окружности, и точки P₂
с координатами

(x₂,
y₂),
принадлежащей параболе, таких, чтобы
расстояние между ними

было минимальным. Для облегчения
дальнейших вычислений расстояние d
можно заменить его квадратом. Выписываем
критерий и ограничения:

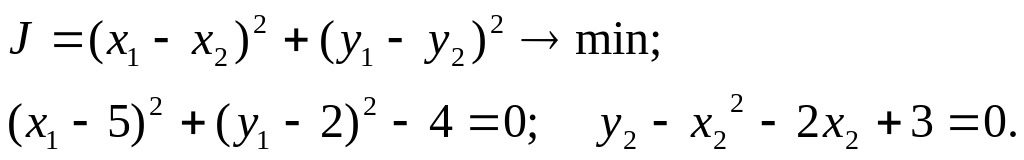
Строим
функцию Лагранжа:

Решение
задачи теперь сводится к отысканию
минимума функции от шести переменных
x₁,
x₂,
y₁,
y₂,
λ₁,
λ₂.
Это можно сделать, приравняв соответствующие
шесть производных нулю:

Заметим,
что два последних уравнения – это просто
описание исходных кривых.

Данная
ыимееи три различных решения. Геометрически
им соответствуют три прямые, показанные
на рис. 3. Все они проходят через центр
окружности и пересекают одну из ветвей
параболы под прямым углом. Заметим, что
ортогональность
кратчайшего отрезка, соединяющего две
кривые, каждой из них – общее свойство
задач о минимальном расстоянии.

Отбрасывая
лишние решения, находим, что минимальное
расстояние между кривыми равно

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

ОДНА
ЗАДАЧА ВАРИАЦИОННОГО АНАЛИЗА, связанная с нахождением кратчайшего расстояния
между кривыми

Постановка
задачи.

Указание.

Теорема.

Доказательство.

Резюме.

Авторы

Манасян Сергей Керопович,
доктор технических наук, профессор, член-корреспондент РАЕ

Красноярский
техникум социальных технологий

КГБПОУ
«КТСТ», преподаватель

Ассоциация
научных сотрудников «СибАК», рецензент

Черняева Ольга, магистрант

Санкт-Петербургский
горный университет, выпускник

Санкт-Петербургский
государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова
(Ленина), магистрант

СПбГЭТУ
«Ленинградский электротехнический институт»

Красноярск
– Санкт-Петербург

2021

ОДНА
ЗАДАЧА ВАРИАЦИОННОГО АНАЛИЗА, связанная с нахождением кратчайшего расстояния
между кривыми

       Имеем две кривые .

Постановка задачи.
Пусть функции  – непрерывные и непрерывно
дифференцируемые. Требуется найти кратчайшее расстояние между ними.

Указание.
Решите задачу разными способами. Для решения используйте методы оптимизации и
вариационный анализ, школьный курс алгебры, понятие производной, уравнение
касательной к графику функции, элементы аналитической геометрии, нормальный
вектор к кривой в точке, нормаль к прямой, расстояние между прямыми, длина дуги
по кривой. Задача сводится к нахождению минимального расстояния между двумя
точками, одна из которых лежит на кривой  а другая – на кривой

Пример.

        
 — ?             (1)

Решение.
1 способ

 ;            (2)

                                                                                               
(3)                 

                 
                 (4)

Ответ:
d(f1,f2)=1,75.

Решение.
2 способ

                          
d=min |f|
= min |-x²-1-x-1|=min
|x**2+x+2|,                          
(5)

                           
                       (6)                            

          (7)

Решение.
3 способ

                           
 , min J(y)=,                        
(8)

где y – экстремальная кривая (точнее, это – экстремаль, и она является
стационарной кривой, – причем понятие стационарной кривой является более общим
по сравнению с понятием «экстремальная кривая»); точка  принадлежит
первой кривой f₁(x), 
точка  – второй кривой f₂(x).

       Пояснение. Подынтегральная
функция зависит только от производной функции, поэтому экстремальная кривая
(экстремаль функционала J(y))
имеет вид:

.

       Возможные
ориентации касательных к экстремали (эта кривая является аналогом «стационарной
точки», если бы J(y)
был не целевым функционалом, т.е. функцией от функции, а целевой функцией) в точках ее пересечения с граничной кривой определяются условием
трансверсальности:

                        
+(—=0.                      
(9)

а)
Применим условие трансверсальности для кривой  в точке  :

= 0.                
(10)

.                                               
(11)

b)
Применим условие трансверсальности для кривой  в точке  :

= 0.                
(10)

.                                                  (11)

c)
Совместим условие трансверсальности для кривой  с экстремалью в точке  :

                .                            (12)

 = 0.                
                                                      (13)

d) Совместим
условие трансверсальности для кривой  с экстремалью в точке  :

                     .                            (14)

 = 0.               
                                                                                            (15)

Выражение (15) принимает вид:

            В результате получаем систему из 4
уравнений с 4 неизвестными:

                                 
                           (16)

;

                                 
                            (17)

.

            Решение системы (16-17)
имеет вид:

 (из уравнения (17)),                                                                   
                           (18)

 (подставляя (18) в (16),     )                                      (19)                                                                                  

 ,                                                     
                   (20)

 (,                                                                            (21)

Решение. 4 способ

Пусть искомые точки, доставляющие минимум целевой функции
«расстояние между кривыми 1 и 2, есть точки М1 и М2, соответственно на кривой 1
и на кривой 2:

         Целевая
функция – евклдово расстояние между М1 и М2, равное длине отрезка М1М2:

 ® min.                             
(22)

         Ограничения
– принадлежность точки М1 кривой f1 и
точки М2 кривой М2:

                                       
                                  
(23)                              

                                                                                                     
(24)

         Составляем
функцию Лагранжа:

L(                                                        
(25)

         Cоставляем систему 6 уравнений
из 6 неизвестных:

Решая данную систему, получим
ответ: D=7/4.

Другие способы решения данной
задачи Вы можете предложить сами.