Фрагмент физической карты Карелии
Для того, чтобы определить расстояние между двумя точками (пунктами, местами) используя физическую карту, можно воспользоваться простым способом: взять циркуль (им лучше, потому что он чётко фиксирует интервал) и затем с помощью линейки узнать, сколько это будет в сантиметрах.
Если линия криволинейная (например, морское побережье), можно воспользоваться курвиметром — специальным приспособлением с колёсиком, «считывающим» дистанцию.
После этого, соотносим получившееся значение с масштабом карты и пересчитываем см (мм) в километры.
Например, если масштаб 1:500000, это значит, что в 1 см — 5 км, и именно на это число нужно умножать.
Конечно, есть ряд составляющих погрешности даже при мелком масштабе карты, но тем не менее, полученное расстояние всё же будет относительно точным.
Таким образом, занимательная физическая карта, с отображёнными на ней континентами, горами, морями, реками…, позволяет не только увидеть многообразие и красоту нашей Земли, хоть и на бумаге, но и «дотянуться» до них из своего места
Примеры решения задач
Формулы для нахождения скорости, времени и расстояния
Условные обозначения
V – скорость (см/сек, м/мин, км/час);
S – расстояние (мм, см, м, км);
t – время (сек, мин, час).
Формула нахождения скорости
V = S : t
Формула нахождения расстояния
S = V · t
Формула нахождения времени
t = S : V
Задача №1
Из двух городов одновременно навстречу друг другу выехали два автомобиля. Встретились они через 3 часа, причём первый автомобиль проехал на 45 км меньше второго. Узнай расстояние между городами, если известно, что второй автомобиль ехал со скоростью 90 км/ч.
Решение:
В первом действии узнаем пройденный путь авто II, для этого применим формулу: S = V · t. Запишем формулу в удобной для решения задачи форме: V · t = S
1) 90 · 3 = 270 (км)
Из условия задачи известно, что за 3 часа авто I проехал на 45 км меньше чем авто II, тогда всего он проехал
2) 270 — 45 = 225 (км)
В третьем действии задачи сложив путь авто II и авто I получаем расстояние между городами
3) 270 + 225 = 495 (км)Ответ: расстояние между городами 495 километров.
Задача №2
Из двух посёлков одновременно навстречу друг другу выехали на велосипедах два спортсмена и встретились через 2 часа. Узнай расстояние между городами, если известно, что первый велосипедист проехал на 6 километров меньше второго, а второй велосипедист ехал со скоростью 12 км/ч.
Решение:
В первом действии узнаем какое расстояние преодолел второй спортсмен
1) 12 · 2 = 24 (км)
Из условия задачи известно, что за 2 часа первый спортсмен проехал на 6 км меньше чем второй спортсмен, тогда всего он проехал
2) 24 — 6 = 18 (км)
В третьем действии сложим пройденный путь обеих спортсменов чтобы узнать расстояние между городами
3) 24 + 18 = 42 (км)Ответ: расстояние между городами 42 километра.
Коротко:
Известные и великие математики
ученые древности, средневековья и современности, и их вклад
в мировую науку
Виктор Буняковский
Русский математик, педагог, историк математики, вице-президент академии наук
Дата рождения: 15 декабря 1804 г.
Место рождения: Бар, Подольская губерния, Российская империя
Дата смерти: 12 декабря 1889 г. (84 года), Санкт-Петербург
Биография
Родился 15 декабря 1804 года в Баре Подольской губернии. Его отец служил в Баре подполковником конно-польского уланского полка и погиб в 1809 году в Финляндии.
Первоначальное образование получил в Москве, в доме друга его отца графа А. П. Тормасова. В 1820 году Буняковский, вместе с сыном графа, отправился за границу, где изучал преимущественно математические науки. Сначала он жил в Кобурге и брал там частные уроки, затем слушал лекции в Лозаннской академии. В течение двух последних лет проживания за границей он жил в Париже, где слушал лекции в Сорбонне. Он имел возможность заниматься у Лапласа, Пуассона, Фурье, Коши, Ампера, Лежандра и других знаменитых учёных. Больше всего Буняковский работал у Коши.
В 1824 году Буняковский получил степени бакалавра и лиценциата, а в 1825 году защитил диссертацию, состоявшую из двух работ: по аналитической механике и математической физике получив от Парижского университета степень доктора математических наук. Пробыв за границей в общей сложности семь лет, Буняковский в 1826 году приехал в Петербург, где занялся педагогической деятельностью.
Все работы Буняковского, ставящие его в число величайших европейских математиков, помимо ценности в научном отношении — по богатству, новизне и оригинальной разработке научно-математических материалов, — отличаются замечательной ясностью и изяществом изложения.
С 1826 по 1831 год состоял преподавателем математики в старших классах в Первом кадетском корпусе. Оставив эту должность в 1831 году, Буняковский принимал участие в различных комиссиях по составлению программы и конспектов для военно-учебных заведений, по экзаменам учителей и по рассмотрению учебных руководств. В течение десяти лет был наставником-наблюдателем в Пажеском корпусе.
С 1846 года в Императорском Санкт-Петербургском университете читал курс аналитической механики (по Пуассону и Остроградскому), затем — дифференциальное и интегральное исчисление (по Коши) и теорию вероятностей (по собственному оригинальному сочинению), а позднее, уже в пятидесятых годах, — интегрирование дифференциальных уравнений, способ вариаций и исчисление конечных разностей. В 1859 году, желая сосредоточиться исключительно на научной работе, Буняковский оставил службу в университете.
При богатстве и глубине содержания, лекции Буняковского всегда отличались поразительной ясностью, увлекательностью и в то же время литературной красотой изложения, делали легко доступными самые сложные математические положения и увлекали даже безучастных слушателей. По отношениям к лекциям Буняковский проявлял замечательную аккуратность и в течение всего времени своей службы в университете не пропустил ни одной лекции и не опоздал ни разу.
Как человек, Буняковский отличался высокими нравственными качествами, и уважение, которым он пользовался, имело причины не только его громкой славы великого учёного, но и в личных достоинствах. Одарённый чувством изящного, Буняковский в молодости увлекался поэзией Байрона, перевёл отрывок из «Чайльд — Гарольда», и несколько стихотворений помещённых им в журналах сороковых годов.
Умер в Санкт-Петербурге 12 декабря 1889 года. Похоронен на Смоленском кладбище в Санкт-Петербурге
Изобрёл:
- планиметр
- пантограф
- прибор для измерения квадратов
- самосчёты Буняковского — вычислительный механизм основанный на принципе действия русских счётов. Аппарат предназначался для сложения большого числа двузначных чисел. Прибор удобен исключительно для сложения большого количества небольших чисел
Кавалер орденов:
- Александра Невского (1875)
- Св. Владимира 3-й ст. (1854)
- Св. Станислава 1-й ст. (1856)
- Св. Анны 1-й ст. с императорской короной (1861)
- Св. Владимира 2-й ст. (1867)
- Белого Орла (1871)
- По случаю 50-летия научной деятельности учёного 19 мая 1875 года была изготовлена юбилейная медаль и Академией наук была учреждена премия имени В. Я. Буняковского за лучшие сочинения по математике.
Помогите пожалуйста. Как найти расстояния на карте,зная на местности и МАСШТАБ
Чтобы найти масштаб, нужно разделить расстояние на местности на расстояние на карте.
При этом необходимо учитывать, что в 1 км — 100000 см.
Как найти расстояние на карте?
Всё просто.
М — масштаб, расстояние на местности, расстояние на карте.
Если , то
Отсюда следует следующее — чтобы найти расстояние на карте (), необходимо расстояние на местности () разделить на масштаб (М).
Масштаб. Измерение расстояний по планам, картам и глобусу. Урок 3
Масштаб плана или карты всегда один, но указываться он может тремя разными способами. Способы обозначения масштаба следующие:
- численные;
- именованные;
- графические (линейные и поперечные).
Численный масштаб имеет вид дроби, например 1:1000, числитель которой показывает единицу измерения на карте, а знаменатель – во сколько раз она уменьшена по сравнению с действительным расстоянием, второе число называется величиной масштаба. Масштаб 1:1000 нужно читать так «один к тысячи», а обозначает он, что 1см на плане соответствует 1000 см на местности. То есть этот масштаб показывает, что действительное расстояние уменьшено в 1000 раз. Числитель и знаменатель дроби численного масштаба указываются в одинаковых единицах – в сантиметрах, ведь у дроби всегда так. Чем больше знаменатель дроби, тем меньше сама дробь, а значит, мельче масштаб. Например, масштаб 1 : 100 000 мельче, чем масштаб 1:10 000.
Масштаб топографическтй карты
Но, зная математику, мы легко можем перевести сантиметры в метры или километры. Чтобы делать это быстрее, переводя в метры, просто зачёркиваем 2 нуля, так как в 1м – 100 см, а в километры – убираем 5 нулей. Пример: 1:1000 – убираем 2 нуля и получаем 10 метров. Если масштаб один к ста тысячам, например, тогда уже можно перевести знаменатель и в километры – 1:100 000, для этого уберём 5 нулей, потому что в 1 км 100 000 см. Получим, что в 1 см на карте 10 км на местности, а это будет уже другой вид масштаба – именованный.
Именованный масштаб указывается на всех картах, он дополняется словами. В 1 см – 10 м, 10 м – это величина масштаба. Для примера переведём численный масштаб в именованный, пользуясь правилом, обсуждаемым выше:
- 1:25 000 000 – 1см-250 км;
- 1:10 000 000 – 1см-100 км;
- 1:20 000 – 1см-200 м.
При необходимости обратного перевода добавляем те же нули, при переводе километров в сантиметры добавим 5 нулей, метров в сантиметры – 2 нуля. Например:
- 1 см-300 м – это 1:30 000;
- 1см-250 км – это 1:25 000 000.
Для непосредственного определения расстояния по картам и планам служит линейный масштаб. Это график, помещаемый внизу карты в виде линейки (масштабная линейка), в России она разделёна на сантиметры. Справа от нуля у каждого деления линейки подписано истинное расстояние на местности, равное одному, двум или нескольким величинам масштаба. Слева от нуля сантиметр линейки разбивают на меньшие деления, например на миллиметры, для получения более точных результатов.
Понятие масштаба. Измерение расстояний на местности и на карте
Самарский областной центр технического творчества учащихся
Самарская городская общественная организация «Детско-молодежный спортивно-технический клуб Контур»
Абрамов А.В.
Самара, 2000 г.
1 часть
Пособие для учащихся учреждений дополнительного образования и для занятий спортивной радиопеленгацией в семье
1.4. Понятие масштаба. Измерение расстояний на местности и на карте.
Вспомним материал параграфа 2. Там говорилось о важнейших свойствах карты. Одно из них гласило: все объекты на карте уменьшены по сравнению с соответствующими объектами местности в одинаковое количество раз. А во сколько же раз карта уменьшена по сравнению с местностью? Наверное, разные карты уменьшены по-разному. Величина, характеризующая степень уменьшения карты, называется масштабом.
Масштаб карты — это дробь, в числителе которой стоит единица, а в знаменателе – величина, показывающая, во сколько раз уменьшены объекты карты по сравнению с соответствующими объектами местности.
Масштаб карты указывается в зарамочном оформлении. Знание масштаба позволяет нам измерять расстояния по карте и переводить их в расстояния на местности. В примере, рассмотренном в предыдущем параграфе, мы, двигаясь к лесному озеру, не знали, сколько нам до него идти. Вдруг мы отклонились от азимута и озеро давно уже позади? Такого вопроса не возникло, если бы мы, измерив расстояние от домика лесника до озера по карте, рассчитали это расстояние на местности.
Пусть масштаб карты составляет 1:15000. Это означает, что все расстояния местности уменьшены при нанесении на карту в 15000 раз. Следовательно, расстояния, измеренные по карте, при переносе на местность должны быть увеличены в 15000 раз. Каждый сантиметр карты составляет 15000 сантиметров на местности или 150 метров. Таким образом, для карты масштаба 1:15000, 1 см на карте соответствует 150 метрам на местности, а 1 мм – 15 метрам.
Как перевести расстояние, измеренное по карте, в расстояние на местности? Очень просто. Нужно расстояние в миллиметрах умножить на 15 (вспомните, ведь 1 мм это 15 м). И тогда мы получим расстояние в метрах.
Обратите внимание, что в значении масштаба не указана единица измерения (1:15000). Это не случайно. Дело в том, что нет никакой разницы в каких единицах вести измерения. Хоть в попугаях и слоненках, как это делалось в известном мультфильме. Выражение масштаба показывает, что 1 единица на карте, будь то миллиметр, сантиметр, попугай, соответствует 15000 таких же единиц на местности (миллиметров, сантиметров, попугаев).
Для удобства работы условимся измерять расстояния на карте в миллиметрах, а на местности в метрах. Тогда для перевода единиц карты в единицы местности можно воспользоваться таким соотношением:
Чтобы найти расстояние между двумя объектами местности в метрах, нужно на карте измерить это расстояние в миллиметрах, умножить на знаменатель масштаба и перевести полученный результат в метры, то есть разделить на тысячу.
Запишем соотношение в виде формулы:
где – F(m) – расстояние на местности в метрах,
K(mm) – расстояние по карте в миллиметрах, M – знаменатель масштаба.
Задания для самостоятельной работы.
- Определите расстояния между КП по картам различных масштабов.
- Выберите на карте перегон заданной длины.
- Вдоль тропы установлены КП с номерами. На карточке нарисован отрезок и указан масштаб. Добежать до «своего» КП.
- Добежать до заданного КП. Нарисовать отрезок в разных масштабах.
- Даны направления (азимуты) и расстояния. Найти КП на местности.
- Идти от КП к КП (с точки каждого КП видны другие) и рисовать маршрут в виде ломаной линии при заданном масштабе.
Как измерять расстояние по карте, плану или глобусу?
Измерять расстояния можно при помощи масштаба или градусной сетки (на плане её нет). Второй способ мы изучим немного позднее. Чтобы узнать расстояние на местности, нужно расстояние между двумя точками на карте или плане измерить при помощи линейки (этот способ подходит для прямых линий, для извилистых пользуются курвиметром или измерением малым раствором циркуля).
Измерения нужно производить очень точно, учитывая миллиметры. Затем полученные данные умножить на величину масштаба. Например, если при измерении мы получили расстояние 1,4 см, а масштаб карты в 1см 10 000 км, нужно умножить 1,4 на 10 000, получится 14 000 км – это и есть расстояние на местности. Нужно знать, что мы узнаём не действительное расстояние, а его проекцию. Линия на карте может иметь разные неточности в связи с углом наклона земной поверхности.
При помощи линейного масштаба измеряют расстояние линейкой или циркулем, переносят это расстояние на масштабную линейку и без дополнительных расчетов получают искомое расстояние. При этом неизбежны ошибки, которые зависят от масштаба и проекции карты. Чем крупнее масштаб карты, тем точнее измеренные расстояния.
Глобус – объёмная модель Земли. Он показывает шарообразную форму нашей планеты. На нём все объекты изображены в неискажённом виде. В отличие от карты, они сохраняют свою форму, площадь, длину. Направления на глобусе совпадают с направлениями на Земле. У глобуса всюду один и тот же масштаб, который обычно надписывается в южной части Тихого океана. Масштабы школьных глобусов очень мелкие: 1:50 000 000, т. е. в 1 см – 500 км, истинное расстояние на нём уменьшается в 50 миллионов раз.
Для определения расстояний по глобусу надо ниткой или полоской бумаги измерить расстояние между заданными пунктами и, зная масштаб глобуса, вычислить истинное расстояние с помощью пропорции, как по обычной карте.
Виды написания масштаба
В топографии принято указывать масштаб тремя способами.
Численный
Численный масштаб относится к самому распространенному виду, применяемому на топографических картах и различных планах. Пишется он в виде: 1:10000, где в числителе единица, а в знаменателе число, указывающее во сколько раз уменьшили реальный объект для указания его на карте. При масштабе 1: 10000 уменьшение будет в 10 тысяч раз.
Обозначение масштаба на карте
| Для карт | 1:1000000, 1:500000, 1:300000, 1:200000, 1:100000, 1:50000, 1: 25000, 1:10000 |
| Для планов | 1:5000, 1:2000, 1:1000, 1:500 |
Запомнить нужно, что чем больше цифра после дроби, тем более мелко изображен объект.
Словесный
Словесный масштаб введен для удобства пользователей. Дело в том, что на топографических материалах измерения проводятся в см, но это неудобно людям, которые, говоря о расстояниях, обычно подразумевают метры или километры. Поэтому рядом с числовым может быть написан словесный масштаб. Например, так:
- 1 : 1 000 в 1 см – 10 м,
- 1 : 20 000 в 1 см – 200 м,
- 1 : 5 000 000 в 1 см – 50 км,
- 1 : 75 000 000 в 1 см – 750 км.
Линейный
Дополнительно к числовому, может быть указан линейный масштаб. Он позволяет определить расстояние на карте или наоборот нанести линию на карту без числовых измерений.
Пример линейного масштаба
Линейный масштаб — это линия, которая делится по всей длине на одинаковые отрезки (обычно они равны 2 см). Справа от о у каждой части отрезков указывается расстояние (оно вычисляется согласно существующему масштабу). Слева от нуля также отложен отрезок с более мелкими делениями (обычно их 10).
Чтобы узнать расстояние на карте прикладываем к точке А и точке Б циркуль. Затем полученный раствор переносим на линейный масштаб, чтобы определить расстояние в метрах или километрах. Справа от нуля устанавливаем конец циркуля на полное значение отрезка, а вторым концом слева от нуля смотрим полученное значение из мелких делений. Объединив эти два значения, получаем реальное расстояние на местности.
LКарты и компас это азы ориентирования на местности. Как пользоваться компасом, вы узнаете из статьи: Ориентирование по компасу в походе – необходимая азбука для туриста-пешеходника
Масштаб и классификация карт по нему
Чем больший участок Земли нужно изобразить, тем в большее количество раз нужно уменьшить расстояния на карте по сравнению с действительным. На такой карте все подробности не покажешь, для этого она слишком мелкомасштабна. Приходится отбирать только те объекты, которые важны именно для цели выполняемой данной картой – этот процесс называется географической генерализацией.
Подробно можно показать небольшую площадь, посёлок, район, город. Тут будет видны уже и форма и размер зданий, расположение лесопарков, небольшие реки и др. Это возможно потому, что расстояния уменьшены несильно, масштаб карты достаточно крупный.
По масштабу карты делят на:
- мелкомасштабные (обзорные) — с масштабом менее 1: 1 000 000;
- среднемасштабные (обзорно-топографические) – в пределах 1: 200 000 до 1: 1 000 000;
- крупномасштабные (топографические) – от 1: 200 000 до 1: 10 000.
Нужно запомнить правило: чем больше величина масштаба, тем мельче масштаб карты, чем крупнее масштаб, тем подробнее карта.
как найти расстояние на карте если известен масштаб и местность?
Чтобы определить расстояние между двумя точками, вначале измеряют это расстояние на карте, а затем, пользуясь численным или линейным масштабом карты, определяют действительное значение этого расстояния на местности. Если требуется найти расстояние не по прямой, а по извилистой дороге, пользуются специальным прибором — курвиметром (рис. 43). Это прибор для измерения длины кривых линий. Основанием курвиметра служит колесико, длина окружности которого известна. Вращение колесика передается на стрелку, поворачивающуюся по круговой шкале. Зная число оборотов колесика, катящегося по измеряемой линии, легко определить и ее длину.
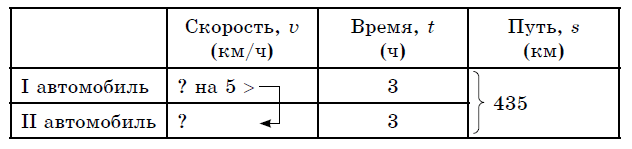
Задача 1. Два автомобиля выехали одновременно навстречу друг другу из двух городов, расстояние между которыми равно 435 км, и встретились через 3 часа. Найти скорость каждого автомобиля, если скорость первого из них на 5 км/ч больше скорости второго.
Краткая запись:
Решение:
1-й способ (арифметический)
- (435:3=145) (км/ч) — скорость сближения;
- (145-5=140) (км/ч) — сумма двух одинаковых скоростей;
- (140:2=70) (км/ч) — скорость II автомобиля;
- (70+5=75) (км/ч) — скорость I автомобиля.
2-й способ (алгебраический)
Пусть (x) км/ч — скорость II автомобиля, тогда ((x+5)) км/ч — скорость I автомобиля.
Скорость сближения: (x+x+5=2x+5) (км/ч).
Так как за 3 ч автомобили вместе прошли 435 км, составим и решим уравнение:
(3(2x+5)=435)
(2x+5=435:3)
(2x+5=145)
(2x=145-5)
(2x=140)
(x=140:2)
(x=70) — vII.
При (x=70), (x+5=70+5=75) (км/ч) — vI.
Ответ: скорость I автомобиля — 75 км/ч, а скорость II автомобиля — 70 км/ч.
Практическая работа №2:
«Определение
расстояний по картам с помощью масштаба»
Цель работы: формирование умений работы с различными видами масштабов;
формирование умений определять расстояния по картам с помощью масштаба.
Оборудование: атлас по географии для 6-го
класса, курвиметр или нитка длиной около 20 см, рабочая тетрадь.
Ход работы
Задание 1. Переведите численный масштаб карты
в именованный:
а) 1:200 000 г)
1:35 000 000
б) 1:10 000 000 д) 1:90 000
в) 1:25 000
Правило для учащихся. Для более легкого перевода
численного масштаба в именованный нужно посчитать, на сколько нулей кончается
число в знаменателе. Например, в масштабе 1: 500 000 в знаменателе
после цифры 5 находится пять нулей.
Если после цифры в знаменателе пять и более нулей, то, закрыв
(пальцем, авторучкой или просто зачеркнув) пять нулей, получим число километров
на местности, соответствующее 1 сантиметру на карте. Пример для масштаба 1:500 000.
В знаменателе после цифры — пять нулей,
закрыв их, получим для именованного масштаба: в 1 см на карте 5 километров на
местности.
Если после цифры в знаменателе менее пяти нулей, то, закрыв два нуля, получим
число метров на местности, соответствующее 1 сантиметру на карте. Если, например,
в знаменателе масштаба 1: 10 000 закроем два нуля, получим: в
1 см — 100 м.
Задание 2. Переведите именованный масштаб в численный:
а) в 1 см — 500 м
б) в 1 см — 10 км
в) в 1 см — 250 км
г) в 1 см – 30 км
д) в 1 см – 5 км
Правило для учащихся. Для более легкого перевода именованного масштаба в численный нужно
перевести расстояние на местности, указанное в именованном масштабе, в
сантиметры. Если расстояние на местности выражено в метрах, чтобы получить знаменатель
численного масштаба, нужно приписать два нуля, если в километрах, то пять
нулей.
Например, для именованного масштаба в 1 см — 100 м расстояние на местности
выражено в метрах, поэтому для численного масштаба приписываем два нуля и
получаем: 1:10 000. Для масштаба в 1 см — 5 км приписываем к пятерке
пять нулей и получаем: 1:500 000.
Задание 3. Определите расстояние между пунктами по физической карте России в
атласе 6-го класса:
а) Москва и Мурманск
б) гора Нaродная (Уральские горы) и гора Белуха (горы Алтай)
в) мыс Дежнева (Чукотский полуостров) и мыс Лопатка (полуостров Камчатка)
Правило для учащихся. При определении расстояния по карте между пунктами следует:
1. Измерить при помощи линейки расстояние в сантиметрах между
пунктами. Например, расстояние между городами Москва и Астрахань на карте
составляет 6,5 см.
2. Узнать по именованному масштабу, сколько километров
(метров) на местности соответствует 1 см на карте.
(На физической карте России в географическом атласе 6-го класса 1
см на карте соответствует 200 км на местности.)
3. Измеренное линейкой расстояние между пунктами умножить на
количество километров (метров) на местности для данного масштаба.
6,5 x 200 = 1300 км.
Задание 4. Измерьте протяженность рек по
физической карте России в атласе 6-го класса:
а) Ока;
б) река Урал;
в) Кама.
Измерения извилистых линий на карте (в данном случае рек)
проводятся при помощи курвиметра либо нитки.
Как измерить длину реки при помощи нитки (правило для
учащихся):
1. Нитку нужно смочить, иначе уложить ее на бумагу трудно.
2. Приложить нитку к кривой линии (к реке — от истока до устья) так, чтобы она
повторяла все изгибы реки.
3. Отметить на нитке (пальцами или пинцетами) точки истока и устья
(можно аккуратно обрезать нитку ножницами по этим точкам).
4. Распрямить нитку, замеченный (или отрезанный) участок нитки приложить к
линейке и измерить, сколько в нем сантиметров. Результат измерения умножить на
количество километров на местности для данного масштаба. (Можно приложить нитку
к линейному масштабу на карте и сразу прочитать длину реки.)
Определение
расстояний по картам с помощью масштаба (ответы)
Задание 1.
Переведите численный масштаб карты в именованный:
а) 1:200 000
б) 1:10 000 000
в) 1:25 000
г) 1:35 000 000
д) 1:90 000
Ответ: а) в 1 см —
2 км; б) в 1 см — 100 км; в) в 1 см — 250 м (0,25 км); г) в 1 см – 900 м (0,9
км).
Задание 2.
Переведите именованный масштаб в численный:
а) в 1 см — 500 м
б) в 1 см — 10 км
в) в 1 см — 250 км
г) в 1 см – 30 км
д) в 1 см – 5 км
Ответы: а) 1:50
000; б) 1:1 000 000; в) 1:25 000 000; г) 1:300 000 д) 1:50 000.
Задание 3.
Определите расстояние между пунктами по физической карте России в атласе 6-го
класса:
а) Москва и
Мурманск
б) гора Нaродная
(Уральские горы) и гора Белуха (горы Алтай)
в) мыс Дежнева
(Чукотский полуостров) и мыс Лопатка (полуостров Камчатка)
Ответы: а) 1460
км; б) 2240 км; в) 2500 км
Задание 4.
Измерьте протяженность рек по физической карте России в атласе 6-го класса:
а) Ока;
б) река Урал;
в) Кама.
Ответы: а)
примерно 920 км; б) примерно 1300 км; в) примерно 1200 км.