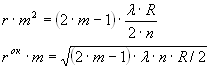Как найти расстояние между интерференционными максимумами - Исправление недочетов и поиск решений вместе с Examum.ru

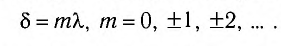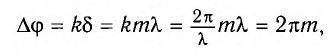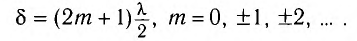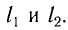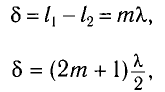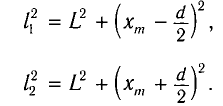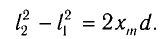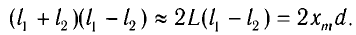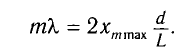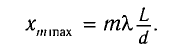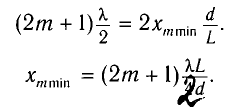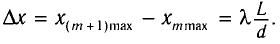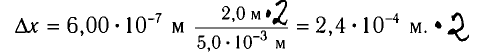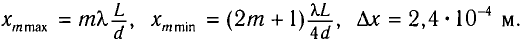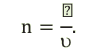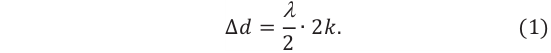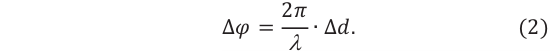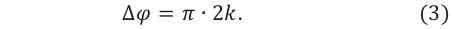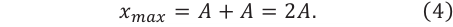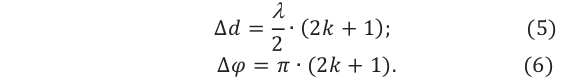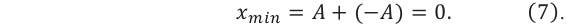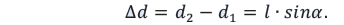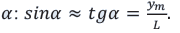
Рис.
6

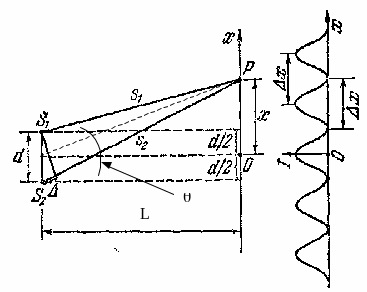
Сделаем рисунок. Здесь (рис.6) приняты
обозначения: L – расстояние от источников
до экрана, 
— угол наблюдения, d – расстояние между
источниками.

В
точке O наблюдается так называемый
нулевой максимум, т.к. в эту точку волны
от обоих источников приходят в одинаковой
фазе. Для того чтобы интерференционная
картина была отчетливо различима,
необходимо выполнение условия

.
Тогда из рисунка можно определить, что

Здесь
x_m

расстояние от центра интерференционной
картины до максимума с номером «m».

Следовательно,

Подстановка
значения 
дает, что максимум
интенсивности будет
наблюдаться при значениях:

Величина x_m
также определяет расстояние от «0»
максимума до максимума с номером «m».

Координаты
минимума
интенсивности определяются
из условия:

,
где m=0,1,2,…

Назовем расстояние
между двумя соседними максимумами
интенсивности расстоянием
между интерференционными полосами,
а расстояние между соседними минимумами
интенсивности 
шириной
интерференционной полосы.
Видно, что расстояние между полосами и
ширина полосы имеют одинаковое значение,
равное

.
Данное значение легко можно получить,
если посчитать расстояние между двумя
соседними максимума или минимумами.
Рекомендуется расчет провести студентам
самостоятельно. Из приведенного выражения
следует, что для получения отчетливой
интерференционной картины необходимо,
чтобы выполнялось условие

,
о чем и говорилось выше.

Ширина
интерференционных полос и расстояние
между ними зависят от длины волны .
Только в центре картины при x=0, совпадут
максимумы всех длин волн. Если в установке
Юнга источник испускает белый цвет, то
только нулевой (главный) максимум
окажется белым (здесь совпадут максимумы
всех длин волн), все остальные максимумы
будут окрашены. По мере удаления от
центра максимумы разных длин волн
(разных цветов) смещаются друг относительно
друга все больше и больше. Это приводит
к смазыванию интерференционной картины
при наблюдении ее в белом цвете. В
монохроматическом свете (монохроматическим
называется свет, которому соответствует
дона определенная длина волны) число
различимых полос интерференции заметно
возрастает.

Измерив
расстояние между полосами x
и зная значения L и d, можно вычислить .
Именно из опытов по интерференции света
были впервые определены длины волн для
световых лучей разного цвета.
Оранжево-красному участку спектра
соответствуют более длинные волны
(_к=780-600нм),
а сине-фиолетовому – более короткие
(_ф=480-420нм).

.52.4. Интерференция в тонких пленках.

Наиболее типичным
и распространенным примером интерференции
света в природе является интерференция
в тонких пленках (мыльные пузыри, радужная
пленка нефти на воде и т.д.).

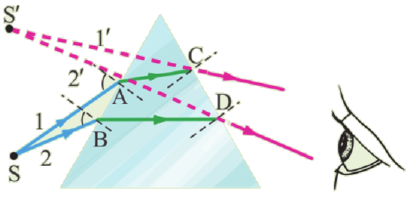
Пусть на прозрачную
тонкую пластинку толщиной d падает
плоская световая волна под углом 
(рис.7). Разность хода, приобретенная
лучами 1 и 2 до того, как они сойдутся в
точке С будет равна:

Рис.
7

где
S₁=ВС;
S₂=АО+ОС.

Но
АО=ОС=d/cos,
поэтому S₂=2d/cos.

В
свою очередь ВС=АСsin,
а АС=2АД=2dtg,
поэтому S₁=2dtgsin.

Воспользовавшись
приведенными равенствами и соотношением

,
получим, что

Для
получения окончательной разности хода
необходимо учесть, что световые волны,
как и всякие другие волны, отражаясь от
оптически более
плотной
среды (луч 1 в точке С) получают
дополнительную разность фаз равную ,
т.е. возникает добавочная разность хода
равная /2.
При отражении от среды оптически менее
плотной (точка О) скачка фазы не происходит.

Таким
образом, при падении на пластинку плоской
волны образуются две отраженные волны,
разность хода которых определяется
формулой:

В
предположении, что лучи 1 и 2 когерентны,
в результате падения на плоскопараллельную
пленку пучка лучей в отраженном и
проходящем свете на экране получаются
чередующиеся темные и светлые полосы
в случае монохроматического света и
цветные полосы в случае белого света.

ДОПОЛНЕНИЕ 1.

Строго
говоря, лучи 1 и 2 (или две плоские
отраженные волны, распространяющиеся
в одном направлении) смогут интерферировать,
если будут соблюдены условия временной
и пространственной когерентности.

Вспомним, что
когерентностью называется согласованное
протекание нескольких колебательных
или волновых процессов. Степень
согласованности может быть различной.
Соответственно можно ввести понятие
степени
когерентности
двух волн.

Различают
временную и пространственную когерентность.
Понятие когерентности является
относительным: две волны могут вести
себя как когерентные при наблюдении с
одним прибором (с малой инерционностью)
и как некогерентные при наблюдении с
другим прибором (с большой инерционностью).
Для характеристики когерентных свойств
волн вводится время
когерентности
t_ког.,
которое определяет такое время, за
которое случайное изменение фазы
достигает значения ~.
За время t_ког.
колебание как бы забывает свою
первоначальную фазу и становится
некогерентным по отношению к самому
себе.

Воспользовавшись
понятием когерентности, можно сказать,
что когда t_{прибора}>>t_ког.,
то прибор не зафиксирует интерференцию.
Если же t_{прибора}<<t_ког.,
то прибор (глаз, фотопластинка и пр.)
обнаружит четкую интерференционную
картину.

Соответственно,
длиной когерентности называется
расстояние

,
на которое перемещается волна за время
t_ког..
Длина когерентности есть то расстояние,
на котором случайное измерение фазы
достигает значения ~.
Для получения интерференционной картины
путем деления естественной волны на
две части необходимо, чтобы оптическая
разность хода была меньше, чем длина
когерентности. Это требование ограничивает
число видимых интерференционных полос.
С увеличением номера полосы “m” разность
хода растет, поэтому четкость полос
делается все хуже и хуже.

При
интерференции немонохроматических
волн время когерентности и длина
когерентности определяются выражениями:

и

.

Пространственная
когерентность.

Рис.
8

усть источник имеет угловые размеры

(рис.8). Если

,
то можно наблюдать интерференцию. Отсюда
следует, что наибольшее расстояние,
между щелями, при котором можно наблюдать
интерференцию от источника с угловым
размером ,
определяется из условия

;

Будем
называть длиной пространственной
когерентности или радиусом когерентности
некое расстояние _ког.,
при смещении на которое вдоль некой
волновой поверхности случайное изменение
фазы достигает значения ~.

.
Для Солнца, например, ~0,01рад;
~0,5мкм

_ког.=0,05мкм.
По мере удаления от источника степень
пространственной когерентности
возрастает.

Вследствие
ограничений, накладываемых временной
и пространственной когерентностями,
интерференция
при освещении тонкой пластинки наблюдается
только в том случае, если толщина
пластинки не
превышает нескольких сотых долей
миллиметра.
При освещении светом с большой степенью
когерентности интерференция наблюдается
и при отражении от более толстых пластинок
и пленок.

      

Рассмотрим
теперь интерференцию монохроматического^⁵
света при падении на пленку или пластинку
расходящегося пучка лучей (например,
при падении сферической волны).

В
этом случае результаты интерференции
отраженного (и проходящего) света в
различных точках пластинки зависят от
углов падения 
лучей. Лучи, падающие под одинаковым
углом ₁,
создадут на экране совокупность одинаково
освещенных точек, образующих криволинейную
темную (или светлую) полосу. Каждой из
этих полос соответствует определенное
значение угла .
Поэтому они называются полосами
равного наклона.
При нарушении плоскопараллельности
пленки или пластинки форма полос равного
наклона искажается. Этим используются
при проверке качества шлифовки
плоскопараллельных стеклянных пластин,
причем обнаруживают отклонение от
плоскопараллельности, равное 0,01мкм.

Справка 3.

—
временная когерентность

Т.к. оптические разности хода для
проходящего и и отраженного света
отличаются на

,
максимум интерференции в отраженном
свете будет соответствовать минимуму
в проходящем и наоборот.

С
увеличением толщины (d) плоскопараллельной
пластины влияние угла наклона становится
все менее заметным, полосы равного
наклона становятся все ближе и ближе
друг к другу. И при больших толщинах
плоскопараллельных пластин интерференцию
света в них наблюдать не удается.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Интерференция волн.

Сложение колебаний.
Когерентные источники.
Условие максимума и минимума.
Интерференционная картина.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: интерференция света.

В предыдущем листке, посвящённом принципу Гюйгенса, мы говорили о том, что общая картина волнового процесса создаётся наложением вторичных волн. Но что это значит — «наложением»? В чём состоит конкретный физический смысл наложения волн? Что вообще происходит, когда в пространстве одновременно распространяются несколько волн? Этим вопросам и посвящён данный листок.

к оглавлению ▴

Сложение колебаний.

Сейчас мы будем рассматривать взаимодействие двух волн. Природа волновых процессов роли не играет — это могут быть механические волны в упругой среде или электромагнитные волны (в частности, свет) в прозрачной среде или в вакууме.

Опыт показывает, что волны складываются друг с другом в следующем смысле.

Принцип суперпозиции. Если две волны накладываются друг на друга в определённой области пространства, то они порождают новый волновой процесс. При этом значение колеблющейся величины в любой точке данной области равно сумме соответствующих колеблющихся величин в каждой из волн по отдельности.

Например, при наложении двух механических волн перемещение частицы упругой среды равно сумме перемещений, создаваемых в отдельности каждой волной. При наложении двух электромагнитных волн напряжённость электрического поля в данной точке равна сумме напряжённостей в каждой волне (и то же самое для индукции магнитного поля).

Разумеется, принцип суперпозиции справедлив не только для двух, но и вообще для любого количества накладывающихся волн. Результирующее колебание в данной точке всегда равно сумме колебаний, создаваемых каждой волной по отдельности.

Мы ограничимся рассмотрением наложения двух волн одинаковой амплитуды и частоты. Этот случай наиболее часто встречается в физике и, в частности, в оптике.

Оказывается, на амплитуду результирующего колебания сильно влияет разность фаз складывающихся колебаний. В зависимости от разности фаз в данной точке пространства две волны могут как усиливать друг друга, так и полностью гасить!

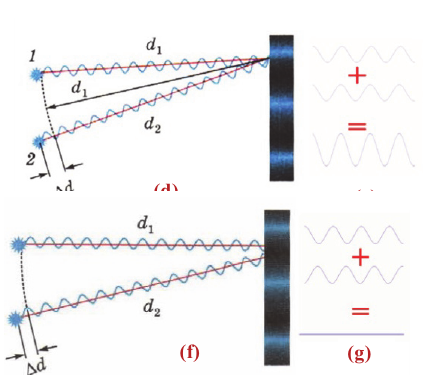
Предположим, например, что в некоторой точке фазы колебаний в накладывающихся волнах совпадают (рис. 1).

Рис. 1. Волны в фазе: усиление колебаний

Мы видим, что максимумы красной волны приходятся в точности на максимумы синей волны, минимумы красной волны — на минимумы синей (левая часть рис. 1). Складываясь в фазе, красная и синяя волны усиливают друг друга, порождая колебания удвоенной амплитуды (справа на рис. 1).

Теперь сдвинем синюю синусоиду относительно красной на половину длины волны. Тогда максимумы синей волны будут совпадать с минимумами красной и наоборот — минимумы синей волны совпадут с максимумами красной (рис. 2, слева).

Рис. 2. Волны в противофазе: гашение колебаний

Колебания, создаваемые этими волнами, будут происходить, как говорят, в противофазе — разность фаз колебаний станет равна . Результирующее колебание окажется равным нулю, т. е. красная и синяя волны попросту уничтожат друг друга (рис. 2, справа).

к оглавлению ▴

Когерентные источники.

Пусть имеются два точечных источника, создающие волны в окружающем пространстве. Мы полагаем, что эти источники согласованы друг с другом в следующем смысле.

Когерентность. Два источника называются когерентными, если они имеют одинаковую частоту и постоянную, не зависящую от времени разность фаз. Волны, возбуждаемые такими источниками, также называются когерентными.

Итак, рассматриваем два когерентных источника $S_{1}$ и $S_{2}$ . Для простоты считаем, что источники излучают волны одинаковой амплитуды, а разность фаз между источниками равна нулю. В общем, эти источники являются «точными копиями» друг друга (в оптике, например, источник $S_{2}$ служит изображением источника $S_{1}$ в какой-либо оптической системе).

Наложение волн, излучённых данными источниками, наблюдается в некоторой точке . Вообще говоря, амплитуды этих волн в точке не будут равны друг другу — ведь, как мы помним, амплитуда сферической волны обратно пропорциональна расстоянию до источника, и при разных расстояниях $S_{1}P$ и $S_{2}P$ амплитуды пришедших волн окажутся различными. Но во многих случаях точка расположена достаточно далеко от источников — на расстоянии гораздо большем, чем расстояние между самими источниками. В такой ситуации различие в расстояниях $S_{1}P$ и $S_{2}P$ не приводит к существенному отличию в амплитудах приходящих волн. Следовательно, мы можем считать, что амплитуды волн в точке также совпадают.

к оглавлению ▴

Условие максимума и минимума.

Однако величина $d=|S_{1}P-S_{2}P|$ , называемая разностью хода, имеет важнейшее значение. От неё самым решительным образом зависит то, какой результат сложения приходящих волн мы увидим в точке .

Рис. 3. Усиление колебаний в точке P

В ситуации на рис. 3 разность хода равна длине волны . Действительно, на отрезке $S_{1}P$ укладываются три полных волны, а на отрезке $S_{2}P$ — четыре (это, конечно, лишь иллюстрация; в оптике, например, длина таких отрезков составляет порядка миллиона длин волн). Легко видеть, что волны в точке складываются в фазе и создают колебания удвоенной амплитуды — наблюдается, как говорят, интерференционный максимум.

Ясно, что аналогичная ситуация возникнет при разности хода, равной не только длине волны, но и любому целому числу длин волн.

Условие максимума. При наложении когерентных волн колебания в данной точке будут иметь максимальную амплитуду, если разность хода равна целому числу длин волн:

(1)

Теперь посмотрим на рис. 4. На отрезке $S_{1}P$ укладываются две с половиной волны, а на отрезке $S_{2}P$ -три волны. Разность хода составляет половину длины волны (d=lambda /2[/math]).

Рис. 4. Гашение колебаний в точке P

Теперь нетрудно видеть, что волны в точке складываются в противофазе и гасят друг друга — наблюдается интерференционный минимум. То же самое будет, если разность хода окажется равна половине длины волны плюс любое целое число длин волн.

Условие минимума.
Когерентные волны, складываясь, гасят друг друга, если разность хода равна полуцелому числу длин волн:

$d=nlambda+frac{displaystyle lambda }{displaystyle 2}.$ (2)

Равенство (2) можно переписать следующим образом:

$d=(2n+1)frac{displaystyle lambda }{displaystyle 2}$ .

Поэтому условие минимума формулируют ещё так: разность хода должна быть равна нечётному числу длин полуволн.

к оглавлению ▴

Интерференционная картина.

А что, если разность хода принимает какое-то иное значение, не равное целому или полуцелому числу длин волн? Тогда волны, приходящие в данную точку, создают в ней колебания с некоторой промежуточной амплитудой, расположенной между нулём и удвоенным значением 2A амплитуды одной волны. Эта промежуточная амплитуда может принимать все значения от 0 до 2A по мере того, как разность хода меняется от полуцелого до целого числа длин волн.

Таким образом, в той области пространства, где происходит наложение волн когерентных источников $S_{1}$ и $S_{2}$ , наблюдается устойчивая интерференционная картина — фиксированное не зависящее от времени распределение амплитуд колебаний. А именно, в каждой точке $S_{1}P$ данной области амплитуда колебаний принимает своё значение, определяемое разностью хода $d=|S_{1}P-S_{2}P|$ приходящих сюда волн, и это значение амплитуды не меняется со временем.

Такая стационарность интерференционной картины обеспечивается когерентностью источников. Если, например, разность фаз источников будет постоянно меняться, то никакой устойчивой интерференционной картины уже не возникнет.

Теперь, наконец, мы можем сказать, что такое интерференция.

Интерференция — это взаимодействие волн, в результате которого возникает устойчивая интерференционная картина, то есть не зависящее от времени распределение амплитуд результирующих колебаний в точках области, где волны накладываются друг на друга.

Если волны, перекрываясь, образуют устойчивую интерференционную картину, то говорят попросту, что волны интерферируют. Как мы выяснили выше, интерферировать могут только когерентные волны. Когда, например, разговаривают два человека, то мы не замечаем вокруг них чередований максимумов и минимумов громкости; интерференции нет, поскольку в данном случае источники некогерентны.

На первый взгляд может показаться, явление интерференции противоречит закону сохранения энергии — например, куда девается энергия, когда волны полностью гасят друг друга? Но никакого нарушения закона сохранения энергии, конечно же, нет: энергия просто перераспределяется между различными участками интерференционной картины. Наибольшее количество энергии концентрируется в интерференционных максимумах, а в точки интерференционных минимумов энергия не поступает совсем.

На рис. 5 показана интерференционная картина, созданная наложением волн двух точечных источников $S_{1}$ и $S_{2}$ . Картина построена в предположении, что область наблюдения интерференции находится достаточно далеко от источников. Пунктиром отмечена ось симметрии интерференционной картины.

Рис. 5. Интерференция волн двух точечных источников

Цвета точек интерференционной картины на этом рисунке меняются от чёрного до белого через промежуточные оттенки серого. Чёрный цвет — интерференционные минимумы, белый цвет — интерференционные максимумы; серый цвет — промежуточное значение амплитуды, и чем больше амплитуда в данной точке, тем светлее сама точка.

Обратите внимание на прямую белую полосу, которая идёт вдоль оси симметрии картины. Здесь расположены так называемые центральные максимумы. Действительно, любая точка данной оси равноудалена от источников (разность хода равна нулю), так что в этой точке будет наблюдаться является интерференционный максимум.

Остальные белые полосы и все чёрные полосы слегка искривлены; можно показать, что они являются ветвями гипербол. Однако в области, расположенной на большом расстоянии от источников, кривизна белых и чёрных полос мало заметна, и выглядят эти полосы почти прямыми.

к оглавлению ▴

Интерференционный опыт, изображённый на рис. 5, вместе с соответствующим методом расчёта интерференционной картины называется схемой Юнга. Эта схема лежит в основе знаменитного
опыта Юнга (речь о котором пойдёт в теме Дифракция света). Многие эксперименты по интерференции света так или иначе сводятся к схеме Юнга.

В оптике интерференционную картину обычно наблюдают на экране. Давайте ещё раз посмотрим на рис. 5 и представим себе экран, поставленный перпендикулярно пунктирной оси.
На этом экране мы увидим чередование светлых и тёмных интерференционных полос.

На рис. 6 синусоида показывает распределение освещённости вдоль экрана. В точке O, расположенной на оси симметрии, находится центральный максимум. Первый максимум в верхней части экрана, соседний с центральным, находится в точке A. Выше идут второй, третий (и такдалее) максимумы.

Рис. 6. Интерференционная картина на экране

Расстояние , равное расстоянию между любыми двумя соседними максимумами или минимумами, называется шириной интерференционной полосы. Сейчас мы займёмся нахождением этой величины.

Пусть источники находятся на расстоянии друг от друга, а экран расположен на расстоянии от источников (рис. 7 ). Экран заменён осью ; начало отсчёта , как и выше, отвечает центральному максимуму.

Рис. 7. Вычисление координат максимумов

Точки $N_{1}$ и $N_{2}$ служат проекциями точек $S_{1}$ и $S_{2}$ на ось и расположены симметрично относительно точки . Имеем: $ON_{1}=ON_{2}=a/2$ .

Точка наблюдения может находиться на оси (на экране) где угодно. Координату точки
мы обозначим . Нас интересует, при каких значениях в точке будет наблюдаться интерференционный максимум.

Волна, излучённая источником $S_{1}$ , проходит расстояние:

$S_{1}P=sqrt{displaystyle S_{displaystyle 1}N_{displaystyle 1}^{displaystyle 2}+PN_{displaystyle 1}^{displaystyle 2}}=sqrt{L^{2}+(x-frac{displaystyle a}{displaystyle 2})^{displaystyle 2}}=Lsqrt{1+(frac{displaystyle 2x-a}{displaystyle 2L})^{displaystyle 2}}$ . (3)

Теперь вспомним, что расстояние между источниками много меньше расстояния от источников до экрана: aleq L . Кроме того, в подобных интерференционных опытах координата точки наблюдения также гораздо меньше . Это означает, что второе слагаемое под корнем в выражении (3) много меньше единицы:

$(frac{displaystyle 2x-a}{displaystyle 2L})^{displaystyle 2}leq 1$ .

Раз так, можно использовать приближённую формулу:

$sqrt{1+alpha }=1+frac{displaystyle alpha }{displaystyle 2}, alpha leq 1$ (4)

Применяя её к выражению (4), получим:

$S_{1}P=L(1+frac{1}{2}(frac{displaystyle 2x-a}{displaystyle 2L})^{displaystyle 2})=L+frac{(displaystyle 2x-a)^{displaystyle 2}}{displaystyle 8L}$ (5)

Точно так же вычисляем расстояние, которое проходит волна от источника $S_{2}$ до точки наблюдения:

$S_{2}P=sqrt{displaystyle S_{displaystyle 1}N_{displaystyle 2}^{displaystyle 2}+PN_{displaystyle 2}^{displaystyle 2}}=sqrt{L^{2}+(x+frac{displaystyle a}{displaystyle 2})^{displaystyle 2}}=Lsqrt{1+(frac{displaystyle 2x+a}{displaystyle 2L})^{displaystyle 2}}$ . (6)

Применяя к выражению (6) приближённую формулу (4), получаем:

$S_{2}P=L(1+frac{1}{2}(frac{displaystyle 2x+a}{displaystyle 2L})^{displaystyle 2})=L+frac{(displaystyle 2x+a)^{displaystyle 2}}{displaystyle 8L}$ . (7)

Вычитая выражения (7) и (5), находим разность хода:

$d=S_{2}P-S_{1}P=frac{(displaystyle 2x+a)^{displaystyle 2}-(displaystyle 2x-a)^{displaystyle 2}}{displaystyle 8L}=frac{displaystyle ax}{displaystyle L}$ . (8)

Пусть lambda — длина волны, излучаемой источниками. Согласно условию (1), в точке будет наблюдаться интерференционный максимум, если разность хода равна целому числу длин волн:

$d=frac{displaystyle ax}{displaystyle L}=nlambda (n=0,1,2,3,...).$

Отсюда получаем координаты максимумов в верхней части экрана (в нижней части максимумы идут симметрично):

$displaystyle x_{displaystyle n}=frac{displaystyle nlambda L}{displaystyle a} (n=0,1,2,3,...).$

При n=0 получаем, разумеется, $displaystyle x_{displaystyle n}=0$ (центральный максимум). Первый максимум рядом с центральным соответствует значению n=1 и имеет координату $displaystyle x_{displaystyle 1}=lambda L/a$ .Такой же будет и ширина интерференционной полосы:

$Delta x=displaystyle x_{displaystyle n+1}-displaystyle x_{displaystyle n}=frac{(displaystyle n+displaystyle 1)lambda L}{displaystyle a}-frac{displaystyle nlambda L}{displaystyle a}=frac{displaystyle lambda L}{displaystyle a}$ .

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Интерференция волн.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
07.05.2023

Источник

1. Интерференция световых волн

1.1. Интерференция от двух источников

1.2. Определим положение m-ого интерференционного максимума. Определим ширину интерференционного максимума

1.3. Интерференция на тонкой плёнке

1.4. Интерференция на клине (полосы равной толщины)

1.5. Кольца Ньютона

2. Дифракция волн

2.1. Дифракция Фраунгофера на узкой длинной щели в непрозрачном экране

2.2. Дифракция света на одномерной дифракционной решётке

2.3. Разрешающая способность дифракционной решётки

2.4. Дифракция рентгеновских лучей

3. Поляризация света

3.1. Поляризованный и естественный свет

3.2. Закон Малюса

3.3. Поляризация при отражении от диэлектриков. Закон Брюстера

3.4. Двойное лучепреломления

3.5. Искусственная оптическая анизотропия

3.6. Вращение плоскости поляризации

1. Интерференция световых волн

Интерференцией волн называется явление усиления колебаний в одних и ослабление колебаний в других точках пространства в результате наложения двух или нескольких волн, приходящих в эти точки пространства.

Для наблюдения устойчивой во времени интерференционной картины необходимы условия, при которых частоты, поляризация и разность фаз интерферирующих волн, были бы постоянными в течение всего времени наблюдения.

Интерферируют когерентные, монохроматические волны.

Когерентные волны — волны одинаковой частоты, колебания в которых отличаются постоянной разностью фаз, не изменяющейся со временем.

1.1. Интерференция от двух источников

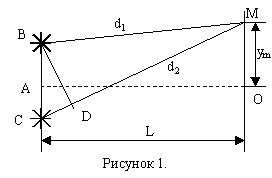
Свет от одного источника с помощью непрозрачного экрана с двумя отверстиями даёт возможность получить два когерентных источника волн (схема Юнга). Расстояние между источниками (В, С) равно l. Длина волны, излучаемая источниками λ, расстояние до экрана, где наблюдается интерференция. О – центр экрана.

Пусть в точке М – экрана происходит наложение когерентных волн. Получим условие усиления и ослабления волнами друг друга. Расстояние от В источника до точки М – d₁, от С до точки М – d₂. Колебания точки М, вызываемые первым. источником волн: , а колебания, вызываемые 2-ым источником: , где А – амплитуда колебаний источников, ω – частота колебаний, k=2π/λ – βолновое число.

Результирующее колебание точки М:

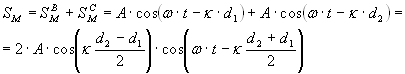
Амплитуда колебаний точки М:

A_M=2Acos(k(d₂-d₁)/2) зависит от положения точки на экране и может быть равной 2А, если волны усиливают друг друга или нулю, если волны ослабляют друг друга.

Получим условие усиления или максимум интерференции. Чтобы А_М=2А, необходимо чтобы

|cos(k(d₂-d₁)/2)|=1

Это выполняется, если

; .

Значит d₂-d₁=±mλ.

Пусть d₂-d₁=Δd – разность хода интерферирующих лучей, а ΔФ=2π(d₂-d₁)/λ=2πΔd/λ – разность фаз интерферирующих волн, тогда

ΔΤ=2π/λ (d₂-d₁) =2π/λ Δd – ρоотношение между разность фаз и разность хода волн.

Если d₂-d₁=Δd=± mλ, γде m=0,1…, то А_М=2А и, следовательно, в этих точках пространства (экрана) наблюдается максимум интерференции. Разность фаз волн при этом будет равна ΔФ=±2πmλ/λ=±2πm.

Условие ослабления или минимум интерференции

А_м=0,

|cos(k(d₂-d₁)/2)|=0.

Это выполняется, если (k(d₂-d₁)/2)=±(2m+1)λ/2; следовательно

Δd=±(2m+1)λ/2.

Волны ослабляют друг друга, если разность хода при этом

ΔΤ=±2πmλ /(2λ)(2m+1)=±(2m+1)π,

m – называется порядком интерференционного максимума или минимума. В центре экрана наблюдается максимум нулевого порядка: d₂-d₁=Δd=0.

1.2. Определим положение m-ого интерференционного максимума. Определим ширину интерференционного максимума

Рисунок 1. В точке М наблюдается максимум m-ого порядка. Обозначим расстояние от центра экрана до точки М – y_m. Воспользуемся геометрией рисунка 1. Отрезок CD=d₂-d₁. Треугольники BCD и AMO – подобны. Из подобия

Чтобы в точке наблюдался максимум m-ого порядка Δd=d₂-d₁=±mλ.

Ширина интерференционного максимума – расстояние между двумя соседними максимумами или минимумами.

Если положение m-ого максимума y_m=mLλ/l, то положение (m+1)-го максимума y_m+1=(m+1)Lλ/l. Тогда Δy= y_m+1-y_m=Lλ/l, γде Δy – ширина интерференционного максимума.

1.3. Интерференция на тонкой плёнке

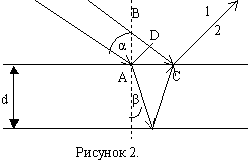
На тонкую плёнку толщиной d и показателем преломления n падает монохроматический свет с длиной волны λ. Угол падения α. Среда около плёнки – воздух. Определим условие наблюдения максимума и минимума интерференции на тонкой плёнке. Интерферирующие лучи показаны на рисунке 2. Часть первого луча проходит через плёнку, преломляясь на границе раздела, отражается от нижней границы плёнки и выходит в точке С. Часть второго луча отражается от верхней поверхности плёнки и в точке С интерферирует с лучом 1. Обозначим Δ – оптическую разность хода волны.

Оптическая разность хода волн 1 и 2:

Δ=n(AB+BC)-(DC+λ/2),

где n(AB+BC) – путь (оптический) первой волны,

(DC+λ/2) – путь второй волны. При отражении волны от поверхности плёнки, фаза волны меняется на π, т.к. отражение происходит от более плотной среды (nb=1);

n>n_b.

Изменение фазы на π соответствует дополнительному ходу, равному λ/2.

Используя геометрию рисунка и законы преломления света, получим, что оптическая разность хода интерферирующихся волн равна:

или ,

где β – угол преломления. Запишем условие усиления волнами друг друга или максимума интерференции: Δ=⁺— mλ. Значит:

Толщина плёнки, при которой интерферирующие волны будут усиливать друг друга:

m – порядок интерференции (m=0,1,2…).

Если m=0, то

– это минимальная толщина плёнки, при которой плёнка будет окрашена цветом соответствующим данной длине волн λ. Условие ослабления при интерференции или минимум интерференции:

Δ=(2m+1)λ/2.

Толщина плёнки, при которой плёнка будет казаться тёмной, т.к. наблюдается ослабление волнами друг друга, равна:

, m=0,1,2…

1.4. Интерференция на клине (полосы равной толщины)

Две поверхности, расположение под малым углом α, образуют систему получившую название клин. Клин имеет разную толщину, а поэтому при освещении поверхности клина монохроматическим светом на поверхности клина будут наблюдаться интерференционные максимумы и минимумы (смотри интерференцию на плёнке), т.к. в одних точках поверхности толщина клина соответствует условию наблюдению максимума, а в других – условию минимума.

Определим ширину интерференционной полосы.

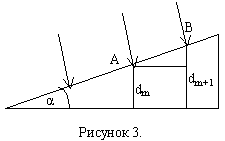
Пусть в точке А поверхности клина возникает максимум m-ого порядка. Толщина клина — d_m+1. В точке В возникает максимум (m+1)-го порядка. Толщина плёнки в этом месте — d_m+1. Условие наблюдения максимума при толщине d_m и d_m+1:

2d_mn=(2m+1)λ/2; 2d_m+1n=(2m+3) λ/2.

Вычтем из второго уравнения первое:

d_m+1-d_m – разность толщины клина в местах наблюдения m-ого и (m+1)-го максимумов. На рисунке 3. Из прямоугольника:

AB=Δy=BD/sinα,

Δy – ширина интерференционной полосы

Если угол при вершине мал, то ,

, α[рад].

Ширина интерференционного минимума или расстояния между соседними минимумами равна ширине интерференционного максимума.

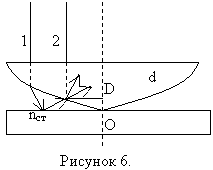
1.5. Кольца Ньютона

Частым случаем полос равной толщины являются кольца Ньютона, которые наблюдаются в схеме, изображённой на рисунке 4.

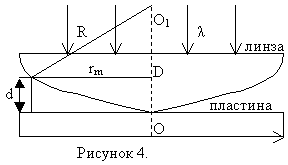
Плосковыпуклая линза с большим радиусом кривизны R выпуклой поверхностью лежит на плоской пластине и соприкасается с ней в точке О. Параллельный пучок света падает нормально на плоскую поверхность промежутка между линзой и пластиной. При наложении отраженных волн возникают интерференционные полосы равной толщины, имеющие вид колец. Вид этих колец в случае монохроматического света показан на рисунке 5.

В центре наблюдается минимум нулевого порядка (тёмное пятно). Центральный минимум окружён системой чередующихся окрашенных и тёмных колец, ширина и интенсивность которых постоянно убывает по мере удаления от центрального пятна.

Расчёт радиусом окрашенных и тёмных колец.

На рисунке 6 изображены интерферирующие волны, распространяются вдоль лучей 1 и 2.

Разность хода волн равна:

где d – толщина зазора между линзой и пластиной, где наблюдается интерференция, n – показатель преломления прослойки, λ/2 – потеря полволны при отражении 1-ой волны от стеклянной пластинки (при условии n<n_стекла).

Для наблюдения максимума интерференции или окрашенного кольца:

где m-ого порядка окрашенного кольца (m=1,2,3…).

Значит,.

Для минимума интерференции , или .

Радиус кольца определим, используя геометрию рисунка 4 OD=d. Из треугольника AO₁D:

Пренебрегая d², получим: .

Если подставим значения d, соответствующее минимуму интерференции, получим выражение для радиуса окрашенного кольца m-ого порядка.

Если между линзой и пластинкой воздушная прослойка, то n=1.

2. Дифракция волн

Огибание волнами препятствий или отклонение от прямолинейного распространения в оптически неоднородной среде получило название дифракции.

Дифракция возникает при прохождении световых волн через отверстия в непрозрачных экранах, вблизи границ непрозрачных тел и т.д.

Различаются два вида дифракции световых волн: дифракция Френеля, или дифракция в расходящихся лучах, и дифракция Фраунгофера, или дифракция в параллельных лучах.

В первом случае на препятствие падает сферическая или плоская волна, а дифракционная картина наблюдается на экране, который находится позади препятствия на конечном расстоянии от него.

Во втором случае на препятствие падает плоская волна, а дифракционная картина наблюдается на экране, который находится в фокальной плоскости собирающей линзы, установленной на пути прошедшего через препятствие света.

2.1. Дифракция Фраунгофера на узкой длинной щели в непрозрачном экране

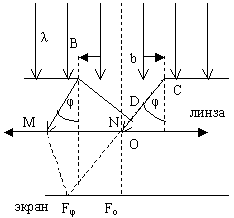
Ширина щели BC=b, длина волны, падающего света λ. Свет падает на щель нормально к её поверхности так что колебания во всех точках щели совершаются в одной фазе. О – оптический центр линзы. Дифракционная картина наблюдается на экране, который установлен в фокальной плоскости линзы. φ – угол дифракции, или угол отклонения от прямолинейного распространения падающих волн, который может принимать значения от 0 до .

F₀ – центр дифракционной картины, где интерферируют лучи, угол дифракции которых равен нулю. В F наблюдается центральный дифракционный максимум.

Параллельные лучи BM и CN, идущие от краёв щели под углом дифракции φ, собираются линзой в побочном фокусе F_φ.

Линза обладает тем свойством, что оптические пути лучей BM и DNF_φ, где D – основание перпендикуляра, опущенного из точки В на направление луча CN, одинаковы.

Результат интерференции в точке F_φ экрана зависит от разности хода волн 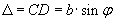и длины волн падающего света. Щель можно разбить по ширине на зоны, которые получили название зон Френеля. Зоны имеют вид параллельных ребру В полосок, разность хода от краев которых равна λ/2.

Число зон Френеля, укладывающихся в отверстие, равно:

Все зоны излучают свет в рассматриваемом направлении с одинаковой амплитудой, причём колебания, вызываемые в точке F_φ двумя соседними зонами противоположны по фазе.

Поэтому, если число зон Френеля в отверстии чётное

где k=1,2…,

то под углом дифракции, удовлетворяющем условию, наблюдается дифракционный минимум. k – порядок дифракционного минимума.

Если число зон Френеля нечётное

, где k=1,2…,

то под углом дифракции φ удовлетворяющему условию

наблюдается дифракционный максимум, соответствующий действию одной зоны Френеля (k — порядок дифракционного минимума).

Самый яркий центральный максимум наблюдается в главном фокусе линзы F₀ (φ=0).

С ростом k ширина зон Френеля уменьшается и интенсивность максимумов быстро падает.

Амплитуда и интенсивность света в точке F_φ равны:

и ,

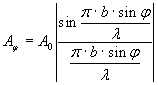
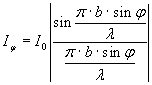
где А₀ – амплитуда, I₀ – интенсивность центрального максимума (φ=0).

2.2. Дифракция света на одномерной дифракционной решётке

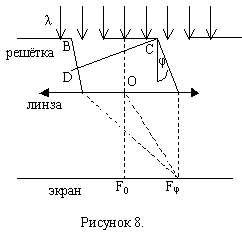
Одномерная дифракционная решётка представляет собой систему из большого число N одинаковых по ширине и параллельных друг другу щелей в экране, раздельных также одинаковыми по ширине непрозрачными промежутками.

На рисунке 8 показаны только две соседние щели решётки. Величина d=a+b, называется периодом решётки (a=KC – ширина непрозрачного промежутка, b=BK – ширина щели,

— ширина решётки). Если плоская монохроматическая волна с длиной λ падает на решётку нормально, то колебания во всех точках щели происходят в одинаковой фазе. Колебания, возбуждаемые в произвольной точке Fφ фокальной плоскости линзы каждой из щелей, совпадают по амплитуде, но отличаются по фазе. Для каждой пары соседних щелей сдвиг по фазе Δφ0 μежду этими колебаниями одинаков. Сдвиг по фазе зависит от разности хода волн, идущих от точек В и С под углом дифракции φ и длины волны λ.

где — разность хода,

D – основание перпендикуляра, опущенного из точки В на направление луча С.

Условие наблюдения главных максимумов: или (k=1,2,3)

k – порядок интерференционного максимума.

Наибольший порядок спектра наблюдается под углом дифракции: ;

;

k может принимать только целые значения, поэтому результат, полученный от деления, нужно округлить до меньшего целого числа. Число максимумов наблюдаемых на экране . В центре экрана в точке F₀ наблюдается центральный максимум (φ=0, k=0).

Условие наблюдения главных минимумов:

или ;

k – порядок главного минимума.

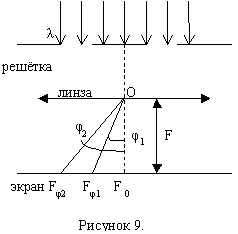
2.3. Разрешающая способность дифракционной решётки

Пусть на дифракционную решётку падает немонохроматический свет с длиной волны λ₁ и λ₂.

; (близкие длины волн).

Период дифракционной решётке d, число щелей N. В спектре k-ого порядка на экране (рисунок 9) под углом φ1 наблюдается максимум для длины волны λ1, а под углом дифракции φ2 – максимум для волны с λ2. (Fφ1 θ Fφ2 – ρоответственно), максимумы для двух длин волн на экране пространственно разделены, если выполняется условие:

(формула Рэлея).

Это условие получило название разрешающей способности дифракционной решётки. λ можно принять равным λ₁ или λ₂.

2.4. Дифракция рентгеновских лучей

Кристаллическую решётку твёрдых тел можно рассматривать как пространственную дифракционную решётку, период которой значительно меньше длины волны видимого света (). Для видимого света кристаллы являются оптически однородной средой.

В тоже время для рентгеновских лучей кристаллы представляют естественные кристаллические решётки ().

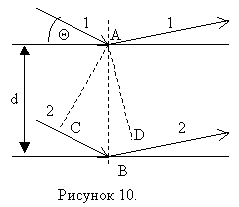
Дифракция рентгеновских лучей на кристаллах рассматривается как результат интерференции рентгеновского излучения, зеркально отражающегося от систем параллельных плоскостей, которые проходят через узлы кристаллической решётке. Расстояние d между двумя сетчатыми плоскостями называется межплоскостным расстоянием, а угол Θ между падающим лучом и плоскостью – угол скольжения. На рисунке 10 изображены две плоскости, которые проходят через углы кристаллической решётки (сетчатые или атомные плоскости).

На поверхности кристалла под углом скольжения Θ падает плоская волна с длиной λ. Рентгеновские лучи не преломляются в кристалле, т.к. показатель преломления для них равен единице (примерно). Разность хода интерферирующих волн (лучи 1 и 2), отражённых от двух параллельных плоскостей равна . Отражение наблюдается в направлениях, соответствующих дифракционным максимумам, которые удовлетворяют условию Вульфа-Брэгга:

, m=1,2,3…

m – порядок дифракционного максимума

Θ – σгол скольжения для наблюдения максимума удовлетворяет этому условию.

Угол скольжения, соответствующий первому дифракционному максимуму (m=1)

3. Поляризация света

3.1. Поляризованный и естественный свет

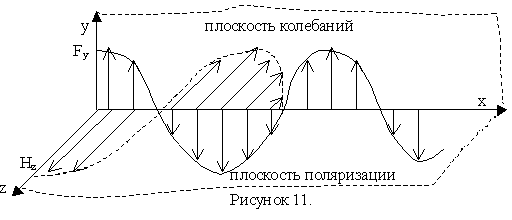
Из теории Максвелла следует, что свет является поперечной электромагнитной волной. Вектор напряжённости электрического поля (электрический или световой вектор) и вектор напряжённости магнитного поля (магнитный вектор) в световой волне колеблется в направлении перпендикулярном скорости распространения волны.

Линейно поляризованной волной называется волна, вектор которой не изменяют направление колебаний в пространстве.

Уравнение плоской монохроматической линейно-поляризованной волны, распространяющейся в направлении оси ОХ:

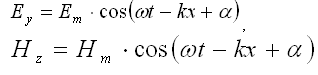
где ω – циклическая частота, — волновое число, υ – скорость распространения волны.

В каждой точке электромагнитного поля электрический вектор совершает гармонические колебания в плоскости XOY, которая называется плоскостью колебания.

Магнитный вектор колеблется в плоскости XOZ – в плоскости поляризации.

Световая волна со всевозможными одинаково вероятными направлениями колебаний электрического и магнитного векторов называется естественным светом.

В естественном свете плоскости поляризации меняют ориентацию в пространстве с течением времени.

Естественный свет можно представить в виде суперпозиции двух волн, которые поляризованы во взаимно-перпендикулярных плоскостях. Запишем уравнение естественного света только для электрического вектора волны:

;

где E_y, E_z – проекции электрического вектора на оси координат, α – сдвиг по фазе между колебаниями по Y и Z. Для естественного света E_oy=E_oz.

Частично поляризованным называется свет, если в нём есть преимущественное направление колебаний вектора

(E_oy>>E_oz) или (E_oz>>E_oy).

Частично поляризованный свет можно рассматривать как смесь одновременно распространяющихся в одном и том же направлении естественного и линейно поляризованного.

Поляризацией света называется выделение линейно поляризованного света естественного или частично поляризованного. Для этой цели используются специальные устройства, называемые поляризаторами.

Для определения характера и степени поляризации используют устройства, называемые анализаторами.

Поляризатор можно использовать в качестве анализатора.

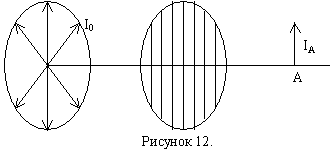
Анализатор или поляризатор условно изображают в виде решётки, “прутья” которой параллельны направлению колебаний вектора в проходящем сквозь неё свете.

Если на такую решётку-анализатор падает естественный свет, то интенсивность проходящей волны не изменяется при вращении анализатора вокруг направления падающего луча вследствие того, что в естественном свете ни одно из направлений плоскости поляризации (плоскости колебаний) не является преобладающим.

где I₀ – интенсивность падающего естественного света,

k – коэффициент прозрачности анализатора,

I_А – интенсивность проходящего света.

На выходе из анализатора-поляризатора имеем линейно поляризованную волну.

Если падающий свет частично поляризован, то I_A при вращении анализатора изменяется в зависимости от ориентации его главной плоскости (т.е. направления прутьев) по отношению к преимущественному направлению колебаний вектора в падающем свете.

3.2. Закон Малюса

Пусть на анализатор падает линейно поляризованный свет интенсивностью I0. Оптическая ось анализатора О-О` (направление прутьев).

Определим интенсивность прошедшей волны в точке А, если анализатор повернуть на угол α вокруг направления распространения луча. Через анализатор пройдёт электрический вектор, величина . Т.к. интенсивность пропорциональна квадрату амплитуды, то — это и есть закон Малюса.

3.3. Поляризация при отражении от диэлектриков. Закон Брюстера

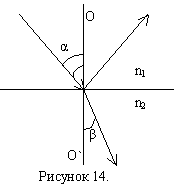
Направим на границу раздела двух диэлектриков (воздух, стекло) тонкий луч естественного света.

Часть световой волны отражается, а часть преломляется, распространяясь во второй среде. На рисунке: φ – угол падения луча, β – угол преломления, n₂ – показатель преломления стекла, n₁ — показатель преломления воздуха, n₁=1.

Если на пути отражённого и преломлённого луча поставить анализатор, то можно исследовать поляризацию при отражении и преломлении.

Оказалось, что в общем случае отражённый и преломлённый лучи поляризованы частично. При некотором строго определённом для данной пары сред (диэлектриков) значение угла падения отражённый свет оказывается линейно поляризованным. Угол падения в этом случае называется углом Брюстера (φ_Б) или углом полной поляризации и определяется законом Брюстера:

где n₂₁ – относительный показатель преломления среды.

3.4. Двойное лучепреломление

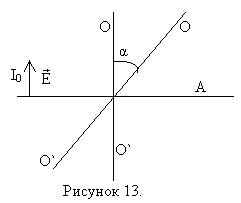
В оптически анизотронных кристаллах наблюдается явление двойного лучепреломления, которое состоит в том, что луч света падающий на поверхность кристалла, раздваивается на два преломлённых луча.

MN – оптическая ось кристалла.

Оптическая ось кристалла – направление в оптически анизотронном кристалле, вдоль которого свет распространяется, не испытывая двойного лучепреломления. Главной плоскостью или главным сечением одностороннего кристалла называется плоскость, проходящая через падающий луч и пересекающую его оптическую ось.

В одноосном кристалле один из преломлённых лучей подчиняется обычным законом преломления света. Этот луч лежит в плоскости падения. Волну, распространяющуюся вдоль направления этого луча, называют обыкновенной волной и обозначают буквой О. Показатель преломления для этой волны n₀.

Вдоль второго луча распространяется необыкновенная волна. Показатель преломления луча для неё n_е. угол преломления для необыкновенного луча зависит от того, как ориентирована поверхность пластинки по отношению к оптической оси кристалла MN. Угол преломления равен нулю в двух случаях:

а) если поверхность пластинки перпендикулярна к оптической оси (свет распространяется вдоль оптической оси, не испытывая двойного лучепреломления).

б) если поверхность пластинки параллельна оптической оси (свет распространяется в пластинке перпендикулярно оптической оси).

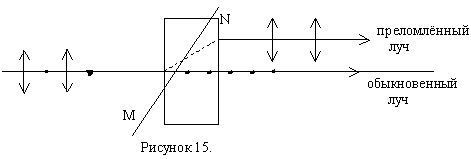
Двойное лучепреломление можно объяснить тем, что падающая на оптически анизотронный кристалл световая волна возбуждает две волны, распространяющиеся в кристалле эти по разным направлениям. В однослойном кристалле эти волны называются обыкновенными и необыкновенными волнами. Обыкновенные и необыкновенные волны линейно поляризованы во взаимно-перпендикулярных плоскостях.

В обыкновенной волне вектор направлен перпендикулярно к главной плоскости кристалла. Электрический вектор необыкновенной волны лежит в главной плоскости кристалла. Направления векторов в обыкновенных и необыкновенных волнах условно показаны на рисунке точками на обыкновенном луче и поперечными чёрточками на необыкновенном. Предполагается, что оба луча и пересекающая их оптическая ось MN кристалла лежат в плоскости рисунка.

3.5. Искусственная оптическая анизотропия

1. Оптически изотропное прозрачное вещество становится анизотропным, если его подвергнуть механической деформации. Это явление называется фотоупругостью, при одностороннем растяжении или сжатии изотропного тела вдоль оси OX оно приобретёт оптические свойства одноосного кристалла, оптическая ось которого параллельна ОХ . Разность показателей преломления обыкновенного (n_o) и необыкновенного (n_е) лучей в направлении перпендикулярном оси ОХ, пропорциональна нормальному напряжению .

n₀-n_е=к

где к- коэффициент пропорциональности, зависящий от свойств вещества.

2. Эффектом Керра называется возникновение оптической неоднородности у прозрачного изотропного диэлектрика, если его поместить во внешнее электрическое поле.

Под действием поля диэлектрик поляризуется и приобретает оптические свойства одноосного кристалла, оптическая ось которого совпадает по направлению с вектором напряженности внешнего поля.

Разность показателей преломления поляризованного диэлектрика для необыкновенного и обыкновенного лучей монохроматического света, распространяющегося перпендикулярно направлению вектора Е, удовлетворяет закону Керра.

n_е-n₀=B_в

где -длина волны в вакууме, В_в-постоянная Керра.

3. Эффектом Коттона-Мутона называется возникновение оптической анизотропии у некоторых изотропных вещество при помещении их в сильное внешнее магнитное поле.

В однородном магнитном поле вещество преображает оптические свойства одноосного кристалла, оптическая ось которого совпадает по направлению с вектором напряженности внешнего поля.

Разность показателей преломления вещества для необыкновенного и обыкновенного лучей монохроматического света при его распространении в направлении перпендикулярном вектору , пропорциональна .

с- постоянная Коттона — Мутона, -длина волны в вакууме.

3.6. Вращение плоскости поляризации

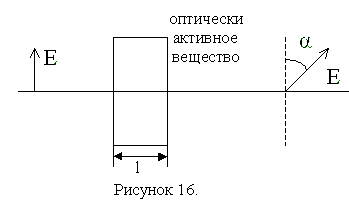
При прохождении линейно поляризованного света через некоторые вещества, называемые оптически активными, плоскость поляризации света поворачивается вокруг направления распространения луча.

Оптически активны некоторые кристалла (кварц, киноварь и др.) чистые жидкости и растворы (скипидар, раствор сахара в воде и др.)

В оптически активных кристаллах и чистых жидкостях угол поворота плоскости поляризации пропорционален толщине слоя вещества, через который проходит свет:

Коэффициент пропорциональности называется удельным вращением, или постоянной вращения.

Угол поворота плоскости поляризации при прохождении света пути в оптически активном растворе равен

С — объемно-массовая концентрация оптически активного вещества в растворе, D- плотность раствора, к=С/D- долевая концентрация по массе, — удельная вращения, зависит от природы оптически активного вещества.

Оптически неактивная среда под действием внешнего магнитного поля приобретает способность вращать плоскость поляризации света, распространяющегося вдоль направления поля.

Это явление называется эффектом Фарадея, или магнитным вращением плоскости поляризации.

где — угол поворота плоскости поляризации,

-напряженность магнитного поля,

— длина пути световой волны,

V — постоянная Верде.

Источник

Содержание:

Интерференция света:

Фаза — аргумент периодической функции, определяющий значение физической величины в любой момент времени t. Она определяет состояние колебательной системы (координаты, скорости, ускорения) в любой момент времени при заданной амплитуде. Монохроматической волной называется электромагнитное излучение постоянной частоты.

Рассмотрим процесс наложения волн длиной

Монохроматические волны одной и той же частоты, приходящие от этих источников в некоторую точку пространства Р, возбуждают в ней гармонические колебания той же частоты.

В силу этого, разность фаз колебаний, возбуждаемых рассматриваемыми источниками в точке Р, остается постоянной с течением времени, даже если начальные фазы этих колебаний различны.

Волны называются когерентными, если разность фаз колебаний, возбуждаемых ими, не изменяется с течением времени. Соответственно, свойство, характеризующее согласованность протекания в пространстве и времени нескольких колебательных или волновых процессов, называется когерентностью (от латинского слова cohaerens — связанный, сцепленный).

Опыт показывает, что амплитуда результирующего колебания в точке Р, создаваемого двумя одинаковыми источниками, зависит от геометрической разности хода волн до рассматриваемой точки:

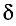
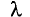
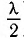
Если разность хода волн равна целому числу длин волн (четному числу полуволн ) то волны приходят в точку Р (см. рис. 33) синфазно и усиливают друг друга. В этом случае говорят о выполнении условия максимума:

Действительно, разность фаз колебаний в рассматриваемой точке в этом случае

т. е. кратна .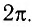

В случае, когда разность хода волн равна нечетному числу полуволн, волны приходят в точку Р в противофазе и ослабляют друг друга. Это соответствует выполнению условия минимума:

Убедитесь самостоятельно, что разность фаз колебаний в этом случае

Таким образом, в результате сложения колебаний, возбуждаемых когерентными волнами на поверхности воды, образуется устойчивая картина распределения минимумов и максимумов результирующего колебания (рис. 34). Это означает, что когерентные волны интерферируют друг с другом.

Интерференция (от латинских слов inter — взаимно, между собой и fеrio — ударяю, поражаю) — явление сложения двух или более когерентных волн, приводящее к образованию в пространстве устойчивой картины чередующихся максимумов и минимумов амплитуд результирующего колебания.

Пространственная картина устойчивого во времени распределения амплитуд результирующего колебания при интерференции называется интерференционной картиной.

Вследствие того, что энергия волны пропорциональна квадрату амплитуды, энергия результирующего колебания в общем случае не равна сумме энергий складываемых колебаний, так как 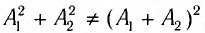. Так, в точках максимума результирующая амплитуда колебаний возрастает в два раза, а энергия, соответственно, в четыре. Однако не будем забывать, что в точках минимума колебания отсутствуют вовсе. Таким образом, явление интерференции приводит к перераспределению энергии в пространстве, причем суммарная энергия колебаний во всех точках среды при этом остается равной сумме энергий интерферирующих волн.

Отметим, что если бы в точке Р складывались две некогерентные волны с одинаковыми амплитудами, то энергия результирующего колебания была бы равна сумме энергий отдельных волн, независимо от положения точки Р относительно источника. Это означало бы просто удвоение энергии, принесенной одной из волн в данную точку.

Закономерности интерференции волн носят универсальный характер, т. е. справедливы для волн любой природы.

При рассмотрении интерференции света (электромагнитных волн) следует учесть, что длина волны света в веществе изменяется в зависимости от показателя преломления вещества. Это эквивалентно замене геометрической разности хода на оптическую разность хода

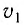
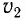
т. е. разность расстояний, пройденных волнами, с учетом различных скоростей и их распространения в средах с показателями преломления

В вакууме (с = 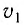=) оптическая разность хода совпадает с геометрической. При оптической разности хода, кратной четному числу полуволн (целому числу длин волн), наблюдается максимум интерференции света, а при оптической разности хода, кратной нечетному числу полуволн, — минимум.

Распространенные бытовые источники света (лампы накаливания, лампы дневного света, свечи и т. д.) не являются когерентными, т. е. не позволяют наблюдать явление интерференции.

Изобретение и распространение когерентных источников излучения — лазеров — сделало демонстрацию явления интерференции достаточно простой.

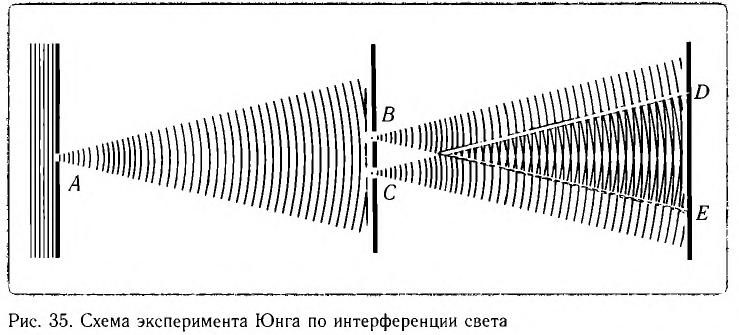
Для получения интерференционной картины при отсутствии лазеров пользуются классической интерференционной схемой (схемой Юнга), где пучок света разделяется на два пучка с помощью отверстий В и С в ширме (рис. 35). Поскольку эти пучки созданы одним и тем же источником, они являются когерентными. На экране в области DE наблюдается интерференционная картина.

Классический эксперимент по наблюдению интерференции Томас Юнг провел в 1801 г. Это позволило измерить длину световой волны и убедительно подтвердить волновую природу света.

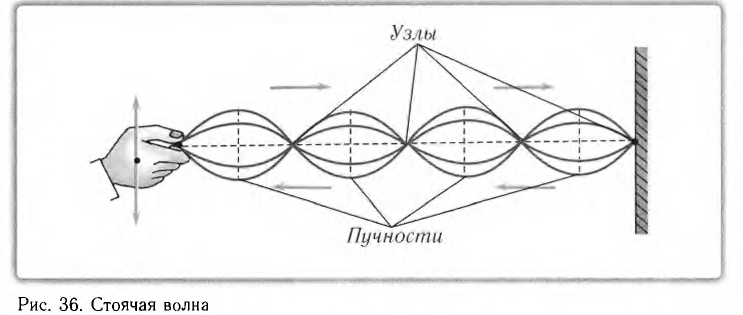
Рассмотрим еще один распространенный случай интерференции — сложение волн с одинаковыми частотами, распространяющихся в противоположных направлениях (например, падающей и отраженной волны), приводящее к образованию в пространстве устойчивой картины чередования максимумов амплитуды колебаний (пучностей) и минимумов (узлов).

Волна, возникающая в результате сложения двух волн одинаковой частоты, распространяющихся в противоположных направлениях, называется стоячей волной (рис. 36).

Пример решения задачи:

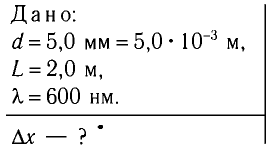
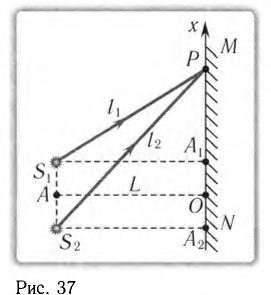
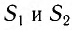
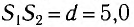
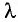
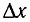
Рассчитайте положения максимумов и минимумов интерференционной картины на экране MN, находящемся на расстоянии L = АО = 2,0 м от двух одинаковых когерентных источников света , которые расположены в вакууме на расстоянии мм друг от друга (рис. 37). Длина волны излучения источников = 600 нм. Найдите расстояние между соседними максимумами.

Решение

До некоторой точки Р на экране волны проходят пути

Максимумы интенсивности будут наблюдаться при условии

а минимумы при условии —

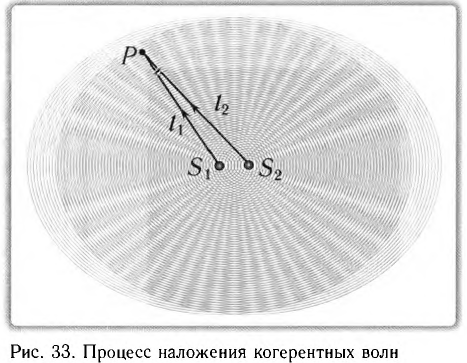
где m = 0, ±1, ±2…..

По теореме Пифагора из треугольников 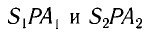находим

Откуда

С учетом того, что 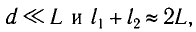находим

С учетом условия максимумов получаем

Откуда расстояние от центра экрана до т-й светлой полосы находится из соотношения

Из условия минимумов находим положение темных полос:

Откуда

Расстояние между соседними максимумами

Из полученной формулы видно, что ширина интерференционных полос увеличивается при уменьшении расстояния d между когерентными источниками.

Ответ:

Волновая природа света и дисперсия света

Показатель преломления среды относительно вакуума называется абсолютным показателем преломления этой среды. Абсолютный показатель преломления среды показывает, во сколько раз скорость света в этой среде меньше скорости света в вакууме:

Луч света, падающий на боковую грань треугольной призмы, отклоняется к основанию призмы.

Природа света

Несколько веков имели место два разных представления о природе света: корпускулярная и волновая природа света.

Основоположником представлений о корпускулярной природе света является И. Ньютон. Он считал, что свет является потоком частиц (корпускул). Прямолинейное распространение света и его отражение легко объяснялись согласно этому представлению.

Основоположником представлений о волновой природе света является голландский ученый Христиан Гюйгенс (1629-1695). Основной причиной возникновения этих представлений является прохождение световых лучей сквозь друг друга при распространении подобно волнам. В XIX веке английский ученый Томас Юнг (1773-1829) провел эксперименты, в которых обнаружил многочисленные факты, подтверждающие волновую природу света. Основоположник теории электромагнитного поля Дж. Максвелл теоретически обосновал электромагнитную волновую природу света. Согласно современным представлениям свет и другие электромагнитные волны обладают двойной — корпускулярной и волновой природой.

Заказать решение задач по физике

Дисперсия света

Одним из явлений, доказывающих волновую природу света, является дисперсия света.

Дисперсия света — это зависимость показателя преломления среды от частоты (длины волны) падающего света.

Впервые это явление исследовал Исаак Ньютон. Он поместил прозрачную стеклянную треугольную призму на пути тонкого пучка солнечного света, попадающего в затемненную комнату через маленькое отверстие в ставнях. Пройдя призму, солнечный луч разделился на спектр из семи составных цветных лучей. Последовательность цветов составных частей в дисперсионном спектре всегда одинакова: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый.

Среди монохроматических (содержащих свет одного цвета) лучей наиболее сильно преломляются фиолетовые лучи, а меньше других — красные (см: а). Причина явления объясняется на основе волновых представлений о свете. Так, абсолютный показатель преломления среды показывает, во сколько раз скорость света в этой среде меньше, чем в вакууме:

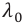
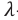
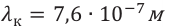
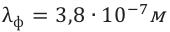
Здесь — длина световой волны в вакууме. — длина световой волны в среде. Значит, подвергающийся наименьшему преломлению красный свет имеет наименьший показатель преломления. А это означает, что красный свет обладает наибольшей длиной волны (или наименьшей частотой). Фиолетовый свет, наоборот, обладает наибольшим показателем преломления и наименьшей длиной волны (или наибольшей частотой). Из проведенных в дальнейшем экспериментов было определено, что дисперсионный спектр видимого света охватывает в шкале электромагнитных волн часть с длинами волн от (красный) до (фиолетовый).

Результат. Таким образом, явление дисперсии показало, что белый свет обладает сложным строением — состоит из монохроматических световых лучей разного цвета. Каждый монохроматический луч света обладает собственной частотой и длиной волны. Поэтому при прохождении монохроматического луча через стеклянную призму он, только преломляясь, изменяет своё направление (не разлагается на составные, не меняет окраски). Если разложенный призмой свет, состоящий из монохроматических составляющих, направить на вторую перевернутую призму, то на выходе из второй призмы опять получится белый свет.

Согласно физике цвета, ни один из трех основных цветов — красный, зеленый и синий, не могут получиться при смешивании двух других. Однако смешиванием основных цветов можно получить все остальные цвета и их оттенки.

Многоцветное восприятие нами окружающего мира объясняется явлениями поглощения, преломления и отражения света. Например, лист бумаги воспринимается нашим зрением белым потому, что он отражает падающий на него белый свет полностью. Если тело полностью поглощает падающий на него свет, то он воспринимается как черный, например, сажа.

Интерференция волн и интерференция света

• Самые часто встречаемые колебания в природе являются колебаниями в связанных системах. В связанных колебательных системах колебания передаются от одного звена системы другой. Например, бросив в воду камень, можно наблюдать распространение концентрических водных кругов из точки падения камня. Нам кажется, что происходит распространение воды в виде выпуклостей и впадин.

Какая связанная система создает волну в воде?

Какие явления происходят в среде при распространении волны?

Обратите внимание на картину, образованную на неподвижной поверхности воды поплавками удочек рыболовов (а). При встрече волн друг с другом происходит их сложение. В результате в определенных точках пространства они усиливают друг друга (а, 1), а в других ослабляют (а, 2).

Интерференция волн

В исследовании вы наблюдали результат сложения когерентных волн, созданных на поверхности воды гармоническими колебаниями шариков генератора с одинаковой частотой.

Когерентные волны — это волны, созданные различными источниками колебания, имеющими одинаковую частоту колебаний и постоянную разность фаз, не зависящую от времени.

Результирующие колебания, образованные сложением когерентных волн, в зависимости от разности между расстояниями от источника колебаний до точки их встречи или усиливаются, или ослабляются — происходит интерференция волн.

Интерференция волн -усиление или ослабление амплитуды колебаний результирующей волны в результате сложения когерентных волн (лат. «интер» взаимно, «ферио» — ударю).

Усиление или ослабление амплитуды результирующей волны определяется условиями максимума и минимума интерференции.

Условие максимума интерференции

Максимум интерференции наблюдается в точках пространства (поверхности), в которых максимумы слагаемых волн накладываются друг на друга. Это зависит от разницы пройденных волнами путей от источника колебаний до этой точки.

Интерференционный максимум результирующей волны образуется в точках, в которых разность хода складываемых волн равна нулю или четному числу полудлин волн (разность фаз равна нулю или четному количеству 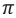) (d):

Здесь 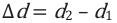— разность путей, проходимых волнами до точки сложения (разность хода), k— порядок максимума, является целым числом: k= 0,1, 2,…. Между разностью фаз и разностью хода когерентных волн существует такая связь:

Учитывая выражение (1) в формуле (2), для разницы фаз максимума интерференции получим:

В этом случае при равенстве амплитуд складываемых волн амплитуда результирующего колебания будет равна сумме амплитуд исходных волн (е):

Условие минимума интерференции

Минимумы интерференции наблюдаются в тех точках пространства, в которые волны доходят в противофазе. При этом максимум одной волны совпадает с минимумом другой. В результате волны ослабляют друг друга.

Минимум интерференции наблюдается в точках, в которых разность хода слагаемых волн равна нечетному числу полудлин волн (разность фаз равна нечетному количеству 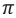) (f):

Если при этом амплитуды складываемых волн равны, то в точке минимума интерференции амплитуда результирующей волны уменьшается до нуля (g):

Интерференция света

Интерференция — характерное свойство всех видов волн, в том числе и световых. Так, две световые волны при сложении в пространстве могут усиливать или ослаблять друг друга, даже может случиться и такой вариант: свет + свет = темнота.

Интерференция света — явление увеличения или уменьшения амплитуды результирующих световых колебаний в разных точках пространства вследствие сложения двух когерентных световых волн.

Долгие годы не могли найти способ получения когерентных световых волн, поэтому невозможно было доказать способность световых волн интерферировать.

Только в начале XIX века с помощью несложного устройства Томас Юнг смог наблюдать интерференцию света (h).

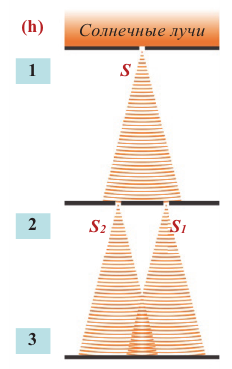
Классический опыт по наблюдению интерференции света состоит в следующем: солнечный свет освещает непрозрачный экран 1 и, пройдя через малое отверстие S в этом экране (проделанное булавкой), попадает на экран 2. Световые лучи, вышедшие из малых отверстий S₁ и S₂ на втором экране, являются когерентными. В результате интерференции этих волн на экране 3 появляются интерференционные полосы. В центральной части экрана наблюдаются чередующиеся цветные и темные полосы. По мере удаления от центра интерференционная картина ослабевает. Используя условие максимумов в этих опытах, Юнг смог на основе формулы (1) измерить длины световых волн для разных цветов. Как ни странно, первый опыт по интерференции света был проведен отрицающим его волновую природу Исааком Ньютоном. Поместив на стеклянной пластине плоско-выпуклую стеклянную линзу выпуклой стороной вниз, он осветил её сверху (i, 1). Посмотрев на линзу сверху, Ньютон увидел чередующиеся светлые и темные концентрические круги (i, 2), которые впоследствии стали называть кольцами Ньютона. Но ни Ньютон, ни повторявшие этот интересный опыт в течение более чем 100 лет ученые не смогли объяснить причину возникновения этих колец. И только в 1802 году Юнгу удалось объяснить происхождение колец Ньютона. Он объяснил кольца Ньютона таким образом: когда пучок света падает на плоскую поверхность линзы, то он, проходя сквозь нее, частично отражается от нижней сферической поверхности линзы (см. i-З, луч 1), а частично — от поверхности стеклянной пластинки, на которой лежит линза (см. i-З, луч 2). Вследствие такого многократного отражения образуются два когерентных луча. Эти лучи, складываясь, в соответствии с максимумами и минимумами интерференции создают интерференционную картину чередующихся темных и светлых концентрических кольца.

Определение длины световой волны

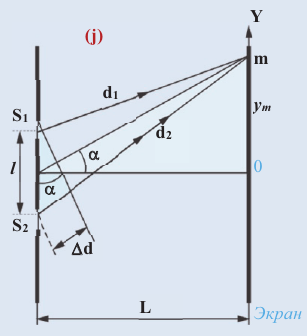
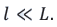
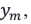
Представим, что расстояние между источниками когерентных волн S₁ и S₂ намного меньше расстояния от источников до экрана (j): В таком случае световые волны, исходящие из этих источников и дошедшие до точки экрана m с координатой , можно считать параллельными. Разность хода между этими лучами:

Вследствие малости угла

Условие интерференционного максимума в этом случае будет:

Отсюда можно найти длину волны:

Дифракция света
Принцип Гюйгенса — Френеля
Прохождение света через плоскопараллельные пластинки и призмы
Поляризация света
Преломление света
Полное отражение
Дисперсия света
Электромагнитная природа света

Источник

Условие максимумов при интерференции d — период дифракционной решетки, м (метр) φ — угол наблюдения максимума, рад (радиан) k — номер максимума, целое число: 0,1,2.. λ — длина волны, м (метр)
Интерференция — это явление, возникающее при наложении нескольких когерентных волн.
Когерентные волны — волны с одинаковой частотой и постоянной разностью фаз.

Дифракционная решетка — оптический прибор, поверхность которого содержит регулярно расположенные штрихи (канавки, щели, выступы). К примеру, компакт-диск является дифракционной решеткой и с его помощью можно наблюдать явление интерференции света.
$diffraction-grating$

Анимация интерференции двух когерентных волн, полученных при помощи дифракционной решетки.

Пример интерференционной картины от нескольких круговых когерентных волн.

Как измеряем? Размер дифракционных щелей задается при выборе решетки, расстояние между интерференционными максимумами измеряется на экране. Из этих данных рассчитывается длина волны источника света.

Как используем? Расстояние между интерференционными максимумами зависит от длины волны светового луча. Это позволяет определить длины световых волн, из которых состоит анализируемый луч света. Метод измерений длин волн при помощи интерференционной картины — называется спектральным анализом.

Для полного понимания явления интерференции, посмотрите этот фильм.

С момента 2:45 — начинается рассказ о том, как формируются максимумы и минимумы.

Задача 56.
На дифракционную решетку с периодом 1,2 мкм падает по нормали монохроматический свет с длиной волны 380 нм. Какой наибольший порядок дифракционного максимума можно получить в данной системе?

Показать ответ

Источник