Как найти расстояние между основаниями треугольника

Как найти расстояние между двумя точками?

Расстоянием между точками также называют прямую,
у которой одна из точек это начало, а соответственно
другая конец. Найти расстояние между этими
двумя точками, значит найти длину прямой,
связывающей точки.

Есть много разных способов найти расстояние между
двумя точками, но самый универсальный, на мой взгляд,
это найти расстояние взяв за основу Теорему Пифагора.
Исходя из этой теоремы, можно сказать, что в нашем
случае расстоянием(прямой), является гипотенуза,
а чем тогда являются точки, сейчас разберемся.

Формулировка великой Теоремы Пифагора звучит так:
в прямоугольном треугольнике квадрат гипотенузы равен
сумме квадратов катетов. Или же кратко, формулой:
( c^2 = a^2 + b^2 ) где c — это гипотенуза, a и b — катеты.

Формулировка этой теоремы применяется почти всегда и везде,
где нужно найти расстояние от чего-то до чего-то. Сейчас, мы
используя эту теорему найдем расстояние между точками.

Итак, для примера возьмем точки с координатами
первой точки — x1 = 0; y1 = 4, второй точки — x2 =3; y2 = 0.
Как же нам теперь выразить точки через катеты a и b ?
Читайте дальше, все гениальное просто.

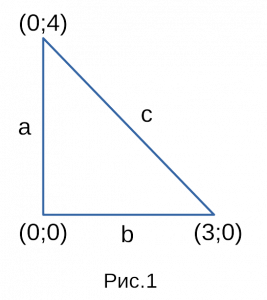
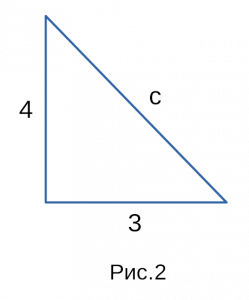
На рисунке 1 мы изобразили для наглядности
прямоугольный треугольник, с координатами
которые мы взяли для примера. На рисунке 2
тот же самый прямоугольный треугольник,
только без координат! Эти два прямоугольных
треугольника идентичные, поэтому вернемся
к Теореме Пифагора.

Заменяем длины катетов a и b, из Теоремы Пифагора,
на разность координат точек. ​Взгляните на формулу,
которая получилась:

Подставляем наши координаты:

В итоге получилось, что расстояние в нашем примере
равно 5(корень из 25). Как видите все просто, и вы можете
смело применять эту формулу, решая не только задачи,
но и на практике, находя расстояние зная только две точки.

Все формулы для треугольника

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c — стороны произвольного треугольника

α , β , γ — противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b — катеты

c — гипотенуза

α , β — острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)

a — равные стороны

α — углы при основании

β — угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

4. Найти длину высоты треугольника

Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

H — высота треугольника

a — сторона, основание

b, c — стороны

β , γ — углы при основании

p — полупериметр, p=(a+b+c)/2

R — радиус описанной окружности

S — площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

Расстояние от точки до прямой

Что называется расстоянием от точки до прямой? Как найти расстояние от точки до прямой?

Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из данной точки на прямую.

Таким образом, чтобы найти расстояние от точки до прямой, надо из точки к прямой провести перпендикуляр и найти его длину.

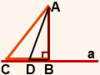
Например, на рисунке 1 расстояние от точки A до прямой a равно длине перпендикуляра AB, опущенного из точки A на прямую a.

Задачи на нахождение расстояния от точки до прямой сводятся к рассмотрению прямоугольного треугольника.

№ 1. Из точки к прямой проведены две наклонные, длины которых относятся как 2:3, а длины их проекций соответственно равны 2 см и 7 см. Найти расстояние от точки до прямой.

Дано: A∉a,

BC и BD — их проекции, BC=2 см, BD=7 см

1) Пусть k — коэффициент пропорциональности. Тогда AC=2k см, AD=3k см.

2) Рассмотрим треугольник ABC — прямоугольный (так как AB — перпендикуляр к прямой a по условию). По теореме Пифагора

3) Аналогично, из треугольника ABD

4) Приравниваем правые части полученных равенств и находим k:

5) Зная k, найдем AB:

№ 2. Из точки к прямой проведены две наклонные, длины которых равны 13 см и 15 см. Найти расстояние от точки до прямой, если разность проекций наклонных равна 4 см.

Дано: A∉a,

AC и AD — наклонные, AC=13 см, AD=15 см,

BC и BD — их проекции, BD-BC=4 см

1) Пусть BC=x см, тогда BD=x+4 см.

2) Рассмотрим треугольник ABC — прямоугольный (так как AB — перпендикуляр к прямой a по условию). По теореме Пифагора

3) Аналогично, из треугольника ABD

4) Приравниваем правые части полученных равенств и находим x:

5) Зная x, найдем AB:

№ 3. Найти расстояние от точки A до прямой a, если известно, что наклонная AF, длина которой равна c, образует с прямой a угол α.

Дано: A∉a,

Треугольник ABF — прямоугольный (так как AB — перпендикуляр к прямой a по условию). AB — катет, противолежащий углу ACB, AF — гипотенуза.

Что такое наклонная к прямой? Сколько наклонных можно провести из одной точки к данной прямой? Как найти расстояние между основаниями наклонных?

Определение.

Наклонной, проведенной из точки A к прямой a, называется отличный от перпендикуляра отрезок,  соединяющий точку A с некоторой точкой на прямой a.

Рисунок наклонной, проведенной из данной точки к данной прямой, начинают с изображения перпендикуляра (даже если в условии задачи о перпендикуляре не упоминается).

Чтобы нарисовать наклонную, нужно соединить точку, из которой проводится наклонная, с любой точкой на данной прямой.

На рисунке 1 AB — перпендикуляр, проведенный из точки A к прямой a, AC — наклонная.

Точка B — основание перпендикуляра, точка C — основание наклонной AC.

Отрезок BC, соединяющий основание перпендикуляра с основанием наклонной, — проекция наклонной AC на прямую a.

Из точки к прямой можно провести бесконечно много наклонных.

Две наклонные проведенные из данной точки к данной прямой, могут быть расположены как по одну сторону от перпендикуляра, так и по разные стороны от него.

На рисунке 2 наклонные AC и AD расположены по одну сторону от перпендикуляра AB.

BC — проекция наклонной AC на прямую a,

BD — проекция наклонной AD на прямую a.

CD — расстояние между основаниями наклонных

AC и AD.

CD=BC-BD.

Если наклонные расположены по одну сторону от перпендикуляра, чтобы найти расстояние между основаниями наклонных, надо найти разность между длинами их проекций.

На рисунке 3 наклонные AC и AD расположены по разные стороны от перпендикуляра AB.

BC — проекция наклонной AC на прямую a,

BD — проекция наклонной AD на прямую a.

CD — расстояние между основаниями наклонных

AC и AD:

CD=BC-BD.

Если наклонные расположены по разные стороны от перпендикуляра, расстояние между основаниями наклонных равно сумме  длин проекций этих наклонных.

В следующий раз рассмотрим свойства наклонных.

Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:

1. Найти все стороны треугольника.
2. Найти все углы треугольника.
3. Найти площадь (S) и периметр (P) треугольника.
4. Найти радиус (r) вписанной окружности.
5. Найти радиус (R) описанной окружности.
6. Найти высоту (h) треугольника.

Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.
 

Сторона треугольника (или длина сторон) может быть найдена различными методами. 
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.

Как найти длину стороны треугольника?

Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.

Для прямоугольного треугольника:

1) Найти катет через гипотенузу и другой катет

где a и b — катеты, с — гипотенуза.

2) Найти гипотенузу по двум катетам

где a и b — катеты, с — гипотенуза.

3) Найти катет по гипотенузе и противолежащему углу

где a и b — катеты, с — гипотенуза,α° и β° — углы напротив катетов.

4) Найти гипотенузу через катет и противолежащий угол

где a и b — катеты, с — гипотенуза,α° и β°- углы напротив катетов.

Для равнобедренного треугольника:

1) Найти основание через боковые стороны и угол между ними

где a — искомое основание, b — известная боковая сторона,α° — угол между боковыми сторонами.

2) Найти основание через боковые стороны и угол при основании

где a — искомое основание,b — известная боковая сторона,β° — угол при осноавнии.

3) Найти боковые стороны по углу между ними

где b — искомая боковая сторона, a — основание,α° — угол между боковыми сторонами.

4) Найти боковые стороны по углу при основании

где b — искомая боковая сторона, a — основание,β° — угол при осноавнии.

​​​​​Для равностороннего треугольника:

1) Найти сторону через площадь

где a — искомая сторона, S — площадь треугольника.

2) Найти сторону через высоту

где a — искомая сторона,h — высота треугольника.

3) Найти сторону через радиус вписанной окружности

где a — искомая сторона,r — радиус вписанной окружности.

4) Найти сторону через радиус описанной окружности

где a — искомая сторона,R — радиус описанной окружности.

​​​​​Для произвольного треугольника:

1) Найти сторону через две известные стороны и один угол (теорема косинусов)

где a — искомая сторона, b и с — известные стороны, α° — угол напротив неизвестной стороны.

2) Найти сторону через одну известную сторону и два угла (теорема синусов)

где a — искомая сторона, b — известная сторона, α° и β° известные углы.

Скачать все формулы в формате Word

Треугольник является базовой фигурой геометрии, встречающейся повсеместно. Расчет всех геометрических фигур и тел основаны на наличии в них тех или иных треугольников, благодаря чему становится возможным применить множество теорем и формул, несвойственных конкретным фигурам по отдельности. Равносторонние треугольники, равнобедренные треугольники и прямоугольные треугольники составляют каркас решения геометрических задач, и обладая множеством дополнительных построений внутри треугольника, они предоставляют огромное количество значений тех или иных длин. Все биссектрисы, медианы, высоты, радиусы окружностей, вписанных или описанных около таких треугольников, можно рассчитать в этом разделе через геометрический калькулятор. Для этого необходимо ввести любые имеющиеся вводные данные, и калькулятор выдаст не только значения всех остальных параметров треугольника, но и объяснит преобразования формул, использованные для этих расчетов.