Как найти расстояние между отрезками 6 класс - Исправление недочетов и поиск решений вместе с Examum.ru

Назовите кто − нибудь
Нам синоним к слову «путь»!

Назовите кто − нибудь
Нам синоним к слову «путь»!
Без труда его найдёте
Вы от точки до другой,

Назовите кто − нибудь
Нам синоним к слову «путь»!
Без труда его найдёте
Вы от точки до другой,
А потом определите
И от точки до прямой.

РАССТОЯНИЕ

РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ

Как найти расстояние между палатками?
РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ

РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ
Расстояние между палатками – это длина отрезка,
который соединяет эти палатки.

РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ

Расстояние − это всегда длина кратчайшего пути.
РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ

РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ
Как проложить кратчайший путь от дома лесника до озера?

Будем проводить окружности с центром в точке А, увеличивая их радиусы, пока одна из них «не достигнет» озера.
РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ

В результате найдём точку озера, ближайшую к дому лесника.
РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ

Длина отрезка АМ и есть расстояние от дома лесника до озера.
РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ

РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ
Как найти расстояние от дома лесника до шоссе,
которое проходит по прямой?

РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ
Расстояние от дома лесника до шоссе – длина перпендикуляра, проведенного из точки А к шоссе, которое проходит по прямой.

ЗАДАЧИ НА ПОСТРОЕНИЕ

РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ
Нахождение расстояния между двумя точками.

РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ
АВ = 13 см
Расстояние между точками А и В − длина отрезка АВ.

РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ
Нахождение расстояния от точки до прямой.

Нахождение расстояния от точки до прямой.
РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ

РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ
Нахождение расстояния от точки до прямой.

Расстояние от точки А до прямой m − длина АК.
РАССТОЯНИЕ ОТ ТОЧКИ ДО ФИГУРЫ
АK = 11 см

РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ

РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ
Нахождение расстояния между прямыми а и b (а ∥ b).

РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ
Расстояние между прямыми а и b − длина MN.
MN= 10 см

Рельсы на прямолинейном участке должны быть параллельными: они не могут сближаться или удаляться.
РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ

Поэтому их крепят к шпалам на одном и том же расстоянии
друг от друга. Это расстояние называют шириной колеи.
РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ

РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ

Как найти расстояние от светильника до пола?
РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ

Расстояние от точки до плоскости измеряют по перпендикуляру.
РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ

ABCDKLMN – куб. Ребро АВ перпендикулярно грани AKND.
РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ

РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ
ABCDKLMN – куб. Ребро АВ перпендикулярно грани AKND. Расстояние от точки В до плоскости AKND равно длине АВ.

РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ
ABCDKLMN – куб. Ребро ВС перпендикулярно грани СМND.

РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ
ABCDKLMN – куб. Ребро ВС перпендикулярно грани СМND. Расстояние от точки В до плоскости СМND равно длине ВС.

Источник

Расстоянием между двумя точками A и B называется длина отрезка, соединяющего эти точки.

Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату левого конца.

Примеры.

Найти расстояние в единичных отрезках между точками:

1) A(-11) и B(3);

2) M(-5,1) и N(-7,2);

3) C (0) и D(-12);

$[4)P( - frac{2}{9})uK(frac{5}{{12}});]$

$[5)E(3frac{3}{8})uF( - 2frac{1}{6}).]$

Решение:

Чтобы найти расстояние между точками на координатной прямой, определим, какая из точек находится правее, и из координаты правого конца отрезка вычтем координату его левого конца.

Из двух точек на координатной прямой точка с большей координатой лежит правее точки с меньшей координатой.

Для точек A(a) и B(b) это означает, что если b>a, то точка B на координатной прямой лежит правее точки A и расстояние между точками A и B равно

1) Так как 3>11, то на координатной прямой точка B с координатой 3 лежит правее точки A с координатой -11. Следовательно, расстояние между точками A и B

2) -5,1>-7,2, поэтому на координатной прямой точка M(-5,1) лежит правее точки N(-7,2). Значит, расстояние между точками M и N равно

3) Так как 0>-12, точка C (0) на координатной прямой лежит правее точки D(-12). Расстояние между точками C и D:

$[4)frac{5}{{12}} > - frac{2}{9},]$

поэтому точка K на координатной прямой расположена правее, чем точка P.

$[left| {PK} right| = frac{5}{{12}} - ( - frac{2}{9}) = frac{{{5^{backslash 3}}}}{{12}} + frac{{{2^{backslash 4}}}}{9} = frac{{15 + 8}}{{36}} = frac{{23}}{{36}}.]$

$[5)3frac{3}{8} > - 2frac{1}{6},]$

значит, точка E на координатной прямой находится справа от точки F. Поэтому длина отрезка EF, а значит, и расстояние между точками E и F

$[left| {EF} right| = 3frac{3}{8} - ( - 2frac{1}{6}) = 3frac{{{3^{backslash 3}}}}{8} + 2frac{{{1^{backslash 4}}}}{6} = 5frac{{9 + 4}}{{24}} = 5frac{{13}}{{24}}.]$

Источник

Простейшие расстояния на плоскости

Расстояние – это длина, на которую объекты удалены друг от друга.

Чтобы измерить длину или расстояние используют различные измерительные приборы: линейку, рулетку, ленты и даже лазерные дальномеры. Все они показывают, как далеко находится один объект до другого. Длина всегда измеряется в определенных величинах: миллиметрах, сантиметрах, дециметрах, метрах, километрах.

РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ:

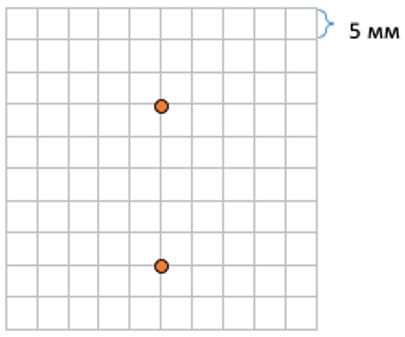
1. Представим тетрадный лист в клетку. Мы знаем, что длина и ширина каждой клетки равна 5 мм или половине сантиметра (5мм х 5мм). Попробуем найти расстояние между двумя точками:

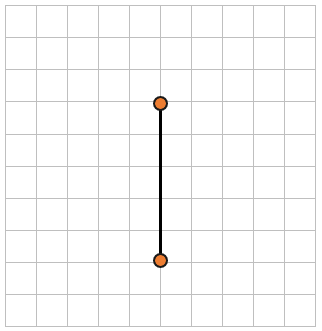
Проведем отрезок между этими точками. Этот отрезок проходит 5 клеток. Каждая клетка = 5 мм.

Значит расстояние между точками равно длине отрезка, заключенного между ними:

(5мм bullet 5 = 25мм).

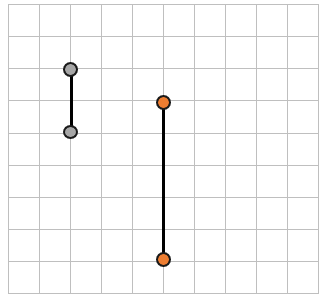
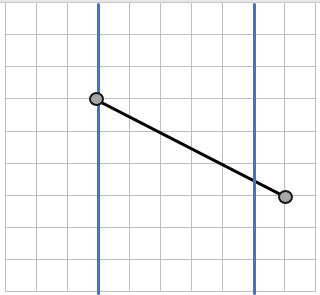
2. Добавим еще две точки на наш лист в клетку и посчитаем расстояние между ними:

Расстояние между этими двумя точками (5мм bullet 2 = 10мм). Теперь мы можем сравнить расстояния до разных точек, зная их длину:

(25мм > 10мм)

Значит расстояние между оранжевыми точками больше, чем расстояние между серыми.

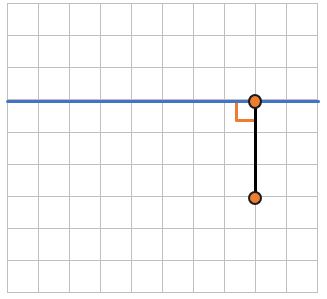
РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПРЯМОЙ:

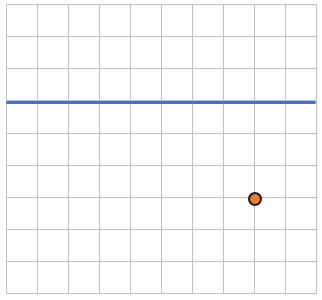
Теперь рассмотрим на клетчатой бумаге, клетки которой равны 1см х 1 см точку и прямую линию:

Найдем расстояние между точкой и прямой. Таким расстоянием будет являться наикратчайшее расстояние.

Наикратчайшее расстояние – это перпендикуляр, проведенный между двумя точками.

Это значит, что расстоянием между точкой и прямой будет длина перпендикуляра между ними.

Перпендикуляр – это отрезок, проходящий под прямым углом к чему-либо.

Теперь если мы посчитаем длину перпендикуляра – найдем расстояние между прямой и точкой:

(1см bullet 3 = 3см)

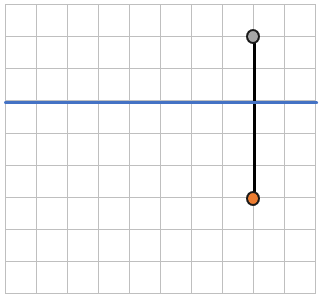
Длины каких отрезков НЕ будут являться расстоянием между прямой и точкой:

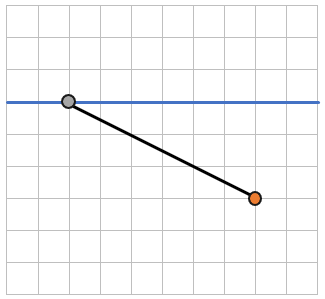
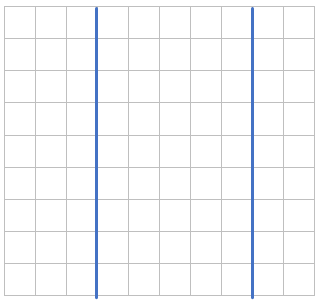
РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ:

Длина любого перпендикуляра между двумя параллельными прямыми везде одинакова, поэтому, чтобы найти расстояние между параллельными прямыми, можно взять любой перпендикуляр между ними и измерить его длину:

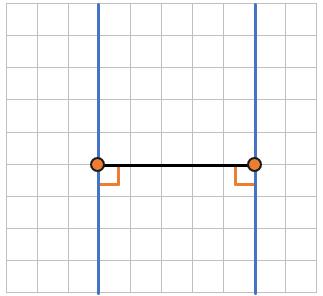
Проведем перпендикуляр между прямыми:

Длина перпендикуляра между прямыми будет равна

расстоянию между ними, т.к. перпендикуляр – кратчайшее расстояние:

(1см bullet 5 = 5см)

Длины каких отрезков НЕ будут являться расстоянием между параллельными прямыми:

Источник

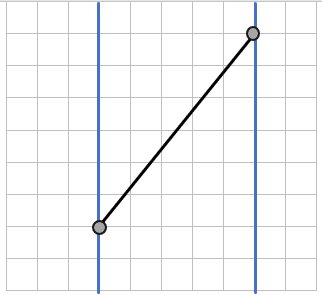
Слайд 1

Расстояние между точками на координатной прямой х 0 1 А В АВ = ρ (А, В)

Слайд 2

Расстояние между точками на координатной прямой Цель урока: — Найти способ (формулу, правило) для нахождения расстояния между точками на координатной прямой. — Научиться находить расстояние между точками н а координатной прямой, используя найденное правило.

Слайд 3

1. Устный счет 15 -22 +8 -31 +43 -27 -14

Слайд 4

2 . Устно решите задание с помощью координатной прямой: сколько целых чисел заключено между числами: а ) – 8,9 и 2 б ) – 10,4 и – 3,7 в ) – 1,2 и 4,6? а ) 10 б ) 8 в ) 6

Слайд 5

0 1 2 7 п оложительные числа -1 -5 о трицательные числа Расстояние от дома до стадиона 6 Расстояние от дома до школы 6 Координатная прямая

Слайд 6

0 1 2 7 -1 -5 Расстояние от стадиона до дома 6 Расстояние от школы до дома 6 Нахождение расстояния между точками на координатной прямой ρ ( -5 ; 1 )=6 ρ ( 7 ; 1 )=6 Расстояние между точками будем обозначать буквой ρ ( ро )

Слайд 7

0 1 2 7 -1 -5 Расстояние от стадиона до дома 6 Расстояние от школы до дома 6 Нахождение расстояния между точками на координатной прямой ρ ( -5 ; 1 )=6 ρ ( 7 ; 1 )=6 ρ (a; b) = ? | a-b |

Слайд 8

Расстояние между точками a и b равно модулю разности координат этих точек. ρ ( a; b)= | a-b | Расстояние между точками на координатной прямой

Слайд 9

Геометрический смысл модуля действительного числа a b a a=b b x x x Расстояние между двумя точками

Слайд 10

0 1 2 7 -1 -5 На йдите расстояния между точками на координатной прямой — 2 — 3 — 4 3 4 5 6 -6 ρ (-6 ; 2 )= ρ (6 ; 3 )= ρ (0 ; 7 )= ρ (1 ; -4 ) = 8 3 7 5

Слайд 11

0 1 2 7 -1 -5 На йдите расстояния между точками на координатной прямой — 2 — 3 — 4 3 4 5 6 -6 ρ (2 ; -6 )= ρ (3 ; 6 )= ρ (7 ; 0 )= ρ (-4 ; 1 ) = 8 3 7 5

Слайд 12

Вывод : значения выражений | a – b | и | b – a | равны при любых значениях а и b =

Слайд 13

–16 –2 0 –3 +8 0 +4 +17 0 ρ(–3; = 11; |(–3) – (+8)| = 11; |(+8) – (–3)| = 11. ρ(–16; –2) = 14; |(–16) – (–2)| = 14; |(–2) – (–16)| = 14. ρ(4; 17) = 13; |(+4) – (+17)| = 13; |(+17) – (+4)| = 13. Расстояние между точками координатной прямой

Слайд 14

Найдите ρ(х; у) , если : 1 ) x = – 14, у = – 23; ρ( х ; у )=| х – у |=|–14–(– 23 )|=|–14+23|=| 9 |=9 2 ) x = 5,9 , у = –6,8; ρ( х ; у )=|5, 9 –(– 6,8 )|=|5,9+6,8|=| 12,7 |=12,7

Слайд 15

Продолжить предложение 1. Координатная прямая – это прямая с указанными на ней … 2. Расстояние между двумя точками — это … 3. Противоположные числа – это числа, … 4. Модулем числа Х называют … 5. — Сравните значения выражений a – b V b – a сделайте вывод … — Сравните значения выражений | a – b | V | b – a | c делайте вывод …

Слайд 16

Винтик и Шпунтик идут по координатному лучу. Винтик находится в точке В(236), Шпунтик – в точке Ш(193) На каком расстоянии друг от друга находятся Винтик и Шпунтик ? ρ (B, Ш ) = 43

Слайд 17

Найдите расстояние между точками А(0 ), В(1 ) А(2 ), В(5 ) А(0 ), В (- 3) А(- 10), В(1 ) АВ = 1 АВ = 3 АВ = 3 АВ = 11

Слайд 18

Найдите расстояние между точками А(- 3,5), В(1,4 ) К(1,8 ), В(4,3 ) А(- 10), С(3 )

Слайд 19

Проверка АВ = КВ = АС =

Слайд 20

С( – 5 ) С(– 3 ) Найдите координату точки — середины отрезка ВА

Слайд 21

На координатной прямой отмечены точки А (–3,25) и В (2,65). Найдите координату точки О – середины отрезка АВ. Решение : 1) ρ(А;В )= |–3,25 – 2,65| = |–5,9| = 5,9 2) 5,9 : 2 = 2,95 3) –3,25 + 2,95 = – 0,3 или 2,65 – 2,95 = – 0,3 Ответ : О(–0,3 )

Слайд 22

На координатной прямой отмечены точки С( – 5,17) и D(2,33). Найдите координату точки А – середины отрезка CD. Решение: 1 ) ρ(С; D )= |– 5 , 17 – 2, 33 | = |– 7 , 5 | = 7 , 5 2 ) 7 , 5 : 2 = 3 , 7 5 3) – 5 , 17 + 3 , 7 5 = – 1 , 42 или 2, 33 – 3 , 7 5 = – 1 , 42 Ответ: A (– 1 , 42 )

Слайд 23

Вывод: Алгоритм нахождения координаты точки – середины данного отрезка: 1. Найти расстояние между точками – концами данного отрезка = 2. Разделить результат-1 на 2 (половина величины) = с 3. Прибавить результат-2 к координате а или вычесть результат-2 из координаты а + с или — с 4. Результат-3 есть координата точки — середины данного отрезка

Слайд 24

Работа с учебником: §19, с.112, А. № 573, 575 В. № 578, 580 Домашнее задание: §19, с.112, А. № 574, 576, В. № 579, 581 подготовиться к КР «Сложение и вычитание рациональных чисел. Расстояние между точками на координатной прямой»

Слайд 25

Сегодня я узнал… Было интересно… Я понял, что… Теперь я могу… Я научился… У меня получилось… Я попробую… Меня удивило… Мне захотелось…

Слайд 26

До новых встреч!

Источник

Математика

6 класс

Урок № 75

Длина отрезка

Перечень рассматриваемых вопросов:

длина отрезка;
единицы измерения длины;
способы измерения длины отрезка;
решение задач на вычисление длины отрезка.

Тезаурус

Отрезок – это часть прямой, ограниченная двумя точками.

Длина отрезка – это расстояние между его концами.

Измерение длины отрезка – это сравнение длины отрезка с выбранной единицей измерения.

Длиной отрезка называется положительная величина, определённая для каждого отрезка.

Любой отрезок имеет определённую длину, большую нуля.

Обязательная литература:

Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.

Дополнительная литература:

Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.

Теоретический материал для самостоятельного изучения

Что такое отрезок?

Отрезок – это часть прямой, ограниченная двумя точками.

Как отрезки обозначаются на чертежах?

Отрезок можно обозначить двумя заглавными буквами – отрезок АВ. Или можно обозначить отрезок одной строчной буквой – отрезок с.

Любой отрезок имеет определённую длину, большую нуля.

Длина может быть выражена натуральным или дробным числом.

Измерить отрезок – значит найти его длину.

Длина отрезка – это расстояние между его концами.

Свойства длин отрезков:

– равные отрезки имеют равные длины;

– если отрезок состоит из двух отрезков, то его длина равна сумме длин его частей.

Эти свойства длины отрезка используются при её измерении. Чтобы измерить длину отрезка, нужно выбрать единицу длины.

Такой единицей может быть длина произвольного отрезка. В мультфильме «38 попугаев» герои измеряли длину удава в попугаях.

Для определения длины отрезка надо узнать, сколько раз в данном отрезке помещается выбранная единица измерения.

Можно сравнивать длины отрезков, не имея под рукой линейки. Например, прикладывать к отрезкам один и тот же карандаш, ластик или использовать циркуль. Для этого нужно установить иглу в начало отрезка, провести дугу, пересекающую отрезок, затем, не меняя расстояния между иглой и карандашом циркуля, переставить иглу в точку пересечения и повторить действия.

В десятичной системе мер единицами измерения длины являются 1 мм, 1 см, 1 дм, 1 м и т. д.

Рассмотрим несколько примеров измерения длины отрезка. Измерения небольших отрезков удобно производить с помощью линейки.

Прикладываем линейку так, чтобы один конец отрезка совместился с нулём. Единичный отрезок 1 см отложился 7 раз, значит, длина отрезка АВ = 7 см.

Если единичный отрезок 1 см отложился n раз, и осталась часть меньшая 1 см, то откладываем отрезки равные 1/10 см. Длина отрезка СD = 8,7 см.

При необходимости можно продолжить откладывать по 1/100 части единичного отрезка и т. д.

Алгоритм измерения длины отрезков:

– выбрать какой-либо отрезок и принять его за единицу длины;

– от одного из концов отрезка отложить последовательно отрезки, равные единичному;

– если единичные отрезки отложились n раз и конец последнего совпал с концом измеряемого отрезка, то значение его длины равно n единиц длины;

– если отрезок или его часть меньше единичного отрезка, то нужно отложить отрезки, равные 1/10 части единичного отрезка;

– если десятые части единичного отрезка отложились ровно n раз, то длина измеряемого отрезка есть конечная десятичная дробь, в которой целая часть равна количеству целых единичных отрезков, а после запятой в разряде десятых стоит количество десятых частей единичного отрезка;

– при необходимости можно откладывать 1/100 часть единичного отрезка и т. д.

Таким образом, для каждого положительного действительного числа существует отрезок, длина которого выражается этим числом.

И для каждого положительного действительного числа существует отрезок, длина которого выражается этим числом.

На практике используют приближённое значение длин отрезков, например, с точностью 1/10 или 1/100 части единичного отрезка, но точность приближения зависит от поставленной задачи.

Рассмотрим фигуры, составленные из отрезков.

Возьмем на плоскости несколько точек и соединим их отрезками. Если никакие два из этих отрезков, имеющих общие точки, не лежат на одной прямой, то линию называют ломаной.

Отрезки, из которых состоит ломаная, называются звеньями, а концы этих отрезков – вершинами ломаной.

Длина ломаной – это сумма длин всех её звеньев.

Если концы ломаной совпадают, то такая ломаная называется замкнутой.

Замкнутая ломаная линия, у которой звенья не пересекаются между собой, называется многоугольником.

Периметр многоугольника равен сумме длин всех его сторон.

Разбор заданий тренировочного модуля

Тип 1. Ввод с клавиатуры пропущенных элементов в тексте.

Впишите верный ответ.

Точка P лежит на отрезке AB. Известно, что отрезок AP больше отрезка PB на 3,6 см, а отрезок AB = 10,4 см. Найдите длину отрезка PB.

Решение:

Пусть PB = x, тогда AP = x + 3,6 см.

По условию AB = 10,4 см.

Если отрезок состоит из двух отрезков, то его длина равна сумме длин его частей.

PB + AP = AB.

Составим и решим уравнение:

x + x + 3,6 = 10,4,

2x + 3,6 = 10,4,

2x = 10,4 – 3,6,

2x = 6,8,

x = 3,4.

Значит, длина отрезка PB = 3,4 см.

Ответ: 3,4 см.

Тип 2. Множественный выбор

Выберите верные ответы.

Задача 2

Известно, что отрезок AС = 3,6 см, а отрезок BС = 7,5 см. Найдите длину отрезка АB, если все три точки лежат на одной прямой.

Варианты ответов: 3,9; 11,1; 4,8; 13,2; 16,5; 2,9.

Первый вариант решения

В этом случае АВ = АС + ВС = 3,6 + 7,5 = 11,1 (см).

Второй вариант

BC = AB + AC,

АВ = ВС – АС = 7,5 – 3,6 = 3,9 (см).

Значит, длина отрезка АВ может быть равна 11,1 см или 3,9 см. Выбираем эти варианты.

Ответ: 11,1; 3,9.

Источник