Координаты концов первого отрезка: A(xa, ya), B(xb, yb).
Координаты концов второго отрезка: C(xc, yc), D(xd, yd).
Для начала проверим не пересекаются ли отрезки.
Пусть для отрезка AB: x = t(xb — xa) + xa, y = t(yb — ya) + ya, тогда для CD: x = s(xd — xc) + xc, y = s(yd — yc) + yc, где 0 ≤ t,s ≤ 1.
Если отрезки пересекаются, то выполняются равенства:
t(xb — xa) — s(xd — xc) = xc — xa и t(yb — ya) — s(yd — yc) = yc — ya.
Полученную систему уравнений решим методом Крамера:
Δ = (xb — xa)(yс — yd) — (yb — ya)(xс — xd).
Δ1 = (xb — xa)(yс — ya) — (yb — ya)(xс — xa).
Δ2 = (xc — xa)(yс — yd) — (yc — ya)(xс — xd).
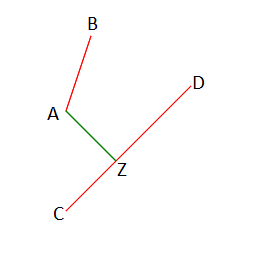
Тогда t = Δ1/Δ, s = Δ2/Δ. Если 0 ≤ t,s ≤ 1 и Δ ≠ 0, то отрезки пересекаются и расстояние между ними min равно 0, иначе с каждого конца отрезка попытаемся опустить высоту на противоположный. Если отрезок, на который опускаем высоту вертикальный, то поменяем местами координаты каждого конца отрезка и точки, с которой опускаем высоту (таким образом сохраним расстояние между точкой и отрезком, а отрезок станет горизонтальным).
Пусть k и d — коэффициенты уравнения прямой, на которую опущена эта высота. Основание высоты будет находится на прямой в точке Z, координаты Z(xz, yz) можно найти по формуле yz = kxz + d. Поскольку высота перпендикулярна отрезку — скалярное произведение их векторов равно 0. Тогда (x2 — x1)(x3 — xz)+(y2 — y1)(y3 — yz) = 0, соответственно xz = (x3x2 — x3x1 + y2y3 — y1y3 + y1d — y2d)/(ky2 — ky1 + x2 — x1), где (x3, y3) — координаты точки, с которой была опущена высота, (x1, y1) и (x2, y2) — координаты концов отрезка, принадлежащего прямой на которую опущена высота.
Вычислим длину dl каждой высоты, основание которой принадлежит одному из данных отрезков: dl = √((x3 — xz)2 + (y3 — kxz — d)2).
Минимальная длина высоты и будет наименьшим расстоянием между отрезками. В случае, если невозможно опустить высоты из одного отрезка на другой: расстояние между ними будет равно минимальному расстоянию между концами двух отрезков: min = √((x1 — x3)2 + (y1 — y3)2), где (x1, y1) — координаты одного из концов первого отрезка, а (x3, y3) — координаты одного из концов второго отрезка.
тупое решение в лоб — идем в поисковик, и просто тупо пишем: расстояние между отрезками
вторая же ссылка (ну лично у меня) — Ю2.30. Расстояние между отрезками
там и описание и решение и код, правда на Си
берем его и переписываем на Python, получаем:
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import math
def ras (x1, y1, x2, y2, x3, y3):
## Если отрезок вертикальный - меняем местами координаты каждой точки.
if x1==x2:
x1, y1 = y1, x1
x2, y2 = y2, x2
x3, y3 = y3, x3
k=(y1-y2)/(x1-x2) ## Ищем коэффициенты уравнения прямой, которому принадлежит данный отрезок.
d=y1-k*x1
xz=(x3*x2-x3*x1+y2*y3-y1*y3+y1*d-y2*d)/(k*y2-k*y1+x2-x1)
dl=-1
if ( xz<=x2 and xz>=x1 ) or ( xz<=x1 and xz>=x2 ):
dl=math.sqrt((x3-xz)*(x3-xz)+(y3-xz*k-d)*(y3-xz*k-d)) ## Проверим лежит ли основание высоты на отрезке.
return dl
## Вводим параметры отрезков
# xa, ya, xb, yb = [1, 1, 2, 2]
# xc, yc, xd, yd = [2, 1, 3, 0]
xa, ya, xb, yb = [int(s) for s in input().split()]
xc, yc, xd, yd = [int(s) for s in input().split()]
min=-1
t=-2
s=-2
o=(xb-xa)*(-yd+yc)-(yb-ya)*(-xd+xc)
o1=(xb-xa)*(yc-ya)-(yb-ya)*(xc-xa)
o2=(-yd+yc)*(xc-xa)-(-xd+xc)*(yc-ya)
if o!=0:
t=o1/o
s=o2/o
if (t>=0 and s>=0) and (t<=1 and s<=1):
min=0 ## Проверим пересекаются ли отрезки.
else:
## Найдём наименьшую высоту опущенную из конца одного отрезка на другой.
dl1=ras(xa,ya,xb,yb,xc,yc)
min=dl1
dl2=ras(xa,ya,xb,yb,xd,yd)
if ( dl2<min and dl2!=-1 ) or min==-1 :
min=dl2
dl3=ras(xc,yc,xd,yd,xa,ya)
if ( dl3<min and dl3!=-1 ) or min==-1 :
min=dl3
dl4=ras(xc,yc,xd,yd,xb,yb)
if ( dl4<min and dl4!=-1) or min==-1 :
min=dl4
if min==-1 :
## В случае, если невозможно опустить высоту найдём минимальное расстояние между точками.
dl1=math.sqrt((xa-xc)*(xa-xc)+(ya-yc)*(ya-yc))
min=dl1
dl2=math.sqrt((xb-xd)*(xb-xd)+(yb-yd)*(yb-yd))
if dl2<min :
min=dl2
dl3=math.sqrt((xb-xc)*(xb-xc)+(yb-yc)*(yb-yc))
if dl3<min :
min=dl3
dl4=math.sqrt((xa-xd)*(xa-xd)+(ya-yd)*(ya-yd))
if dl4<min :
min=dl4
print (min)PS: ну, …. пробовали?? или нужно на подносе?
Во-первых, для нахождения расстояния от точки (x, y) до отрезка (ax, ay)-(bx, by) не нужна никакая «бинарка». Использовать поисковый алгоритм для нахождения этого расстояния — безобразие. Это элементарная задача вычислительной геометрии. Например, в целых числах (не выжимая процессорные такты и не беспокоясь о переполнениях)
int point_to_segment_distance_sq(int x, int y, int ax, int ay, int bx, int by)
{
// Обеспечим, чтобы наш отрезок был более горизонтальным, чем вертикальным
int dx = bx - ax, dy = by - ay;
if (std::abs(dx) < std::abs(dy))
{
std::swap(x, y);
std::swap(ax, ay);
std::swap(bx, by);
std::swap(dx, dy);
}
// Обеспечим, чтобы наш отрезок шел слева направо
if (dx < 0)
{
std::swap(ax, bx);
std::swap(ay, by);
dx = -dx;
dy = -dy;
}
// Действия, выполненные выше, нужны только для того, чтобы впоследствии
// мы могли проверить, попадает ли точка (px, py) (см. ниже) внутрь нашего
// отрезка (ax, ay)-(bx, by). Теперь это можно сделать простым сравнением
// `px < ax` и `px > bx`
// Строим уравнение прямой
int A = dy, B = -dx, C = -(A * ax + B * bx);
// Вычисляем ненормированное ориентированное расстояние от точки до прямой
int d = A * x + B * y + C;
// Находим проекцию нашей точки на прямую
int absq = A * A + B * B;
int px = x - A * d / absq, py = y - B * d / absq;
// Проверяем, не попали ли мы за пределы отрезка
if (px < ax)
{
px = ax;
py = ay;
}
else if (px > bx)
{
px = bx;
py = by;
}
// Возвращаем квадрат расстояния
x -= px;
y -= py;
return x * x + y * y;
}
Во-вторых, достаточно применить эту функцию четыре раза — для поиска расстояния от каждого из четырех концов, чтобы найти минимальное расстояние для непересекающихся отрезков. А вот именно этот особый случай — пересекающиеся отрезки — и надо еще уметь отлавливать и обрабатывать. (На самом деле вышеприведенная функция вычисляет всю необходимую информацию для такой проверки.)
|
1125 / 294 / 74 Регистрация: 16.03.2020 Сообщений: 926 |
|
|
15.02.2023, 14:40 [ТС] |
7 |
|
Немного поспорив и поизменяв формулировки я добился следующего: Кликните здесь для просмотра всего текста Да, формула, которую я привел в прошлом ответе, не учитывает случай перпендикулярных отрезков. Для таких отрезков можно использовать следующий алгоритм: Найти проекции начальной и конечной точек каждого отрезка на другой отрезок. Вычислить вектора отрезков AB и CD и их длины. Код AB = sqrt((xB-xA)^2 + (yB-yA)^2) # Длина отрезка AB
CD = sqrt((xD-xC)^2 + (yD-yC)^2) # Длина отрезка CD
AC = (xC-xA)*(xB-xA) + (yC-yA)*(yB-yA) # Скалярное произведение векторов AC и AB
BD = (xD-xB)*(xB-xA) + (yD-yB)*(yB-yA) # Скалярное произведение векторов BD и AB
if AB == 0 and CD == 0:
distance = sqrt((xA-xC)^2 + (yA-yC)^2) # Отрезки совпадают
elif AB == 0:
distance = point_to_segment_distance(xA, yA, xC, yC, xD, yD) # Отрезок AB вырожден
elif CD == 0:
distance = point_to_segment_distance(xC, yC, xA, yA, xB, yB) # Отрезок CD вырожден
elif AC <= 0 and BD <= 0:
distance = point_to_segment_distance(xA, yA, xC, yC, xD, yD) # Проекции лежат на отрезке CD
elif AC <= 0:
distance = point_to_segment_distance(xA, yA, xC, yC, xD, yD) # Проекция точки A лежит на отрезке CD
elif BD <= 0:
distance = point_to_segment_distance(xB, yB, xC, yC, xD, yD) # Проекция точки B лежит на отрезке CD
else:
distance = min(point_to_point_distance(xA, yA, xC, yC),
point_to_point_distance(xA, yA, xD, yD),
point_to_point_distance(xB, yB, xC, yC),
point_to_point_distance(xB, yB, xD, yD)) # Проекции лежат за пределами отрезка CD
То есть вроде бы и ответ есть, но используются якобы имеющиеся функции point_to_point_distance и point_to_segment_distance. Не по теме: Интересно, что псевдокод он выдал практически полностью питоном. Вот она, пропаганда! Уже до нейросетей добралась. И язык ответа на вопрос по программированию по умолчанию в нем тоже питон…
0 |
Расстояния между двумя точками
На данной странице калькулятор поможет рассчитать расстояние между двумя точками онлайн в плоскости и пространстве. Для расчета задайте координаты.
Расстояние между двумя точками — это длина отрезка, которая соединяет эти точки.
Расстояния между двумя точками
Формула вычисления расстояния между двумя точками A(xa; ya) и B(xb; yb) на плоскости:
Формула вычисления расстояния между двумя точками A(xa; ya; za) и B(xb; yb; zb) в пространстве:
Вывод формулы для вычисления расстояния между двумя точками на плоскости
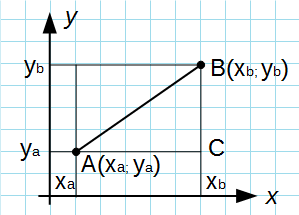
Из точек A и B опустим перпендикуляры на оси координат x и y.
Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:
Спомощью теоремы Пифагора, вычислим длину отрезка AB:
Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.
Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично.
Расстояние между отрезками
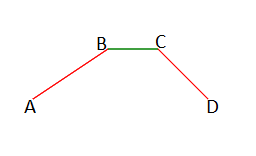
Координаты концов первого отрезка: A(xa, ya), B(xb, yb).
Координаты концов второго отрезка: C(xc, yc), D(xd, yd).
Тогда t = Δ1/Δ, s = Δ2/Δ. Если 0 ≤ t,s ≤ 1 и Δ ≠ 0, то отрезки пересекаются и расстояние между ними min равно 0, иначе с каждого конца отрезка попытаемся опустить высоту на противоположный. Если отрезок, на который опускаем высоту вертикальный, то поменяем местами координаты каждого конца отрезка и точки, с которой опускаем высоту (таким образом сохраним расстояние между точкой и отрезком, а отрезок станет горизонтальным).
Пусть k и d — коэффициенты уравнения прямой, на которую опущена эта высота. Основание высоты будет находится на прямой в точке Z, координаты Z(xz, yz) можно найти по формуле yz = kxz + d. Поскольку высота перпендикулярна отрезку — скалярное произведение их векторов равно 0. Тогда (x2 — x1)(x3 — xz)+(y2 — y1)(y3 — yz) = 0, соответственно xz = (x3x2 — x3x1 + y2y3 — y1y3 + y1d — y2d)/(ky2 — ky1 + x2 — x1), где (x3, y3) — координаты точки, с которой была опущена высота, (x1, y1) и (x2, y2) — координаты концов отрезка, принадлежащего прямой на которую опущена высота.
Вычислим длину dl каждой высоты, основание которой принадлежит одному из данных отрезков: dl = √((x3 — xz) 2 + (y3 — kxz — d) 2 ).
Минимальная длина высоты и будет наименьшим расстоянием между отрезками. В случае, если невозможно опустить высоты из одного отрезка на другой: расстояние между ними будет равно минимальному расстоянию между концами двух отрезков: min = √((x1 — x3) 2 + (y1 — y3) 2 ), где (x1, y1) — координаты одного из концов первого отрезка, а (x3, y3) — координаты одного из концов второго отрезка.
Отрезок. Формула длины отрезка.
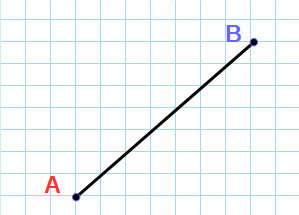
Отрезком обозначают ограниченный двумя точками участок прямой. Точки – концы отрезка.
Общеизвестный факт, что каждая точка А плоскости имеет свои координаты (х, у).
В данном примере вектор AB задан координатами (х2— х1, y2— y1). Квадрат длины вектора будет равен сумме квадратов его координат. Следовательно, расстояние d между точками А и В, или, что то же самое, длина вектора АВ, вычисляется согласно формуле:
Эта формула длины отрезка предоставляет возможность рассчитывать расстояние между двумя произвольными точками плоскости, при условии, что известны координаты этих точек
Вышеуказанную формулу длины отрезка можно доказать и другим способом. В системе координат заданы координаты крайних точек отрезка координатами его концов(х1y1) и (х2,у2).
Прочертим прямые лини через эти точки перпендикулярно к осям координат, в результате имеем прямоугольный треугольник. Первоначальный отрезок является гипотенузой образовавшегося треугольника. Катеты треугольника сформированы отрезками, их длиной будет проекция гипотенузы на оси координат.
Установим длину этих проекций.
На ось у длина проекции равна y2 — y1, а на ось х длина проекции равна х2 — х1. На основании теоремы Пифагора видим, что |AB|² = (y2 – y1)² + (x2 – x1)².
В рассмотренном случае |AB| выступает длиной отрезка.
Вычислим длину отрезка АВ, для этого извлечем квадратный корень. Результатом является все та же формула длины отрезков по известным координатам конца и начала.