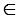Любовь Петровна Гаврилюк
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Для наиболее полного понимания темы следует ознакомиться с основными определениями, поэтому давайте узнаем, что же такое параллельные прямые и с чем их едят, а также некоторую другую основную терминологию и теоремы, которые касаются данной темы.
Используемые термины и понятия
Определение 1
Расстояние — это мера удалённости, используемая для характеристики местоположения двух объектов относительно друг друга.
Иногда расстояние можно измерить с помощью измерительных приборов, например, линейки или штангенциркуля, в случае поездки на автомобиле расстояние можно вычислить через измеритель скорости. Но чаще всего приходится прибегать к каким-либо вычислениям.
Определение 2
Параллельные прямые в пространстве — это такие прямые, которые не имеют каких-либо совместных точек и при этом лежат в одной плоскости. То есть по сути выходит, что есть два необходимых критерия для того чтобы назвать пару прямых параллельными друг другу:
1) обе такие прямые можно поместить в некую одиночную плоскость
2) 2 параллели никогда не встретятся
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Не стоит путать такие прямые со скрещивающимися. Эти прямые также никогда не встречаются между собой, но рассматривая их, становится очевидно, что их нельзя расположить в одной плоскости.
Параллельные прямые можно встретить много где в окружающем нас мире: это и линии пола и потолка, и противопложные стороны поверхности стола, и стороны двери.
Теорема 1
Расстояние между такими прямыми есть не что иное, как длина перпендикуляра, опущенного из одной точки любой из двух изучаемых прямых, на другую. Эта длина всегда будет одинаковой вне зависимости от того, из какой точки проведёна линия под прямым углом.
Докажем теорему, приведённую выше.
Доказательство теоремы о расстоянии между параллельными прямыми
Рисунок 1. Расстояние между параллельными прямыми
«Расстояние между двумя параллельными прямыми в пространстве» 👇
Рассмотрим наши прямые, про которые заранее известно, что они параллельны, назовём их $l$ и $k$.
Выберем пару рандомных точек $X$ и $Y$, возлежащих на $l$, и опустим из них под прямым углом линии на $k$.
Здесь совсем неважно, где именно вы выберете точки, главное правило — они не должны совпадать друг с другом.
Точки пересечения построенных линий с прямой $k$ назовём $A$ и $B$.
Так как наши прямые параллельны, то по условию параллельности накрест лежащие углы $XBA$ и $BXY$ при гипотенузе $XB$ получившегося прямоугольника равны между собой. Гипотенуза в данном случае является секущей к исследуемым прямым.
Собираем всё вместе о треугольниках $XBA$ и $BXY$:
- У них есть общая сторона $XB$.
- Стороны этих треугольников $XY$ и $AB$ равны между собой.
- Значения углов $XBA$ $BXY$ тоже одинаковы, а сами по себе эти углы образованы сторонами, которые также равны между собой.
Из всего вышеперечисленного следует, что $XBA$ и $BXY$ являются равными по первому признаку равенства треугольников, и следовательно, длины перпендикуляров $XA$ и $YB$ равны.
Данное соотношение будет соблюдаться для любых произвольно выбранных точек $X$ и $Y$ — то есть длины перпендикуляров, опущенных с одной параллельной прямой на другую, всегда будут равны, что и требовалось доказать.
Доказанное утверждение справедливо как для параллельных прямых, рассматриваемых в планиметрии, так и для прямых, рассматриваемых в объёмном мире, так как 2 параллельные между собой прямые всегда образуют плоскость.
Задачи на определение расстояния между параллельными прямыми в объёмном мире
Мы с вами уже немного разобрались в теме, а это значит, что пришло время для задач с нахождением расстояния между параллельными прямыми в пространстве.
Пример 1
Найти расстояние между параллельными прямыми $l$ и $k$.
Рисунок 2. Параллельные прямые, образующие плоскость
Рассмотрим рисунок 2. По теореме, изложенной выше, кратчайшим расстоянием между двумя этими прямыми будет длина перпендикуляра, опущенного с одной прямой на другую, поэтому опустим из точки $X$ на прямую $k$ перпендикуляр, назовём его $h$. Длина этого перпендикуляра и будет решением нашей задачи.
На практике чаще всего нет возможности использования подручных методов типа линейки из-за невозможности исполнения чертежа в масштабе 1:1, поэтому обычно нужно найти расстояние между двумя параллельными прямыми в пространстве имея на руках функции, описывающие данные прямые.
Выше мы показали, что совсем неважно, где именно выбрать точку на одной из двух параллельных прямых, из которой нужно опустить перпендикуляр.
Поэтому в случае параллельности прямых эта задача фактически есть не что иное, как поиск расстояния между точкой, лежащей на одной из этих прямых, и другой прямой.
Формула для нахождения расстояния между параллельными прямыми $d$ и $k$ в один этап в пространстве следующая:
Определение 3
$ρ(d, k) = frac{sqrt{begin{array}{|cc|} y_2 – y_1 & z_2 — z_1\ m_1 & n_1 \ end{array}^2 + begin{array}{|cc|} x_2 – x_1 & z_2 — z_1\ l_1 & n_1 \ end{array}^2 + begin{array}{|cc|} x_2 – x_1 & y_2 – y_1\ l_1 & m_1 \ end{array}^2}}{sqrt{l_1^2 + m_1^2 + n_1^2}}$
В этой формуле $x_1, y_1, z_1$ — координаты нормального вектора прямой $d$, а $l, m, n$ — направляющий вектор этой прямой, его координаты — это знаменатели из канонических уравнений прямой в пространстве; $x_2, y_2, z_2$ — это координаты нормального вектора второй прямой.
Пример 2
Даны уравнения двух параллельных несовпадающих прямых:
Прямая $d$ задана уравнением $frac{x + 1}{1}=frac{y — 2}{3}=frac{z + 4}{5}$,
а её параллель $k$ уравнением $frac{x — 3}{1}=frac{y + 1}{3}=frac{z – 2}{5}$.
Найдите длину перпендикуляра, опущенного с одной прямой на другую.
Координаты нормального вектора для прямой $k$ ${3;-1;2}$, а для прямой $d$ ${-1; 2; -4}$. Координаты направляющего вектора для первой прямой ${1; 3; 5}$.
Подставим данные числа в обозначенную выше формулу:
$ρ(d, k) = frac{sqrt{begin{array}{|cc|} 2 + 1 & -4 — 2\ 3 & 5 \ end{array}^2 + begin{array}{|cc|} -1 – 3 & -4 — 2\ 1 & 5 \ end{array}^2 + begin{array}{|cc|} -1 -3 & 2 + 1\ 1 & 3 \ end{array}^2}}{sqrt{1^2 + 3^2 + 5^2}}$
$ρ(d, k) = frac{sqrt{begin{array}{|cc|} 3 & -6\ 3 & 5 \ end{array}^2 + begin{array}{|cc|} -4 & -6\ 1 & 5 \ end{array}^2 + begin{array}{|cc|} -4 & 3\ 1 & 3 \ end{array}^2}}{sqrt{35}} =frac{ (15 +18)^2 +(-20+6)^2 +(-12-3)^2}{sqrt{35}}≈6,568$
Решение примера, приведённого выше, реализовано по формуле, полученной через векторное произведение, кому-то такой способ может показаться более просты, а кому-то наоборот — сложным.
Но в любом случае воспользовавшись обоими вариантами решения оба алгоритма легко можно проверить.
Алгоритм с векторным произведением рассмотрен нами ниже для этой же задачи, из него становится понятно, каким образом получена используемая выше формула.
Пример 3
Найдите расстояние между параллельными прямыми из задачи, изложенной выше, через векторное произведение.
В этом случае вычисление расстояния между прямыми осуществляется по формуле:
$ρ = frac{overline{M_0M_1}×overline{s}}{|overline{s}|}$,
где $M_0M_1$ — вектор, соединяющий 2 произвольных точки на двух параллельных прямых
Нормальные вектора для первой и второй прямых соответственно будут ${3;-1;2}$ и ${-1; 2;-4}$.
Направляющий вектор для обеих прямых совпадает, его координаты $s={1;3;5}$
Найдём векторную разность между нормальными векторами, которая будет координатами вектора $M_0M_1$
$overline{M_0M_1} = overline{r_2} — overline{r_2} = {3;-1;2} — {-1; 2;-4} = {4; -3; 6}$
Теперь необходимо высчитать векторное произведение вектора $overline{M_0M_1}$ на вектор $overline{s}$:
$overline{M_0M_1} ×overline{s} = begin{array}{|ccc|} i & j & k \ 4 & -3 & 6 \ 1 & 3 & 5 \ end{array} = i begin{array}{|cc|} -3 & 6\ 3 & 5 \ end{array} + j begin{array}{|cc|} 4 & 6\ 1 & 5 \ end{array} + k begin{array}{|cc|} 4 & -3\ 1 & 3 \ end{array} = -33i + 14j + 15k = {-33; 14; 15}$
$|overline{M_0M_1} ×overline{s}| =sqrt{(-33)^2 + 14^2 + 15^2} = sqrt{1510} ≈ 38,859$
А сейчас пришла очередь определить длину направляющего вектора $s$:
$|overline{s}| = sqrt{1^2 + 3^2 + 5^2} = 5, 916$
В результате конечный ответ составит:
$ρ = frac{ 38,859}{ 5, 916} = 6,568$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
2.5.6. Как найти расстояние между параллельными прямыми?
Ответим на этот вопрос конкретной задачей:
Задача 82
Найти расстояние 
между двумя параллельными прямыми, заданными в декартовой
системе координат: 
.
Решение: расстояние между параллельными прямыми найдём как расстояние от точки до прямой. Для этого
достаточно найти одну точку, принадлежащую любой прямой. Из уравнения 
легко
усмотреть точку 
. Вычислим расстояние:
Примечание: последним действием домножили числитель и знаменатель на 
– чтобы
избавиться от иррациональности в знаменателе.
Ответ: 
Как видите, здесь бесконечно много способов решения.
Едем дальше:
2.5.7. Как найти угол между прямыми?
2.5.5. Как вычислить расстояние от точки до прямой?
| Оглавление |
Автор: Aлeксaндр Eмeлин
Как называется расстояние между двумя параллельными прямыми в пространстве
Две линии могут пересекаться или не иметь общих точек. Во втором случае прямые будут располагаться параллельно относительно друг друга. Для данного положения существует ряд характеристик, одной из которых является расстояние.
Расстоянием между двумя параллельными прямыми называется длиной отрезка, мысленно прочерченного от некоторой произвольно отмеченной точки на одной из линий до другой.
Схематично такие прямые можно представить следующим образом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
На рисунке представлен чертеж с двумя параллельными прямыми a и b. Точка М1 отмечена на прямой a. От нее можно опустить перпендикулярную линию к прямой b. Отрезок М1Н1 будет представлять расстояние между этими точками или параллельными линиями, на которых они расположены.
Примечание
Представленное определение расстояния между двумя линиями, расположенными параллельно относительно друг друга, применимо в условиях плоскости. Такой же способ определения расстояния подходит для расчетов, выполняемых в трехмерном пространстве.
Доказательство теоремы, формула вычисления
Расстояние между двумя параллельными прямыми описывается теоремой. Звучит утверждение следующим образом: «На двух параллельных прямых все точки на одной из них равноудалены от точек, отмеченных на другой линии».
В качестве доказательства этой теории необходимо схематично представить две параллельные прямые линии a и b. На первой прямой можно отметить точку М1 и точку М2. С помощью перпендикуляров, пересекающих прямую b, можно отметить на ней аналогичные точки Н1 и Н2. Согласно определению расстояния между двумя параллельными прямыми, отрезок М1Н1 является расстоянием между прямой a и прямой b. Исходя из теоретического утверждения, необходимо доказать следующее отношение:
М1Н1 = М2Н2.
Схему можно дополнить с помощью некой секущей линии, которая представляет собой отрезок, пересекающий параллельные прямые. Исходя из условия параллельности двух прямых, можно заметить, что внутренние углы, образованные при пересечении секущей двух параллельных линий и лежащие накрест, равны друг другу. Таким образом:
угол М2М1Н2 = угол Н1Н2М1.
Согласно методике построения, отрезок М2Н2 перпендикулярен прямой b и расположен перпендикулярно к прямой a. Образованные в результате треугольники М1Н1Н2 и М2М1Н2 обладают прямыми углами и считаются равными по следующим характеристикам:
- Общая гипотенуза М1Н2.
- Равные острые углы М2М1Н2 и Н1Н2М1.
Исходя из утверждения, что у равных треугольников стороны также будут равны,
М1Н1 = М2Н2.
Таким образом, доказательства теоремы представлены.
Примечание
У расстояния, на которое удалены две прямые, расположенные параллельно друг другу, есть важная особенность. Этот отрезок будет являться наименьшим расстоянием от точек на одной линии до точек на другой параллельной линии.
Нахождение расстояния между параллельными прямыми
Определить удаленность двух линий, которые располагаются параллельно относительно друг друга, не составит труда. Достаточно измерить длину перпендикуляра, соединяющего две точки на этих прямых. Существует несколько способов, чтобы произвести данные вычисления:
- теорема Пифагора;
- признак равенства или подобия треугольников;
- метод координат в прямоугольной системе.
Подробнее следует рассмотреть последний способ. Если зафиксировать прямоугольную систему координат и задать в ней две параллельные линии a и b, то необходимо вычислить, насколько эти прямые удалены друг от друга. Решение задачи базируется на вычислении расстояния между этими линиями. Для этого необходимо выполнить следующие действия:
- Определить координаты, соответствующие точке М1, отмеченной на одной из прямых линий.
- Вычислить, каково расстояние от точки М1 до линии, к которой она не относится.
Исходя из примеров уравнений прямой на плоскости или в пространстве, можно достаточно просто вычислить координаты точки М1. Можно представить, что линия a соответствует следующему уравнению:
АХ + ВУ + С1 = 0
Пусть линия b соответствует такому уравнению:
АХ + ВУ + С2 = 0
Определить расстояние, на которое удалены эти параллельные прямые, можно по формуле:
(left|M1H1right|=frac{left|C_{2}-C_{1} right|}{sqrt{A^{2}+B^{2}}})
Если выбрать какую-то точку М1(х1, у1) на прямой а, ее координаты будут соответствовать следующему уравнению:
Ах1 + Ву1 + С1 = 0.
В этом случае стоит отметить справедливость равенства:
Ах1 + Ву1 + С1 = 0, из которого получается следующая формула:
Ах1 + Ву1 = — С1.
В случае, если С2 меньше 0, то вид нормального уравнения прямой b будет следующим:
(frac{A}{sqrt{A^{2}+B^{2}}}x+frac{B}{sqrt{A^{2}+B^{2}}}y+frac{C_{2}}{sqrt{A^{2}+B^{2}}}=0)
Когда С2 равно либо больше 0, можно представить нормальное уравнение для прямой b таким образом:
(frac{A}{sqrt{A^{2}+B^{2}}}x+frac{B}{sqrt{A^{2}+B^{2}}}y-frac{C_{2}}{sqrt{A^{2}+B^{2}}}=0)
Найти расстояние между двумя параллельными прямыми, если С2 меньше 0, можно, используя такую формулу:
(left|M1H1right|=left| frac{A}{sqrt{A^{2}+B^{2}}}x_{1}+frac{B}{sqrt{A^{2}+B^{2}}}y_{1}+frac{C_{2}}{sqrt{A^{2}+B^{2}}}right|)
В случаях, когда С2 больше либо равно 0, расстояние вычисляется по следующей формуле:
(left|M1H1right|=left| -frac{A}{sqrt{A^{2}+B^{2}}}x_{1}-frac{B}{sqrt{A^{2}+B^{2}}}y_{1}-frac{C_{2}}{sqrt{A^{2}+B^{2}}}right|=left| frac{A}{sqrt{A^{2}+B^{2}}}x_{1}+frac{B}{sqrt{A^{2}+B^{2}}}y_{1}+frac{C_{2}}{sqrt{A^{2}+B^{2}}}right|)
В таком случае расстояние между двумя параллельными прямыми не зависит от величины С2 и определяется по формуле:
(left|M1H1right|)=( left| frac{A}{sqrt{A^{2}+B^{2}}}x_{1}+frac{B}{sqrt{A^{2}+B^{2}}}y_{1}+frac{C_{2}}{sqrt{A^{2}+B^{2}}}right|)
Следует применить формулу, полученную ранее:
(Ах1 + Ву1 = — С1)
Тогда окончательные расчеты будут выглядеть следующим образом:
(left|M1H1right|=left| frac{-C_{1}}{sqrt{A^{2}+B^{2}}}+frac{C_{2}}{sqrt{A^{2}+B^{2}}}right|=left| frac{C_{2}-C_{1}}{sqrt{A^{2}+B^{2}}}right|)
Таким образом, получилась формула, характерная для алгоритма метода координат. Данное уравнение можно применять для вычисления расстояние между двумя параллельными прямыми.
Примеры задач с решением
Пример №1
По условиям задачи необходимо определить расстояние между двумя параллельными прямыми:
(y=frac{2}{3}x-1)
(begin{cases} & text{ if } x= 4+3*lambda \ & text{ if } x= -5+2*lambda end{cases})
Решение
С помощью параметрических уравнений достаточно просто определить координаты точки, через которую проходит линия, соответствующая параметрическим уравнениям. Исходя из этих данных, получается:
точка М1 (4, -5).
Таким образом, необходимо рассчитать расстояние, на которое удалена точка М1 (4, -5) от прямой (y=frac{2}{3}x-1)
Получение нормального уравнения прямой основано на преобразовании заданного уравнения прямой с угловым коэффициентом (y=frac{2}{3}x-1). Выполнить это можно путем перехода к общему уравнению прямой:
(y=frac{2}{3}x-1)
(frac{2}{3}x-1-y=0)
2x – 3y – 3 = 0
Далее необходимо вычислить нормирующий множитель:
(frac{1}{sqrt{2^{2}+(-3^{2})}}=frac{1}{sqrt{13}})
Полученный нормирующий множитель следует умножить на обе части последней формулы, чтобы в конечном итоге вывести формулу нормального уравнения прямой:
(frac{1}{sqrt{13}}times (2x-3y-3)=frac{1}{sqrt{13}}times 0)
(frac{2}{sqrt{13}}x-frac{3}{sqrt{13}}y-frac{3}{sqrt{13}}=0)
Расчет модуля значения крайнего равенства при условии, что х = 4, у = -5, позволит вычислить искомое расстояние между двумя параллельными прямыми:
(left|frac{2}{sqrt{13}}times 4-frac{3}{sqrt{13}}times (-5)-frac{3}{sqrt{13}} right|= frac{20}{sqrt{13}})
Ответ: расстояние между двумя параллельными прямыми составляет (frac{20}{sqrt{13}})
Пример №2
На фиксированной прямоугольной системе координат Оху расположены две линии, параллельно относительно друг друга. Данные прямые определяются с помощью следующих уравнений:
х – 3 = 0
(frac{x+5}{0}=frac{y-1}{1})
Необходимо рассчитать расстояние, на которое две прямые отдалены друг от друга.
Решение
Исходя из условий задачи, в которых указано одно общее уравнение, выделим формулу для одной из исходных линий:
х – 3 = 0.
С помощью исходного канонического уравнения можно вычислить общую формулу:
(frac{x+5}{0}=frac{y-1}{1})
х + 5 = 0
При переменной х наблюдается равенство коэффициентов в обоих уравнениях (также равны и при у — нулю). Исходя из данного условия, представляется возможным использовать формулу, чтобы вычислить расстояние, на которое удалены эти параллельные прямые друг от друга:
(left|M1H1 right|=frac{left|C_{2}-C_{1} right|}{sqrt{A^{2}+B^{2}}}=frac{left|5-(-3) right|}{sqrt{1^{2}+0^{2}}}=8)
Ответ: расстояние между двумя параллельными прямыми равно 8.
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Соотношения между сторонами и углами треугольника
- Расстояние между параллельными прямыми
Теорема
Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
Доказательство:
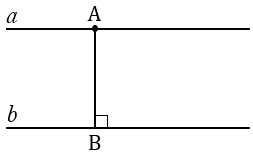
Рассмотрим параллельные прямые 
и 
.
Отметим точку А на прямой и проведем из этой точки перпендикуляр АВ к прямой .
Отметим точку Х на прямой и докажем, что расстояние от точки Х до прямой равно АВ. Проведем из точки Х перпендикуляр ХУ к прямой .
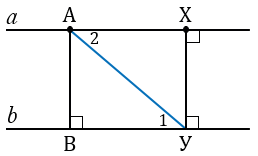
ХУ
, следовательно, ХУ (т.к. прямая перпендикулярная к одной из параллельных прямых перпендикулярна и ко второй из них).
Рассмотрим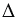 
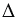
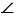
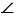
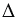
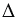
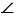
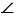
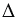
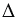
АВУ и АХУ: 
В =Х = 900, т.е. АВУ и АХУ прямоугольные, АУ — общая гипотенуза, 1 = 2 (т.к. они накрест лежащие при пересечении параллельных прямых и секущей АУ), следовательно, АВУ =АХУ (по гипотенузе и острому углу), ХУ = АВ.
Точка Х находится на расстоянии АВ от прямой , а так как эту точку мы выбрали произвольно, все точки каждой из двух параллельных прямых и равноудалены от другой прямой. Что и требовалось доказать.
Из доказанной выше теоремы следует, что расстояние между параллельными прямыми — это наименьшее расстояние (перпендикуляр) от каждой точки одной из этих прямых до другой прямой.
Замечание 1
Все точки плоскости, расположенные по одну сторону от данной прямой и равноудаленные от нее, лежат на прямой параллельной данной.
Доказательство:
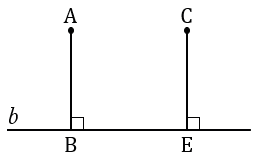
Дано: прямая , А, С
, АВ, СE, АВ = СЕ.
Доказать: А, С
и 
.
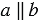
Доказательство:
По аксиоме параллельных прямых через точку А проходит единственная прямая параллельная прямой . Проведем через точку А прямую параллельную .
По теореме, доказанной выше, все точки, лежащие на прямой равноудалены от точек прямой .
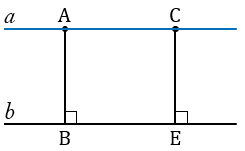
Предположим, что точка С не лежит на прямой , тогда расстояние от точки С до прямой будет больше или меньше, чем расстояние АВ.
Но по условию АВ = СЕ, следовательно, получили противоречие, значит, наше предположение неверно и А, С, при этом по построению . Что и требовалось доказать.
Замечание 2
Множество всех точек плоскости, находящихся на данном расстоянии от данной прямой и лежащих по одну сторону от нее, есть прямая, параллельная данной прямой.
Доказательство:
Пусть — данная прямая, d — данное расстояние. Отметим на прямой произвольную точку А и проведем отрезок АВ длины d так, что АВ, через точку В по аксиоме параллельных прямых проходит единственная прямая параллельная прямой . Проведем через точку В прямую параллельную .
По доказанной выше теореме все точки прямой находятся на расстоянии d от прямой , т.е. все эти точки принадлежат искомому множеству. В силу обратной теоремы любая точка искомого множества лежит на прямой . Значит, прямая является геометрическим местом всех точек, удовлетворяющих данному условию. Что и требовалось доказать.
Геометрическое место точек, удовлетворяющих данному условию — множество всех точек, удовлетворяющих какому-либо условию.
Советуем посмотреть:
Теорема о сумме углов треугольника
Остроугольный, прямоугольный и тупоугольный треугольники
Теорема о соотношениях между сторонами и углами треугольника
Неравенство треугольника
Некоторые свойства прямоугольных треугольников
Признаки равенства прямоугольных треугольников
Уголковый отражатель
Расстояние от точки до прямой
Построение треугольника по двум сторонам и углу между ними
Построение треугольника по стороне и двум прилежащим к ней углам
Построение треугольника по трем его сторонам
Соотношения между сторонами и углами треугольника
Правило встречается в следующих упражнениях:
7 класс
Задание 279,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 281,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 282,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 283,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 293,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 294,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 17,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 18,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 20,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 813,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник