Расстояние между плоскостями.
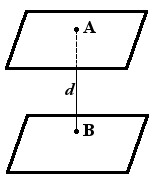
Определение. Расстояние между плоскостями — равно длине перпендикуляра, опущенного с одной плоскости на другую.
Формула для вычисления расстояния между плоскостями
Если заданы уравнения параллельных плоскостей Ax + By + Cz + D1 = 0 и Ax + By + Cz + D2 = 0, то расстояние между плоскостями можно найти, используя следующую формулу
| d = | |D2 — D1| |
| √A2 + B2 + C2 |
Примеры задач на вычисление расстояния между плоскостями
Пример 1.
Найти расстояние между плоскостями 2x + 4y — 4z — 6 = 0 и x + 2y — 2z + 9 = 0.
Решение. Проверим, параллельны ли плоскости, для этого умножим уравнение второй плоскости на 2
2x + 4y — 4z + 18 = 0
Так как коэффициенты при неизвестных величинах у полученного уравнения и первого уравнения равны, то для вычисления расстояния между плоскостями можно использовати приведенную выше формулу:
| d = | |18 — (-6)| | = | |24| | = | 24 | = 4 |
| √22 + 42 + (-4)2 | √36 | 6 |
Ответ: расстояние между плоскостями равно 4.
Расстояние между плоскостями. Онлайн калькулятор
Страница обновляется. Могут возникнуть ошибки. Спасибо за понимание!
С помощю этого онлайн калькулятора можно найти расстояние между плоскостями. Дается подробное решение с пояснениями. Для нахождения расстояния между плоскостями, введите элементы уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Расстояние между плоскостями − теория
Заметим, сначала, что расстояние между плоскостями определена, если плоскости параллельны или, что то же самое, нормальные векторы этих плоскостей коллинеарны. Вычисление расстояния между двумя плоскостями можно свести к вычислению расстояния от точки первой плоскости до второй плоскости. Вычисление расстояния от точки до плоскости (онлайн калькулятор, теория, примеры) посмотрите на странице Расстояние от точки до плоскости онлайн.
Алгоритм вычисления расстояния между плоскостями содержит следующие шаги:
- Проверка коллинеарности нормальных векторов плоскостей.
- Нахождение некоторой точки M0 на первой плоскости.
- Вычисление расстояния между точкой M0 и второй плоскостью.
Выведем формулу вычисления расстояния между плоскостями.
Запишем уравнения двух плоскостей:
1. Проверяем коллинеарность нормальных векторов n1=(A1, B1, C1) и n2=(A2, B2, C2).
Очевидно, что нормальные векторы n1 и n2 не могут быть нулевыми векторами.Если из пары коэффициентов (A1,A2),(B1,B2), (C1,C2) один нулевой а другой − нет, то нормальные векторы n1 и n2 неколлинеарны. Т.е. задача неразрешима.
Пусть A1≠0, A2≠0. Уравнение плоскости (2) не изменится, если умножим на A1/A2:
Нормальный вектор уравнения (2′) имеет следующий вид:
Для коллинеарности векторов n1 и n’2(или n1 и n2) необходимо и достаточно выполнение следующих равенств:
или
Если удовлетворяется условие (3) (или (3′)), то векторы n1 и n’2(или n1 и n2) коллинеарны, т.е. плоскости (1) и (2′) (или (1) и (2) ) параллельны. Тогда уравнение плоскости (2′) можно представить так:
где
2. Найдем некоторую точку на плоскости (1).
Легко убедится, что точка
принадлежит плоскости (1):
3. Расстояние от точки M0(x0, y0, z0) до плоскости (2») вычисляется с помощью выражения (подробнее смотрите на странице расстояние от точки до плоскости):
Подставляя координаты точки M0 из (4) в (5), получим формулу вычисления расстояния между плоскостями (1) и (2») (или (1) и (2)):
где
Расстояние между плоскостями − примеры и решения
Пример 1. Найти расстояние между плоскостями
и
Решение.
Проверим, являются ли эти плоскости параллельными. Для этого умножим второе уравнение на 1/3.
Общее уравнение плоскости имеет вид:
где n=(A,B,C)− называется нормальным вектором плоскости.
Нормальный вектор плоскости (7) равен n1=(1, 2, −4), нормальный вектор плоскости (8′) равен n2=(1, 2, −4). n1=n2. Следовательно эти плоскости параллельны.
Найдем расстояние между плоскостями (7) и (8′), используя следующую формулу:
Подставим значения A, B, C, D1, D2 в (9):
Упростим и решим:
Ответ. Расстояние между плоскостями равен:
Пример 2. Найти расстояние между плоскостями
и
Решение.
Эти плоскости не параллельны, так как коэффициент переменного z уравнения (10) нулевой а коэффициент переменного z уравнения (11)−нет. Невозможно найти расстояние между непараллельными плоскостями.
Пример 3. Найти расстояние между плоскостями
и
Решение.
Проверим, являются ли эти плоскости параллельными. Для этого умножим второе уравнение на 4/3.
Нормальный вектор плоскости (12) равен n1=(4, 2, 8), нормальный вектор плоскости (13′) равен n2=(4, 16/3, 64/3). n1≠n2. Нормальные векторы этих плоскостей неколлинеарны. Тогда эти плоскости не параллельны и, следовательно, задача неразрешима.
({color{red}{textbf{Факт 1. Про векторы}}})
(bullet) Если в пространстве заданы две точки (A(x_1;y_1;z_1)) и (B(x_2;y_2;z_2)), то вектор (overrightarrow{AB}) имеет координаты [overrightarrow{AB} = {x_2-x_1;y_2-y_1;z_2-z_1}]
(bullet) Если в пространстве заданы два вектора (vec{a}
={x_1;y_1;z_1}) и (vec{b}=
{x_2;y_2;z_2}), то:
(qquad blacktriangleright) сумма этих векторов (vec{a}+vec{b}={x_1+x_2;y_1+y_2;z_1+z_2})
(qquad blacktriangleright) разность этих векторов (vec{a}-vec{b}={x_1-x_2;y_1-y_2;z_1-z_2})
(qquad blacktriangleright) произведение вектора на число (lambda
vec{a}={lambda x_1;lambda
y_1;lambda z_1})
(bullet) Если в пространстве заданы две точки (A(x_1;y_1;z_1)) и (B(x_2;y_2;z_2)), а точка (O) — середина отрезка (AB), то (O) имеет координаты [Oleft(dfrac{x_1+x_2}2;dfrac{y_1+y_2}2;dfrac{z_1+z_2}2right)]
(bullet) Длина вектора (vec{a}={x;y;z}) обозначается (|vec{a}|) и вычисляется по формуле [|vec{a}|=sqrt{x^2+y^2+z^2}]
(bullet) Заметим, что расстояние между двумя точками есть не что иное, как длина вектора с началом и концом в этих точках.
({color{red}{textbf{Факт 2. Про скалярное произведение}}})
(bullet) Скалярным произведением двух векторов называется произведение длин этих векторов на косинус угла между ними: [{large{(vec{a},
vec{b})=|vec{a}|cdot|vec{b}|cdotcos angle (vec{a},
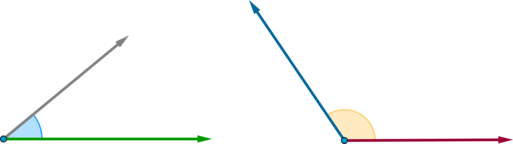
vec{b})}}] На рисунке показано, что такое угол между векторами:
(bullet) Справедливы следующие утверждения:
I. Скалярное произведение ненулевых векторов (их длины не равны нулю) равно нулю тогда и только тогда, когда они перпендикулярны: [(vec{a}, vec{b})=0 quadLeftrightarrowquad
vec{a}perp vec{b}]
II. Длина вектора равна квадратному корню из скалярного произведения вектора на себя: [|vec{a}|=sqrt{(vec{a},
vec{a})}]
III. Переместительный закон: [(vec{a}, vec{b})=(vec{b},
vec{a})]
IV. Распределительный закон: [(vec{a}+vec{b},
vec{c})=(vec{a}, vec{c})+(vec{b}, vec{c})]
V. Сочетательный закон ((lambda) – число): [lambda(vec{a}, vec{b})=(lambda
vec{a}, vec{b})]
(bullet) Скалярное произведение двух векторов (vec{a}
={x_1;y_1;z_1}) и (vec{b}= {x_2;y_2;z_2}) можно вычислить с помощью координат этих векторов: [{large{(vec{a},
vec{b})=x_1x_2+y_1y_2+z_1z_2}}]
(bullet) Косинус угла между векторами (vec{a} ={x_1;y_1;z_1}) и (vec{b}= {x_2;y_2;z_2}) вычисляется по формуле: [{large{cosangle(vec{a}, vec{b})=dfrac{x_1x_2+y_1y_2+z_1z_2}
{sqrt{x^2_1+y^2_1+z^2_1}cdot
sqrt{x^2_2+y^2_2+z^2_2}}}}]
({color{red}{textbf{Факт 3. Про уравнение плоскости}}})
(bullet) Если (vec{n}={a;b;c}) – нормаль к плоскости, то уравнение плоскости имеет вид [ax+by+cz+d=0] Для того, чтобы найти (d), нужно подставить в уравнение плоскости вместо (x, y, z) координаты любой точки, лежащей в этой плоскости.
Пример: если (vec{n}={1;2;3}) – нормаль к плоскости, (O(4;5;6)) – точка из плоскости, то справедливо: (1cdot 4+2cdot 5+3cdot
6+d=0), откуда (d=-32), следовательно, уравнение плоскости имеет вид (x+2y+3z-32=0).
(bullet) Уравнение плоскости можно составить, используя три точки из плоскости, не лежащие на одной прямой.
Пусть (A(1;0;0),
B(0;3;4), C(2;0;5)) – точки из плоскости. Тогда уравнение плоскости можно найти, решив систему: [begin{cases}
1cdot a+0cdot b+0cdot c+d=0\
0cdot a+3cdot b+4cdot c+d=0\
2cdot a+0cdot b+5cdot c+d=0end{cases} quadRightarrowquad
begin{cases}
d=-a\
3b+4c-a=0\
a+5c=0end{cases}quadRightarrowquad begin{cases} d=-a\
a=-5c\
b=-3cend{cases}quadRightarrowquadbegin{cases}a=-5c\
b=-3c\
d=5cend{cases}] Следовательно, уравнение плоскости имеет вид: [-5ccdot x-3ccdot y+ccdot z+5c=0] Можно разделить обе части на (c), так как (cne 0) (иначе (a=b=c=d=0)), следовательно, уравнение плоскости имеет вид [-5x-3y+z+5=0]
({color{red}{textbf{Факт 4. Про углы между прямыми, плоскостями}}})
(bullet) Если векторы (vec{a} ={x_1;y_1;z_1}) и (vec{b}=
{x_2;y_2;z_2}) являются направляющими прямых (p) и (q), то косинус угла между этими прямыми равен: [cos phi=dfrac{|x_1x_2+y_1y_2+z_1z_2|}
{sqrt{x^2_1+y^2_1+z^2_1}cdot sqrt{x^2_2+y^2_2+z^2_2}}]
(bullet) Если (vec{a}) — направляющий вектор прямой (p), а (vec{n}) — нормаль к плоскости (phi) (перпендикуляр к плоскости), то синус угла между прямой (p) и плоскостью (phi) равен модулю косинуса угла между векторами (vec{a}) и (vec{n}): [sin
angle(p, phi)=|cos angle(vec{a}, vec{n})|]
(bullet) Если две плоскости заданы уравнениями (a_1x+b_1y+c_1z+d_1=0) и (a_2x+b_2y+c_2z+d_2=0), то косинус угла между плоскостями ищется по формуле: [{large{cos phi=left| dfrac{a_1a_2+b_1b_2+c_1c_2}
{sqrt{a^2_1+b^2_1+c^2_1}cdot
sqrt{a^2_2+b^2_2+c^2_2}}right|}}]
({color{red}{textbf{Факт 5. Про расстояния от точки до плоскости,
между скрещивающимися прямыми}}})
(bullet) Если (M(x_0;y_0;z_0)) — некоторая точка вне плоскости (phi), (ax+by+cz+d=0) — уравнение плоскости (phi), то расстояние от точки (M) до плоскости (phi) ищется по формуле: [rho(M, phi)=dfrac{|ax_0+by_0+cz_0+d|}{sqrt{a^2+b^2+c^2}}]
(bullet) Для того, чтобы найти расстояние между скрещивающимися прямыми, нужно
— построить плоскость, проходящую через одну из них и параллельную другой;
— найти уравнение этой плоскости;
— найти расстояние от любой точки первой прямой до этой плоскости.
Лекция
№5
Взаимное
расположение двух и трех плоскостей.
Расстояние от точки до плоскости.
Расстояние между двумя параллельными
плоскостями. Угол между плоскостями.
Лемма 5.1.
(Условие
параллельности вектора и плоскости).
Пусть в
аффинной системе координат задана
плоскость
общим уравнением
и вектор
.
Вектор
параллелен плоскости
тогда
и только тогда, когда
выполняется условие:
.
Доказательство.
Пусть
.
Докажем, что выполняется условие
.
1.
Рассмотрим
.
Отложим
от неё вектор
.
2. Пусть
,
тогда вектор
.
Запишем условие равенства векторов
и
:
3. Так как
,
то
ее координаты удовлетворяют уравнению
плоскости, т.е.
,
где
(точка
принадлежит плоскости ).
(<=)
повторить
все рассуждения в обратном направлении.
Ч.т.д.
Лемма 5.2.
Пусть в
прямоугольной системе координат
плоскость
задана общим уравнением:
.
Тогда
вектор
перпендикулярен
плоскости
.
Доказательство.
Пусть
вектор
параллелен плоскости .
Применяя
условие параллельности вектора и
плоскости, получим:
вектор
перпендикулярен
плоскости
.
Ч.т.д.
Взаимное
расположение двух плоскостей.
В аффинной системе
координат поверхность, заданная
уравнением первой степени, является
плоскостью. Выясним, при каких условиях
два уравнения
и
:
I.
Определяют одну и ту же плоскость;
II.
Определяют две параллельные плоскости;
III.
Определяют две пересекающиеся плоскости.
I.
Условия, при которых уравнения
и
определяют
одну и ту же плоскость.
Теорема 5.3.
Для
того чтобы два
уравнения
и
в аффинной системе координат определяли
одну и ту же плоскость, необходимо и
достаточно, чтобы все коэффициенты в
уравнениях были пропорциональны.
Необходимость:
Дано: уравнения
плоскостей
:
(1)
(2)
Докажем:
.
Доказательство:
1.
Данные уравнения определяют одну и ту
же плоскость
.
Значит, векторы нормалей
и
будут коллинеарны, т.е.
или
.
2.
Подставим выражения в уравнение (1) и
выразим
:
3.
Найдем отношение
:
.
4.
Значит,
Достаточность:
Дано:
уравнения:
:
(1)
(2)
.
Докажем,
что уравнения (1) и (2) задают одну и ту же
плоскость
.
Доказательство:
1.
Выразим из условия теоремы
коэффициенты
:
-
Подставим
данные выражения в уравнение (1):
или
3.
Значит, уравнениями (1) и (2) задаётся одна
плоскость в аффинной системе координат.
II.
Условие параллельности двух прямых.
Теорема
5.4.
Два
уравнения
и
в аффинной системе координат определяют
две параллельные плоскости, если
коэффициенты при переменных
в уравнениях пропорциональны.
III.
Условие пересечения двух прямых.
Теорема
5.5.
Два
уравнения
и
в аффинной системе координат определяют
две пересекающие плоскости, если
коэффициенты при переменных
в уравнениях не пропорциональны.
Взаимное расположение
плоскостей
и
определяется и рангами расширенной и
основной матриц, соответствующих системе
уравнений данных плоскостей:
Пусть:
-
— расширенная
матрица ранга
-
-основная
матрица ранга
.
-
Если
,
то плоскости
и
пересекаются; -
Если
,
то плоскости
и
совпадают; -
Если
,
то плоскости
и
параллельны.
Пучок плоскостей.
Определение
5.6. Пучком
плоскостей называется совокупность
плоскостей пространства, проходящих
через одну прямую.
Пусть плоскости
и
пересекаются, причем
:
;
:
Помножим уравнения
плоскостей
и
соответственно на числа
и q,одновременно
не равные 0, и сложим полученные равенства:
(*)
,
где
Коэффициенты при
х,у,z
не равны
нулю одновременно,
т.к. одновременное равенство нулю
позволяет говорить, что
.
По условию параллельности плоскостей
имеем, что
=> противоречит
условию.
Уравнение (*)
есть
уравнение плоскости, проходящей через
общую прямую двух данных плоскостей.
—
уравнение пучка
плоскостей.
Пример.
Задача:
Составить
уравнение плоскости, проходящей через
точку А(2,3,1) и прямую, определяемую
плоскостями:х+у-2z+1=0
и 2x—y+z-4=0.
Определение
5.7.
Совокупность
всех плоскостей, проходящих через точку
пересечения трех основных плоскостей,
называются связкой
плоскостей.
—уравнение
связки.
Расстояние от
точки до плоскости.
З
Найти расстояние от точки
до
плоскости :
.
Решение:
1.
,
2.
3. Вектор
=>
4. Так как точка
принадлежит
плоскости, то имеем:
5.
или
— расстояние
от точки Мо до плоскости.
Расстояние
между двумя параллельными плоскостями.
Задача:
Найти расстояние между параллельными
плоскостями
и
,
заданными своими уравнениями:
и
.
Угол между
плоскостями.
Определение
5.8.
Углом между плоскостями называется
любой из двух двугранных углов,
образованный
этими плоскостями.

угла между
и
.
Соседние файлы в папке вопрос 6
- #
- #
There is another way of finding the distance. Write $C_1$ and $C_2$ as functions $z=f_i(x,y)$:
$$C_1,:,z=f_1(x,y)=2-frac12 x-frac12 yqquadtext{ and}$$
$$C_2,:,z=f_1(x,y)=3-frac12 x-frac12 y.$$
To find the intersections we assume that $(x,y,z)in C_1cap C_2$ and solve the simultaneous equations.
$$begin{align}
2-frac12 x-frac12 y&=3-frac12 x-frac12 y
\ Rightarrow 2&=3,
end{align}$$
a contradiction and so $C_1cap C_2$ is empty and so $C_1parallel C_2$.
Find a point on one plane, say $(0,0,2)$ on $C_2$.
Write a function $d(x,y)=operatorname{dist}((x,y,f_1(x,y)),(0,0,2))$ using Pythagoras a couple of times:
$$d(x,y)=sqrt{x^2+y^2+(1-x/2-y/2)^2}.$$
Minimise $d(x,y)$ — or even easier $(d(x,y))^2$ — using partial differentiation:
$$begin{align}
frac{partial d^2}{partial x}&=2x+2(1-x/2-y/2)(-1/2)
\&=frac52 x -1+frac{y}{2},text{ and}
\ frac{partial d^2}{partial y}&= frac52 y -1+frac{x}{2}.
end{align}
$$
Solve both partial derivatives equal to zero to find that the minimum of $d^2$ occurs at $(x,y)=(1/3,1/3)$. Plug these into $d(x,y)$ to find
$$d_min=sqrt{frac23}.$$
For $C_3$ to be parallel to $C_1$ and $C_2$ it must be of the form:
$$f_3(x,y)=lambda-frac12 x-frac12 y,$$
for $lambdaneq 2,3$.
Note that
$$f_1(x,y)=-x/2-y/2+2,$$
and
$$f_2(x,y)=-x/2-y/2+3=f_1(x,y)+1,$$
and so $C_2$ is just $C_1$ shifted upwards by one. Therefore shift upwards again by one and you will find $C_3$:
$$f_3(x,y)=-x/2-y/2+4Leftrightarrow x+y+2z=8.$$
You wouldn’t even have to solve the first part to do this.