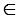Расстояние между двумя параллельными прямыми – определение и примеры нахождения.
В этой статье дано определение расстояния между двумя параллельными прямыми на плоскости и в трехмерном пространстве, а также разобран метод координат, позволяющий вычислять расстояние между параллельными прямыми. Сначала приведена необходимая теория, после чего приведены подробные решения примеров и задач, в которых находится расстояние между двумя параллельными прямыми.
Навигация по странице.
Расстояние между двумя параллельными прямыми – определение.
Определение расстояния между двумя параллельными прямыми дается через расстояние от точки до прямой.
Расстояние между двумя параллельными прямыми – это расстояние от произвольной точки одной из параллельных прямых до другой прямой.
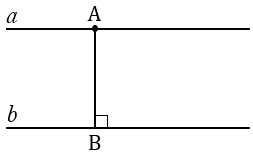
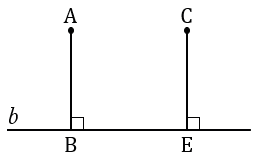
Для наглядности изобразим две параллельные прямые a и b , отметим на прямой а произвольную точку М1 , опустим перпендикуляр из точки М1 на прямую b , обозначив его H1 . Отрезок М1H1 соответствует расстоянию между параллельными прямыми a и b .
Приведенное определение расстояния между двумя параллельными прямыми справедливо как для параллельных прямых на плоскости, так и для прямых в трехмерном пространстве. Более того, такое определение расстояния между двумя параллельными прямыми принято не случайно. Оно тесно связано со следующей теоремой.
Все точки одной из двух параллельных прямых удалены на одинаковое расстояние от другой прямой.
Рассмотрим параллельные прямые a и b . Отметим на прямой a точку М1 , опустим из нее перпендикуляр на прямую b . Основание этого перпендикуляра обозначим как H1 . Тогда длина перпендикуляра М1H1 есть расстояние между параллельными прямыми a и b по определению. Докажем, что равно , где М2 – произвольная точка прямой a , отличная от точки M1 , а H2 – основание перпендикуляра, проведенного из точки М2 на прямую b . Доказав этот факт, мы докажем и саму теорему.
Так как внутренние накрест лежащие углы, образованные при пересечении двух параллельных прямых секущей, равны (об этом говорилось в статье параллельные прямые, параллельность прямых), то , а прямая M2H2 , перпендикулярная прямой b по построению, перпендикулярна и прямой a . Тогда треугольники М1H1H2 и М2М1H2 прямоугольные, и, более того, они равны по гипотенузе и острому углу: М1H2 – общая гипотенуза, . Из равенства треугольников следует равенство их соответствующих сторон, поэтому, . Теорема доказана.
Следует заметить, что расстояние между двумя параллельными прямыми является наименьшим из расстояний от точек одной прямой до точек другой прямой.
Нахождение расстояния между параллельными прямыми – теория, примеры, решения.
Итак, нахождение расстояния между параллельными прямыми сводится к нахождению длины перпендикуляра, проведенного из некоторой точки одной из прямых на другую прямую. При этом подбирается метод, позволяющий это расстояние отыскать. Выбор метода зависит от условий конкретной задачи. В некоторых случаях можно использовать теорему Пифагора, в других — признаки равенства или подобия треугольников, определения синуса, косинуса или тангенса угла и т.п. Если же параллельные прямые заданы в прямоугольной системе координат, то расстояние между заданными параллельными прямыми можно вычислить методом координат. На нем и остановимся.
Сформулируем условие задачи.
Пусть на плоскости или в трехмерном пространстве зафиксирована прямоугольная система координат, заданы две параллельные прямые a и b и требуется найти расстояние между этими прямыми.
Решение этой задачи строится на определении расстояния между параллельными прямыми — чтобы найти расстояние между двумя заданными параллельными прямыми нужно:
- определить координаты некоторой точки М1 , лежащей на прямой a (или на прямой b );
- вычислить расстояние от точки М1 до прямой b (или a ).
С определением координат точки М1 , лежащей на какой-нибудь из заданных параллельных прямых, проблем не возникнет, если, конечно, Вам знакомы основные виды уравнения прямой на плоскости и уравнения прямой в пространстве. Для нахождения расстояния от точки М1 до нужной из заданных параллельных прямых Вам будет полезна информация из раздела нахождение расстояния от точки до прямой.
В частности, если в прямоугольной системе координат Oxy на плоскости прямую a задает общее уравнение прямой вида , а прямую b , параллельную прямой a , — общее уравнение прямой , то расстояние между этими параллельными прямыми можно вычислить по формуле .
Покажем вывод этой формулы.
Возьмем точку , которая лежит на прямой a , тогда координаты точки М1 удовлетворяют уравнению , то есть, справедливо равенство , откуда имеем .
Если , то нормальное уравнение прямой b имеет вид , а если , то нормальное уравнение прямой b имеет вид . Тогда при расстояние от точки до прямой b вычисляется по формуле , а при — по формуле
То есть, при любом значении С2 расстояние от точки до прямой b можно вычислить по формуле . А если учесть равенство , которое было получено выше, то последняя формула примет вид . На этом вывод формулы для вычисления расстояние между двумя параллельными прямыми, заданными общими уравнениями прямых вида и завершен.
Разберем решения примеров.
Начнем с нахождения расстояния между двумя параллельными прямыми, заданными в прямоугольной системе координат Oxy на плоскости.
Найдите расстояние между параллельными прямыми и .
Очевидно, что прямая, которой соответствуют параметрические уравнения прямой на плоскости вида , проходит через точку .
Искомое расстояние между параллельными прямыми равно расстоянию от точки до прямой . Вычислим его.
Получим нормальное уравнение прямой, которой отвечает уравнение прямой с угловым коэффициентом вида . Для этого сначала запишем общее уравнение прямой: . Теперь вычислим нормирующий множитель: . Умножив на него обе части последнего уравнения, имеем нормальное уравнение прямой: . Искомое расстояние равно модулю значения выражения , вычисленного при . Итак, расстояние между заданными параллельными прямыми равно
Второй способ решения.
Получим общие уравнения заданных параллельных прямых.
Выше мы выяснили, что прямой соответствует общее уравнение прямой . Перейдем от параметрических уравнений прямой вида к общему уравнению этой прямой:
Коэффициенты при переменных x и y в полученных общих уравнениях параллельных прямых равны, поэтому мы сразу можем применить формулу для вычисления расстояния между параллельными прямыми на плоскости: .
.
На плоскости введена прямоугольная система координат Oxy и даны уравнения двух параллельных прямых и . Найдите расстояние между указанными параллельными прямыми.
Канонические уравнения прямой на плоскости вида позволяют сразу записать координаты точки М1 , лежащей на этой прямой: . Расстояние от этой точки до прямой равно искомому расстоянию между параллельными прямыми. Уравнение является нормальным уравнением прямой, следовательно, мы можем сразу вычислить расстояние от точки до прямой : .
Второй способ решения.
Общее уравнение одной из заданных параллельных прямых нам уже дано . Приведем каноническое уравнение прямой к общему уравнению прямой: . Коэффициенты при переменной x в общих уравнениях заданных параллельных прямых равны (при переменной y коэффициенты тоже равны — они равны нулю), поэтому можно применять формулу, позволяющую вычислить расстояние между заданными параллельными прямыми: .
Осталось рассмотреть пример нахождения расстояния между параллельными прямыми в трехмерном пространстве.
Найдите расстояние между двумя параллельными прямыми, которым в прямоугольной системе координат Oxyz соответствуют канонические уравнения прямой в пространстве вида и .
Очевидно, прямая проходит через точку . Вычислим расстояние от этой точки до прямой — оно даст нам искомое расстояние между параллельными прямыми.
Прямая проходит через точку . Обозначим направляющий вектор прямой как , он имеет координаты . Вычислим координаты вектора (при необходимости смотрите статью координаты вектора по координатам точек): . Найдем векторное произведение векторов и :
Теперь осталось применить формулу, позволяющую вычислить расстояние от точки до прямой в пространстве: .
расстояние между заданными параллельными прямыми равно .
Расстояние между двумя параллельными прямыми: определение и примеры нахождения
В материале этой статьи разберем вопрос нахождения расстояния между двумя параллельными прямыми, в частности, при помощи метода координат. Разбор типовых примеров поможет закрепить полученные теоретические знания.
Расстояние между двумя параллельными прямыми: определение
Расстояние между двумя параллельными прямыми – это расстояние от некоторой произвольной точки одной из параллельных прямых до другой прямой.
Приведем иллюстрацию для наглядности:
На чертеже изображены две параллельные прямые a и b . Точка М 1 принадлежит прямой a , из нее опущен перпендикуляр на прямую b . Полученный отрезок М 1 Н 1 и есть расстояние между двумя параллельными прямыми a и b .
Указанное определение расстояния между двумя параллельными прямыми справедливо как на плоскости, так и для прямых в трехмерном пространстве. Кроме того, данное определение взаимосвязано со следующей теоремой.
Когда две прямые параллельны, все точки одной из них равноудалены от другой прямой.
Пусть нам заданы две параллельные прямые a и b . Зададим на прямой а точки М 1 и М 2 , опустим из них перпендикуляры на прямую b , обозначив их основания соответственно как Н 1 и Н 2 . М 1 Н 1 – это расстояние между двумя параллельными прямыми по определению, и нам необходимо доказать, что | М 1 Н 1 | = | М 2 Н 2 | .
Пусть будет также существовать некоторая секущая, которая пересекает две заданные параллельные прямые. Условие параллельности прямых, рассмотренное в соответствующей статье, дает нам право утверждать, что в данном случае внутренние накрест лежащие углы, образованные при пересечении секущей заданных прямых, являются равными: ∠ M 2 M 1 H 2 = ∠ H 1 H 2 M 1 . Прямая М 2 Н 2 перпендикулярна прямой b по построению, и, конечно, перпендикулярна прямой a . Получившиеся треугольники М 1 Н 1 Н 2 и М 2 М 1 Н 2 являются прямоугольными и равными друг другу по гипотенузе и острому углу: М 1 Н 2 – общая гипотенуза, ∠ M 2 M 1 H 2 = ∠ H 1 H 2 M 1 . Опираясь на равенство треугольников, мы можем говорить о равенстве их сторон, т.е.: | М 1 Н 1 | = | М 2 Н 2 | . Теорема доказана.
Отметим, что расстояние между двумя параллельными прямыми – наименьшее из расстояний от точек одной прямой до точек другой.
Нахождение расстояния между параллельными прямыми
Мы уже выяснили, что, по сути, чтобы найти расстояние между двумя параллельными прямыми, необходимо определить длину перпендикуляра, опущенного из некой точки одной прямой на другую. Способов, как это сделать, несколько. В каких-то задачах удобно воспользоваться теоремой Пифагора; другие предполагают использование признаков равенства или подобия треугольников и т.п. В случаях, когда прямые заданы в прямоугольной системе координат, возможно вычислить расстояние между двумя параллельными прямыми, используя метод координат. Рассмотрим его подробнее.
Зададим условия. Допустим, зафиксирована прямоугольная система координат, в которой заданы две параллельные прямые a и b . Необходимо определить расстояние между заданными прямыми.
Решение задачи построим на определении расстояния между параллельными прямыми: для нахождения расстояния между двумя заданными параллельными прямыми необходимо:
— найти координаты некоторой точки М 1 , принадлежащей одной из заданных прямых;
— произвести вычисление расстояния от точки М 1 до заданной прямой, которой эта точка не принадлежит.
Опираясь на навыки работы с уравнениями прямой на плоскости или в пространстве, определить координаты точки М 1 просто. При нахождении расстояния от точки М 1 до прямой пригодится материал статьи о нахождении расстояния от точки до прямой.
Вернемся к примеру. Пусть прямая a описывается общим уравнением A x + B y + C 1 = 0 , а прямая b – уравнением A x + B y + C 2 = 0 . Тогда расстояние между двумя заданными параллельными прямыми возможно вычислить, используя формулу:
M 1 H 1 = C 2 — C 1 A 2 + B 2
Выведем эту формулу.
Используем некоторую точку М 1 ( x 1 , y 1 ) , принадлежащую прямой a . В таком случае координаты точки М 1 будут удовлетворять уравнению A x 1 + B y 1 + C 1 = 0 . Таким образом, справедливым является равенство: A x 1 + B y 1 + C 1 = 0 ; из него получим: A x 1 + B y 1 = — C 1 .
Когда С 2 0 , нормальное уравнение прямой b будет иметь вид:
A A 2 + B 2 x + B A 2 + B 2 y + C 2 A 2 + B 2 = 0
При С 2 ≥ 0 нормальное уравнение прямой b будет выглядеть так:
A A 2 + B 2 x + B A 2 + B 2 y — C 2 A 2 + B 2 = 0
И тогда для случаев, когда С 2 0 , применима формула: M 1 H 1 = A A 2 + B 2 x 1 + B A 2 + B 2 y 1 + C 2 A 2 + B 2 .
А для С 2 ≥ 0 искомое расстояние определяется по формуле M 1 H 1 = — A A 2 + B 2 x 1 — B A 2 + B 2 y 1 — C 2 A 2 + B 2 = = A A 2 + B 2 x 1 + B A 2 + B 2 y 1 + C 2 A 2 + B 2
Таким образом, при любом значении числа С 2 длина отрезка | М 1 Н 1 | (от точки М 1 до прямой b ) вычисляется по формуле: M 1 H 1 = A A 2 + B 2 x 1 + B A 2 + B 2 y 1 + C 2 A 2 + B 2
Выше мы получили: A x 1 + B y 1 = — C 1 , тогда можем преобразовать формулу: M 1 H 1 = — C 1 A 2 + B 2 + C 2 A 2 + B 2 = C 2 — C 1 A 2 + B 2 . Так мы, собственно, получили формулу, указанную в алгоритме метода координат.
Разберем теорию на примерах.
Заданы две параллельные прямые y = 2 3 x — 1 и x = 4 + 3 · λ y = — 5 + 2 · λ . Необходимо определить расстояние между ними.
Решение
Исходные параметрические уравнения дают возможность задать координаты точки, через которую проходит прямая, описываемая параметрическими уравнениями. Таким образом, получаем точку М 1 ( 4 , — 5 ) . Требуемое расстояние – это расстояние между точкой М 1 ( 4 , — 5 ) до прямой y = 2 3 x — 1 , произведем его вычисление.
Заданное уравнение прямой с угловым коэффициентом y = 2 3 x — 1 преобразуем в нормальное уравнение прямой. С этой целью сначала осуществим переход к общему уравнению прямой:
y = 2 3 x — 1 ⇔ 2 3 x — y — 1 = 0 ⇔ 2 x — 3 y — 3 = 0
Вычислим нормирующий множитель: 1 2 2 + ( — 3 ) 2 = 1 13 . Умножим на него обе части последнего уравнения и, наконец, получим возможность записать нормальное уравнение прямой: 1 13 · 2 x — 3 y — 3 = 1 13 · 0 ⇔ 2 13 x — 3 13 y — 3 13 = 0 .
При x = 4 , а y = — 5 вычислим искомое расстояние как модуль значения крайнего равенства:
2 13 · 4 — 3 13 · — 5 — 3 13 = 20 13
Ответ: 20 13 .
В фиксированной прямоугольной системе координат O x y заданы две параллельные прямые, определяемые уравнениями x — 3 = 0 и x + 5 0 = y — 1 1 . Необходимо найти расстояние между заданными параллельными прямыми.
Решение
Условиями задачи определено одно общее уравнение, задаваемое одну из исходных прямых: x-3=0. Преобразуем исходное каноническое уравнение в общее: x + 5 0 = y — 1 1 ⇔ x + 5 = 0 . При переменной x коэффициенты в обоих уравнениях равны (также равны и при y – нулю), а потому имеем возможность применить формулу для нахождения расстояния между параллельными прямыми:
M 1 H 1 = C 2 — C 1 A 2 + B 2 = 5 — ( — 3 ) 1 2 + 0 2 = 8
Ответ: 8 .
Напоследок рассмотрим задачу на нахождение расстояния между двумя параллельными прямыми в трехмерном пространстве.
В прямоугольной системе координат O x y z заданы две параллельные прямые, описываемые каноническими уравнениями прямой в пространстве: x — 3 1 = y — 1 = z + 2 4 и x + 5 1 = y — 1 — 1 = z — 2 4 . Необходимо найти расстояние между этими прямыми.
Решение
Из уравнения x — 3 1 = y — 1 = z + 2 4 легко определются координаты точки, через которую проходит прямая, описываемая этим уравнением: М 1 ( 3 , 0 , — 2 ) . Произведем вычисление расстояния | М 1 Н 1 | от точки М 1 до прямой x + 5 1 = y — 1 — 1 = z — 2 4 .
Прямая x + 5 1 = y — 1 — 1 = z — 2 4 проходит через точку М 2 ( — 5 , 1 , 2 ) . Запишем направляющий вектор прямой x + 5 1 = y — 1 — 1 = z — 2 4 как b → с координатами ( 1 , — 1 , 4 ) . Определим координаты вектора M 2 M → :
M 2 M 1 → = 3 — ( — 5 , 0 — 1 , — 2 — 2 ) ⇔ M 2 M 1 → = 8 , — 1 , — 4
Вычислим векторное произведение векторов :
b → × M 2 M 1 → = i → j → k → 1 — 1 4 8 — 1 — 4 = 8 · i → + 36 · j → + 7 · k → ⇒ b → × M 2 M 1 → = ( 8 , 36 , 7 )
Применим формулу расчета расстояния от точки до прямой в пространстве:
M 1 H 1 = b → × M 2 M 1 → b → = 8 2 + 36 2 + 7 2 1 2 + ( — 1 ) 2 + 4 2 = 1409 3 2
Геометрия. 7 класс
Конспект урока
Расстояние от точки до прямой. Расстояние между параллельными прямыми
Перечень рассматриваемых вопросов:
- Понятие наклонной.
- Расстояние от точки до прямой.
- Расстояние между параллельными прямыми.
- Теорема о равноудалённости точек параллельных прямых.
Наклонной, проведенной из данной точки к данной прямой, называется любой отрезок, соединяющий данную точку с точкой прямойине являющийся перпендикуляром к прямой.
Длина перпендикуляра, проведенного из точки к прямой, называется расстоянием от этой точки до прямой.
Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
Все точки плоскости, расположенные по одну сторону от данной прямой и равноудаленные от неё, лежат на прямой, параллельной данной.
Расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми.
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
Расстояние между двумя точками – длина отрезка, соединяющего эти точки. Введём также следующие понятия:
1) расстояние от точки до прямой;
2) расстояние между параллельными прямыми.
Пусть отрезок АН – перпендикуляр, проведённый из точки А к прямой а, М – любая точка прямой а, отличная от Н. Отрезок АМ называется наклонной, проведённой из точки А к прямой а. В прямоугольном треугольнике АНМ катет АН меньше гипотенузы АМ. Следовательно, перпендикуляр, проведённый из точки к прямой, меньше любой наклонной, проведённой из той же точки к этой прямой.
Длина перпендикуляра, проведённого из точки к прямой, называется расстоянием от этой точки до прямой.
Отметим, что расстояние от точки до прямой равно наименьшему из расстояний от этой точки до точек прямой.
На рисунке расстояние от точки В до прямой р равно 3 см, а расстояние от точки С до этой прямой равно 5 см.
Прежде чем ввести понятие расстояния между параллельными прямыми, рассмотрим одно из важнейших свойств параллельных прямых.
Теорема. Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
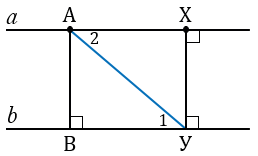
Доказательство. Рассмотрим параллельные прямые а и b. Отметим на прямой a точку A и проведём из этой точки перпендикуляр AB к прямой b. Докажем, что расстояние от любой точки X прямой а до прямой b равно АВ.
Проведём из точки Х перпендикуляр XY к прямой b. Так как XY перпендикулярно b, то XY перпендикулярно а. Прямоугольные треугольники ABY и YXA равны по гипотенузе и острому углу (AY – общая гипотенуза, а углы 1 и 2 равны как накрест лежащие углы при пересечении параллельных прямых a и b секущей AY). Следовательно, XY = AB.
Итак, любая точка X прямой a находится на расстоянии AB от прямой b. Очевидно, что все точки прямой b находятся на таком же расстоянии от прямой a. Теорема доказана.
Из доказанной теоремы следует, что точка, движущаяся по одной из параллельных прямых, все время находится на одном и том же расстоянии от другой прямой.
Расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми.
Отметим, что расстояние между параллельными прямыми равно наименьшему из расстояний от точек одной прямой до точек другой прямой.
Замечание. Справедливо утверждение, обратное доказанной теореме: все точки плоскости, расположенные по одну сторону от данной прямой и равноудалённые от неё, лежат на прямой, параллельной данной.
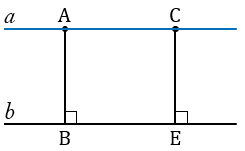
Доказательство: по аксиоме параллельных прямых, через точку A проведем прямую b, b║a, тогда все точки b║a равноудаленыот точек прямой a. Докажем, что B, C∈ b.
Пусть B∉ b, C∉ b, значит, расстояние от точки B до a и C будет больше или меньше, чем расстояние h. Но это противоречит AA1 = BB1 = CC1.
Следовательно, наше предположение неверно и A, B и С ∈ b || a, что и требовалось доказать.
Разбор заданий тренировочного модуля.
В равностороннем треугольнике ABC проведена биссектриса AD. Расстояние от точки D до прямой AC равно 12 см. Найти расстояние от точки A до прямой BC.
Объяснение: равносторонним треугольником называется треугольник с тремя равными сторонами (значит, и с тремя равными углами, то есть – по 60°). Равносторонний треугольник является частным случаем равнобедренного, поэтому все свойства, присущие равнобедренному треугольнику, распространяются и на равносторонний. Поэтому АD – не только биссектриса, но ещё и высота, стало быть AD⊥BC
Поскольку расстояние от точки D до прямой АС – это длина перпендикуляра, опущенного из точки D на прямую AC, то DH – данное расстояние. Рассмотрим треугольник AHD. В нём угол H = 90°, так как DH – перпендикуляр к AC (по определению расстояния от точки до прямой). Кроме этого, в данном треугольнике катет DH лежит против угла DAH = 30°, поэтому AD = 2 ∙ 12= 24см (по свойству).
Расстояние от точки А до прямой ВС – это длина опущенного на прямую ВС перпендикуляра. По доказанному AD⊥ BC, значит, AD = 24 см.
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/rasstojanie-mezhdu-dvumja-parallelnymi-prjamymi/
http://resh.edu.ru/subject/lesson/7306/conspect/
Геометрия
7 класс
Урок № 26
Расстояние от точки до прямой. Расстояние между параллельными прямыми
Перечень рассматриваемых вопросов:
- Понятие наклонной.
- Расстояние от точки до прямой.
- Расстояние между параллельными прямыми.
- Теорема о равноудалённости точек параллельных прямых.
Тезаурус:
Наклонной, проведенной из данной точки к данной прямой, называется любой отрезок, соединяющий данную точку с точкой прямойине являющийся перпендикуляром к прямой.
Длина перпендикуляра, проведенного из точки к прямой, называется расстоянием от этой точки до прямой.
Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
Все точки плоскости, расположенные по одну сторону от данной прямой и равноудаленные от неё, лежат на прямой, параллельной данной.
Расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми.
Основная литература:
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Дополнительная литература:
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
Расстояние между двумя точками – длина отрезка, соединяющего эти точки. Введём также следующие понятия:
1) расстояние от точки до прямой;
2) расстояние между параллельными прямыми.
Пусть отрезок АН – перпендикуляр, проведённый из точки А к прямой а, М – любая точка прямой а, отличная от Н. Отрезок АМ называется наклонной, проведённой из точки А к прямой а. В прямоугольном треугольнике АНМ катет АН меньше гипотенузы АМ. Следовательно, перпендикуляр, проведённый из точки к прямой, меньше любой наклонной, проведённой из той же точки к этой прямой.
Длина перпендикуляра, проведённого из точки к прямой, называется расстоянием от этой точки до прямой.
Отметим, что расстояние от точки до прямой равно наименьшему из расстояний от этой точки до точек прямой.
На рисунке расстояние от точки В до прямой р равно 3 см, а расстояние от точки С до этой прямой равно 5 см.
Прежде чем ввести понятие расстояния между параллельными прямыми, рассмотрим одно из важнейших свойств параллельных прямых.
Теорема. Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
Доказательство. Рассмотрим параллельные прямые а и b. Отметим на прямой a точку A и проведём из этой точки перпендикуляр AB к прямой b. Докажем, что расстояние от любой точки X прямой а до прямой b равно АВ.
Проведём из точки Х перпендикуляр XY к прямой b. Так как XY перпендикулярно b, то XY перпендикулярно а. Прямоугольные треугольники ABY и YXA равны по гипотенузе и острому углу (AY – общая гипотенуза, а углы 1 и 2 равны как накрест лежащие углы при пересечении параллельных прямых a и b секущей AY). Следовательно, XY = AB.
Итак, любая точка X прямой a находится на расстоянии AB от прямой b. Очевидно, что все точки прямой b находятся на таком же расстоянии от прямой a. Теорема доказана.
Из доказанной теоремы следует, что точка, движущаяся по одной из параллельных прямых, все время находится на одном и том же расстоянии от другой прямой.
Расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми.
Отметим, что расстояние между параллельными прямыми равно наименьшему из расстояний от точек одной прямой до точек другой прямой.
Замечание. Справедливо утверждение, обратное доказанной теореме: все точки плоскости, расположенные по одну сторону от данной прямой и равноудалённые от неё, лежат на прямой, параллельной данной.
Дано:
AA1= BB1= CC1
Доказать: точкиA, B, C– принадлежатодной прямой, АА1║ ВВ1║СС1.
Доказательство: по аксиоме параллельных прямых, через точку A проведем прямую b, b║a, тогда все точки b║a равноудаленыот точек прямой a. Докажем, что B, C∈ b.
Пусть B∉ b, C∉ b, значит, расстояние от точки B до a и C будет больше или меньше, чем расстояние h. Но это противоречит AA1 = BB1 = CC1.
Следовательно, наше предположение неверно и A, B и С ∈ b || a, что и требовалось доказать.
Разбор заданий тренировочного модуля.
В равностороннем треугольнике ABC проведена биссектриса AD. Расстояние от точки D до прямой AC равно 12 см. Найти расстояние от точки A до прямой BC.
Объяснение: равносторонним треугольником называется треугольник с тремя равными сторонами (значит, и с тремя равными углами, то есть – по 60°). Равносторонний треугольник является частным случаем равнобедренного, поэтому все свойства, присущие равнобедренному треугольнику, распространяются и на равносторонний. Поэтому АD – не только биссектриса, но ещё и высота, стало быть AD⊥BC
Поскольку расстояние от точки D до прямой АС – это длина перпендикуляра, опущенного из точки D на прямую AC, то DH – данное расстояние. Рассмотрим треугольник AHD. В нём угол H = 90°, так как DH – перпендикуляр к AC (по определению расстояния от точки до прямой). Кроме этого, в данном треугольнике катет DH лежит против угла DAH = 30°, поэтому AD = 2 ∙ 12= 24см (по свойству).
Расстояние от точки А до прямой ВС – это длина опущенного на прямую ВС перпендикуляра. По доказанному AD⊥ BC, значит, AD = 24 см.
Ответ: 24 см.
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Соотношения между сторонами и углами треугольника
- Расстояние между параллельными прямыми
Теорема
Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
Доказательство:
Рассмотрим параллельные прямые 

Отметим точку А на прямой 

Отметим точку Х на прямой 


ХУ

Рассмотрим 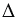
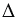
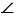
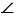


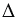
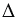
Точка Х находится на расстоянии АВ от прямой 


Из доказанной выше теоремы следует, что расстояние между параллельными прямыми — это наименьшее расстояние (перпендикуляр) от каждой точки одной из этих прямых до другой прямой.
Замечание 1
Все точки плоскости, расположенные по одну сторону от данной прямой и равноудаленные от нее, лежат на прямой параллельной данной.
Доказательство:
Дано: прямая 



Доказать: А, С
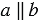
Доказательство:
По аксиоме параллельных прямых через точку А проходит единственная прямая параллельная прямой 


По теореме, доказанной выше, все точки, лежащие на прямой 

Предположим, что точка С не лежит на прямой 

Но по условию АВ = СЕ, следовательно, получили противоречие, значит, наше предположение неверно и А, С
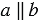
Замечание 2
Множество всех точек плоскости, находящихся на данном расстоянии от данной прямой и лежащих по одну сторону от нее, есть прямая, параллельная данной прямой.
Доказательство:
Пусть 





По доказанной выше теореме все точки прямой 



Геометрическое место точек, удовлетворяющих данному условию — множество всех точек, удовлетворяющих какому-либо условию.
Советуем посмотреть:
Теорема о сумме углов треугольника
Остроугольный, прямоугольный и тупоугольный треугольники
Теорема о соотношениях между сторонами и углами треугольника
Неравенство треугольника
Некоторые свойства прямоугольных треугольников
Признаки равенства прямоугольных треугольников
Уголковый отражатель
Расстояние от точки до прямой
Построение треугольника по двум сторонам и углу между ними
Построение треугольника по стороне и двум прилежащим к ней углам
Построение треугольника по трем его сторонам
Соотношения между сторонами и углами треугольника
Правило встречается в следующих упражнениях:
7 класс
Задание 279,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 280,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 283,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 284,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 293,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 294,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 17,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 19,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 20,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1095,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Определение:
Расстоянием
между двумя точками А и В является длина отрезка АВ,
соединяющего эти точки.
При
этом следует отметить, что точки А и В можно соединить
и таким образом:
Но
именно кратчайший путь, то есть отрезок АВ, является расстоянием между данными
точками.
Возьмём
некоторую прямую b
и
точку А, которая не лежит на этой прямой. Опустим
перпендикуляр из точки А к прямой b:
Полученный
отрезок АН и будет называться расстоянием
от точки А до
прямой, так как это кратчайшее расстояние между данными точкой и прямой.
Действительно
так. Отметим точку В на прямой b и рассмотрим прямоугольный
треугольник АНВ:
АВ
— гипотенуза, а АН — катет этого треугольника. Известно, что катет всегда
меньше гипотенузы.
Отрезок
АВ называется наклонной, проведённой из точки А к
прямой b.
Перпендикуляр,
проведённый из точки к прямой, меньше любой наклонной, проведённой из той же
точки к этой прямой.,
Определение:
Длина
перпендикуляра, проведённого из точки к прямой,
называется расстоянием от этой точки до прямой.
Обозначают
следующим образом:
Пусть
а и b
—
параллельные прямые. Отметим на прямой а две точки А
и В и опустим из них перпендикуляры АМ и BN на
прямую b:
Если
прямая a||b,
а отрезки AM⊥b, BN⊥b, то АМ=BN и равняется расстоянию между
параллельными прямыми а и b.
Проведём
отрезок АN
и
рассмотрим полученные треугольники АBN и АМN:
Так
как AM⊥b, а a||b, то AM⊥a. То есть ВN⊥b, а a||b, то и ВN⊥a.
Получили,
что АBN
и АМN
—
прямоугольные треугольники. У них сторона АN —
общая, она является гипотенузой для обоих треугольников. Углы ВАN и АNМ равны, так как являются
внутренними накрест лежащими при параллельных прямых
АВ и MN
и секущей АN.
Следовательно,
получаем, что прямоугольные треугольники АBN и АМN равны по гипотенузе и острому
углу. Из этого следует, что АМ=ВN.
Получили,
что отрезки АМ и BN
равны.
Расстоянием между параллельными прямыми
является длина их общего перпендикуляра.
Обозначают
следующим образом:
Верно
и обратное утверждение:
Все
точки плоскости, расположенные по одну сторону от прямой и находящиеся на
равном расстоянии от неё, лежат на прямой параллельной
данной.
Пример.
На
рисунке отрезок АВ=6 см, ∠В=30 градусов. Найти
расстояние от точки А до прямой а.
Опустим
из точки А к прямой а перпендикуляр АС, который
и есть расстояние от точки А до прямой а:
Получили
прямоугольный треугольник АВС. У которого ∠В=30
градусов, АВ=6см.
Известно,
что катет прямоугольного треугольника, лежащий против угла в 30 градусов, равен
половине гипотенузы. Получаем:
Пример.
На
рисунке расстояние между параллельными прямыми а
и b
равно 5 сантиметров, а расстояние между параллельными прямыми а и с
равно 9 сантиметров. Чему равно расстояние между параллельными
прямыми b
и с?
Известно,
что:
Из
этого следует:
Описание презентации по отдельным слайдам:
-
1 слайд
Расстояние от точки
до прямой.
Расстояние между параллельными прямыми
Учитель математики:
МБОУ СОШ № 38, г.Воронеж
Клыга Лариса Фёдоровна -
2 слайд
Цели и задачи:
Познакомиться с понятием «наклонная», расстояние от точки до прямой, расстояние между параллельными прямыми.
Научится решать задачи на нахождение кратчайшего расстояния от точки до прямой.
Воспитывать математическую культуру речи. -
3 слайд
Повторим
Какое расположение прямых относительно друг друга вы знаете?2. Какие прямые называются перпендикулярными?
3. Сколько перпендикуляров можно провести из точки не лежащей на прямой, к данной прямой?
А -
4 слайд
Повторим
4. Как построить перпендикуляр из точки не лежащей на прямой к данной прямой?
А
5. Назовите:
отрезок перпендикулярный к прямой а;
основание перпендикуляра;
отрезок наименьшей длины
В
а
Н
А
С -
5 слайд
Какие прямые называются параллельными?
2. Назовите свойство параллельных прямых?
Повторим
a
b
c
Если a || b и a || c, то b || c -
6 слайд
Расстояние от точки до прямой
А
В
Расстояние между двумя точками называется длина отрезка, соединяющего эти точки -
7 слайд
Что называется расстояние от точки до прямой?
Расстояние от точки до прямой
В
а
Н
наклонная
С
Пусть ВН прямой а.
Точка С – любая точка прямой а, отличная от Н.
Отрезок ВС – называется наклонной, проведенной из точки В к прямой а.Треугольник ВНС – какой ?
ВН – это ?
ВС – это ?
Что больше ВС или ВН — ?Перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведенной из той же точки к этой прямой
Длина перпендикуляра, проведенного из точки к прямой называется расстоянием от этой точки до прямой
Наименьшее расстояние
-
8 слайд
Теорема. Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
Расстояние между параллельными прямыми -
9 слайд
AC b, DB b, a || b
Так как DB b то DB a.
Треугольники ABC и ADB равны (по гипотенузе и прилежащим углам)
Следовательно АС = DB.Расстояние между параллельными прямыми
Теорема. Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
а
b
A
B
C
D
Расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми.
Наименьшее расстояние -
10 слайд
Замечание 1. Все точки плоскости, расположенные по одну сторону от данной прямой и равноудаленные от неё, лежат на прямой, параллельной данной.
Расстояние между параллельными прямыми
a
A
В
Расстояние от точки А до прямой а равно расстоянию от точки В до прямой а
АА1=ВВ1A1
В1 -
11 слайд
Расстояние между параллельными прямыми
Замечание 2. Множество всех точек плоскости, находящихся на данном расстоянии от данной прямой и лежащих по одну сторону от нее, есть прямая, параллельная данной прямой.a
d
A
B
b -
12 слайд
На этом факте основано устройство инструмента, называемого рейсмусом.
Расстояние между параллельными прямыми -
13 слайд
Закрепление изученного материала
Решить задачи № 271, 272 -
14 слайд
Вариант 1.
m || n. Расстояние от точки М до прямой m равно 4,5 см, а до прямой n равно 14,8.
Найти расстояние между прямыми m и n.Самостоятельная работа
Вариант 2.
AB || CD. CB = 24,5 см, <BCD = 30 0 .
Найти расстояние между прямыми AB и CD
m
М
n
A
B
C
D -
15 слайд
Какой отрезок называется наклонной?
Перпендикуляр, проведенный из точки к прямой, меньше или больше наклонной, поведенной из этой же точки?
Что называется расстоянием от точки до прямой?
Какое расстояние считается наименьшим от точки до прямой?
Итог урока
5. Что называется расстоянием между параллельными прямыми?Мне было все понятно
Мне нужно еще раз разобраться в теме
Я ничего не понял -
16 слайд
Спасибо за урок!