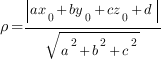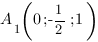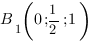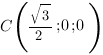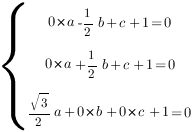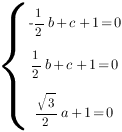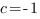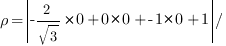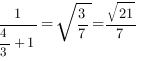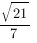Сергей Евгеньевич Грамотинский
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Скрещивающиеся прямые — это прямые, не лежащие в одной плоскости и не пересекающиеся между собой.
Наименьшим расстоянием между двумя скрещивающимися прямыми является перпендикуляр, опущенный с одной прямой на другую. У каждой пары скрещивающихся прямых при этом есть только один такой общий перпендикуляр.

Рисунок 1. Кратчайшее расстояние между скрещивающимися прямыми. Автор24 — интернет-биржа студенческих работ
Через каждую из скрещивающихся прямых возможно провести лишь одну плоскость, параллельную второй скрещивающейся прямой, соответственно, для определения расстояния между скрещивающимися прямыми, достаточно определить расстояние между одной из скрещивающихся прямых и плоскостью, на которой лежит вторая прямая.
Соответственно, задачу поиска расстояния между прямой и параллельной ей плоскостью можно свести к поиску расстояния между любой точкой, лежащей на вышеозначенной прямой, и плоскостью.
Как найти расстояние между скрещивающимися прямыми: координатный метод
Рассмотрим методику нахождения расстояния между двумя скрещивающимися прямыми $L_1$ и $L_2$ через координатный метод.
Прямая $L_1$ задана каноническими уравнениями $frac{x-x_1}{l_1} =frac{y-y_1}{m_1}=frac{z-z_1}{n_1}$, а прямая $L_2$ — $frac{x-x_2}{l_2}=frac{y-y_2}{m_2}=frac{z-z_2}{n_2}$.
Прежде всего необходимо найти уравнение плоскости $β$, параллельной прямой $L_1$. Для этого необходимо найти векторное произведение направляющих векторов прямых $L_1$ и $L_2$, данное произведение представляет собой координаты нормального вектора плоскости $β$:
«Расстояние между скрещивающимися прямыми: формула» 👇
$[ {l_1;m_1;n_1} cdot {l_2;m_2;n_2}]=begin{array}{|ccc|} i & j & k \ l_1 & m_1 &n_1 \ l_2 & m_2 &n_2 \ end{array}left(1right)$.
При вычислении выражения $(1)$ мы получим коэффициенты для общего уравнения плоскости $β$ — $A, B$ и $C$.
Для того чтобы записать всё общее выражение плоскости, подставим координаты любой точки, лежащей на $L_2$ в общую форму, например, можно подставить точку с координатами $(x_2;y_2; z_2)$, получим следующее:
$A (x-x_2) + B (y – y_2) + C(z- z_2) + D=0$.
Теперь достаточно выбрать любую точку на прямой $L_1$, пусть это будет точка $M_1$ с координатами $(x_1;y_1; z_1)$.
Расстояние от плоскости $β$ до точки $M_1$ составит:
$ρ=frac{|Ax_1 + By_1 + Cz_1 + D|}{sqrt{A^2 + B^2 + C^2}}left(2right)$,
где $A, B, C$ и $D$ — коэффициенты уравнения плоскости $β$, а $(x_1;y_1; z_1)$ — координаты точки, лежащей на прямой $L_1$.
Замечание 1
Данная формула позволяет высчитать расстояние между двумя скрещивающимися прямыми.
Пример 1
Определить расстояние между скрещивающимися прямыми $L_1$ и $L_2$.
Уравнения прямых —
$L_1: frac{x-2}{2}=frac{y+1}{-3}=frac{z}{-1}$
$L_2: frac{x+1}{1}=frac{y}{-2}; z-1=0$.
Найдём нормальный вектор плоскости, в которой лежит прямая $L_2$, для этого выпишем направляющие вектора для каждой из прямых:
$L_1: vec{s_1}= {2;-3;-1}$, точка на этой прямой — $(2;-1;0)$
$L_2: vec{s_2}= {1;-2;0}$, точка на этой прямой — $(-1;0;1)$
Теперь найдём векторное произведение векторов $vec{s_1}$ и $vec{s_2}$, полученный вектор является нормальным вектором плоскости, в которой лежит $L_2 $:
$[vec{s_1}cdot vec{s_2}]= begin{array}{|ccc|} i &j &k \ 2 &-3 &-1 \ 1 &-2 &0 \ end{array}=((-3) cdot 0 -2) cdot vec{i} + (2 cdot 0 + 1)vec{j} + ((-4) + 3) cdot vec{k} = -2vec{i} + vec{j} -k = {-2;1;-1}$
Подставим координаты точки $(-1;0;1)$, принадлежащей прямой $L_2$, в общее уравнение плоскости:
$-2 cdot (x+1) + (y-0) – 1 cdot(z-1)=0$
Упрощаем и в конечном итоге имеем следующее уравнение плоскости:
$-2x+y-z+1=0$
Теперь, используя координаты точки $(2;-1;0)$, лежащей на первой прямой, можно воспользоваться формулой $(2)$ для вычисления расстояния между двумя скрещивающимися прямыми:
$ρ=frac{|(-2) cdot 2 + 1 cdot(-1) + (-1) cdot(0) + 1|}{sqrt{(-2)^2+1^2+(-1)^2}}=frac{|(-4)+(-1)+1|}{sqrt{4+1+1}}=frac{4}{sqrt{6}}$
Координатная формула вычисления расстояния между скрещивающимися прямыми
Также аналогичное уравнение для поиска расстояния между скрещивающимися прямыми можно использовать сразу в полной координатной форме:
$ρ=frac{begin{array}{|ccc|} l_1 & m_1 &n_1\ l_2 &m_2 &n_2\ (x_2 – x_1) &(y_2-y_1) &(z_2-z_1) \ end{array}}{sqrt{begin{array}{|cc|} m_1 &n_1 \ m_2 &n_2 \ end{array}^2 + begin{array}{|cc|} l_1 &n_1 \ l_2 &n_2 \ end{array}^2 + begin{array}{|cc|} l_1 &m_1 \ l_2 &m_2 \ end{array}^2}}left(3right)$
Для того чтобы воспользоваться данной формулой, возможно нужно освежить в памяти способы нахождения определителей матриц.
Пример 2
Найти расстояние между вышеприведёнными прямыми с помощью формулы $(3)$.
Выпишем сначала точки, принадлежащие данным прямым и их направляющие векторы:
$L_1$ имеет направляющий вектор ${2; -3; -1}$, а принадлежащая ей точка имеет координаты $(2; -1; 0)$.
$L_2$ имеет направляющий вектор ${1; -2; 0 }$, а принадлежащая ей точка имеет координаты $(-1; 0; 1)$.
Воспользуемся формулой $(3)$:
$ρ=frac{begin{array}{|ccc|} 2 & -3 &-1\ 1 &-2 &0\ (-1 -2) &(0+ 1) &(1-0) \ end{array}}{sqrt{begin{array}{|cc|} -3 &-1 \ -2 &0 \ end{array}^2 + begin{array}{|cc|} 2 & -1 \ 1 &0 \ end{array}^2 + begin{array}{|cc|} 2 & -3 \ 1 & -2 \ end{array}^2}}=frac{|4|}{sqrt{2^2 + 1^2 + 1^2}}=frac{4}{sqrt{6}}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Расстояние между прямыми в пространстве онлайн
С помощю этого онлайн калькулятора можно найти расстояние между прямыми в пространстве. Дается подробное решение с пояснениями. Для вычисления расстояния между прямыми в пространстве, задайте вид уравнения прямых («канонический» или «параметрический» ), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить».
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Расстояние между прямыми в пространстве − теория, примеры и решения
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2:
где M1(x1, y1, z1) и M2(x2, y2, z2) − точки, лежащие на прямых L1 и L2, а q1={m1, p1, l1} и q2={m2, p2, l2} − направляющие векторы прямых L1 и L2, соответственно.
Прямые (1) и (2) в пространстве могут совпадать, быть паралленьными, пересекаться, или быть скрещивающимся. Если прямые в пространстве пересекаются или совпадают, то расстояние между ними равно нулю. Мы рассмотрим два случая. Первый − прямые параллельны, и второй − прямые скрещиваются. Остальные являются частыми случаями. Если при вычислении расстояния между параллельными прямыми мы получим расстояние равным нулю, то это значит, что эти прямые совпадают. Если же расстояние между скрещивающимися прямыми равно нулю, то эти прямые пересекаются.
1. Расстояние между параллельными прямыми в пространстве
Рассмотрим два метода вычисления расстояния между прямыми.
Метод 1. От точки M1 прямой L1 проводим плоскость α, перпендикулярно прямой L2. Находим точку M3(x3, y3, y3) пересечения плоскости α и прямой L3. По сути мы находим проекцию точки M1 на прямую L2. Как найти проекцию точки на прямую посмотрите здесь. Далее вычисляем расстояние между точками M1(x1, y1, z1) и M3(x3, y3, z3):
которое и является расстоянием между прямыми L1 и L2 (Рис.1).
Пример 1. Найти расстояние между прямыми L1 и L2:
Решение. Прямая L1 проходит через точку M1(x1, y1, z1)=M1(1, 2, 1) и имеет направляющий вектор
Прямая L2 проходит через точку M2(x2, y2, z2)=M2(8, 4, 1) и имеет направляющий вектор
Найдем проекцию точки M1 на прямую L2. Для этого построим плоскость α, проходящей через точку M1 и перпендикулярной прямойL2.
Для того, чтобы плоскость α было перепендикулярна прямой L2, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L2, т.е. в качестве нормального вектора плоскости α можно взять направляющий вектор прямой L2. Тогда уравнение искомой плоскости, проходящей через точку M1(x1, y1, z1) имеет следующий вид:
Подставляя значения m2, p2, l2, x1, y1, z1 в (5) получим :
После упрощения получим уравнение плоскости, проходящей через точку M1 и перпендикулярной прямой L2:
Найдем точку пересечения прямой L2 и плоскости α, для этого построим параметрическое уравнение прямой L2.
Выразив переменные x, y, z через параметр t, получим параметрическое уравнение прямой L2:
Чтобы найти точку пересечения прямой L2 и плоскости α, подставим значения переменных x, y, z из (7) в (6):
Решив уравнение получим:
Подставляя полученное значение t в (7), получим точку пересеченияпрямой L2 и плоскости α:
Остается найти расстояние между точками M1 и M3:
Ответ: Расстояние между прямыми L1 и L2 равно d=7.2506.
Метод 2. Найдем расстояние между прямыми L1 и L2 (уравнения (1) и (2)). Во первых, проверяем параллельность прямых L1 и L2. Если направляющие векторы прямых L1 и L2 коллинеарны, т.е. если существует такое число λ, что выполнено равенство q1=λq2, то прямые L1 и L2 параллельны.
Данный метод вычисления расстояния между параллельными векторами основана на понятии векторного произведения векторов. Известно, что норма векторного произведения векторов 
Вычислим координаты вектора 
Вычислим векторное произведение векторов 
Вычисляя определители второго порядка находим координаты вектора c:
Далее находим площадь параллелограмма:
Расстояние между прямыми L1 и L2 равно:
где
Пример 2. Решим пример 1 методом 2. Найти расстояние между прямыми
и
Решение. Прямая L1 проходит через точку M1(x1, y1, z1)=M1(1, 2, 1) и имеет направляющий вектор
Прямая L2 проходит через точку M2(x2, y2, z2)=M2(8, 4, 1) и имеет направляющий вектор
Векторы q1 и q2 коллинеарны. Следовательно прямые L1 и L2 параллельны. Для вычисления расстояния между параллельными прямыми воспользуемся векторным произведением векторов.
Построим вектор 
Вычислим векторное произведение векторов 

Вычислим определитель этой матрицы, разложив ее по первой строке. Результатом этих вычислений получим векторное произведение векторов 
Таким образом, результатом векторного произведения векторов 
Поскольку векторное произведение векторов 
Ответ: Расстояние между прямыми L1 и L2 равно d=7.25061.
2. Расстояние между скрещивающимися прямыми в пространстве
Пусть задана декартова прямоугольная симтема координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2 (уравнения (1) и (2)).
Пусть прямые L1 и L2 не параллельны (паралельные прямые мы расстотрели в предыдущем параграфе). Чтобы найти расстояние между прямыми L1 и L2 нужно построить параллельные плоскости α1 и α2 так, чтобы прямая L1 лежал на плоскости α1 а прямая L2 − на плоскости α2. Тогда расстояние между прямыми L1 и L2 равно расстоянию между плоскостями L1 и L2 (Рис. 3).
Поскольку плоскость α1, проходит через прямую L1, то он проходит также через M1(x1, y1, z1). Следовательно справедливо следующее равенство:
где n1={A1, B1, C1} − нормальный вектор плоскости α1. Для того, чтобы плоскость α1 проходила через прямую L1, нормальный вектор n1 должен быть ортогональным направляющему вектору q1 прямой L1, т.е. скалярное произведение этих векторов должен быть равным нулю:
Так как плоскость α1 должна быть параллельной прямой L2, то должна выполнятся условие:
Решая систему линейных уравнений (27)−(29), с тремя уравнениями и четыремя неизвестными A1, B1, C1, D1, и подставляя в уравнение
получим уравнение плоскости α1. (Как построить уравнение плоскости, проходящей через прямую, параллельно другой прямой подробно изложено здесь).
Аналогичным образом находим уравнение плоскости α2:
Плоскости α1 и α2 параллельны, следовательно полученные нормальные векторыn1={A1, B1, C1} и n2={A2, B2, C2} этих плоскостей коллинеарны. Если эти векторы не равны, то можно умножить (31) на некторое число так, чтобы полученный нормальный вектор n2 совпадал с нормальным вектором уравнения (30).
Тогда расстояние между параллельными плоскостями вычисляется формулой:
Полученное расстояние между плоскостями α1 и α2 является также расстоянием между прямыми L1 и L2.
Пример 3. Найти расстояние между прямыми
и
Решение. Прямая L1 проходит через точку M1(x1, y1, z1)=M1(2, 1, 4) и имеет направляющий вектор q1={m1, p1, l1}={1, 3, −2}.
Прямая L2 проходит через точку M2(x2, y2, z2)=M2(6, −1, 2) и имеет направляющий вектор q2={m2, p2, l2}={2, −3, 7}.
Шаг 1.
Построим плоскость α1, проходящую через прямую L1, параллельно прямой L2.
Поскольку плоскость α1 проходит через прямую L1 , то она проходит также через точку M1(x1, y1, z1)=M1(2, 1, 4) и нормальный вектор n1={m1, p1, l1} плоскости α1 перпендикулярна направляющему вектору q1 прямой L1. Тогда уравнение плоскости должна удовлетворять условию:
а условие параллельности прямой L1 и искомой плоскости α1 представляется следующим условием:
Так как плоскость α1 должна быть параллельной прямой L2, то должна выполнятся условие:
Таким образом мы должны решить систему трех уравнений с четырьмя неизвестными (34)−(36). Подставим значения x1, y1, z1, m1, p1, l1, m2, p2, l2 в (27)−(29):
Представим эти уравнения в матричном виде:
Решим систему линейных уравнений (40) отностительно A1, B1, C1, D1:
Искомая плоскость может быть представлена формулой:
Подставляя значения A1, B1, C1, D1 в (42), получим:
Упростим уравнение, умножив на число 17.
Шаг 2.
Построим плоскость α2, проходящую через прямую L2, параллельно прямой L1.
Поскольку плоскость α2 проходит через прямую L2 , то она проходит также через точку M2(x2, y2, z2)=M2(6, −1, 2) и нормальный вектор n2={m2, p2, l2} плоскости α2 перпендикулярна направляющему вектору q2 прямой L2. Тогда уравнение плоскости должна удовлетворять условию:
а условие параллельности прямой L2 и искомой плоскости α2 представляется следующим условием:
Так как плоскость α2 должна быть параллельной прямой L1, то должна выполнятся условие:
Таким образом мы должны решить систему трех уравнений с четырьмя неизвестными (37)−(39). Подставим значения x2, y2, z2, m2, p2, l2, m1, p1, l1 в (37)−(39):
Представим эти уравнения в матричном виде:
Решим систему линейных уравнений (50) отностительно A2, B2, C2, D2:
Искомая плоскость может быть представлена формулой:
Подставляя значения A2, B2, C2, D2 в (52), получим:
Упростим уравнение, умножив на число −83.
Шаг 3.
Расстояние между построенными плоскостями (43) и (53) будет расстоянием между прямыми (1) и (2).
Запишем формулы уравнений плоскостей α1 и α2 :
где n1={A1, B1, C1}={15, −11, −9} и n2={A2, B2, C2}={15, −11, −9} − нормальные векторы плоскостей α1 и α2, соответственно, а свободные члены равны D1=17, D2=−83, соответственно.
Поскольку нормальные векторы плоскостей α1 и α2 совпадают, то можно найти расстояние между плоскостями α1 и α2, используя следующую формулу:
Подставим значения A1, B1, C1, D1, D2 в (54):
Упростим и решим:
Расстояние между прямыми равно: d=4.839339
({color{red}{textbf{Факт 1. Про векторы}}})
(bullet) Если в пространстве заданы две точки (A(x_1;y_1;z_1)) и (B(x_2;y_2;z_2)), то вектор (overrightarrow{AB}) имеет координаты [overrightarrow{AB} = {x_2-x_1;y_2-y_1;z_2-z_1}]
(bullet) Если в пространстве заданы два вектора (vec{a}
={x_1;y_1;z_1}) и (vec{b}=
{x_2;y_2;z_2}), то:
(qquad blacktriangleright) сумма этих векторов (vec{a}+vec{b}={x_1+x_2;y_1+y_2;z_1+z_2})
(qquad blacktriangleright) разность этих векторов (vec{a}-vec{b}={x_1-x_2;y_1-y_2;z_1-z_2})
(qquad blacktriangleright) произведение вектора на число (lambda
vec{a}={lambda x_1;lambda
y_1;lambda z_1})
(bullet) Если в пространстве заданы две точки (A(x_1;y_1;z_1)) и (B(x_2;y_2;z_2)), а точка (O) — середина отрезка (AB), то (O) имеет координаты [Oleft(dfrac{x_1+x_2}2;dfrac{y_1+y_2}2;dfrac{z_1+z_2}2right)]
(bullet) Длина вектора (vec{a}={x;y;z}) обозначается (|vec{a}|) и вычисляется по формуле [|vec{a}|=sqrt{x^2+y^2+z^2}]
(bullet) Заметим, что расстояние между двумя точками есть не что иное, как длина вектора с началом и концом в этих точках.
({color{red}{textbf{Факт 2. Про скалярное произведение}}})
(bullet) Скалярным произведением двух векторов называется произведение длин этих векторов на косинус угла между ними: [{large{(vec{a},
vec{b})=|vec{a}|cdot|vec{b}|cdotcos angle (vec{a},
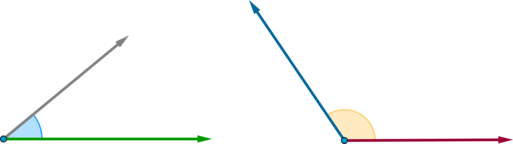
vec{b})}}] На рисунке показано, что такое угол между векторами:
(bullet) Справедливы следующие утверждения:
I. Скалярное произведение ненулевых векторов (их длины не равны нулю) равно нулю тогда и только тогда, когда они перпендикулярны: [(vec{a}, vec{b})=0 quadLeftrightarrowquad
vec{a}perp vec{b}]
II. Длина вектора равна квадратному корню из скалярного произведения вектора на себя: [|vec{a}|=sqrt{(vec{a},
vec{a})}]
III. Переместительный закон: [(vec{a}, vec{b})=(vec{b},
vec{a})]
IV. Распределительный закон: [(vec{a}+vec{b},
vec{c})=(vec{a}, vec{c})+(vec{b}, vec{c})]
V. Сочетательный закон ((lambda) – число): [lambda(vec{a}, vec{b})=(lambda
vec{a}, vec{b})]
(bullet) Скалярное произведение двух векторов (vec{a}
={x_1;y_1;z_1}) и (vec{b}= {x_2;y_2;z_2}) можно вычислить с помощью координат этих векторов: [{large{(vec{a},
vec{b})=x_1x_2+y_1y_2+z_1z_2}}]
(bullet) Косинус угла между векторами (vec{a} ={x_1;y_1;z_1}) и (vec{b}= {x_2;y_2;z_2}) вычисляется по формуле: [{large{cosangle(vec{a}, vec{b})=dfrac{x_1x_2+y_1y_2+z_1z_2}
{sqrt{x^2_1+y^2_1+z^2_1}cdot
sqrt{x^2_2+y^2_2+z^2_2}}}}]
({color{red}{textbf{Факт 3. Про уравнение плоскости}}})
(bullet) Если (vec{n}={a;b;c}) – нормаль к плоскости, то уравнение плоскости имеет вид [ax+by+cz+d=0] Для того, чтобы найти (d), нужно подставить в уравнение плоскости вместо (x, y, z) координаты любой точки, лежащей в этой плоскости.
Пример: если (vec{n}={1;2;3}) – нормаль к плоскости, (O(4;5;6)) – точка из плоскости, то справедливо: (1cdot 4+2cdot 5+3cdot
6+d=0), откуда (d=-32), следовательно, уравнение плоскости имеет вид (x+2y+3z-32=0).
(bullet) Уравнение плоскости можно составить, используя три точки из плоскости, не лежащие на одной прямой.
Пусть (A(1;0;0),
B(0;3;4), C(2;0;5)) – точки из плоскости. Тогда уравнение плоскости можно найти, решив систему: [begin{cases}
1cdot a+0cdot b+0cdot c+d=0\
0cdot a+3cdot b+4cdot c+d=0\
2cdot a+0cdot b+5cdot c+d=0end{cases} quadRightarrowquad
begin{cases}
d=-a\
3b+4c-a=0\
a+5c=0end{cases}quadRightarrowquad begin{cases} d=-a\
a=-5c\
b=-3cend{cases}quadRightarrowquadbegin{cases}a=-5c\
b=-3c\
d=5cend{cases}] Следовательно, уравнение плоскости имеет вид: [-5ccdot x-3ccdot y+ccdot z+5c=0] Можно разделить обе части на (c), так как (cne 0) (иначе (a=b=c=d=0)), следовательно, уравнение плоскости имеет вид [-5x-3y+z+5=0]
({color{red}{textbf{Факт 4. Про углы между прямыми, плоскостями}}})
(bullet) Если векторы (vec{a} ={x_1;y_1;z_1}) и (vec{b}=
{x_2;y_2;z_2}) являются направляющими прямых (p) и (q), то косинус угла между этими прямыми равен: [cos phi=dfrac{|x_1x_2+y_1y_2+z_1z_2|}
{sqrt{x^2_1+y^2_1+z^2_1}cdot sqrt{x^2_2+y^2_2+z^2_2}}]
(bullet) Если (vec{a}) — направляющий вектор прямой (p), а (vec{n}) — нормаль к плоскости (phi) (перпендикуляр к плоскости), то синус угла между прямой (p) и плоскостью (phi) равен модулю косинуса угла между векторами (vec{a}) и (vec{n}): [sin
angle(p, phi)=|cos angle(vec{a}, vec{n})|]
(bullet) Если две плоскости заданы уравнениями (a_1x+b_1y+c_1z+d_1=0) и (a_2x+b_2y+c_2z+d_2=0), то косинус угла между плоскостями ищется по формуле: [{large{cos phi=left| dfrac{a_1a_2+b_1b_2+c_1c_2}
{sqrt{a^2_1+b^2_1+c^2_1}cdot
sqrt{a^2_2+b^2_2+c^2_2}}right|}}]
({color{red}{textbf{Факт 5. Про расстояния от точки до плоскости,
между скрещивающимися прямыми}}})
(bullet) Если (M(x_0;y_0;z_0)) — некоторая точка вне плоскости (phi), (ax+by+cz+d=0) — уравнение плоскости (phi), то расстояние от точки (M) до плоскости (phi) ищется по формуле: [rho(M, phi)=dfrac{|ax_0+by_0+cz_0+d|}{sqrt{a^2+b^2+c^2}}]
(bullet) Для того, чтобы найти расстояние между скрещивающимися прямыми, нужно
— построить плоскость, проходящую через одну из них и параллельную другой;
— найти уравнение этой плоскости;
— найти расстояние от любой точки первой прямой до этой плоскости.
Нахождение кратчайшего расстояния между прямыми в пространстве
Содержание:
- Что такое расстояние между прямыми в пространстве
- Метод координат для определения расстояния
-
Примеры задач с решением
- Задача 1
- Задача 2
Что такое расстояние между прямыми в пространстве
Для начала дадим определение этому понятию.
Определение
Расстояние между прямыми в пространстве — это отрезок, который соединяет две прямые линии по самому короткому пути. Иными словами, он перпендикулярен обеим этим прямым.
Но не всегда две линии могут быть параллельны друг другу.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определение
Расстояние между двумя скрещивающимися прямыми в пространстве — это расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через вторую прямую параллельно первой.
Таким образом, чтобы найти расстояние между этими скрещивающимися прямыми, нужно от одной из прямых провести перпендикуляр на плоскость, в которой лежит другая прямая.
Между параллельными прямыми расстояние одинаково на протяжении всей их длины: перпендикуляр, опущенный из любой точки одной из этих линий, всегда будет одной и той же величины.
Метод координат для определения расстояния
Разберем пошагово способ определения расстояния между двумя скрещивающимися прямыми с помощью метода координат.
- Определить координаты точек (М_1) и (М_2), лежащих соответственно на прямых a и b.
- Найти x, y и z направляющих векторов для прямых a и b.
- Найти вектор-нормаль для плоскости, в которой лежит прямая b с помощью векторного произведения (overrightarrow a) и (overrightarrow b).
- Записать общее уравнение плоскости: (A(x-x_0)+B(y-y_0)+C(z-z_0)=0) и потом записать к нормированному виду уравнения плоскости, которое выглядит так: (xtimescosleft(alpharight)+ytimescosleft(betaright)+ztimescosleft(gammaright)-p=0), где p — свободный член (число, которое равно расстоянию точки начала координат до плоскости), а (cosleft(alpharight),;cosleft(betaright)) и (cosleft(gammaright)) — координаты единичного нормального вектора плоскости.
- Далее, для определения расстояния от точки M до искомой плоскости, воспользуемся следующим уравнением: (M_1H_1=left|x_1timescosleft(alpharight)+y_1timescosleft(betaright)+z_1cosleft(gammaright)-pright|), где (x_1), (y_1) и (z_1) — координаты точки (M_1), лежащей на прямой a, а (H_1) — точка, лежащая на искомой плоскости.
Примеры задач с решением
Задача 1
Дан куб (ABCDA_1B_1C_1D_1) с ребром равным (sqrt{32}) см. Найти расстояние между прямыми (DB_1) и (CC_1).
Решение
Расстояние между скрещивающимися прямыми будем искать в качестве расстояния между прямой (CC_1) и плоскостью, проходящей через (DB_1) параллельно (CC_1). Так как (DD_1parallel CC_1), плоскость ((B_1D_1D)) параллельна (СС_1).
Сначала нужно доказать, что (CO) — перпендикуляр, проведенный к этой плоскости. (COperp BD) (как диагонали квадрата) и (COperp DD_1) (так как ребро (DD_1) перпендикулярно всей плоскости ((ABC))). Получается, (CO) перпендикулярен двум пересекающимся прямым из плоскости. Значит, (COperp(B_1D_1D)).
(AC) — диагонально квадрата — равна (ABsqrt2), то есть (AC=sqrt{32}timessqrt2=sqrt{64}=8) см. Следовательно, (CO=frac12times AC=4) см.
Ответ: 4 см.
Задача 2
В трехмерном пространстве в прямоугольной системе координат Oxyz заданы две скрещивающиеся прямые a и b. Прямую a определяют параметрические уравнения прямой в пространстве:
(left{begin{array}{l}x=-2\y=1+2timeslambda\z=4-3timeslambdaend{array}right.)
А прямую b канонические уравнения прямой в пространстве:
(frac x1=frac{y-1}{-2}=frac{z+4}6).
Вычислить расстояние между заданными прямыми.
Решение
Прямая a проходит через точку (M_1(-2, 1, 4)) и имеет направляющий вектор (overrightarrow a=(0, 2, -3)). Прямая b проходит через точку (M_2 (0, 1, -4)), а ее направляющий вектором является вектор (overrightarrow b=(1, -2, 6)).
Найдем векторное произведение векторов( overrightarrow a=(0, 2, -3)) и (overrightarrow b=(1, -2, 6): left[overrightarrow atimesoverrightarrow bright]=begin{vmatrix}overrightarrow i&overrightarrow j&overrightarrow k\0&2&-3\1&-2&6end{vmatrix}=6timesoverrightarrow i-3timesoverrightarrow j-2timesoverrightarrow k).
Так, (overrightarrow n=left[overrightarrow atimesoverrightarrow bright]) плоскости X, проходящей через прямую b параллельно прямой a, имеет координаты (6, -3, -2).
Таким образом, уравнение плоскости X есть уравнение плоскости, проходящей через точку (M_2(0, 1, -4)) и имеющей нормальный вектор (overrightarrow n=(6, -3, -2)):
(6times(x-0)-3times(y-1)-2times(z-(-4))=0;leftrightarrow6x-3y-2z-5=0)
Нормирующий множитель для общего уравнения плоскости (6x-3y-2z-5=0) равен (frac1{sqrt{6^2+{(-3)}^2+{(-2)}^2}}=frac17). Значит, нормальное уравнение этой плоскости выглядит как (frac67x-frac37y-frac27z-frac57=0).
Воспользуемся формулой для вычисления расстояния от точки (M_1(-2, 1, 4)) до плоскости (frac67x-frac37y-frac27z-frac57=0: left|M_1H_1right|=left|frac67times(-2)-frac37times1-frac27times4-frac57right|=left|frac{-28}7right|=4) см.
Ответ: 4 см.
Расстояние между двумя прямыми. Метод координат. Задание 14
В этой статье я хочу показать решение задачи на нахождение расстояния между скрещивающимися прямыми, которую мы уже решали геометрическим способом, но теперь с помощью метода координат. Я специально показываю решение одной задачи разными способами, чтобы у вас была возможность выбрать наиболее удобный для вас.
Итак, аналитический способ решения задачи:
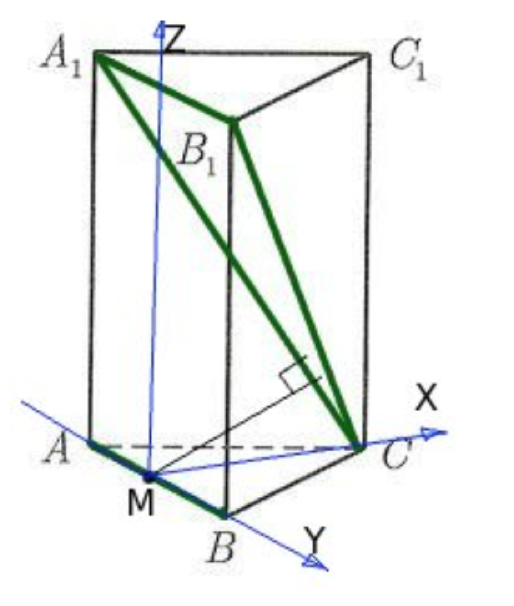
В правильной треугольной призме 

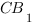

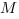

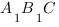
Рассстояние 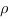
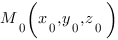

Поместим нашу призму в систему координат. Если мы решаем задачу с кубом или прямоугольным параллелепипедом, то выбор системы координат очевиден: мы помещаем начало координат в одну из вершин куба, а оси направляем вдоль ребер. В случае призмы это не столь очевидно.
Нам надо выбрать систему координат таким образом, чтобы координаты точки 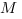
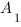
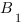
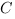
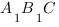
Запишем координаты нужных нам точек:
Чтобы найти коэффициенты 

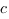
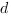

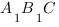
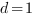
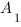
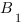
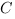
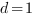
Получим систему уравнений:
Отсюда:
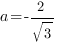
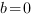
Подставим значения коэффициентов и координаты точки 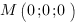
Ответ:
И.В. Фельдман, репетитор по математике.