Расстояние между плоскостями.
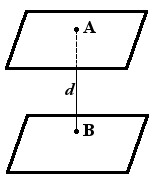
Определение. Расстояние между плоскостями — равно длине перпендикуляра, опущенного с одной плоскости на другую.
Формула для вычисления расстояния между плоскостями
Если заданы уравнения параллельных плоскостей Ax + By + Cz + D1 = 0 и Ax + By + Cz + D2 = 0, то расстояние между плоскостями можно найти, используя следующую формулу
| d = | |D2 — D1| |
| √A2 + B2 + C2 |
Примеры задач на вычисление расстояния между плоскостями
Пример 1.
Найти расстояние между плоскостями 2x + 4y — 4z — 6 = 0 и x + 2y — 2z + 9 = 0.
Решение. Проверим, параллельны ли плоскости, для этого умножим уравнение второй плоскости на 2
2x + 4y — 4z + 18 = 0
Так как коэффициенты при неизвестных величинах у полученного уравнения и первого уравнения равны, то для вычисления расстояния между плоскостями можно использовати приведенную выше формулу:
| d = | |18 — (-6)| | = | |24| | = | 24 | = 4 |
| √22 + 42 + (-4)2 | √36 | 6 |
Ответ: расстояние между плоскостями равно 4.
[{Large{text{Скрещивающиеся прямые}}}]
Заметим, что если две прямые лежат в одной плоскости, то, как и в планиметрии, они могут либо пересекаться, либо быть параллельны, либо совпадать. Значит, и угол между такими прямыми ищется так же, как и в планиметрии (напомним, что угол между параллельными прямыми считается равным (0^circ)). А если через две прямые нельзя провести одну плоскость?
Поэтому к трем видам взаимного расположения прямых в плоскости (пересекаются, параллелельны или совпадают) в пространстве добавляется еще один вид: скрещивающиеся прямые.
Определение
Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости.
Угол (alpha) между прямыми — это угол (0^circleqslant
alphaleqslant
90^circ).
Теорема 1: признак скрещивающихся прямых
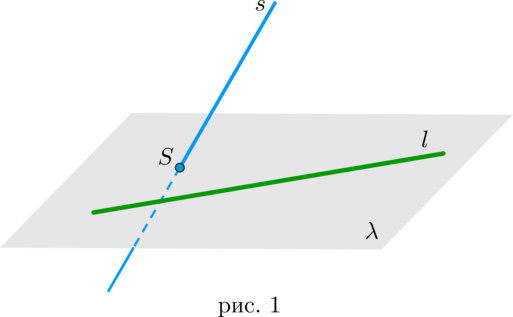
Пусть прямая (l) лежит в плоскости (lambda). Если прямая (s) пересекает плоскость (lambda) в точке (S), не лежащей на прямой (l), то прямые (l) и (s) скрещиваются (рис. 1).
Доказательство
Необходимо доказать, что через прямые (l) и (s) нельзя провести плоскость. Предположим, что это не так, то есть проведем через эти прямые плоскость (pi). Т.к. плоскость (pi) содержит прямую (l) и точку (S), то она совпадает с плоскостью (lambda) по следствию 1 из аксиом. Значит, т.к. прямая (s) лежит в плоскости (pi), то она лежит и в плоскости (lambda), что противоречит условию. Чтд.
Теорема 2
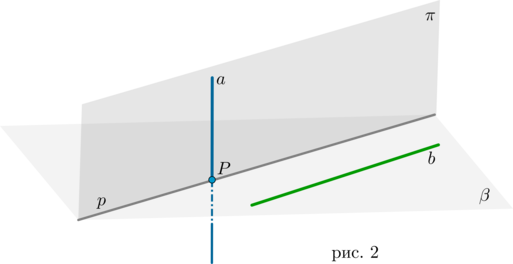
Через каждую из двух скрещивающихся прямых проходит единственная плоскость, параллельная другой прямой (рис. 2).
Доказательство
Пусть прямые (a) и (b) скрещиваются. Проведем плоскость (beta) через прямую (b) так, чтобы она пересекала прямую (a) в точке (P) (как в предыдущей теореме). Через точку (P) проведем прямую (pparallel b). Т.к. прямые (a) и (p) пересекаются (в точке (P)), то через них проходит единственная плоскость (назовем ее (pi)). Прямая (b) параллельна плоскости (pi) по признаку параллельности прямой и плоскости.
Построенная таким образом плоскость (pi) единственна. Любая другая плоскость, проходящая через прямую (a), будет уже пересекать прямую (p), а следовательно, будет пересекать прямую (b). Чтд.
[{Large{text{Угол между скрещивающимися прямыми}}}]
Определение
Угол между скрещивающимися прямыми – это угол между пересекающимися прямыми, соответственно параллельными двум скрещивающимся прямым.
Таким образом, можно определить следующий алгоритм нахождения угла между скрещивающимися прямыми (рис. 2):
Шаг 1. Через одну из двух скрещивающихся прямых (a) провести плоскость (pi) параллельно другой прямой (b) (по алгоритму, приведенному в теореме 2);
Шаг 2. В этой плоскости найти угол между прямыми (a) и (p) ((pparallel b)). Угол между ними будет равен углу между скрещивающимися прямыми (a) и (b).
[{Large{text{Перпендикулярность прямой и плоскости в пространстве}}}]
Определение
Две прямые в пространстве называются перпендикулярными, если угол между ними равен (90^circ).
Таким образом, перпендикулярными могут быть как и пересекающиеся прямые (лежащие в одной плоскости), так и скрещивающиеся прямые (не лежащие в одной плоскости).
Утверждение 1
Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и вторая прямая перпендикулярна этой прямой:
[aparallel b, aperp c Longrightarrow bperp c]
Утверждение 2
Две прямые, перпендикулярные третьей прямой, не пересекаются (то есть либо параллельны, либо скрещиваются):
[aperp c, bperp c Longrightarrow acap b=varnothing]
Определение
Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
Следствие 1
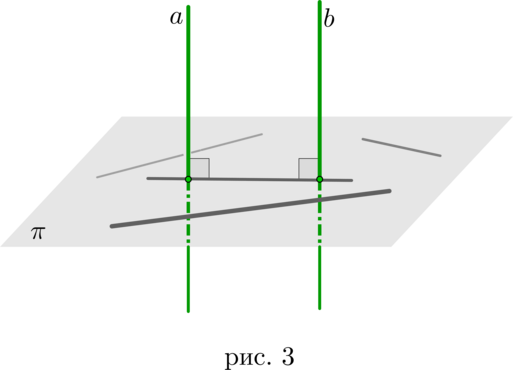
Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости (рис. 3).
(Данное утверждение напрямую следует из утверждения 1.)
Верно и обратное утверждение:
Следствие 2
Если две прямые перпендикулярны плоскости, то они параллельны (рис. 3).
Теорема 3: признак перпендикулярности прямой и плоскости
Если прямая перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости, то она перпендикулярна этой плоскости.
Доказательство
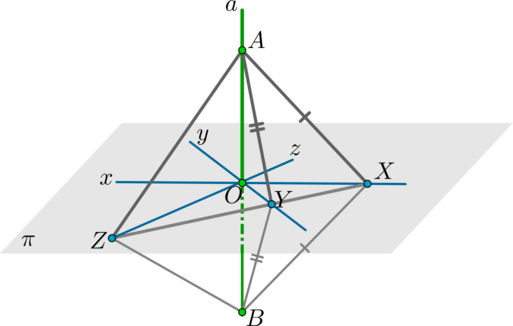
Пусть прямая (aperp x,aperp y), причем прямые (x, yin pi).
Предположим, что прямая (a) уже проходит через точку (O) пересечения прямых (x) и (y) (если это не так, то проведем через точку (A) прямую (a’), параллельную (a); если (a’) будет перпендикулярна плоскости, то и (a) будет ей перпендикулярна по следствию 1).
Проведем через точку (O) в плоскости (pi) некоторую прямую (z). Проведем также прямую, пересекающую прямые (x, y, z) в точках (X, Y,
Z) соответственно. На прямой (a) по разные стороны от плоскости (pi) отметим точки (A, B) так, чтобы (AO=OB).
Рассмотрим (triangle AXB). Т.к. (XO) – высота (по условию) и медиана (по построению), то (AX=XB). Аналогично для (triangle AYB): (AY=YB). Таким образом, (triangle AXY=triangle BXY) по трем сторонам. Отсюда (angle AXY=angle BXY).
Значит, по двум сторонам и углу между ними (triangle AXZ=triangle
BXZ). Значит, (AZ=BZ). Теперь (triangle AZB) – равнобедренный, причем (ZO) – медиана (по построению). Значит, (ZO) – высота, то есть прямая (a) перпендикулярна прямой (z).
Т.к. прямую (z) мы выбрали произвольно, то это значит, что прямая (a) перпендикулярна любой прямой из плоскости (pi), проходящей через точку (O). Но это значит, что прямая (a) перпендикулярна вообще любой прямой из плоскости, т.к. для любой прямой (z’), не проходящей через точку (O), существует параллельная ей прямая (z), проходящая через точку (O). А раз (aperp z, zparallel z’
Rightarrow aperp z’) (по утверждению 1).
Следствие 3
Через любую точку пространства можно провести плоскость, перпендикулярную данной прямой, и притом только одну.
Следствие 4
Через любую точку пространства проходит прямая, перпендикулярная данной плоскости, и притом только одна.
[{Large{text{Расстояния}}}]
Определение
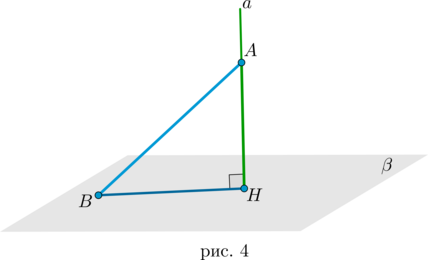
Пусть (aperp beta), причем (acap beta=H). Пусть (Ain a, Bin
beta):
Отрезок (AH) называется перпендикуляром к плоскости (beta).
Отрезок (AB) называется наклонной к плоскости (beta).
Отрезок (BH) называется проекцией наклонной (AB) на плоскость (beta).
Расстояние от точки до плоскости
Длина перпендикуляра (AH) к плоскости (beta) равна расстоянию от точки (A) до плоскости (beta) (рис. 4).
Расстояние между параллельными плоскостями
Для того, чтобы найти расстояние между параллельными плоскостями, нужно из любой точки одной плоскости опустить перпендикуляр к другой плоскости. Длина этого перпендикуляра и есть расстояние между параллельными плоскостями.
Заметим, что расстояние между пересекающимися плоскостями равно нулю.
Расстояние между скрещивающимися прямыми
Длина общего перпендикуляра (h) к обеим скрещивающимся прямым (a) и (b) и есть расстояние между этими скрещивающимися прямыми.
То есть (hperp a, hperp b).
Для того, чтобы найти расстояние между скрещивающимися прямыми, удобно найти расстояние между одной из них и плоскостью, проходящей через вторую прямую параллельно первой.
[{Large{text{Теорема о трех перпендикулярах (ТТП)}}}]
ТТП
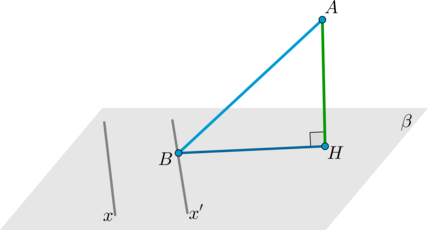
Пусть (AH) – перпендикуляр к плоскости (beta). Пусть (AB, BH) – наклонная и ее проекция на плоскость (beta). Тогда прямая (x) в плоскости (beta) будет перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции.
Доказательство
1. Докажем, что из (xperp AB) следует, что (xperp BH).
Заметим, что т.к. (AHperp beta), то (AH) перпендикулярна любой прямой из плоскости (beta).
Проведем прямую (x’parallel x) через точку (B). Рассмотрим плоскость ((AHB)). Прямая (x’) перпендикулярна этой плоскости, т.к. перпендикулярна двум пересекающимся прямым (AB) и (AH) из этой плоскости. Но т.к. (xparallel x’), то и (xperp(AHB) Rightarrow
xperp BH).
2. Случай, когда из перпендикулярности проекции следует перпендикулярность наклонной, доказывается аналогично.
Замечание
Данная теорема является очень важным и незаменимым инструментов во многих задачах стереометрии.
[{Large{text{Угол между прямой и плоскостью. Угол между плоскостями}}}]
Определение
Угол между наклонной прямой и плоскостью — это угол между этой прямой и ее проекцией на данную плоскость. Таким образом, данный угол принимает значения из промежутка ((0^circ;90^circ)).
Если прямая лежит в плоскости, то угол между ними считается равным (0^circ). Если прямая перпендикулярна плоскости, то, исходя из определения, угол между ними равен (90^circ).
Замечание
Таким образом, чтобы найти угол между наклонной прямой и плоскостью, необходимо отметить некоторую точку (A) на этой прямой и провести перпендикуляр (AH) к плоскости. Если (B) – точка пересечения прямой с плоскостью, то (angle ABH) и есть искомый угол (рис. 4).
Определение
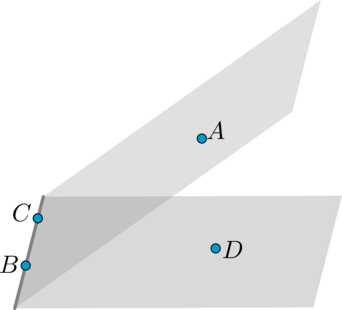
Двугранный угол – это геометрическая фигура, образованная прямой (a) (называемой ребром) и двумя полуплоскостями (называемыми гранями), общей границей которых является прямая (a).
Будем считать, что данные полуплоскости не принадлежат одной плоскости (т.к. в этом случае двугранный угол представляет собой просто плоскость с прямой из этой плоскости).
Если отметить по одной точке на каждой полуплоскости, а также две точки на прямой (a) (как показано на рисунке), то двугранный угол можно обозначить как (ABCD).
Замечание
Прямая (a) в данном случае является аналогом вершины плоского угла, а полуплоскости – аналогом сторон плоского угла.
Таким образом, при пересечении двух плоскостей образуется четыре двугранных угла.
Определение
Если к ребру (a) двугранного угла провести перпендикулярную плоскость (через любую точку), то она пересечет грани двугранного угла по лучам. Угол, образованный данными лучами, называется линейным углом данного двугранного угла.
Замечание
Таким образом, при пересечении двух плоскостей образуется четыре двугранных угла, которым соответствуют четыре линейных угла.
Градусная мера угла между данными плоскостями — это градусная мера меньшего из четырех линейных углов. Таким образом, данный угол принимает значения из промежутка ([0^circ;90^circ]).
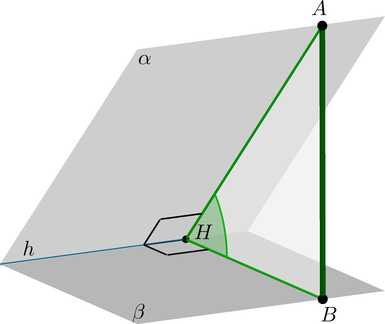
Для того, чтобы найти угол между плоскостями (alpha) и (beta), можно действовать по следующему алгоритму:
Отметить произвольную точку (A) в плоскости (alpha).
Провести (AHperp h), где (h) — линия пересечения плоскостей.
Провести (AB) перпендикулярно плоскости (beta).
Тогда (AB) – перпендикуляр к плоскости (beta), (AH) – наклонная, следовательно, (HB) – проекция. Тогда по ТТП (HBperp h).
Следовательно, плоскость, проходящая через прямые (AH) и (BH), и есть плоскость, перпендикулярная ребру (h) двугранного угла. Значит, (angle AHB) — линейный угол двугранного угла между плоскостями. Градусная мера этого угла равна градусной мере угла между плоскостями.
Заметим, что мы получили прямоугольный треугольник (triangle AHB). Как правило, находить (angle AHB) удобно из него.
[{Large{text{Перпендикулярность плоскостей}}}]
Определение
Две плоскости называются перпендикулярными, если угол между ними равен (90^circ).
Теорема 4: признак перпендикулярности плоскостей
Если плоскость проходит через прямую, перпендикулярную другой плоскости, то она перпендикулярна этой плоскости.
Доказательство
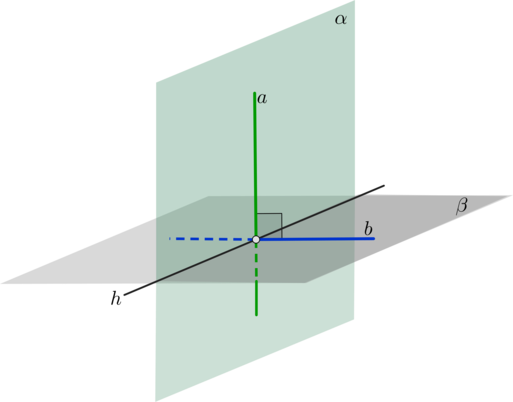
Пусть прямая (a) лежит в плоскости (alpha) и перпендикулярна плоскости (beta). Докажем, что тогда плоскости (alphaperp beta).
Пусть плоскости пересекаются по прямой (h). Тогда (aperp h) (т.к. (a) перпендикулярна любой прямой из плоскости (beta), а (h), очевидно, лежит в (beta)). Проведем через точку пересечения прямых (a) и (h) прямую (b) в плоскости (beta). Углы, образованные при пересечении прямых (a) и (b) – линейные углы двугранных углов, образованных плоскостями (alpha) и (beta). Но (aperp b), значит, углы, образованные ими, равны (90^circ). Чтд.
Задание 3035
Основанием пирамиды SABC является равносторонний треугольник ABC, длина стороны которого равна $$4sqrt{2}$$ . Боковое ребро SC перпендикулярно плоскости основания и имеет длину 2.
а) Докажите, что угол между скрещивающимися прямыми, одна из которых проходит через точку S и середину ребра BC, а другая проходит через точку С и середину ребра AB равен 45°.
б) Найдите расстояние между этими скрещивающимися прямыми.
Ответ: $$frac{2}{sqrt{3}}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1) Введем ортогональную систему координат: $$CM=CBcdotsin60^{circ}=4sqrt{2}cdotfrac{sqrt{3}}{2}=2sqrt{6}$$
$$left.begin{matrix}S(0;0;2)\L(sqrt{2};sqrt{6};0)end{matrix}right}$$ $$Rightarrow$$ $$SL left { sqrt{2};sqrt{6};-2 right }$$
$$left.begin{matrix}C(0;0;0)\M(0;2sqrt{6};0)end{matrix}right}$$ $$Rightarrow$$ $$CMleft{0;2sqrt{6};0right}$$
$$cos(SL;CM)=frac{|sqrt{2}cdot0+sqrt{6}cdot2sqrt{6}+(-2)cdot0|}{sqrt{2+6+4}cdotsqrt{4cdot6}}=$$
$$=frac{2sqrt{36}}{sqrt{12}cdotsqrt{24}}=frac{2cdot6}{2sqrt{3}cdot2sqrt{6}}=frac{sqrt{2}}{2}$$
$$angle (SL;CM)=45^{circ}$$ ч.т.д.
2) Пусть $$LKparallel CMRightarrow d(SL;CM)=d(C;(SLK))$$
$$K(sqrt{2}; 2sqrt{6}; 0)$$ Пусть $$ax+by+cz+d=0$$ — уравнение $$(SLK)$$
$$left{begin{matrix}0cdot a+0cdot b+2cdot c+d=0\sqrt{2}a+sqrt{6}b+0cdot c+d=0\sqrt{2}a+2sqrt{6}b+0cdot c+d=0end{matrix}right.$$
$$b=0;c=-frac{d}{2};a=-frac{sqrt{2}d}{2}$$ $$-frac{sqrt{2}d}{2}x+0y-frac{d}{2}z+d=0$$ $$Rightarrow$$<
$$-frac{sqrt{2}}{2}x+0y-frac{1}{2}z+1=0$$
$$d(C;(SLK))=frac{|ax_{0}+by_{0}+cz_{0}+d|}{sqrt{a^{2}+b^{2}+c^{2}}}=$$<
$$=frac{|-frac{sqrt{2}}{2}cdot0+0cdot0-frac{1}{2}cdot0+1|}{sqrt{frac{2}{4}+0+frac{1}{4}}}=frac{1}{frac{sqrt{3}}{2}}=frac{2}{sqrt{3}}$$
Задание 3159
В правильной треугольной пирамиде SABC точка К – середина ребра АВ. На ребре SC взята точка М так, что SM : СМ = 1:3.
а) Докажите, что прямая МК пересекает высоту SО пирамиды в её середине.
б) Найдите расстояние между прямыми МК и АС, если известно, что АВ=6, SA=4.
Ответ: $$frac{3sqrt{21}}{7}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 3662
В кубе $$ABCDA_{1}B_{1}C_{1}D_{1}$$ точка О1 – центр квадрата АВСD, точка О2 – центр квадрата $$CC_{1}D_{1}D$$
а) Докажите, что прямые А1О1 и В1О2 – скрещивающиеся.
б) Найдите расстояние между прямыми А1О1 и В1О2, если ребро куба равно 2.
Ответ: $$frac{2sqrt{3}}{3}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1) Опустим $$O_{2}Mperp C_{1}D_{1}$$ $$Rightarrow$$ $$B_{1}M$$ — проекция $$B_{1}O_{2}$$ на $$(A_{1}B_{1}C_{1}D_{1})Rightarrow(B_{1}MO_{2})$$ плоскость $$B_{1}O_{2}$$; достроим её до $$(B_{1}MM_{1}B)$$
2) Опустим $$O_{1}Lperp AD$$ $$Rightarrow$$ $$A_{1}L$$ — проекция $$A_{1}O_{1}$$ на $$(AA_{1}D_{1}D)Rightarrow(A_{1}O_{1}L)$$ плоскость $$A_{1}O_{1}$$; достроим её до $$(A_{1}LL_{1}B_{1})$$
3) $$BM_{1}cap LL_{1}=H$$ $$B_{1}$$ — общая $$Rightarrow$$ $$B_{1}H$$ -линия пересечения $$(A_{1}LL_{1}B_{1})$$ и $$(B_{1}MM_{1}B)$$ $$Rightarrow$$ $$A_{1}O_{1}cap(B_{1}MM_{1}B)$$ по $$B_{1}H$$ $$Rightarrow$$ $$A_{1}O_{1}$$ не пересекает $$B_{1}O_{2}$$ и $$A_{1}O_{1}$$ не параллельна $$B_{1}O_{2}$$ $$Rightarrow$$ $$B_{1}O_{2}$$ и $$A_{1}O_{1}$$ — скрещивающиеся
б) 1) Введем ортогональную систему координат как на рисунке: $$B_{1}(0;0;2)$$; $$O_{2}(2;1;1)$$; $$A_{1}(0;2;2)$$
2) Пусть $$B_{1}L_{2}parallel A_{1}L$$, тогда $$(B_{1}O_{2}L_{2})parallel A_{1}L$$, $$d(A_{1}L; B_{1}O_{2})=d((B_{1}O_{2}L_{2});A_{1})$$
$$L_{2}(1;-1;0)$$
3) Пусть $$ax+by+cz+d=0$$ — уравнение $$(B_{1}O_{2}L_{2})$$
$$left{begin{matrix}0cdot x+0cdot y+2z+d=0\2x+1y+1z+d=0\1x+(-1)cdot y+0cdot z+d=0end{matrix}right.$$
$$left{begin{matrix}2z+d=0\2x+y+z+d=0\x-y+d=0end{matrix}right.$$
$$left{begin{matrix}z=-frac{d}{2}\3x+z+2d=0\x-y+d=0end{matrix}right.$$
$$3x-0,5d+2d=0$$
$$3x=-1,5d$$
$$x=-0,5d$$
$$-y+0,5d=0$$
$$y=0,5d$$
$$d((B_{1}O_{2}L_{2});A_{1})=frac{|ax_{0}+by_{0}+cz_{0}+d|}{sqrt{a^{2}+b^{2}+c^{2}}}=$$
$$=frac{|1cdot0-1cdot2+1cdot2-2}{sqrt{1^{2}+(-1)^{2}+1^{2}}}=frac{2}{sqrt{3}}=frac{2sqrt{3}}{3}$$
Задание 4332
В правильной треугольной призме ABCA1B1C1, все рёбра которой равны 1, найдите расстояние между прямыми AA1 и BC1.
Ответ:
Задание 4333
Расстояние между боковыми ребрами AA1 и BB1 прямой треугольной призмы ABCA1B1C1 равно 5, а расстояние между боковыми ребрами AA1 и CC1 равно 8. Найдите расстояние от прямой AA1 до плоскости BC1C, если известно, что двугранный угол призмы при ребре AA1 равен 60°.
Ответ:
Задание 4334
Дана правильная треугольная призма ABCA1B1C1, все рёбра основания которой равны $$2sqrt{7}$$. Сечение, проходящее через боковое ребро AA1 и середину M ребра B1C1, является квадратом. Найдите расстояние между прямыми A1B и AM.
Ответ:
Задание 4335
Дан правильный тетраэдр MABC с ребром 1. Найдите расстояние между прямыми AL и MO, где L — середина ребра MC O — центр грани ABC.
Ответ:
Задание 5241
Дан куб $$ABCDA_{1}B_{1}C_{1}D_{1}$$. Пусть $$l$$ – линия пересечения плоскостей $$ACD_{1}$$ и $$BDC_{1}$$
А) Докажите, что прямые $$DB_{1}$$ и $$l$$ перпендикулярны.
Б) Найдите расстояние между прямыми $$DB_{1}$$ и $$l$$, если ребро куба равно 2.
Ответ: $$frac{1}{sqrt{6}}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
A) введем систему координат. Пусть ребро куба 2. Тогда :$$H(1;1;0), M(1;0;1), D(0;0;0), B_{1}(2;2;2)$$
$$vec{HM} (0;-1;1)$$; $$vec{DB_{1}} (2;2;2)$$
$$cos (HM; BD)=frac{10*2+(-1)*2+1*2}{sqrt{2}*sqrt{12}}=0Rightarrow$$ угол равен 90
Б) Построим из H прямую $$HKleft | right | DB_{1}$$$$Rightarrow Delta DB_{1}Bsim Delta HKB$$; H-середина DB, то и K-середина
$$BB_{1}Rightarrow K(2;2;1)$$
Зададим уравнение (HKM):
$$left{begin{matrix}a+b+d-0\a+c+d=0 \2a+ab+c+d=0 end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}b=c \a+c+d=0 \2a+3c+d=0end{matrix}right.$$$$left{begin{matrix}a=-c-d \-2c-2d+3c+d=0 \b=c end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}c=d \b=c \a=-2cend{matrix}right.$$
Получим: $$-2cx+cy+cz+c=0|:c Leftrightarrow$$$$-2x+y+z+1=0$$
Найдем расстояние от D до (HKM)
$$r=frac{left | -2*0+1*0+1*0+1 right |}{sqrt{4+1+1}}=frac{1}{sqrt{6}}$$
Задание 6569
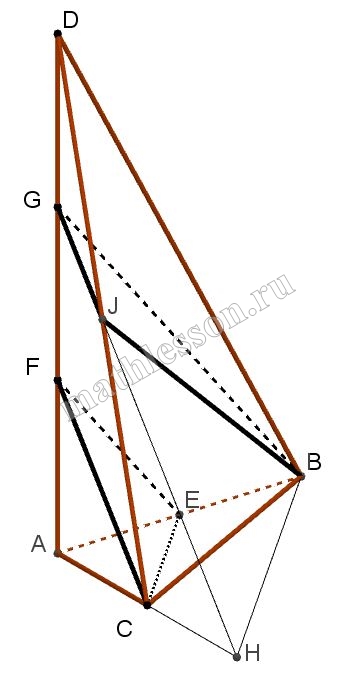
Ребро SA пирамиды SABC перпендикулярно плоскости АВС, ,AB=2, AC=1, $$angle BAC=120^{circ}, SA=3sqrt{2}$$ . Сечения пирамиды двумя параллельными плоскостями, одна из которых проходит через точку С и середину ребра АВ, а другая – через точку В, имеют равные площади.
А) Найти объемы многогранников, на которые разбивают пирамиду плоскости сечений
Б) Найти расстояние между секущими плоскостями.
Ответ: А)$$frac{sqrt{6}}{12};frac{sqrt{6}}{3}; frac{sqrt{6}}{12}$$ Б)$$frac{sqrt{2}}{3}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
A) 1) Пусть E-середина $$ABRightarrow$$ пусть $$CEin alpha$$ и $$alpha cap AD=F$$, тогда $$alpha =(CEF)$$
2)Пусть $$B in beta$$ и $$alpha left | right |beta$$ и $$beta cap AD=G$$; $$beta cap CD=J$$. Тогда : $$EFleft | right |BG$$ и т.к. $$Delta AEFsim Delta ABG$$, то $$frac{AE}{AB}=frac{EF}{BG}=frac{1}{2}Rightarrow$$ $$BG=2 EF(1)$$
3) $$S_{CFE}=S_{JGB}Rightarrow$$$$frac{1}{2}CF*FE*sin F=frac{1}{2}JG*GB sin F$$; $$angle F=angle GRightarrow$$$$CF*FE=JG*GB$$. С учетом (1) получаем, что $$JG=frac{1}{2}CF$$. Но $$Delta SGTsim Delta SFCRightarrow$$ $$frac{GT}{CF}=frac{SG}{SF}=frac{1}{2}Rightarrow$$ $$AF=FG=GS=frac{1}{3}AS=sqrt{2}$$
4) $$V_{FACE}=frac{1}{3}S_{AEC}*AF=$$$$frac{1}{3}*frac{1}{2}*S_{ABC}*frac{1}{3}AS=$$$$frac{1}{6}V_{SABC}$$;
$$frac{V_{SGBJ}}{V_{SABC}}=frac{SG*SJ*SB}{SA*SC*SB}=$$$$frac{1}{3}*frac{1}{2}=frac{1}{6}Rightarrow$$ $$V_{SGBJ}=frac{1}{6}V_{SABC}$$, $$V _{FECGBJ}=frac{4}{6} V_{SABC}$$; $$V_{SABC}=frac{1}{3}*frac{1}{2}*2*1*frac{sqrt{3}}{2}*3sqrt{2}=frac{sqrt{6}}{2}$$
Найдем $$V_{FACE}=V_{SGJB}=frac{sqrt{6}}{12}$$; $$V_{FCEGBJ}=frac{4}{6}*frac{sqrt{6}}{2}=frac{2sqrt{6}}{6}$$
Б) 1)Построим $$ANperp EC$$ . Опустим перпендикуляр из G на FN :$$GMperp FN$$ и $$GMcap FN=G$$. Тогда GMFи FNAявляются одной плоскостью
2) FNperp CE(по построению) , AN- проекция FN на $$(ABC)Rightarrow$$ $$CEperp (FCE)Rightarrow$$ $$CEperp MG$$ с учетом , что $$GMperp FN$$, то $$GMperp (CEF)Rightarrow$$ GM — расстояние от (GJB) до (CEF)
3) $$Delta GFM$$: $$GM=FG sin angle MFG$$
$$angle MFG=angle AFN$$( вертикальные ), тогда $$sin angle MFG=sin angle AFN=frac{AN}{FN}$$
$$Delta ANC$$: $$AN=frac{1}{2}AC=frac{1}{2}$$
$$Delta AFN$$: $$FN=sqrt{2+frac{1}{4}}=frac{3}{2}$$
$$sin angle AFN=frac{1}{2}:frac{3}{2}=frac{1}{3}$$
$$GM=sqrt{2}*frac{1}{3}=frac{sqrt{2}}{3}$$
Задание 6825
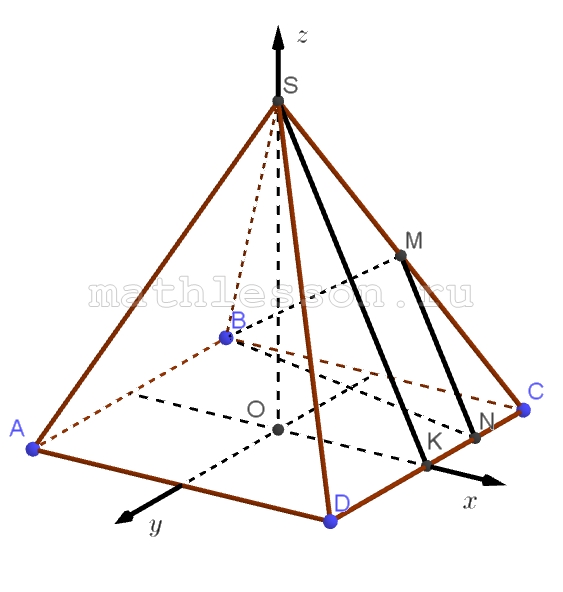
Диагональ основания ABCD правильной пирамиды SABCD равна 8, высота пирамиды SO равна 1. Точка М – середина ребра SC, точка К – середина ребра CD.
А) Найдите угол между прямыми ВМ и SK
Б) Найдите расстояние между прямыми ВМ и SK
Ответ: А)$$arccos frac{23}{27}$$ Б) $$frac{4sqrt{2}}{5}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
A) 1) Зададим ортогальную систему координат как показано на рисунке:
2)из $$Delta ABD$$: $$AB=BD sin D=8*frac{sqrt{2}}{2}=4sqrt{2}$$
3) Найдем координаиты точек:
$$B (-frac{BC}{2}; -frac{AB}{2},0)Rightarrow$$ $$B(-2sqrt{2};-2sqrt{2},0)$$
$$S(0;0; SO)$$$$Rightarrow$$ $$S(0;0;1)$$
$$K (frac{AD}{2};0;0)Rightarrow$$ $$k(2sqrt{2};0;0)$$
Опустим $$MM_{1}perp (ABC)$$, $$Delta SOC sim Delta MM_{1}C$$, тогда:
$$M(frac{AD}{4};-frac{CD}{4};frac{SO}{2})Rightarrow$$ $$M (sqrt{2};-sqrt{2};frac{1}{2})$$
Тогда: $$bar{BM} (3sqrt{2}; sqrt{2};frac{1}{2})$$, $$bar{SK}(2sqrt{2};0;-1)$$
Найдем угол между данными векторами:
$$cos angle (bar{BM}, bar{SK})=$$$$frac{3sqrt{2}*2sqrt{2}+sqrt{2}*0+frac{1}{2}(-1)}{sqrt{(3sqrt{2})^{2}+(sqrt{2})^{2}+(frac{1}{2})^{2}}* sqrt{(2sqrt{2})^{2}+0^{2}+(-1)^{2}}}=$$$$frac{23}{27}Rightarrow$$ $$angle (bar{BM}; bar{SK})=arccos frac{23}{27}$$
Б) 1) Построим $$MN left | right |SK (MNcap DC=N)Rightarrow$$ $$(BMN)left | right |SKRightarrow$$ $$rho (SK; (BMN))=rho (BM; SK)$$
2) $$N (frac{AD}{2}; -frac{CD}{4};0) Rightarrow$$ $$N (2sqrt{2}; -sqrt{2},0)$$
Зададим уравнение (BMN):
$$left{begin{matrix}-2sqrt{2}a-2sqrt{2}b +d=0\sqrt{2}a -sqrt{2}b +frac{1}{2}c+d=0\2sqrt{2}a-sqrt{2}b +d=0end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}b=frac{sqrt{2}d}{3}\c=-frac{d}{3}\a=-frac{sqrt{2}d}{12}end{matrix}right.$$
Тогда уравнение (BMN): $$-frac{sqrt{2}}{12}x+frac{sqrt{2}}{3}y-frac{1}{3}z+1=0$$
Тогда расстояние между прямыми: $$rho (BM, SK) =frac{left | -frac{sqrt{2}}{12}*2sqrt{2}+1 right |}{sqrt{(-frac{sqrt{2}}{12})^{2}+(frac{sqrt{2}}{3})^{2}+(-frac{1}{2})^{2}}}=frac{4sqrt{2}}{5}$$
Задание 7364
В правильной четырехугольной пирамиде SABCD точка Р – середина ребра SA, точка Q – середина ребра SC.
А) Докажите, что расстояние между прямыми ВР и DQ не зависит от высоты пирамиды.
Б) Найдите это расстояние, если площадь основания пирамиды равна 5.
Ответ: $$sqrt{2}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 7731
В правильном тетраэдре ABCD точка К – центр грани ABD, точка М – центр грани ACD.
а) Докажите, что прямые ВС и КМ параллельны.
б) Найдите угол между прямой КМ и плоскостью ABD.
Ответ: $$arccosfrac{sqrt{3}}{3}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 8893
Основанием пирамиды SABCD является прямоугольник ABCD со сторонами AB=15 и BC=25. Все боковые рёбра пирамиды равны $$5sqrt{17}$$. На рёбрах AB и BC отмечены соответственно точки K и N так, что AK=CN=8. Через точки K и N проведена плоскость $$alpha$$, перпендикулярная ребру SB.
а) Докажите, что плоскость $$alpha$$ проходит через точку M-середину ребра SB.
б) Найдите расстояние между прямыми DS и KM
Ответ: $$frac{5sqrt{17}}{2}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 8913
Основанием пирамиды TABCD является прямоугольник ABCD со сторонами AB=26 и BC=18. Все боковые рёбра пирамиды равны $$10sqrt{5}$$. На рёбрах AB и CD отмечены соответственно точки N и M так, что BN=DM=12. Через точки N и M проведена плоскость $$alpha$$, перпендикулярная ребру TA.
а) Докажите, что плоскость $$alpha$$ проходит через точку K — середину ребра TA.
б) Найдите расстояние между прямыми TC и KN.
Ответ: $$5sqrt{5}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 9046
В основании пирамиды SABCD лежит квадрат ABCD со стороной 2. Боковое ребро SA перпендикулярно основанию и равно 1. Точка F – середина АВ.
а) Найдите угол между прямыми SF и AC
б) Найдите площадь сечения пирамиды плоскостью, проходящей через точку F параллельно прямым BD и SС.
Ответ: а) 60 градусов; б) $$frac{3sqrt{2}}{8}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Лекция
№5
Взаимное
расположение двух и трех плоскостей.
Расстояние от точки до плоскости.
Расстояние между двумя параллельными
плоскостями. Угол между плоскостями.
Лемма 5.1.
(Условие
параллельности вектора и плоскости).
Пусть в
аффинной системе координат задана
плоскость
общим уравнением
и вектор
.
Вектор
параллелен плоскости
тогда
и только тогда, когда
выполняется условие:
.
Доказательство.
Пусть
.
Докажем, что выполняется условие
.
1.
Рассмотрим
.
Отложим
от неё вектор
.
2. Пусть
,
тогда вектор
.
Запишем условие равенства векторов
и
:
3. Так как
,
то
ее координаты удовлетворяют уравнению
плоскости, т.е.
,
где
(точка
принадлежит плоскости ).
(<=)
повторить
все рассуждения в обратном направлении.
Ч.т.д.
Лемма 5.2.
Пусть в
прямоугольной системе координат
плоскость
задана общим уравнением:
.
Тогда
вектор
перпендикулярен
плоскости
.
Доказательство.
Пусть
вектор
параллелен плоскости .
Применяя
условие параллельности вектора и
плоскости, получим:
вектор
перпендикулярен
плоскости
.
Ч.т.д.
Взаимное
расположение двух плоскостей.
В аффинной системе
координат поверхность, заданная
уравнением первой степени, является
плоскостью. Выясним, при каких условиях
два уравнения
и
:
I.
Определяют одну и ту же плоскость;
II.
Определяют две параллельные плоскости;
III.
Определяют две пересекающиеся плоскости.
I.
Условия, при которых уравнения
и
определяют
одну и ту же плоскость.
Теорема 5.3.
Для
того чтобы два
уравнения
и
в аффинной системе координат определяли
одну и ту же плоскость, необходимо и
достаточно, чтобы все коэффициенты в
уравнениях были пропорциональны.
Необходимость:
Дано: уравнения
плоскостей
:
(1)
(2)
Докажем:
.
Доказательство:
1.
Данные уравнения определяют одну и ту
же плоскость
.
Значит, векторы нормалей
и
будут коллинеарны, т.е.
или
.
2.
Подставим выражения в уравнение (1) и
выразим
:
3.
Найдем отношение
:
.
4.
Значит,
Достаточность:
Дано:
уравнения:
:
(1)
(2)
.
Докажем,
что уравнения (1) и (2) задают одну и ту же
плоскость
.
Доказательство:
1.
Выразим из условия теоремы
коэффициенты
:
-
Подставим
данные выражения в уравнение (1):
или
3.
Значит, уравнениями (1) и (2) задаётся одна
плоскость в аффинной системе координат.
II.
Условие параллельности двух прямых.
Теорема
5.4.
Два
уравнения
и
в аффинной системе координат определяют
две параллельные плоскости, если
коэффициенты при переменных
в уравнениях пропорциональны.
III.
Условие пересечения двух прямых.
Теорема
5.5.
Два
уравнения
и
в аффинной системе координат определяют
две пересекающие плоскости, если
коэффициенты при переменных
в уравнениях не пропорциональны.
Взаимное расположение
плоскостей
и
определяется и рангами расширенной и
основной матриц, соответствующих системе
уравнений данных плоскостей:
Пусть:
-
— расширенная
матрица ранга
-
-основная
матрица ранга
.
-
Если
,
то плоскости
и
пересекаются; -
Если
,
то плоскости
и
совпадают; -
Если
,
то плоскости
и
параллельны.
Пучок плоскостей.
Определение
5.6. Пучком
плоскостей называется совокупность
плоскостей пространства, проходящих
через одну прямую.
Пусть плоскости
и
пересекаются, причем
:
;
:
Помножим уравнения
плоскостей
и
соответственно на числа
и q,одновременно
не равные 0, и сложим полученные равенства:
(*)
,
где
Коэффициенты при
х,у,z
не равны
нулю одновременно,
т.к. одновременное равенство нулю
позволяет говорить, что
.
По условию параллельности плоскостей
имеем, что
=> противоречит
условию.
Уравнение (*)
есть
уравнение плоскости, проходящей через
общую прямую двух данных плоскостей.
—
уравнение пучка
плоскостей.
Пример.
Задача:
Составить
уравнение плоскости, проходящей через
точку А(2,3,1) и прямую, определяемую
плоскостями:х+у-2z+1=0
и 2x—y+z-4=0.
Определение
5.7.
Совокупность
всех плоскостей, проходящих через точку
пересечения трех основных плоскостей,
называются связкой
плоскостей.
—уравнение
связки.
Расстояние от
точки до плоскости.
З
Найти расстояние от точки
до
плоскости :
.
Решение:
1.
,
2.
3. Вектор
=>
4. Так как точка
принадлежит
плоскости, то имеем:
5.
или
— расстояние
от точки Мо до плоскости.
Расстояние
между двумя параллельными плоскостями.
Задача:
Найти расстояние между параллельными
плоскостями
и
,
заданными своими уравнениями:
и
.
Угол между
плоскостями.
Определение
5.8.
Углом между плоскостями называется
любой из двух двугранных углов,
образованный
этими плоскостями.

угла между
и
.
Соседние файлы в папке вопрос 6
- #
- #
Расстояние между плоскостями. Онлайн калькулятор
Страница обновляется. Могут возникнуть ошибки. Спасибо за понимание!
С помощю этого онлайн калькулятора можно найти расстояние между плоскостями. Дается подробное решение с пояснениями. Для нахождения расстояния между плоскостями, введите элементы уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Расстояние между плоскостями − теория
Заметим, сначала, что расстояние между плоскостями определена, если плоскости параллельны или, что то же самое, нормальные векторы этих плоскостей коллинеарны. Вычисление расстояния между двумя плоскостями можно свести к вычислению расстояния от точки первой плоскости до второй плоскости. Вычисление расстояния от точки до плоскости (онлайн калькулятор, теория, примеры) посмотрите на странице Расстояние от точки до плоскости онлайн.
Алгоритм вычисления расстояния между плоскостями содержит следующие шаги:
- Проверка коллинеарности нормальных векторов плоскостей.
- Нахождение некоторой точки M0 на первой плоскости.
- Вычисление расстояния между точкой M0 и второй плоскостью.
Выведем формулу вычисления расстояния между плоскостями.
Запишем уравнения двух плоскостей:
1. Проверяем коллинеарность нормальных векторов n1=(A1, B1, C1) и n2=(A2, B2, C2).
Очевидно, что нормальные векторы n1 и n2 не могут быть нулевыми векторами.Если из пары коэффициентов (A1,A2),(B1,B2), (C1,C2) один нулевой а другой − нет, то нормальные векторы n1 и n2 неколлинеарны. Т.е. задача неразрешима.
Пусть A1≠0, A2≠0. Уравнение плоскости (2) не изменится, если умножим на A1/A2:
Нормальный вектор уравнения (2′) имеет следующий вид:
Для коллинеарности векторов n1 и n’2(или n1 и n2) необходимо и достаточно выполнение следующих равенств:
или
Если удовлетворяется условие (3) (или (3′)), то векторы n1 и n’2(или n1 и n2) коллинеарны, т.е. плоскости (1) и (2′) (или (1) и (2) ) параллельны. Тогда уравнение плоскости (2′) можно представить так:
где
2. Найдем некоторую точку на плоскости (1).
Легко убедится, что точка
принадлежит плоскости (1):
3. Расстояние от точки M0(x0, y0, z0) до плоскости (2») вычисляется с помощью выражения (подробнее смотрите на странице расстояние от точки до плоскости):
Подставляя координаты точки M0 из (4) в (5), получим формулу вычисления расстояния между плоскостями (1) и (2») (или (1) и (2)):
где
Расстояние между плоскостями − примеры и решения
Пример 1. Найти расстояние между плоскостями
и
Решение.
Проверим, являются ли эти плоскости параллельными. Для этого умножим второе уравнение на 1/3.
Общее уравнение плоскости имеет вид:
где n=(A,B,C)− называется нормальным вектором плоскости.
Нормальный вектор плоскости (7) равен n1=(1, 2, −4), нормальный вектор плоскости (8′) равен n2=(1, 2, −4). n1=n2. Следовательно эти плоскости параллельны.
Найдем расстояние между плоскостями (7) и (8′), используя следующую формулу:
Подставим значения A, B, C, D1, D2 в (9):
Упростим и решим:
Ответ. Расстояние между плоскостями равен:
Пример 2. Найти расстояние между плоскостями
и
Решение.
Эти плоскости не параллельны, так как коэффициент переменного z уравнения (10) нулевой а коэффициент переменного z уравнения (11)−нет. Невозможно найти расстояние между непараллельными плоскостями.
Пример 3. Найти расстояние между плоскостями
и
Решение.
Проверим, являются ли эти плоскости параллельными. Для этого умножим второе уравнение на 4/3.
Нормальный вектор плоскости (12) равен n1=(4, 2, 8), нормальный вектор плоскости (13′) равен n2=(4, 16/3, 64/3). n1≠n2. Нормальные векторы этих плоскостей неколлинеарны. Тогда эти плоскости не параллельны и, следовательно, задача неразрешима.