Среди огромного количества стереометрических
задач в учебниках геометрии, в различных
сборниках задач, пособиях по подготовке в ВУЗы
крайне редко встречаются задачи на нахождение
расстояния между скрещивающимися прямыми.
Возможно, это обусловлено как узостью их
практического применения (относительно школьной
программы, в отличие от «выигрышных» задач на
вычисление площадей и объемов), так и сложностью
данной темы.
Практика проведения ЕГЭ показывает, что многие
учащиеся вообще не приступают к выполнению
заданий по геометрии, входящих в экзаменационную
работу. Для обеспечения успешного выполнения
геометрических заданий повышенного уровня
сложности необходимо развивать гибкость
мышления, способность анализировать
предполагаемую конфигурацию и вычленять в ней
части, рассмотрение которых позволяет найти путь
решения задачи.
Школьный курс предполагает изучение четырех
способов решения задач на нахождение расстояния
между скрещивающимися прямыми. Выбор способа
обусловлен, в первую очередь, особенностями
конкретной задачи, предоставленными ею
возможностями для выбора, и, во вторую очередь,
способностями и особенностями
«пространственного мышления» конкретного
учащегося. Каждый из этих способов позволяет
решить самую главную часть задачи — построение
отрезка, перпендикулярного обеим скрещивающимся
прямым (для вычислительной же части задач
деление на способы не требуется).
Основные способы решения задач на нахождение
расстояния между скрещивающимися прямыми
Нахождение длины общего перпендикуляра двух
скрещивающихся прямых, т.е. отрезка с концами на
этих прямых и перпендикулярного каждой из этих
прямых.
Нахождение расстояния от одной из
скрещивающихся прямых до параллельной ей
плоскости, проходящей через другую прямую.
Нахождение расстояния между двумя
параллельными плоскостями, проходящими через
заданные скрещивающиеся прямые.
Нахождение расстояния от точки, являющейся
проекцией одной из скрещивающихся прямых, на
перпендикулярную ей плоскость (так называемый
«экран») до проекции другой прямой на ту же
самую плоскость.
Проведем демонстрацию всех четырех способов на
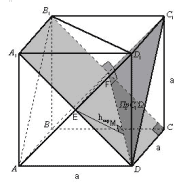
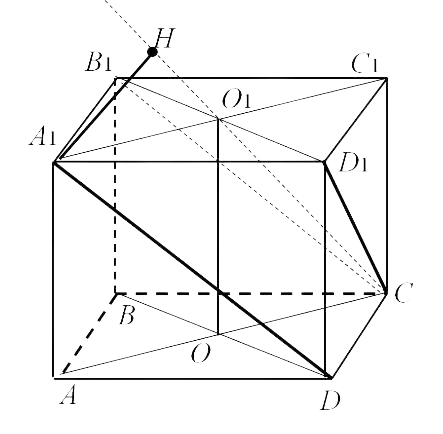
следующей простейшей задаче: «В кубе с
ребром а найти расстояние между любым ребром
и диагональю не пересекающей его грани». Ответ: .
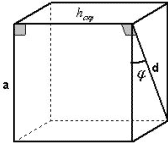
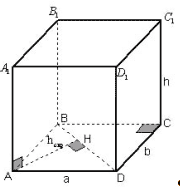
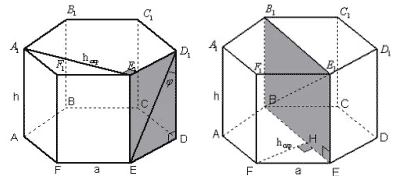
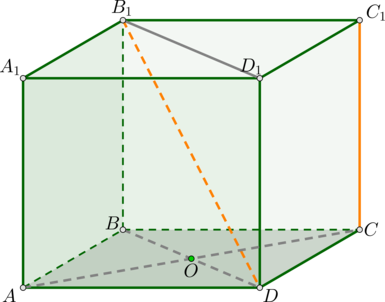
1 способ.
Рисунок 1
hскр перпендикулярна плоскости боковой
грани, содержащей диагональ d и
перпендикулярна ребру, следовательно, hскр
и является расстоянием между ребром а и
диагональю d.
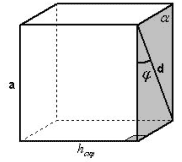
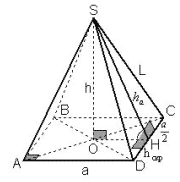
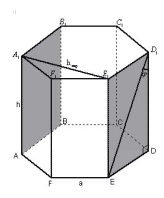
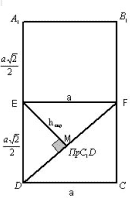
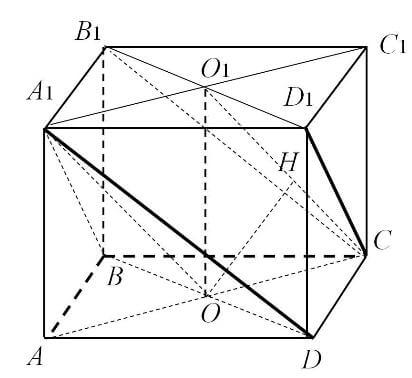
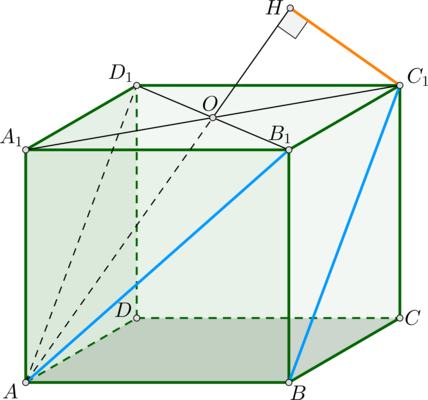
2 способ.
Рисунок 2
Плоскость A параллельна ребру и проходит через
данную диагональ, следовательно, данная hскр
является не только расстоянием от ребра до
плоскости A, но и расстоянием от ребра до данной
диагонали.
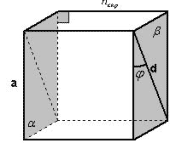
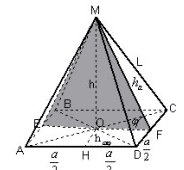
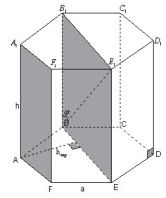
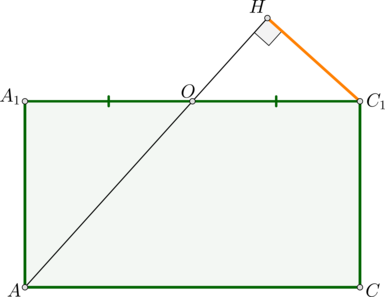
3 способ.
Рисунок 3
Плоскости A и B параллельны и проходят через две
данные скрещивающиеся прямые, следовательно,
расстояние между этими плоскостями равно
расстоянию между двумя скрещивающимися прямыми.
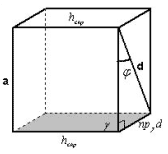
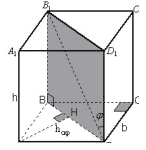
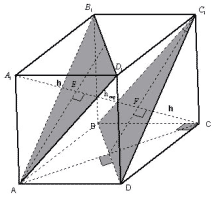
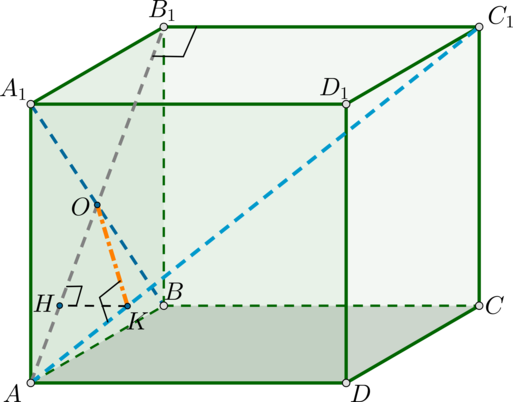
4 способ.
Рисунок 4
Плоскость A перпендикулярна ребру куба. При
проекции на A диагонали d данная диагональ
обращается в одну из сторон основания куба.
Данная hскр является расстоянием между
прямой, содержащей ребро, и проекцией диагонали
на плоскость C, а значит и между прямой,
содержащей ребро, и диагональю.
Остановимся подробнее на применении каждого
способа для изучаемых в школе многогранников.
СПОСОБ I.
Применение первого способа достаточно
ограничено: он хорошо применяется лишь в
некоторых задачах, так как достаточно сложно
определить и обосновать в простейших задачах
точное, а в сложных — ориентировочное
местоположение общего перпендикуляра двух
скрещивающихся прямых. Кроме того, при
нахождении длины этого перпендикуляра в сложных
задачах можно столкнуться с непреодолимыми
трудностями.
Примеры
Задача 1. В прямоугольном параллелепипеде с
размерами a, b, h найти расстояние между
боковым ребром и не пересекающейся с ним
диагональю основания.
Рисунок 5
Пусть AHBD.
Так как А1А перпендикулярна плоскости АВСD ,
то А1А
AH.
AH перпендикулярна обеим из двух скрещивающихся
прямых, следовательно AH?- расстояние между
прямыми А1А и BD. В прямоугольном
треугольнике ABD, зная длины катетов AB и AD, находим
высоту AH, используя формулы для вычисления
площади прямоугольного треугольника. Ответ:
Задача 2. В правильной 4-угольной пирамиде с
боковым ребром L и стороной основания a
найти расстояние между апофемой и стороной
основания, пересекающей боковую грань,
содержащую эту апофему.
Рисунок 6
SHCD как
апофема, ADCD,
так как ABCD — квадрат. Следовательно, DH —
расстояние между прямыми SH и AD. DH равно половине
стороны CD. Ответ:
СПОСОБ II
Применение этого способа также ограничено в
связи с тем, что если можно быстро построить (или
найти уже готовую) проходящую через одну из
скрещивающихся прямых плоскость, параллельную
другой прямой, то затем построение
перпендикуляра из любой точки второй прямой к
этой плоскости (внутри многогранника) вызывает
трудности. Однако в несложных задачах, где
построение (или отыскивание) указанного
перпендикуляра трудностей не вызывает, данный
способ является самым быстрым и легким, и поэтому
доступен.
Примеры
Задача 2. Решение уже указанной выше задачи
данным способом особых трудностей не вызывает.
Рисунок 7
Плоскость EFM параллельна прямой AD, т. к AD || EF.
Прямая MF лежит в этой плоскости, следовательно,
расстояние между прямой AD и плоскостью EFM равно
расстоянию между прямой AD и прямой MF. Проведем OHAD. OH
EF, OH
MO,
следовательно, OH(EFM),
следовательно, OH — расстояние между прямой AD и
плоскостью EFM, а значит, и расстояние между прямой
AD и прямой MF. Находим OH из треугольника AOD.
Ответ:
Задача 3. В прямоугольном параллелепипеде с
размерами a,b и h найти расстояние между
боковым ребром и не пересекающейся с ним
диагональю параллелепипеда.
Рисунок 8
Прямая AA1 параллельна плоскости BB1D1D,
B1D принадлежит этой плоскости,
следовательно расстояние от AA1 до
плоскости BB1D1D равно расстоянию между
прямыми AA1 и B1D. Проведем AHBD. Также, AH
B1B,
следовательно AH(BB1D1D), следовательно AH
B1D, т. е. AH —
искомое расстояние. Находим AH из прямоугольного
треугольника ABD.
Ответ:
Задача 4. В правильной шестиугольной призме
A:F1 c высотой h и стороной основания a
найти расстояние между прямыми:
Рисунок 9 Рисунок 10
а) AA1 и ED1.
Рассмотрим плоскость E1EDD1. A1E1EE1, A1E1
E1D1,
следовательно
A1E1 (E1EDD1). Также A1E1
AA1.
Следовательно, A1E1 является
расстоянием от прямой AA1 до плоскости E1EDD1.
ED1(E1EDD1).,
следовательно AE1 — расстояние от прямой AA1
до прямой ED1. Находим A1E1 из
треугольника F1A1E1 по теореме
косинусов. Ответ:
б) AF и диагональю BE1.
Проведем из точки F прямую FH перпендикулярно BE.
EE1FH, FH
BE, следовательно
FH(BEE1B1),
следовательно FH является расстоянием между
прямой AF и (BEE1B1), а значит и
расстоянием между прямой AF и диагональю BE1.
Ответ:
СПОСОБ III
Применение этого способа крайне ограничено,
так как плоскость, параллельную одной из прямых
(способ II) строить легче, чем две параллельные
плоскости, однако способ III можно использовать в
призмах, если скрещивающиеся прямые принадлежат
параллельным граням, а также в тех случаях, когда
в многограннике несложно построить параллельные
сечения, содержащие заданные прямые.
Примеры
Задача 4.
Рисунок 11
а) Плоскости BAA1B1 и DEE1D1
параллельны, так как AB || ED и AA1 || EE1. ED1DEE1D1,
AA1(BAA1B1),
следовательно, расстояние между прямыми AA1
и ED1 равно расстоянию между плоскостями BAA1B1
и DEE1D1. A1E1AA1, A1E1
A1B1, следовательно, A1E1
BAA1B1.
Аналогично доказываем, что A1E1(DEE1D1). Т.о., A1E1
является расстоянием между плоскостями BAA1B1
и DEE1D1, а значит, и между прямыми AA1
и ED1. Находим A1E1 из треугольника
A1F1E1, который является
равнобедренным с углом A1F1E1,
равным .
Ответ:
Рисунок 12
б) Расстояние между AF и диагональю BE1
находится аналогично.
Ответ:.
Задача 5. В кубе с ребром а найти
расстояние между двумя непересекающимися
диагоналями двух смежных граней.
Данная задача рассматривается как
классическая в некоторых пособиях, но, как
правило, ее решение дается способом IV, однако
является вполне доступной для решения с помощью
способа III.
Рисунок 13
Некоторую трудность в данной задаче вызывает
доказательство перпендикулярности диагонали A1C
обеим параллельным плоскостям (AB1D1 ||
BC1D). B1CBC1 и BC1
A1B1, следовательно,
прямая BC1 перпендикулярна плоскости A1B1C,
и следовательно, BC1A1C. Также, A1C
BD.
Следовательно, прямая A1C перпендикулярна
плоскости BC1D. Вычислительная же часть
задачи особых трудностей не вызывает, так как hскр
= EF находится как разность между диагональю куба
и высотами двух одинаковых правильных пирамид A1AB1D1
и CC1BD.
Ответ:
СПОСОБ IV.
Данный способ имеет достаточно широкое
применение. Для задач средней и повышенной
трудности его можно считать основным. Нет
необходимости применять его только тогда, когда
один из трех предыдущих способов работает проще
и быстрее, так как в таких случаях способ IV может
только усложнить решение задачи, или сделать его
труднодоступным. Данный способ очень выгодно
использовать в случае перпендикулярности
скрещивающихся прямых, так как нет необходимости
построения проекции одной из прямых на «экран»
Примеры.
Задача 5. Все та же «классическая» задача
(с непересекающимися диагоналями двух смежных
граней куба) перестает казаться сложной, как
только находится «экран» — диагональное
сечение куба.
Рисунок 14
Экран:
Рисунок 15
Рассмотрим плоскость A1B1CD. C1F (A1B1CD),
т. к. C1FB1C
и C1FA1B1.
Тогда проекцией C1D на «экран» будет
являться отрезок DF. Проведем EMDF. Отрезок EM и будет являться расстоянием
между двумя непересекающимися диагоналями двух
смежных граней. Находим EM из прямоугольного
треугольника EDF. Ответ:.
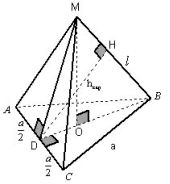
Задача 6. В правильной треугольной пирамиде
найти расстояние и угол между скрещивающимися
прямыми: боковым ребром l и стороной
основания a.
Рисунок 16
В данной и аналогичных ей задачах способ IV
быстрее других способов приводит к решению, так
как построив сечение, играющее роль «экрана»,
перпендикулярно AC (треугольник BDM), видно, что
далее нет необходимости строить проекцию другой
прямой (BM) на этот экран. DH — искомое расстояние. DH
находим из треугольника MDB, используя формулы
площади. Ответ: .
Скачать материал

Скачать материал


- Сейчас обучается 22 человека из 17 регионов


- Сейчас обучается 105 человек из 36 регионов


- Сейчас обучается 1160 человек из 83 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
О некоторых способах вычисления расстояния между скрещивающимися прямыми
-
2 слайд
Две прямые называются скрещивающимися, если они не лежат в одной плоскости.
Определение -
3 слайд
Отрезок, концы которого лежат на скрещивающихся прямых, и перпендикулярный обеим прямым, называется общим перпендикуляром к скрещивающимся прямым.
-
4 слайд
1. Расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, проходящими через эти прямые.
2. Расстояние между скрещивающимися прямыми равно расстоянию от одной из них до параллельной ей плоскости,
проходящей через вторую прямую. -
5 слайд
Задача. Ребро куба равно 1. Найдите расстояние между скрещивающимися диагоналями двух соседних граней куба.
-
6 слайд
Решение: 1 способ (геометрический)
Рассмотрим плоскость А 1 ДВ,
А 1 Д ║ В 1 С А 1 ДВ ║ В 1 С. Найдем расстояние от любой точки до этой плоскости, например от точки С.
ВД ┴ АС и А А 1 ВД ┴ АС А 1 , тогда
Плоскость А 1 ДВ ┴ АС А 1 . Перпендикуляр СН к плоскости А 1 ДВ будет лежать в плоскости АС А 1 , точка Н – на линии пересечения этих плоскостей, т.е. на прямой О А 1 .
Из подобия треугольников СНО и А 1 АО следует, что СН А 1 А = СО А 1 О , откуда
СН = А 1 А∙СО А 1 О ,
А А 1 =1, СО= 1 2 АС= 2 2 . А 1 О= 3 2 .
СН = 1 3 .
Ответ: 𝟏 𝟑 . -
7 слайд
2 способ (использование формулы объёма тетраэдра.)
Объём тетраэдра может быть вычислен по формуле V = 1 6 abd sinα, где a и b – длины скрещивающихся рёбер, d — расстояние между этими прямыми, α – угол между содержащими этими прямыми.
Выражая расстояние из формулы, получим :
d= 6𝑉 В А 1 ·С В 1 ∙sinД А 1 В
V= 1 3 · 𝑆 𝐵𝐶 𝐵 1 · 𝐴 1 𝐵 1 = 1 3 · 1 2 ·1= 1 6 ,
В А 1 =С В 1 = 2 , угол Д А 1 В = 60 0 .
d= 𝟏 𝟑 .Ответ: 𝟏 𝟑 .
-
8 слайд
3 способ (координатный.)
Рассмотрим плоскость А 1 ДВ, напишем уравнение данной плоскости, проходящей через точки
Д(0;0;0), В(1;1;0), А 1 (1;0;1). Уравнение будет иметь вид
х-у-z =0.
Далее по формуле
ρ= а х 𝟎 +в у 𝟎 +с 𝒛 𝟎 +𝒅 а 𝟐 + в 𝟐 + с 𝟐
Найдем расстояние от точки
С(0;1;0) до плоскости А 1 ДВ.
ρ= 0·0−1·1−0·1 1 2 +(−1 ) 2 +(−1 ) 2 = 1 3 .Ответ: 𝟏 𝟑 .
-
9 слайд
4 способ (координатно-векторный.)
Пусть КР – общий перпендикуляр.
Найдем координаты точек Р и К, чтобы найти длину вектора КР.
К∈ В 1 С, К (k;1;k).
Р∈ А 1 В, Р(1; p;1-p)
Т.к. КР ⊥ С В 1 (1;0;1) и В А 1 (0;-1;1), то скаляр. произведение векторов равно нулю.
Имеем систему уравнений
1−𝑘+1−𝑝−𝑘=0 1−𝑝+1−𝑝−𝑘=0,
Решая систему находим k=p= 2 3 .
КР = ( 1 3 ) 2 +(− 1 3 ) 2 +(− 1 3 ) 2 = 𝟏 𝟑Ответ: 𝟏 𝟑 .
-
10 слайд
5 способ (метод проекции)
Пусть КР – общий перпендикуляр.
Спроецируем отрезок КР на плоскости ВС С 1 и АВ В 1 . Его проекциями будут отрезки К Р 1 и Р К 1.
т.к. В 1 С⊥РК, то по теореме, обратной
о трех перпендикулярах⟹
В 1 С⊥К Р 1 ,
А 1 В⊥РК, то по теореме, обратной
о трех перпендикулярах⟹
А 1 В⊥Р К 1 . ∆ В 1 К Р 1 и ∆ВР К 1 — прямоугольные и равнобедренные.
К К 1 и Р Р 1 — медианы.
В 1 К 1 = К 1 Р 1 = Р 1 В= 1 3 . Р Р 1 = 1 3 , К Р 1 = 2 3 .
По теореме Пифагора находим
КР= 𝟏 𝟑 .
Ответ: 𝟏 𝟑 . -
11 слайд
В правильной треугольной призме
АВС А 𝟏 В 𝟏 С 𝟏 , все ребра которой равны 1, найдите расстояние между прямыми АВ и С В 𝟏 . -
12 слайд
1 способ (геометрический)
Решение:
Прямая А 1 В 1 параллельна прямой АВ. Проведем через прямые А 1 В 1 и В 1 С плоскость А 1 В 1 С, параллельную прямой АВ. Возьмем точку М, являющуюся серединой отрезка АВ. Проведем через эту точку плоскость МС С 1 . МС С 1 ⊥ АВ и значит перпендикулярна А 1 В 1 С. Рассмотрим △МКС и проведем высоту МР (h). МС = 3 2 , КМ =1.
Ответ: 21 7 -
13 слайд
2 способ (использование формулы объёма тетраэдра)
Рассмотрим пирамиду А 1 В 1 СМ. V= 1 3 МР· 𝑆 А 1 В 1 С𝑉 А 1 В 1 СМ = 1 3 𝑉 АВС А 1 В 1 С 1 ; 𝑆 АВС = 3 4 , h=1.
𝑉 АВС А 1 В 1 С 1 = 3 4 . 𝑉 А 1 В 1 СМ = 3 12 . 𝑆 А 1 В 1 С = КС∙ А 1 В 1 2 = 7 2 ∙1 2 = 7 4 .
Выражаем МР из формулы
МР = 3 12 ∙3∙ 4 7 = 3 7 = 21 7
Ответ: 21 7 -
14 слайд
3 способ (координатный)
Нам надо выбрать систему координат таким образом, чтобы координаты точки М и точек А 1 , В 1 и С, задающих плоскость А 1 В 1 С вычислялись наиболее простым способом и содержали как можно больше нулей. Поэтому удобно выбрать систему координат вот таким образом.
М(0;0;0)
А 1 0;− 1 2 ;1
В 1 0; 1 2 ;1
С( 3 2 ;0;0). Уравнение плоскости А 1 В 1 С будет иметь вид — 2 3 х-z+1=0
ρ= 21 7
Ответ: 21 7 -
15 слайд
Сравнивая различные способы решения задачи на нахождение расстояния между скрещивающимися прямыми, видим, что наиболее универсальным является координатно-векторный метод, а наиболее рациональным, алгоритмичным и доступным большинству учащихся – метод, основанный на применении формулы с объемом пирамиды. Но, несомненно, показателем высокой математической культуры школьника, будущего абитуриента, будет классический способ решения задачи – нахождение длины общего перпендикуляра на основе чисто геометрических рассуждений.
-
16 слайд
Использованная литература
1. Журнал «Математика в школе» 2008 год, №1.
2. http://ege-ok.ru/2012/03/09/2534/
3. http://ege-ok.ru/2012/03/08/rasstoyanie-mezhdu-dvumya-pryamyimi-zadanie-s2/
Краткое описание документа:
Одним из наиболее трудных вопросов учебной программы школьной геометрии является вычисление расстояния между скрещивающимися прямыми. Как показывает опыт не только школьники, но и абитуриенты испытывают при его выполнении определенные затруднения. Это связано с тем, что в школьном курсе математики практически не рассматриваются упражнения на формирование умения находить общий перпендикуляр двух прямых, хотя в учебнике упоминается о существовании и единственности такого перпендикуляра, а также приводится правило его построения.
Стоит заметить, что задача на построение общего перпендикуляра к двум скрещивающимся прямым требует весьма кропотливой работы. В то же время при нахождении расстояния между скрещивающимися прямыми нет необходимости строить их общий перпендикуляр. Часто бывает достаточно лишь увидеть(провести) более подходящий отрезок, длина которого и будет искомым расстоянием.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 266 972 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 25.01.2015
- 5160
- 45
- 25.01.2015
- 3511
- 3
- 25.01.2015
- 774
- 1
Напомним, что скрещивающимися прямыми называют прямые, не принадлежащие одной плоскости и не имеющие между собой общих точек.
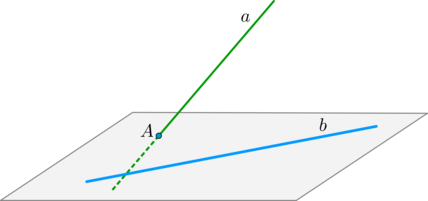
Признак скрещивания прямых: если прямая a пересекается с плоскостью, в которой лежит прямая b и при этом точка пересечения не принадлежит a, то a и b скрещиваются.
В качестве наглядного представления скрещивающихся прямых можно привести транспортную развязку. Верхнюю из дорог следует считать за одну прямую, нижнюю принять за другую.
Теорема 1
Пусть мы имеем две скрещивающиеся в пространстве прямые. Через каждую из них можно провести плоскость, параллельную другой скрещивающейся прямой, причём только одну.
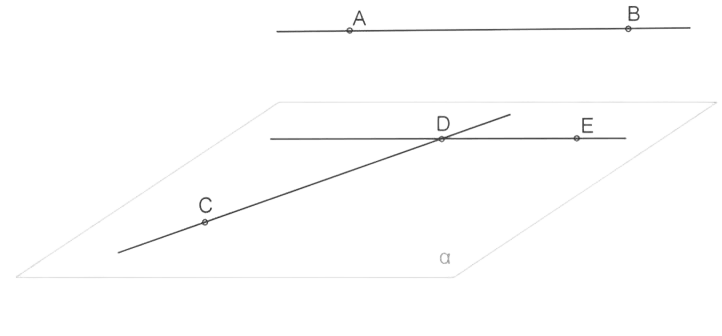
Доказательство:
Через точку D у нас получится провести прямую DE, которая будет параллельной AB.
Через CD и DE (смотрите рис. выше) можно провести плоскость α.
В связи с тем, что AB не принадлежит этой плоскости и при этом параллельна DE, то она будет параллельной и плоскости.
Указанная плоскость единственная. Это ясно из того, что любая другая плоскость, которая проходит через CD, неизбежно пересечёт DE и AB, которая ей параллельна.
Доказательство завершено.
Различные определения расстояния между скрещивающимися прямыми
Определения 1 — 5
Расстоянием между скрещивающимися в пространстве прямыми именуют длину промежутка, отделяющего одну из скрещивающихся прямых от параллельной плоскости, которая пересекает другую прямую.
Расстоянием между скрещивающимися прямыми это расстояние между самыми близкими точками этих прямых.
Расстоянием между двумя скрещивающимися прямыми называют расстояние, разделяющее две плоскости, которым они принадлежат.
Расстоянием между двумя скрещивающимися прямыми считают длину, которую имеет их общий перпендикуляр.
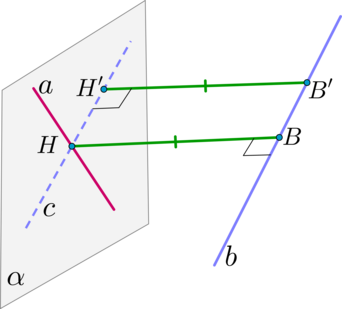
Пусть нам даны скрещивающиеся прямые a и b. Произвольно выберем на a некоторую точку M1. На b наложим плоскость χ, которая будет параллельна a. Из точки M1 на указанную плоскость χ проведём перпендикуляр M1H1. Его длина и есть расстояние, разделяющее скрещивающиеся прямые.
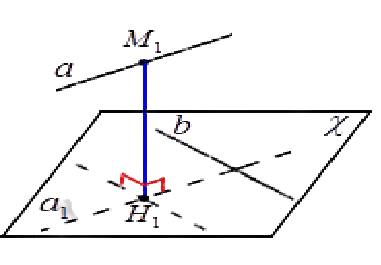
Ка найти расстояние между скрещивающимися прямыми
Главная трудность здесь состоит в построении отрезка равного по своей длине расстоянию, которое нам требуется найти. Если его удалось построить, то используя теорему Пифагора, признаки подобия или равенства треугольников либо иные подобные пути, расстояние получится найти достаточно легко.
Как следует искать расстояние между скрещивающимися прямыми методом координат
Он основан на определении 5 и использовании формулы расстояния от точки M до плоскости α.
r(M, a) = (ax0 + by0 + cz0 + d)/ √(a2 + b2 + c2)
Последовательность действий здесь следующая:
- Выясняем, какие координаты имеют точки M1 (x1, y1, z1)и M2(x2, y2,z2) , принадлежащие прямым a и b;
- Выясняем координаты (ax,ay,az) и (bx,by,bz), принадлежащие направляющим векторам a и b;
- Выясняем, какие координаты (A,B,C) имеет нормальный вектор n плоскости χ, который проходит через b, параллельной a. Проще всего это сделать из равенства
[mathrm{n}=left[begin{array}{llll}
mathrm{a} X mathrm{~b}
end{array}right]=begin{array}{ccc}
i & j & k \
ax & ay & a z \
b x & b y & b z
end{array}]
- Записываем общее уравнение плоскости χ как
[mathrm{A}left(mathrm{x}-mathrm{x}_{1}right)+mathrm{B}left(mathrm{y}-mathrm{y}_{1}right)+mathrm{C}left(mathrm{z}-mathrm{z}_{1}right)=0;] - Приводим полученное уравнение к нормальному виду
[cos alpha * mathrm{x}+cos beta * mathrm{y}+cos gamma * mathrm{z}-mathrm{p}=0;] - Вычисляем величину промежутка M1H1 от точки M(x1,y1,z1) до плоскости χ по формуле
[mathrm{M}_{1} mathrm{H}_{1}=cos alpha mathrm{x}_{1}+cos beta mathrm{y}_{1}+cos gamma mathrm{z}_{1}-mathrm{p}]
Пример 1
В системе координат заданы скрещивающиеся прямые a и b.
Первая определена параметрическими уравнениями [mathrm{x}=-2, mathrm{y}=1+2 * lambda, mathrm{z}=4-3^{*} lambda]
Вторая задана каноническим уравнением [mathrm{x} / 1=(mathrm{y}-1) /-2=(mathrm{z}+4) / 6]
Нужно выяснить расстояние между этими прямыми.
Решение: Из уравнений прямых ясно, что первая из них проходит через точку M1(-2, 1,4), а вторая через точку M2(0,1,-4).
Направляющий вектор первой прямой a = (0,2,-3). Второй – b = (1,-2,6).
Вычислим векторное произведение указанных векторов.
[mathrm{n}=left[begin{array}{llcc}
a mathrm{X} b
end{array}right]=begin{array}{ccc}
i & j & k \
0 & 2 & -3 \
1 & -2 & 6
end{array}=6 * I-3* mathrm{j}-2* mathrm{k}]
У n будут координаты (6, -3, -2).
Из этого получается, что уравнение плоскости χ является уравнением той плоскости, которой принадлежит точка M2(0,1,-4). Она имеет нормальный вектор n = (6,-3,-2).
6*(x-0) — 3(y-1) – 2(z-(-4)) = 0
6x – 3y – 2z – 5 = 0
Нормирующим множителем выше указанного уравнения плоскости будет
1/ √((62) – (-3)2 – (-22)) = 1/7
Отсюда следует, что у уравнения данной плоскости будет вид
(6/7)*x – (3/7)*y – (2/7)*z – 5/7 = 0
Теперь нам осталось лишь воспользоваться формулой расстояния от точки M1(-2,1,4) до плоскости (6/7)*x – (3/7)*y – (2/7)*z – 5/7 = 0
В результате несложных вычислений мы получаем
M1H1= ((6/7)*(-2) – (3/7)*1 – (2/7)*4 – (5/7) = (-28/7) = 4
Ответ: расстояние между прямыми равно 4.
Нет времени решать самому?
Наши эксперты помогут!
Метод базирующийся на определении 1
Его покажем сразу на решении конкретно задачи. Так будет понятнее и яснее.
Пример 2
Основанием прямоугольной призмы АВСDA1B1C1D1 является квадрат ABCD. Каждая из его сторон равна 4. Высота призмы 2√2. Требуется найти величину промежутка между прямыми DA1 и CD1.
Решение: Т. к. прямая CD1 принадлежит плоскости CB1D1 . DA1||CB1, прямая DA1 является параллельной плоскости CB1D1. Из сказанного следует, что нужно найти разделяющее их расстояние. Оно и будет ответом на наш вопрос. Упомянутое расстояние, есть расстояние от точки A1 до плоскости CB1D1.
BD1 перпендикулярна плоскости ACC1. Из этого следует, что плоскость ACC1 будет перпендикулярной плоскости CB1D1. Их пересечением является прямая O1C. O и O1 есть центры верхнего и нижнего оснований призмы.
Из точки A1, которая принадлежит плоскости ACC1 опустим перпендикуляр A1H на прямую CO1. Длина A1H будет тем расстоянием, которое мы ищем.
Из прямоугольного треугольника A1HO1, зная, что его гипотенуза AO1 равна 2√2, и
sin(HO1A1) = √2/2 находим катет HA1 = A1O1sin(HO1A1) = 2.
Ответ: величина промежутка между прямыми DA1 и CD1 равно 2.
Метод объёмов
Он использует вспомогательную пирамиду, высота которой и будет искомым расстоянием, разделяющем скрещивающиеся прямые. Для нахождения упомянутой высоты сначала нужно узнать объём указанной пирамиды. Отсюда и название метода.
Отметим, что данный метод исключает проведение перпендикуляра к скрещивающимся прямым.
Пример 3
Выясните, чему равна величина промежутка между прямыми A1D и D1C. Сторона квадрата равна 4. Высота призмы 2√2.
Решение: Т. к. DA1||CB1 и CD1||BA1 , то (BDA1 )||(CB1D1). Расстояние между указанными плоскостями равняется расстоянию от точки C до плоскости A1BD.
Посмотрите на пирамиду BCDA1. H – высота, соединяющая вершину С с основанием BDA1.
Длина высоты равняется расстоянию между DA1 и DC1.
BD = AC = √32 = 4√2. AO = 2√2
Из прямоугольного треугольника легко находим
A1O = CO1 = √(AA12 + AO2) = √(4*2 + 4*2) = 4
Находим объём пирамиды CA1BD. Она имеет основание A1BD и высоту h. Он будет равен
V(1) = (1/3)SABD * h = (1/3)*(1/2)A1O * BD * h = (4 * 4√2)*h/6 = (8√2)*h/3
Вычислим теперь той же самой пирамиды объём, считая её основанием BCD, а высоту AA1.
V{2} = (1/3)SBCD*AA1 = (1/3)*(1/2)*16*2√2 = 16*(√2/3)
Теперь приравняем эти выражения
[(8√2)*h/3] = [16*(√2/3)]
Из этого выражения очень легко найти расстояние между прямыми DA1 и CD1. Упрощаем и получаем, что h = 2.
Ответ: величина промежутка равна 2.
14. Задачи по стереометрии
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Нахождение расстояния между скрещивающимися прямыми
(blacktriangleright) Скрещивающиеся прямые – это прямые, через которые нельзя провести одну плоскость.
Признак скрещивающихся прямых: если первая прямая пересекает плоскость, в которой лежит вторая прямая, в точке, не лежащей на второй прямой, то такие прямые скрещиваются.
(blacktriangleright) Т.к. через одну из скрещивающихся прямых проходит ровно одна плоскость, параллельная другой прямой, то расстояние между скрещивающимися прямыми — это расстояние между одной из этих прямых и плоскостью, проходящей через вторую прямую параллельно первой.
Таким образом, если прямые (a) и (b) скрещиваются, то:
Шаг 1. Провести прямую (cparallel b) так, чтобы прямая (c) пересекалась с прямой (a). Плоскость (alpha), проходящая через прямые (a) и (c), и будет плоскостью, параллельной прямой (b).
Шаг 2. Из точки пересечения прямых (a) и (c) ((acap c=H)) опустить перпендикуляр (HB) на прямую (b) (первый способ).
Или из любой точки (B’) прямой (b) опустить перпендикуляр на прямую (c) (второй способ).
В зависимости от условия задачи какой-то из этих двух способов может быть гораздо удобнее другого.
Задание
1
#2452
Уровень задания: Легче ЕГЭ
В кубе (ABCDA_1B_1C_1D_1), ребро которого равно (sqrt{32}), найдите расстояние между прямыми (DB_1) и (CC_1).
Прямые (DB_1) и (CC_1) скрещиваются по признаку, т.к. прямая (DB_1) пересекает плоскость ((DD_1C_1)), в которой лежит (CC_1), в точке (D), не лежащей на (CC_1).
Расстояние между скрещивающимися прямыми будем искать как расстояние между прямой (CC_1) и плоскостью, проходящей через (DB_1) параллельно (CC_1). Т.к. (DD_1parallel CC_1), то плоскость ((B_1D_1D)) параллельна (CC_1).
Докажем, что (CO) – перпендикуляр на эту плоскость. Действительно, (COperp BD) (как диагонали квадрата) и (COperp DD_1) (т.к. ребро (DD_1) перпендикулярно всей плоскости ((ABC))). Таким образом, (CO) перпендикулярен двум пересекающимся прямым из плоскости, следовательно, (COperp (B_1D_1D)).
(AC), как диагональ квадрата, равна (ABsqrt2), то есть (AC=sqrt{32}cdot sqrt2=8). Тогда (CO=frac12cdot AC=4).
Ответ: 4
Задание
2
#2453
Уровень задания: Сложнее ЕГЭ
Дан куб (ABCDA_1B_1C_1D_1). Найдите расстояние между прямыми (AB_1) и (BC_1), если ребро куба равно (a).
1) Заметим, что эти прямые скрещиваются по признаку, т.к. прямая (AB_1) пересекает плоскость ((BB_1C_1)), в которой лежит (BC_1), в точке (B_1), не лежащей на (BC_1).
Расстояние между скрещивающимися прямыми будем искать как расстояние между прямой (BC_1) и плоскостью, проходящей через (AB_1) параллельно (BC_1).
Для этого проведем (AD_1) — она параллельна (BC_1). Следовательно, по признаку плоскость ((AB_1D_1)parallel BC_1).
2) Опустим перпендикуляр (C_1H) на эту плоскость и докажем, что точка (H) упадет на продолжение отрезка (AO), где (O) – точка пересечения диагоналей квадрата (A_1B_1C_1D_1).
Действительно, т.к. по свойству квадрата (C_1Operp B_1D_1), то по теореме о трех перпендикуляр проекция (HOperp B_1D_1). Но (triangle AB_1D_1) равнобедренный, следовательно, (AO) – медиана и высота. Значит, точка (H) должна лежать на прямой (AO).
3) Рассмотрим плоскость ((AA_1C_1)).
(triangle AA_1Osim triangle OHC_1) по двум углам ((angle
AA_1O=angle OHC_1=90^circ), (angle AOA_1=angle HOC_1)). Таким образом,
[dfrac{C_1H}{AA_1}=dfrac{OC_1}{AO} qquad (*)]
По теореме Пифагора из (triangle AA_1O): [AO=sqrt{a^2+dfrac{a^2}2}=dfrac{sqrt6}2a.]
Следовательно, из ((*)) теперь можно найти перпендикуляр
[C_1H=dfrac a{sqrt3}.]
Ответ:
(dfrac a{sqrt3})
Задание
3
#2439
Уровень задания: Сложнее ЕГЭ
Дан куб (ABCDA_1B_1C_1D_1). Найдите расстояние между прямыми (A_1B) и (AC_1), если ребро куба равно (sqrt6).
По определению угол между скрещивающимися прямыми — это угол между одной прямой и плоскостью, проходящей через вторую прямую параллельно первой. Найдем плоскость, проходящую через (A_1B) параллельно (AC_1).
Заметим, что данные прямые являются скрещивающимися. Т.к. (B_1C_1perp (AA_1B_1)), то проекция наклонной (AC_1) на эту плоскость – это прямая (AB_1).
Пусть (AB_1cap A_1B=O). Опустим из точки (O) на (AC_1) перпендикуляр (OK) и докажем, что это и есть искомое расстояние. Т.к. по определению расстояние между скрещивающимися прямыми – длина отрезка, перпендикулярного обеим прямым, то осталось доказать, что (OK) перпендикулярен прямой (A_1B).
Действительно, проведем (KHparallel B_1C_1) (следовательно, (Hin
AB_1)). Тогда т.к. (B_1C_1perp (AA_1B_1)), то и (KHperp
(AA_1B_1)). Тогда по теореме о трех перпендикулярах (т.к. проекция (HOperp A_1B)) наклонная (KOperp A_1B), чтд.
Таким образом, (KO) – искомое расстояние.
Заметим, что (triangle AOKsim triangle AC_1B_1) (по двум углам). Следовательно,
[dfrac{AO}{AC_1}=dfrac{OK}{B_1C_1} quad Rightarrow quad
OK=dfrac{sqrt6cdot sqrt2}{2sqrt3}=1.]
Ответ: 1

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды