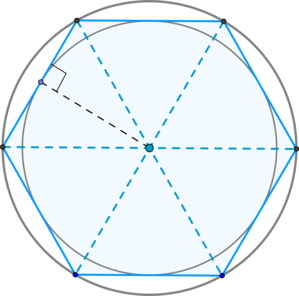
Это хорошо, что в поставленной задаче все многоугольники оснащены чётным количеством сторон. Ведь не секрет, что именно у таких фигур имеются пары параллельных сторон. Но, мало того, расстояние между такими сторонами является диаметром вписанной окружности. И тут мне сразу вспомнились картинки из предыдущего ответа, который я давал по теме «Площади 6-угольников».
То есть в шестиугольнике мы банально делим диаметр вписанной окружности на корень из трёх и всё:
- t6 = 2 * r / √3 = d / √3 = 5,7735027 см
Что же, лиха беда начало. Берём справочник и находим в нём формулу для аналогичных расчётов в тех случаях, когда число углов равно восьми. Нашлась такая и выглядит она следующим образом:
- t8 = 2 / (1 + √2) * r = d / (1 + √2) = 4,1421356 см
Однако при переходе к двенадцатиугольнику дело застопорилось. Быстро отыскать подходящую формулу мне не удалось. Но, может быть, это и к лучшему, потому что мне на глаза попалась другая — универсальная. Такая формула, которая вычисляет длину стороны многоугольника через радиус вписанной окружности. И в этом случае мы можем первым делом перепроверить уже сделанные вычисления, а потом разобраться и двенадцатью углами.
- t6 = 2 * r * Tg (π / n) = 10 * Tg (π / 6) = 5,7735027 см
- t8 = 10 * Tg (π /
= 4,1421356 см
- t12 = 10 * Tg (π / 12) = 2,6794919 см
По окончании проделанной работы я по старой привычке нашёл ещё один альтернативный способ, который может послужить нам средством для проверки. Идём в Интернет, где находим площадку, предназначенную для выполнения расчётов такого рода. Подставляем в форму одно за другим значения радиуса вписанной окружности и количества вершин многоугольника, а потом подшиваем скриншоты и показываем здесь:
На сколько я вижу, все ответы сошлись. И мы можем привести их отдельными строками:
- t6 = 5,7735026919 см
- t8 = 4,1421356237 см
- t12 = 2,6794919243 см.
6. Геометрия на плоскости (планиметрия). Часть II
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Правильный шестиугольник (страница 2)
Правильный шестиугольник — выпуклый шестиугольник, у которого все углы равны и все стороны равны.
(blacktriangleright) Каждый угол правильного шестиугольника равен (120^circ).
(blacktriangleright) Около правильного шестиугольника можно описать окружность: ее радиус равен его стороне.
(blacktriangleright) Большие диагонали правильного шестиугольника делят его на (6) равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности.
(blacktriangleright) Центры вписанной и описанной около правильного шестиугольника окружностей есть точка пересечения больших диагоналей этого шестиугольника.
(blacktriangleright) Площадь правильного шестиугольника со стороной (a) равна [S=dfrac{3sqrt3}2a^2]
Задание
8
#667
Уровень задания: Равен ЕГЭ
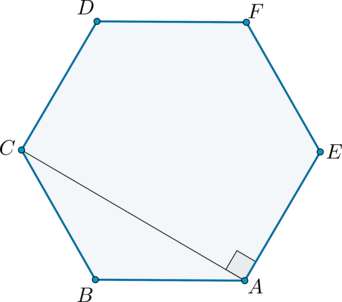
Сторона правильного шестиугольника (ABCDEF) равна (sqrt[4]{3}). Найдите его площадь.
Пусть (O) – центр описанной около (ABCDEF) окружности
тогда треугольники (AOF), (AOB), (BOC), (COD), (DOE), (EOF) – равносторонние и все они попарно равны.
[S_{triangle{AOF}} = 0,5 AF^2 cdot sin{60^{circ}} = dfrac{AF^2sqrt{3}}{4}, qquadqquad S_{ABCDEF} = 6cdot S_{triangle{AOF}} = dfrac{3sqrt{3}AF^2}{2}.] В данной задаче (S_{ABCDEF} = 6cdot S_{triangle{AOF}} = dfrac{3sqrt{3}AF^2}{2} = 4,5).
Ответ: 4,5
Задание
9
#2428
Уровень задания: Сложнее ЕГЭ
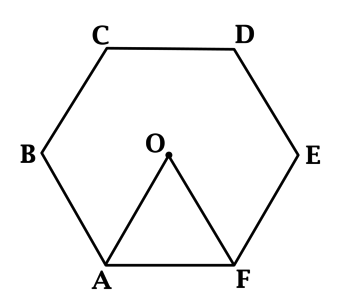
Найдите расстояние между двумя параллельными сторонами правильного шестиугольника со стороной (sqrt{108}).
Рассмотрим правильный шестиугольник (ABCDFE) и в нем треугольник (ABC). Параллельными сторонами являются пары (AB) и (DF), (BC) и (FE), (CD) и (EA).
Помним, что угол правильного шестиугольника равен (120^circ).
(triangle ABC) равнобедренный ((AB=BC,)), следовательно, (angle
BAC=0,5cdot (180^circ-120^circ)=30^circ). Таким образом, (angle
CAE=120^circ-30^circ=90^circ).
Следовательно, (AC) – расстояние между сторонами (AE) и (CD) (по определению расстояние между двумя параллельными прямыми – отрезок, проведенный из любой точки одной прямой перпендикулярно ко второй прямой).
Найдем (AC) по теореме косинусов ((AB=BC=a=sqrt{108})):
(AC^2=a^2+a^2-2a^2cdot cos120^circ=2a^2(1-cos120^circ)=2cdot
108cdot left(1+frac12right)=3cdot 108 quad Rightarrow
)
(Rightarrow quad AC=sqrt{3cdot 108}=sqrt{3cdot 3cdot
36}=3cdot 6=18.)
Ответ: 18
Задание
10
#2431
Уровень задания: Сложнее ЕГЭ
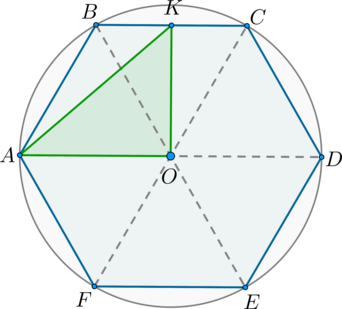
Около правильного шестиугольника (ABCDEF) описана окружность с центром в точке (O). Во сколько раз площадь этого шестиугольника больше площади треугольника (AOK), где (K) – середина стороны (BC).
По свойству правильного шестиугольника центр описанной окружности лежит на пересечении больших его диагоналей. Следовательно, (AO) – радиус описанной окружности. Также по свойству радиус описанной окружности равен стороне правильного шестиугольника, следовательно, (AB=AO=x).
Т.к. (triangle AOB) – правильный, то (angle AOB=60^circ). (triangle BOC) также правильный. Т.к. по условию (OK) – медиана в правильном (triangle BOC), то она и биссектриса, то есть (angle
BOK=frac12cdot 60^circ=30^circ). Таким образом, (angle
AOK=90^circ), то есть (triangle AOK) – прямоугольный.
Следовательно, [S_{triangle AOK}=dfrac12cdot AOcdot OK=dfrac
x2cdot OK]
Площадь правильного шестиугольника равна сумме площадей шести правильных треугольников:
[S_{ABCDEF}=6cdot dfrac12cdot BCcdot OK=6cdot dfrac x2cdot OK]
Таким образом, [dfrac{S_{ABCDEF}}{S_{triangle AOK}}=6.]
Ответ: 6
Задание
11
#2432
Уровень задания: Сложнее ЕГЭ
Около правильного шестиугольника (ABCDEF) описана окружность с центром в точке (O). Найдите большую сторону треугольника (AOK), где (K) – середина стороны (BC=sqrt7) шестиугольника (ABCDEF).
По свойству правильного шестиугольника центр описанной окружности лежит на пересечении больших его диагоналей. Следовательно, (AO) – радиус описанной окружности. Также по свойству радиус описанной окружности равен стороне правильного шестиугольника, следовательно, (AB=AO=sqrt7).
Т.к. (triangle AOB) – правильный, то (angle AOB=60^circ). (triangle BOC) также правильный. Т.к. по условию (OK) – медиана в правильном (triangle BOC), то она и биссектриса, то есть (angle
BOK=frac12cdot 60^circ=30^circ). Таким образом, (angle
AOK=90^circ), то есть (triangle AOK) – прямоугольный.
Следовательно, большая сторона в (triangle AOK) – это гипотенуза (AK). По теореме Пифагора из (triangle BOK) ((OK) также является в нем высотой):
[OK=sqrt{BO^2-BK^2}=sqrt{(sqrt7)^2-left(dfrac{sqrt7}2right)^2}=
dfrac{sqrt3}2cdot sqrt7]
Таким образом, по теореме Пифагора из (triangle AOK):
[AK=sqrt{AO^2+OK^2}=sqrt{(sqrt7)^2+left(dfrac{sqrt3}2cdot sqrt7right)^2}=
dfrac72=3,5.]
Ответ: 3,5

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Расстояние между паралл.сторонами правильных: шестиугольника… Как решить? Подскажите, если можно
Расстояние между параллельными сторонами правильных<
равно 10 см. Найдите сторону соответствующего многоугольника.
Это хорошо, что в поставленной задаче все многоугольники оснащены чётным количеством сторон. Ведь не секрет, что именно у таких фигур имеются пары параллельных сторон. Но, мало того, расстояние между такими сторонами является диаметром вписанной окружности. И тут мне сразу вспомнились картинки из предыдущего ответа, который я давал по теме «Площади 6-угольников»< √3 = 5,7735027 см
Что же, лиха беда начало. Берём справочник и находим в нём формулу для аналогичных расчётов в тех случаях, когда число углов равно восьми. Нашлась такая и выглядит она следующим образом:
t8 = 2 n) = 10 * Tg (π li>
Правильный шестиугольник, многоугольнике с 6 вершинами, вычислить его параметры. Шестиугольник-это фигура, из которой можно складывать мозаику (черепицу). Введите одно из известных значений. Затем нажмите кнопку вычислить.
.
Поделиться расчетом:
Калькулятор шестиугольников
Длина стороны(a)
Большая диагональ(d1)
Меньшая диагональ(d2)
Периметр(p)
Площадь(S)
Радиус вписанной окружности(r)
Вычислить
Очистить
Формулы:

d2 = √3 * a
p = 6 * a
S = 3/2 * √3 * a2
r = √3 / 2 * a
Высота = d2 = 2 * r
Радиус окружности = a
Внутренние углы: 120°, 9 диагоналей





Шестиугольная шестиугольная форма появляется в некоторых неожиданных местах: ячейки сот, формы, которые мыльные пузыри образуют, когда они разбиваются вместе, внешний край болтов и даже шестигранные базальтовые колонны Дорожки Гиганта, природные скальные образования на северном побережье Ирландии. Предполагая, что вы имеете дело с обычным шестиугольником, а это означает, что все его стороны имеют одинаковую длину, вы можете использовать периметр шестиугольника или его площадь, чтобы найти длину его сторон.
TL; DR (слишком долго; не читал)
Самый простой и, безусловно, наиболее распространенный способ определения длины сторон правильного шестиугольника заключается в использовании следующей формулы:
s = P ÷ 6, где P — периметр шестиугольника, а s — длина любой из его сторон.
Расчет сторон шестиугольника от периметра
Поскольку обычный шестиугольник имеет шесть сторон одинаковой длины, найти длину любой из этих сторон так же просто, как разделить периметр шестиугольника на 6. Так что, если ваш шестиугольник имеет периметр 48 дюймов, у вас есть:
48 дюймов ÷ 6 = 8 дюймов.
Каждая сторона вашего шестиугольника имеет длину 8 дюймов.
Расчет сторон шестиугольника от области
Точно так же, как квадраты, треугольники, круги и другие геометрические фигуры, с которыми вы могли иметь дело, есть стандартная формула для расчета площади правильного шестиугольника. Это:
A = (1.5 × √3) × s 2, где A — площадь шестиугольника, а s — длина любой из его сторон.
Очевидно, что вы можете использовать длину сторон шестиугольника для расчета площади. Но если вы знаете площадь шестиугольника, вы можете использовать ту же формулу, чтобы найти длину его сторон. Рассмотрим шестиугольник площадью 128 в 2:
-
Подставляемая область в уравнение
-
Изолировать переменную
-
Упростите термин справа
-
Возьмите квадратный корень обеих сторон
Начнем с подстановки площади шестиугольника в уравнение:
128 = (1, 5 × √3) × s 2
Первым шагом в решении для s является выделение его с одной стороны уравнения. В этом случае деление обеих частей уравнения на (1, 5 × √3) дает вам:
128 ÷ (1, 5 × √3) = с 2
Условно переменная идет в левой части уравнения, поэтому вы также можете записать это как:
s 2 = 128 ÷ (1, 5 × √3)
Упростите термин справа. Ваш учитель может позволить вам приблизить √3 к 1.732, в этом случае у вас будет:
s 2 = 128 ÷ (1, 5 × 1, 732)
Что упрощает до:
с 2 = 128 ÷ 2, 598
Что, в свою очередь, упрощает:
s 2 = 49, 269
Вы можете, вероятно, сказать, что путем проверки s будет близко к 7 (потому что 7 2 = 49, что очень близко к уравнению, с которым вы имеете дело). Но, взяв квадратный корень с обеих сторон с помощью калькулятора, вы получите более точный ответ. Не забудьте также написать в своих единицах измерения:
√ s 2 = √49.269 тогда становится:
s = 7, 019 дюймов



 = 4,1421356 см
= 4,1421356 см