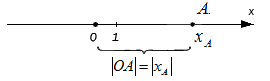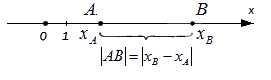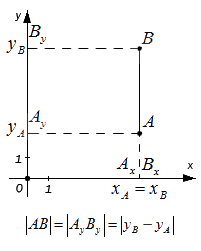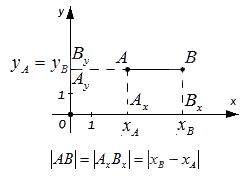The study of geometry requires you to deal with angles and their relation to other measurements, such as distance. When looking at straight lines, calculating the distance between two points is straightforward: simply measure the distance with a ruler, and use the Pythagorean Theorem when dealing with right triangles. When working with a circle, however, there is no instrument to accurately measure a curve. Therefore, you may have to calculate the distance between two points on a circle using mathematics.
- Ruler
- Calculator
- Protractor
Measure the circle’s radius with a ruler, or record the figure given to you in the math problem. The radius of a circle measures the distance from the center to any point along the outside of the circle.
Multiply this measurement by two to calculate the diameter, or distance through the center of the circle.
Multiply this measurement by pi. Pi is an irrational number, but for most everyday purposes and in school, you can round it to two decimal places: 3.14. The diameter of a circle multiplied by pi gives you the circumference, or the distance around the circle.
Draw two lines from the radius of your circle, each connecting to one of the two points you’re using to measure arc distance.
Measure the angle made by those lines with a protractor and record the measurement.
Set the angle you measured as a ratio of 360. According to The Geometer’s Sketchpad on the Rice University website, there are 360 degrees in any circle, so any angle you measure can be taken as a ratio to determine the proportion of an arc length.
Cross-multiply your numbers using the equation: a/C = T/360. A is your arc length, C is your circumference and T is the angle you measured. Multiply C by T. Set the result equal to 360 times a. Divide both sides of the equation by 360 to solve for a.
Things You’ll Need
GIS-LAB
Географические информационные системы и дистанционное зондирование
Вычисление расстояния и начального азимута между двумя точками на сфере
Измерение расстояния и начального азимута между точками без проекционных преобразований
Содержание
[править] Введение
Длина дуги большого круга – кратчайшее расстояние между любыми двумя точками находящимися на поверхности сферы, измеренное вдоль линии соединяющей эти две точки (такая линия носит название ортодромии) и проходящей по поверхности сферы или другой поверхности вращения. Сферическая геометрия отличается от обычной Эвклидовой и уравнения расстояния также принимают другую форму. В Эвклидовой геометрии, кратчайшее расстояние между двумя точками – прямая линия. На сфере, прямых линий не бывает. Эти линии на сфере являются частью больших кругов – окружностей, центры которых совпадают с центром сферы.
Начальный азимут — азимут, взяв который при начале движения из точки А, следуя по большому кругу на кратчайшее расстояние до точки B, конечной точкой будет точка B. При движении из точки A в точку B по линии большого круга азимут из текущего положения на конечную точку B постоянно меняется. Начальный азимут [angles-rhumb.html отличен от постоянного], следуя которому, азимут из текущей точки на конечную не меняется, но маршрут следования не является кратчайшим расстоянием между двумя точками.
Через любые две точки на поверхности сферы, если они не прямо противоположны друг другу (то есть не являются антиподами), можно провести уникальный большой круг. Две точки, разделяют большой круг на две дуги. Длина короткой дуги – кратчайшее расстояние между двумя точками. Между двумя точками-антиподами можно провести бесконечное количество больших кругов, но расстояние между ними будет одинаково на любом круге и равно половине окружности круга, или pi*R, где R – радиус сферы.
На плоскости (в прямоугольной системе координат), большие круги и их фрагменты, как было упомянуто выше, представляют собой дуги во всех проекциях, кроме гномонической, где большие круги — прямые линии. На практике это означает, что самолеты и другой авиатранспорт всегда использует маршрут минимального расстояния между точками для экономии топлива, то есть полет осуществляется по расстоянию большого круга, на плоскости это выглядит как дуга.
Форма Земли может быть описана как сфера, поэтому уравнения для вычисления расстояний на большом круге важны для вычисления кратчайшего расстояния между точками на поверхности Земли и часто используются в навигации.
Вычисление расстояния этим методом более эффективно и во многих случаях более точно, чем вычисление его для спроектированных координат (в прямоугольных системах координат), поскольку, во-первых, для этого не надо переводить географические координаты в прямоугольную систему координат (осуществлять проекционные преобразования) и, во-вторых, многие проекции, если неправильно выбраны, могу привести к значительным искажениям длин в силу особенностей проекционных искажений.
Известно, что более точно описывает форму Земли не сфера, а эллипсоид, однако в данной статье рассматривается вычисление расстояний именно на сфере, для вычислений используется сфера радиусом 6372795 метров, что может привести к ошибке вычисления расстояний порядка 0.5%.
[править] Формулы
Существует три способа расчета сферического расстояния большого круга (подробнее).
[править] Сферическая теорема косинусов
В случае маленьких расстояний и небольшой разрядности вычисления (количество знаков после запятой), использование формулы может приводить к значительным ошибкам связанным с округлением. Графическое изображение формул здесь и далее — из Википедии.
— широта и долгота двух точек в радианах
— разница координат по долготе
— угловая разница
Для перевода углового расстояния в метрическое, нужно угловую разницу умножить на радиус Земли (6372795 метров), единицы конечного расстояния будут равны единицам, в которых выражен радиус (в данном случае — метры).
[править] Формула гаверсинусов
Используется, чтобы избежать проблем с небольшими расстояниями.
[править] Модификация для антиподов
Предыдущая формула также подвержена проблеме точек-антиподов, чтобы ее решить используется следующая ее модификация.
[править] Реализация на Avenue
На языке Avenue, используя последнюю формулу для вычисления расстояния большого круга между двумя точками, можно использовать следующий код. Точки для вычисления передаются другим скриптом, либо добавляются в начало данного в виде pnt = point.make(long, lat) (скачать скрипт):
Для вызова процедуры расчета длин приведенной выше, можно также воспользоваться следующим скриптом, результатом его работы будет расчет длин между точкой testpont до всех точек активной темы вида и запись результата в поле Newdist атрибутивной таблицы этой темы:
[править] Реализация на языке Python
Реализует полный вариант расчета через atan2(), более универсальнее, чем вариант для Avenue. (скачать скрипт)
[править] Реализация в Excel
Скачать пример расчета расстояния большого круга и начального азимута в Excel. Демонстрирует расчеты через закон косинусов, гаверсинус, полное уравнение и полное уравнение через atan2().
Можно также воспользоваться следующей функцией:
[править] Проверочный набор данных
Если все считается правильно, должны быть получены следующие результаты (координаты точек даны как широта/долгота, расстояние в метрах, начальный угол в десятичных градусах):
| # | Точка 1 | Точка 2 | Расстояние | Угол |
| 1 | 77.1539/-139.398 | -77.1804/-139.55 | 17166029 | 180.077867811 |
| 2 | 77.1539/120.398 | 77.1804/129.55 | 225883 | 84.7925159033 |
| 3 | 77.1539/-120.398 | 77.1804/129.55 | 2332669 | 324.384112704 |
[править] Ссылки по теме
Последнее обновление: 2014-05-14 23:41
Дата создания: 06.06.2006
Автор(ы): Максим Дубинин
Как найти расстояние между двумя точками окружности
Окружность
Привет, друг! Ниже собрана вся информация по окружности: что это такое, как найти ее величины, как круг связан с тригонометрией. Это поможет тебе еще лучше разобраться с этими темами, а также верно решать задачи! Время прочтения — 10 минут.
Что такое окружность?
Окружность — это множество всех точек на плоскости, находящихся на одинаковом расстоянии от данной точки, а ее радиусом называют отрезок, который соединяет любую её точку с центром (все радиусы окружности равны). У окружности также есть диаметр — отрезок, соединяющий две точки окружности и проходящий через её центр.
Выделяют также такое понятие как единичная окружность. Она представляет из себя такую окружность, центр которой располагается в начале координат, а ее радиус равен единице.
Есть еще один вид окружности — числовая. Это обычная единичная окружность, но с уже установленным соответствием между действительными числами и точками.
Как найти длину окружности
Зачастую в задачах просят найти длину окружности, как это сделать?
Так, для того чтобы найти длину окружности, нужно:
- Диаметр этой окружности умножить на , число ≈ 3,1415926535…
- Найти удвоенное произведение радиуса и числа
Формулы:
Где r — это радиус окружности, а d — ее диаметр, а число — это математическая константа (отношение длины окружности к длине ее диаметра)
Чему равен радиус окружности
Радиус окружности необходимо знать, чтобы решить многие задачи, поэтому давай вместе разберем, как его можно найти.
- Через площадь окружности : R=s, где S — площадь круга, — это математическая константа, которая объяснена выше.
- Через длину круга: R=P2, где P — длина круга.
- Через диаметр окружности: R=d2, где d — диаметр.
- Через диагональ вписанного треугольника: R=d2, где d=a2 b2.
- Через сторону описанного квадрата: R= a2, где а — сторона описанного квадрата.
- Через стороны и площадь вписанного треугольника: R=abc4S, где abc — стороны вписанного треугольника, а S — его площадь.
- Через площадь и полупериметр описанного треугольника: R=sp, где S — площадь треугольника, а p — полупериметр.
- Через площадь сектора и его центральный угол: R=360Spa, где S — площадь сектора круга, α — его центральный угол.
- Через сторону вписанного правильного многоугольника: R=a2sin(180N), где a — сторона правильного многоугольника (все его стороны равны), N — количество сторон многоугольника.
Окружность в тригонометрии
Окружность используется и в тригонометрии:
Что значат на рисунке все обозначение?
- Присутствует перевод градусов в радианы (и наоборот). В полном круге — 360 градусов ( радиан);
- Значение косинуса угла — на оси Х, а значение синуса — на У;
- Синус и косинус имеют значения от -1 до 1;
- На тригонометрическом круге видно, что косинус как и синус — периодические (один период равен 2).
Что еще важно знать?
Полный круг — 360 градусов.
Точка с координатами (1;0) — угол 0 градусов соответствует углу ноль градусов, а точка с координатами (-1;0) соответствует углу 180 градусов, точка с координатами (0;1) — в 90 градусов.
Косинус угла — абсцисса точки на единичной окружности, которая соответствует приведенному углу.
Синус угла — ордината точки на единичной окружности, которая соответствует приведенному углу.
Потому как окружность единичная, то для любого угла и синус, и косинус находятся в пределах от -1 до 1. Так:
Из этого можно выделить основное тригонометрическое тождество:
cos^2 a + sin^2 a = 1
По рисунку видно, что
,
Углы могут быть и больше 360 градусов. Например, угол 720 — это два полных оборота по часовой стрелке. Из этого можно сделать такой вывод:
Если же применять в этих формулах не градусы, а радианы, то:
Можно также по рисунку тригонометрической окружности определить тангенс угла и котангенс:
В результате, мы получаем таблицу:
Углы поворота
Угол поворота — это угол, образованный положительным направлением оси OX и лучом OA.
Их величина не имеет зависимости от радиуса приведенной окружности.
Угол в первом квадранте(четверти круга), имеет все положительные значения тригонометрических функций.
Во втором квадранте все функции (кроме sin и cos) — отрицательные.
В третьем квадранте значения всех функций (помимо tg и ctg) меньше 0.
В четвертом квадранте все функции (кроме cos и sec) с отрицательным значением.
Декартовы координаты точек плоскости. Уравнение окружности
Числовая ось
Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление
указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.
Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .
Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .
Прямоугольная декартова система координат на плоскости
Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).
Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.
Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA1 и AA2 на прямые Ox и Oy соответственно (рис.3).
Определение 4 . Абсциссой точки A называют координату точки A1 на числовой оси Ox , ординатой точки A называют координату точки A2 на числовой оси Oy .
Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).
Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .
Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).
Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.
Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .
Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.
Формула для расстояния между двумя точками координатной плоскости
Утверждение 1 . Расстояние между двумя точками координатной плоскости
вычисляется по формуле
Доказательство . Рассмотрим рисунок 6.
| | A1A2| 2 = = ( x2 – x1) 2 + ( y2 – y1) 2 . |
(1) |
что и требовалось доказать.
Уравнение окружности на координатной плоскости
Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:
Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A0 (x0 ; y0) .
Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид
Нахождение расстояния между двумя точками
В данной публикации мы рассмотрим, чему равно расстояние между двумя точками, и по какой формуле оно считается (на плоскости и в пространстве). Также разберем примеры решения задач по этой теме.
Расчет расстояния между двумя точками
Расстояние между двумя точками — это длина отрезка (d), который получится, если их соединить.
Если точки и расположены на плоскости, то расстояние между ними считается по формуле:
Если точки и находятся в трехмерном пространстве, расстояние вычисляется так:
Примеры задач
Задание 1
На плоскости даны две точки: и . Найдем расстояние между ними.
Решение:
Воспользуемся первой формулой, представленной выше:
Задание 2
Найдем расстояние между точками и .
Решение:
Применим соответствующую формулу, подставив в нее известные нам значения:
Всё про окружность и круг
Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Центральный угол — это угол, вершина которого совпадает с центром окружности.
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
http://b4.cooksy.ru/articles/kak-nayti-rasstoyanie-mezhdu-dvumya-tochkami-okruzhnosti
http://www.stranamam.ru/post/8974384/
Как найти расстояние между точками на окружности
Содержание
- Расстояние между точками на координатной прямой
- Расстояние между точками на плоскости
- Расстояние между точками в пространстве
- Примеры решения задач на нахождение расстояния между точками
- Содержание
- Общие определения
- Касательная к окружности
- Углы в окружности
- Вписанная окружность
- Описанная окружность
- Теорема Птолемея
Имеем окружность (радиус не имеет значения, например 1), на которой расположены некие точки, полученные при пересечении этой окружности лучом, исходящим из центра окружности под произвольным углом. Как реализовать алгоритм нахождения ближайшей из точек А, В, С, Д и тд N (доступных по варианту) к точке X, являющейся известной заранее. Пробовал по формуле нахождения минимальной хорды и минимального угла — получаю неверный результат. Реализовать мне это нужно в Excel.
Alex Nikush: Итак, решение я нашел: =МИН(ABS(ЕСЛИ($C$2:$C$4-$E$2 19 Ноября в 15:42 и в 19:10 .
«Шапка» табл.1 (Объект/Луч/Субъект/Код) — A1:D1
Данные табл.1 A2:C6
«Шапка» табл.2 (Субъект/Код/Луч) — A9:C9
Данные табл.2 A10:C15
В D2 формула массива:
Протянуть формулу по строкам (D2:D6)
Формула тяжелая, облегчение возможно, но нужно «щупать» живой файл.
Без файла Excel воспроизведение решения трудоемкое.
В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.
Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе. Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.
Расстояние между точками на координатной прямой
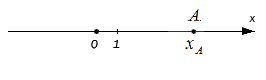
Исходные данные: координатная прямая O x и лежащая на ней произвольная точка А . Любой точке прямой присуще одно действительное число: пусть для точки А это будет некое число х A , оно же – координата точки А .
В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.
Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой О А отрезки – единицы длины, мы можем определить длину отрезка O A по итоговому количеству отложенных единичных отрезков.
К примеру, точке А соответствует число 3 – чтобы попасть в нее из точки О , необходимо будет отложить три единичных отрезка. Если точка А имеет координату — 4 – единичные отрезки откладываются аналогичным образом, но в другом, отрицательном направлении. Таким образом в первом случае, расстояние О А равно 3 ; во втором случае О А = 4 .
Если точка A имеет в качестве координаты рациональное число, то от начала отсчета (точка О ) мы откладываем целое число единичных отрезков, а затем его необходимую часть. Но геометрически не всегда возможно произвести измерение. К примеру, затруднительным представляется отложить на координатной прямой дробь 4 111 .
Вышеуказанным способом отложить на прямой иррациональное число и вовсе невозможно. К примеру, когда координата точки А равна 11 . В таком случае возможно обратиться к абстракции: если заданная координата точки А больше нуля, то O A = x A (число принимается за расстояние); если координата меньше нуля, то O A = — x A . В общем, эти утверждения справедливы для любого действительного числа x A .
Резюмируя: расстояние от начала отсчета до точки, которой соответствует действительное число на координатной прямой, равно:
- 0, если точка совпадает с началом координат;
- x A , если x A > 0 ;
- — x A , если x A 0 .
При этом очевидно, что сама длина отрезка не может быть отрицательной, поэтому, используя знак модуля, запишем расстояние от точки O до точки A с координатой x A : O A = x A
Верным будет утверждение: расстояние от одной точки до другой будет равно модулю разности координат. Т.е. для точек A и B , лежащих на одной координатной прямой при любом их расположении и имеющих соответственно координаты x A и x B : A B = x B — x A .
Расстояние между точками на плоскости
Исходные данные: точки A и B , лежащие на плоскости в прямоугольной системе координат O x y с заданными координатами: A ( x A , y A ) и B ( x B , y B ) .
Проведем через точки А и B перпендикуляры к осям координат O x и O y и получим в результате точки проекции: A x , A y , B x , B y . Исходя из расположения точек А и B далее возможны следующие варианты:
— если точки А и В совпадают, то расстояние между ними равно нулю;
— если точки А и В лежат на прямой, перпендикулярной оси O x (оси абсцисс), то точки и совпадают, а | А В | = | А y B y | . Поскольку, расстояние между точками равно модулю разности их координат, то A y B y = y B — y A , а, следовательно A B = A y B y = y B — y A .
— если точки A и B лежат на прямой, перпендикулярной оси O y (оси ординат) – по аналогии с предыдущим пунктом: A B = A x B x = x B — x A
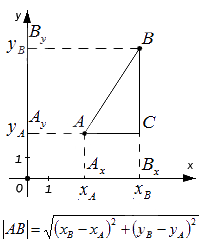
— если точки A и B не лежат на прямой, перпендикулярной одной из координатных осей, найдем расстояние между ними, выведя формулу расчета:
Мы видим, что треугольник А В С является прямоугольным по построению. При этом A C = A x B x и B C = A y B y . Используя теорему Пифагора, составим равенство: A B 2 = A C 2 + B C 2 ⇔ A B 2 = A x B x 2 + A y B y 2 , а затем преобразуем его: A B = A x B x 2 + A y B y 2 = x B — x A 2 + y B — y A 2 = ( x B — x A ) 2 + ( y B — y A ) 2
Сформируем вывод из полученного результата: расстояние от точки А до точки В на плоскости определяется расчётом по формуле с использованием координат этих точек
A B = ( x B — x A ) 2 + ( y B — y A ) 2
Полученная формула также подтверждает ранее сформированные утверждения для случаев совпадения точек или ситуаций, когда точки лежат на прямых, перпендикулярных осям. Так, для случая совпадения точек A и B будет верно равенство: A B = ( x B — x A ) 2 + ( y B — y A ) 2 = 0 2 + 0 2 = 0
Для ситуации, когда точки A и B лежат на прямой, перпендикулярной оси абсцисс:
A B = ( x B — x A ) 2 + ( y B — y A ) 2 = 0 2 + ( y B — y A ) 2 = y B — y A
Для случая, когда точки A и B лежат на прямой, перпендикулярной оси ординат:
A B = ( x B — x A ) 2 + ( y B — y A ) 2 = ( x B — x A ) 2 + 0 2 = x B — x A
Расстояние между точками в пространстве
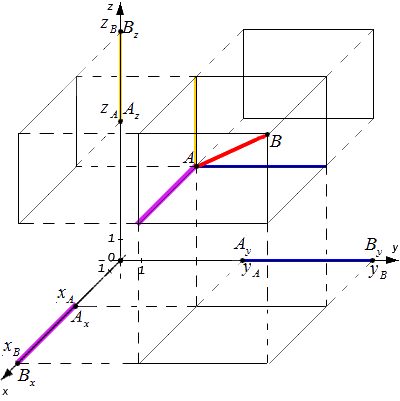
Исходные данные: прямоугольная система координат O x y z с лежащими на ней произвольными точками с заданными координатами A ( x A , y A , z A ) и B ( x B , y B , z B ) . Необходимо определить расстояние между этими точками.
Рассмотрим общий случай, когда точки A и B не лежат в плоскости, параллельной одной из координатных плоскостей. Проведем через точки A и B плоскости, перпендикулярные координатным осям, и получим соответствующие точки проекций: A x , A y , A z , B x , B y , B z
Расстояние между точками A и B являет собой диагональ полученного в результате построения параллелепипеда. Согласно построению измерения этого параллелепипеда: A x B x , A y B y и A z B z
Из курса геометрии известно, что квадрат диагонали параллелепипеда равен сумме квадратов его измерений. Исходя из этого утверждения получим равенство: A B 2 = A x B x 2 + A y B y 2 + A z B z 2
Используя полученные ранее выводы, запишем следующее:
A x B x = x B — x A , A y B y = y B — y A , A z B z = z B — z A
A B 2 = A x B x 2 + A y B y 2 + A z B z 2 = x B — x A 2 + y B — y A 2 + z B — z A 2 = = ( x B — x A ) 2 + ( y B — y A ) 2 + z B — z A 2
Итоговая формула для определения расстояния между точками в пространстве будет выглядеть следующим образом:
A B = x B — x A 2 + y B — y A 2 + ( z B — z A ) 2
Полученная формула действительна также для случаев, когда:
— лежат на одной координатной оси или прямой, параллельной одной из координатных осей.
Примеры решения задач на нахождение расстояния между точками
Исходные данные: задана координатная прямая и точки, лежащие на ней с заданными координатами A ( 1 — 2 ) и B ( 11 + 2 ) . Необходимо найти расстояние от точки начала отсчета O до точки A и между точками A и B .
Решение
- Расстояние от точки начала отсчета до точки равно модулю координаты этой точки, соответственно O A = 1 — 2 = 2 — 1
- Расстояние между точками A и B определим как модуль разности координат этих точек: A B = 11 + 2 — ( 1 — 2 ) = 10 + 2 2
Ответ: O A = 2 — 1 , A B = 10 + 2 2
Исходные данные: задана прямоугольная система координат и две точки, лежащие на ней A ( 1 , — 1 ) и B ( λ + 1 , 3 ) . λ – некоторое действительное число. Необходимо найти все значения этого числа, при которых расстояние А В будет равно 5 .
Решение
Чтобы найти расстояние между точками A и B , необходимо использовать формулу A B = ( x B — x A ) 2 + y B — y A 2
Подставив реальные значения координат, получим: A B = ( λ + 1 — 1 ) 2 + ( 3 — ( — 1 ) ) 2 = λ 2 + 16
А также используем имеющееся условие, что А В = 5 и тогда будет верным равенство:
λ 2 + 16 = 5 λ 2 + 16 = 25 λ = ± 3
Ответ: А В = 5 , если λ = ± 3 .
Исходные данные: задано трехмерное пространство в прямоугольной системе координат O x y z и лежащие в нем точки A ( 1 , 2 , 3 ) и B — 7 , — 2 , 4 .
Решение
Для решения задачи используем формулу A B = x B — x A 2 + y B — y A 2 + ( z B — z A ) 2
Подставив реальные значения, получим: A B = ( — 7 — 1 ) 2 + ( — 2 — 2 ) 2 + ( 4 — 3 ) 2 = 81 = 9
Сначала разберемся в отличии между кругом и окружностью. Чтобы увидеть эту разницу, достаточно рассмотреть, чем являются обе фигуры. Это бесчисленное количество точек плоскости, располагающиеся на равном расстоянии от единственной центральной точки. Но, если круг состоит и из внутреннего пространства, то окружности оно не принадлежит. Получается, что круг это и окружность, ограничивающая его (о-кру(г)жность), и бесчисленное число точек, что внутри окружности.
Содержание
Общие определения
Окружность — это множество точек, которое располагается на одинаковом расстоянии от ее центра, представленного точкой.
Для любой точки L , лежащей на окружности, действует равенство OL=R . (Длина отрезка OL равняется радиусу окружности).
Отрезок, который соединяет две точки окружности, является ее хордой.
Хорда, проходящая прямо через центр окружности, является диаметром этой окружности (D) . Диаметр можно вычислить по формуле: D=2R
Длина окружности вычисляется по формуле: C=2pi R
Площадь круга: S=pi R^
Дугой окружности называется та ее часть, которая располагается между двух ее точек. Эти две точки и определяют две дуги окружности. Хорда CD стягивает две дуги: CMD и CLD . Одинаковые хорды стягивают одинаковые дуги.
Центральным углом называется такой угол, который находится между двух радиусов.
Длину дуги можно найти по формуле:
- Используя градусную меру: CD = frac<pi R alpha ^<circ>><180^<circ>>
- Используя радианную меру: CD = alpha R
Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.
В случае, если хорды AB и CD окружности имеют пересечение в точке N , то произведения отрезков хорд, разделенные точкой N , равны между собой.
ANcdot NB = CN cdot ND
Касательная к окружности
Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью.
Если же у прямой есть две общие точки, ее называют секущей.
Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.
Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.
Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть.
Можно сделать вывод: произведение целого отрезка первой секущей на его внешнюю часть равняется произведению целого отрезка второй секущей на его внешнюю часть.
AC cdot BC = EC cdot DC
Углы в окружности
Градусные меры центрального угла и дуги, на которую тот опирается, равны.
angle COD = cup CD = alpha ^
Вписанный угол — это угол, вершина которого находится на окружности, а стороны содержат хорды.
Вычислить его можно, узнав величину дуги, так как он равен половине этой дуги.
angle AOB = 2 angle ADB
Опирающийся на диаметр, вписанный угол, прямой.
angle CBD = angle CED = angle CAD = 90^
Вписанные углы, которые опираются на одну дугу, тождественны.
angle ADB = angle AEB = angle AFB
Опирающиеся на одну хорду вписанные углы тождественны или их сумма равняется 180^ <circ>.
angle ADB + angle AKB = 180^
angle ADB = angle AEB = angle AFB
На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.
Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.
angle DMC = angle ADM + angle DAM = frac<1> <2>left ( cup DmC + cup AlB
ight )
Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.
angle M = angle CBD — angle ACB = frac<1> <2>left ( cup DmC — cup AlB
ight )
Вписанная окружность
Вписанная окружность — это окружность, касающаяся сторон многоугольника.
В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.
Окружность может быть вписанной не в каждый многоугольник.
Площадь многоугольника с вписанной окружностью находится по формуле:
p — полупериметр многоугольника,
r — радиус вписанной окружности.
Отсюда следует, что радиус вписанной окружности равен:
Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.
В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.
Радиус вписанной окружности вычисляется по формуле:
Описанная окружность
Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника.
В точке пересечения серединных перпендикуляров сторон этой фигуры будет находиться центр описанной окружности.
Радиус можно найти, вычислив его как радиус окружности, которая описана около треугольника, определенного любыми 3 -мя вершинами многоугольника.
Есть следующее условие: окружность возможно описать около четырехугольника только, если сумма его противоположных углов равна 180^ < circ>.
angle A + angle C = angle B + angle D = 180^
Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.
Радиус описанной окружности можно вычислить по формулам:
a , b , c — длины сторон треугольника,
S — площадь треугольника.
Теорема Птолемея
Под конец, рассмотрим теорему Птолемея.
Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.
Диаграмма, показывающая расстояние по большому кругу (нарисовано красным) между двумя точками на сфере, P и Q. Две противоположные точки также показаны точки u и v.
расстояние по большому кругу, ортодромное расстояние или сферическое расстояние — это кратчайшее расстояние между двумя точками на поверхности сферы, измеренных по поверхности сферы (в отличие от прямой линии, проходящей через внутреннюю часть сферы). Расстояние между двумя точками в евклидовом пространстве — это длина прямой линии между ними, но на сфере прямых линий нет. В пространствах с кривизной прямые линии заменяются на геодезические. Геодезические на сфере — это круги на сфере, центры которых совпадают с центром сферы, и называются большими кругами.
. Определение расстояния большого круга является частью более общей проблемы большой окружности. -круговая навигация, которая также вычисляет азимуты в конечных точках и промежуточных точках пути.
Через любые две точки на сфере, которые не находятся прямо напротив друг друга, проходит уникальный большой круг. Две точки разделяют большой круг на две дуги. Длина более короткой дуги — это расстояние по большому кругу между точками. Большой круг с таким расстоянием называется римановой окружностью в римановой геометрии.
. Между двумя точками, которые находятся прямо напротив друг друга, называемыми антиподальными точками, находятся бесконечно много больших окружностей, и все дуги большого круга между противоположными точками имеют длину, равную половине окружности окружности, или π r { displaystyle pi r}
, где r — радиус сферы.
Земля почти сферическая (см. Радиус Земли ), поэтому формулы расстояния по дуге большого круга дают расстояние между точками на поверхности Земли с точностью до 0,5%. (См. Длина дуги § Дуги больших кругов на Земле.)
Содержание
- 1 Формулы
- 1.1 Вычислительные формулы
- 1.2 Векторная версия
- 1.3 От длины хорды
- 2 Радиус сферической Земли
- 3 См. Также
- 4 Ссылки и примечания
- 5 Внешние ссылки
Формулы
Иллюстрация центрального угла Δσ между двумя точками P и Q. λ и φ — продольный и широтный углы P соответственно.
Пусть λ 1, ϕ 1 { displaystyle lambda _ {1}, phi _ {1}}
и λ 2, ϕ 2 { displaystyle lambda _ {2}, phi _ {2}}
— географическая долгота и широта в радианах, равных двум. точки 1 и 2, а Δ λ, Δ ϕ { displaystyle Delta lambda, Delta phi}
— их абсолютные разности; тогда Δ σ { displaystyle Delta sigma}
, центральный угол между ними, задается сферическим законом косинусов, если один из полюса используется как вспомогательная третья точка на сфере:
- Δ σ = arccos (sin ϕ 1 sin ϕ 2 + cos ϕ 1 cos ϕ 2 cos (Δ λ)). { Displaystyle Delta sigma = arccos { bigl (} sin phi _ {1} sin phi _ {2} + cos phi _ {1} cos phi _ {2} cos ( Delta lambda) { bigr)}.}
Проблема обычно выражается в терминах определения центрального угла Δ σ { displaystyle Delta sigma}. Учитывая этот угол в радианах, фактическая длина дуги d на сфере радиуса r может быть тривиально вычислена как
- d = r Δ σ. { displaystyle d = r , Delta sigma.}
Вычислительные формулы
В компьютерных системах с низкой точностью с плавающей запятой формула сферического закона косинусов может иметь большие ошибки округления, если расстояние небольшое (если две точки находятся на расстоянии километра друг от друга на поверхности Земли, косинус центрального угла составляет около 0,99999999). Для современных 64-битных чисел с плавающей запятой формула сферического закона косинусов, приведенная выше, не имеет серьезных ошибок округления для расстояний, превышающих несколько метров на поверхности Земли. Формула гаверсинуса является численно лучше обусловленной для малых расстояний:
- Δ σ = archav (hav (Δ ϕ) + cos ϕ 1 cos ϕ 2 hav (Δ λ)) Δ σ = 2 arcsin sin 2 (Δ ϕ 2) + cos ϕ 1 cos ϕ 2 sin 2 (Δ λ 2). { displaystyle { begin {align} Delta sigma = operatorname {archav} left ( operatorname {hav} left ( Delta phi right) + cos phi _ {1} cos phi _ {2} operatorname {hav} left ( Delta lambda right) right) \\ Delta sigma = 2 arcsin { sqrt { sin ^ {2} left ({ frac { Delta phi} {2}} right) + cos { phi _ {1}} cos { phi _ {2}} sin ^ {2} left ({ frac { Дельта лямбда} {2}} right)}}. \ end {align}}}
Исторически использование этой формулы упрощалось доступностью таблиц для функции haversine : hav (θ) = sin (θ / 2).
Хотя эта формула верна для большинства расстояний на сфере, она также страдает от ошибок округления для особого (и несколько необычного) случая точек противоположных точек (на противоположных концах сферы). Формула, которая является точной для всех расстояний, представляет собой следующий частный случай формулы Винсенти для эллипсоида с равной большой и малой осями:
- Δ σ = arctan (cos ϕ 2 sin (Δ λ)) 2 + (cos ϕ 1 sin ϕ 2 — sin ϕ 1 cos ϕ 2 cos (Δ λ)) 2 sin ϕ 1 sin ϕ 2 + cos ϕ 1 cos ϕ 2 cos (Δ λ). { displaystyle Delta sigma = arctan { frac { sqrt { left ( cos phi _ {2} sin ( Delta lambda) right) ^ {2} + left ( cos phi _ {1} sin phi _ {2} — sin phi _ {1} cos phi _ {2} cos ( Delta lambda) right) ^ {2}}} { sin phi _ {1} sin phi _ {2} + cos phi _ {1} cos phi _ {2} cos ( Delta lambda)}}.}
Векторная версия
Другое представление аналогичных формул, но с использованием нормальных векторов вместо широты и долготы для описания позиций, находится с помощью трехмерной векторной алгебры с использованием скалярное произведение, кросс-произведение или комбинация:
- Δ σ = arccos (n 1 ⋅ n 2) = arcsin | n 1 × n 2 | = arctan | n 1 × n 2 | n 1 ⋅ N 2 { displaystyle { begin {align} Delta sigma = arccos left ( mathbf {n} _ {1} cdot mathbf {n} _ {2} right) \ = arcsin left | mathbf {n} _ {1} times mathbf {n} _ {2} right | \ = arctan { frac { left | mathbf {n} _ { 1} times mathbf {n} _ {2} right |} { mathbf {n} _ {1} cdot mathbf {n} _ {2}}} \ конец {выровнено}}}
где n 1 { displaystyle mathbf {n} _ {1}}
и n 2 { displaystyle mathbf {n} _ {2}}
— нормали к эллипсоиду в двух положениях 1 и 2. Подобно приведенным выше уравнениям, основанным на широте и долготе, выражение, основанное на arctan, является единственным, которое хорошо обусловлено для всех углов. Выражение на основе arctan требует величины перекрестного произведения на скалярное произведение.
По длине хорды
Линия, проходящая через трехмерное пространство между интересующими точками на сферической Земле, является хордой большого круга между точками. Центральный угол между двумя точками можно определить по длине хорды. Расстояние большого круга пропорционально центральному углу.
Длина хорды большого круга, C h { displaystyle C_ {h} , !}
, может быть вычислена следующим образом для соответствующей единичной сферы с помощью Декартово вычитание :
- Δ X = cos ϕ 2 cos λ 2 — cos ϕ 1 cos λ 1; Δ Y = cos ϕ 2 sin λ 2 — cos ϕ 1 sin λ 1; Δ Z = sin ϕ 2 — sin ϕ 1; С знак равно (Δ Икс) 2 + (Δ Y) 2 + (Δ Z) 2 { displaystyle { begin {align} Delta {X} = cos phi _ {2} cos lambda _ {2 } — cos phi _ {1} cos lambda _ {1}; \ Delta {Y} = cos phi _ {2} sin lambda _ {2} — cos phi _ {1} sin lambda _ {1}; \ Delta {Z} = sin phi _ {2} — sin phi _ {1}; \ C = { sqrt {( Delta {X}) ^ {2} + ( Delta {Y}) ^ {2} + ( Delta {Z}) ^ {2}}} end {align}}}
Центральный угол:
- Δ σ = 2 arcsin C 2. { displaystyle Delta sigma = 2 arcsin { frac {C} {2}}.}
Радиус сферической Земли
Экваториальный (a), полярный (b) и средний радиус Земли, как определено в 1984 Мировая геодезическая система, редакция. (Не в масштабе.)
Форма Земли очень напоминает сплюснутую сферу (сфероид ) с экваториальным радиусом a { displaystyle a}
из 6378,137 км; расстояние b { displaystyle b}
от центра сфероида до каждого полюса составляет 6356,7523142 км. При вычислении длины короткой линии север-юг на экваторе круг, который наилучшим образом соответствует этой линии, имеет радиус b 2 / a { displaystyle b ^ {2} / a}
(что соответствует меридиану semi-latus rectum ), или 6335,439 км, в то время как сфероид на полюсах лучше всего аппроксимируется сферой радиуса a 2 / b { displaystyle a ^ {2} / b}
, или 6399,594 км, разница в 1%. Пока предполагается сферическая Земля, любая формула для расстояния на Земле гарантированно верна только в пределах 0,5% (хотя возможна более высокая точность, если формула предназначена только для применения к ограниченной области). Используя средний радиус Земли, R 1 = 1 3 (2 a + b) ≈ 6371,009 км { displaystyle R_ {1} = { frac {1} {3}} (2a + б) приблизительно 6371.009 , mathrm {km}}
(для эллипсоида WGS84 ) означает, что в пределе небольшого уплощения средняя квадратичная относительная погрешность в оценках расстояния сведено к минимуму.
См. также
- Аэронавигация
- Изоазимутал
- Центральный угол
- Кругосветное плавание
- Планирование полета
- Геодезия
- Геодезия на эллипсоиде
- Геодезическая система
- Географическое расстояние
- Навигация по большому кругу
- Формула Хаверсина
- Дуга меридиана
- Линия Румба
- Сферическая Земля
- Сферическая геометрия
- Сферическая тригонометрия
Ссылки и примечания
Внешние ссылки
- GreatCircle на MathWorld
Если есть под рукой карта Google, то расстояние между двумя точками с заданными координатами можно определить с помощью инструмента Линейка.
Если этот инструмент не включен, его необходимо включить в Лаборатории карт (в левом нижнем углу).
Координаты можно нанести на карту либо через окно Поиск, либо через задание Маршрута.
Кратчайшим расстоянием между двумя точками на сфере является длина дуги большого круга (круга, проходящего через эти две точки и центр сферы). Эта дуга называется ортодромией (имеется в виду наименьшая из двух дуг большого круга).
Кратчайшее расстояние или длина ортодромии определяется формулой:
L = R x Y
где R – радиус сферы,
Y – центральный угол в радианах.
или
L = пR x A/180 град.
где A — центральный угол в градусах (п — «пи»).
Пусть x1, y1 и x2, y2 — широта и долгота двух точек. Тогда центральный угол будет определяться сферическим законом косинусов:
Y = arccos(sin x1 sin x2 + cos x1 cos x2 cos (y2 — y1))
Следует заметить, что при вычислениях с невысокой точностью (а тем более на калькуляторе) по этой формуле особенно при небольших расстояниях между точками, точность результата будет весьма невысока, поскольку центральный угол будет 0,99999999. (На 64-разрядных компьютерах точность может достигать нескольких метров на километр.)
Поэтому для практических целей применялись другие формулы с использованием синус-верзусов (обращенных синусов), которые сыграли важную роль в навигации.
В следующей формуле использован haversine (haversin, гаверсинус) — квадрат синуса половинного угла.
где переменные: кратчайшее расстояние, радиус сферы, широта и долгота точек соответственно.
Формула гаверсинусов хорошо работает при сравнительно небольших расстояниях, но имеет проблему для антиподов. Формула через арктангенс устраняет эту проблему. Центральный угол равен:
Для расчета расстояния между двумя точками по GPS-координатам можно написать несложную программу. Вот тут можно «поиграть» с программкой на JavaScript.
Для координат, приведенных в вопросе: L = 751 м. (эта цифра неплохо сходится с результатом, полученным Линейкой в картах Google).
Скрипты: JavaScript, Python