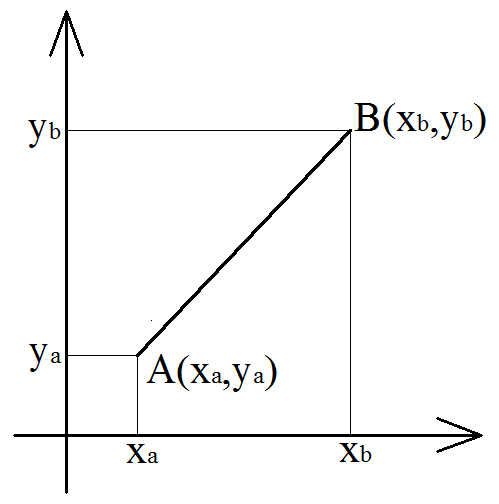Онлайн калькулятор. Длина отрезка. Расстояние между точками.
Предлагаю вам воспользоваться онлайн калькулятором для вычисления расстояния между точками.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление расстояния между точками и закрепить пройденный материал.
Калькулятор для вычисления расстояния между двумя точками
Выберите необходимую вам размерность:
Размерность:
Введите координаты точек.
Вводить можно числа или дроби (-2.4, 5/7, …). Более подробно читайте в правилах ввода чисел.
Формула вычисления расстояния между двумя точками A(xa; ya) и B(xb; yb) на плоскости:
Формула вычисления расстояния между двумя точками A(xa; ya; za) и B(xb; yb; zb) в пространстве:
Вывод формулы для вычисления расстояния между двумя точками на плоскости
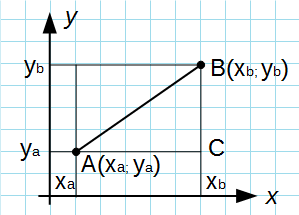
Из точек A и B опустим перпендикуляры на оси координат x и y.
Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:
AC = xb — xa;
BC = yb — ya.
Спомощью теоремы Пифагора, вычислим длину отрезка AB:
Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.
Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично.
Онлайн калькуляторы
Calculatorium.ru — это бесплатные онлайн калькуляторы для самых разнообразных целей: математические калькуляторы,
калькуляторы даты и времени, здоровья, финансов. Инструменты для работы с текстом. Конвертеры. Удобное решение различных задач — в учебе, работе, быту.
Актуальная информация
Помимо онлайн калькуляторов, сайт также предоставляет актуальную информацию по курсам валют и
криптовалют, заторах на дорогах, праздниках и значимых событиях, случившихся в этот день.
Информация из официальных источников, постоянное обновление.
На этой странице находится все необходимое, чтобы найти расстояние между двумя точками. Просто введите координаты точек и получите ответ и подробное решение с помощью наших онлайн-калькуляторов. Кроме того на сайте можно найти координаты середины отрезка.
Расстояние между двумя точками — это длина отрезка, соединяющего эти точки.
Формула расстояния между двумя точками на плоскости:
d=sqrt{{(x_b — x_a)}^2 + {(y_b — y_a)^2}}
xa и ya — координаты первой точки A,
xb и yb — координаты второй точки B
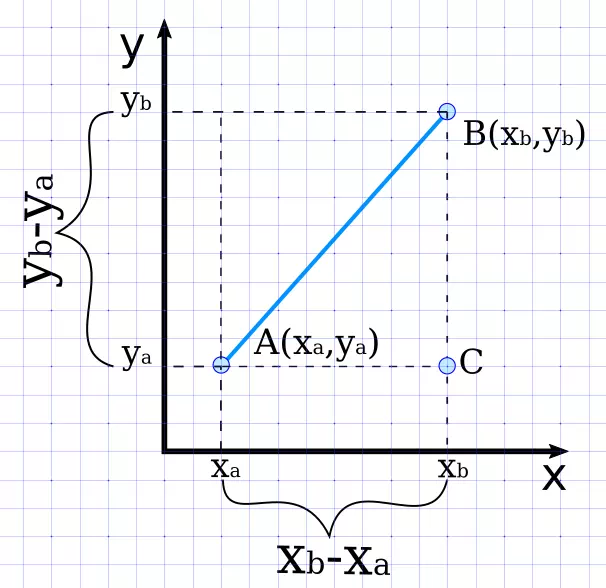
Нахождение расстояния между двумя точками на плоскости сводится к решению треугольника, а точнее — нахождению его гипотенузы. Для этого используется теорема Пифагора. Посмотрите на рисунок.
Соединив отрезком точки A и B, а также опустив перпендикуляры на оси мы получим треугольник ABC. В этом треугольнике стороны AC и BC являются катетами прямоугольного треугольника, а AB — его гипотенузой. Длины катетов AC и BC найти довольно просто:
AC = xb — xa
BC = yb — ya
Осталось применить теорему Пифагора и получить сторону AB, которая является гипотенузой прямоугольного треугольника и расстоянием между точками A и B:
AB=sqrt{{AC}^2 + {BC^2}}
Подставив вместо отрезков AC и BC их длины, получим итоговую формулу расстояния между двумя точками:
AB=sqrt{{(x_b — x_a)}^2 + {(y_b — y_a)^2}} или d=sqrt{{(x_b — x_a)}^2 + {(y_b — y_a)^2}}
Формула расстояния между двумя точками в пространстве:
{d=sqrt{{(x_b — x_a)}^2 + {(y_b — y_a)^2} + {(z_b — z_a)^2}}}
xa, ya и za — координаты первой точки A,
xb, yb и zb — координаты второй точки B
Примеры задач на вычисление середины отрезка
Задача 1
Найдите расстояние между точками А и В, если А(2; 7), В(-2; 7).
Решение
Подставим координаты точек в формулу расстояния между двумя точками на плоскости и вычислим результат:
d=sqrt{{(x_b — x_a)}^2 + {(y_b — y_a)^2}} = sqrt{{(-2 — 2)}^2 + {(7 — 7)^2}} = sqrt{{-4}^2 + {0^2}} = sqrt{16 + 0} = sqrt{16} = 4
Мы получили расстояние между точками и оно равно 4.
Ответ: 4.
Проверим результат с помощью калькулятора .
Расстояние между двумя точками на плоскости онлайн
Калькулятор рассчитывает расстояние между двумя точками на плоскости по координатам. В поля можно вводить целые или десятичные числа.
Введите координаты точки A
Введите координаты точки B
Определение длины отрезка
Длина отрезка это положительное число, показывающее, сколько раз единичный отрезок и его части укладываются в данном отрезке.
Формула расчёта растояния между двумя точками на плоскости
A(xa, ya), B(xb, yb) — координаты концов отрезка
Примеры задач
Найти длину отрезка с концами в точках A(1, 5) и B(2, 9)
Вычислить расстояние между двумя точками с координатами A(1, 6) и B(1, 25)
Вычислить расстояние между двумя точками с координатами A(5, 2) и B(3, 2).
Вычислить расстояние между двумя точками с координатами A(2, 1) и B(-1, 4).
Вычислить расстояние между двумя точками с координатами A(-6, -2) и B(1, -5).
Вычислить расстояние между двумя точками с координатами A(1, -6) и B(-2, 1).
Вычислить расстояние между двумя точками с координатами A(-7, 5) и B(5, -6).
Похожие калькуляторы