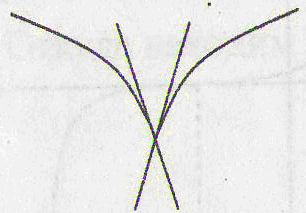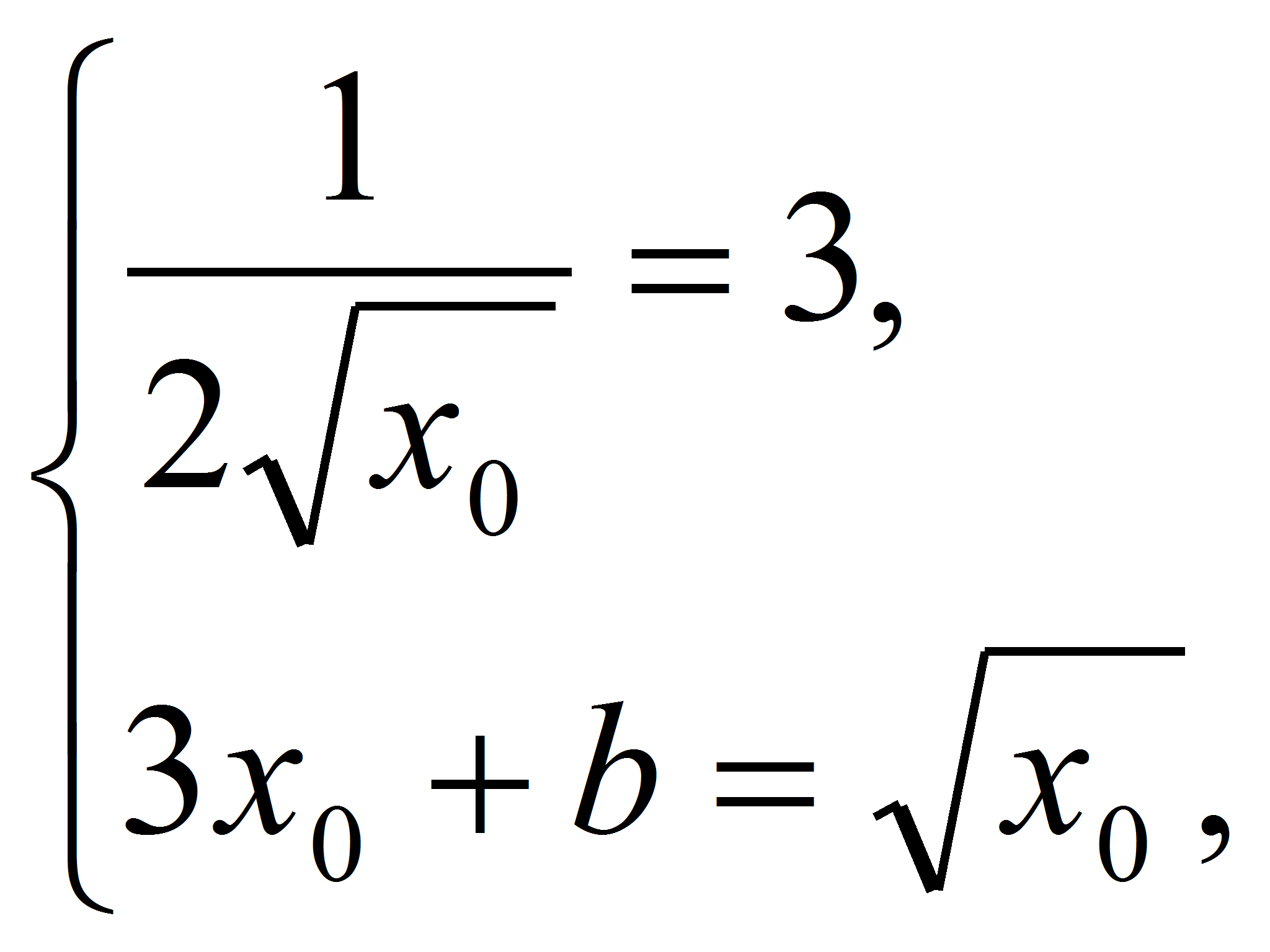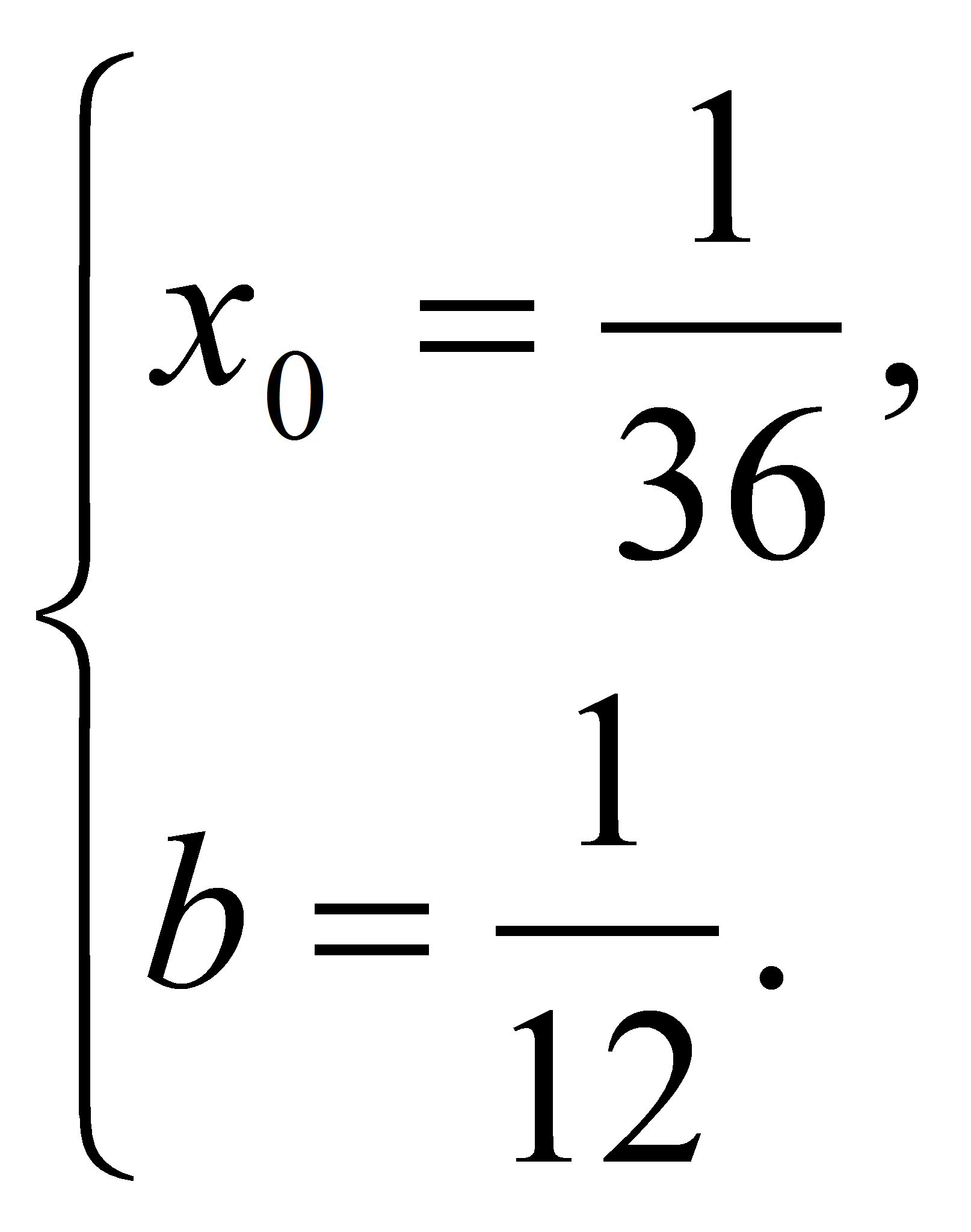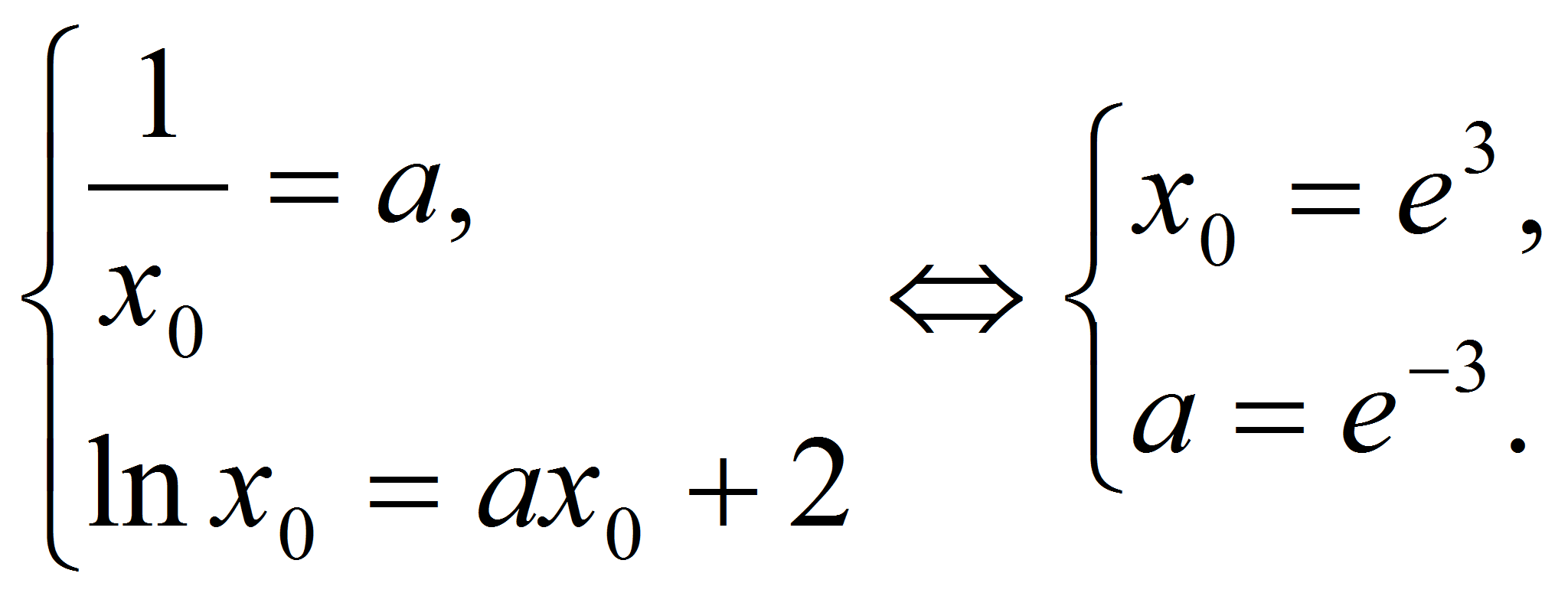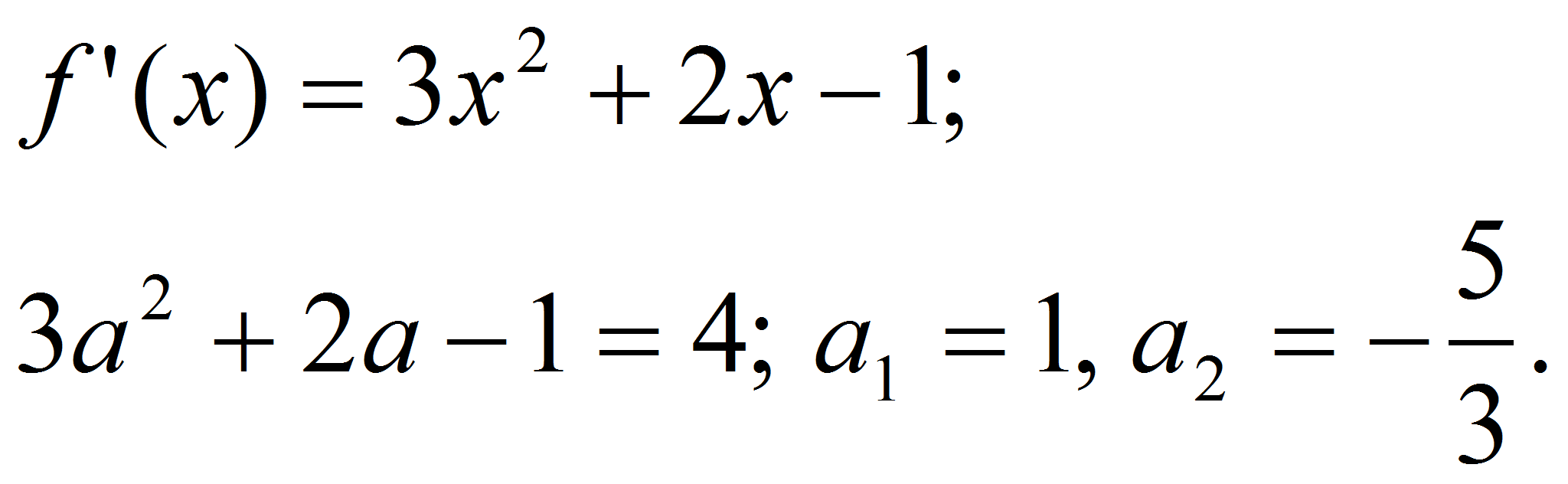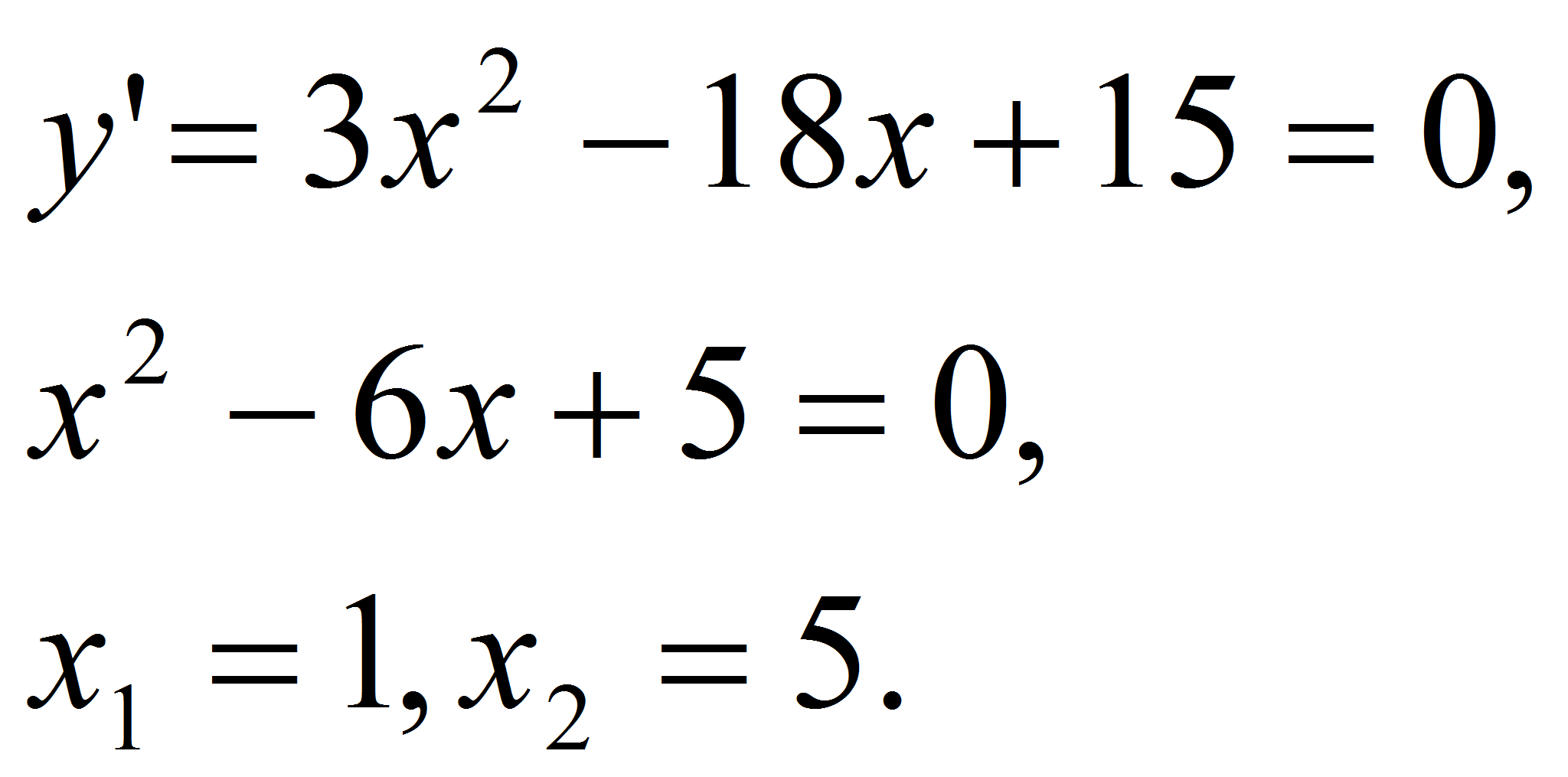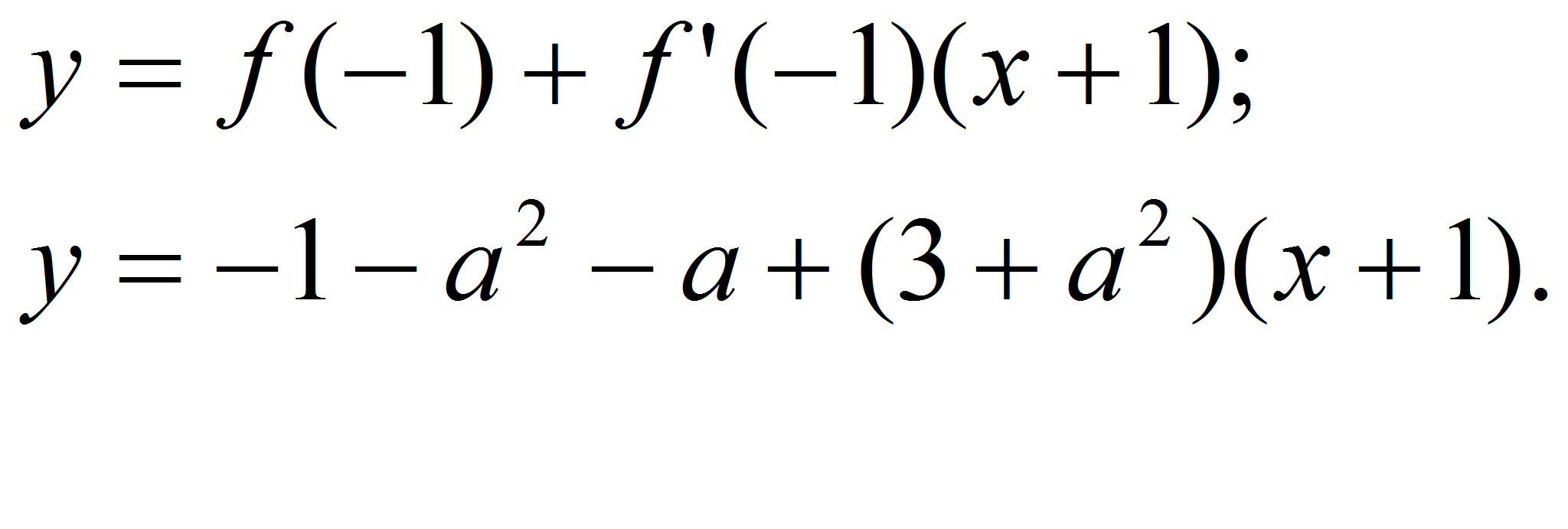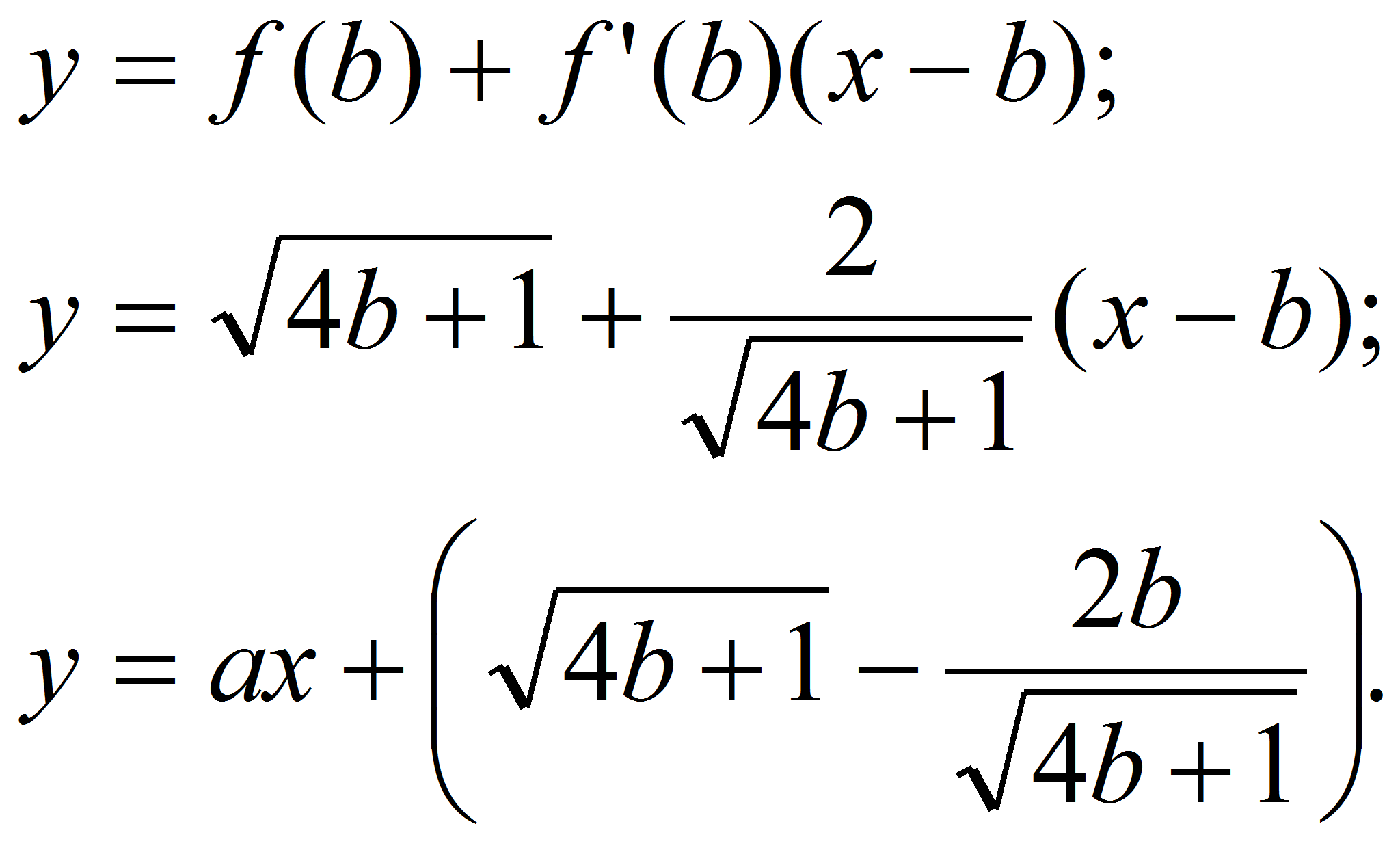Как найти расстояние между точками общей касательной

Расстояние между точками касания окружности

Касание окружностей

Говорят, что две окружности касаются, если они имеют единственную общую точку. Эта точка называется точкой касания окружностей. Касание окружностей бывает внутренним и внешним.

Внутреннее касание

Касание называется внутренним, если центры окружностей лежат по одну сторону от точки касания окружностей. Построим две окружности, первая с центром A и радиусом AC, отметим на радиусе AC точку B, это будет центр второй окружности с радиусом BC:

Построенные окружности имеют только одну общую точку C. Говорят, что они касаются внутренним образом.

При внутреннем касании двух окружностей, расстояние между их центрами равно разности их радиусов.

Внешнее касание

Касание называется внешним, если центры окружностей лежат по разные стороны от точки касания. Построим две окружности, первая с центром A и радиусом AC, вторая с центром B и радиусом BC:

Построенные окружности имеют только одну общую точку C. Говорят, что они касаются внешним образом.

При внешнем касании двух окружностей, расстояние между их центрами равно сумме их радиусов.

Две окружности на плоскости.
Общие касательные к двум окружностям

Взаимное расположение двух окружностей

Фигура Рисунок Свойства
Две окружности на плоскости

Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей

Каждая из окружностей лежит вне другой

Расстояние между центрами окружностей больше суммы их радиусов

Внешнее касание двух окружностей

Расстояние между центрами окружностей равно сумме их радиусов

Внутреннее касание двух окружностей

Расстояние между центрами окружностей равно разности их радиусов

Окружности пересекаются в двух точках

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов

r1 – r2 лежит внутри другой

Расстояние между центрами окружностей меньше разности их радиусов

d r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей

Каждая из окружностей лежит вне другой

Расстояние между центрами окружностей больше суммы их радиусов

Внешнее касание двух окружностей

Расстояние между центрами окружностей равно сумме их радиусов

Внутреннее касание двух окружностей

Расстояние между центрами окружностей равно разности их радиусов

Окружности пересекаются в двух точках

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов

r1 – r2 лежит внутри другой

Расстояние между центрами окружностей меньше разности их радиусов

d r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей

Каждая из окружностей лежит вне другой

Расстояние между центрами окружностей больше суммы их радиусов

Внешнее касание двух окружностей

Расстояние между центрами окружностей равно сумме их радиусов

Внутреннее касание двух окружностей

Расстояние между центрами окружностей равно разности их радиусов

Окружности пересекаются в двух точках

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов

r1 – r2 лежит внутри другой

Расстояние между центрами окружностей меньше разности их радиусов

d внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Внутренняя касательная к двум окружностям

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Внутреннее касание двух окружностей

Существует единственная общая внешняя касательная. Других общих касательных нет.

Окружности пересекаются в двух точках

Существуют две общих внешних касательных. Других общих касательных нет.

Внешнее касание двух окружностей

Существует единственная общая внутренняя касательная, а также
две общих внешних касательных. Других общих касательных нет.

Каждая из окружностей лежит вне другой

Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.

Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

Внешняя касательная к двум окружностям
Внутренняя касательная к двум окружностям
Внутреннее касание двух окружностей
Окружности пересекаются в двух точках
Внешнее касание двух окружностей
Каждая из окружностей лежит вне другой

Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.

Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

Формулы для длин общих касательных и общей хорды двух окружностей

Внешняя касательная к двум окружностям
Внутренняя касательная к двум окружностям
Внутреннее касание двух окружностей
Окружности пересекаются в двух точках
Внешнее касание двух окружностей
Каждая из окружностей лежит вне другой
Фигура Рисунок Формула
Внешняя касательная к двум окружностям

Длина общей внешней касательной к двум окружностям вычисляется по формуле

Внутренняя касательная к двум окружностям

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Общая хорда двух пересекающихся окружностей

Длина общей хорды двух окружностей вычисляется по формуле

Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Длина общей хорды двух окружностей вычисляется по формуле

Внешняя касательная к двум окружностям
Внутренняя касательная к двум окружностям
Общая хорда двух пересекающихся окружностей

Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Внешняя касательная к двум окружностям
Внутренняя касательная к двум окружностям
Общая хорда двух пересекающихся окружностей

Длина общей хорды двух окружностей вычисляется по формуле

Доказательства формул для длин общих касательных и общей хорды двух окружностей

Утверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле

что и требовалось доказать.

Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле

что и требовалось доказать.

Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле

Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3,

Окружность. Относительное взаимоположение окружностей.

Если две окружности имеют только одну общую точку, то говорят, что они касаются.

Если же две окружности имеют две общие точки, то говорят, что они пересекаются.

Трех общих точек две не сливающиеся окружности иметь не могут, потому, что в противном случае через три точки можно было бы провести две различные окружности, что невозможно.

Будем называть линией центров прямую, проходящую через центры двух окружностей (например, прямую OO1).

Теорема.

Если две окружности имеют общую точку по одну сторону от линии центров, то они имеют общую точку и по другую сторону от этой линии, т.е. такие окружности пересекаются.

Пусть окружности O и O1 имеют общую точку A, лежащую вне линии центров OO1. Требуется доказать, что эти окружности имеют еще общую точку по другую сторону от прямой OO1.

Опустим из A на прямую OO1 перпендикуляр AB и продолжим его на расстояние BA1, равное AB. Докажем теперь, что точка A1 принадлежит обеим окружностям. Из построения видно, что точки O и O1 лежат на перпендикуляре, проведенном к отрезку AA1 через его середину. Из этого следует, что точка O одинаково удалена от A и A1. То же можно сказать и о точке O1. Значит обе окружности, при продолжении их, пройдут через A1.Таким образом, окружности имеют две общие точки : A (по условию) и A1 (по доказанному). Следовательно, они пересекаются.

Следствие.

Общая хорда (AA1) двух пересекающихся окружностей перпендикулярна к линии центров и делится ею пополам.

Теоремы.

1. Если две окружности имеют общую точку на линии их центров или на ее продолжении, то они касаются.

2. Обратно: если две окружности касаются, то общая их точка лежит на линии центров или на ее продолжении.

Признаки различных случаев относительного положения окружностей.

Пусть имеем две окружности с центрами O и O1, радиусами R и R1 и расстоянием между центрами d.

Эти окружности могут находиться в следующих 5-ти относительных положениях:

1. Окружности лежат одна вне другой, не касаясь. В этом случае, очевидно, d > R + R1 .

2. Окружности имеют внешнее касание. Тогда d = R + R1, так как точка касания лежит на линии центров O O1.

3. Окружности пересекаются. Тогда d R + R1, потому что в треугольнике OAO1 сторона OO1 меньше суммы, но больше разности двух других сторон.

4. Окружности имеют внутреннее касание. В этом случае в d = R — R1, потому что точка касания лежит на продолжении линии OO1.

5. Одна окружность лежит внутри другой, не касаясь. Тогда, очевидно,

d R + R1, то окружности расположены одна вне другой, не касаясь.

2. Если d = R + R1, то окружности касаются извне.

3. Если d R — R1, то окружности пересекаются.

4. Если d = R — R1, то окружности касаются изнутри.

5. Если d R Е R1. Значит, все эти случаи исключаются. Остается один возможный, именно тот, который требовалось доказать. Таким образом, перечисленные признаки различных случаев относительно положения двух окружностей не только необходимы, но и достаточны.

Please wait.

We are checking your browser. mathvox.ru

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6d2af6a44c1f00b0 • Your IP : 85.95.179.65 • Performance & security by Cloudflare

Окружность. Относительное взаимоположение окружностей.

Если две окружности имеют только одну общую точку, то говорят, что они касаются.

Если же две окружности имеют две общие точки, то говорят, что они пересекаются.

Трех общих точек две не сливающиеся окружности иметь не могут, потому, что в противном случае через три точки можно было бы провести две различные окружности, что невозможно.

Будем называть линией центров прямую, проходящую через центры двух окружностей (например, прямую OO1).

Теорема.

Если две окружности имеют общую точку по одну сторону от линии центров, то они имеют общую точку и по другую сторону от этой линии, т.е. такие окружности пересекаются.

Пусть окружности O и O1 имеют общую точку A, лежащую вне линии центров OO1. Требуется доказать, что эти окружности имеют еще общую точку по другую сторону от прямой OO1.

Опустим из A на прямую OO1 перпендикуляр AB и продолжим его на расстояние BA1, равное AB. Докажем теперь, что точка A1 принадлежит обеим окружностям. Из построения видно, что точки O и O1 лежат на перпендикуляре, проведенном к отрезку AA1 через его середину. Из этого следует, что точка O одинаково удалена от A и A1. То же можно сказать и о точке O1. Значит обе окружности, при продолжении их, пройдут через A1.Таким образом, окружности имеют две общие точки : A (по условию) и A1 (по доказанному). Следовательно, они пересекаются.

Следствие.

Общая хорда (AA1) двух пересекающихся окружностей перпендикулярна к линии центров и делится ею пополам.

Теоремы.

1. Если две окружности имеют общую точку на линии их центров или на ее продолжении, то они касаются.

2. Обратно: если две окружности касаются, то общая их точка лежит на линии центров или на ее продолжении.

Признаки различных случаев относительного положения окружностей.

Пусть имеем две окружности с центрами O и O1, радиусами R и R1 и расстоянием между центрами d.

Эти окружности могут находиться в следующих 5-ти относительных положениях:

1. Окружности лежат одна вне другой, не касаясь. В этом случае, очевидно, d > R + R1 .

2. Окружности имеют внешнее касание. Тогда d = R + R1, так как точка касания лежит на линии центров O O1.

3. Окружности пересекаются. Тогда d R + R1, потому что в треугольнике OAO1 сторона OO1 меньше суммы, но больше разности двух других сторон.

4. Окружности имеют внутреннее касание. В этом случае в d = R — R1, потому что точка касания лежит на продолжении линии OO1.

5. Одна окружность лежит внутри другой, не касаясь. Тогда, очевидно,

d R + R1, то окружности расположены одна вне другой, не касаясь.

2. Если d = R + R1, то окружности касаются извне.

3. Если d R — R1, то окружности пересекаются.

4. Если d = R — R1, то окружности касаются изнутри.

5. Если d R Е R1. Значит, все эти случаи исключаются. Остается один возможный, именно тот, который требовалось доказать. Таким образом, перечисленные признаки различных случаев относительно положения двух окружностей не только необходимы, но и достаточны.

источники:

http://mathvox.ru/geometria/treugolniki/glava-13/tochki-kasaniya-vpisannoi-okrujnosti-svoistvo-2/

http://www.calc.ru/Otnositelnoye-Vzaimopolozheniye-Okruzhnostey.html
Источник

Пятый тип задач на касательную — уравнение общей касательной нескольких кривых

Говорят, что прямая
y=kx
+ b
является общей касательной графиков
функций y=f1(x)
и y=f2(x),
если она касается как одного, так и
другого графиков, но не обязательно в
одной и той же точке.

Правило.

Функции y=f1(x)
и y=f2(x)
имеют в точке пересечения M(x0;y0)
общую невертикальную касательную, если

f1’(x0)
= f2’(x0)

ЗАДАЧА. Докажите,
что параболы y1=3x²-5x-2
и y2=2x²-x-6
имеют в их общей точке общую касательную.
Найти уравнение этой общей касательной.

  1. Найдем точку
    пересечения парабол

3x²-5x-2
= 2x²-x-6

x²-4x+4
= 0

(x-2)²
= 0

x
= 2

y(2)=
2·4-2-6=0 y(2)=3·4-5·2-2=0

значит, у парабол
одна точка пересечения (2;0)

  1. Теперь перейдем
    к составлению уравнений касательных

y(1)=6x
-5 y(1)(2)
= 12-5=7

y(2)=4x-1
y(2)(2)
= 8-1=7

Получим уравнение
касательной

y=0+7(x-2)

y=7x-14

Ответ: y=7x-14

ЗАДАЧА. Найти
уравнение всех общих касательных к
графикам функции y=x²+1
и y=4x²-2

  1. Составим уравнение
    касательной в точке x0
    = a
    к графику

y=x²+1

y(a)=a²+1

y’=2x

y’(a)=2a

Получим уравнение
касательной

y=a²+1+2a(x-a)

y=a²+1+2ax-2a²

y=2ax-a²+1

  1. Составим уравнение
    касательной в точке с абсциссой x0=b
    к графику y=4x²-2

y(b)=4b²-2

y’=8x

y’(b)=8b

Получим уравнение
касательной

y=4b²-2+8b(x-b)

y= 4b²-2+8bx-8b²

y=8bx-4b²-2

  1. Уравнения прямых
    совпадают, если угловые коэффициенты
    и свободные члены равны, т.е.

Подставим a=4b
во второе уравнение, получим

-16b2
 +1 = -4b2
-2

12b2
 = 3

b2
=




Получим уравнения
касательных

y=4x-3 y=-4x-3

Ответ: y=4x-3 y=-4x-3

Шестой тип задач на касательную – расстояние между кривыми.

Пусть дана функция
y
= f(x)
и прямая y
= kx
+b,
тогда можно составить уравнение
касательной, параллельной данной прямой.
Проведенная касательная разделит
плоскость на две части: в одной из них
будет находиться заданная прямая, а в
другой график функции y
= f(x).

Кратчайшее
расстояние между кривой y
= f(x)
и прямой y
= kx
+b
можно посчитать по формуле :


=

Задача. Найти
кратчайшее расстояние между параболой
y
= x2
и прямой y
=

  1. Убедимся,
    что графики не имеют общих точек, для
    этого решим уравнение:

x2
=
,

3x2
– 4x
+6 = 0,

D
= 16-72< 0.

Нет корней, нет
общих точек.

  1. Найдем
    точку, в которой касательная параллельна
    прямой y
    =

y = x2,

y’
= 2x,

2x =
,

x=
,

x0
=
,

y0
=
.

  1. Получим касательную
    y
    =

y
=

Прямая y
=

и парабола y
= x2
лежат по разные стороны от касательной
y
=
,
тогда расстояние от прямой y
=

до параболы y
= x2,
это расстояние от точки M
(x0;y0),
лежащей на параболе, до прямой y
=
,
находим его по формуле


=


=
.

Ответ:

Задача. Найти
расстояние между касательными к графику
функции
,
образующими с положительным направлением
оси Ох угол 450.

  1. y’
    =

    =

  2. y0’
    = tg 450



  3. = 1


x= 3 x= 1

x0=
3 x0=
1

  1. Составим
    уравнение касательной в точке x0=
    3

  2. y(3)
    = 0

y = 0 +
1
(x-3)

y = x-3

  1. Составим уравнение
    касательной в точке x0=
    1

  2. y(1)
    = 2

y = 2 +
1
(x-3)

y = x+1

  1. Пусть
    y
    = x
    +1 – данная прямая,



— данная кривая,

y
= x-3
— данная касательная,


=

Ответ :

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Чтобы
правильно и рационально решать задачи, связанные
с уравнением касательной, нужно четко понимать, что такое
касательная, владеть техникой составления
уравнения касательной к графику функции и
представлять себе, для решения каких задач (в том
числе и задач с параметрами) можно использовать метод касательной.

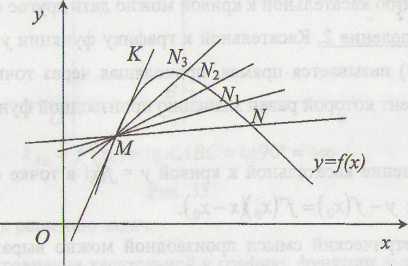
Опр.
1. Касательной к графику функции у
= f(x)
называется
предельное положение секущей MN
при

(рис. 1).

Рис. 1

Касательная к кривой может
иметь с ней несколько общих точек или пересекать ее. Можно дать и
другое определение касательной к кривой.

Опр.
2. Касательной к графику функции у
= f(x) в
точке A0(x0;
f(x0))
называется
прямая, проходящая через точку A0,
угловой
коэффициент которой
равен значению производной функции у
=f(x)
в точке
с абсциссой x0.

Уравнение
касательной
к кривой у =
f(x)
в точке с
абсциссой х0
имеет вид:
.

Между
понятием касательной и понятие производной имеется тесная
связь. Геометрический
смысл производной можно выразить так: если функция
у = f(x)
в точке
х0
имеет
производную, то в точке с этой абсциссой определена касательная к
графику функции
,
причем ее
угловой коэффициент
равен
.
Вывод: если в точке х0
есть производная
функции
,
то в точке с
этой абсциссой есть касательная к графику
функции

и наоборот; если
в точке х0
нет производной
функции
,
то в точке с
этой абсциссой нет касательной к графику функции

и наоборот.

Укажем
случаи, когда
функция не имеет в точке касательной, и, следовательно, не
имеет и производной. Таких случаев три: угловая точка, точка
возврата, узловая точка
(рис. 2 а, б, в). Особо
отметим случай, когда в точке функция имеет бесконечную
производную (рис. 2 г).

угловая точка
точка возврата узловая
точка

а) б) в) г)

Рис. 2

Рассмотрим решение
некоторых задач.

Задачи,
связанные с определением того, является ли прямая
у = kx
+ b
касательной к графику функции
у = f(x).
Можно указать два способа решения таких задач.

  1. Находим общие
    точки графиков, т. е. решаем уравнение f(x)
    =     kx
    +     b,
    а затем для каждого из его решений
    вычисляем
    .
    В тех случаях, когда

    = k,
    имеет место касание, в других —
    пересечение.

  2. Находим корни
    уравнения

    = k
    и для каждого из них проверяем, выполняется ли
    равенство f(x)
    =     kx
    +     b.
    При его выполнении получаем абсциссы точек
    касания.

Обобщая
оба способа, заметим, что для того чтобы прямая у
= kx
+ b
была касательной к графику функции
у = f(x),
необходимо и достаточно существование хотя
бы одного числа х0,
для которого выполняется система

  1. При каких
    значениях b
    прямая у = 3х +b
    является касательной к графику функции у
    =    ?

Решение.
Записав условие касания

получим

Ответ:
.

  1. При каких
    значениях а прямая
    у=ах+2
    является касательной к графику функции

Указание.

Ответ:
а = e-3

  1. При каких
    значениях а прямая

    является касательной к графику функции

Указание.

Ответ:
а = 7 или а =
-1.

  1. Является ли
    прямая

    касательной к графику функции
    ?
    Если является, то найти координаты точки касания.

Решение.
Пусть
.
Из условия следует, что должны выполняться равенство
,
где
—
возможная абсцисса точки касания. Имеем:

Если теперь
составить уравнение касательной к графику заданной функции в каждой
из двух найденных точек, то окажется, что в точке

как раз и получится
.
Значит, точка касания имеет координаты (1;-1).

  1. К графику
    функции
    проведена
    касательная, параллельная прямой
    .
    Найти ординату точки касания.

Решение.
.
Абсцисса интересующей нас точки касания удовлетворяет уравнению
.
Имеем:

Таким образом,
.
Значит,
—
абсцисса точки касания. Чтобы найти ординату точки касания
преобразуем выражение, задающее функцию:

Ответ: 1.

  1. Написать
    уравнение всех касательных к графику функции
    ,
    параллельных прямой
    .

Решение.
Так как касательная должна быть параллельна прямой
,
то ее угловой коэффициент, равный у'(х0),
где х0
— абсцисса точки касания, совпадает с
угловым коэффициентом данной прямой, т. е.
.
Отсюда

или
.
Далее составляем уравнение касательной для каждой точки.

Ответ:
,.

  1. Найти все
    значения
    ,
    при каждом из которых касательная к графикам функций

    и
    в
    точках с абсциссой

    параллельны.

Решение.
Известно, что тангенс угла наклона касательной к графику функций

в точке с абсциссой

равен
.
Следовательно, все искомые значения

будут корнями уравнения
,
откуда
.
Используя формулу разности синусов углов, будем иметь
.
Решая полученное уравнение, получаем

  1. Найти
    расстояние между касательными к графику функции
    ,
    расположенными параллельно оси
    .

Решение.
Найдем критические точки заданной функции:

Так как,
производная в точках

и

равна нулю, то касательные, проведенные к кривой в точках с этими
абсциссами, параллельны оси
.
Найдем значения функций в этих точках.

Итак,
расстояние d
между касательными, параллельными оси
,
равно

С составлением
уравнения касательной, параллельной данной прямой, связана задача о
нахождении кратчайшего расстояния между графиком
некоторой функции f(x)
и прямой
.

Во многих
случаях удается найти касательную к графику
,
параллельную данной прямой

и делящую плоскость на две части, в одной из
которых расположен график функции, а в другой — заданная
прямая. Тогда кратчайшим расстоянием между графиком функции и прямой

является расстояние от точки М(х0;
у0),
в которой проведена параллельная касательная,
до заданной прямой у =
kx
+ b;
это расстояние можно вычислить по формуле

  1. Найти
    кратчайшее расстояние между параболой

    и прямой

Решение.
Убедившись, что графики не имеют общих
точек (уравнение

не имеет решений), запишем
уравнение такой касательной к графику функции
,
которая параллельна прямой

Уравнение касательной имеет
вид

касание происходит в точке

Прямая у =
х
– 2 и парабола у
= х2
расположены по разные
стороны от касательной. Таким образом, кратчайшее
расстояние между параболой и прямой равно
расстоянию от точки М до
прямой
.

Ответ:

Довольно
сложной является задача составления уравнения всех касательных к
графику функции у = f(x),
проходящих через заданную точку М(х0;
у0),
вообще говоря, не лежащую на графике.
Приведем алгоритм решения этой задачи.

1. Составляем
уравнение касательной к графику функции
у = f(x)
в произвольной
точке графика с абсциссой
t:

2. Решаем
относительно t
уравнение

и для каждого его
решения t
записываем
соответствующую
касательную в виде
.

  1. Написать
    уравнение всех касательных к графику функции
    ,
    проходящих через точку
    М(2; -2).

Указание.
Уравнение касательной в точке с абсциссой t
имеет вид
.
Так как эта
касательная проходит через точку
(2; -2), то
,
откуда
.

Ответ:
.

  1. Найти
    площадь треугольника, образованного касательными, проведенными
    к графику функции

    через точку

    и секущей,
    проходящей через точки касания.

Указание.
Уравнение

дает два
решения: t1
= 1, t2
= 4. Таким
образом, точки K1
(1;1) и
K2(4;2)
являются точками касания.

Ответ:
0,25.

Говорят, что
прямая

является общей касательной графиков функции


и
,
если она касается как одного, так и другого
графиков (но совершенно не обязательно в одной и той же точке).
Например, прямая

является общей касательной графиков функций

(в точке М(2; 5) и

(в точке K(0,5;
-1)). Заметим, что графики функций
и

имеют в точке их пересечения М(х0;
у0)
общую невертикальную касательную тогда и
только тогда, когда
.

  1. Доказать,
    что параболы

    и
    имеют
    в их общей точке общую касательную. Найти
    уравнение этой общей касательной. Решение.
    Уравнение
    имеет
    единственный корень х=2,
    т. е. параболы имеют единственную общую точку
    М(2;0). Убедимся, что значения производных для
    обеих функций в точке х =
    2 равны; действительно,
    и
    .
    Далее составляем уравнение касательной.

Ответ:.

В завершении рассмотрим
решение еще нескольких задач на касательную с параметром.

  1. При
    каких значениях параметра
    касательная
    к графику функции

    в точке

    проходит через точку (2;3)?

Решение.
Составим уравнение касательной к графику заданной функции в точке
:

Так как эта прямая проходит через точку (2;3), то имеет место
равенство
,
откуда находим:
.

  1. Может ли
    касательная к кривой

    в какой-либо ее точке составлять острый угол с положительным
    направлением оси
    ?

Решение.
Найдем производную функции
.
В любой точке, в которой функция определена, производная
отрицательна. Но производная есть тангенс угла наклона касательной, а
так как он отрицателен, то угол тупой.

Ответ: Не
может.

  1. Найти
    значение параметра
    ,
    при котором касательная к графику функции

    в точке

    проходит через точку М(1;7).

Решение.
Пусть
тогда
.
Составим уравнение касательной:

По условию эта
касательная проходит через точку М(1;7), значит,
,
откуда получаем:

  1. При каких
    значениях параметра

    прямая

    является касательной к графику функции
    ?

Решение.
Из условия следует, что должно выполнятся равенство
где

абсцисса
точки касания. Значит,
и

связаны между собой равенством

(1). Составим уравнение касательной к графику заданной функции в
точке

Из условия
следует, что должно выполняться равенство
.
Решив это уравнение, получим
.
Тогда из (1) получаем, что
.

  1. При каком
    значении

    прямая

    является касательной у графику
    ?

Решение.
Так как прямая

является касательной к графику функции
,
то в точке касания угловой коэффициент касательной равен 3. Но
угловой коэффициент касательной равен значению производной функции в
этой точке, то есть
,
откуда
,
следовательно,
—
абсцисса точки касания. Найдем теперь
из
условия равенства значений функций
и

при
.
Имеем
,
откуда
.

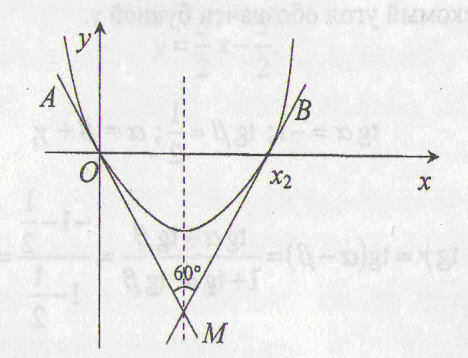
  1. При каких
    значениях параметра а касательные к графику функции
    ,
    проведенные в точках его пересечения с осью оx,
    образуют между собой угол 60о?

Решение.
В этой задаче, как и в предыдущих, речь идет о касательных к графику
функции. Составлять уравнение касательной не надо, достаточно
использовать геометрический смысл производной, то есть угловые
коэффициенты касательных. Графиком данной функции является парабола с
ветвями, направленными вверх, пересекающая ось оx
в двух точках (случай а=0
нас не устраивает):

и
учитываем,
что х2>0
(рис. 3)

Рис. 3

Касательные АМ
и ВМ пересекаются под углом 60о
в точке М, лежащей на оси параболы, причем возможны два случая: либо
,
либо смежный угол равен 60о.
в первом случае угол между касательной АО и осью х равен 120о,
следовательно, угол коэффициента касательной равен tg120o,
то есть равен

Далее имеем:
.
Таким образом, получаем, что
,
то
.
Во втором случае
,
поэтому угол между касательной АО и остью ох
равен 150о.
Значит, угловой коэффициент касательной равен tg150o
, то есть он равен
.
Таким образом, получаем, что
,
то есть

Ответ:
.

Литература:

  1. Далингер,
    В.А. Начала математического анализа в задачах [Текст]: учебное
    пособие / В.А. Далингер. – Омск: Изд-во ГОУ ОМГПУ, 2009. –
    312 с.

  2. Звавич, Л.И. Алгебра и
    начала анализа. 8-11 кл. [Текст]: пособие для школ и классов с
    углубл. изучением математики / Л. И. Звавич, Л.Я. Шляпочник, М.В.
    Чинкина.– М.: Дрофа, 1999. – 352 с.

Основные термины (генерируются автоматически): график функции, касательная, уравнение касательной, прямая, решение, абсцисса, касание, график функций, кратчайшее расстояние, угловой коэффициент.

Источник

Утверждение

Если две окружности касаются внешне, то длина отрезка общей внешней касательной равна удвоенному среднему пропорциональному их радиусов.

dlina-obshchej-kasatelnoj-okruzhnostej Дано: окр. (O1; R) и окр.(O2; r) касаются внешне в точке D, AB — общая касательная,

окр. (O1; R)∩AB=A, окр.(O2; r)∩AB=B.

Доказать:

    [AB = 2sqrt {Rr} ]

Доказательство:

dlina-obshchej-kasatelnojСоединим центры окружностей с точками касания.

ABO2O1 — прямоугольная трапеция (по доказанному).

Из точки O2 на сторону AO1 опустим перпендикуляр O2F. Четырёхугольник ABO2F — прямоугольник (так как у него все углы прямые). Поэтому его противоположные стороны равны: FO2=AB, AF=BO2=r.

Рассмотрим прямоугольный треугольник O1O2F.

FO1=AO1-AF=R-r, O1O2=O1D+O2D=R+r.

По теореме Пифагора

    [{O_1}O_2^2 = FO_1^2 + FO_2^2,]

    [F{O_2} = sqrt {{O_1}O_2^2 - FO_1^2} ]

    [F{O_2} = sqrt {{{(R + r)}^2} - {{(R - r)}^2}} = ]

    [ = sqrt {{R^2} + 2Rr + {r^2} - {R^2} + 2Rr - {r^2}} = 2sqrt {Rr} ,]

а значит, и

    [AB = 2sqrt {Rr} .]

Что и требовалось доказать.

Источник

Как найти расстояние между точками касания окружности

Найдите расстояние между точками касания окружностей, вписанных в треугольники ABC и CDA , со стороной AC , если

а) AB = 5, BC = 7, CD = DA ;

б) AB = 7, BC = CD , DA = 9.

Подсказка

Расстояние от вершины треугольника до ближайшей точки касания с вписанной окружностью равно разности между полупериметром и противолежащей стороной треугольника ( x = p — a ).

Решение

а) Пусть вписанная окружность треугольника ABC касается стороны AC в точке K , а вписанная окружность треугольника CDA — в точке M . Поскольку расстояние от вершины треугольника до точки касания с вписанной окружностью равно разности между полупериметром и противолежащей стороной треугольника, то

Об отрезках касательной к окружности

Чаще всего именно геометрические задачи вызывают затруднения у абитуриентов, выпускников, участников математических олимпиад. Если посмотреть статистику ЕГЭ 2010 года, то видно, что к геометрической задаче С4 приступило около 12% участников, а получило полный балл только 0,2% участников, а в целом задача оказалась самой сложной из всех предложенных.

Очевидно, что чем раньше мы предложим школьникам красивые или неожиданные по способу решения задачи, тем больше вероятность заинтересовать и увлечь всерьёз и надолго. Но, как же трудно найти интересные и сложные задачи на уровне 7 класса, когда только начинается систематическое изучение геометрии. Что можно предложить интересующемуся математикой школьнику, знающему только признаки равенства треугольников, свойства смежных и вертикальных углов? Однако, можно ввести понятие касательной к окружности, как прямой, имеющей с окружностью одну общую точку; принять, что радиус, проведённый в точку касания, перпендикулярен касательной. Конечно, стоит рассмотреть все возможные случаи расположения двух окружностей и общих касательных к ним, которых можно провести от нуля до четырёх. Доказав ниже предложенные теоремы, можно значительно расширить набор задач для семиклассников. При этом попутно доказать важные или просто интересные и занимательные факты. Причём, поскольку многие утверждения не входят в школьный учебник, то обсуждать их можно и на занятиях кружка и с выпускниками при повторении планиметрии. Актуальными эти факты оказались в прошлом учебном году. Так как многие диагностические работы и сама работа ЕГЭ содержали задачу, для решения которой необходимо было использовать доказываемое ниже свойство отрезка касательной.

Т1Отрезки касательных к окружности, проведённые из
одной точки равны (рис. 1)

Вот именно с теоремой можно сначала познакомить семиклассников.
В процессе доказательства использовали признак равенства прямоугольных треугольников, сделали вывод о том, что центр окружности лежит на биссектрисе угла ВСА.
Попутно вспомнили, что биссектриса угла есть геометрическое место точек внутренней области угла, равноудалённых от его сторон. На этих доступных даже только начинающим изучать геометрию фактах основывается решение уже далеко нетривиальной задачи.

1. Биссектрисы углов А, В и С выпуклого четырёхугольника АВСD пересекаются в одной точке. Лучи АВ и DC пересекаются в точке Е, а лучи
ВС и АD в точке F. Докажите, что у невыпуклого четырёхугольника AECF суммы длин противоположных сторон равны.

Решение (рис. 2). Пусть О – точка пересечения данных биссектрис. Тогда О равноудалена от всех сторон четырёхугольника АВСD, то есть
является центром окружности вписанной в четырёхугольник. По теореме 1 верны равенства: AR = AK, ER = EP, FT = FK. Почленно сложим левые и правые части, получим верное равенство:

(AR + ER) + FT = (AK +FK) + EP; AE + (FC + CT) = AF + (ЕC + PC). Так как СТ = РС, то АЕ + FC = AF + ЕC, что и требовалось доказать.

Рассмотрим необычную по формулировке задачу, для решения которой достаточно знание теоремы 1.

2. Существует ли n-угольник, стороны которого последовательно 1, 2, 3, …, n, в который можно вписать окружность?

Решение. Допустим, такой n-угольник существует. А1А2 =1, …, Аn-1Аn = n – 1, АnА1 = n. B1, …, Bn – соответствующие точки касания. Тогда по теореме 1 A1B1 = A1Bn < 1, n – 1 < AnBn < n. По свойству отрезков касательных AnBn = AnBn-1. Но, AnBn-1 < An-1Аn = n – 1. Противоречие. Следовательно, нет n-угольника, удовлетворяющего условию задачи.

Т2 Суммы противолежащих сторон четырёхугольника, описанного около
окружности, равны (рис. 3)

Школьники, как правило, легко доказывают это свойство описанного четырёхугольника. После доказательства теоремы 1, оно является тренировочным упражнением. Можно обобщить этот факт – суммы сторон описанного чётноугольника, взятых через одну, равны. Например, для шестиугольника ABCDEF верно: AB + CD + EF = BC + DE + FА.

3. МГУ. В четырёхугольнике ABCD расположены две окружности: первая окружность касается сторон AB, BC и AD, а вторая – сторон BC, CD и AD. На сторонах BC и AD взяты точки E и F соответственно так, отрезок EF касается обеих окружностей, а периметр четырёхугольника ABEF на 2p больше периметра четырёхугольника ECDF. Найти AB, если CD = a.

Решение (рис. 1). Так как четырёхугольники ABEF и ECDF вписанные, то по теореме 2 РABEF = 2(AB + EF) и РECDF = 2(CD + EF), по условию

РABEF – РECDF = 2(AB + EF) – 2(CD + EF) = 2p. AB – CD = p. АВ = а + р.

Опорная задача 1. Прямые АВ и АС – касательные в точках В и С к окружности с центром в точке О. Через произвольную точку Х дуги ВС
проведена касательная к окружности, пересекающая отрезки АВ и АС в точках М и Р соответственно. Докажите, что периметр треугольника АМР и величина угла МОР не зависят от выбора точки Х.

Решение (рис. 5). По теореме 1 МВ = МХ и РС = РХ. Поэтому периметр треугольника АМР равен сумме отрезков АВ и АС. Или удвоенной касательной, проведённой к вневписанной окружности для треугольника АМР. Величина угла МОР измеряется половиной величины угла ВОС, который не зависит от выбора точки Х.

Опорная задача 2а. В треугольник со сторонами а, b и c вписана окружность, касающаяся стороны АВ и точке К. Найти длину отрезка АК.

Решение (рис. 6). Способ первый (алгебраический). Пусть АК = АN = x, тогда BK = BM = c – x, CM = CN = a – c + x. АС = АN + NC, тогда можем составить уравнение относительно х: b = x + (a – c + x). Откуда .

Способ второй (геометрический). Обратимся к схеме. Отрезки равных касательных, взятые по одному, в сумме дают полупериметр
треугольника. Красный и зелёный составляют сторону а. Тогда интересующий нас отрезок х = р – а. Безусловно, полученные результаты совпадают.

Опорная задача 2б. Найти длину отрезка касательной АК, если К – точка касания вневписанной окружности со стороной АВ. Решение (рис. 7). АК = АM = x, тогда BK = BN = c – x, CM = CN. Имеем уравнение b + x = a + (c – x). Откуда . Заметим, что из опорной задачи 1 следует, что СМ = р Δ АВС. b + x = p; х = р – b. Полученные формулы имеют применение в следующих задачах.

4. Найдите радиус окружности, вписанной в прямоугольный треугольник с катетами а, b и гипотенузой с. Решение (рис. 8). Так как OMCN – квадрат, то радиус вписанной окружности равен отрезку касательной CN. .

5. Докажите, что точки касания вписанной и вневписанной окружности со стороной треугольника симметричны относительно середины этой стороны.

Решение (рис. 9). Заметим, АК – отрезок касательной вневписанной окружности для треугольника АВС. По формуле (2) . ВМ – отрезок касательной вписанной окружности для треугольника АВС. По формуле (1) . АК = ВМ, а это и означает, что точки К и М равноудалены от середины стороны АВ, что и требовалось доказать.

6. К двум окружностям проведены две общие внешние касательные и одна внутренняя. Внутренняя касательная пересекает внешние в точках А, В и касается окружностей в точках А1и В1. Докажите, что АА1 = ВВ1.

Решение (рис. 10). Стоп… Да что тут решать? Это же просто другая формулировка предыдущей задачи. Очевидно, что одна из окружностей является вписанной, а другая вневписанной для некоего треугольника АВС. А отрезки АА1 и ВВ1соответствуют отрезкам АК и ВМ задачи 5. Примечательно, что задача, предлагавшаяся на Всероссийской олимпиаде школьников по математике, решается столь очевидным образом.

7. Стороны пятиугольника в порядке обхода равны 5, 6, 10, 7, 8. Доказать, что в этот пятиугольник нельзя вписать окружность.

Решение (рис. 11). Предположим, что в пятиугольник АВСDE можно вписать окружность. Причём стороны AB, BC, CD, DE и ЕA равны соответственно 5, 6, 10, 7 и 8. Отметим последовательно точки касания – F, G, H, M и N. Пусть длина отрезка AF равна х.

Тогда BF = FD – AF = 5 – x = BG. GC = BC – BG = = 6 – (5 – x) = 1 + x = CH. И так далее: HD = DM = 9 – x; ME = EN = x – 2, AN = 10 – х.

Но, AF = AN. То есть 10 – х = х; х = 5. Однако, отрезок касательной AF не может равняться стороне АВ. Полученное противоречие и доказывает, что в данный пятиугольник нельзя вписать окружность.

8. В шестиугольник вписана окружность, его стороны в порядке обхода равны 1, 2, 3, 4, 5. Найти длину шестой стороны.

Решение. Конечно, можно отрезок касательной обозначить за х, как и в предыдущей задаче, составить уравнение и получить ответ. Но, гораздо эффективнее и эффектнее использовать примечание к теореме 2: суммы сторон описанного шестиугольника, взятых через одну, равны.

Тогда 1 + 3 + 5 = 2 + 4 + х, где х – неизвестная шестая сторона, х = 3.

9. МГУ, 2003 г. химический факультет, № 6(6). В пятиугольник АВСDE вписана окружность, Р – точка касания этой окружности со стороной ВС. Найдите длину отрезка ВР, если известно, что длины всех сторон пятиугольника есть целые числа, АВ = 1, СD = 3.

Решение (рис.12). Так как длины всех сторон являются целыми числами, то равны дробные части длин отрезков BT, BP, DM, DN, AK и AT. Имеем, АТ + ТВ = 1, и дробные части длин отрезков AT и TB равны. Это возможно только тогда, когда АТ + ТВ = 0,5. По теореме 1 ВТ + ВР.
Значит, ВР = 0,5. Заметим, что условие СD = 3 оказалось невостребованным. Очевидно, авторы задачи предполагали какое-то другое решение. Ответ: 0,5.

10. В четырёхугольнике ABCD AD = DC, AB = 3, BC = 5. Окружности, вписанные в треугольники ABD и CBD касаются отрезка BD в точках M и N соответственно. Найти длину отрезка MN.

Решение (рис. 13). MN = DN – DM. По формуле (1) для треугольников DBA и DBС соответственно, имеем:

11. В четырёхугольник ABCD можно вписать окружность. Окружности, вписанные в треугольники ABD и CBD имеют радиусы R и r соответственно. Найти расстояние между центрами этих окружностей.

Решение (рис. 13). Так как по условию четырёхугольник ABCD вписанный, по теореме 2 имеем: AB + DC = AD + BC. Воспользуемся идеей решения предыдущей задачи. . Это означает, что точки касания окружностей с отрезком DM совпадают. Расстояние между центрами окружностей равно сумме радиусов. Ответ: R + r.

Фактически доказано, что условие – в четырёхугольник ABCD можно вписать окружность, равносильно условию – в выпуклом четырехугольнике ABCD окружности, вписанные в треугольники ABC и ADC касаются друг друга. Верно обратное.

Доказать эти два взаимно-обратных утверждения предлагается в следующей задаче, которую можно считать обобщением данной.

12. В выпуклом четырехугольнике ABCD (рис. 14) окружности, вписанные в треугольники ABC и ADC касаются друг друга. Докажите, что окружности, вписанные в треугольники ABD и BDC также касаются друг друга.

13. В треугольнике АВС со сторонами а, b и c на стороне ВС отмечена точка D так, что окружности, вписанные в треугольники АВD и ACD касаются отрезка AD в одной точке. Найти длину отрезка BD.

Решение (рис. 15). Применим формулу (1) для треугольников ADC и ADB, вычислив DM двумя

Оказывается, D – точка касания со стороной ВС окружности, вписанной в треугольник АВС. Верно обратное: если вершину треугольника соединить с точкой касания вписанной окружности на противоположной стороне, то окружности, вписанные в получившиеся треугольники, касаются друг друга.

14. Центры О1, О2 и О3 трёх непересекающихся окружностей одинакового радиуса расположены в вершинах треугольника. Из точек О1, О2, О3 проведены касательные к данным окружностям так, как показано на рисунке.

Известно, что эти касательные, пересекаясь, образовали выпуклый шестиугольник, стороны которого через одну покрашены в красный и синий цвета. Докажите, что сумма длин красных отрезков равна сумме длин синих.

Решение (рис. 16). Важно понять, как использовать тот факт, что заданные окружности имеют одинаковые радиусы. Заметим, что отрезки ВR и DМ равны, что следует из равенства прямоугольных треугольников О1ВR и O2BM. Аналогично DL = DP, FN = FK. Почленно складываем равенства, затем вычитаем из полученных сумм одинаковые отрезки касательных, проведенных из вершин А, С, и Е шестиугольника ABCDEF: АR и AK, CL и CM, EN и EP. Получаем требуемое.

Вот пример задачи по стереометрии, предлагавшейся на XII Международном математическом турнире старшеклассников “Кубок памяти А. Н. Колмогорова”.

16. Дана пятиугольная пирамида SA1A2A3A4A5. Существует сфера w , которая касается всех ребер пирамиды и другая сфера w 1, которая касается всех сторон основания A1A2A3A4A5и продолжений боковых рёбер SA1, SA2, SA3, SA4, SA5за вершины основания. Докажите, что вершина пирамиды равноудалена от вершин основания. (Берлов С. Л., Карпов Д. В.)

Решение. Пересечение сферы w с плоскостью любой из граней сферы – это вписанная окружность грани. Пересечение сферы w 1 с каждой из граней SAiAi+1 – вневписанная окружность, касающаяся стороны AiAi+1 треугольника SAiAi+1 и продолжений двух других сторон. Обозначим точку касания w 1 с продолжением стороны SAi через Bi. По опорной задаче 1 имеем, что SBi = SBi+1 = pSAiAi+1 , следовательно, периметры всех боковых граней пирамиды равны. Обозначим точку касания w со стороной SAi через Сi. Тогда SC1 = SC2 = SC3 = SC4 = SC5= s,
так как отрезки касательных равны. Пусть CiAi = ai. Тогда pSAiAi+1 = s+ai+ai+1, и из равенства периметров следует, что a1 = a3 = a5 = a2 = a4, откуда SA1 = SA2 = SA3 = SA4 = SA5.

17. ЕГЭ. Диагностическая работа 8.12.2009 г, С–4. Дана трапеция ABCD, основания которой BC = 44, AD = 100, AB = CD = 35. Окружность, касающаяся прямых AD и AC, касается стороны CD в точке K. Найдите длину отрезка CK.

Найдем диагональ AC. Опустим из вершин B и C на сторону AD перпендикуляры BE и CF соответственно. AE = FD, так как трапеция равнобедренная. BCFE – прямоугольник.

Возможны две геометрические конфигурации.

Первый случай (рис. 18): окружность вписана в треугольник ACD.

Второй вариант (рис.19): окружность касается продолжений сторон AC и AD за точками C и D соответственно и отрезка CD.

18. ЕГЭ. 4.6. 2010 г. В треугольнике АВС АВ = 13, ВС = 11, СА = 9. Точка D лежит на прямой АС, причём АD : DС = 1 : 9. Окружности, вписанные в каждый из треугольников ВDС и ВDА, касаются стороны ВD в точках Е и F. Найдите длину отрезка EF.

Решение. Возможны два случая (рис. 20 и рис. 21). По формуле (1) найдём длины отрезков DE и DF.

В первом случае AD = 0,1АС, СD = 0,9AC. Во втором – AD = 0,125АС, СD = 1,125AC. Подставляем данные и получаем ответ: 4,6 или 5,5.

Задачи для самостоятельного решения/

1. Периметр равнобедренной трапеции, описанной около окружности равен 2р. Найдите проекцию диагонали трапеции на большее основание. (1/2р)

2. Открытый банк задач ЕГЭ по математике. В4. К окружности, вписанной в треугольник ABC (рис. 22), проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника. (24)

3. В треугольник АВС вписана окружность. MN – касательная к окружности, M Î АС, N Î ВС, ВС = 13, АС = 14, АВ = 15. Найдите периметр треугольника MNC. (12)

4. К окружности, вписанной в квадрат со стороной а, проведена касательная, пересекающая две его стороны. Найдите периметр отсечённого треугольника. (а)

5. Окружность вписана в пятиугольник со сторонами а, d, c, d и e. Найдите отрезки, на которые точка касания делит сторону, равную а.

6. В треугольник со сторонами 6, 10 и 12 вписана окружность. К окружности проведена касательная так, что она пересекает две большие стороны. Найдите периметр отсечённого треугольника. (16)

7. CD – медиана треугольника ABC. Окружности, вписанные в треугольники ACD и BCD, касаются отрезка CD в точках M и N. Найдите MN, если АС – ВС = 2. (1)

8. В треугольнике АВС со сторонами а, b и c на стороне ВС отмечена точка D. К окружностям, вписанным в треугольники АВD и ACD, проведена общая касательная, пересекающая AD в точке М. Найти длину отрезка АМ. (Длина АМ не зависит от положения точки D и
равна ½ (c + b – a))

9. В прямоугольный треугольник вписана окружность радиуса а. Радиус окружности, касающейся гипотенузы и продолжений катетов, равен R. Найдите длину гипотенузы. (R – a)

10. В треугольнике АВС известны длины сторон: АВ = с, АС = b, ВС = а. Вписанная в треугольник окружность касается стороны АВ в точке С1. Вневписанная окружность касается продолжения стороны АВ за точку А в точке С2. Определите длину отрезка С1С2. (b)

11. Найдите длины сторон треугольника, разделённых точкой касания вписанной окружности радиуса 3 см на отрезки 4 см и 3 см. (7, 24 и 25 см в прямоугольном треугольнике)

12. Соросовская олимпиада 1996 г, 2 тур, 11 класс. Дан треугольник АВС, на сторонах которого отмечены точки А1, В1, С1. Радиусы окружностей вписанных в треугольники АС1В1, ВС1А1, СА1В1 равны по r. Радиус окружности, вписанной в треугольник А1В1С1равен R. Найти радиус окружности, вписанной в треугольник АВС. (R + r).

Задачи 4–8 взяты из задачника Гордина Р. К. “Геометрия. Планиметрия.” Москва. Издательство МЦНМО. 2004.

Две окружности на плоскости.
Общие касательные к двум окружностям

Взаимное расположение двух окружностей

Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также
две общих внешних касательных. Других общих касательных нет.

Каждая из окружностей лежит вне другой

Общие касательные к двум окружностям

Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.

Общие касательные к двум окружностям

Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

Общие касательные к двум окружностям

Общие касательные к двум окружностям

Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Общие касательные к двум окружностям

Общие касательные к двум окружностям

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Общие касательные к двум окружностям

Общие касательные к двум окружностям

Существует единственная общая внешняя касательная. Других общих касательных нет.

Общие касательные к двум окружностям

Общие касательные к двум окружностям

Существуют две общих внешних касательных. Других общих касательных нет.

Общие касательные к двум окружностям

Общие касательные к двум окружностям

Общие касательные к двум окружностям

Общие касательные к двум окружностям

Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.

Общие касательные к двум окружностям

Общие касательные к двум окружностям

Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

Формулы для длин общих касательных и общей хорды двух окружностей

Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Длина общей хорды двух окружностей вычисляется по формуле

Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Длина общей хорды двух окружностей вычисляется по формуле

Формулы для длин общих касательных и общей хорды двух окружностей

Формулы для длин общих касательных и общей хорды двух окружностей

Длина общей внешней касательной к двум окружностям вычисляется по формуле

Формулы для длин общих касательных и общей хорды двух окружностей

Формулы для длин общих касательных и общей хорды двух окружностей

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Длина общей хорды двух окружностей вычисляется по формуле

Доказательства формул для длин общих касательных и общей хорды двух окружностей

Утверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле

Доказательство формул для длин общих касательных и общей хорды двух окружностей

Доказательство формул для длин общих касательных и общей хорды двух окружностей

что и требовалось доказать.

Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле

Доказательство формул для длин общих касательных и общей хорды двух окружностей

Доказательство формул для длин общих касательных и общей хорды двух окружностей

что и требовалось доказать.

Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле

Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3,

Источник

Like this post? Please share to your friends:
  • Как найти женщину в саранске
  • Если в озу ошибки как их исправить
  • Как можно найти телефон по имей коду
  • Как исправить ошибку в файле журнала
  • Как составить портфолио воспитателя детского сада образец