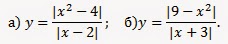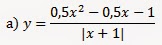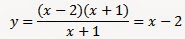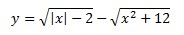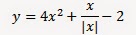- Математика — уроки для подготовки к экзаменам ЕГЭ ОГЭ
- Математика ЕГЭ, ОГЭ, высшая
- Подготовка к олимпиаде ФИЗТЕХ. вычисление расстояний между точками пересечения графиков функций.
Подготовка к олимпиаде ФИЗТЕХ. вычисление расстояний между точками пересечения графиков функций.
Смотреть видео:
Свежая информация для ЕГЭ и ОГЭ по Математике (листай):
С этим видео ученики смотрят следующие ролики:
Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):
- Комментарии
Нет комментариев. Ваш будет первым!
Пусть f(x)=kx+b. Тогда точки пересечения графиков для первого случая имеют вид (x1,y1), (x2,y2), где абсциссы — корни квадратного уравнения x^2-kx-(b+2)=0. Ясно, что y1-y2=k(x1-x2), поэтому квадрат расстояния между точками пересечения равен (x1-x2)^2+(y1-y2)^2=(1+k^2)(x1-x2)^2=(1+k^2)D, где (x1-x2)^2=(x1+x2)^2-4x1x2=k^2+4(b+2) есть дискриминант квадратного уравнения. Отсюда имеем 26=(1+k^2)(k^2+4(b+2)).
Для второго случая имеем уравнение x^2-kx-(b+1)=0, откуда 18=(1+k^2)(k^2+4(b+1)). Наконец, для третьего случая квадратное уравнение имеет вид x^2-kx-b=0, и надо найти (1+k^2)(k^2+4b). Очевидно, что вторая величина есть среднее арифметическое первой и третьей, что даёт ответ 10.
МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ
Функции, содержащие знак модуля
Модулем (абсолютной величиной) действительного числа а называется само это число а, если оно неотрицательно, и противоположное число (-а), если число а отрицательно.
При построении графиков функций, содержащих знак модуля, применяются те же приемы, что и при решении уравнений с модулем. Также при построении графика функции можно воспользоваться геометрическими преобразованиями.
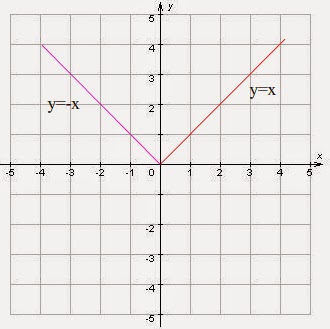
Пример. Построить график функции y =|x|.
Первый способ.
Раскроем знак модуля согласно его определению:
y = x при x ≥ 0,
y = −x при x < 0.
Таким образом, искомый график совпадает с графиком функции y = x при x ≥ 0 и с графиком функции y = −x при x < 0. Cтроим график.
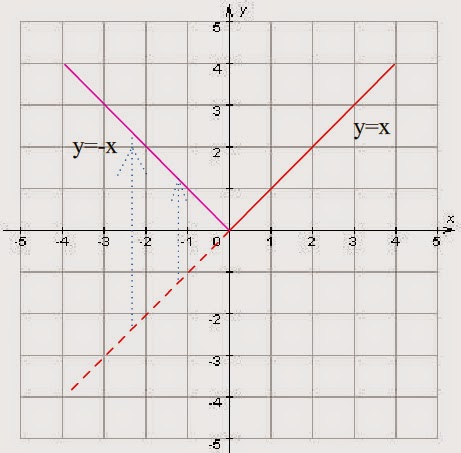
Второй способ.
Можно рассматривать функцию y = |x| как модуль функции y = x. Т.к. модуль не может принимать отрицательные значения, то график в верхней полуплоскости останется прежним, а график в нижней полуплоскости отразится в верхнюю полуплоскость симметрично координатной оси ОХ.
Пример. Построить график функции y=|x2-2x-3|.
Построим график функции у= x2-2x-3, после чего отразим часть графика, которая находится в нижней полуплоскости в верхнюю полуплоскость симметрично координатной оси ОХ.
1. Вершина параболы имеет координаты: х=1, у=-4.
2. Пересечение с осью ОХ: D=16, х1=3, x2=-1.
3. Пересечение с осью ОУ: у=-3.
4. Ветви параболы направлены вверх.
Пример. Построить график функции y = |x| − |2 − x| .
Так как знак модуля входит в два различных слагаемых, то его нужно «снимать» тем
же методом, который применяется при решении уравнений и неравенств:
Рассмотрим значение функции на трех промежутках:
1. x≤0: y=-x-2+x; y=-2.
2. 0<x≤2: y=x-2+x; y=2x-2.
3. x>2: y=x+2-x; y=2.
Построим график функции:
Пример. Построить график функции y=x2-2|x|-3.
При х≤0 y=x2+2x-3.
При x>0 y=x2-2x-3.
Построим график функции y=x2+2x-3 и оставим только ту часть графика, где х≤0.
Построим график функции y=x2-2x-3 и оставим только ту часть графика, где х>0.
Расстояние между точками
Расстояние между двумя точками A1(x1;y1) и A2(x2;y2) в прямоугольной системе координат выражается формулой:
Пример. Найти расстояние между точками А1(-2; 1) и А2(2; 3).
УПРАЖНЕНИЯ
1. Какие из уравнений задают функцию от х?
а) 1) y=5x2+x-1; 2) 4y2=2x+3; 3) |y|=3x;
4) x=y2+1.
б) 1) |y-1|=x; 2) x2=y2+9 3) 10,5y2=-2x; 4) y=-x2+4x-1.
Решение:
а) По определению функции каждому значению х должно соответствовать единственное значение у. Следовательно, уравнение y=5x2+x-1 задает функцию у от х.
2. а) При каких значениях х значения функции y=|x-2| больше 3?
б) При каких значениях х значения функции y=|3-х| больше 4?
Решение:
а) Значение функции больше 3, т.е.y>3 и, следовательно|x|>3.
Ответ: (-∞; -3) U (3; +∞).
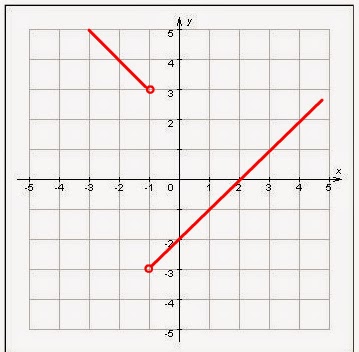
3. а) Найдите количество корней уравнения |x|=2-x2, построив графики функций y=|x| и y=2-x2.
б) Найдите количество корней уравнения -|x|=x2-2, построив графики функций y=-|x| и y=x2-2.
Решение:
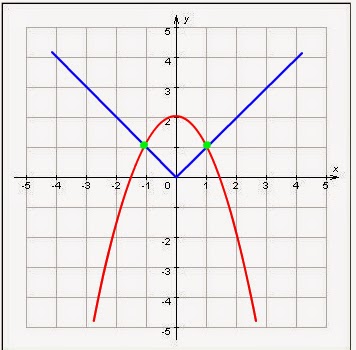
а) Построим графики функций y=|x| — функция модуля и y=2-x2— парабола.
y=2-x2— ветви направлены вниз, вершина х0=0, у0=2.
Количество точек пересечения графиков данных функций — это количество корней уравнения.
Ответ: 2.
4. Найдите область определения функций:
Решение:
а) Т.к. функция содержит арифметический корень, то |x|-6≥0.
Решим это неравенство:
|x|-6≥0;
|x|≥6;
x≥6 или х≤-6.
Ответ: (-∞; -6) U (6; +∞).
5. Найдите площадь параллелограмма ABCD, если:
а) A(3; 2), В(1; -2), а точки С и D симметричны вершинам А и В относительно начала координат;
б) A(-4; 2), D(-1; -2), а точки С и D симметричны вершинам А и В относительно начала координат.
Решение:
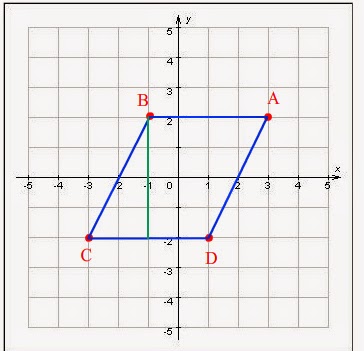
а) Построим точки A(3; 2), В(1; -2). Точка С симметрична точке А относительно начала координат, следовательно С(-3; -2). Точка D симметрична точке B относительно начала координат, следовательно B(-1; 2).
Построим параллелограмм:
Найдем площадь параллелограмма: высоту умножим на сторону к которой она проведена.
S=4*4=16.
Ответ: 16
6. Найдите расстояние между точками А и В, если точка А — вершина параболы, а точка В — точка пересечения параболы с осью ОУ:
а) парабола y=x2+2x-15; б) парабола y=x2+4x-12.
Решение:
а) Найдем вершину параболы y=x2+2x-15:
х0=-2:2=-1; у0=1-2-15=-16.
Точка А имеет координаты (-1; -16).
Точка В — точка пересечения параболы с осью ОУ, следовательно точка В имеет координаты (0; -15).
Найдем расстояние между точками А и В:
7. Найдите нули и промежутки знакопостоянства функции:
а) y=|3x-6|-4; б) y=|2x-4|-3.
Решение:
7. а) y=|3x-6|-4.
Найдем нули функции:
|3x-6|-4=0;
|3x-6|=4;
3х-6=4
или 3х-6=-4
3х=10 или
3х=2
Найдем промежутки знакопостоянства функции:
Функция принимает положительные значения на промежутках (-∞;
2/3) U (3 1/3 ; +∞).
Функция принимает отрицательные значения на промежутке (2/3;
3 1/3).
8. Найдите область определения функции и постройте ее график:
Решение:
а) Найдем область определения функции:
|x-2|≠0
x≠2. D=(-∞; 2)U(2;
+∞).
Для построения графика данной функции упростим ее:
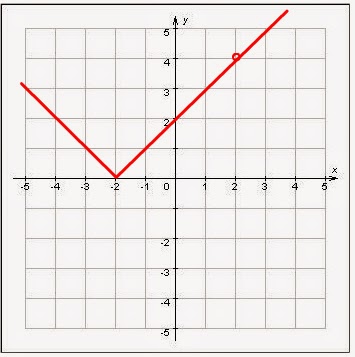
Построим график функции y=|x+2|на области определения D=(-∞; 2)U(2; +∞).
Если х+2≥0, то у=х+2.
Если х+2≤0, то у=-х-2.
На промежутке (-∞; -2) строим график функции
у=-х-2, на промежутке (-2; +∞)
строим график функции у=х+2.
9. Постройте график функции:
Решение:
Область определения выражения D=(-∞; -1)U(-1; +∞).
Разложим числитель на множители:
0,5х2-0,5х-1=0
D=0,25+2=2,25
x1=2, x2=-1
0,5x2-0,5x-1=0,5(x-2)(x+1).
Рассмотрим х+1>0; x
>-1:
Построим график функции на области определения
10. а) Изобразите на координатной плоскости фигуры, которые образуют точки с координатами (х; у), если координаты удовлетворяют условиям: 1≤|x|≤4, 2≤|y|≤3. Найдите сумму площадей полученных фигур.
б) Изобразите на координатной плоскости фигуры, которые образуют точки с координатами (х; у), если координаты удовлетворяют условиям: 2≤|x|≤4, 1≤|y|≤5. Найдите сумму площадей полученных фигур.
Решение:
а) Из неравенства 1≤|x|≤4 следует, что |x|≤4 и |x|≥1. Значит -4≤х≤4 и х≤-1 или х ≥1.
Из неравенства 2≤|у|≤5 следует, что |у|≤5 и |у|≥2. Значит -5≤у≤5 и у≤-2 или у ≥2.
Обозначим на координатной плоскости решения данных неравенств:
На пересечении решений каждого из неравенств мы получили четыре прямоугольника S1, S2, S3, S4. Площадь фигур S1+S2+S3+S4 равна 4*3=12.
Ответ: 12.
11. Постройте график функции и укажите промежутки возрастания и убывания функции:
а) y=|x2-2x|; б) y=|x2+4x|.
Решение:
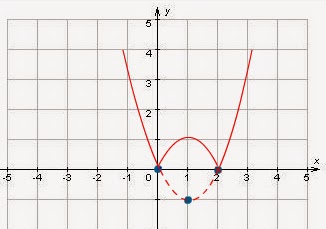
а) y=|x2-2x|. Построим график функции y=x2-2x и отразим часть графика, которая находится в нижней полуплоскости в верхнюю полуплоскость симметрично координатной оси ОХ.
График функции y=x2-2x — парабола. Вершина (1; -1). Нули функции: х=0; х=2.
Функция возрастает: [0; 1] U [2; +∞).
Функция убывает: (-∞; 0) U (1; 2).
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1.Определите, проходит ли график функции y=|x-4|+2 через точки
а) А(1; 5); б) В(1; -5).
2. Найдите расстояние между точками А и В, если:
а) А(-5; -4), В(2; 1); б) А(-2; 1), В(2; 3).
3. Укажите область определения функции, заданной формулой:
4. Постройте график функции y=-x2+4|x|-6.
5. Найдите расстояние между точками пересечения прямой 2у-6х=9 с осями координат.
6. Найдите нули функции y=|2x-1|-2x2+5.
7. Найдите область определения функции:
8. Найдите количество корней уравнения |x-2|=х-0,25x2, построив графики функций y=|x-2| и y=х-0,25x2.
9. Найдите промежутки знакопостоянства функции:
10. Найдите, при каких значениях аргумента значения функции y=| x2-6x+1| меньше значений функции y=|x2-4|.
ПРОВЕРЬТЕ СЕБЯ
|
���������: 3- ������: 8,9 |
�������� ����������� |
�������
������� ���������� ����� ������ A(1, 7) � ������
����������� ������ x – y – 1 = 0 � x + 3y – 12 = 0.
�������
����� �������, ���ģ� ����� B(15/4, 11/4) ����������� ������ ������. �� ������� ��� ���������� ����� ����� �������
AB2 = (15/4 – 1)2 + (11/4 – 1)2 = (11/4)2 + (17/4)2 = 1/16 + (121 + 289) = 410/16.
�����
.
��������� � ���������� �������������
| web-���� | |
| �������� | ������� ����� �� ��������� �.�.������� |
| URL | http://zadachi.mccme.ru |
| ������ | |
| ����� | 4221 |
Содержание
- — Как найти точку пересечения графиков в Excel?
- — Как определить точку пересечения двух прямых?
- — Как найти точки пересечения двух графиков без построения?
- — Как найти точки пересечения с графиком?
- — Как найти точки пересечения графиков квадратичной функции?
- — Как соединить две диаграммы в Excel?
- — Как найти точку пересечения двух графиков функций?
- — Как найти точку пересечения двух отрезков?
- — Как доказать что прямые пересекаются?
- — Какие графики не пересекаются?
- — Как найти точки пересечения параболы?
- — Как правильно построить график функции?
- — Как узнать что графики параллельны?
- — Как показать пересечение?
- — Какое название имеет точка пересечения осей координат?
Чтобы найти координаты точки пересечения графиков функций нужно приравнять обе функции друг к другу, перенести в левую часть все члена, содержащие x , а в правую остальные и найти корни, полученного уравнения. Третий способ подразумевает графическое построение функций и визуальное определение точки пересечения.
Как найти точку пересечения графиков в Excel?
Выделяем диапазоны данных, на вкладке «Вставка» в группе «Диаграммы» подбираем нужный тип графика. Как: Нужно найти точки пересечения графиков со значением Х, поэтому столбчатые, круговые, пузырьковые и т.
Как определить точку пересечения двух прямых?
Две прямые называются пересекающимися, если они имеют одну общую точку. Определение. Точка, в которой пересекаются две прямые, называется точкой пересечения этих прямых. Если точка M, является точкой пересечения двух прямых, то она должна принадлежать этим прямым, а ее координаты удовлетворять уравнения этих прямых.
Как найти точки пересечения двух графиков без построения?
Можно точки пересечения находить без построения графиков – аналитически. Для этого приравнивают правые части обоих уравнений и решают получившееся уравнение. Итак, запишем уравнение из правых частей заданных функций: 2х – 1 = 5 – х.
Как найти точки пересечения с графиком?
Для того чтобы найти точки пересечения графика функции с осью ординат (Oy), необходимо подставить в уравнения функции x=0 , тем самым, найти y. Аналогично, чтобы найти точки пересечения графика функции с осью абсцисс (Ox), необходимо подставить в уравнение функции y=0 и найти x.
Как найти точки пересечения графиков квадратичной функции?
Значит, чтобы найти точки пересечения графика квадратичной функции (параболы) с осью Ox, надо решить квадратное уравнение ax²+bx+c=0. В зависимости от дискриминанта, парабола пресекает ось абсцисс в одной точке или в двух точках либо не пересекает Ox. В точке пересечения графика с осью Oy x=0. y=a∙0²+b∙0+c=с.
Как соединить две диаграммы в Excel?
На вкладке Конструктор нажмите кнопку Изменить тип диаграммы, а затем выберите плоскую диаграмму, которую требуется добавить к существующей. Примечание: Для объединения диаграмм необходимо не менее двух рядов данных.
Как найти точку пересечения двух графиков функций?
Чтобы найти координаты точки пересечения графиков функций нужно приравнять обе функции друг к другу, перенести в левую часть все члена, содержащие x , а в правую остальные и найти корни, полученного уравнения. Третий способ подразумевает графическое построение функций и визуальное определение точки пересечения.
Как найти точку пересечения двух отрезков?
Если нужно найти пересечение отрезков, то нужно лишь проверить, лежат ли ua и ub на промежутке [0,1]. Если какая-нибудь из этих двух переменных 0 <= ui <= 1, то соответствующий отрезок содержит точку пересечения. Если обе переменные приняли значения из [0,1], то точка пересечения прямых лежит внутри обоих отрезков.
Как доказать что прямые пересекаются?
Две прямые называют пересекающимися прямыми , если они имеют единственную общую точку. Две прямые называют скрещивающимися прямыми , если не существует плоскости, содержащей обе прямые. Две прямые называют пересекающимися прямыми , если они имеют единственную общую точку.
Какие графики не пересекаются?
Если даны две линейные функции вида y = kx + m, то их графики (прямые) могут вообще не пересекаться, если параллельны друг другу. … Пример: графики функций y = 2x – 3 и y = 2x + 1 параллельны и, следовательно, не пересекаются.
Как найти точки пересечения параболы?
Чтобы найти точки пересечения параболы с прямой нужно:
- приравнять правые части функций (те части функций, в которых содержатся «x»);
- решить полученное уравнение относительно «x»;
- подставить полученные числовые значения «x» в любую из функций и найти координаты точек по оси «Оy».
Как правильно построить график функции?
Для построения графика функции f(x) нужно найти все точки плоскости, координаты х, у которых удовлетворяют уравнению y = f(x). В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью.
Как узнать что графики параллельны?
Таким образом, если 2 линейные функции имеют одинаковый угловой коэффициент, то их графики будут параллельны. Если же угловые коэффициенты не равны, то графики будут пересекаться.
Как показать пересечение?
Как обозначается пересечение прямых
В тексте пересечение прямых обозначают символом ∩. Информацию на рисунке выше можно записать следующим образом: b ∩ c — прямые b и с пересекаются; a ∩ c — прямые a и с пересекаются.
Какое название имеет точка пересечения осей координат?
Чтобы найти координаты точки на плоскости, нужно опустить из этой точки перпендикуляры на оси координат. Точка пересечения с осью «x» называется абсциссой точки «А», а с осью y называется ординатой точки «А».
Интересные материалы:
Как называется работа Дарвина?
Как называется работа в магазине раскладывать товар?
Как называется работник магазина?
Как называется рамка для фотографии?
Как называется ранняя форма египетской гробницы?
Как называется раскладная дубинка?
Как называется распитие спиртных напитков в общественном месте?
Как называется расположение листьев друг за другом?
Как называется расположение листьев когда они находятся друг за другом по спирали?
Как называется расстояние между бровями?