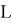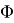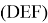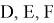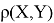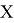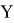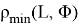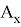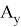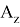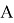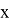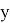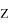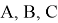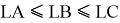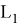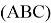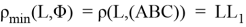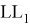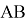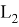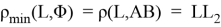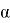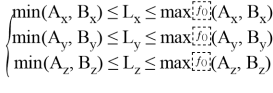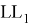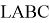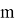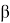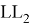Как найти расстояние между точками в многограннике

22 января 2014

Это первый урок из серии видеоуроков, посвященных задачам B13. Перед нами стандартная задача, которую часто дают на пробниках и контрольных работах. Однако решать ее мы будем весьма нестандартным методом.:)

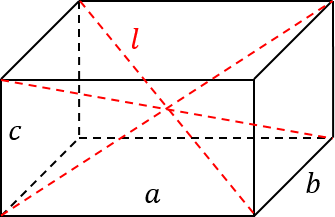
Задача B13. Дан многогранник, изображенный на рисунке. Все двугранные углы прямые. Найдите, насколько расстояние между вершинами
A
и C2 отличается от квадрата расстояния между вершинами
E
и G1. В ответ запишите положительное число.

Для решения любых таких задач нам потребуется обобщенная теорема Пифагора. Давайте отмотаем время назад и вспомним, что такое обычная теорема Пифагора. У нас есть прямоугольный треугольник с катетами
a
,
b
и гипотенузой
c
:

В этом случае квадрат гипотенузы равен сумме квадратов катетов:

c

² =
a

² +
b

²

Теорема Пифагора в пространстве

Но все это рассматривается лишь на плоскости, потому что треугольник — это плоская фигура. Однако та же самая формула работает и в пространстве.

Теорема Пифагора в пространстве. Рассмотрим прямоугольный параллелепипед, или, просто говоря, кирпич. Такой параллелепипед однозначно задается своими сторонами
a
,
b
и
c
. Кроме того, у него есть главная диагональ. Эта диагональ соединяет наиболее удаленные точки параллелепипеда. Разумеется, если параллелепипед прямоугольный, то таких диагоналей сразу несколько, при этом все они будут равны и будут считаться по одной и той же формуле.

Диагональ обозначим буквой
l
. В этом случае можно записать формулу:

l

² =
a

² +
b

² +
c

²

Как связана теорема Пифагора и расстояния между точками в пространстве

Возможно, кто-то сейчас спросит: а какое отношение диагональ, тем более, в параллелепипеде имеет к нашему прямоугольному треугольнику со сторонами
a
,
b
и
c
? Отношение, на самом деле, самое прямое. Давайте достроим наш треугольник до прямоугольника, и получим, что гипотенуза
c
является диагональю на прямоугольнике.

Таким образом, перед нами, по сути, аналог теоремы Пифагора для трехмерного пространства. Давайте немножко перепишем ее:

Внимательные ученики наверняка заметят, что эта формула очень похожа на формулу расстояния в трехмерном пространстве между точками
a
и
b
. Разумеется, при условии, что точка
A
лежала бы в начале координат, а точка
B
имела координаты, равные длинам сторон нашего параллелепипеда:

A
= (0; 0; 0);

B
= (
a
,
b
,
c
).

Однако ничего удивительного в этом нет, потому что длина диагонали
l
— это как раз и есть расстояние между наиболее удаленными точками параллелепипеда.

Метод обхода точек

Но хватит теории, давайте перейдем непосредственно к нашей задаче. Итак, в первую очередь нужно найти расстояние от точки
A
до точки
C

₂. И вот для того, чтобы найти это расстояние, сейчас мы воспользуемся замечательным приемом, который называется обход точек.

Метод обхода точек заключается в следующем:

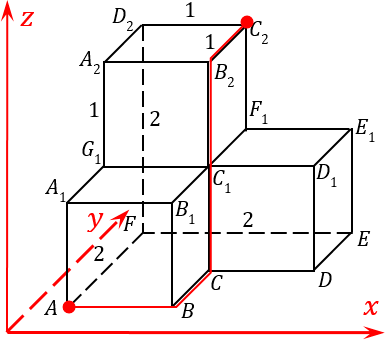
1. Построим систему координат с осями, параллельными ребрам нашего многогранника. Назовем эти оси x, y и z.
2. А теперь давайте поставим ручку в нашу точку A и попытаемся каким-то образом, двигаясь по ребрам, добраться до точки C
   ₂.

Нахождение диагонали методом обхода точек

Разумеется, последовательность осей может быть любой, решение и ответ от этого не изменится. И двигаться из одной точки в другую тоже можно по-разному. Например, можно идти к точке
B
, затем к точке
C
, затем вверх до точки
B

₂ и, наконец, двигаться вдаль — и мы попадем в точку
C

₂:

Давайте разметим, полученный нами путь:

1. Из точки A в точку B мы двигались вдоль оси x в положительном направлении. Запишем: 1x;
2. От точки B в точку C мы двигались вдоль оси игрек опять же по положительному направлению, то есть вглубь. Так и запишем 1y;
3. Затем мы шагнули на два шага вверх из точки C в точку B
   ₂. так и напишем: 2z;
4. Еще один шаг из точки B
   ₂ в точку C
   ₂ вдоль y, т. е. вглубь нашего рисунка. Запишем: 1y.

А теперь, когда мы отметили каждое звено нашей ломанной, соединяющие точки
A
и
C

₂, выпишем, сколько шагов мы получили вдоль каждой координатной оси с учетом знаков:

1. x: 1;
2. y: 1 + 1 = 2;
3. z: 2.

Теперь возвращается к нашей обобщенной теореме Пифагора и замечаем, что оси
x
,
y
и
z
— это, по сути,
a
,
b
и
c
, т. е. длины сторон параллелепипеда. Следовательно, мы можем посчитать длину диагонали этого параллелепипеда:

Вот и все! Мы получили расстояние от точки
A
до
C

₂, согласно рисунку нашего многогранника.

Диагональ параллелепипеда не зависит от маршрута обхода

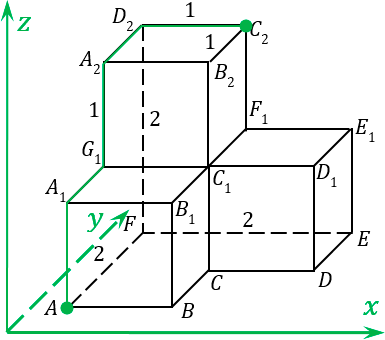
Однако внимательные ученики спросят: а что будет, если мы пойдем по другому пути? Ведь от точки
A
до точки
C

₂ можно идти и другим путем: сначала вверх до точки
A
₁, затем вглубь до точки
G

₁, затем вверх до точки
A

₂, затем снова в глубину до точки
D

₂, и, наконец вправо до точки
C

₂:

Получили совсем другой маршрут, и возникает логичный вопрос: не будет длина на этом маршруте иметь совсем другое значение координат
x
,
y
и
z
, и, соответственно, другое значение
l
? Давайте проверим.

Размечаем наш второй маршрут:

1. из точки A в точку A
   ₁ мы попадаем, смещением оси z на единичку: 1z;
2. из точки A
   ₁ в точку G
   ₁ мы попадаем, смещением по y на единичку: 1y;
3. из точки G
   ₁ в точку A
   ₂ — смещение по z: 1z;
4. из точки A
   ₂ в точку D
   ₂ — смещение по y: 1y;
5. от D
   ₂ до C
   ₂ — смещение вправо, т.е. в положительную сторону по x: 1x.

Выписываем полученные смещения:

1. x: 1
2. y: 1 + 1 = 2
3. z: 1 + 1 = 2

Итого выражение для диагонали
l
получилось в точности тем же самым:

Таким образом, мы убедились, что итоговое значение величины
l
, т. е. расстояние между точками
A
и
C

₂ не зависит от того, каким маршрутом мы будем идти из одной точки в другую. Следовательно, при решении реальных задач вы вправе выбрать любой маршрут, который будет удобен именно вам. И вообще, тот факт, что расстояние между двумя точками не зависит от того, как это расстояние мерить, на самом деле вполне логичен. Мы же занимаемся математикой, а не гаданием на кофейной гуще. Поэтому, по какому бы пути мы не пошли, ответ получится одним и тем же.

Расстояние между двумя точками в пространстве не зависит от того, как мы это расстояние считаем. Если все расчеты выполнены правильно, ответ получится одним и тем же.

Вычисление квадрата расстояния методом обхода точек

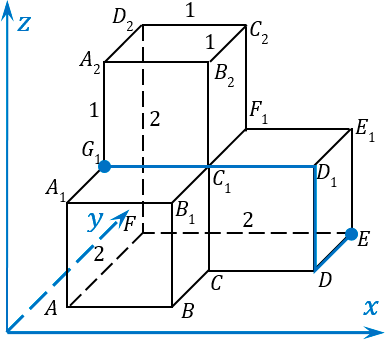
Возвращаемся к нашему заданию и переходим ко второй его части. Нужно найти расстояние между точкой
E
и точкой
G

₁. Опять предлагаю воспользоваться методом обхода точек. Начнем путь от точки
E
, будем двигаться к точке
D
, потом из точки
D
в точку
D

₁, и потом от
D

₁ напрямую в точку
G

₁:

Размечаем нашу ломанную:

1. из точки E в точку D мы попадаем смещением по оси y на единицу в сторону, противоположную положительному направлению оси: -1y;
2. затем мы поднимаемся вверх на одну единицу по оси z, т. е. этот отрезок ломанной обозначаем как 1z;
3. потом мы смещаемся влево из точки D
   ₁ в точку G
   ₁ на две единицы вдоль оси x и получаем -2x.

Давайте запишем, что у нас получилось:

1. x: -2
2. y: -1
3. z: 1

По каждой из осей зафиксировано лишь одно смещение, ничего складывать, как в предыдущих случаях, не надо. Просто находим длину отрезка, соединяющего точки
E
и
G

₁. Давайте назовем этот отрезок
l

₂. Его длина равна:

Окончательное решение задачи B13

Вспоминаем, что от нас требуется найти в условии задачи. А от нас требуется квадрат расстояния между этими вершинами. Следовательно, нам нужна величина:

l

₂
² = 6

При произведении в квадрат корень исчезает.

Внимательно читайте условие задачи. Недостаточно просто найти длину отрезка или значение переменной — нужно предъявить именно ту величину, которую у нас спрашивают.

Осталось найти ту самую разницу, которую от нас требуют найти в условии задачи. Назовем ее ∆:

∆ = 6 − 3 = 3

Вот мы и нашли ответ — он равен 3.

Ключевой прием — обход точек

Еще раз — ключевая идея решения всей этой задачи. Она состоит в том, чтобы прямо на рисунке начертить путь из одной искомой точки в другую и посмотреть: вдоль каких координатных осей выполняется смещение и насколько. Затем мы выписываем эти смещения и считаем общее расстояние по обобщенной теореме Пифагора.

При этом возникает замечательный эффект: итоговое расстояние, которое мы считаем, не зависит от того, какой маршрут обхода мы выберем. В любом случае, как бы мы ни шли из одной точки в другую, расстояние получится одним и тем же. Разумеется, при условии, что все вычисления будут выполнены верно.

Аналогичным образом мы считаем второе расстояние. Пусть вас совершенно не смущает, что тут получаются отрицательные координаты, потому что при возведении в квадрат минусы сжигаются. Наконец, остается сосчитать ту самую разницу, которую требуется найти в условии задачи. Тут вообще все очень просто, и никаких дополнительных пояснений не требуется.

Краткая сводка по задачам B13

Итак, мы решили задачу B13 мы будем методом обхода точек. Давайте еще раз посмотрим, из каких шагов состояло наше решение:

1. Добавить к рисунку оси координат, параллельные ребрам многогранника;
2. Начертить «траекторию движения» от одной точки до другой, двигаясь исключительно по ребрам исходного многогранника;
3. Выяснить, вдоль какой оси происходит смещение на каждом отрезке полученной ломаной, и посчитать общее смещение;
4. Найти итоговое расстояние по обобщенной теореме Пифагора: l
   ² = a
   ² + b
   ² + c
   ², где a, b, c — суммарные смещения вдоль каждой из осей.

Но что будет, если выбрать другой маршрут? Не случится ли так, что при этом возникнут другие суммарные смещения и, следовательно, другое расстояние? Спешу вас обрадовать: суммарные смещения и расстояние между точками не зависит от выбранного маршрута. Мы убедились в этом лично, когда рассмотрели альтернативный маршрут обхода.

В общем, чертите путь так, как вам удобно — ответ всегда будет одним и тем же. В этом и состоит прелесть метода обхода точек.

Смотрите также:

1. Обход точек в стереометрии — 2
2. Разбор задачи 8 из ЕГЭ на площадь полной поверхности призмы/параллелепипеда.
3. Решение ЕГЭ-2011: вариант 1, часть B
4. Метод коэффициентов, часть 1
5. Задача B5: площадь сектора
6. Решение задач на движение по воде



В данной работе рассмотрена задача поиска минимального расстояния между многогранником и точкой, не лежащей внутри него. Предложен алгоритм решения этой задачи и способ его применения в 3D-моделировании.

Ключевые слова:



многогранник, расстояние, алгоритм



.

Введение

При реализации метода 3D-моделирования Ray Marching необходимым является определение минимального расстояния от некоторой точки до трехмерного объекта [1]. В данной статье предлагается алгоритм поиска такого расстояния от точки до выпуклого многогранника.

Математическая постановка задачи

Определение 1.

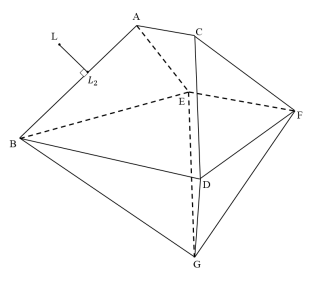
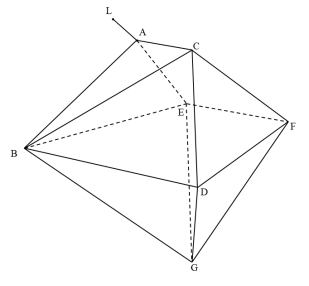
Пусть дан выпуклый многогранник и точка вне его. Минимальным расстоянием от этой точки до данного многогранника назовем длину отрезка между указанной точкой и ближайшей к ней точкой, принадлежащей многограннику.

Задача.

Втрехмерном евклидовом пространстве найти минимальное расстояние от точки

с известными координатами до выпуклого многогранника

с известными координатами вершин.

Обозначения, используемые в


статье

и

— точка вне многогранника и многогранник соответственно, между которыми определяется минимальное расстояние;

— плоскость, содержащая произвольные точки

, не лежащие на одной прямой;

— расстояние между объектами

и

, каждый из которых может быть точкой, прямой или плоскостью;

— минимальное расстояние между точкой

и выпуклым многогранником

;

,

,

— координаты точки

по осям

,

,

соответственно.

Алгоритм решения

Определим, какие из вершин многогранника

являются тремя ближайшими к

и назовем их

так, что

Проверим выполнение следующего условия:

1. 
   Проекция точки
   

   

   
   на
   

   

   
   находится внутри треугольника
   

   

   
   или на его границе
   

Рис. 1.

Пусть

— проекция

на плоскость

(рис. 1). Если она находится внутри треугольника

или на его границе, то выполнено равенство:

(см. доказательство Теоремы 1). Для того, чтобы проверить выполнение этого условия, находим координаты точки

.

Зная координаты точек

, составляем уравнение плоскости

и определяем координаты вектора нормали к ней. Используя координаты точки

и координаты направляющего вектора прямой

(являющегося вектором нормали

) составляем каноническое уравнение прямой

. Зная его и уравнение плоскости

определяем координаты точки

, которая является точкой пересечения прямой

и

. Далее проверяем принадлежность точки

треугольнику

. Метод проверки описан в статье [2]. При выполнении данного условия

. Находим его как расстояние между двумя точками в пространстве.

В случае невыполнения условия пункта 1, переходим к проверке следующего условия.

1. 
   Проекция точки
   

   

   
   на прямую
   

   

   
   принадлежит отрезку
   

   

Рис. 2.

Пусть

— проекция

на прямую

(рис. 2). Если

принадлежит отрезку

, то выполнено равенство:

(см. доказательство Теоремы 2). Для проверки выполнения этого условия находим координаты точки

.

Для этого определяем координаты вектора

, являющегося направляющим вектором прямой

, и подставляем их в каноническое уравнение прямой

. Далее составляем уравнение плоскости

, проходящей через точку

перпендикулярно прямой

и находим координаты точки пересечения плоскости

с прямой

, являющиеся координатами точки

.

Если выполнена система неравенств:

, то

принадлежит отрезку

.

При выполнении данного условия

. Находим его как расстояние между двумя точками в пространстве.

При невыполнении пунктов 1 и 2 (рис. 3) задача сводится к поиску расстояния между

и

, поскольку расстояние от

до

не является ни расстоянием от

до ближайшей грани

, ни расстоянием от

до ближайшего ребра

.

Рис. 3.

Для проверки корректности данного алгоритма рассмотрим следующие теоремы.

Теорема 1.

Минимальное расстояние от некоторой точки

, лежащей вне выпуклого многогранника, до этого многогранника равно расстоянию от

до ближайшей к ней грани этого многогранника тогда и только тогда, когда проекция точки

на плоскость, содержащую эту грань, принадлежит треугольнику, образованному тремя ближайшими к

вершинами многогранника.

Доказательство

. Пусть

— ближайшие к

вершины многогранника

, при этом

. Пусть

— проекция точки

на

.

Пусть

лежит принадлежит треугольнику

. Тогда

— ближайшая к

точка треугольника

, поскольку

— высота пирамиды

. Поскольку треугольник

принадлежит ближайшей к

грани многогранника, то расстоянием от

до этой грани является длина отрезка

. Расстояние до ближайшей к

грани многогранника меньше, чем расстояние от

до любой другой грани многогранника, следовательно, длина отрезка

и есть минимальное расстояние от

до многогранника.

Пусть

находится вне треугольника

. Следовательно,

находится вне грани, которой принадлежит этот треугольник. Эта грань — единственная, принадлежащая плоскости

, поскольку многогранник выпуклый. Поэтому

не принадлежит многограннику, следовательно, отрезок

не является минимальным расстоянием от

до многогранника.

Теорема 2.

Минимальное расстояние от некоторой точки

, лежащей вне выпуклого многогранника, до этого многогранника равно расстоянию от

до ближайшего к ней ребра этого многогранника тогда и только тогда, когда проекция точки

на прямую, содержащую это ребро, принадлежит этому ребру, а проекция точки

на плоскость, образованную тремя ближайшими к

вершинами многогранника совпадает с проекцией

на ближайшее к ней ребро многогранника или лежит вне треугольника, образованного тремя ближайшими к

вершинами многогранника.

Доказательство.

Пусть

— ближайшие к

вершины многогранника

, при этом

;

— прямая, содержащая отрезок

;

— проекция точки

на

;

— проекция точки

на

.

Пусть

принадлежит отрезку

,

лежит вне треугольника

. Проведем плоскость

, содержащую

и не имеющую общих точек с двумя гранями многогранника, пересекающимися по ребру

. Все точки многогранника, за исключением точек, принадлежащих ребру

, будут находится по другую сторону плоскости

относительно точки

, поэтому расстояние от

до любой точки многогранника будет больше, чем расстояние от

до

. Поскольку

и есть расстояние от

до

и

принадлежит многограннику, длина отрезка

является минимальным расстоянием от

до многогранника.

Пусть

принадлежит отрезку

,

совпадает с

. В этом случае по теореме 1 минимальное расстояние от

до многогранника есть

. Поскольку

совпадает с

,

является минимальным расстоянием от

до многогранника.

Пусть

не принадлежит отрезку

. Отрезок

— единственное ребро многогранника, принадлежащее

, поскольку многогранник выпуклый, следовательно,

не принадлежит многограннику, и поэтому отрезок

не является минимальным расстоянием от

до многогранника.

Применение данного алгоритма

Ray Marching — одна из относительно новых технологий, используемых для рендеринга трехмерных сцен. При ее реализации для рендеринга непрозрачных объектов можно использовать поля расстояний со знаком, что позволит оптимизировать вычислительный процесс. Поле расстояния — это функция, определяющая расстояние от точки до поверхности объекта [3]. Вышеописанный метод может быть использован для определения минимальных расстояний до любых выпуклых многогранников.

Литература:

1. Ray Marching Distance Fields in Real-time on WebGL. — Текст: электронный // semanticscholar: [сайт]. — URL: https://pdfs.semanticscholar.org/a964/750aa212bd490d258221bc9756e7e58c5317.pdf (дата обращения: 18.07.2020).
2. Weisstein, Eric W. Triangle Interior. — Текст: электронный // mathworld: [сайт]. — URL: https://mathworld.wolfram.com/TriangleInterior.html (дата обращения: 18.07.2020).
3. GPU Ray Marching of Distance Fields / J. T. Lukasz. — Текст: электронный // DTU.compute: [сайт]. — URL: http://www2.imm.dtu.dk/pubdb/edoc/imm6392.pdf (дата обращения: 19.07.2020).

01
Янв 2012

05 Задание (2022)

Задание В5: ищем расстояние между двумя точками

|
Отзывов нет
| Метки: решение задания В9

В данной статье хочу рассказать вам об определённом типе задач по стереометрии, одну из которых, возможно, предстоит решить именно вам на ЕГЭ по математике. Это задачи на решение составных многогранников:

Обычно требуется найти расстояние (или квадрат расстояния) между двумя точками; какой-либо угол, либо значение одной из тригонометрических функций обозначенного в условии угла.

Для решения  необходимо знать совсем не много теории: теорему Пифагора; определения синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике; значения углов тригонометрических функций.

Рассмотрим задачи:

Найдите расстояние между вершинами А и С₂  многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Результат умножьте на  корень из шести  и запишите ответ.

Соединим точки  А и С₂   и рассмотрим  прямоугольный треугольник АА₂С₂:

По теореме Пифагора:

Ответ: 6

Найдите угол САD₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.

Соединим точки C, А, D₂:

Рассмотрим треугольник CАD₂:  AC = CD₂ = AD₂, так как являются диагоналями квадратов со сторонами равными 8. Следовательно, треугольник CАD₂ – равносторонний, то есть все его  углы равны 60°.

Таким образом, угол CАD₂ = 60°.

Ответ: 60

Найдите квадрат расстояния между вершинами В₂ и D₃ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Соединим точки B₂, B₃ и D₃. Рассмотрим прямоугольный треугольник B₂B₃D₃:

По теореме Пифагора:

Ответ: 12

Найдите тангенс угла АBB₃ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Соединим точки В и B₃, из точки B₃ опустим перпендикуляр на ребро АВ, точку пересечения обозначим как К. Рассмотрим прямоугольный треугольник КВB₃:

Ответ: 2

Найдите квадрат расстояния между вершинами D и C₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Соединим точки В  и C₂, а так же C₂  и С:

Рассмотрим прямоугольный треугольник СВС₂.  По теореме Пифагора:

Ответ: 46

245376. Найдите квадрат расстояния между вершинами В₂ и D₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Посмотреть решение

245380. Найдите тангенс угла AВB₃ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Посмотреть решение

245382. Найдите квадрат расстояния между вершинами D и C₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Посмотреть решение

При решении подобных заданий главное – это «увидеть» треугольник, в который входит искомый элемент (отрезок, угол) и построить этот треугольник.  А далее уже использовать указанную в начале статьи теорию.

Есть ещё задачи с параллелепипедами:

245359   245360   245361   245362   245363

Процесс решения в них сводится к решению прямоугольного треугольника: нужно найти расстояние между вершинами (квадрат расстояния), либо заданный угол.

Мы продолжим рассматривать задачи по стереометрии? не пропустите! На этом всё. Как видите, ничего сложного. Успеха вам!

С уважением, Александр.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Многогранник – это поверхность, составленная из многоугольников, ограничивающая некоторое геометрическое тело.

В данной теме мы рассмотрим составные многогранники (многогранники, состоящие обычно из нескольких параллелепипедов).

Объемы различных многогранников:

• Призма $V=S_{осн}·h$
• Пирамида $V={1}/{3}S_{осн}·h$
• Параллелепипед $V=a·b·c$, где $a, b$ и $c$ — длина, ширина и высота.
• Куб $V=а^3$, где $а$ — сторона куба

Задачи на нахождение объема составного многогранника:

• Первый способ.

1. Составной многогранник надо достроить до полного параллелепипеда или куба.
2. Найти объем параллелепипеда.
3. Найти объем лишней части фигуры.
4. Вычесть из объема параллелепипеда объем лишней части.

• Второй способ

1. Разделить составной многогранник на несколько параллелепипедов.
2. Найти объем каждого параллелепипеда.
3. Сложить объемы.

Задачи на нахождение площади поверхности составного многогранника.

— Если можно составной многогранник представить в виде прямой призмы, то находим площадь поверхности по формуле:

$S_{полн.пов.}=P_{осн}·h+2S_{осн}$

Чтобы найти площадь основания призмы, надо разделить его на прямоугольники и найти площадь каждого.

— Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.

Задачи на нахождение расстояния между точками составного многогранника.

В данных задачах приведены составные многогранники, у которых двугранные углы прямые. Надо соединить расстояние между заданными точками и достроить его до прямоугольного треугольника. Далее остается воспользоваться теоремой Пифагора для нахождения нужной стороны.

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

$АС^2+ВС^2=АВ^2$