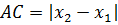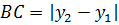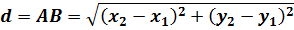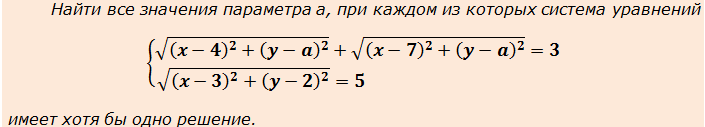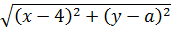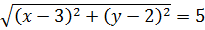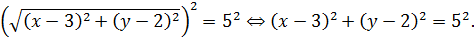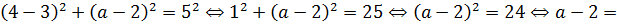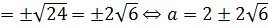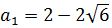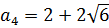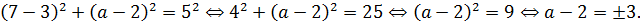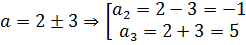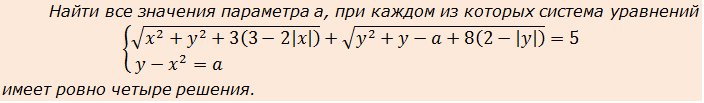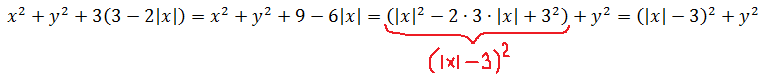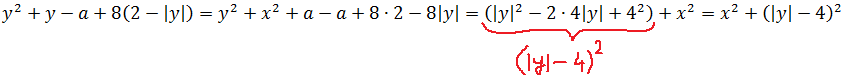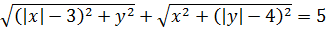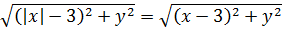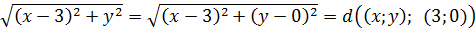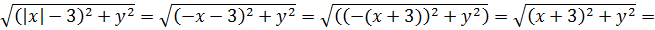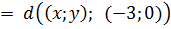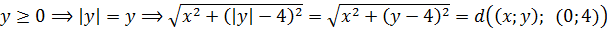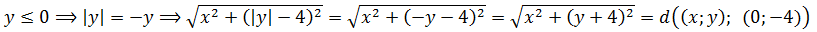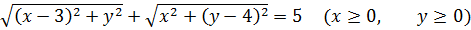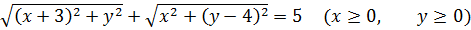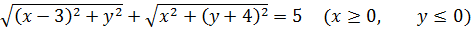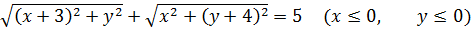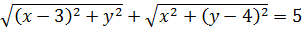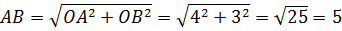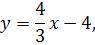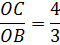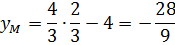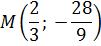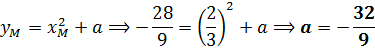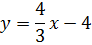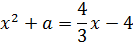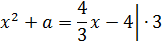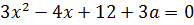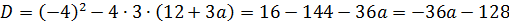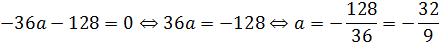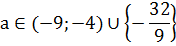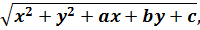Как найти расстояние на графике зависимости - Исправление недочетов и поиск решений вместе с Examum.ru

Вычисление перемещения по графику проекции скорости

Из кодификатора по физике, 2020.
«1.1.3. Вычисление перемещения по графику зависимости υ(t).»

Теория

Пусть задан график зависимости проекции скорости ${ v }_{ x }$ от времени t (рис. 1).

Проекция перемещении тела ${ s }_{ x }$ за промежуток времени от ${ t }_{ 1 }$ до ${ t }_{ 2 }$ численно равна по величине площади фигуры, ограниченной графиком ${ v }_{ x }(t)$ , осью времени 0t и перпендикулярами к ${ t }_{ 1 }$ и ${ t }_{ 2 }$ (см. рис. 1, площадь выделена штриховкой).

Проекцию перемещения на ось 0Х будем считать:

— положительной, если проекция скорости на данную ось будет положительной (тело движется по направлению оси) (см. рис. 1);

— отрицательной, если проекция скорости на данную ось будет отрицательной (тело движется против оси) (рис. 2).

Путь s может быть только положительным:

Напоминаем формулы для расчета площадей фигур:

— прямоугольника –

— треугольника – $S=frac { acdot h }{ 2 }$

— трапеции – $S=frac { a+b }{ 2 } cdot h$

Задачи

Задача 1. По графику проекции скорости тела (рис. 3) определите проекцию его перемещения между 1 и 5 с.

Ответ: ____ м.

Решение. Проекция перемещения за промежуток времени Δt= ${ t }_{ 2 }$ – ${ t }_{ 1 }$ =5с–1с=4c численно равна площади фигуры, ограниченной графиком ${ v }_{ x }(t)$ , осью времени 0t и перпендикулярами к ${ t }_{ 1 }=1$ с и ${ t }_{ 2 }=5$ с (рис. 4, площадь выделена штриховкой). Фигура ABCD — это трапеция, ее площадь равна

$S=frac { a+b }{ 2 } cdot h=frac { AD+BC }{ 2 } cdot DC$

где DC = Δt = 4 c, AD = 3 м/c, BC = 5 м/c. Тогда S = 16 м.
Проекция перемещения ${ s }_{ x }>0$ , т.к. проекция скорости ${ v }_{ x }>0$ .
${ s }_{ x }=S=16$ м.

Ответ: 16.

Задача 2. Автомобиль движется по прямой улице вдоль оси X. На рисунке 5 представлен график зависимости проекции скорости автомобиля от времени. Определите путь, пройденный автомобилем в течение указанных интервалов времени.

Интервал времени	Путь
от 0 до 10 с	Ответ: м.
от 30 до 40 с	Ответ: м.

В бланк ответов перенесите только числа, не разделяя их пробелом или другим знаком.

Решение. Путь за промежуток времени Δt = ${ t }_{ 2 }$ – ${ t }_{ 1 }$ численно равна площади фигуры, ограниченной графиком ${ v }_{ x }(t),$ осью времени 0t и перпендикулярами к ${ t }_{ 1 }$ и ${ t }_{ 2 }$ .

На интервале [0 с, 10 с] ищем площадь треугольника (рис. 6).

${ S }_{ 1 }=frac { acdot h }{ 2 }$ ,

где a = 20 м/c, $h=triangle { t }_{ 1 }=10c-0c=10c$ . Тогда ${ S }_{ 1 }=100$ м.

Путь равен значению площади (путь всегда положительный, т.е. s > 0).

${ s }_{ 1 }={ S }_{ 1 }=100$ м.

На интервале [30 с, 40 с] ищем площадь трапеции (см. рис. 6).

${ S }_{ 2 }=frac { a+b }{ 2 } cdot h$ ,

где a = 10 м/c, b = 15 м/c, h = Δt = 40 c – 30 с = 10 с. Тогда ${ s }_{ 2 }={ S }_{ 2 }=125$ м.

Ответ: 100125.

Задача 3. Определите за первые 4 с (рис. 7):

а) проекцию перемещения тела;

б) пройденный путь.

Ответ: а) ____ м; б) ____ м.

Решение. Проекция перемещения за время $triangle t={ t }_{ 2 }-{ t }_{ 1 }=4c-0=4c$ (пер-вые 4 с) численно равна площади фигуры, ограниченной графиком ${ v }_{ x }(t)$ , осью времени 0t и перпендикулярами к ${ t }_{ 1 }=0$ с и ${ t }_{ 2 }=4$ с (рис. 8, площадь выделена штриховкой).

Так как при ${ t }_{ 0 }=3$ с проекция скорости поменяла знак, то получили две фигуры, два треугольника, площади которых равны:

${ S }_{ 1 }=frac { { a }_{ 1 }cdot { h }_{ 1 } }{ 2 } ,quad { S }_{ 2 }=frac { { a }_{ 2 }cdot { h }_{ 2 } }{ 2 }$ ,

где

${ a }_{ 1 }=30quad$ м/с, $quad { h }_{ 1 }=triangle { t }_{ 1 }=3c-0c=3c$

${ a }_{ 2 }$ =|-10 м/c|=10 м/c, $quad { h }_{ 2 }=triangle { t }_{ 2 }=4c-3c=1c$ .

Тогда ${ S }_{ 1 }=45$ м, $quad { S }_{ 2 }=5$ м.

а) Проекция перемещения ${ s }_{ 1x }>0$ , т.к. проекция скорости ${ v }_{ 1x }>0$ ; проекция перемещения ${ s }_{ 2x }<0$ , т.к. проекция скорости ${ v }_{ 2x }<0$ . В итоге получаем: ${ s }_{ x }={ s }_{ 1x }+{ s }_{ 2x }={ S }_{ 1 }-{ S }_{ 2 },quad { s }_{ 1x }=$ 45м — 5м = 40 м. б) Путь равен значению площади (путь всегда положительный, т.е. s>0).

$s={ S }_{ 1 }+{ S }_{ 2 }$ , s = 45 м + 5 м = 50 м.

Ответ: а) 40; б) 50.

Задача 4. График зависимости проекции скорости материальной точки, движущейся вдоль оси 0Х, от времени изображен на рисунке 9. Определите перемещение точки, которое она совершила за первые 6 с.

Ответ: ____ м.

Решение. Проекция перемещения за время $triangle t={ t }_{ 2 }-{ t }_{ 1 }=6c-0=6c$ (пер-вые 6 с) численно равна площади фигуры, ограниченной графиком ${ v }_{ x }(t)$ , осью времени 0t и перпендикулярами к ${ t }_{ 1 }=0 c$ и ${ t }_{ 2 }=6 c$ (рис. 10, площадь выделена штриховкой).

Так как при ${ t }_{ 01 }=2c$ и ${ t }_{ 02 }=4c$ проекция скорости меняет знак, то получили три фигуры, три треугольника, площади которых равны:

${ S }_{ 1 }=frac { { a }_{ 1 }cdot { h }_{ 1 } }{ 2 } ,quad { S }_{ 2 }=frac { { a }_{ 2 }cdot { h }_{ 2 } }{ 2 } ,quad { S }_{ 3 }=frac { { a }_{ 3 }cdot { h }_{ 3 } }{ 2 } ,$

где

${ a }_{ 1 }=3$ м/с, $h_{ 1 }=triangle { t }_{ 1 }=2c-0c=2c$

${ a }_{ 2 }=$ |-2 м/c| = 2 м/с, $h_{ 2 }=triangle { t }_{ 2 }=4c-2c=2c$

${ a }_{ 2 }=$ 3м/c, $h_{ 3 }=triangle { t }_{ 3 }=6c-4c=2c$ .

Тогда ${ S }_{ 1 }=3$ м, ${ S }_{ 2 }=2$ м, ${ S }_{ 3 }=3$ м.

Проекция перемещения ${ s }_{ 1x }>0$ , т.к. проекция скорости ${ v }_{ 1x }>0$ .

Проекция перемещения ${ s }_{ 2x }<0$ , т.к. проекция скорости ${ v }_{ 2x }<0$ . Проекция перемещения ${ s }_{ 3x }>0$ , т.к. проекция скорости ${ v }_{ 3x }>0$ . В итоге получаем:

${ s }_{ x }={ s }_{ 1x }+{ s }_{ 2x }+{ s }_{ 3x }={ S }_{ 1 }-{ S }_{ 2 }+{ S }_{ 3 },quad { s }_{ x }=$ 3 м – 2 м + 3 м = 4 м.

Ответ: 4.

Задача 5. На рисунке приведен график зависимости v_x скорости тела от времени .

Определите путь, пройденный телом в интервале времени от 0 до 5 с.

Ответ: ____ м.

Решение. Решение любых графических задач основывается на умении «читать» графики. В данной задаче рассматривается зависимость проекции скорости тела от времени. На интервале от 0 до 3с проекция скорости уменьшается от значения 15 м/с до 0. На интервале от 3 до 5с модуль проекции начинает возрастать от нулевого значения до 10 м/с. Причем важно «увидеть», что тело в этом временном интервале начинает движение в направлении, противоположном оси ОХ.

Пройденный путь будет определяться площадью геометрической фигуры, образованной под графиком проекции скорости.

Рис.1

Дальнейшее решение задачи сводится к нахождению площадей двух треугольников, заштрихованных на рис.1

$S_1=frac{15cdot 3}{2}=22,5$ (м).

$S_2=frac{10cdot 2}{2}=10$ (м).

Тогда, общий путь в интервале времени от 0 до 5с будет определяться суммой отдельных путей S_1 и S_2 .

(м).
Ответ: 32,5 м

По условию этой задачи можно поставить второй вопрос: найти проекцию перемещения в интервале времени от 0 до 5с.

В этом случае надо учесть, что проекция перемещения в интервале времени от 0 до 3 с положительная и её значение равно пройденному пути на этом интервале.

$S_{1x}=S_1=22,5$ (м).

В интервале времени от 3 с до 5 с проекция перемещения отрицательная, так как тело движется в направлении противоположном оси ОХ.

$S_{2x}=-10$ (м).

Проекция перемещения за весь интервал времени будет равна $S_{o.x}=S_{1x}+S_{2x}$
$S_{o.x}=22,5+(-10)=12,5$ (м).

Ответ: 12,5 м

Задача 6. На рисунке представлен график зависимости модуля скорости v прямолинейно движущегося тела от времени t. Определите по графику путь, пройденный телом в интервале времени от 1 до 5 с.

Ответ: ____ м.

Решение. Для нахождения пройденного пути в интервале времени от 1с до 5с необходимо рассчитать площадь геометрической фигуры под графиком модуля скорости.

Рис.1

Дальнейшее решение сводится к расчету площади трапеции, заштрихованной на графике (см. рис.1).

$S=frac{4+2}{2}cdot 10=30$ (м).

Особенностью подобной задачи является то, что при решении, необходимо внимательно отследить временной интервал, на котором требуется рассчитать пройденный путь.
Ответ: 30 м.

Задача 7. Из двух городов навстречу друг другу с постоянной скоростью двиижутся два автомобиля. На графике показана зависимость расстояния между автомобилями от времени. Скорость первого автомобиля равна 15 м/с. Какова скорость второго автомобиля?

Ответ: ____ м.

Решение. При движении навстречу друг к другу расстояние между двумя автомобилями уменьшается от значения 144 км до 0. На графике видно, что встреча автомобилей произошла в момент времени 60 минут, так как расстояние между автомобилями стало равным 0. Расчеты в этой задаче требуют обязательного применения системы «СИ».

144 км = 144000 м; 60 мин = 3600 с.
Используя эти данные, можно рассчитать скорость сближения автомобилей.

$v=frac{144000}{3600}=40$ м/с

Так как автомобили движутся навстречу друг другу, то отсюда скорость второго автомобиля можно выразить как

(м/с)

Ответ: 25 м/с.

Задача 8. На рисунке представлен график зависимости модуля скорости тела от времени. Найдите путь, пройденный телом за время от момента времени 0 с до момента времени 5 с. (Ответ дайте в метрах.)

Ответ: ____ м.

Решение. Для нахождения пройденного пути необходимо рассчитать площадь геометрической фигуры (трапеции) под графиком модуля скорости (см.рис.1). Это относится к интервалу времени от 0 до 3 с. От 3 с до 5 с скорость тела равна 0, следовательно, тело находилось в состоянии покоя и пройденный путь в этом интервале равен 0.

Рис.1

$S_1=frac{3+1}{2}cdot 10=20$ (м).
S_2=0
(м).

Сакович А.Л., 2020

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Вычисление перемещения по графику проекции скорости» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

1. Нахождение пути по графику зависимости скорости от времени

Покажем, как можно найти пройденный телом путь с помощью графика зависимости скорости от времени.

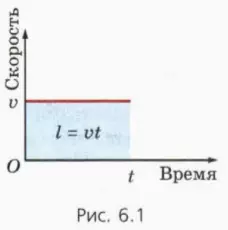
Начнем с самого простого случая – равномерного движения. На рисунке 6.1 изображен график зависимости v(t) – скорости от времени. Он представляет собой отрезок прямой, параллельной осн времени, так как при равномерном движении скорость постоянна.

Фигура, заключенная под этим графиком, – прямоугольник (он закрашен на рисунке). Его площадь численно равна произведению скорости v на время движения t. С другой стороны, произведение vt равно пути l, пройденному телом. Итак, при равномерном движении

путь численно равен площади фигуры, заключенной под графиком зависимости скорости от времени.

Покажем теперь, что этим замечательным свойством обладает и неравномерное движение.

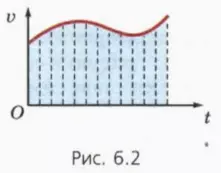
Пусть, например, график зависимости скорости от времени имеет вид кривой, изображенной на рисунке 6.2.

Разобьем мысленно все время движения на столь малые промежутки, чтобы в течение каждого из них движение тела можно было считать практически равномерным (это разбиение показано штриховыми линиями на рисунке 6.2).

Тогда путь, пройденный за каждый такой промежуток, численно равен площади фигуры под соответствующим ком графика. Поэтому и весь путь равен площади фигур заключенной под всем графиком. (Использованный нами прием лежит в основе интегрального исчисления, основы которого вы будете изучать в курсе «Начала математического анализа».)

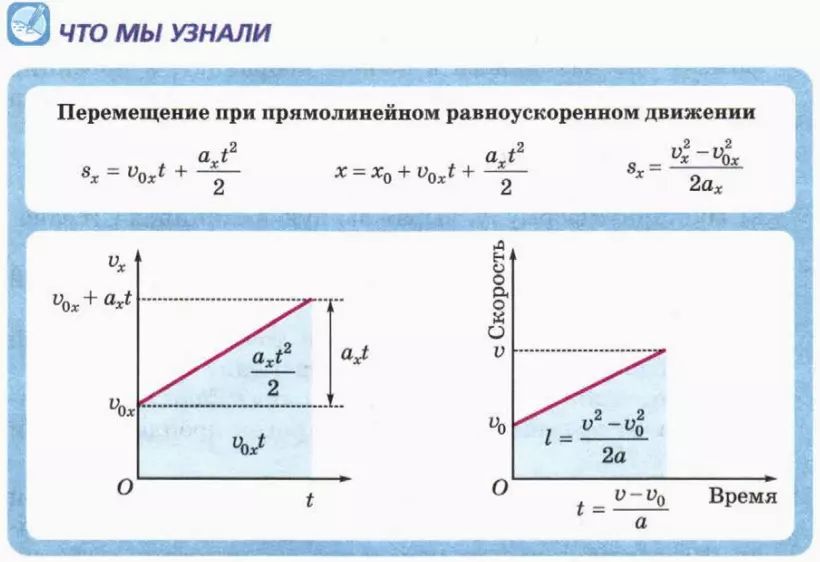
2. Путь и перемещение при прямолинейном равноускоренном движении

Применим теперь описанный выше способ нахождения пути к прямолинейному равноускоренному движению.

Начальная скорость тела равна нулю

Направим ось x в сторону ускорения тела. Тогда a_x = a, v_x = v. Следовательно,

v = at. (1)

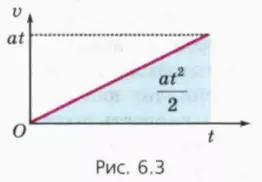
На рисунке 6.3 изображен график зависимости v(t).

? 1. Используя рисунок 6.3, докажите, что при прямолинейном равноускоренном движении без начальной скорости путь l выражается через модуль ускорения a и время движения t формулой

l = at²/2. (2)

Главный вывод:

при прямолинейном равноускоренном движении без начальной скорости пройденный телом путь пропорционален квадрату времени движения.

Этим равноускоренное движение существенно отличается от равномерного.

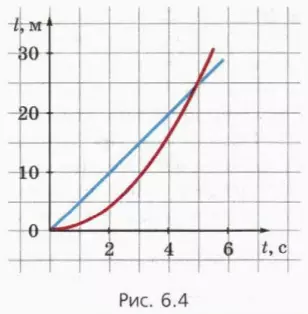
На рисунке 6.4 приведены графики зависимости пути от времени для двух тел, одно из которых движется равномерно, а другое – равноускоренно без начальной скорости.

? 2. Рассмотрите рисунок 6.4 и ответьте на вопросы.
а) Каким цветом изображен график для тела, движущегося равноускоренно?
б) Чему равно ускорение этого тела?
в) Чему равны скорости тел в тот момент, когда они прошли одинаковый путь?
г) В какой момент времени скорости тел равны?

? 3. Тронувшись с места, автомобиль за первые 4 с проехал расстояние 20 м. Движение автомобиля считайте прямолинейным равноускоренным. Не вычисляя ускорения автомобиля, определите, какое расстояние проедет автомобиль:
а) за 8 с? б) за 16 с? в) за 2 с?

Найдем теперь зависимость проекции перемещения s_x от времени. В данном случае проекция ускорения на ось x положительна, поэтому s_x = l, a_x = a. Таким образом, из формулы (2) следует:

s_x = a_xt²/2. (3)

Формулы (2) и (3) очень похожи, что приводит порой к ошибкам при решении простых задач. Дело в том, что значение проекции перемещения может быть отрицательным. Так будет, если ось x направлена противоположно перемещению: тогда s_x < 0. А путь отрицательным быть не может!

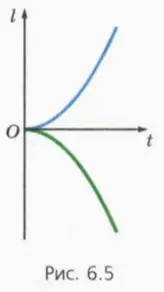
? 4. На рисунке 6.5 изображены графики зависимости от времени пути и проекции перемещения для некоторого тела. Какой цвет у графика проекции перемещения?

Начальная скорость тела не равна нулю

Напомним, что в таком случае зависимость проекции скорости от времени выражается формулой

v_x = v_0x + a_xt, (4)

где v_0x – проекция начальной скорости на ось x.

Мы рассмотрим далее случай, когда v_0x > 0, a_x > 0. В этом случае снова можно воспользоваться тем, что путь численно равен площади фигуры под графиком зависимости скорости от времени. (Другие комбинации знаков проекции начальной скорости и ускорения рассмотрите самостоятельно: в результате получится та же общая формула (5).

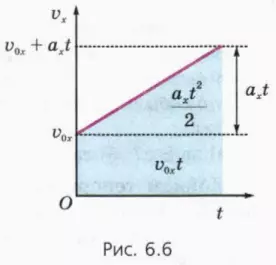
На рисунке 6.6 изображен график зависимости v_x(t) при v_0x > 0, a_x > 0.

? 5. Используя рисунок 6.6, докажите, что при прямолинейном равноускоренном движении с начальной скоростью проекция перемещения

s_x = v_0x + a_xt²/2. (5)

Эта формула позволяет найти зависимость координаты x тела от времени. Напомним (см. формулу (6), § 2), что координата x тела связана с проекцией его перемещения s_x соотношением

s_x = x – x₀,

где x₀ — начальная координата тела. Следовательно,

x = x₀ + s_x, (6)

Из формул (5), (6) получаем:

x = x₀ + v_0xt + a_xt²/2. (7)

6. Зависимость координаты от времени для некоторого тела, движущегося вдоль оси x, выражается в единицах СИ формулой x = 6 – 5t + t².
а) Чему равна начальная координата тела?
б) Чему равна проекция начальной скорости на ось x?
в) Чему равна проекция ускорения на ось x?
г) Начертите график зависимости координаты x от времени.
д) Начертите график зависимости проекции скорости от времени.
е) В какой момент скорость тела равна нулю?
ж) Вернется ли тело в начальную точку? Если да, то в какой момент (моменты) времени?
з) Пройдет ли тело через начало координат? Если да, то в какой момент (моменты) времени?
и) Начертите график зависимости проекции перемещения от времени.
к) Начертите график зависимости пути от времени.

3. Соотношение между путем и скоростью

При решении задач часто используют соотношения между путем, ускорением и скоростью (начальной v₀, конечной v или ими обеими). Выведем эти соотношения. Начнем с движения без начальной скорости. Из формулы (1) получаем для времени движения:

t = v/a. (8)

Подставим это выражение в формулу (2) для пути:

l = at²/2 = a/2(v/a)² = v²/2a. (9)

Главный вывод:

при прямолинейном равноускоренном движении без начальной скорости пройденный телом путь пропорционален квадрату конечной скорости.

? 7. Тронувшись с места, автомобиль набрал скорость 10 м/с на пути 40 м. Движение автомобиля считайте прямолинейным равноускоренным. Не вычисляя ускорения автомобиля, определите, какой путь от начала движения проехал автомобиль, когда его скорость была равна: а) 20 м/с? б) 40 м/с? в) 5 м/с?

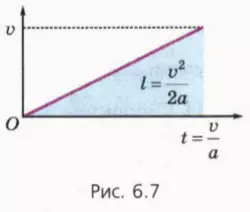
Соотношение (9) можно получить также, вспомнив, что путь численно равен площади фигуры, заключенной под графиком зависимости скорости от времени (рис. 6.7).

Это соображение поможет вам легко справиться со следующим заданием.

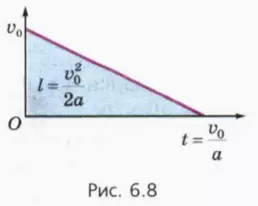
? 8. Используя рисунок 6.8, докажите, что при торможении с постоянным ускорением тело проходит до полной остановки путь l_т = v₀²/2a, где v₀ – начальная скорость тела, a – модуль ускорения.

В случае торможения транспортного средства (автомобиль, поезд) путь, пройденный до полной остановки, называют тормозным путём. Обратите внимание: тормозной путь при начальной скорости v₀ и путь, пройденный при разгоне с места до скорости v₀ с тем же по модулю ускорением a, одинаковы.

? 9. При экстренном торможении на сухом асфальте ускорение автомобиля равно по модулю 5 м/с². Чему равен тормозной путь автомобиля при начальной скорости: а) 60 км/ч (максимальная разрешенная скорость в городе); б) 120 км/ч? Найдите тормозной путь при указанных скоростях во время гололеда, когда модуль ускорения равен 2 м/с². Сравните найденные вами значения тормозного пути с длиной классной комнаты.

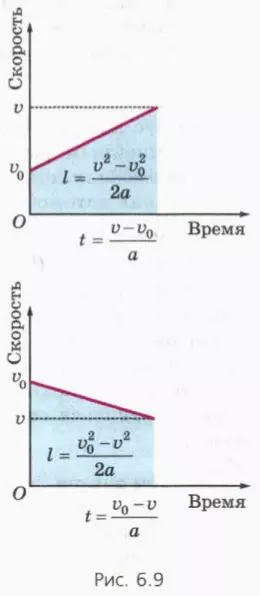
? 10. Используя рисунок 6.9 и формулу, выражающую площадь трапеции через ее высоту и полусумму оснований, докажите, что при прямолинейном равноускоренном движении:
а) l = (v² – v₀²)/2a, если скорость тела увеличивается;
б) l = (v₀² – v²)/2a, если скорость тела уменьшается.

? 11. Докажите, что проекции перемещения, начальной и конечной скорости, а также ускорения связаны соотношением

s_x = (v_x² – v_0x²)/2ax (10)

? 12. Автомобиль на пути 200 м разогнался от скорости 10 м/с до 30 м/с.
а) С каким ускорением двигался автомобиль?
б) За какое время автомобиль проехал указанный путь?
в) Чему равна средняя скорость автомобиля?

Лютый опыт

Дополнительные вопросы и задания

13. От движущегося поезда отцепляют последний вагон, после чего поезд движется равномерно, а вагон – с постоянным ускорением до полной остановки.
а) Изобразите на одном чертеже графики зависимости скорости от времени для поезда и вагона.
б) Во сколько раз путь, пройденный вагоном до остановки, меньше пути, пройденного поездом за то же время?

14. Отойдя от станции, электричка какое-то время ехала равноускоренно, затем в течение 1 мин – равномерно со скоростью 60 км/ч, после чего снова равноускоренно до остановки на следующей станции. Модули ускорений при разгоне и торможении были различны. Расстояние между станциями электричка прошла за 2 мин.
а) Начертите схематически график зависимости проекции скорости электрички от времени.
б) Используя этот график, найдите расстояние между станциями.
в) Какое расстояние проехала бы электричка, если бы на первом участке пути она разгонялась, а на втором – тормозила? Какова была бы при этом ее максимальная скорость?

15. Тело движется равноускоренно вдоль оси x. В начальный момент оно находилось в начале координат, а проекция его скорости была равна 8 м/с. Через 2 с координата тела стала равной 12 м.
а) Чему равна проекция ускорения тела?
б) Постройте график зависимости v_x(t).
в) Напишите формулу, выражающую в единицах СИ зависимость x(t).
г) Будет ли скорость тела равна нулю? Если да, то в какой момент времени?
д) Побывает ли тело второй раз в точке с координатой 12 м? Если да, то в какой момент времени?
е) Вернется ли тело в начальную точку? Если да, то в какой момент времени, и чему будет равен пройденный при этом путь?

16. После толчка шарик вкатывается вверх по наклонной плоскости, после чего возвращается в начальную точку. На расстоянии b от начальной точки шарик побывал дважды через промежутки времени t₁ и t₂ после толчка. Вверх и вниз вдоль наклонной плоскости шарик двигался с одинаковым по модулю ускорением.
а) Направьте ось x вверх вдоль наклонной плоскости, выберите начало координат в точке начального положения шарика и напишите формулу, выражающую зависимость x(t), в которую входят модуль начальной скорости шарика v0 и модуль ускорения шарика a.
б) Используя эту формулу и тот факт, что на расстоянии b от начальной точки шарик побывал в моменты времени t₁ и t₂ составьте систему двух уравнений с двумя неизвестными v₀ и a.
в) Решив эту систему уравнений, выразите v₀ и a через b, t₁ и t₂.
г) Выразите весь пройденный шариком путь l через b, t₁ и t₂.
д) Найдите числовые значения v₀, a и l при b = 30 см, t₁ = 1с, t₂ = 2 с.
е) Постройте графики зависимости v_x(t), s_x(t), l(t).
ж) С помощью графика зависимости sx(t) определите момент, когда модуль перемещения шарика был максимальным.

Источник

Если траектория движения точки известна, то зависимость пути

, пройденного точкой, от истекшего промежутка времени

дает полное описание этого движения. Мы видели, что для равномерного движения такую зависимость можно дать в виде формулы (9.2). Связь между

и

для отдельных моментов времени можно задавать также в виде таблицы, содержащей соответственные значения промежутка времени и пройденного пути. Пусть нам дано, что скорость некоторого равномерного движения равна 2 м/с. Формула (9.2) имеет в этом случае вид

. Составим таблицу пути и времени такого движения:

t, с	1	2	3	4	5	6	…
s, м	2	4	6	8	10	12	…

Зависимость одной величины от другой часто бывает удобно изображать не формулами или таблицами, а графиками, которые более наглядно показывают картину изменения переменных величин и могут облегчать расчеты. Построим график зависимости пройденного пути от времени для рассматриваемого движения. Для этого возьмем две взаимно перпендикулярные прямые — оси координат; одну из них (ось абсцисс) назовем осью времени, а другую (ось ординат) — осью пути. Выберем масштабы для изображения промежутков времени и пути и примем точку пересечения осей за начальный момент и за начальную точку на траектории. Нанесем на осях значения времени и пройденного пути для рассматриваемого движения (рис. 18). Для «привязки» значений пройденного пути к моментам времени проведем из соответственных точек на осях (например, точек 3 с и 6 м) перпендикуляры к осям. Точка пересечения перпендикуляров соответствует одновременно обеим величинам: пути

и моменту

, — этим способом и достигается «привязка». Такое же построение можно выполнить и для любых других моментов времени и соответственных путей, получая для каждой такой пары значений время — путь одну точку на графике. На рис. 18 выполнено такое построение, заменяющее обе строки таблицы одним рядом точек. Если бы такое построение было выполнено для всех моментов времени, то вместо отдельных точек получилась бы сплошная линия (также показанная на рисунке). Эта линия и называется графиком зависимости пути от времени или, короче, графиком пути.

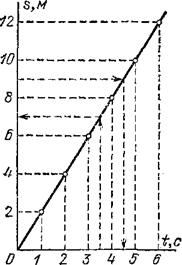
Рис. 18. График пути равномерного движения со скоростью 2 м/с

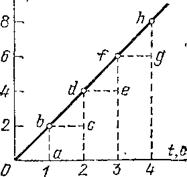
Рис. 19. К упражнению 12.1

В нашем случае график пути оказался прямой линией. Можно показать, что график пути равномерного движения всегда есть прямая линия; и обратно: если график зависимости пути от времени есть прямая линия, то движение равномерно.

Повторяя построение для другой скорости движения, найдем, что точки графика для большей скорости лежат выше, чем соответственные точки графика для меньшей скорости (рис. 20). Таким образом, чем больше скорость равномерного движения, тем круче прямолинейный график пути, т. е. тем больший угол он составляет с осью времени.

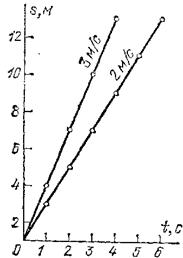
Рис. 20. Графики пути равномерных движений со скоростями 2 и 3 м/с

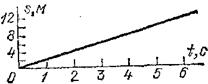
Рис. 21. График того же движения, что на рис. 18, вычерченный в другом масштабе

Наклон графика зависит, конечно, не только от числового значения скорости, но и от выбора масштабов времени и длины. Например, график, изображенный на рис. 21, дает зависимость пути от времени для того же движения, что и график рис. 18, хотя и имеет другой наклон. Отсюда ясно, что сравнивать движения по наклону графиков можно только в том случае, если они вычерчены в одном и том же масштабе.

С помощью графиков пути можно легко решать разные задачи о движении. Для примера на рис. 18 штриховыми линиями показаны построения, необходимые для того, чтобы решить следующие задачи для данного движения: а) найти путь, пройденный за время 3,5 с; б) найти время, за которое пройден путь 9 м. На рисунке графическим путем (штриховые линии) найдены ответы: а) 7 м; б) 4,5 с.

На графиках, описывающих равномерное прямолинейное движение, можно откладывать по оси ординат вместо пути

координату

движущейся точки. Такое описание открывает большие возможности. В частности, оно позволяет различать направление движения по отношению к оси

. Кроме того, приняв начало отсчета времени за нуль, можно показать движение точки в более ранние моменты времени, которые следует считать отрицательными.

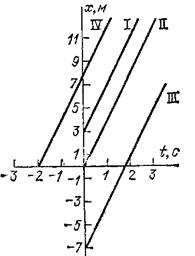
Рис. 22. Графики движений с одной и той же скоростью, но при различных начальных положениях движущейся точки

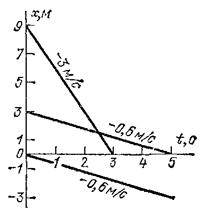
Рис. 23. Графики нескольких движений с отрицательными скоростями

Например, на рис. 22 прямая I есть график движения, происходящего с положительной скоростью 4 м/с (т. е. в направлении оси

), причем в начальный момент движущаяся точка находилась в точке с координатой

м. Для сравнения на том же рисунке дан график движения, которое происходит с той же скоростью, но при котором в начальный момент движущаяся точка находится в точке с координатой

(прямая II). Прямая. III соответствует случаю, когда в момент

движущаяся точка находилась в точке с координатой

м. Наконец, прямая IV описывает движение в случае, когда движущаяся точка имела координату

в момент

с.

Мы видим, что наклоны всех четырех графиков одинаковы: наклон зависит только от скорости движущейся точки, а не от ее начального положения. При изменении начального положения весь график просто переносится параллельно самому себе вдоль оси

вверх или вниз на соответственное расстояние.

Графики движений, происходящих с отрицательными скоростями (т. е. в направлении, противоположном направлению оси

), показаны на рис. 23. Они представляют собой прямые, наклоненные вниз. Для таких движений координата

точки с течением времени уменьшается.

12.3.
График пути для точки, движущейся со скоростью

, отсекает на оси ординат отрезок

. Как зависит от времени расстояние

от начальной точки? Напишите формулу этой зависимости.

12.4.
Точка, движущаяся со скоростью

, в момент

находится на расстоянии

от начальной. Как зависит от времени расстояние

?

12.5.
Точка, двигаясь равномерно вдоль оси

, имела координаты

м и

м в моменты времени

с и

с соответственно. Найдите графически, в какой момент точка проходила через начало координат и какова была координата

в начальный момент. Найдите проекцию скорости на ось

.

12.6.
Найдите при помощи графика пути, когда и на каком расстоянии от точки А автомашину, вышедшую из точки А, догонит вторая автомашина, вышедшая из той же точки через 20 мин после первой, если первая машина движется со скоростью 40 км/ч, а вторая — со скоростью 60 км/ч.

12.7.
Найдите при помощи графика пути, где и когда встретятся автомашины, вышедшие одновременно навстречу друг другу со скоростями 40 и 60 км/ч из пунктов А и В, лежащих на расстоянии 100 км друг от друга.

Графики пути можно строить и для случаев, в которых тело движется равномерно в течение определенного промежутка времени, затем движется равномерно, но с другой скоростью в течение другого промежутка времени, затем снова меняет скорость и т. д. Например, на рис. 26 показан график движения, в котором тело двигалось в течение первого часа со скоростью 20 км/ч, в течение второго часа — со скоростью 40 км/ч и в течение третьего часа — со скоростью 15 км/ч.

12.8.
Постройте график пути для движения, в котором за последовательные часовые промежутки тело имело скорости 10, -5, 0, 2, -7 км/ч. Чему равно суммарное перемещение тела?

Источник

График скорость-время представляет собой соотношение скорости и времени движущегося объекта. Сообщите нам, как найти расстояние на графике скорости и времени.

Построив график скорости-времени для полного пути движущегося тела, мы также можем найти пройденное расстояние. Расстояние определяется путем вычисления площади под графиком как с положительной, так и с отрицательной стороны.

График скорости и времени показывает скорость объекта в конкретное время. При построении этого графика мы берем значение скорости по вертикальной оси, которая является осью Y. Точно так же время отсчитывается по оси абсцисс, вертикальной. Так же, как график позиции-времени, мы можем найти наклон графика скорость-время. Уклон рассчитывается по формуле:

Здесь,

Поскольку мы берем время по оси x, то:

Кроме того,

По оси ординат берем скорость так:

Следовательно, формула для графика скорость-время принимает следующий вид:

Наклон = (v₂-v₁) / (t₂-t₁)

Единица измерения скорости — метр в секунду (м / с), а времени — секунда (с).

Следовательно, если мы введем единицу измерения в приведенную выше формулу наклона, мы получим.

наклон = мс^-2

Мы знаем, что единицей измерения является ускорение. Таким образом, наклон графика скорости и времени дает значение ускорения объекта.

Если крутизна склона направлена вниз, то ее значение будет отрицательным. Следовательно, ускорение также будет отрицательным. отрицательное ускорение означает, что скорость уменьшается. Следовательно, нисходящий наклон будет означать, что тело замедляется. Плавный подъем наклона графика означает, что его значение положительно, поэтому тело ускоряется.

Когда наклон графика равен нулю, то есть он параллелен оси времени. В этом случае ускорение становится равным нулю. Следовательно, это означает, что скорость остается постоянной на протяжении всего путешествия.

Теперь дайте нам знать, как найти расстояние на графике скорости и времени. Площадь графика дает значение всего расстояния, которое проходит объект. Чтобы понять это шаг за шагом, проверьте ниже.

На приведенном выше графике показано соотношение скорости и времени движущегося автомобиля. Мы можем ясно видеть, что первоначально тело ускорялось, затем скорость стала постоянной, а затем оно начало замедляться. Чтобы найти расстояние, разделите график на треугольники и трапеции, как показано выше. Теперь последнее — найти значения цифр и сложить их.

Площадь треугольника 1 =

(1/2)*база*высота

(1/2)*2*8

Площадь треугольника 1 = 8

Площадь трапеции 2 =

(1/2)*(а+б)*рост

(1/2)*(8+12)*3

Площадь трапеции = 30

Площадь треугольника 3

=(1/2)*основание*высота

=(1/2)*3*12

Площадь треугольника 3 = 18

Чтобы найти область графика, добавьте все три области:

Пройденное расстояние = Зона 1 + Зона 2 + Зона 3

Пройденное расстояние = 8 + 30 + 18

Пройденное расстояние = 56

Это общая площадь, которую покрыла машина. Таким образом, расстояние на графике скорости и времени рассчитывается путем нахождения площади графика.

Как найти расстояние по криволинейному графику скорости и времени

Для изогнутого графика скорости и времени расстояние определяется путем нахождения области под графиком. Возьмите приведенный выше график; склон здесь не прямой. Он изогнутый; то есть он продолжает увеличиваться или уменьшаться.

Самый первый шаг — это примерно разделить график на треугольники и трапеции. Минуты вверх и вниз можно проигнорировать. Таким образом, мы узнаем правильное значение расстояния, пройденного телом. После разделения графика на треугольники и трапеции нужно найти площадь каждой фигуры. Следовательно, площадь треугольников и трапеций рассчитывается как:

Площадь 1 = (1/2)*(4+8)*2

Площадь = 12

Area 2 =(1/2)*(8+9)*4

Площадь 2 = 34

Area 3 =(1/2)*(9+10)*2

Площадь 3 = 19

Последний шаг — добавить области приблизительного рисунка и получить значение пройденного расстояния.

Пройденное расстояние = Зона 1+ Зона 2+ Зона 3

Пройденное расстояние = 12 + 34 + 19

Пройденное расстояние = 65

Следовательно, расстояние для приведенного выше графика составляет 65

Часто задаваемые вопросы (FAQ)

Что такое график скорости-времени?

График, показывающий зависимость между скоростью и временем движущегося тела, известен как график скорости-времени.

На графике скорости и времени мы откладываем скорости объекта по оси ординат, а время — по оси абсцисс. Он сообщает скорость движущейся частицы в определенный момент времени. Возрастающий наклон говорит о том, что скорость увеличивается, а крутизна спуска говорит о том, что скорость уменьшается.

Что показывает наклон графика скорости-времени?

Крутизна линии графика — это ее наклон. Он дает значение некоторой физической величины.

В разделе график скорость-время, найдя наклон, получим значение ускорения тела. Если наклон положительный, это означает, что тело ускоряется. Если наклон направлен вниз, это означает, что скорость продолжает уменьшаться со временем.

Как показать, что скорость постоянна, на графике скорости и времени?

С помощью графика скорости и времени мы можем показать все виды скорости, увеличивающие, уменьшающиеся, изменяющиеся или даже постоянные.

Когда наклон равен нулю, это означает, что он параллелен горизонтальной оси x; то есть время означает, что скорость постоянна. Это показывает, что в разное время значение скорости остается неизменным; следовательно, он постоянен.

Как найти расстояние на графике скорости и времени?

С помощью графика скорости и времени мы можем легко найти общее расстояние, пройденное объектом за все время путешествия.

Область графика скорости и времени используется для определения точного расстояния, пройденного объектом. Чтобы найти площадь, мы делим график на треугольники и трапеции, а затем находим их площадь и складываем их. Следовательно, величина расстояния известна.

Можем ли мы найти смещение по графику скорости и времени?

Нет, график скорость-время не дает информации о перемещении.

Найдя площадь под графиком скорости и времени, мы получим пройденное расстояние, а не смещение. Мы не можем найти смещение по графику скорость-время. Это потому, что для смещения нам нужно знать начальную и конечную позиции, которые не представлены на этом графике.

Источник

Графические способы решения задач с параметрами. Формула расстояния между двумя точками на плоскости.

В данном материале будет рассмотрен один из очень красивых геометрических методов решения задач с параметрами — метод расстояний. А именно — применение формулы расстояния между двумя точками прямоугольной декартовой системы координат OXY.

Выводится она довольно просто.

Пусть на плоскости OXY заданы две точки А(x₁; y₁) и B(x₂; y₂) (см. рисунок). И наша задача — определить расстояние между этими точками. Или длину отрезка АВ.

Как видно из рисунка, отрезок АВ является гипотенузой прямоугольного треугольника АВС с катетами АС и ВС. Их длины равны разности абсцисс и ординат концов А и В отрезка АВ:

Модули ставятся для того, чтобы было неважно, как именно ориентирован наш отрезок и какая из координат больше — первая или вторая: модуль просто отсекает возможный минус, если, вдруг, скажем, х₂ окажется меньше, чем х₁. Ведь длина отрезка, очевидно, величина неотрицательная.

Теперь, призвав на помощь ~~тяжёлую артиллерию~~ великую и могучую теорему Пифагора, получим наше искомое расстояние:

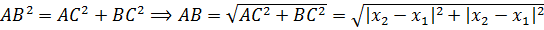
Поскольку как квадрат, так и модуль обладают одним весьма удобным и замечательным свойством — чётностью, то модули под корнем можно совершенно спокойно и без последствий заменить на обычные скобки.

Итого:

Вот такая полезная формула. Что ж, на этом краткая теоретическая часть закончена. Пора теперь посмотреть, как именно эта формула работает на примере некоторых задач с параметрами из профильного ЕГЭ по математике.

Пример 1

Иными словами, от нас требуется найти такие а, при которых система имеет решение в принципе. Хотя бы одно. Ни сами решения, ни их количество находить при этом не нужно.

Проанализируем наши уравнения.

Первое уравнение представляет собой сумму квадратных корней из выражений с двумя переменными. Обычно, как только ученик видит уравнение с квадратными корнями, первое что приходит в голову, — срочно возвести обе части в квадрат!) Однако, традиционный «лобовой» способ решения путём возведения в квадрат обеих частей уравнения здесь вряд ли приведёт к чему-либо хорошему. А вы возведите! После первого возведения — да, квадраты обоих корней дадут просто подкоренные выражения, но… согласно бескомпромиссной формуле квадрата суммы (a+b)²=a²+2ab+b², выплывет удвоенное произведение слагаемых, где корни сохранятся! Что потребует возводить в квадрат повторно… И в результате полной ликвидации корней у вас получится уравнение аж четвёртой степени, да ещё и с иксом и игреком… Короче, ужас!

Нет, надо идти каким-то обходным путём. Каким же?

В данном примере как раз таки здорово выручает формула расстояния между двумя точками на плоскости. Давайте присмотримся к первому уравнению системы:

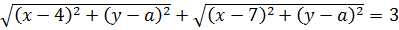
Каждый из корней, фигурирующих в уравнении, очень похож на формулу расстояния между некими точками. Это намёк.) Займёмся расшифровкой каждого корня.

Сопоставим первый корень с выведенной только что формулой расстояния:

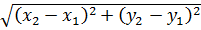
Просто присматриваемся к этим двум корням и сравниваем. Похожи ведь, правда? Тогда, согласно нашей формуле расстояния, можно принять:

x₁ = 4;

x₂ = x;

y₁ = a;

y₂ = y.

Значит, первый корень — это на самом деле расстояние от точки (4; a) до точки (x; y).

Аналогично сопоставив с формулой второй корень, увидим, что он тоже представляет собой расстояние от точки (7; a) опять же до точки (x; y).

А теперь переведём первое уравнение с алгебраического языка (языка формул) на геометрический (язык расстояний).

Алгебра:

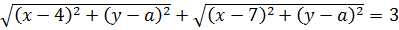
Геометрия:

Сумма расстояний от точки (x; y) до точек (4; a) и (7; a) равна трём.

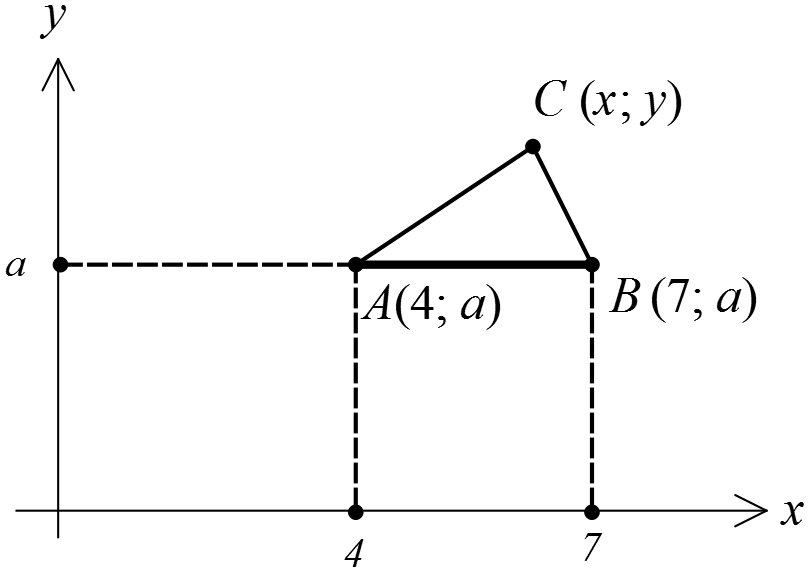
Для наглядности нарисуем картинку, чтобы представлять, а чего, собственно, от нас хотят.)

Значит, согласно рисунку, с геометрической точки зрения первое уравнение системы выглядит так:

AC + BC = 3,

где точки А и В зафиксированы (для конкретного значения параметра), а третья точка С как-то «гуляет» по координатной плоскости.

Вообще говоря, множество точек плоскости, сумма расстояний от которых до двух фиксированных точек постоянна и равна некому положительному числу, представляет собой замкнутую кривую, которая называется красивым словом эллипс, а данные фиксированные точки являются фокусами эллипса. Но проблема состоит в том, что понятие эллипса не входит в школьную программу (зачастую даже физико-математических классов), а изучается уже в ВУЗе в курсе аналитической геометрии.) Так как же обойти это незнакомое (пока) понятие? Может, в данной (и подобных этой) задаче всё гораздо проще?

Вынужден признаться. Да, всё гораздо проще!

Дело всё в том, что понятие эллипса справедливо только в том случае, если эта самая сумма расстояний будет больше расстояния между самими фиксированными точками. Если же сумма расстояний от точки С(x; y) до двух фиксированных точек (в данном случае A и B) точно равна расстоянию AB между ними, то точка С(x; y) обязательно будет лежать на отрезке AB, и никакого эллипса уже не будет, а будет просто отрезок AB с «гуляющей» по нему третьей точкой.

Давайте посмотрим, чему же равно расстояние между нашими фиксированными точками:

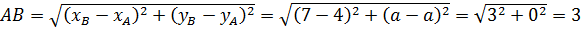
Итак, длина отрезка АВ в точности получилась равной трём, как и правая часть уравнения. Это не случайно!) Что это означает? Это означает то, что наша точка С(x; y) обязательно лежит на отрезке AB и как-то по нему гуляет.) И только на отрезке! Ведь в противном случае, если бы точка С лежала где-то за его пределами (скажем, где-то выше или где-то ниже), то сумма расстояний от неё до концов отрезка АВ была бы строго больше тройки, что противоречило бы первому уравнению.

Что ещё важного можно заметить в данном уравнении и на рисунке? А то, что при любом значении параметра «а» игрековые координаты А и В концов нашего отрезка совпадают (обе равны а). Это означает, что в любом случае наш отрезок АВ будет строго горизонтален (то бишь, параллелен оси ОХ), а его концы, в зависимости от значения параметра, будут как бы скользить вдоль направляющих прямых x=4 и x=7 (поскольку абсциссы его концов никак не зависят от «а», оставаясь всё время равными 4 и 7).

Итак, первое уравнение разложили по полочкам, переходим ко второму.

Вот тут возведение обеих частей в квадрат вполне прокатит. Возводим:

Ну как, знакомо? Да, это классическое уравнение окружности с центром в точке (3;2) и радиусом 5.

Кстати сказать, а как понять, что второе уравнение задаёт именно окружность не через возведение в квадрат, а через расстояние между точками? Снова переводим второе уравнение с алгебры на геометрию, используя нашу формулу расстояния.

Алгебра:

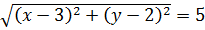
Геометрия:

Расстояние от точки (x;y) до точки (3;2) равно пяти.

А что же это за множество точек, находящихся от фиксированной точки (3;2) на расстоянии 5? Ну, конечно! Окружность радиуса 5 с центром в данной точке.

Что ж, у нас уже имеется всё необходимое, чтобы нарисовать общий чертёж к задаче. Поехали!

1) Итак, сначала, как водится, чертим координатные оси X и Y.

2) Проводим пунктиром вспомогательные вертикальные прямые x=4 и x=7. Вдоль этих прямых, в зависимости от параметра «а», будет скользить наш отрезок АВ, всё время оставаясь горизонтальным. Как вагонная ось катится по рельсам.))

3) Отмечаем точку (3; 2) — центр нашей окружности.

4) Собственно, рисуем саму окружность с центром в данной точке и радиусом — пятёрка.

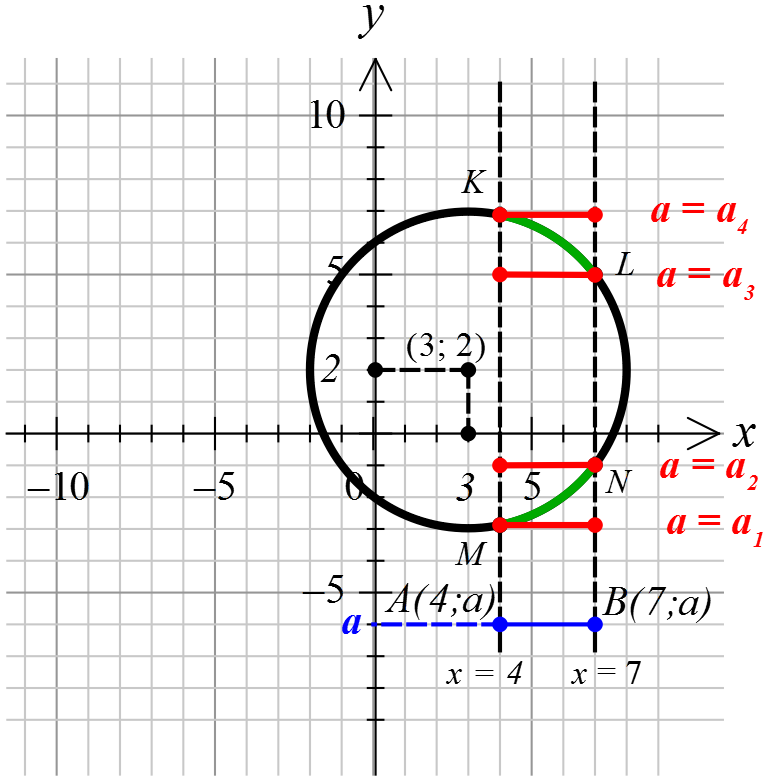
5) Готово! Что в конечном итоге получилось — смотрим рисунок ниже.

А теперь пора рассуждать и включать воображение.) В задаче от нас требуется, чтобы система имела хотя бы одно решение. Что это означает с точки зрения нашего рисунка? А то, что наши отрезок (первое уравнение) и окружность (второе уравнение) должны иметь хотя бы одну общую точку. Когда такое возможно?

Пусть при каком-то конкретном сильно отрицательном (например, -6) значении параметра а наш отрезок АВ (синего цвета) лежит где-то внизу и пока что вообще не пересекает окружность. Теперь мысленно начинаем двигать отрезок вверх по нашим «рельсам».)

Имеем четыре граничные ситуации.

Первое граничное положение отрезка, которое нас устроит, — когда его левый конец совпадёт с точкой М окружности (а = а₁). И пересечение отрезка с окружностью будет до того момента, пока его правый конец не совпадёт с точкой N (а = а₂). То есть, хотя бы одно (и единственное!) решение системы будет при таких а, когда отрезок пересекается с дугой MN окружности (показана зелёным цветом).

Двигаем отрезок вверх дальше. При a > a₂ отрезок оказывается целиком внутри окружности и, следовательно, решений у нашей системы снова нет. И следующие два граничных положения — момент, когда правый конец попадает в точку L (a = a₃) и момент, когда левый конец попадает в точку K (a = a₄). И пересечение будет тогда, когда отрезок находится между этими крайними положениями, пересекая уже верхнюю дугу KL. Все граничные положения отрезка показаны красным цветом. При дальнейшем движении отрезка вверх (то есть росте параметра «а») пересечений (а, следовательно, и решений системы) больше не будет.

Итак, можно даже составить заготовку для будущего ответа:

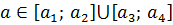
Причём граничные значения параметра а нас тоже устраивают, посему все скобки квадратные.

Что ж, остаются сущие пустяки — определить эти самые граничные значения параметра.)

Начнём с левого конца отрезка. То есть, точки А(4; a). Подставим координаты точки А в уравнение окружности (ведь мы же как раз отлавливаем пересечение отрезка с окружностью!):

Получили два значения параметра. Очевидно, знак минус соответствует крайнему нижнему положению отрезка при a = a₁, а знак плюс — крайнему верхнему при а = а₄. Таким образом,

Аналогично расправляемся и с правым концом — с точкой B(7; a):

То есть,

Итак, а₂ = -1; a₃ = 5.

Всё! Все интересующие нас значения параметра найдены, и теперь можно с чистой совестью записывать окончательный ответ.)

Ответ:

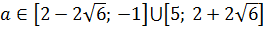
В рассмотренном примере формула расстояния между точками ~~была подана на блюдечке~~ прослеживалась довольно явно. А вот следующий пример будет гораздо сложнее. Там, во-первых, в нагрузку добавятся модули, а во-вторых, потребуются дополнительные преобразования. Но ничего, мы тоже его распутаем.)

Итак, приступим!

Пример 2

Во, накрутили… Сумма корней, под корнями модули… Кошмар!

Как здесь можно узнать формулу расстояния между точками? Ясно, что надо как-то преобразовывать и приводить к красивому виду первое уравнение.

Посмотрим, что получается под первым корнем. Раскроем скобки:

Здесь мы воспользовались тем фактом, что и квадрат и модуль — функции чётные, а значит, x² и |x|² — одно и то же, поэтому без ущерба для здоровья мы заменили выражение x² на |x|², что позволило свернуть выражение с иксом по формуле квадрата суммы.

А вот второй корень сразу так красиво преобразовать не выйдет: ведь там у нас совсем нет икса в квадрате, а вместо этого затесался параметр а, да ещё и игрек в первой степени. Чтобы избавиться от а и y, воспользуемся вторым уравнением и подставим в первое уравнение вместо y выражение x²+a:

Вот так. И теперь первое уравнение системы стало выглядеть гораздо симпатичнее:

Уже потихоньку вырисовывается нечто знакомое, правда? Что делать дальше? Ясно, что надо раскрывать модули. Лучше, когда их нет.) Давайте начнём с первого корня, то есть с икса.

Если x≥0, то модуль раскрывается с плюсом (|x| = x), и тогда

Таким образом, если x≥0, то первый корень представляет собой расстояние между точками (x; y) и (3; 0). С какой такой стати? Элементарно!

Ведь можно же записать данное выражение вот так:

Аналогично, если x<0, то наш модуль раскрывается с минусом (|x| = —x), и тогда

Точно так же, раскрывая модуль игрека во втором радикале, получим:

Значит, первое уравнение нашей системы разбивается на четыре случая раскрытия модулей:

Каждое из полученных четырёх уравнений выражает сумму расстояний от неких двух фиксированных точек плоскости ОXY до точки (x; y), «гуляющей» где-то по плоскости. И эта сумма расстояний у нас постоянна и равна пяти.

Здесь опять таки не будем выпендриваться и сделаем вид, что понятия не имеем про эллипс, а вместо этого снова посчитаем расстояния между точками.)

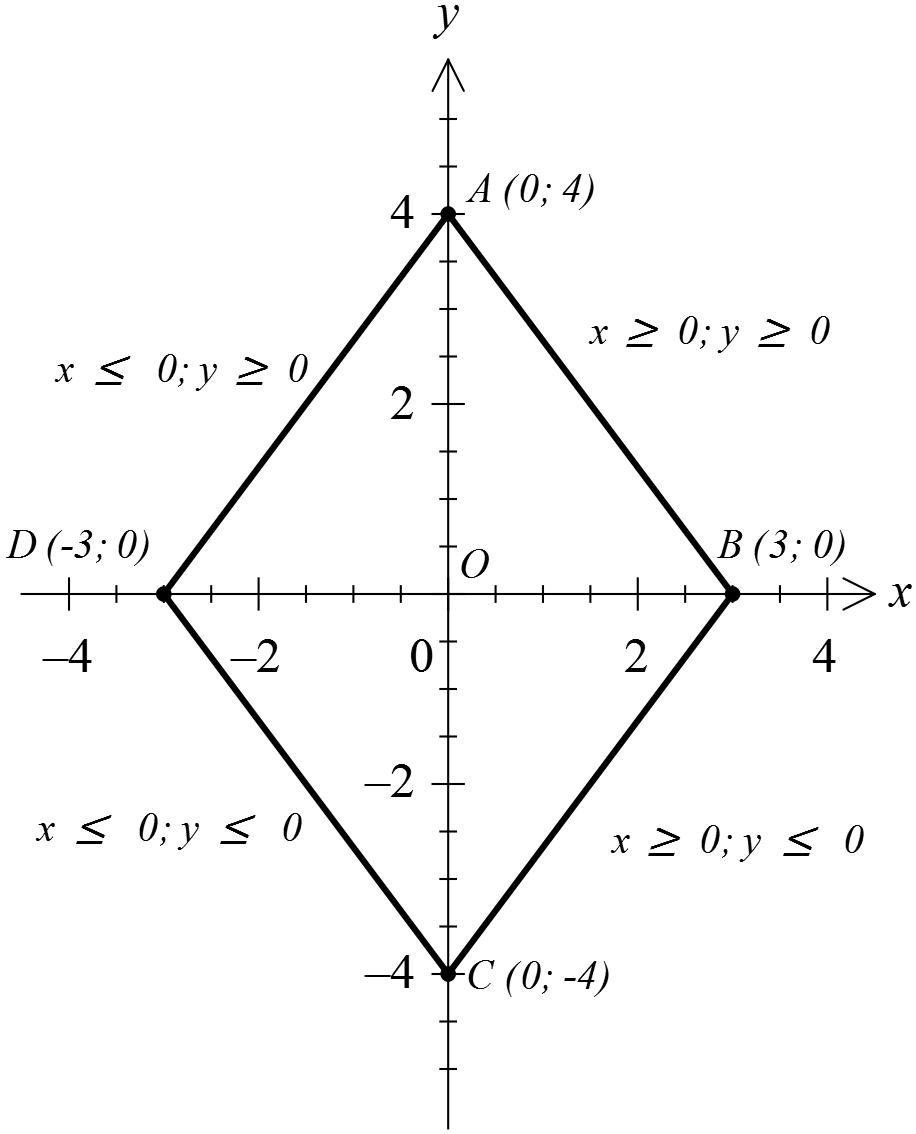
Для этого изобразим все наши точки на координатой плоскости и соединим их отрезками. Это будут точки A(0; 4), B(3; 0), C(0; -4) и D(-3; 0). Вот наша картинка:

Теперь подробно рассмотрим, к примеру, первый случай:

Он представляет собой сумму расстояний от точки (x; y) до точек A и B.

Вычислим длину отрезка АВ из треугольника AOB:

Получили в точности пятёрку. То есть, длину отрезка AB! Что это означает? Это означает, что наша точка с координатами (x; y) обязательно лежит на отрезке АВ и как-то по нему гуляет! Таким же образом доказывается, что и в остальных трёх случаях точка (x; y) лежит на соответствующем отрезке. Итак, множество точек, описывающих первое уравнение системы, — ромб ABCD со стороной 5. Каждая сторона ромба отвечает за свой случай раскрытия модулей.

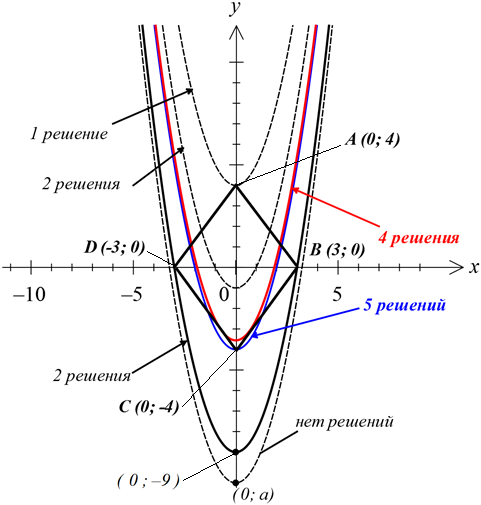
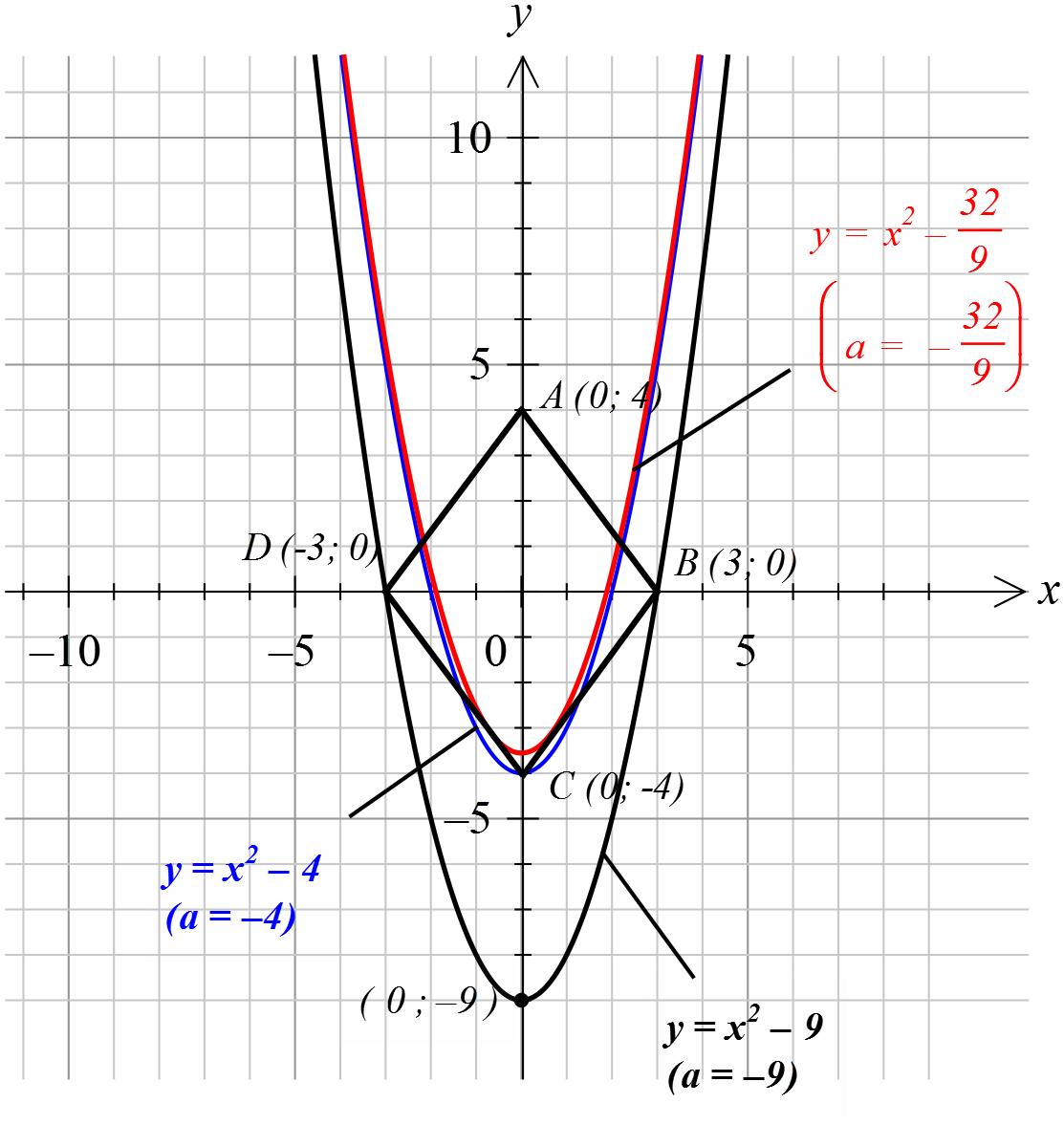
А вот второе уравнение нашей системы — обычная парабола y = x² с вершиной в точке (0; a), гуляющая вверх-вниз вдоль оси игреков в зависимости от параметра. Вот наша картинка:

А теперь (внимание!) начинаем двигать нашу параболу снизу вверх вдоль оси OY, меняя тем самым параметр а!

Тогда видно, что, если вершина находится где-то совсем низко, то пересечений у параболы и ромба вообще не будет. Первый граничный случай соответствует a = -9, когда ветви параболы проходят через точки B и D ромба (показан чёрным цветом). В этом случае решений будет два. Как только вершина параболы сместится чуть выше -9, то каждая её ветвь пересечёт по две стороны ромба, и решений станет уже четыре — как раз то что нам и нужно. И так будет продолжаться до тех пор, пока вершина параболы не окажется в точке С (синий цвет), то есть, а = -4, когда решений станет пять.

Таким образом, первая часть ответа будет такая:

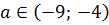
Сами границы нас не устраивают и в ответ, естественно, не включаются.

Но… Это ещё не всё!) Продолжим дальше двигать вверх по оси ОY нашу параболу. Когда вершина окажется чуть выше точки С, то пересечений станет уже шесть: по два с нижними сторонами ромба и по одному с верхними. И так будет до тех пор, пока ветви параболы не станут касаться сторон CD и CB ромба (красный цвет). В случае касания решений снова станет четыре, что от нас и требуется. И это значение параметра а, при котором парабола касается нижних сторон ромба, теперь нам и предстоит «отловить».)

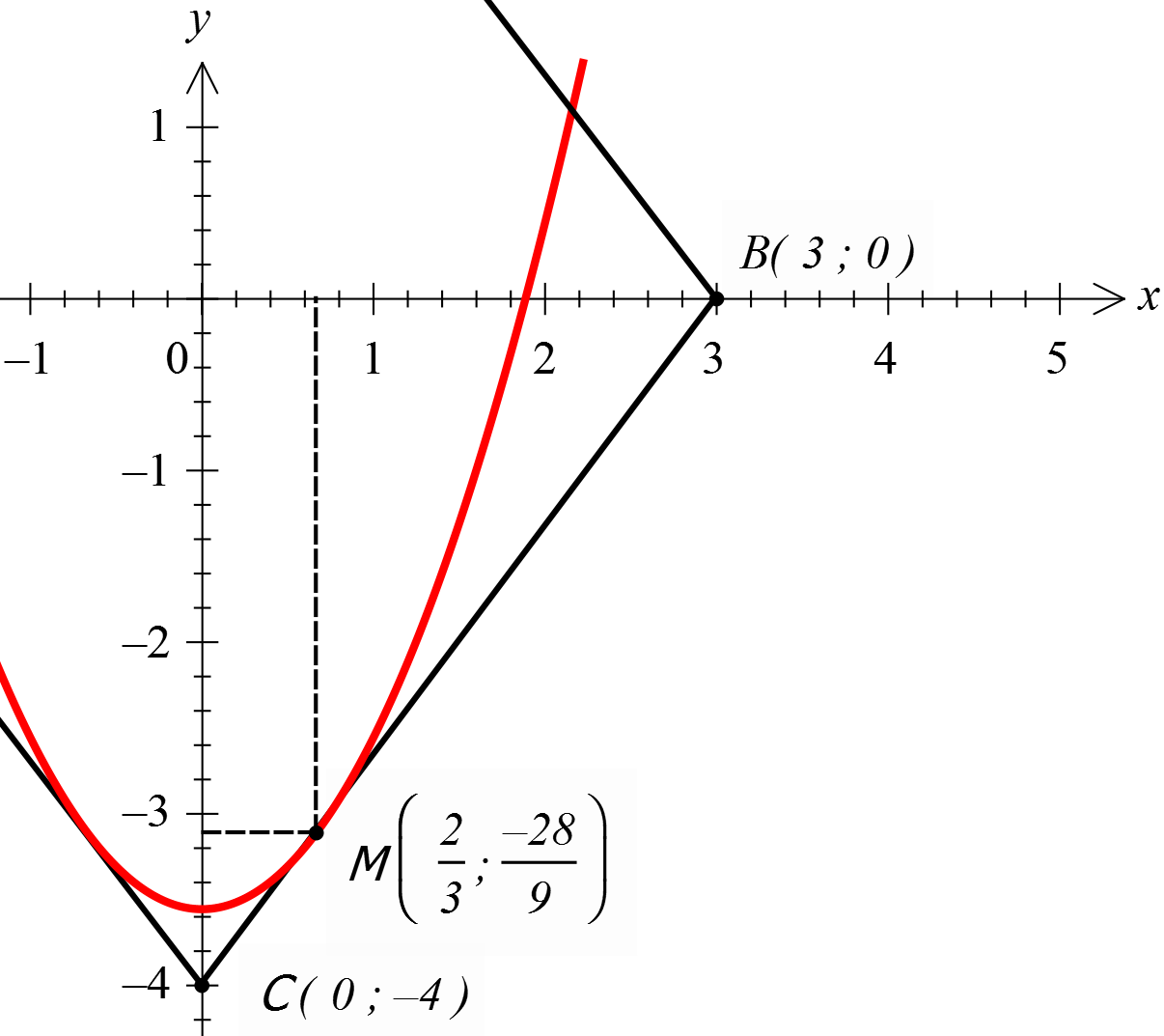
На помощь придёт такой мощный инструмент, как производная. В силу симметрии картинки, рассматривать будем только правую ветвь параболы. Итак, пусть наша красная парабола касается нижнего отрезка ромба СВ в какой-то точке М.

Уравнение прямой, задающей отрезок СВ, будет

поскольку тангенс угла наклона прямой CB к оси ОХ равен:

Уравнение нашей параболы будет y = x² + a. Мы не знаем пока, чему равно «а», но зато твёрдо знаем, что отрезок CB её касается, а значит, производная нашей параболы в точке касания M должна быть равна 4/3.

Вычислим эту самую производную:

(x²+a)’ = (x²)’ + a’ = 2x

Тогда 2x = 4/3 и тогда x = 2/3 — абсцисса точки касания M.

Поскольку точка M лежит на отрезке CB, то её координаты обязательно удовлетворяют уравнению этого отрезка:

Значит, координаты нашей точки касания следующие:

Но! Точка M принадлежит не только отрезку, но ещё и параболе! Поэтому, подставив координаты точки M в уравнение параболы, мы теперь уже без труда найдём интересующее нас значение а:

Вот теперь всё. Все характерные положения параболы представлены на картинке.

Легко видеть, что при дальнейшем росте параметра а четырёх решений уже не будет, а будет либо два, либо одно, либо ни одного.

Кстати сказать, а можно ли в данной ситуации обойтись без производной? Уж больно напряжно с ней возиться, как правило…

Что ж, специально для разумных халявщиков предлагаю способ-лайт.) Но, следует предупредить, что он срабатывает только в случае каких-нибудь простеньких графиков — в основном для параболы. В случае более сложных функций способ с производной — самый надёжный.)

Итак, нам требуется отыскать значение параметра, при котором происходит касание прямой

и параболы

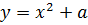
Что означает сей факт с алгебраической точки зрения? Только то, что уравнение

имеет строго один корень! То есть, дискриминант получившегося квадратного уравнения обязан быть равен нулю!

Что ж, остаётся только привести наше уравнение к стандартному виду, посчитать дискриминант да приравнять его к нулю.) Действуем:

Как и следовало ожидать, результат получился тем же самым.)

Ответ:

Заключение: если в примере предложено какое-то зверское на вид уравнение или неравенство с корнями, но подкоренные выражения представляют собой какие-то квадратичные конструкции от x и y вида

то ни в коем случае не возводим обе части в квадрат с целью избавиться от корней и не тратим своё время! Вместо этого пробуем выделить полные квадраты под корнями по каждой из переменных.

Очень часто в таких конструкциях срабатывает именно формула расстояния между двумя точками, что значительно упрощает дальнейшее решение примера и тем самым открывает дорогу к успеху.

Заметим, что данный приём работает только тогда, когда наше подкоренное выражение именно такого вида — то есть, переменные под корнем стоят в квадрате и в первой степени (а не в кубе или более высоких степенях) и именно сами по себе, без попарных произведений xy . Если данное требование не выполняется, и под корнем затесалось, скажем, ещё и произведение xy, то либо его надо на что-то заменять (скажем, если оно выражается из второго уравнения), либо данный пример решается как-то по-другому.

Успехов!

Источник