Как найти расстояние от основания пирамиды - Исправление недочетов и поиск решений вместе с Examum.ru

Достаточно знать длину бокового ребра пирамиды, количество сторон многоугольника, лежащего в основании пирамиды, а также длину стороны основания (сторону многоугольника).

В основании правильной пирамиды всегда лежит правильный многоугольник. Любой правильный многоугольник можно вписать в окружность.

Есть такая формула:

a — длина стороны n-угольника (для правильного многоугольника).

L — длина окружности, описывающей этот многоугольник.

n — это количество сторон этого многоугольника

Если выразить эту формулу наоборот, то можно по стороне многоугольника найти длину окружности.

L=a*π/sin(180/n)

Зная длину окружности, можно найти радиус этой окружности:

L=2πR

R=L/(2π)

Подставляя L из первой формулы, получаем:

R = L/(2π) = a*π/(2π*sin(180/n)) = a/(2sin(180/n))

Теперь если приглядитесь к рисунку, то увидите, что радиус описанной окружности является также и катетом в прямоугольном треугольнике (игреком «y» на левой картинке).

А вертикальное ребро пирамиды это гипотенуза этого прямоугольного треугольника.

А искомая нам высота это второй катет этого прямоугольного треугольника.

По теореме Пифагора:

X²=Y²+h²

h²=X²-Y²

h=√(X²-Y²)

X нам известен — это длина боковой стороны пирамиды.

Y тоже известен — это расстояние от одного из углов основания пирамиды до центра пирамиды, и это же радиус описанной вокруг этого многоугольника окружности.

Y=R, а R равен: R=a/(2sin(180/n))

Итак подведём итог:

h=√(X²-Y²) = √(X²-R²) = √(X²-(a/(2sin(180/n)))²)

X — размер боковой стороны (ребра) пирамиды.

n — количество сторон многоугольника в основании.

a — размер стороны этого многоугольника в основании.

Более удобно эту формулу я отразил на рисунке.

Источник

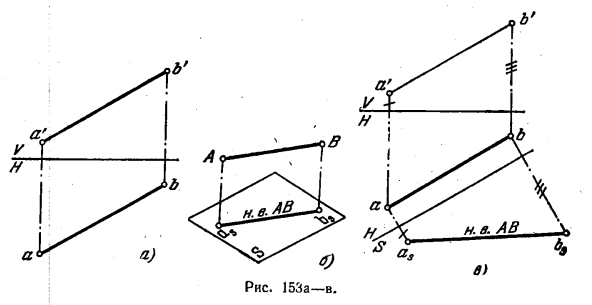
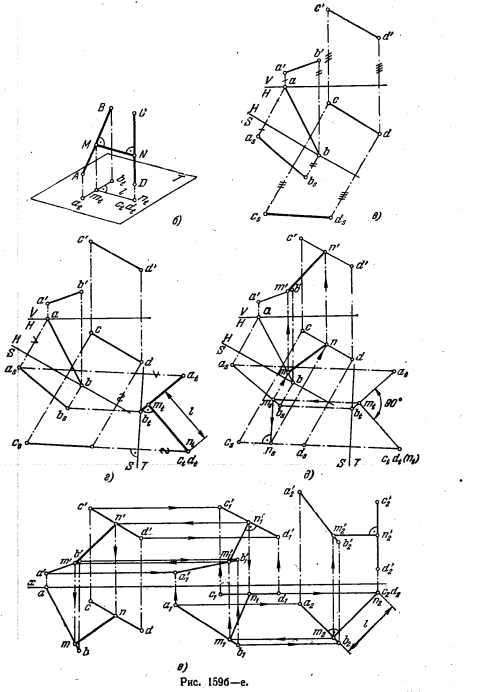
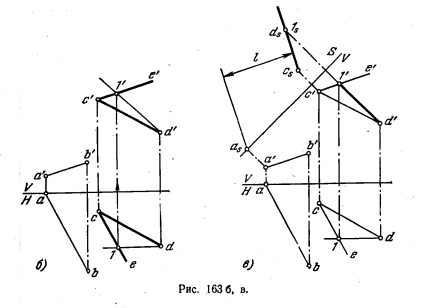
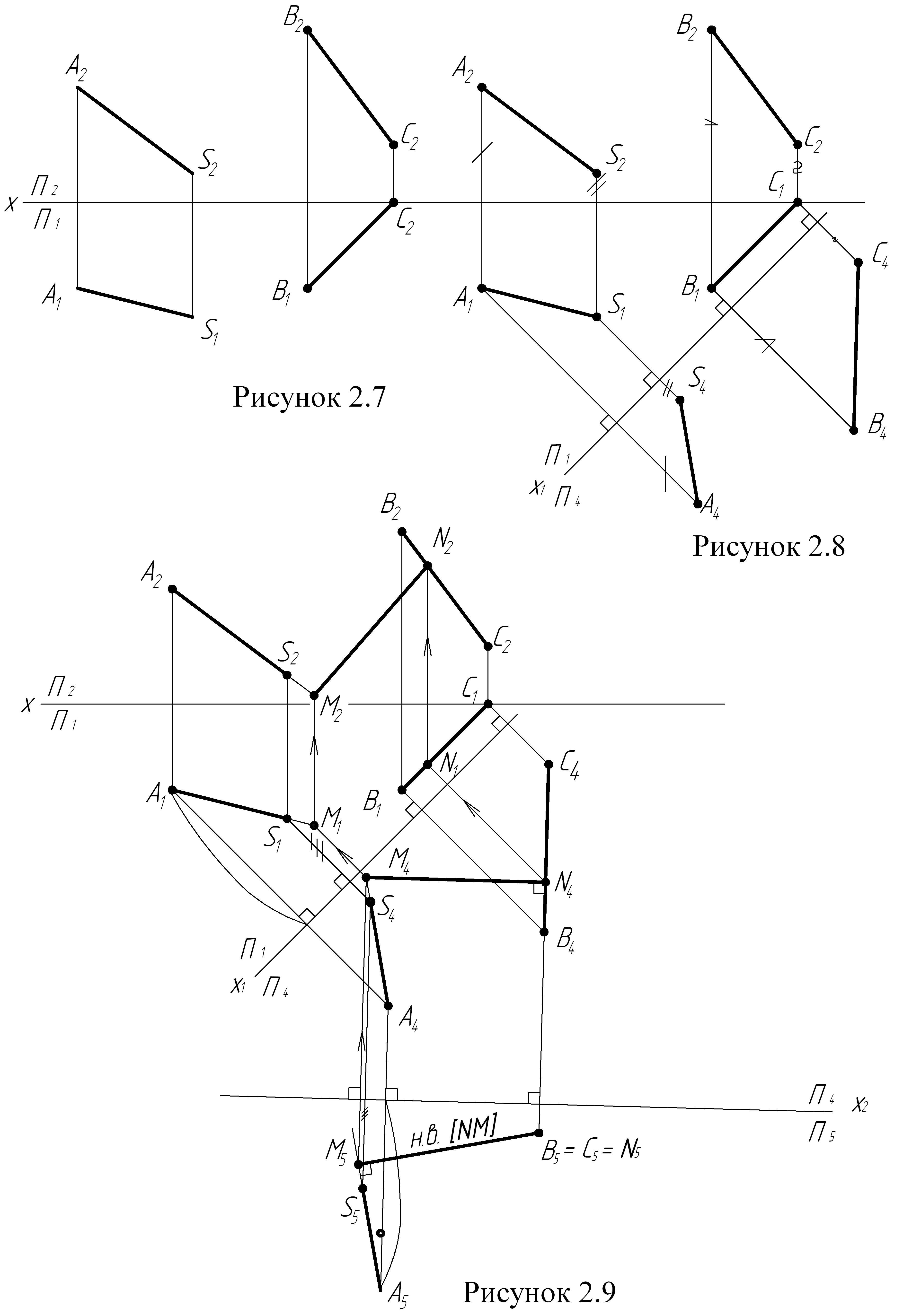
155*. Определить натуральную величину отрезка АВ прямой общего положения (рис. 153, а).

Решение. Как известно, проекция отрезка прямой на какой-либо плоскости равна самому отрезку (с учетом масштаба чертежа), если он параллелен этой плоскости

(рис. 153, б). Из этого следует, что путем преобразования чертежа надо добиться параллельности данного отрезка пл. V или пл. Н или же дополнить систему V, Н еще одной плоскостью, перпендикулярной к пл. V или к пл. H и в то же время параллельной данному отрезку.

На рис. 153, в показано введение дополнительной плоскости S, перпендикулярной к пл. H и параллельной заданному отрезку АВ.

Проекция a_sb_s равна натуральной величине отрезка AB.

На рис. 153, г показан другой прием: отрезок АВ повернут вокруг прямой, проходящей через точку В и перпендикулярной к пл. Н, до положения, параллельного

пл. V. При этом точка В остается на месте, а точка А занимает новое положение А₁. В новом положении горизонт. проекция а₁b || оси х. Проекция a’₁b’ равна натуральной величине отрезка АВ.

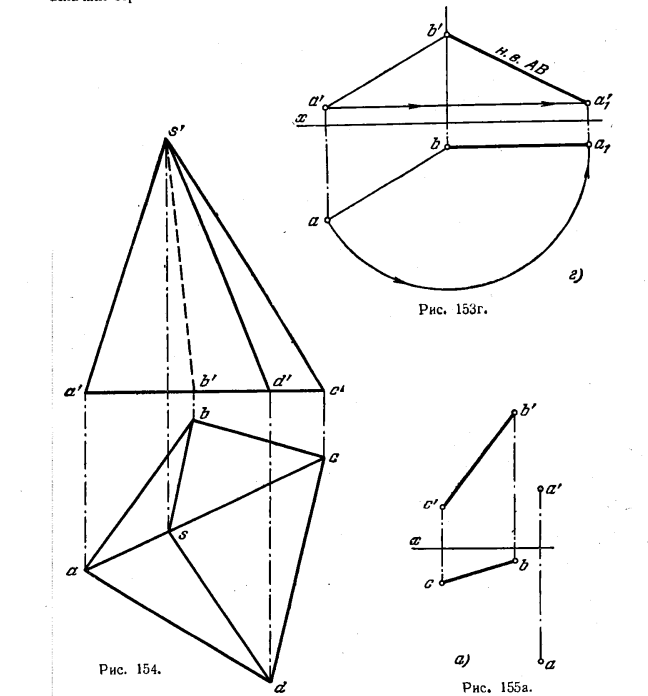
156. Дана пирамида SABCD (рис. 154). Определить натуральную величину ребер пирамиды AS и CS, используя способ перемены плоскостей проекций, и ребер BS и DS, используя способ вращения, причем взять ось вращения перпендикулярно к пл. H.

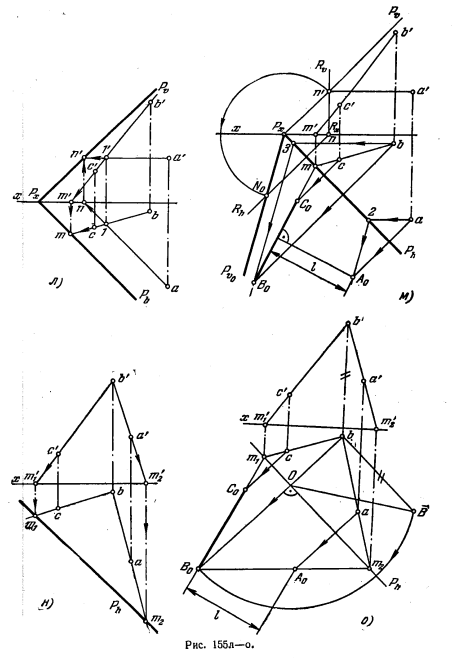
157*. Определить расстояние от точки А до прямой ВС (рис. 155, а).

Решение. Расстояние от точки до прямой измеряется отрезком перпендикуляра, проведенного из точки на прямую.

Если прямая перпендикулярна к какой-либо плоскости (рис. 155,6), то расстояние от точки до прямой измеряется расстоянием между проекцией точки и точкой- проекцией прямой на этой плоскости. Если прямая занимает в системе V, H общее положение, то, чтобы определить расстояние от точки до прямой способом перемены плоскостей проекций, надо ввести в систему V, H еще две дополнительные плоскости.

Сначала (рис. 155, в) вводим пл. S, параллельную отрезку ВС (новая ось S/H параллельна проекции bс), и строим проекции b_sc_s и a_s. Затем (рис. 155, г) вводим еще пл. Т, перпендикулярную к прямой ВС (новая ось T/S перпендикулярна к b_sс_s). Строим проекции прямой и точки — с_t(b_t) и a_t. Расстояние между точками a_t и с_t(b_t) равно расстоянию l от точки А до прямой ВС.

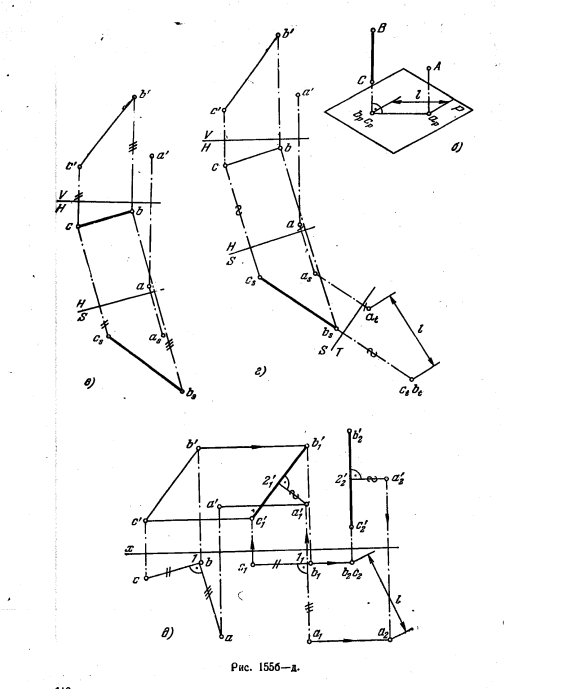
На рис. 155, д эта же задача выполнена с помощью способа вращения в той его форме, которую называют способом параллельного перемещения. Сначала прямую ВС и точку А, сохраняя неизменным их взаимное положение, поворачиваем вокруг некоторой (не обозначенной на чертеже) прямой, перпендикулярной к пл. H, так, чтобы прямая ВС расположилась параллельно пл. V. Это равносильно перемещению точек А, В, С в плоскостях, параллельных пл. H. При этом горизонт. проекция заданной системы (BC + A) не изменяется ни по величине, ни по конфигурации, лишь изменяется ее положение относительно оси х. Располагаем горизонт. проекцию прямой ВС параллельно оси х (положение b₁c₁) и определяем проекцию a₁, откладывая c₁1₁ = с—1 и а₁1₁ = а—1, причем a₁1₁ ⊥ c₁1₁. Проведя прямые b’b’₁, a’a’₁, с’с’₁ параллельно оси х, находим на них фронт. проекции b’₁,а’₁, с’₁. Далее, перемещаем точки В₁, С₁ и A₁ в плоскостях, параллельных пл. V (также не изменяя их взаимного расположения), так, чтобы получить В₂С₂ ⊥ пл. H. При этом фронту проекция прямой расположится перпендикулярно к оси x,b₂c’₂ = b’₁с’₁, а для построений проекции а’₂ надо взять b’₂2′₂ = b’₁2′₁, провести 2’a’₂ ⊥ b’₂с’₂ и отложить а’₂2′₂ = а’₁2′₁. Теперь, проведя с₁с₂ и а₁а₂ || х₁ получим проекции b₂с₂ и а₂ и искомое расстояние l от точки А до прямой ВС. Определить расстояние от А до ВС можно, повернув плоскость, определяемую точкой А и прямой ВС, вокруг горизонтали этой плоскости до положения Т || пл. H (рис. 155, е).

В плоскости, задаваемой точкой А и прямой ВС, проводим горизонталь А—1 (рис. 155, ж) и поворачиваем вокруг нее точку В. Точка В перемещается в пл. R (заданной на чертеже следом R_h), перпендикулярной к А—1; в точке О находится центр вращения точки В. Определяем теперь натуральную величину радиуса вращения ВО, (рис. 155, в). В требуемом положении, т. е. когда пл. Т, определяемая точкой А и прямой ВС, станет || пл. H, точка В получится на R_h на расстоянии Оb₁ от точки О (может быть и другое положение на том же следе R_h, но по другую сторону от О). Точка b₁ — это горизонт. проекция точки В после перемещения ее в положение В₁ в пространстве, когда плоскость, определяемая точкой А и прямой ВС, заняла положение Т.

Проведя (рис. 155, и) прямую b₁1, получаем горизонт. проекцию прямой ВС, уже расположенной || пл. H в одной плоскости с А. В этом положении расстояние от а до b₁1 равно искомому расстоянию l. Плоскость Р, в которой лежат заданные элементы, можно совместить с пл. H (рис. 155, к), повернув пл. Р вокругее горизонт. следа. Перейдя от задания плоскости точкой А и прямой ВС к заданию прямыми ВС и А—1 (рис. 155, л), находим следы этих прямых и проводим через них следы Р_ϑ и P_h. Строим (рис. 155, м) совмещенное с пл. H положение фронт. следа — P_ϑ0.

Через точку а проводим горизонт. проекцию фронтали; совмещенная фронталь проходит через точку 2 на следе Р_h параллельно Р_ϑ0. Точка А₀ — совмещенное с пл. H положение точки А. Аналогично находим точку В₀. Прямая ВС в совмещенном с пл. H положении проходит через точку В₀ и точку m (горизонт. след прямой).

Расстояние от точки A₀ до прямой В₀С₀ равно искомому расстоянию l.

Можно выполнить указанное построение, найдя только один след Р_h (рис. 155, н и о). Все построение аналогично повороту вокруг горизонтали (см. рис. 155, ж, в, и): след Р_h — это одна из горизонталей пл. Р.

Из приведенных для решения данной задачи способов преобразования чертежа предпочтительным является способ вращения вокруг горизонтали или фронтали.

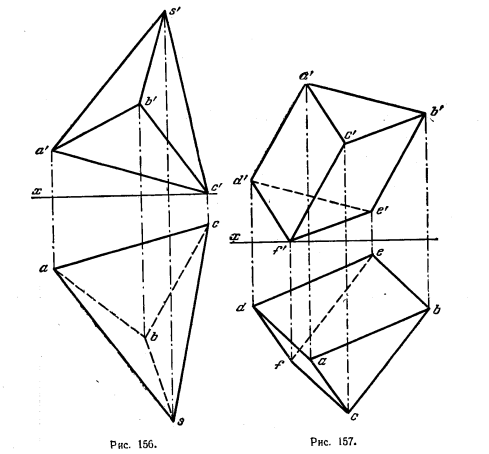
158. Дана пирамида SABC (рис. 156). Определить расстояния:

а) от вершины В основания до его стороны АС способом параллельного перемещения;

б) от вершины S пирамиды до сторон ВС и АВ основания способом вращения вокруг горизонтали;

в) от вершины S до стороны AС основания способом перемены плоскостей проекций.

159. Дана призма (рис. 157). Определить расстояния:

а) между ребрами AD и CF способом перемены плоскостей проекций;

б) между ребрами BE и CF вращением вокруг фронтали;

в) между ребрами AD и BE способом параллельного перемещения.

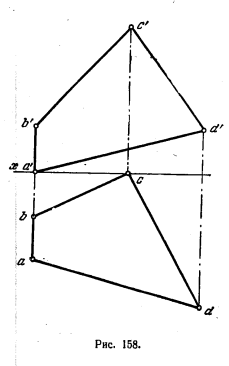
160. Определить натуральную величину четырехугольника ABCD (рис. 158) совмещением с пл. Н. Пользоваться только горизонтальным следом плоскости.

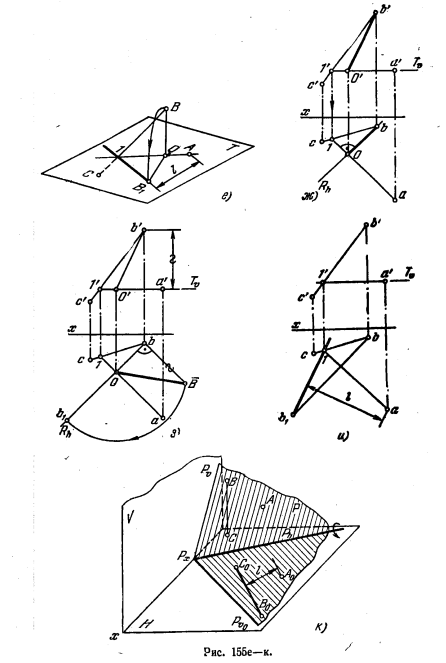
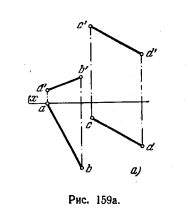
161*. Определить расстояние между скрещивающимися прямыми АВ и CD (рис. 159, а) и построить проекции общего к ним перпендикуляра.

Решение. Расстояние между скрещивающимися прямыми измеряется отрезком (MN) перпендикуляра к обеим прямым (рис. 159, б). Очевидно, если одну из прямых расположить перпендикулярно к какой-либо пл. Т, то

отрезок MN перпендикуляра к обеим прямым окажется параллельным пл. Т него проекция на этой плоскости отобразит искомое расстояние. Проекция прямого угла менаду MN н АВ на пл. Т оказывается также прямым углом между m_tn_t и а_tb_t, так как одна из сторон прямого угла AMN, а именно MN. параллельна пл. Т.

На рис. 159, в и г искомое расстояние l определено способом перемены плоскостей проекций. Сначала вводим дополнительную пл. проекций S, перпендикулярную к пл. H и параллельную прямой CD (рис. 159, в). Затем вводим еще одну дополнительную пл. Т, перпендикулярную к пл. S и перпендикулярную к той же прямой CD (рис. 159, г). Теперь можно построить проекцию общего перпендикуляра проведя m_tn_t из точки c_t(d_t) перпендикулярно к проекции a_tb_t. Точки m_t и n_t — проекции точек пересечения этого перпендикуляра с прямыми АВ и CD. По точке m_t (рис. 159, д) находим m_s на a_sb_s: проекция m_sn_s должна быть параллельна оси Т/S. Далее, по m_s и n_s находим m и n на ab и cd, а по ним m’ и n’ на а’b’ и c’d’.

На рис. 159, в показано решение этой задачи по способу параллельного перемещений. Сначала ставим прямую CD параллельно пл. V: проекция c₁d₁ || х. Далее перемещаем прямые CD и АВ из положений C₁D₁ и А₁В₁ в положения С₂B₂ и А₂В₂ так, чтобы С₂D₂ расположилась перпендикулярно Н: проекция с’₂d’₂ ⊥ х. Отрезок искомого перпендикуляра располагается || пл. H, и, следовательно, m₂n₂ выражает искомое расстояние l между АВ и CD. Находим положение проекций m’₂, и n’₂ на а’₂b’₂ и c’₂d’₂, затем проекций и m₁ и m’₁, n₁ и n’₁, наконец, проекций m’ и n’, m и n.

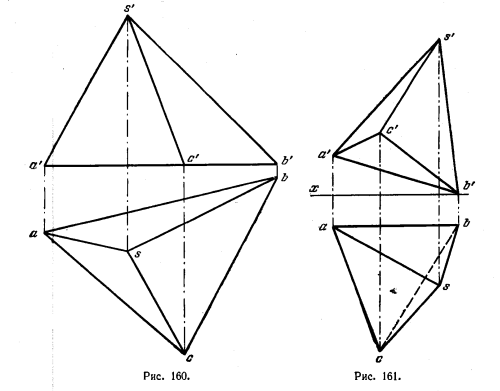
162. Дана пирамида SABC (рис. 160). Определить расстояние между ребром SB и стороной АС основания пирамиды и построить проекции общего перпендикуляра к SB и АС, применив способ пере-мены плоскостей проекций.

163. Дана пирамида SABC (рис. 161). Определить расстояние между ребром SH и стороной ВС основания пирамиды и построить проекции общего перпендикуляра к SX и ВС, применив способ параллельного перемещения.

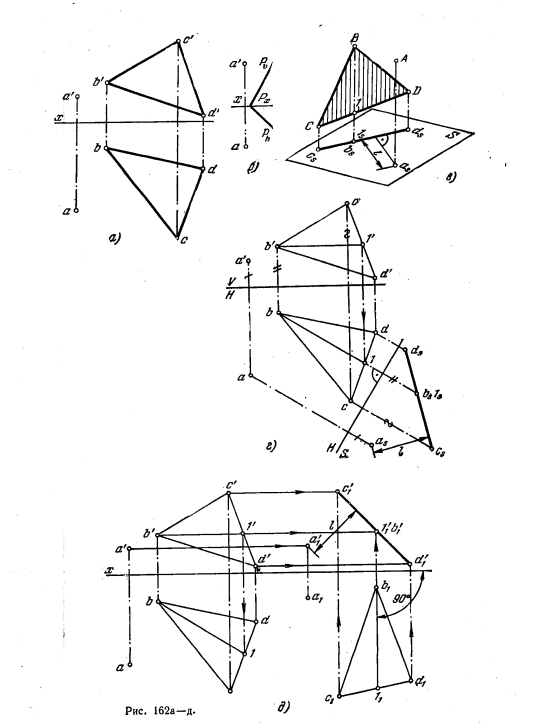
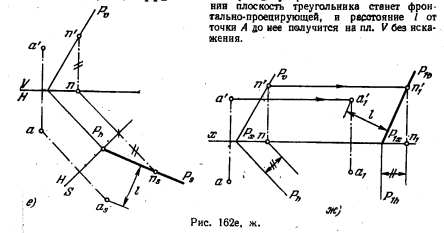
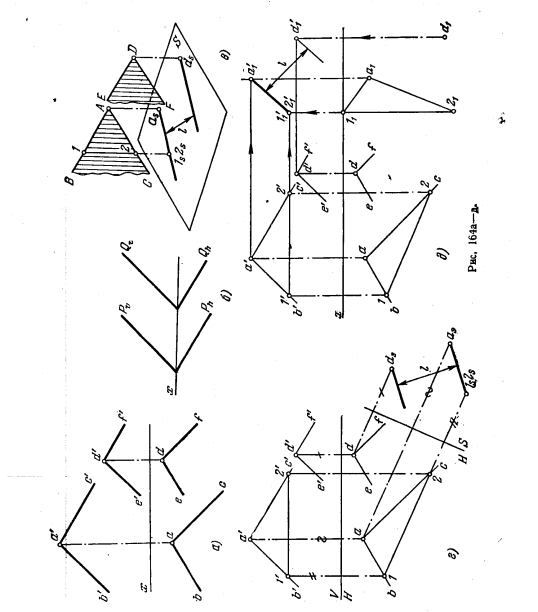
164*. Определить расстояние от точки А до плоскости в случаях, когда плоскость задана: а) треугольником BCD (рис. 162, а); б) следами (рис. 162, б).

Решение. Как известно, расстояние от точки до плоскости измеряется величиной перпендикуляра, проведенного из точки на плоскость. Это расстояние проецируется на какую-либо пл. проекций в натуральную величину, если данная плоскость перпендикулярна к пл. проекций (рис. 162, в). Добиться такого положения можно, преобразуя чертеж, например, способом перемены пл. проекций. Введем пл. S (рис. 16ц, г), перпендикулярную к пл. треугольника BCD. Для этого проводим в пл. треугольника горизонталь В—1 и располагаем ось проекций S перпендикулярно к проекции b—1 горизонтали. Строим проекции точки и плоскости — а_sи отрезок c_sd_s. Расстояние от a_s до c_sd_s равно искомому расстоянию l точки до плоскости.

На рио. 162, д применен способ параллельного перемещения. Перемещаем всю систему до тех пор, пока горизонталь В—1 плоскости не станет перпендикулярна к плоскости V: проекция b₁1₁ должна быть перпендикулярна к оси x. В этом положении плоскость треугольника станет фронтально-проецирующей, и расстояние l от точки А до нее получится на пл. V без искажения.

На рис. 162, б плоскость задана следами. Вводим (рис. 162, е) дополнительную пл. S, перпендикулярную к пл. P: ось S/Н перпендикулярна к Р_h. Дальнейшее ясно из чертежа. На рис. 162, ж задача решена при помощи одного перемещения: пл. Р переходит в положение Р₁, т. е. становится фронтально-проецирующей. След. Р_1h перпендикулярен к оси х. Строим в этом положении плоскости фронт. след горизонтали — точку n’₁,n₁. След P_1ϑ пройдет через Р_1x и n₁. Расстояние от a’₁, до Р_1ϑ равно
искомому расстоянию l.

165. Дана пирамида SABC (см. рис. 160). Определить расстояние от точки А до грани SBC пирамиды, применив способ параллельного перемещения.

166. Дана пирамида SABC (см. рис. 161). Определить высоту пирамиды, применив способ параллельного перемещения.

167*. Определить расстояние между скрещивающимися прямыми АВ и CD (см.рис. 159,а) как расстояние между параллельными плоскостями, проведенными через эти прямые.

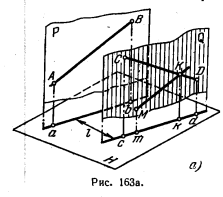
Решение. На рис. 163, а показаны параллельные между собой плоскости Р и Q, из которых пл. Q проведена через CD параллельно АВ, а пл. Р — через АВ параллельно пл. Q. Расстояние между такими плоскостями и считается расстоянием между скрещивающимися прямыми АВ и CD. Однако можно ограничиться построением только одной плоскости, например Q, параллельно АВ, а затем определить расстояние хотя бы от точки А до этой плоскости.

На рис. 163, в показана плоскость Q, проведенная через CD параллельно АВ; в проекциях проведено с’е’ || а’b’ и се || аb. Применяя способ перемены пл. проекций (рис. 163, в), введем дополнительную пл. S, перпендикулярную к пл. V и в то же время

перпендикулярную к пл. Q. Чтобы провести ось S/V, берем в этой плоскости фронталь D—1. Теперь проводим S/V перпендикулярно к d’1′ (рис. 163, в). Пл. Q изобразится на пл. S в виде прямой с_sd_s. Остальное ясно из чертежа.

168. Дана пирамида SABC (см. рис, 160). Определить расстояние между ребрами SC и AB.Применить: 1) способ перемены пл. проекций, 2) способ параллельного перемещения.

169*. Определить расстояние между параллельными плоскостями, из которых одна задана прямыми АВ и АС, а другая — прямыми DE и DF (рис. 164, а). Выполнить также построение для случая, когда плоскости заданы следами (рис. 164, б).

Решение. Расстояние (рис. 164, в) между параллельными плоскостями можно определить, проведя перпендикуляр из любой точки одной плоскости на другую плоскость. На рис. 164, г введена дополнительная пл. S перпендикулярно к пл. Н и к обеим данным плоскостям. Ось S.H перпендикулярна к горизонт. проекции горизонтали, проведенной в одной из плоскостей. Строим проекцию этой плоскости и точки В другой плоскости на пл. 5. Расстояние точки d_s до прямой l_sa_s равно искомому расстоянию между параллельными плоскостями.

На рис. 164, д дано другое построение (по способу параллельного перемещения). Для того чтобы плоскость, выраженная пересекающимися прямыми АВ и АС,оказалась перпендикулярна к пл. V, горизонт. проекцию горизонтали этой плоскости ставим перпендикулярно к оси х: 1₁2₁ ⊥ х. Расстояние между фронт. проекцией d’₁ точки D и прямой а’₁2′₁ (фронт. проекцией плоскости) равно искомому расстоянию между плоскостями.

На рис. 164, е показано введение дополнительной пл. S, перпендикулярной к пл.H и к данным плоскостям Р и Q (ось S/H перпендикулярна к следам Р_h, и Q_h). Строим следы Р_s, и Q_s. Расстояние между ними (см. рис. 164, в) равно искомому расстоянию l между плоскостями Р и Q.

На рис. 164, ж показано перемещение плоскостей Р₁ н Q₁, в положение P₁ и Q₁, когда горизонт. следы оказываются перпендикулярными к оси x. Расстояние между новыми фронт. следами P_1ϑ и Q_1ϑ равно искомому расстоянию l.

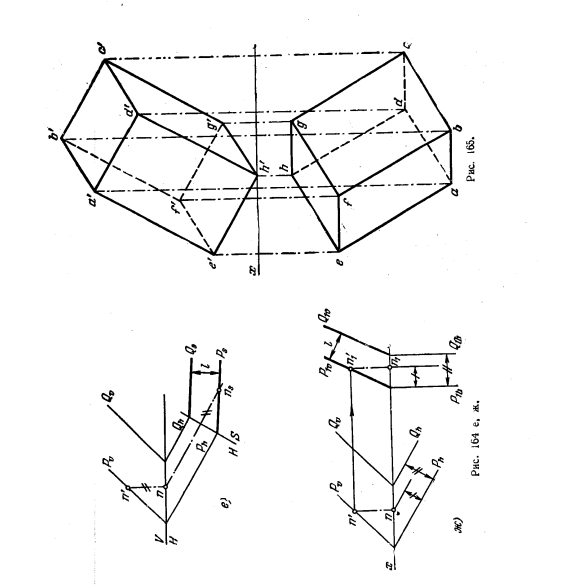
170. Дан параллелепипед ABCDEFGH (рис. 165). Определить расстояния: а) между основаниями параллелепипеда — l₁; б) между гранями ABFE и DCGH — l₂; в) между гранями ADHE и BCGF—l₃.

Источник

2.1. Содержание эпюра:

Дано:
Координаты вершин пирамиды SABC.

Требуется:

задача
1 — определить
натуральную величину основания пирамиды
АВС.

задача
2 — определить
расстояние от вершины пирамиды S
до плоскости ее основания АВС.

задача
3 — найти
кратчайшее расстояние между ребрами
пирамиды SА
и ВС.

задача
4 — определить
величину двугранного угла при ребре
пирамиды АВ.

Рекомендации
по выполнению эпюра:

Чертеж
должен быть выполнен в соответствии с
ГОСТми: 2.301 – 68^*
(Форматы), 2.302 — 68^*
(Масштабы), 2.303 — 68^*
(Линии), 2.304 – 81 (Шрифты) (приложение 4);

2. После выполнения
чертежа выполнить его обводку (возможно
оформление в цвете):

исходный чертеж
(цвет черный) и результат построений
(цвет красный) выполнить сплошными
основными толстыми линиями;
промежуточные
построения (цвет синий) – сплошными
тонкими;
невидимые линии
– штриховой.

Указания
к выполнению эпюра:

1.
Студенты факультета МСХ выполняют
задачи 1 – 4 на двух форматах А3. Задачи
1, 2 совместить на первом листе эпюра,
задачи 3, 4 – на втором. Студенты факультета
ПГС выполняют задачи 1 – 3 на двух форматах
А3.

2.
Данные для выполнения эпюра взять из
таблицы 2 в соответствии с вариантом.
Координаты точек даны в миллиметрах.
Все задания выполнить в масштабе 1:1.
Основная надпись выбирается в соответствии
с факультетом из приложения 3.

Задачи
эпюра должны быть решены следующими
способами:

— плоскопараллельное
перемещение (задача 2);

— вращение
вокруг горизонтали или фронтали (задача
1);

— замена
плоскостей проекций (задачи 3, 4).

Примечание:
при решении задач 3 и 4 расстояния
переносимые из одной плоскости в другую
отмечать засечками или другими знаками
(рисунки 2.8, 2.9).

Внимание!
Не разрешается все задачи решать одним
способом.

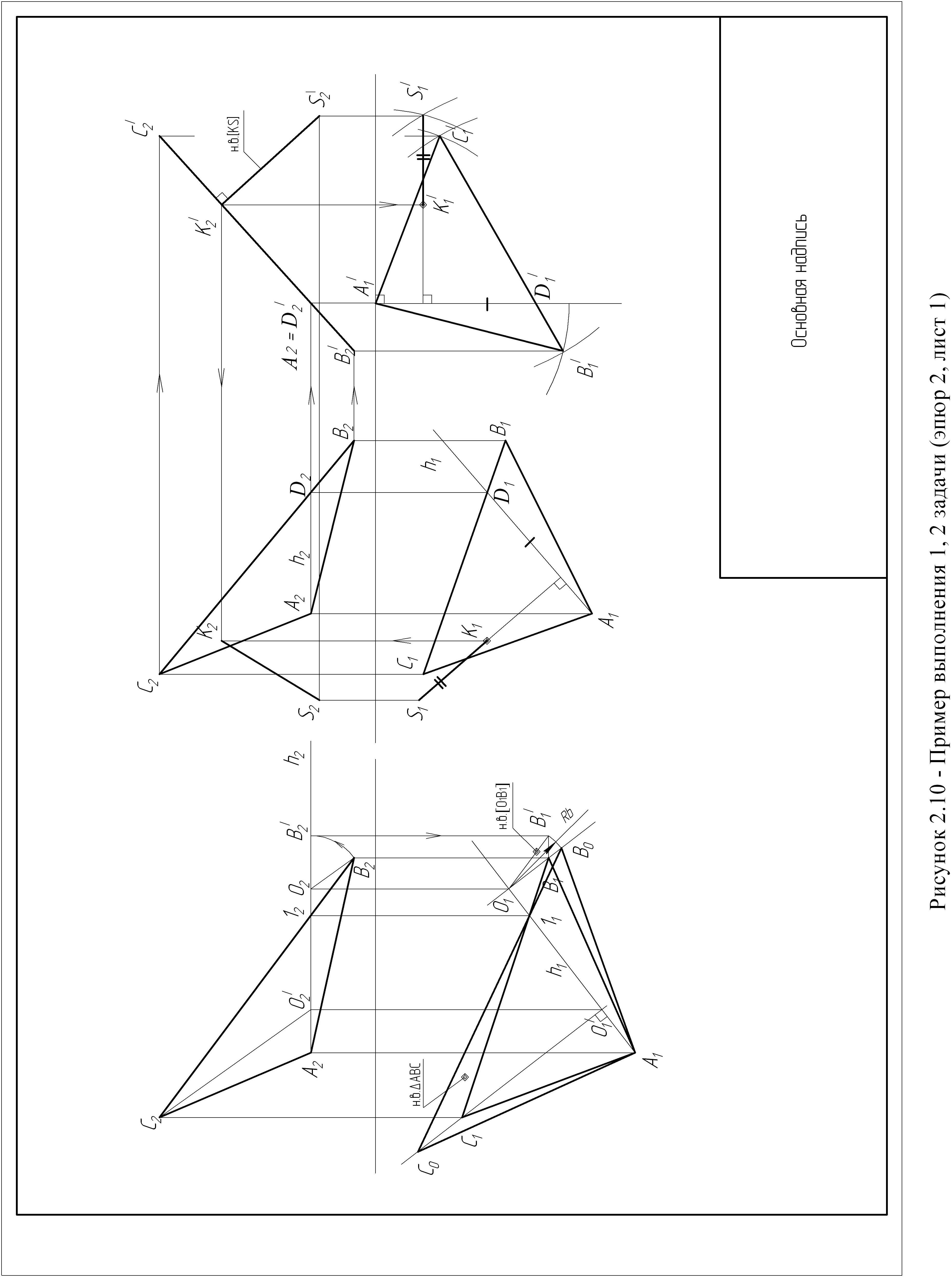
2.2. Порядок выполнения эпюра

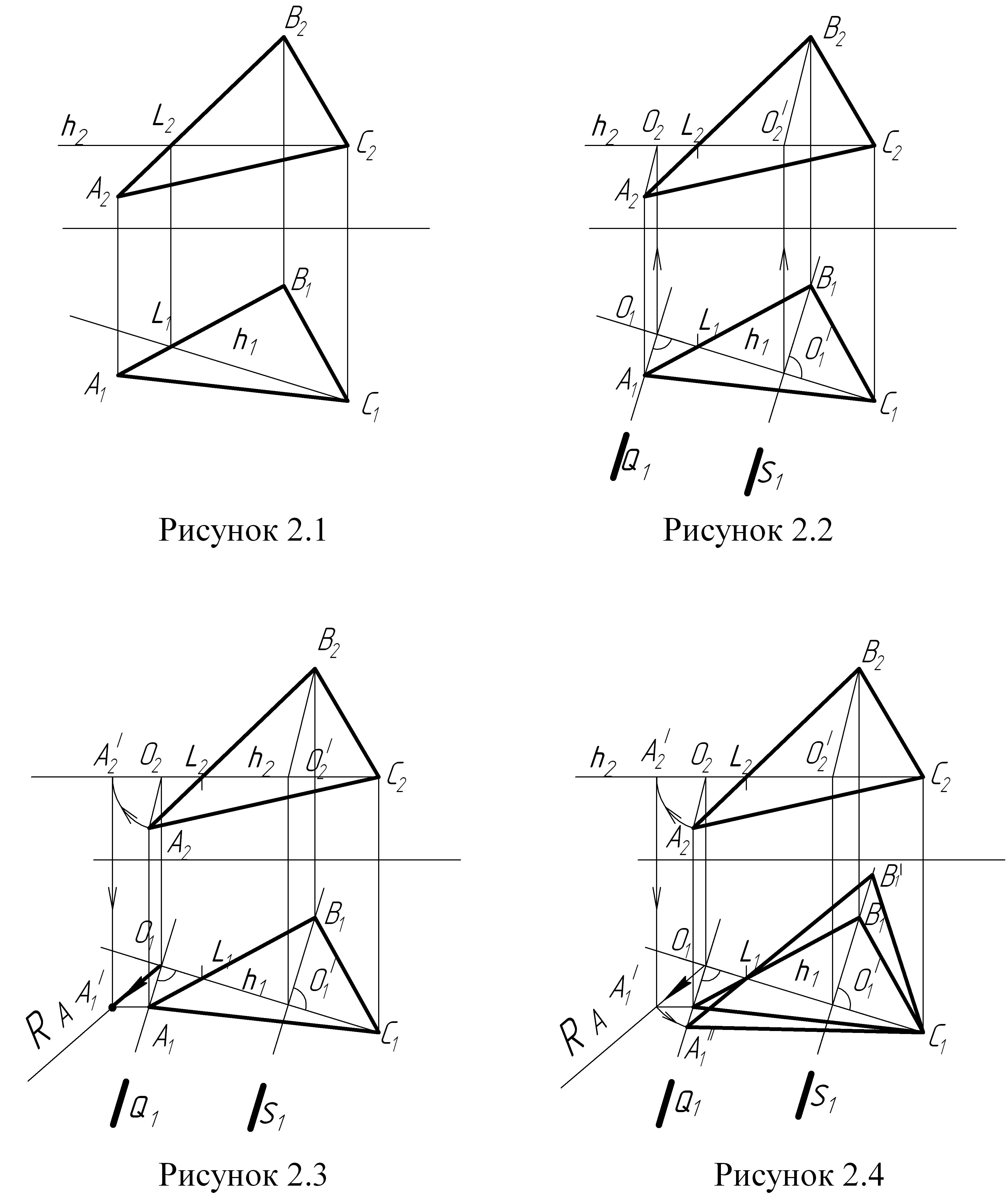
Задача
1 (рисунки
2.1, 2.2, 2.3, 2.4)

Для решения задачи 1 необходимо
преобразовать чертеж так, чтобы основание
пирамиды (треугольник {АВС}), представляющее
собой плоскость общего положения, в
результате вращения оказалось параллельным
одной из плоскостей проекций.

За
ось вращения принимаем горизонталь СL
(С₂L₂,
С₁L₁).
Каждая точка треугольника {АВС},
вращаясь вокруг горизонтали СL, будет
описывать дугу окружности в плоскости,
перпендикулярной к этой горизонтали,
а следовательно, и к плоскости П₁.

Окружности,
которые описывают вершины А и В
треугольника АВС, находясь в горизонтально
– проецирующих плоскостях Q
и S,
спроецируются на плоскость П₁
в виде прямых, совмещенных со следами
Q₁
и S₁
плоскостей Q и S.

Центры
вращения точек А и В будут лежать на
оси вращения (горизонтали CL). Для вершины
А– точка О ( О₁,О₂
), для вершины В – точка О´( О₁´,О₂´
).

Когда
плоскость треугольника АВС будет
параллельна плоскости П₁,
горизонтальная проекция каждой из
перемещающихся вершин окажется удаленной
от оси вращения (горизонтали СL)
на расстояние, равное радиусу вращения
данной точки.

Порядок
построения:

По
координатам точек А, В, С строим проекции
треугольника {АВС};
В
плоскости треугольника {АВС}
проводим
горизонталь СL
(С₂L₂,
С₁L₁)
являющуюся осью вращения треугольника
{АВС} (
рисунок 2.1 );
Из
горизонтальных проекций вершин А и В
проводим прямые, перпендикулярные
горизонтали СL,
по которым будут перемещаться
горизонтальные проекции вращающихся
точек ( рисунок 2.2);
Отмечаем
проекции центров вращения вершин
треугольника. Для вершины А–точка О
( О₁,О₂
), для вершины В – точка О´( О₁´,О₂´
). Радиус вращения вершины А – [АО]
([А₁О₁],
[А₂О₂]),
радиус вращения вершины В – [ВО’]
([В₁О₁‘],
[В₂О₂‘]);
По
двум проекциям определяем натуральную
величину R_А
радиуса вращения вершины А (рисунок
2.3). Натуральная величина R_А
определяется способом вращения отрезка
[АО] вокруг оси , проходящей через точку
О перпендикулярно плоскости П₂;
Отрезок
R_А
откладываем от точки О₁
вдоль прямой, по которой
перемещается горизонтальная проекция
вершины А₁.
Получим точку А₁»;
Через
полученную точку В₁‘
и точку L₁
проводим прямую до пересечения с прямой,
по которой перемещается горизонтальная
проекция вершины В;
Получим
точку В₁‘
( рисунок 2.4);
Соединяя
найденные точки А₁»
и В₁‘
с вершиной С₁
, получаем новую горизонтальную проекцию
треугольника {А₁»В₁‘С₁}.
Эта проекция определяет натуральную
величину плоскости треугольника {АВС}.

Задача
2 (рисунки
2.5, 2.6)

Для
решения задачи 2 необходимо преобразовать
чертеж так, чтобы основание пирамиды –
треугольник {АВС},
представляющий собой плоскость общего
положения, в результате перемещения
оказалось перпендикулярным плоскости
П₂
(плоскости П₁),
т.е. стало фронтально – проецирующей
плоскостью (горизонтально – проецирующей
плоскостью).

Порядок построения:

По
координатам точек S,
A,
B,
C
строим проекции основания пирамиды
треугольника {АВС}
и ее вершину
точки S;
В
плоскости треугольника {АВС}
проводим
горизонталь ВД (В₁Д₁,
В₂Д₂)
(рисунок 2.5);
По
координатам точек S,
A,
B,
C
строим проекции основания пирамиды
треугольника {АВС}
и ее вершину
точки S;
В
плоскости треугольника {АВС}
проводим
горизонталь ВД (В₁Д₁,
В₂Д₂)
(рисунок 2.5);
Переместим
треугольник {АВС}
так, чтобы
горизонтальная проекция В₁Д₁горизонтали
заняла положение перпендикулярное оси
Х, а фронтальная проекция треугольника
{А₂В₂С₂}
превратилась
в прямую линию, т.е. треугольник {АВС}
станет
фронтально — проецирующей плоскостью;
Найдем
новое положение точки S
(при помощи засечек);
Перпендикуляр
из точки S
к фронтально проецирующей плоскости
будет искомым расстоянием (рисунок
2.6);
Покажем
перпендикуляр [SК]
в исходных проекциях;
Определить
видимость перпендикуляра [SK].

Примечание:
задачу можно решать, преобразовав
треугольник АВС в горизонтально –
проецирующую плоскость, тогда в плоскости
треугольника необходимо построить
фронталь.

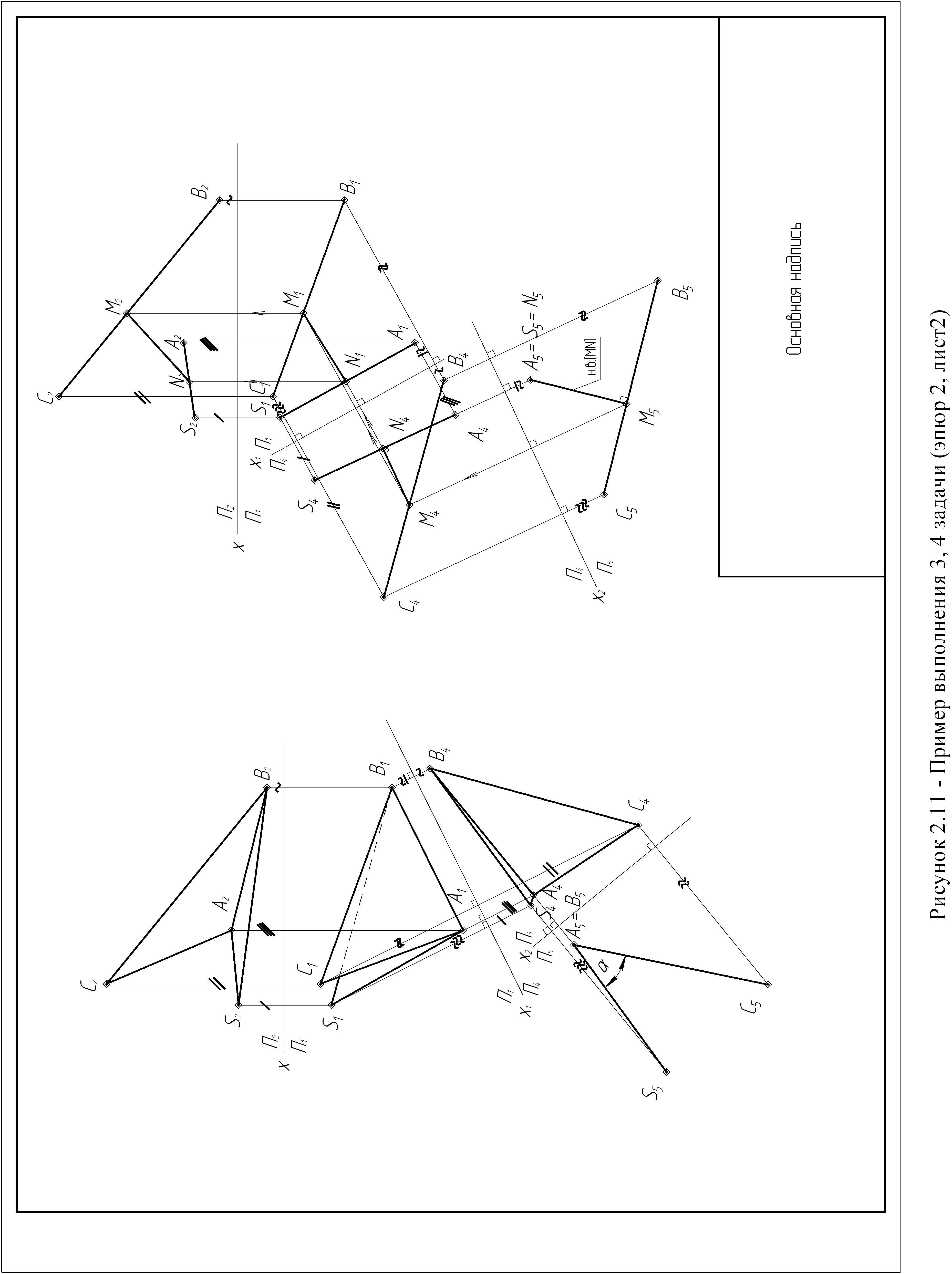
Задача
3 (рисунки
2.7, 2.8, 2.9)

Если
одна из заданных прямых является
проецирующей прямой, то кратчайшее
расстояние между такими прямыми
измеряется длиной перпендикуляра [MN],
общего к заданным прямым. В этом случае
перпендикуляр [MN] будет параллелен одной
из плоскостей проекций и равен длине
его проекции на эту плоскость.

Для
решения данной задачи необходимо одну
из прямых общего положения (SA)
или (BC)
преобразовать в прямую проецирующую,
применив две замены плоскостей проекций.

Порядок
построения:

По
координатам точек S,
A,
B,
C
построить проекции ребра пирамиды
SA
и проекцию стороны основания BC
(рисунок 2.7);
При
первой замене чертеж преобразуем так,
чтобы прямая общего положения
(ВС) оказалась параллельной одной из
плоскостей проекций, для этого вводим
новую плоскость П₄,
перпендикулярную плоскости П₁
и параллельную отрезку [ВС]. Ось Х₁
проведем параллельно [В₁С₁].
Измеряя расстояния от оси х до точек
А₂,
S₂,
В₂
и С₂
и откладывая их в плоскости П₄
от оси х₁,
получаем проекции [S₄A₄]
и [В₄C₄]
прямых (SA)
и (ВС) (рисунок 2.8);
При
второй замене чертеж преобразуем так,
чтобы отрезок прямой [ВС], параллельный
в системе П₄/П₁
плоскости П₄,
стал перпендикулярен плоскости П₅
в системе П₄/П₅
(рисунок 2.9);
Вводим
новую плоскость П₅,
перпендикулярно плоскости П₄
и отрезку [ВС], т.е. ось Х₂
пройдет перпендикулярно [В₄С₄].
Измерив расстояния от оси Х₁
до точек А₁,
S₁,
В₁,
С₁
и отложить их в плоскости П₅
от оси Х₂
на соответствующих линиях связи, получим
проекции [В₅С₅]
и [S₅А₅];
Находим
кратчайшее расстояние [МN]
между прямыми (SА)
и (ВС). Кратчайшим расстоянием будет
являться перпендикуляр, опущенный из
точки В₅=С₅
на проекцию [S₅А₅];
По
линиям связи находим проекции кратчайшего
расстояния между прямыми (SА)
и (ВС) в исходных проекциях.

Примечание:
данную задачу
можно решить, используя только одну
замену плоскостей проекций, если одна
из данных прямых (AS)
или (BC)
является прямой уровня.

Задача
4

Если
двугранный угол образован проецирующими
плоскостями и ребро АВ двугранного угла
перпендикулярно этой плоскости, то
двугранный угол спроецируется в
натуральную величину.

Для
решения данной задачи необходимо ребро
АВ (прямую общего положения) преобразовать
в проецирующую прямую, применив две
замены плоскостей проекций.

Порядок
построения:

По
координатам точек S,
А, В, С строим проекции двугранного
угла;
При
первой замене чертеж преобразуем так,
чтобы ребро АВ двугранного угла оказалось
параллельным одной из плоскостей
проекций, т.е. вводим новую плоскость
П₄,
перпендикулярно плоскости П₂
и параллельно ребру АВ; ось Х₁
пройдет параллельно [А₁В₁]
(рисунок 2.11);
По
линиям связи, перпендикулярным оси Х₁,
двугранный угол проецируем на плоскость
П₄.
Получаем проекцию S₄А₄В₄С₄
двугранного угла SАВС.
При
второй замене чертеж преобразуем так,
чтобы ребро АВ стало перпендикулярно
новой плоскости П₅;
Вводим
новую плоскость П₅
перпендикулярно плоскости П₄
и ребру АВ, т.е. ось Х₂
пойдет перпендикулярно А₄В₄.
По линиям связи, перпендикулярным оси
Х₂,
проецируем двугранный угол SАВС
на плоскость П₅.
Получаем проекцию двугранного угла на
плоскости П₅;
Натуральной
величиной двугранного угла будет угол
α, между проекциями сторон двугранного
угла [А₅=В₅
S₅]
и [А₅=В₅
С₅].

Примечание:
если ребро
АВ двугранного угла является прямой
уровня, то задача решается с помощью
одной замены плоскостей проекций.

Таблица
2 — Индивидуальные
задания к эпюру 2.

№

вар.

Точки

Координаты

№

вар.

Точки

Координаты

Продолжение
таблицы 2

Продолжение таблицы
2

Продолжение
таблицы 2

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Решение задач по теме «Пирамида» координатным методом

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Мой урок 2.ppt

Описание презентации по отдельным слайдам:

Я хочу чтобы Вы хорошо сдали экзамены

Три пути ведут к знанию: Путь размышления – это путь самый благородный, Путь подражания – это путь самый легкий, И путь опыта – это путь самый горький. (Конфуций)

Путь подражания – это путь самый легкий

Основные определения Определение 1. Ненулевой вектор называется направляющим вектором прямой a, если он лежит либо на прямой a , либо на прямой, параллельной a. a Определение 2. Угол между векторами – это угол между векторами, равными данным и отложенными от одной точки . А О В

Основные определения Определение 3. Углом между прямыми в пространстве будем называть острый из вертикальных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным. α Определение 4. Угол между прямой и плоскостью это угол между прямой и ее проекцией на эту плоскость.

Определение 5. Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях. Определение 6. Отрезок, имеющий концы на двух скрещивающихся прямых и перпендикулярный к ним, называется общим перпендикуляром скрещивающихся прямых. Определение 7. Расстояние между скрещивающимися прямыми равно длине общего перпендикуляра скрещивающихся прямых.

Определение 8. Расстояние от точки до прямой – не содержащей эту точку, есть длина отрезка перпендикуляра, проведенного из этой точки на прямую. Определение 9. Расстояние от точки до плоскости– длина перпендикуляра, опущенного из точки на плоскость. Определение 10. Расстояние между прямой и параллельной ей плоскостью длина перпендикуляра, опущенного из любой точки прямой на плоскость. Определение 11-12. Расстояние между параллельными прямыми (плоскостями)– длина перпендикуляра, опущенного из любой точки одной прямой (плоскости) на другую прямую (плоскость).

Определение 13 Нормальный вектор плоскости это любой ненулевой вектор, лежащий на любой прямой перпендикулярной к данной плоскости. Общее уравнение плоскости, где <А;В;С>– вектор нормали Ах+Ву+Сz+D = 0 Общее уравнение плоскости, проходящей через точку М (х0; у0;z0) и вектор нормали <А;В;С>– вектор нормали А(х – х0 ) +В( у- у0 )+С (z — z0 ) = 0

Уравнение плоскости (Оху) : z=0 Уравнение плоскости (Охz) : y=0 Уравнение плоскости (Оyz) : x=0

1. 2. ( 3. 4. 5. 6. 7. 8. 1 2 3 4 5 6 7 8 1П 2 3 4 5 6 7 8 1П 2И 3 4 5 6 7 8 1П 2И 3Р 4 5 6 7 8 1П 2И 3Р 4А 5 6 7 8 1П 2И 3Р 4А 5М 6 7 8 1П 2И 3Р 4А 5М 6И 7 8 1П 2И 3Р 4А 5М 6И 7Д 8 1П 2И 3Р 4А 5М 6И 7Д 8А

ТЕМА УРОКА: Решение задач по теме «Пирамида» координатным методом.

ПРИМЕНИТЬ ФОРМУЛУ, ВЫПОЛНИТЬ ВЫЧИСЛЕНИЯ. ВЫПИСАТЬ КООРДИНАТЫ ВСЕХ НЕОБХОДИМЫХ ТОЧЕК ВВЕСТИ ПРЯМОУГОЛЬНУЮ СИСТЕМУ КООРДИНАТ ВЫЧИСЛИТЬ КООРДИНАТЫ НЕОБХОДИМЫХ ВЕКТОРОВ ЗАПИСАТЬ ОТВЕТ Алгоритм для решения С2 методом координат

Путь размышления – это путь самый благородный,

1. В правильной шестиугольной пирамиде SАВСDEF, стороны основания равны 1, а боковые ребра равны 2, точка К – середина ребра SF. Найдите градусную меру угла между прямой ВК плоскостью основания. 2. В правильной четырехугольной пирамиде FABCD сторона квадрата АВСD, лежащего в основании, равна , а высота, опущенная на основание, равна 2. Найдите расстояние от вершины А до плоскости DFС. 3. Сторона основания АВС правильной треугольной пирамиды DАВС равна 3 , а боковое ребро 5. Найдите объем пирамиды DАРК, где Р и К – середины ребер DВ и DС.

Электронная физкультминутка для глаз

A B C D E S O F В правильной шестиугольной пирамиде SАВСDEF, стороны основания равны 1, а боковые ребра равны 2, точка К – середина ребра SF. Найдите градусную меру угла между прямой ВК плоскостью основания. К

A B C D E S O F К х у Z Дано: пирамида, АВСDEF — правильный шестиугольник, АВ=1, SF=2, К- середина SF Найти: угол между ВК и (АВС). Решение: Введем прямоугольную систему координат. 2. В этой системе координат найдем координаты нужных точек В , К. В К 3. Найдем координаты вектора ВК. 4. Уравнение плоскости (АВС) 5. Найдем угол между прямой и плоскостью. Ответ:

A B D F O В правильной четырехугольной пирамиде FABCD сторона квадрата АВСD, лежащего в основании, равна , а высота, опущенная на основание, равна 2. Найдите расстояние от вершины А до плоскости DFС. C

И путь опыта – это путь самый горький.

А С В D О Р К Сторона основания АВС правильной треугольной пирамиды DАВС равна 3 , а боковое ребро 5. Найдите объем пирамиды DАРК, где Р и К – середины ребер DВ и DС.

В жизни нет ничего лучше собственного опыта. Скотт В.

Источник шаблона: Ранько Елена Алексеевна, учитель начальных классов, МАОУ лицей №21, г. Иваново Сайт: http://pedsovet.su/ Домашнее задание: решить задачи геометрическим методом

Выбранный для просмотра документ Урок пирамида.doc

Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа с углубленным изучением отдельных предметов №68, г. Липецка

Решение задач по теме «Пирамида » координатным методом

Способствовать развитию навыка решения задач координатным методом на примере решения задач по теме «Пирамида» типа С2 ЕГЭ.

систематизировать знания учащихся;

совершенствовать навыки решения задач методом координат;

способствовать развитию внимательности, воображения;

способствовать воспитанию самостоятельности, активности.

Мотивация (самоопределение) к учебной деятельности (2мин)
«Я хочу»
Ребята, вы хотите хорошо сдать ЕГЭ по математике?
Хотите научиться решать задачи по геометрии?

Если да, то многое будет зависеть от вас. Вы должны переключить все свое внимание на урок, убрать лишние вещи, на время забыть жизненные проблемы.

Три пути ведут к знанию:

Путь размышления – это путь самый благородный,

Путь подражания – это путь самый легкий,

И путь опыта – это путь самый горький.

Эти три пути нам предстоит пройти сегодня на уроке. Если вам что-то не будет понятно, обращайтесь к учителю. Проблемы, которые вы будете решать на уроке, вполне преодолимы, нужно всего лишь сделать небольшое усилие, напрячь мозги.

Актуализация знаний и фиксация индивидуального затруднения в пробном действии (5 минут).

Путь подражания – это путь самый легкий

Задание 1: Продолжи предложение, вставив недостающие слова. Основные определения стереометрии:

Ненулевой вектор называется направляющим вектором прямой a , если он лежит либо на прямой a , либо на прямой, параллельной a .

Угол между векторами – это угол между векторами, равными данным и отложенными от одной точки.

Углом между прямыми в пространстве будем называть острый из вертикальных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Угол между прямой и плоскостью это угол между прямой и ее проекцией на эту плоскость.

Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.

Отрезок, имеющий концы на двух скрещивающихся прямых и перпендикулярный к ним, называется общим перпендикуляром скрещивающихся прямых.

Расстояние между скрещивающимися прямыми равно длине общего перпендикуляра скрещивающихся прямых.

Расстояние от точки до прямой – длина перпендикуляра, опущенного из точки на прямую.

Расстояние от точки до плоскости– длина перпендикуляра, опущенного из точки на плоскость.

Расстояние между параллельными прямой и плоскостью длина перпендикуляра, опущенного из любой точки прямой на плоскость.

Расстояние между параллельными прямыми (плоскостями)– длина перпендикуляра, опущенного из любой точки одной прямой (плоскости) на другую прямую (плоскость).

Нормальный вектор плоскости это любой ненулевой вектор, лежащий на любой прямой перпендикулярной к данной плоскости.

Общее уравнение плоскости, проходящей через точку М (х₀; у₀; z ₀) и вектор нормали <А;В;С>– вектор нормали

Выявление места и причины затруднения (2 минуты)

Задание : Угадай формулу

Тему урока учащиеся формулирую самостоятельно, отвечая на вопрос « Для чего мы сегодня повторяли данные формулы?»

ТЕМА урока: Решение задач по теме «Пирамида » координатным методом.

Построение проекта выхода из затруднения(5 мин)

В чем заключается цель нашей дальнейшей работы?(применение метода координат в решении задач по «Пирамида» )

Что необходимо знать для решения задач данным методом? ( основной алгоритм решения задач координатным методом)

Что для ВАС самое сложное в данном алгоритме? (выбрать систему координат и определить координаты необходимых точек)

Мозговой штурм.

Задание: Найди ошибку.

Каждая группа из 3-4 учащихся разрабатывает план решения с проговариванием решения вслух .

Выслушиваются все мнения.
Отмечаем плюсы и минусы каждого решения( Принцип вариативности ) и сравниваем с решением, который приведен на слайде.

Физкультминутка для глаз (3 минуты)

5. Реализация построенного проекта, самостоятельное решение задач по группам (задачи дифференцированы по сложности) (15 мин)

Путь размышления – это путь самый благородный,

1 группа : : В правильной шестиугольной пирамиде S АВС DEF , стороны основания равны 1, а боковые ребра равны 2, точка К – середина ребра SF . Найдите градусную меру угла между прямой ВК плоскостью основания.

В правильной четырехугольной пирамиде FABCD сторона квадрата АВС D , лежащего в основании, равна , а высота, опущенная на основание, равна 2. Найдите расстояние от вершины А до плоскости DF С.

Как рассчитать объем пирамиды по координатам вершин? Методика и пример задачи

Часто в задачах школьного курса геометрии приходится решать задания, которые требуют использования комплексного подхода. Одной из таких задач является вычисление объема пирамиды по координатам вершин. Как решить эту геометрическую задачу — ответит приведенная ниже статья.

Что представляет собой пирамида?

Говоря простыми словами, под этой фигурой понимают пространственный объект, ограниченный треугольными сторонами и одной многоугольной гранью, которая называется основанием. Многоугольное основание может быть произвольным n-угольником на плоскости, например, правильным треугольником, параллелограммом и так далее.

Вам будет интересно: Какую роль играет репродуктивная клетка животных и растений?

Любая пирамида имеет n + 1 грань, 2 * n ребер и n + 1 вершину. Вершины фигуры не являются равноправными. Так, существует единственная вершина, которая не принадлежит основанию. Она называется главной. Расстояние от нее до плоскости основания — это высота фигуры.

Пирамиды могут быть наклонными, если высота пересекает основание не в его центре, или прямыми, когда высота с основанием пересекается в геометрическом центре последнего. Также фигуры могут быть неправильными и правильными. Пирамиды правильные состоят из равноугольного и равностороннего основания и нескольких равнобедренных треугольников, которые друг другу равны.

Как рассчитывается объем пирамиды?

Прежде чем приводить методику вычисления по координатам вершин объема пирамиды, следует привести формулу, при помощи которой можно рассчитать эту величину для фигуры любого типа из рассматриваемого класса. Итак, объем пирамиды рассчитывается так:

Здесь So — это основания площадь, h — расстояние от главной вершины до основания, то есть высота пирамиды.

Таким образом, любая геометрическая задача на нахождение объема пирамиды сводится к расчету величин So и h.

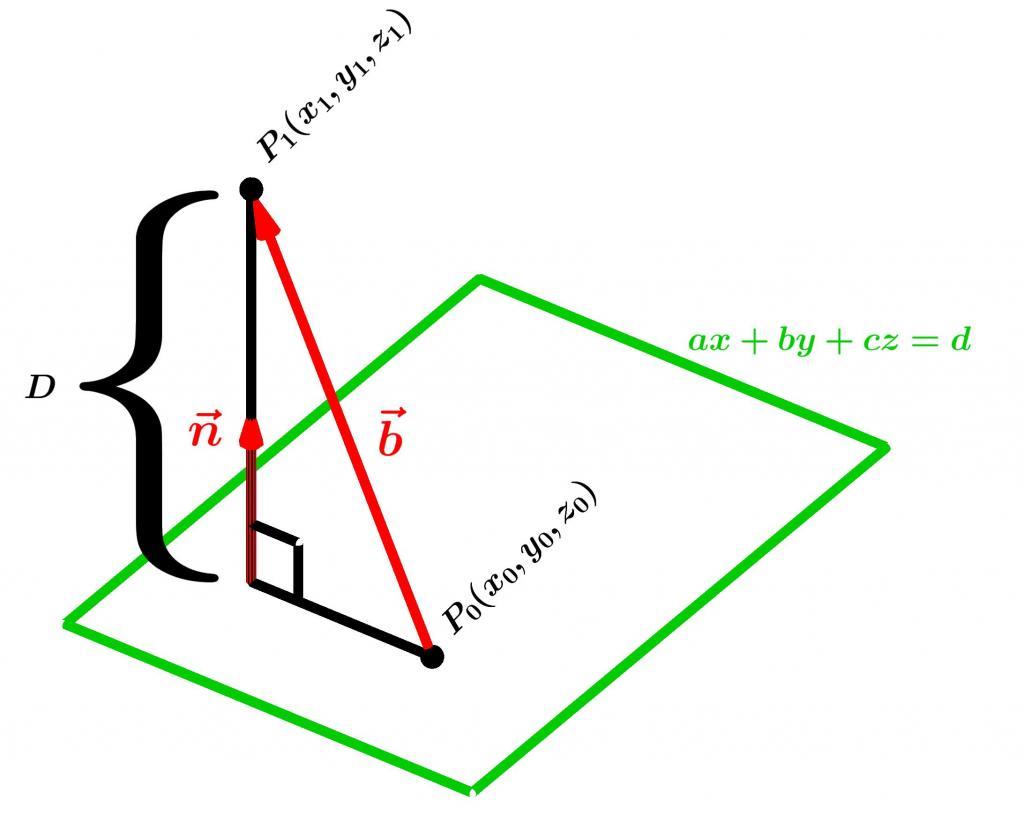
Как найти объем пирамиды по координатам вершин: методика

Пирамида может быть представлена произвольным n-угольным основанием. Чтобы рассчитать его площадь, следует внимательно изучить условие задачи, в котором должно быть сказано, о каком типе n-угольника идет речь. Если это треугольник или параллелограмм, то расчет его площади по известным координатам очень прост: необходимо лишь найти векторное произведение соответствующих векторов сторон.

Вычислить высоту пирамиды также не представляет особого труда. Для этого следует из любых трех точек основания получить уравнение плоскости в общем виде, а затем нужно воспользоваться формулой расстояния между плоскостью и точкой (вершиной пирамиды). Формула имеет вид:

d = |(A * x1 + B * y1 + C * z1 + D)| / √(A2 + B2 + C2).

Здесь (x1; y1; z1) — координаты точки.

Уравнение плоскости имеет вид:

A * x + B * y + C * z + D = 0.

Задача с треугольной пирамидой

Решим задачу на примере самой простой пирамиды — треугольной. Условие простое: ниже даны координаты вершин пирамиды, объем найти нужно для фигуры, которая на этих координатах построена:

Положим, что основание пирамиды является треугольником ABC. Найдем длины векторов AB¯ и AC¯:

Векторное произведение AB¯ и AC¯ даст нам, с одной стороны, двойную площадь треугольника, то есть 2 * So, а с другой стороны, мы получим координаты нормального к плоскости вектора n¯, имеем:

n¯ = [AB¯ * AC¯] = (8; -10; -7).

Площадь треугольного основания равна полудлине вектора n¯, то есть:

So = √(82 + 102 + 72) / 2 = 7,3.

Прежде чем рассчитывать расстояние от D до плоскости ABC, необходимо записать уравнение плоскости. Три его коэффициента (A, B, C) мы уже знаем, они соответствуют координатам нормали n¯. Свободный член можно получить, подставив в уравнение координаты любой точки плоскости, например точки A, имеем:

D = -1 * (A * x1 + B * y1 + C * z1) = -1 * (8 * 1 + (-10) * 0 + (-7) * 3) = 13.

Тогда уравнение плоскости основания пирамиды принимает форму:

8 * x — 10 * y — 7 * z + 13 = 0.

Теперь применяем приведенную выше формулу для расчета расстояния от точки D(4; 3; 4) до найденной плоскости, получаем:

d = |(8 * 4 — 10 * 3 — 7 * 4 + 13)| / √(82 + 102 + 72) = 0,89.

Поскольку найденное значение расстояния d соответствует высоте пирамиды треугольной h, то можно воспользоваться формулой для объема фигуры:

V = 1 / 3 * So * h = 1 / 3 * 7,3 * 0,89 ≈ 2,166.

Полученное значение объема выражено в кубических единицах выбранной координатной системы.

источники:

http://infourok.ru/reshenie-zadach-po-teme-piramida-koordinatnim-metodom-272675.html

http://1ku.ru/obrazovanie/51574-kak-rasschitat-obem-piramidy-po-koordinatam-vershin-metodika-i-primer-zadachi/

Источник

Трудность мизерная.

Смотрим фасад правильной пирамиды. Нужно найти [math]x[/math].

Из подобия треугольников [math]BCD[/math] и [math]AEC[/math], а также из заданных условий, можем написать систему трех уравнений, решая которую неминуемо найдем, что [math]x=3[/math]

Гораздо интересней вот что: при решении системы находятся два варианта положительных значений других трех параметров:

1) [math]a=1 , ; quad h=12 , ; quad l=4[/math]

2) [math]a=2 , ; quad h=3 , ; quad l=2[/math]

Но эти варианты не удовлетворяют условию

[math]l=sqrt{frac{a^2}{4}+h^2}[/math]

Решение есть, но оно кубическое, довольно сложное (причем комплексное). То есть пирамиду такую реально сделать нельзя. Нужны иные значения объема и площади боковой поверхности.

Источник

X²=Y²+h²

h²=X²-Y²

h=√(X²-Y²)

h=√(X²-Y²) = √(X²-R²) = √(X²-(a/(2sin(180/n)))²)

2.1. Содержание эпюра:

2.2. Порядок выполнения эпюра

Решение задач по теме «Пирамида» координатным методом

«Снятие эмоционального напряжения у детей и подростков с помощью арт-практик и психологических упражнений»

Выберите документ из архива для просмотра:

Описание презентации по отдельным слайдам:

Как рассчитать объем пирамиды по координатам вершин? Методика и пример задачи

Что представляет собой пирамида?

Как рассчитывается объем пирамиды?

Как найти объем пирамиды по координатам вершин: методика

Задача с треугольной пирамидой

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»