Определение расстояния от точки до прямой
Расстояние от точки до прямой – это длина перпендикуляра, опущенного из точки на прямую. В начертательной геометрии она определяется графическим путем по приведенному ниже алгоритму.
Алгоритм
- Прямую переводят в положение, в котором она будет параллельна какой-либо плоскости проекции. Для этого применяют методы преобразования ортогональных проекций.
- Из точки проводят перпендикуляр к прямой. В основе данного построения лежит теорема о проецировании прямого угла.
- Длина перпендикуляра определяется путем преобразования его проекций или с использованием способа прямоугольного треугольника.
Пример
На следующем рисунке представлен комплексный чертеж точки M и прямой b, заданной отрезком CD. Требуется найти расстояние между ними.
Решение
Согласно нашему алгоритму, первое, что необходимо сделать, это перевести прямую в положение, параллельное плоскости проекции. При этом важно понимать, что после проведенных преобразований фактическое расстояние между точкой и прямой не должно измениться. Именно поэтому здесь удобно использовать метод замены плоскостей, который не предполагает перемещение фигур в пространстве.
Результаты первого этапа построений показаны ниже. На рисунке видно, как параллельно b введена дополнительная фронтальная плоскость П4. В новой системе (П1, П4) точки C»1, D»1, M»1 находятся на том же удалении от оси X1, что и C», D», M» от оси X.
Выполняя вторую часть алгоритма, из M»1 опускаем перпендикуляр M»1N»1 на прямую b»1, поскольку прямой угол MND между b и MN проецируется на плоскость П4 в натуральную величину. По линии связи определяем положение точки N’ и проводим проекцию M’N’ отрезка MN.
На заключительном этапе нужно определить величину отрезка MN по его проекциям M’N’ и M»1N»1. Для этого строим прямоугольный треугольник M»1N»1N0, у которого катет N»1N0 равен разности (YM1 – YN1) удаления точек M’ и N’ от оси X1. Длина гипотенузы M»1N0 треугольника M»1N»1N0 соответствует искомому расстоянию от M до b.
Второй способ решения
- Параллельно CD вводим новую фронтальную плоскость П4. Она пересекает П1 по оси X1, причем X1∥C’D’. В соответствии с методом замены плоскостей определяем проекции точек C»1, D»1 и M»1, как это изображено на рисунке.
- Перпендикулярно C»1D»1 строим дополнительную горизонтальную плоскость П5, на которую прямая b проецируется в точку C’2 = b’2.
- Величина расстояния между точкой M и прямой b определяется длиной отрезка M’2C’2, обозначенного красным цветом.
Похожие задачи:
- Определение расстояния от точки до плоскости
- Определение натуральной величины отрезка
- Расстояние между параллельными прямыми
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Соотношения между сторонами и углами треугольника
- Расстояние от точки до прямой
Пусть нам даны прямая 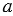
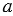
Отрезок АМ называется наклонной, проведенной из точки А к прямой 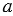
Следовательно, перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведенной из той же точки к этой прямой.
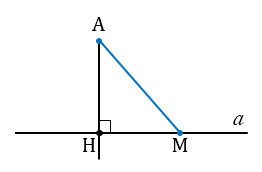
Расстояние от точки до прямой — это длина перпендикуляра (т.е. наименьшее расстояние), проведенного из данной точки к данной прямой.
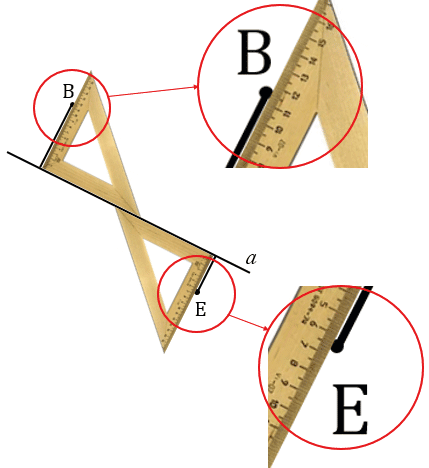
Для того, чтобы найти расстояние от точки до прямой, нужно с помощью чертежного угольника провести перпендикуляр из данной точки к данной прямой, а затем измерить длину этого перпендикуляра.
Расстояние от точки Е до прямой 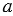
Советуем посмотреть:
Теорема о сумме углов треугольника
Остроугольный, прямоугольный и тупоугольный треугольники
Теорема о соотношениях между сторонами и углами треугольника
Неравенство треугольника
Некоторые свойства прямоугольных треугольников
Признаки равенства прямоугольных треугольников
Уголковый отражатель
Расстояние между параллельными прямыми
Построение треугольника по двум сторонам и углу между ними
Построение треугольника по стороне и двум прилежащим к ней углам
Построение треугольника по трем его сторонам
Соотношения между сторонами и углами треугольника
Правило встречается в следующих упражнениях:
7 класс
Задание 275,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 276,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 285,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 301,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 321*,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 14,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 17,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 434,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 565,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 939,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Что называется расстоянием от точки до прямой? Как найти расстояние от точки до прямой?
Определение.
Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из данной точки на прямую.
рисунок 1
Таким образом, чтобы найти расстояние от точки до прямой, надо из точки к прямой провести перпендикуляр и найти его длину.
Например, на рисунке 1 расстояние от точки A до прямой a равно длине перпендикуляра AB, опущенного из точки A на прямую a.
Задачи на нахождение расстояния от точки до прямой сводятся к рассмотрению прямоугольного треугольника.
Задачи.
№ 1. Из точки к прямой проведены две наклонные, длины которых относятся как 2:3, а длины их проекций соответственно равны 2 см и 7 см. Найти расстояние от точки до прямой.

AC и AD — наклонные, AC:AD=2:3,
BC и BD — их проекции, BC=2 см, BD=7 см
Найти: AB.
Решение:
1) Пусть k — коэффициент пропорциональности. Тогда AC=2k см, AD=3k см.
2) Рассмотрим треугольник ABC — прямоугольный (так как AB — перпендикуляр к прямой a по условию). По теореме Пифагора
откуда
3) Аналогично, из треугольника ABD
4) Приравниваем правые части полученных равенств и находим k:
5) Зная k, найдем AB:
Ответ: 4√2 см.
№ 2. Из точки к прямой проведены две наклонные, длины которых равны 13 см и 15 см. Найти расстояние от точки до прямой, если разность проекций наклонных равна 4 см.

AC и AD — наклонные, AC=13 см, AD=15 см,
BC и BD — их проекции, BD-BC=4 см
Найти: AB.
Решение:
1) Пусть BC=x см, тогда BD=x+4 см.
2) Рассмотрим треугольник ABC — прямоугольный (так как AB — перпендикуляр к прямой a по условию). По теореме Пифагора
откуда
3) Аналогично, из треугольника ABD
4) Приравниваем правые части полученных равенств и находим x:
5) Зная x, найдем AB:
Ответ: 12 см.
№ 3. Найти расстояние от точки A до прямой a, если известно, что наклонная AF, длина которой равна c, образует с прямой a угол α.

AF — наклонная,
AF=c, ∠AFB=α.
Найти: AB.
Решение:
Треугольник ABF — прямоугольный (так как AB — перпендикуляр к прямой a по условию). AB — катет, противолежащий углу ACB, AF — гипотенуза.
По определению синуса
Ответ: c∙sinα.
Что такое расстояние от точки до прямой
Определение
Расстояние от точки до прямой – это длина перпендикуляра, опущенного из точки на прямую.
При этом перпендикуляр – это наименьшее из расстояний от этой точки до точек прямой.
Расстояние от точки до прямой на плоскости, методы нахождения
Найти расстояние от точки до прямой можно двумя способами. С помощью теоремы Пифагора или прямоугольной системы координат. Рассмотрим первый метод.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Теорема Пифагора гласит, что прямоугольная система координат OXY имеет точку М1 (x1, y1). Из нее к плоскости проведена прямая а. Уравнение плоскости имеет вид:
cos ax + cos by — p = 0.
Это уравнение равно по модулю значению, которое получается в левой части уравнения прямой при x = x1, а y = y1. Это значит, что:
M1H1 = cos ax1 + cos by1 — p
Доказательство
Прямой а соответствует уравнение плоскости, которое имеет вид:
cos ax + cos by — p = 0.
Тогда n → = (сos a, cos b) – это нормальный вектор прямой а с расстоянием от начала координат до прямой а с р единицами. При этом радиус вектор точки М1 — ОМ1 → = (х1, у1).
М1Н1 – прямая от точки до прямой. Проекции М2 и Н2 точек М1 и Н1 проходят через точку О с направляющим вектором n → = (cos a, cos b). Числовая проекция вектора ОМ1 → = (х1, у1) направлена к n → = (cos a, cos b) как npn → OM1 →. В итоге получаем М1Н1 = npn → ОМ → 1 — р.
Далее приводим равенство к виду М1Н1 = cos x1 + cos b1 — p. Из этого выходит npn → OM → 1 = cos ax1 + cos by1. Cкалярное произведение векторов дает формулу n → OM → 1 = n → npn → OM1 → = 1npn → OM1 → = npn → OM1 →.
Эта формула – произведение в координатной форме вида n →, OM1 → = cos ax1 + cos by1. Из этого npn → OM1 → = cos ax1 +cos by1. Отсюда следует, что M1H1 = npn → OM1 → — p = cos ax1 + cos by1 — p.
Что и следовало доказать.
Согласно теореме Пифагора, чтобы найти расстояние от точки до прямой, нужно совершить следующие шаги:
- Вывести уравнение прямой cos ax + cos by — p = 0, если его нет в задании.
- Вычислить cos ax + cos by — p, где значение принимает М1Н1.
Рассмотрим второй метод. Если у точки Н1 есть координаты (х2, у2), тогда расстояние от точки до прямой можно найти по формуле:
(left|M1H1right|=sqrt{left(x2-x1right)^2+left(y2-y1right)^2})
Найдем координаты точки Н1.
Прямая линия в ОХУ равна уравнению прямой на плоскости. Необходимо составить уравнение прямой b, проходящей через точку М1 перпендикулярно прямой а. Н1 – это точка пересечения прямых a и b. Для начала нужно найти общее уравнение прямой а, которое имеет вид А1х + В1у + С1 = 0. Либо можно воспользоваться уравнением с угловым коэффициентом у = k1x + b1.
Далее нужно вывести уравнение прямой b, которое имеет вид А2х + В2у + С2 = 0. Либо можно использовать уравнение по аналогии с прямой а: у = k2x + b2. Чтобы определить координаты точки Р1, нужно решить систему линейных уравнений:
(left{begin{array}{lc}А1х;+;В1у;+;С1;=;0&\А2х;+;В2у;+;С2;=;0&end{array}right.) либо ( left{begin{array}{l}у;=;k1x;+;b1\у;=;k2x;+;b2end{array}right.)
Конечное расстояние получают с помощью формулы:
(left|M1H1right|=sqrt{left(x2-x1right)^2+left(y2-y1right)^2})
Формулы для нахождения расстояния
Длину перпендикуляра также можно найти с помощью следующей формулы:
(d;=;;frac{left|Atimes M_x+Btimes M_y+Cright|}{sqrt{A^2+B^2}})
Решение уравнений
Пример 1
Вычислить расстояние между прямой 3x + 4y — 6 = 0 и точкой M(-1, 3).
Решение
(d;=;;frac{left|3times(-1)+4times3-6right|}{sqrt{3^2+4^2}}=frac{left|-3+12-6right|}{sqrt{9+16}}=frac{left|3right|}{sqrt{25}}=frac{left|3right|}5=0,6)
Ответ: 0,6.
Пример 2
Найти расстояние между прямой 12x + 5y — 17 = 0 и точкой M(-3, 8).
Решение
(d;=;;frac{left|12times(-3)+5times8-17right|}{sqrt{12^2+5^2}}=frac{left|-36+40-17right|}{sqrt{144+25}}=frac{left|-13right|}{sqrt{169}}=frac{left|13right|}{13}=1)
Ответ: 1.
Пример 3
Вычислить расстояние между прямой 4x + 3y — 3 = 0 и точкой M(-2, 5).
Решение
(d;=;;frac{left|4times(-2)+3times5-3right|}{sqrt{4^2+3^2}}=frac{left|-8+15-3right|}{sqrt{16+9}}=frac{left|4right|}{sqrt{25}}=frac{left|4right|}5=0,8)
Ответ: 0,8.
Примеры задач для нахождения расстояния от точки до прямой
Задача 1
Дана треугольная пирамида АВСD. Ее грани ABС и ABD представляют собой равные равнобедренные треугольники с прямыми углами при вершине A.
Найти расстояние от точки A до грани ACD, если высота пирамиды равна h и равна CD.
Решение
Так как △BCD равнобедренный, то BC ⊥ CD, K – середина CD. Так же AK ⊥ CD. Получается, перпендикуляр BH на плоскость ACD упадет на прямую AK (удовлетворяет теореме о трех перпендикулярах: HK – проекция, BK – наклонная, обе перпендикулярны CD).
По теореме Пифагора (BK=frac{hsqrt3}2).
Тогда (tg ∠ AKB = frac{AB}{BK}=frac{2sqrt3}3=frac{BH}{HK}).
Значит, (BH = 2sqrt3x), (HK = 3x).
По теореме Пифагора из △ BHK находим (x = frac1{2sqrt7}h ⇒ BH = sqrt{frac37}h).
Ответ: (sqrt{frac37}h).
Задача 2
Дана правильная четырехугольная пирамида ABCDE с вершиной A. Через точку пересечения диагоналей основания провели плоскость α перпендикулярно ребру AB.
Найти расстояние от точки N до плоскости α, если N – середина (BE = 2sqrt2), а высота пирамиды равна 11.
Решение
По теореме о трех перпендикулярах AB ⊥ CE как наклонная (AO ⊥ (BCD), OB ⊥ CE – проекция). Получаем две пересекающиеся прямые OK и СЕ из плоскости α. Значит, сечением является треугольник СKЕ.
Проведем MN ∥ СЕ. Тогда MN ∥ α. Так как расстояние от любой точки прямой, параллельной плоскости, до этой плоскости одинаково, то:
ρ(N,α)=ρ(Q,α)
где ρ — расстояние.
Т.к. по условию SA⊥α, то проведем QH∥SA⇒QH⊥α. По построению MN – средняя линия △BAD, следовательно:
ВQ = QO ⇒ QH – средняя линия △ KВO ⇒ QH = frac12 ВK.
Рассмотрим △ АВO = 2. Из △ ВKO ∼ △ ВАO (⇒ frac{ВК}{ВО}=frac{ВО}{ВА} ⇒ ВK = frac{4sqrt5}{25} ⇒ QH = frac{2sqrt5}{25}).
Ответ: (frac{2sqrt5}{25}).
Задача 3
Дано: в цилиндре параллельно диаметру ВС = 10 в нижнем основании проведена прямая, пересекающая окружность нижнего основания в точках Р и Z, причем PZ = 6. Через отрезок PZ проведена плоскость α под углом 15 градусов к плоскости осевого сечения ВСDE.
Найти расстояние от центра нижнего основания до плоскости α.
Решение
Обозначим за OQ – ось цилиндра. Тогда OQ ⊥ BC ⇒ OQ ⊥ p (OQ ∩ p = L).
Проведем OR ⊥ PZ ⇒ по теореме о трех перпендикулярах RL ⊥ PZ ⇒ RL ⊥ p ⇒ ∠ RLO – угол между плоскостями BCDE и α.
Так как и OR⊥PZ и LR⊥PZ, то перпендикуляр из точки O на плоскость α упадет на прямую LR.
Рассмотрим △ OPR: OP = 5, PR = 3, ∠ ORP = 90° ⇒ OR = 4.
Рассмотрим △ LOR: (∠ HOR = ∠ RLO = 15° ⇒ OH = OR ⋅ cos15° = 4 ⋅ cos(45° − 30°) = sqrt6+sqrt2).
Ответ: (sqrt6+sqrt2).
В данной публикации мы рассмотрим, что такое расстояние от точки до прямой, и по какой формуле оно считается. Также разберем пример решения задачи по этой теме.
- Расчет расстояния от точки до прямой
- Пример задачи
Расчет расстояния от точки до прямой
Чтобы найти расстояние от произвольной точки для прямой, нужно от нее опустить перпендикуляр на эту прямую.
Длина перпендикуляра (d) и является искомым расстоянием.
Формула для расчета
Допустим, есть прямая, заданная уравнением Ax + By + C = 0. Расстояние от нее до точки L с координатами (Lx, Ly) считается следующим образом:
Пример задачи
Дана прямая 2x + 6y – 5 = 0. Найдем расстояние от нее до точки M (1, -3).
Решение:
Воспользуемся формулой выше, подставив в нее известные нам по условиям задачи данные: