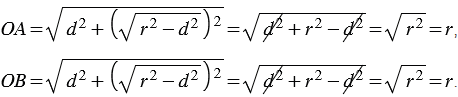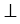Всё про окружность и круг
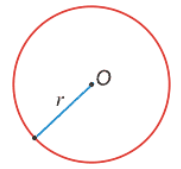
Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Центральный угол — это угол, вершина которого совпадает с центром окружности.
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
Расстояние между двумя фигурами
Общее определение расстояния между двумя произвольными фигурами выходит за рамки школьной программы, и мы его не приводим. Ряд частных случаев, когда расстояние между двумя фигурами можно ввести на базе школьного материала, перечислен в следующей таблице.
| Фигуры | Рисунок | Определение расстояния |
| Две точки | 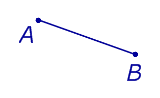 |
Расстоянием между двумя точками называют длину отрезка AB. |
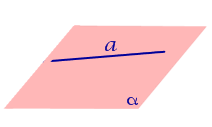
| Точка, лежащая на прямой | 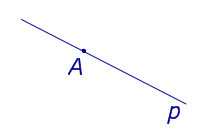 |
Расстояние равно 0. |
| Точка, не лежащая на прямой | 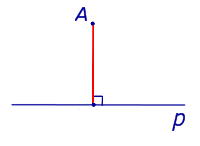 |
Расстоянием от точки до прямой называют длину перпендикуляра, опущенного из точки на прямую. |
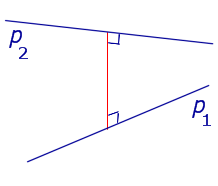
| Две параллельные прямые | 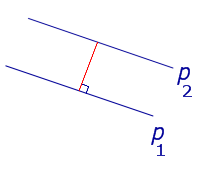 |
Расстоянием между параллельными прямыми называют длину перпендикуляра, опущенного из любой точки одной прямой на другую прямую. |
| Две пересекающиеся прямые |  |
Расстояние равно 0. |
| Две скрещивающиеся прямые | 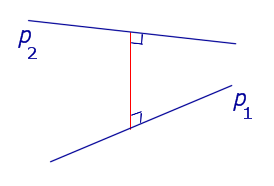 |
Расстоянием между скрещивающимися прямыми называют длину общего перпендикуляра к этим прямым. |
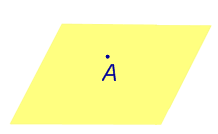
| Точка, лежащая на плоскости |  |
Расстояние равно 0. |
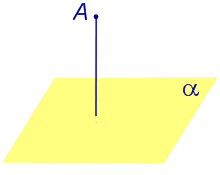
| Точка, не лежащая на плоскости | 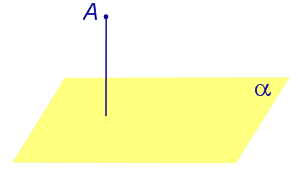 |
Расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из этой точки на плоскость. |
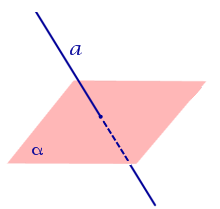
| Прямая, пересекающая плоскость | 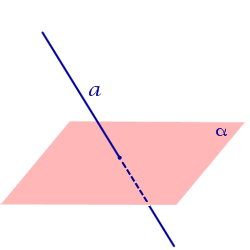 |
Расстояние равно 0. |
| Прямая, лежащая на плоскости |  |
Расстояние равно 0. |
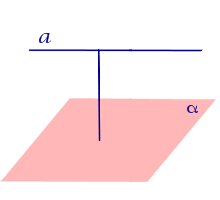
| Прямая, параллельная плоскости | 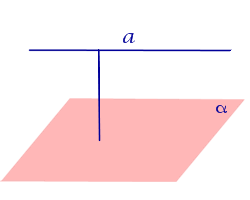 |
Расстоянием от прямой, параллельной плоскости, до плоскости называют длину перпендикуляра, опущенного из любой точки данной прямой на плоскость. |
| Две пересекающиеся плоскости |  |
Расстояние равно 0. |
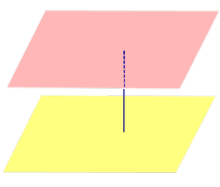
| Две параллельные плоскости | 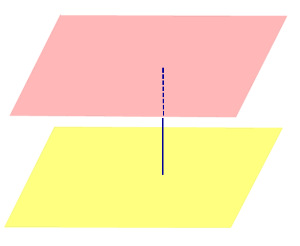 |
Расстоянием между параллельными плоскостями называют длину перпендикуляра, опущенного из любой точки одной плоскости на другую плоскость (все такие перпендикуляры имеют одну и ту же длину). |
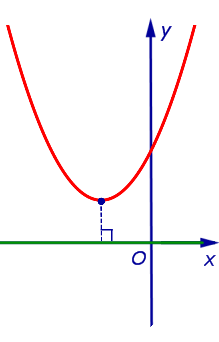
| Парабола y = a x 2 + b x + c , не пересекающая ось абсцисс, и ось абсцисс |
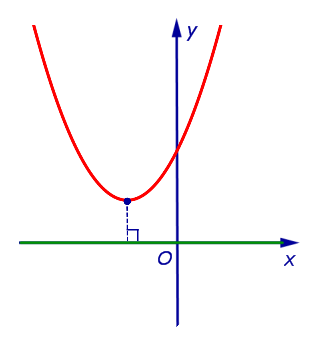 |
Расстоянием от параболы, не пересекающей ось абсцисс, до оси абсцисс называют длину кратчайшего отрезка, один из концов которого лежит на параболе, а другой на оси абсцисс. Этим кратчайшим отрезком является перпендикуляр, опущенный из вершины параболы на ось абсцисс. |
| Окружность и не пересекающая ее прямая | 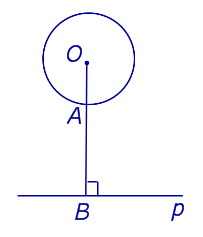 |
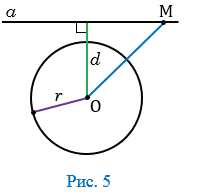
Расстоянием между окружностью и непереcекающей ее прямой называют длину кратчайшего отрезка, один из концов которого лежит на окружности, а другой конец – на прямой. Если перпендикуляр OB , опущенный из центра O окружности на прямую, пересекает окружность в точке A, то расстояние от окружности до прямой равно длине отрезка AB. |
| Две непересекающиеся окружности, каждая из которых лежит вне другой | 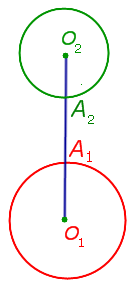 |
Расстоянием между непересекающимися окружностями называют длину кратчайшего отрезка, один из концов которого лежит на одной окружности , а другой конец – на другой окружности. Если линия центров O1O2 пересекает окружность с центром O1 в точке A1, а окружность с центром O2 – в точке A2, то расстояние между окружностями будет равно длине отрезка A1A2. |
Гипербола 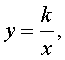 где k – любое, отличное от нуля, число, и ось абсцисс. где k – любое, отличное от нуля, число, и ось абсцисс. |
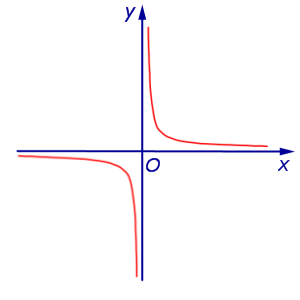 |
Расстояние между гиперболой и осью абсцисс считается равным 0, поскольку гипербола неограниченно приближается к оси абсцисс (длина отрезка, один из концов которого лежит на гиперболе, а другой конец – на оси абсцисс, может быть сколь угодно малой). |
| Две точки |
 |
Определение расстояния:
Расстоянием между двумя точками называют длину отрезка AB.
Точка, лежащая на прямой
Расстояние равно 0.
Точка, не лежащая на прямой
Определение расстояния:
Расстоянием от точки до прямой называют длину перпендикуляра, опущенного из точки на прямую.
Две параллельные прямые параллельные прямые
Определение расстояния:
Расстоянием между параллельными прямыми называют длину перпендикуляра, опущенного из любой точки одной прямой на другую прямую.
Две пересекающиеся прямые пересекающиеся прямые
Расстояние равно 0.
Определение расстояния:
Расстоянием между скрещивающимися прямыми называют длину общего перпендикуляра к этим прямым.
Точка, лежащая на плоскости
Расстояние равно 0.
Точка, не лежащая на плоскости
Определение расстояния:
Расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из этой точки на плоскость.
Расстояние равно 0.
Расстояние равно 0.
Определение расстояния:
Расстоянием от прямой, параллельной плоскости, до плоскости называют длину перпендикуляра, опущенного из любой точки данной прямой на плоскость.
Две пересекающиеся плоскости
Расстояние равно 0.
Две параллельные плоскости
Определение расстояния:
Расстоянием между параллельными плоскостями называют длину перпендикуляра, опущенного из любой точки одной плоскости на другую плоскость (все такие перпендикуляры имеют одну и ту же длину).
Парабола y = a x 2 + b x + c , не пересекающая ось абсцисс, и ось абсцисс
Определение расстояния:
Расстоянием от параболы, не пересекающей ось абсцисс, до оси абсцисс называют длину кратчайшего отрезка, один из концов которого лежит на параболе, а другой на оси абсцисс.
Этим кратчайшим отрезком является перпендикуляр, опущенный из вершины параболы на ось абсцисс.
Окружность и не пересекающая ее прямая
Определение расстояния:
Расстоянием между окружностью и непереcекающей ее прямой называют длину кратчайшего отрезка, один из концов которого лежит на окружности , а другой конец – на прямой.
Если перпендикуляр OB , опущенный из центра O окружности на прямую, пересекает окружность в точке A , то расстояние от окружности до прямой равно длине отрезка AB.
Две непересекающиеся окружности, каждая из которых лежит вне другой Две непересекающиеся окружности, каждая из которых лежит вне другой
Определение расстояния:
Расстоянием между непересекающимися окружностями называют длину кратчайшего отрезка, один из концов которого лежит на одной окружности, а другой конец – на другой окружности.
Если линия центров O1O2 пересекает окружность с центром O1 в точке A1, а окружность с центром O2 – в точке A2, то расстояние между окружностями будет равно длине отрезка A1A2.
Окружность
Вы будете перенаправлены на Автор24
Определение окружности
Окружность — геометрическая фигура, состоящая из всех точек, расположенных на равном расстоянии от заданной точки.
В рамках определения 1, заданная точка называется центром окружности.
Отрезок, соединяющий центр окружности с любой ее точкой называется радиусом окружности $(r)$ (Рис. 1).
Рисунок 1. Окружность с центром в точке $O$ и радиусом $r$
Отрезок, соединяющий две любые точки окружности, называется хордой.
Хорда, проходящая через центр окружности, называется диаметром $(d)$.
Взаимное расположение прямой и окружности
Окружность имеет три возможных взаимных расположений относительно прямой:
Если расстояние от центра окружности до прямой меньше радиуса, то прямая имеет две точки пересечения с окружностью.
Если расстояние от центра окружности до прямой равно радиусу, то прямая имеет две точки пересечения с окружностью.
Если расстояние от центра окружности до прямой больше радиуса, то прямая имеет две точки пересечения с окружностью.
Уравнение окружности
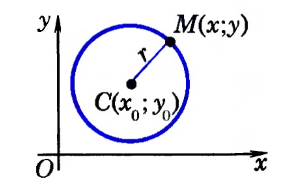
Выведем уравнение окружности в декартовой системе координат $xOy$. Пусть центр окружности $C$ имеет координаты $(x_0,y_0)$, а радиус окружности равен $r$. Пусть точка $M$ с координатами $(x,y)$ — произвольная точка этой окружности (рис. 2).
Рисунок 2. Окружность в декартовой системе координат
Готовые работы на аналогичную тему
Расстояние от центра окружности до точки $M$ вычисляется следующим образом
Но, так как $M$ лежит на окружности, то по определению 3, получаем $CM=r$. Тогда получим следующее
Уравнение (1) и есть уравнение окружности с центром в точке $(x_0,y_0)$ и радиусом $r$.
В частности, если центр окружности совпадает с началом координат. То уравнение окружности имеет вид
Длина окружности
Выведем формулу длины окружности $C$ через её радиус. Для этого рассмотрим две окружности с длинами $C$ и $C’$ и радиусами $R$ и $R’$. Впишем в ним правильные $n-угольники$ с периметрами $P$ и $P’$ и длинами сторон $a$ и $a’$ соответственно. Как нам известно, сторона вписанного -угольника равна
Неограниченно увеличивая количество сторон правильных многоугольников $n$ получим, что
Получили, что отношение длины окружности к её диаметру постоянное число для любой окружности. Эту константу принято обозначать числом $pi approx 3,14$. Таким образом, получим
Формула (2) и есть формула для вычисления длины окружности.
Пример задачи на понятие окружность
Найти уравнение окружности с центром в точке $(1, 2)$. Проходящей через начало координат и найти длину данной окружности.
Решение.
Найдем сначала уравнение данной окружности. Для этого будем использовать формулу (1). Так как центр окружности лежит в точке $(1, 2)$, получим
Найдем радиус окружности как расстояние от точки $(1, 2)$ до точки $(0,0)$
Получаем, уравнение окружности имеет вид:
Найдем длину окружности по формуле (2). Получим
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 29 03 2022
http://www.resolventa.ru/uslugi/uslugischoolotr.htm
http://spravochnick.ru/matematika/okruzhnost/
Касательная и секущая к окружности
На плоскости прямая и окружность могут либо пересекаться друг с другом, либо не пересекаться:
Расстояние от центра O до прямой m равно длине перпендикуляра OA. Следовательно, расстояние от центра окружности до прямой всегда будет равно перпендикуляру, опущенному из центра окружности на прямую.
Если расстояние от центра окружности до прямой больше радиуса данной окружности, то прямая и окружность не пересекаются и не имеют общих точек:
Касательная
Если расстояние от центра окружности до прямой равно радиусу данной окружности, то прямая касается окружности и они имеют одну общую точку, такая прямая называется касательной к окружности:
Прямая m — касательная. Точка соприкосновения прямой и окружности, то есть их общая точка, называется точкой касания: точка A — точка касания.
Касательная – это прямая линия, имеющая с окружностью одну общую точку.
Секущая
Если расстояние от центра окружности до прямой меньше радиуса данной окружности, то прямая пересекает окружность и они имеют две точки касания, такая прямая называется секущей к окружности:
Линейная алгебра. Векторная алгебра. Аналитическая геометрия: Конспект лекций , страница 13
а) уравнение медианы , б) высоты , в) найти угол между и (рис. 25).
а) – середина ВС (см. (2.4)). Напишем уравнение (3.4) прямой, проходящей через две точки: . Вектор – направляющий вектор прямой .
Перепишем уравнение медианы в общем виде:
б) – нормаль . Уравнение прямой (3.1), проходящей через точку перпендикулярно вектору :
в) . По формуле (3.7)
РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ НА ПЛОСКОСТИ
Пусть в некоторой пдск задана прямая и точка Найдем расстояние от точки до прямой
Пусть – проекция точки на (рис. 26), тогда . Нормаль
, где – искомое расстояние, а – скалярное произведение.
Так как , то . Поэтому
(3.8) – формула для вычисления расстояния от точки до прямой на плоскости.
ПРИМЕР. Найти длину высоты
Уравнение (3.4): – искомая длина высоты АН.
КРИВЫЕ ВТОРОГО ПОРЯДКА.
ОПРЕДЕЛЕНИЕ. Кривые второго порядка – плоские линии, которые в пдск задаются уравнениями второй степени относительно двух переменных
ОПРЕДЕЛЕНИЕ. Окружностью называется совокупность точек плоскости, равноудаленных от фиксированной точки, называемой ее центром.
Выведем уравнение окружности. Зададим пдск . Пусть – фиксированная точка (центр окружности), а – расстояние от точек окружности до ее центра (радиус окружности). Если – произвольная точка окружности, то длина равна .
Если точка не лежит на окружности, то и ее координаты уравнению (3.9) не удовлетворяют, поэтому, (3.9) – уравнение окружности с центром радиуса .
Если , то уравнение окружности примет вид:
(3.10) – каноническое уравнение окружности.
ПРИМЕР. Показать, что уравнение задает окружность (то есть найти ее центр и радиус).
Приведем данное уравнение к виду (3.9), выделив полный квадрат по переменной :
ПРИМЕР. Написать уравнение линии центров окружностей и .
Найдем центр второй окружности:
Уравнение прямой (3.4), проходящей через две точки:
ОПРЕДЕЛЕНИЕ. Эллипс – совокупность точек плоскости, сумма расстояний от которых до двух фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная и большая, чем расстояние между фокусами.
Чтобы вывести уравнение эллипса, выберем пдск следующим образом: ось абсцисс проведем через фокусы и , а ось ординат – посередине отрезка перпендикулярно оси абсцисс. Обозначим расстояние между фокусами , тогда . Пусть – произвольная точка, лежащая на эллипсе, а – сумма расстояний от точек на эллипсе до и ,
по определению эллипса.
Запишем в виде уравнения свойство точек, принадлежащих эллипсу, сформулированное в определении:
(3.11) – уравнение эллипса в выбранной системе координат. Преобразуем его к более простому (каноническому) виду. Для этого умножим (3.11) на сопряженное выражение:
Сложим (3.11) и (3.12) и результат возведем в квадрат:
Так как по определению , то есть , то обозначим . Тогда из (3.13) получим:
Расстояние от точки до прямой на плоскости и в пространстве: определение и примеры нахождения
Данная статья рассказывает о теме «расстояния от точки до прямой», рассматриваются определения расстояния от точки к прямой с иллюстрированными примерами методом координат. Каждый блок теории в конце имеет показанные примеры решения подобных задач.
Расстояние от точки до прямой – определение
Расстояние от точки до прямой находится через определение расстояния от точки до точки. Рассмотрим подробней.
Пусть имеется прямая a и точка М 1 , не принадлежащая заданной прямой. Через нее проведем прямую b , расположенную перпендикулярно относительно прямой a . Точка пересечения прямых возьмем за Н 1 . Получим, что М 1 Н 1 является перпендикуляром, который опустили из точки М 1 к прямой a .
Расстоянием от точки М 1 к прямой a называется расстояние между точками М 1 и Н 1 .
Бывают записи определения с фигурированием длины перпендикуляра.
Расстоянием от точки до прямой называют длину перпендикуляра, проведенного из данной точки к данной прямой.
Определения эквивалентны. Рассмотрим рисунок, приведенный ниже.
Известно, что расстояние от точки до прямой является наименьшим из всех возможных. Рассмотрим это на примере.
Если взять точку Q , лежащую на прямой a , не совпадающую с точкой М 1 , тогда получим, что отрезок М 1 Q называется наклонной, опущенной из М 1 к прямой a . Необходимо обозначить, что перпендикуляр из точки М 1 является меньше, чем любая другая наклонная, проведенная из точки к прямой.
Чтобы доказать это, рассмотрим треугольник М 1 Q 1 Н 1 , где М 1 Q 1 является гипотенузой. Известно, что ее длина всегда больше длины любого из катетов. Значим, имеем, что M 1 H 1 < M 1 Q . Рассмотрим рисунок, приведенный ниже.
Расстояние от точки до прямой на плоскости – теория, примеры, решения
Исходные данные для нахождения от точки до прямой позволяют использовать несколько методов решения: через теорему Пифагора, определения синуса, косинуса, тангенса угла и другими. Большинство заданий такого типа решают в школе на уроках геометрии.
Когда при нахождении расстояния от точки до прямой можно ввести прямоугольную систему координат, то применяют метод координат. В данном пункте рассмотрим основных два метода нахождения искомого расстояния от заданной точки.
Первый способ подразумевает поиск расстояния как перпендикуляра, проведенного из М 1 к прямой a . Во втором способе используется нормальное уравнение прямой а для нахождения искомого расстояния.
Если на плоскости имеется точка с координатами M 1 ( x 1 , y 1 ) , расположенная в прямоугольной системе координат, прямая a , а необходимо найти расстояние M 1 H 1 , можно произвести вычисление двумя способами. Рассмотрим их.
Первый способ
Если имеются координаты точки H 1 , равные x 2 , y 2 , тогда расстояние от точки до прямой вычисляется по координатам из формулы M 1 H 1 = ( x 2 — x 1 ) 2 + ( y 2 — y 1 ) 2 .
Теперь перейдем к нахождению координат точки Н 1 .
Известно, что прямая линия в О х у соответствует уравнению прямой на плоскости. Возьмем способ задания прямой a через написание общего уравнения прямой или уравнения с угловым коэффициентом. Составляем уравнение прямой, которая проходит через точку М 1 перпендикулярно заданной прямой a . Прямую обозначим буковой b . Н 1 является точкой пересечения прямых a и b , значит для определения координат необходимо воспользоваться статьей, в которой идет речь о координатах точек пересечения двух прямых.
Видно, что алгоритм нахождения расстояния от заданной точки M 1 ( x 1 , y 1 ) до прямой a проводится согласно пунктам:
- нахождение общего уравнения прямой a , имеющее вид A 1 x + B 1 y + C 1 = 0 ,или уравнение с угловым коэффициентом, имеющее вид y = k 1 x + b 1 ;
- получение общего уравнения прямой b , имеющее вид A 2 x + B 2 y + C 2 = 0 или уравнение с угловым коэффициентом y = k 2 x + b 2 , если прямая b пересекает точку М 1 и является перпендикулярной к заданной прямой a ;
- определение координат x 2 , y 2 точки Н 1 , являющейся точкой пересечения a и b , для этого производится решение системы линейных уравнений A 1 x + B 1 y + C 1 = 0 A 2 x + B 2 y + C 2 = 0 или y = k 1 x + b 1 y = k 2 x + b 2 ;
- вычисление искомого расстояния от точки до прямой, используя формулу M 1 H 1 = ( x 2 — x 1 ) 2 + ( y 2 — y 1 ) 2 .
Второй способ
Теорема способна помочь ответить на вопрос о нахождении расстояния от заданной точки до заданной прямой на плоскости.
Прямоугольная система координат имеет О х у имеет точку M 1 ( x 1 , y 1 ) , из которой проведена прямая а к плоскости, задаваемая нормальным уравнением плоскости, имеющее вид cos α · x + cos β · y — p = 0 , равно по модулю значению, получаемому в левой части нормального уравнения прямой, вычисляемому при x = x 1 , y = y 1 , значит, что M 1 H 1 = cos α · x 1 + cos β · y 1 — p .
Прямой а соответствует нормальное уравнение плоскости, имеющее вид cos α · x + cos β · y — p = 0 , тогда n → = ( cos α , cos β ) считается нормальным вектором прямой a при расстоянии от начала координат до прямой a с p единицами. Необходимо изобразить все данные на рисунке, добавить точку с координатами M 1 ( x 1 , y 1 ) , где радиус-вектор точки М 1 — O M 1 → = ( x 1 , y 1 ) . Необходимо провести прямую от точки до прямой, которое обозначим M 1 H 1 . Необходимо показать проекции М 2 и Н 2 точек М 1 и Н 2 на прямую, проходящую через точку O с направляющим вектором вида n → = ( cos α , cos β ) , а числовую проекцию вектора обозначим как O M 1 → = ( x 1 , y 1 ) к направлению n → = ( cos α , cos β ) как n p n → O M 1 → .
Вариации зависят от расположения самой точки М 1 . Рассмотрим на рисунке, приведенном ниже.
Результаты фиксируем при помощи формулы M 1 H 1 = n p n → O M → 1 — p . После чего приводим равенство к такому виду M 1 H 1 = cos α · x 1 + cos β · y 1 — p для того, чтобы получить n p n → O M → 1 = cos α · x 1 + cos β · y 1 .
Скалярное произведение векторов в результате дает преобразованную формулу вида n → , O M → 1 = n → · n p n → O M 1 → = 1 · n p n → O M 1 → = n p n → O M 1 → , которая является произведением в координатной форме вида n → , O M 1 → = cos α · x 1 + cos β · y 1 . Значит, получаем, что n p n → O M 1 → = cos α · x 1 + cos β · y 1 . Отсюда следует, что M 1 H 1 = n p n → O M 1 → — p = cos α · x 1 + cos β · y 1 — p . Теорема доказана.
Получаем, что для нахождения расстояния от точки M 1 ( x 1 , y 1 ) к прямой a на плоскости необходимо выполнить несколько действий:
- получение нормального уравнения прямой a cos α · x + cos β · y — p = 0 , при условии, что его нет в задании;
- вычисление выражения cos α · x 1 + cos β · y 1 — p , где полученное значение принимает M 1 H 1 .
Решение задач на нахождение расстояния от заданной точки до заданной прямой на плоскости
Применим данные методы на решении задач с нахождением расстояния от точки до плоскости.
Найти расстояние от точки с координатами M 1 ( — 1 , 2 ) к прямой 4 x — 3 y + 35 = 0 .
Применим первый способ для решения.
Для этого необходимо найти общее уравнение прямой b , которая проходит через заданную точку M 1 ( — 1 , 2 ) , перпендикулярно прямой 4 x — 3 y + 35 = 0 . Из условия видно, что прямая b является перпендикулярной прямой a , тогда ее направляющий вектор имеет координаты, равные ( 4 , — 3 ) . Таким образом имеем возможность записать каноническое уравнение прямой b на плоскости, так как имеются координаты точки М 1 , принадлежит прямой b . Определим координаты направляющего вектора прямой b . Получим, что x — ( — 1 ) 4 = y — 2 — 3 ⇔ x + 1 4 = y — 2 — 3 . Полученное каноническое уравнение необходимо преобразовать к общему. Тогда получаем, что
x + 1 4 = y — 2 — 3 ⇔ — 3 · ( x + 1 ) = 4 · ( y — 2 ) ⇔ 3 x + 4 y — 5 = 0
Произведем нахождение координат точек пересечения прямых, которое примем за обозначение Н 1 . Преобразования выглядят таким образом:
4 x — 3 y + 35 = 0 3 x + 4 y — 5 = 0 ⇔ x = 3 4 y — 35 4 3 x + 4 y — 5 = 0 ⇔ x = 3 4 y — 35 4 3 · 3 4 y — 35 4 + 4 y — 5 = 0 ⇔ ⇔ x = 3 4 y — 35 4 y = 5 ⇔ x = 3 4 · 5 — 35 4 y = 5 ⇔ x = — 5 y = 5
Из выше написанного имеем, что координаты точки Н 1 равны ( — 5 ; 5 ) .
Необходимо вычислить расстояние от точки М 1 к прямой a . Имеем, что координаты точек M 1 ( — 1 , 2 ) и H 1 ( — 5 , 5 ) , тогда подставляем в формулу для нахождения расстояния и получаем, что
M 1 H 1 = ( — 5 — ( — 1 ) 2 + ( 5 — 2 ) 2 = 25 = 5
Второй способ решения.
Для того, чтобы решить другим способом, необходимо получить нормальное уравнение прямой. Вычисляем значение нормирующего множителя и умножаем обе части уравнения 4 x — 3 y + 35 = 0 . Отсюда получим, что нормирующий множитель равен — 1 4 2 + ( — 3 ) 2 = — 1 5 , а нормальное уравнение будет вида — 1 5 · 4 x — 3 y + 35 = — 1 5 · 0 ⇔ — 4 5 x + 3 5 y — 7 = 0 .
По алгоритму вычисления необходимо получить нормальное уравнение прямой и вычислить его со значениями x = — 1 , y = 2 . Тогда получаем, что
— 4 5 · — 1 + 3 5 · 2 — 7 = — 5
Отсюда получаем, что расстояние от точки M 1 ( — 1 , 2 ) к заданной прямой 4 x — 3 y + 35 = 0 имеет значение — 5 = 5 .
Видно, что в данном методе важно использование нормального уравнения прямой, так как такой способ является наиболее коротким. Но первый метод удобен тем, что последователен и логичен, хотя имеет больше пунктов вычисления.
На плоскости имеется прямоугольная система координат О х у с точкой M 1 ( 8 , 0 ) и прямой y = 1 2 x + 1 . Найти расстояние от заданной точки до прямой.
Решение первым способом подразумевает приведение заданного уравнения с угловым коэффициентом к уравнению общего вида. Для упрощения можно сделать иначе.
Если произведение угловых коэффициентов перпендикулярных прямых имеют значение — 1 , значит угловой коэффициент прямой перпендикулярной заданной y = 1 2 x + 1 имеет значение 2 . Теперь получим уравнение прямой, проходящее через точку с координатами M 1 ( 8 , 0 ) . Имеем, что y — 0 = — 2 · ( x — 8 ) ⇔ y = — 2 x + 16 .
Переходим к нахождению координат точки Н 1 , то есть точкам пересечения y = — 2 x + 16 и y = 1 2 x + 1 . Составляем систему уравнений и получаем:
y = 1 2 x + 1 y = — 2 x + 16 ⇔ y = 1 2 x + 1 1 2 x + 1 = — 2 x + 16 ⇔ y = 1 2 x + 1 x = 6 ⇔ ⇔ y = 1 2 · 6 + 1 x = 6 = y = 4 x = 6 ⇒ H 1 ( 6 , 4 )
Отсюда следует, что расстояние от точки с координатами M 1 ( 8 , 0 ) к прямой y = 1 2 x + 1 равно расстоянию от точки начала и точки конца с координатами M 1 ( 8 , 0 ) и H 1 ( 6 , 4 ) . Вычислим и получим, что M 1 H 1 = 6 — 8 2 + ( 4 — 0 ) 2 20 = 2 5 .
Решение вторым способом заключается в переходе от уравнения с коэффициентом к нормальному его виду. То есть получим y = 1 2 x + 1 ⇔ 1 2 x — y + 1 = 0 , тогда значение нормирующего множителя будет — 1 1 2 2 + ( — 1 ) 2 = — 2 5 . Отсюда следует, что нормальное уравнение прямой принимает вид — 2 5 · 1 2 x — y + 1 = — 2 5 · 0 ⇔ — 1 5 x + 2 5 y — 2 5 = 0 . Произведем вычисление от точки M 1 8 , 0 к прямой вида — 1 5 x + 2 5 y — 2 5 = 0 . Получаем:
M 1 H 1 = — 1 5 · 8 + 2 5 · 0 — 2 5 = — 10 5 = 2 5
Необходимо вычислить расстояние от точки с координатами M 1 ( — 2 , 4 ) к прямым 2 x — 3 = 0 и y + 1 = 0 .
Получаем уравнение нормального вида прямой 2 x — 3 = 0 :
2 x — 3 = 0 ⇔ 1 2 · 2 x — 3 = 1 2 · 0 ⇔ x — 3 2 = 0
После чего переходим к вычислению расстояния от точки M 1 — 2 , 4 к прямой x — 3 2 = 0 . Получаем:
M 1 H 1 = — 2 — 3 2 = 3 1 2
Уравнение прямой y + 1 = 0 имеет нормирующий множитель со значением равным -1. Это означает, что уравнение примет вид — y — 1 = 0 . Переходим к вычислению расстояния от точки M 1 ( — 2 , 4 ) к прямой — y — 1 = 0 . Получим, что оно равняется — 4 — 1 = 5 .
Ответ: 3 1 2 и 5 .
Подробно рассмотрим нахождение расстояния от заданной точки плоскости к координатным осям О х и О у .
В прямоугольной системе координат у оси О у имеется уравнение прямой, которое является неполным имеет вида х = 0 , а О х — y = 0 . Уравнения являются нормальными для осей координат, тогда необходимо найти расстояние от точки с координатами M 1 x 1 , y 1 до прямых. Это производится, исходя из формул M 1 H 1 = x 1 и M 1 H 1 = y 1 . Рассмотрим на рисунке, приведенном ниже.
Найти расстояние от точки M 1 ( 6 , — 7 ) до координатных прямых, расположенных в плоскости О х у .
Так как уравнение у = 0 относится к прямой О х , можно найти расстояние от M 1 с заданными координатами, до этой прямой, используя формулу. Получаем, что 6 = 6 .
Так как уравнение х = 0 относится к прямой О у , то можно найти расстояние от М 1 к этой прямой по формуле. Тогда получим, что — 7 = 7 .
Ответ: расстояние от М 1 к О х имеет значение 6 , а от М 1 к О у имеет значение 7 .
Расстояние от точки до прямой в пространстве – теория, примеры, решения
Когда в трехмерном пространстве имеем точку с координатами M 1 ( x 1 , y 1 , z 1 ) , необходимо найти расстояние от точки A до прямой a .
Рассмотрим два способа, которые позволяют производить вычисление расстояние от точки до прямой a , расположенной в пространстве. Первый случай рассматривает расстояние от точки М 1 к прямой, где точка на прямой называется Н 1 и является основанием перпендикуляра, проведенного из точки М 1 на прямую a . Второй случай говорит о том, что точки этой плоскости необходимо искать в качестве высоты параллелограмма.
Первый способ
Из определения имеем, что расстояние от точки М 1 , расположенной на прямой а, является длиной перпендикуляра М 1 Н 1 , тогда получим, что при найденных координатах точки Н 1 , тогда найдем расстояние между M 1 ( x 1 , y 1 , z 1 ) и H 1 ( x 1 , y 1 , z 1 ) , исходя из формулы M 1 H 1 = x 2 — x 1 2 + y 2 — y 1 2 + z 2 — z 1 2 .
Получаем, что все решение идет к тому, чтобы найти координаты основания перпендикуляра, проведенного из М 1 на прямую a . Это производится следующим образом: Н 1 является точкой, где пересекаются прямая a с плоскостью, которая проходит через заданную точку.
Значит, алгоритм определения расстояния от точки M 1 ( x 1 , y 1 , z 1 ) к прямой a пространства подразумевает несколько пунктов:
- составление уравнение плоскости χ в качестве уравнения плоскости, проходящего через заданную точку, находящуюся перпендикулярно прямой;
- определение координат ( x 2 , y 2 , z 2 ) , принадлежавших точке Н 1 , которая является точкой пересечения прямой a и плоскости χ ;
- вычисление расстояния от точки до прямой при помощи формулы M 1 H 1 = x 2 — x 1 2 + y 2 — y 1 2 + z 2 — z 1 2 .
Второй способ
Из условия имеем прямую a , тогда можем определить направляющий вектор a → = a x , a y , a z с координатами x 3 , y 3 , z 3 и определенной точки М 3 ,принадлежащей прямой a . При наличии координат точек M 1 ( x 1 , y 1 ) и M 3 x 3 , y 3 , z 3 можно произвести вычисление M 3 M 1 → :
M 3 M 1 → = ( x 1 — x 3 , y 1 — y 3 , z 1 — z 3 )
Следует отложить векторы a → = a x , a y , a z и M 3 M 1 → = x 1 — x 3 , y 1 — y 3 , z 1 — z 3 из точки М 3 , соединим и получим фигуру параллелограмма. М 1 Н 1 является высотой параллелограмма.
Рассмотрим на рисунке, приведенном ниже.
Имеем, что высота М 1 Н 1 является искомым расстоянием, тогда необходимо найти его по формуле. То есть ищем M 1 H 1 .
Обозначим площадь параллелограмма за букву S , находится по формуле, используя вектор a → = ( a x , a y , a z ) и M 3 M 1 → = x 1 — x 3 . y 1 — y 3 , z 1 — z 3 . Формула площади имеет вид S = a → × M 3 M 1 → . Также площадь фигуры равняется произведению длин его сторон на высоту, получим, что S = a → · M 1 H 1 с a → = a x 2 + a y 2 + a z 2 , являющимся длиной вектора a → = ( a x , a y , a z ) , являющейся равной стороне параллелограмма. Значит, M 1 H 1 является расстоянием от точки до прямой. Ее нахождение производится по формуле M 1 H 1 = a → × M 3 M 1 → a → .
Для нахождения расстояния от точки с координатами M 1 ( x 1 , y 1 , z 1 ) до прямой a в пространстве, необходимо выполнить несколько пунктов алгоритма:
- определение направляющего вектора прямой a — a → = ( a x , a y , a z ) ;
- вычисление длины направляющего вектора a → = a x 2 + a y 2 + a z 2 ;
- получение координат x 3 , y 3 , z 3 , принадлежавших точке М3, находящейся на прямой а;
- вычисление координат вектора M 3 M 1 → ;
- нахождение векторного произведения векторов a → ( a x , a y , a z ) и M 3 M 1 → = x 1 — x 3 , y 1 — y 3 , z 1 — z 3 в качестве a → × M 3 M 1 → = i → j → k → a x a y a z x 1 — x 3 y 1 — y 3 z 1 — z 3 для получения длины по формуле a → × M 3 M 1 → ;
- вычисление расстояния от точки до прямой M 1 H 1 = a → × M 3 M 1 → a → .
Решение задач на нахождение расстояния от заданной точки до заданной прямой в пространстве
Найти расстояние от точки с координатами M 1 2 , — 4 , — 1 к прямой x + 1 2 = y — 1 = z + 5 5 .
Первый способ начинается с записи уравнения плоскости χ , проходящей через М 1 и перпендикулярно заданной точке. Получаем выражение вида:
2 · ( x — 2 ) — 1 · ( y — ( — 4 ) ) + 5 · ( z — ( — 1 ) ) = 0 ⇔ 2 x — y + 5 z — 3 = 0
Нужно найти координаты точки H 1 , являющейся точкой пересечения с плоскостью χ к заданной по условию прямой. Следует переходить от канонического вида к пересекающемуся. Тогда получаем систему уравнений вида:
x + 1 2 = y — 1 = z + 5 5 ⇔ — 1 · ( x + 1 ) = 2 · y 5 · ( x + 1 ) = 2 · ( z + 5 ) 5 · y = — 1 · ( z + 5 ) ⇔ x + 2 y + 1 = 0 5 x — 2 z — 5 = 0 5 y + z + 5 = 0 ⇔ x + 2 y + 1 = 0 5 x — 2 z — 5 = 0
Необходимо вычислить систему x + 2 y + 1 = 0 5 x — 2 z — 5 = 0 2 x — y + 5 z — 3 = 0 ⇔ x + 2 y = — 1 5 x — 2 z = 5 2 x — y + 5 z = 3 по методу Крамера, тогда получаем, что:
∆ = 1 2 0 5 0 — 2 2 — 1 5 = — 60 ∆ x = — 1 2 0 5 0 — 2 3 — 1 5 = — 60 ⇔ x = ∆ x ∆ = — 60 — 60 = 1 ∆ y = 1 — 1 0 5 5 2 2 3 5 = 60 ⇒ y = ∆ y ∆ = 60 — 60 = — 1 ∆ z = 1 2 — 1 5 0 5 2 — 1 3 = 0 ⇒ z = ∆ z ∆ = 0 — 60 = 0
Отсюда имеем, что H 1 ( 1 , — 1 , 0 ) .
Необходимо рассчитать расстояние между точками с координатами M 1 ( 2 , — 4 , — 1 ) и H 1 ( 1 , — 1 , 0 ) по формуле:
M 1 H 1 = 1 — 2 2 + — 1 — — 4 2 + 0 — — 1 2 = 11
Второй способ необходимо начать с поиска координат в каноническом уравнении. Для этого необходимо обратит внимание на знаменатели дроби. Тогда a → = 2 , — 1 , 5 является направляющим вектором прямой x + 1 2 = y — 1 = z + 5 5 . Необходимо вычислить длину по формуле a → = 2 2 + ( — 1 ) 2 + 5 2 = 30 .
Понятно, что прямая x + 1 2 = y — 1 = z + 5 5 пересекает точку M 3 ( — 1 , 0 , — 5 ) , отсюда имеем, что вектор с началом координат M 3 ( — 1 , 0 , — 5 ) и его концом в точке M 1 2 , — 4 , — 1 является M 3 M 1 → = 3 , — 4 , 4 . Находим векторное произведение a → = ( 2 , — 1 , 5 ) и M 3 M 1 → = ( 3 , — 4 , 4 ) .
Мы получаем выражение вида a → × M 3 M 1 → = i → j → k → 2 — 1 5 3 — 4 4 = — 4 · i → + 15 · j → — 8 · k → + 20 · i → — 8 · j → = 16 · i → + 7 · j → — 5 · k →
получаем, что длина векторного произведения равняется a → × M 3 M 1 → = 16 2 + 7 2 + — 5 2 = 330 .
Имеются все данные для использования формулы вычисления расстояния от точки для прямлой, поэтому применим ее и получим:
Прежде
чем приступить к новой теме, давайте вспомним, что такое окружность и вспомним
основные элементы окружности.
Напомню,
что окружностью называется геометрическая фигура, состоящая из всех
точек, равноудаленных от точки О, которую называют центром окружности. Отрезок, соединяющий центр окружности с любой
точкой на окружности, называется радиусом. Отрезок,
соединяющий две любые точки окружности, называется хордой. Хорда,
проходящая через центр окружности, называется диаметром и равна двум
радиусам.
Сегодня
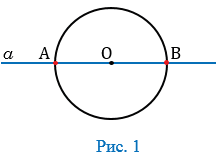
мы выясним, сколько общих точек могут иметь окружность и прямая. Если прямая p проходит через центр окружности, то,
очевидно, она имеет с окружностью две общие точки.
Теперь
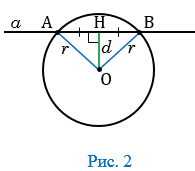
давайте рассмотрим случай, когда прямая p не проходит через центр окружности. Опустим на прямую перпендикуляр из
центра окружности и обозначим его буквой d. Длина этого перпендикуляра – расстояние от центра окружности до
данной прямой p.
Теперь
давайте попробуем определить взаимное расположение прямой и окружности в
зависимости от соотношения d и
радиуса окружности. Возможны три случая:
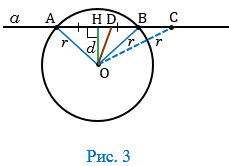
Первый случай.
Получим,
что ОА и ОB равны радиусу
окружности, то есть точки А и B
лежат на окружности. А, значит, они являются общими точками прямой p и окружности.
А
может быть есть еще общие точки, у прямой и окружности? Допустим, что,
действительно, есть еще одна общая точка C. Тогда медиана ОD
равнобедренного треугольника OBC,
проведенная к основанию AC,
является высотой, то есть перпендикулярна прямой p. Поскольку середина отрезка AB – точка H не совпадает с
серединой отрезка AC – точкой D, значит, отрезки ОD и ОH не совпадают.
Получается, что из точки О проведены два перпендикуляра к прямой p, а такого быть не может.
То
есть доказали, что если расстояние от центра окружности до прямой меньше
радиуса окружности, то прямая и окружность имеют две общие точки. В таком
случае, прямая называется секущей по отношению к окружности.
Рассмотрим
второй случай.
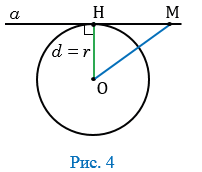
В
этом случае, длина перпендикуляра ОH=r, то есть точка H лежит на окружности. Больше общих точек у
прямой и окружности нет.
Докажем
это. Возьмем на прямой точку М. В любом случае ОМ будет больше OH, следовательно, точка М не будет лежать на
окружности.
Таким
образом, если расстояние от центра окружности до прямой равно радиусу
окружности, то прямая и окружность имеют только одну общую точку. В таком
случае, прямая называется касательной к окружности.
Теперь,
давайте, рассмотрим третий случай.
В
этом случае, , то есть, окружность и прямая не имеют общих точек. Можно сказать, что
если расстояние от центра окружности до прямой больше радиуса окружности, то
прямая и окружность не имеют общих точек.
Задача.
Определить взаимное расположение прямой и окружности,
если:
а) ,
; б)
,
; в)
,
;
Решение.
а)
, прямая является секущей для окружности и они
имеют две общие точки
б)
, прямая и окружность не пересекаются
в)
, прямая и окружность имеют одну общую точку
Задача.
Диаметр окружности равен см
а расстояние от центра окружности до прямой равно:
см
дм
мм
см
дм
см.
Решение.
Найдем
радиус окружности.
см
Теперь
сравним получившийся радиус с расстоянием от центра окружности до прямой. Не
забудем все перевести в одни единицы измерения.
дм
см
мм
см
дм
см
Получим,
что с прямой, расстояние до которой равно четырем целым пятнадцать сотых
сантиметра, окружность имеет две общие точки.
С
прямой, расстояние до которой равно двум дециметрам или двадцати сантиметрам,
окружность не имеет общих точек.
С
прямой, расстояние до которой равно сто три миллиметра, окружность не имеет
общих точек.
Задача.
Даны окружность с центром в точке и точка
. Где находится точка
, если
см, а длина отрезка
равна:
см,
см,
мм.
Решение. Для определения места положения точки А, сравним длину отрезка ОА с
радиусом окружности.
Получим,
что в случае, когда длина отрезка равна 4 сантиметрам, точка А лежит внутри
окружности), в случае, когда ОА равно 10 сантиметрам, точка
А лежит вне окружности (). В случае, когда ОА равно 50 миллиметрам или, что тоже самое, 5
сантиметрам, точка А лежит на окружности( мм
см)
Итак,
сегодня на уроке мы рассмотрели три случая взаимного расположения прямой и
окружности, в зависимости от соотношения расстояния от центра окружности до
прямой и радиуса окружности. Повторим их.
Если
расстояние от центра окружности до прямой меньше радиуса окружности, то прямая
и окружность имеют две общие точки.
Если
расстояние от центра окружности до прямой равно радиусу окружности, то прямая и
окружность имеют только одну общую точку.
Если
расстояние от центра окружности до прямой больше радиуса окружности, то прямая
и окружность не имеют общих точек.
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Окружность
- Взаимное расположение прямой и окружности
Если прямая проходит через центр окружности, то она пересекает окружность в двух точках — концах диаметра, лежащего на на этой прямой. На рисунке 1 прямая 
Если прямая 


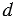

1 случай
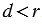

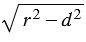

Проверим, лежат ли точки А и В на окружности.
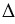
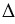
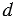

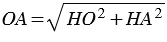
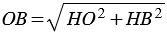
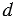
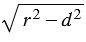
Поэтому точки А и В лежат на окружности и, значит, являются общими точками прямой 
Докажем, что прямая 

Тогда медиана ОD равнобедренного 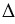




Вывод:
Если расстояние от центра окружности до прямой меньше радиуса окружности (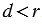
В этом случае прямая называется секущей по отношению к окружности (на рисунке 2 прямая 
2 случай
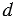


Прямая 

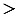

Вывод:
В этом случае прямая называется касательной по отношению к окружности (на рисунке 4 прямая 
3 случай



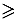

Вывод:
Советуем посмотреть:
Касательная к окружности
Градусная мера дуги окружности
Теорема о вписанном угле
Свойство биссектрисы угла
Свойства серединного перпендикуляра к отрезку
Теорема о пересечении высот треугольника
Вписанная окружность
Описанная окружность
Окружность
Правило встречается в следующих упражнениях:
7 класс
Задание 631,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 633,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 646,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 647,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 658,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 670,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 672,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 2,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 4,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 877,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Взаимное расположение прямой и окружности
Выясним количество общих точек прямой и окружности в зависимости от их взаимного расположения. Если прямая l проходит через центр O окружности (Рис.1), то она пересекает окружность в двух точках, которые являются концами диаметра окружности.
Пусть прямая не проходит через центр окружности. Проведем перпендикуляр OH к прямой l (Рис.2, Рис.3, Рис.4). Обозначим расстояние от центра окружности до прямой l буквой d. Рассмотрим сколько общих точек будут иметь прямая и окружность в зависимости от соотношения d и r.
Теорема 1. Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.
В этом случае прямая называется секущей по отношению к окружности.
Доказательство. Пусть расстояние от центра окружности до прямой меньше радиуса окружности: d<r (Рис.2). На прямой l от точки H отложим два отрезка HM и HN, которые имеют длину ( small sqrt{r^2-d^2}) (Рис.2). Вычислим расстояния OM и ON используя теорему Пифагора:
Получили, что расстояние от центра окружности O до точек M и N равно r. Тогда эти точки лежат на окружности и являются общими для прямой l и данной окружности.
Докажем, далее, что прямая l и данная окружность не имеют других общих точек. Предположим, что они имеют еще одну общую точку P. Поскольку эта точка находится на окружности, то OM=OP=r. Тогда треугольник MOP равнобедренный и медиана OD, проведенная к основанию MP является высотой треугольника MOP. Поэтому ( small OD ⊥ MP .) Отрезки ( small OD ) и ( small OH ) не совпадают, так как середина D отрезка MP не совпадает с точкой H, которая является серединой отрезка MN. Получили, что из точки O проведены два перпендикуляра OH и OD к прямой l, что невозможно (см. статью Перпендикуляр к прямой). Таким образом, если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.
Теорема 2. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну общую точку.
Доказательство. Пусть расстояние от центра окружности до прямой равно радиусу окружности: d=r (Рис.3). В этом случае OH=r, т.е. точка H лежит на окружности и является общей точкой прямой l и окружности. Возьмем на прямой l любую точку M отличной от H. Тогда расстояние от OM больше расстояния OH=r, поскольку наклонная OM больше перпендикуляра OH к прямой l. Следовательно точка M не лежит на окружности. Получили, что точка H единственная общая точка прямой l и окружности.
Теорема 3. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.
Доказательство. Пусть расстояние от центра окружности до прямой больше радиуса окружности:d>r (Рис.4). Тогда ( small OH > r). Возьмем на прямой l любую точку M отличной от H. Тогда ( small OM > OH>r). Следовательно точка M не лежит на окружности. Таким образом, если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.