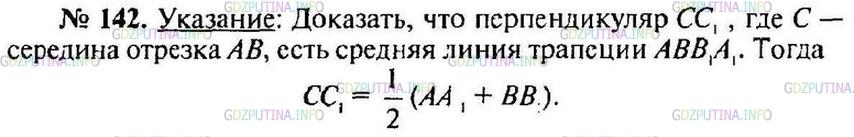Как найти расстояние от середины до плоскости - Исправление недочетов и поиск решений вместе с Examum.ru

Я, я!

Рассмотрим два случая:
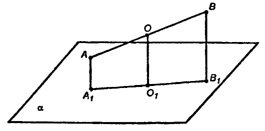
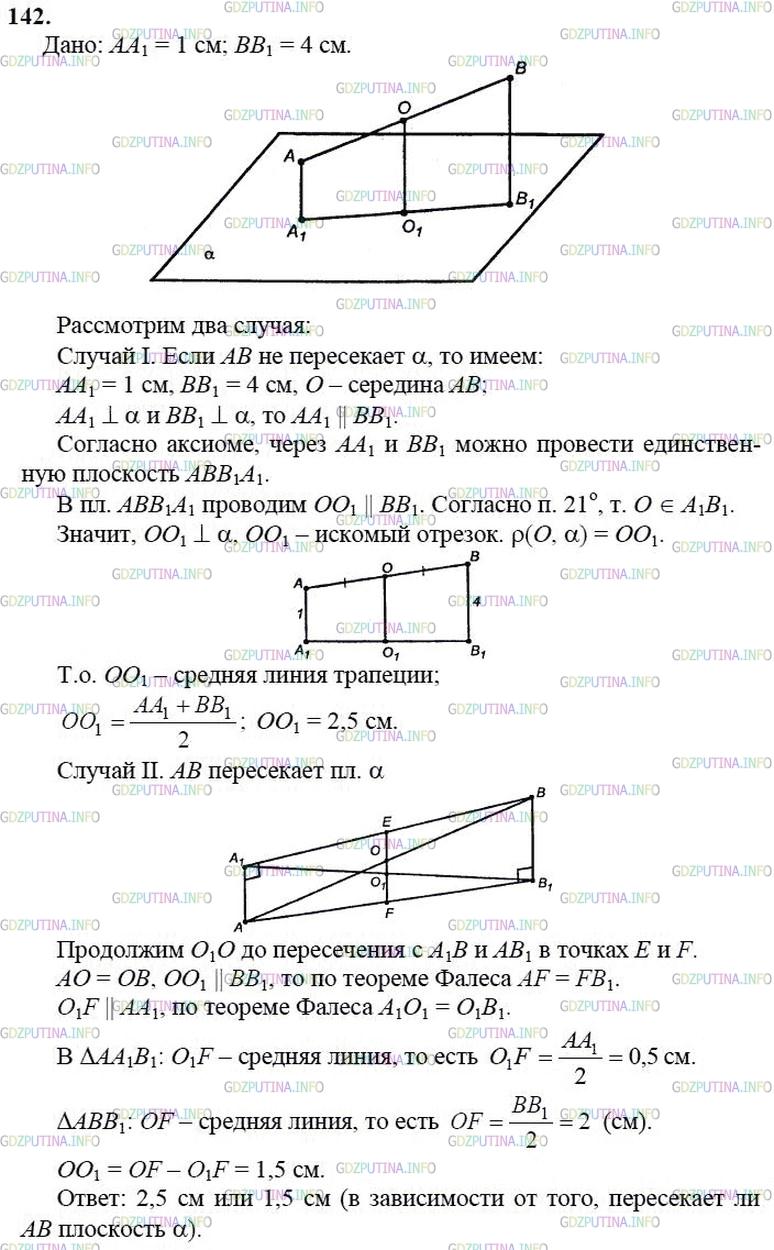
Случай I. Если АВ не пересекает а, то имеем:
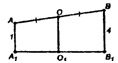
АА₁ = 1 см, ВВ₁ = 4 см, О — середина АВ;
то АА₁ || ВВ₁ .
Согласно аксиоме, через АА₁ и ВВ₁ можно провести единственную плоскость АВВ₁А₁ .
В пл. АВВ₁А₁ проводим ОО₁ || ВВ₁ . Согласно п. 21°, т. 0 € А₁В₁
Значит, ОО₁ ОО₁ — искомый отрезок, ρ(О, α) = ОО₁

Т.о. ОО₁ — средняя линия трапеции;
ОО₁ = 2,5 см.
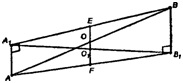
Случай II. АВ пересекает пл. α

Продолжим О₁О до пересечения с А₁В и АВ₁ в точках Е и F. АО = ОВ, ОО₁ || ВВ₁ , то по теореме Фалеса AF = FB₁ .
O₁F || АА₁ по теореме Фалеса А₁О₁ = О₁В₁.
В ΔАА₁В₁ : O₁F- средняя линия, то есть
ΔАВВ₁ : OF- средняя линия, то есть
ОО₁ = OF — O₁F- 1,5 см.
Ответ: 2,5 см или 1,5 см (в зависимости от того, пересекает ли АВ плоскость а).

Источник

Так как в условии ничего нет про угол, под которым отрезок пересекает плоскость, примем его за 90°. В этом случае действительно можно говорить о том, что расстояния от концов отрезка до плоскости являются частями самого отрезка, то есть перпендикуляры из концов отрезка на плоскость совпадают с самим отрезком.
Тогда длина отрезка: L = h₁+h₂ = 3 + 12 = 15 (cм)
и L/2 = 7,5 (cм)
Так как концы отрезка находятся по разные стороны плоскости, расстояние от середины отрезка до плоскости будет меньше половины длины отрезка на величину расстояния от ближнего к плоскости конца отрезка до самой плоскости. То есть:
h = L/2 — h₁ = 7,5 — 3 = 4,5 (см)

Ответ: расстояние от середины отрезка до плоскости 4,5 см

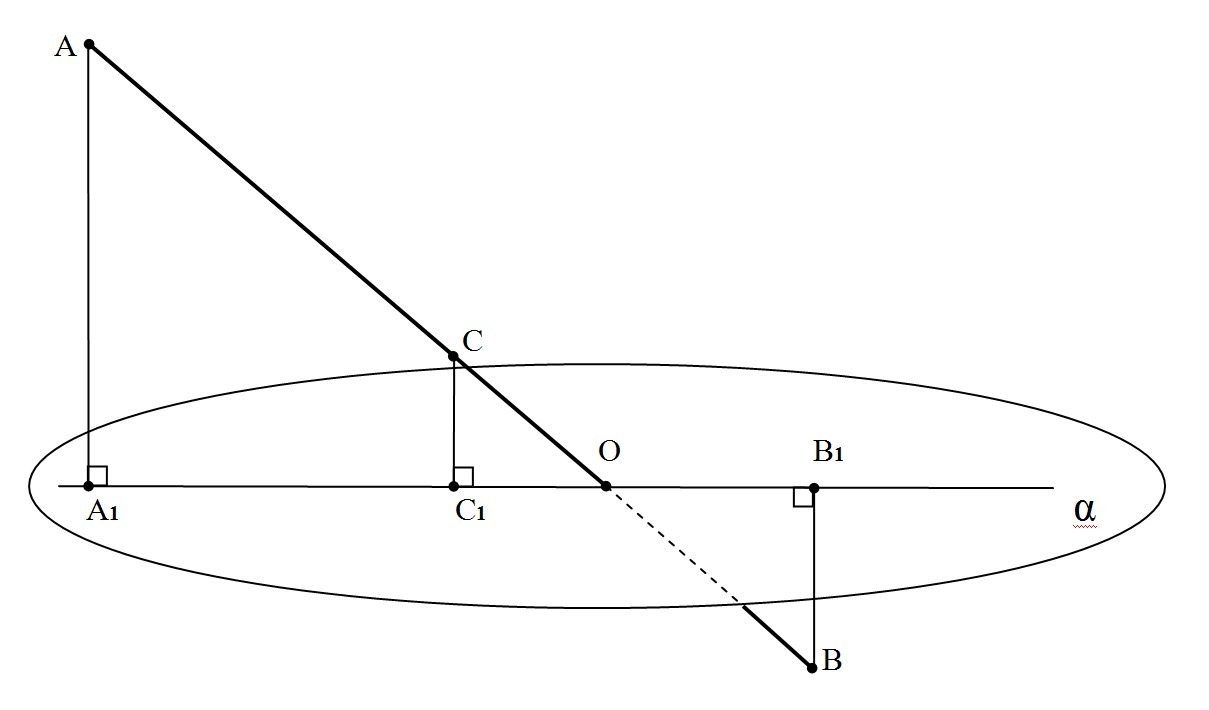
Решение через подобие треугольников. (см. рис.)

Расстоянием от точки до плоскости является перпендикуляр, опущенный из этой точки на данную плоскость.
Следовательно, АА₁⊥α и ВВ₁⊥α.
Через точки А₁ и В₁ проведем прямую А₁В₁.
Рассмотрим треугольники АА₁О и ВВ₁О:
Данные треугольники являются прямоугольными и
∠АОА₁=∠ВОВ₁, как вертикальные.
Значит, данные треугольники подобны по двум углам, и АО/ОВ = 12/3 = 4
Обозначим ОВ₁=х, тогда ОА₁=4х
Весь отрезок АВ=х+4х=5х, и половина отрезка АВ:2 = АС = СВ = 5х:2 = 2,5х
Тогда отрезок ОС = 4х-2,5х = 1,5х

Рассмотрим треугольники АОА₁ и СОС₁:
   Так как СС₁⊥α => CC₁⊥A₁B₁
   ∠АОА₁ — общий
Следовательно, эти треугольники также подобны по двум углам, и
   АО/CO = 12/CC₁
   4x/1,5x = 12/CC₁
   CC₁ = 12*1,5/4 = 4,5 (см)

Ответ: 4,5 см

Приложения:

Источник

ГДЗ (готовое домашние задание из решебника) на Номер №142 по учебнику Геометрия. 10-11 классы: учебник для общеобразовательных учреждений : базовый и профильный уровни / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. — 22-е изд. — Просвещение, 2013-2019г

Условие

Концы отрезка отстоят от плоскости α на расстояниях 1 см и 4 см. Найдите расстояние от середины отрезка до плоскости α.

Решение 1

Решение 2

Решение 3

Решение 4

Решение 5

Другие задачи из этого учебника

Популярные решебники

Ваше сообщение отправлено
и скоро будет рассмотрено

Источник

Решение.
Пусть отрезок пересекает плоскость в точке D, середину отрезка обозначим как M. Перпендикуляр отрезка, опущенный на плоскость (и определяющий расстояние от середины отрезка до плоскости) пусть касается плоскости в точке M1. Точки A и B проецируются на плоскость соответственно в точках A1 и B1.
Достроим отрезок AB до треугольника ABK, где точка К лежит на плоскости, параллельной исходной.
Отрезок пересекающий плоскость

Найдем длину отрезка MM1, который и будет расстоянием от середины отрезка AB до плоскости.
Учтем что MM1 = MC — M1C

Для треугольника ВАВ1 по теореме Фалеса, МС будет средней линией треугольника. То есть
МС = ВВ1 / 2.

Для треугольника АА1В1 отрезок М1С также является средней линией.
Откуда
М1С = АА1/2

Так как ММ1 = МС – М1С

MM1 = ( BB1 − AA1 ) / 2

Если AA1 ≥ BB1, путем аналогичных рассуждений получим
MM1 = ( AA1 − BB1 ) / 2

То есть для общего случая
MM1 = | BB1 − AA1 | / 2

Подставим значения:
MM1 = | 10 − 6 | / 2 = 2

Ответ: 2 см.

Источник

Ответ:
10 см.
Объяснение:
Искомое расстояние — средняя линия трапеции с основаниями, рваными 12см и 8см. Найдем по формуле: (12+8)/2 =10см.
Или так:
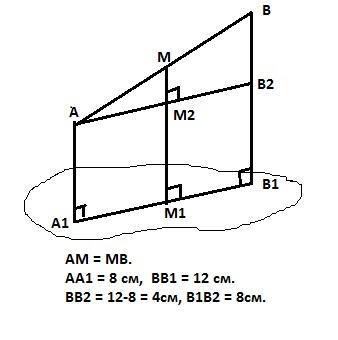
Пусть отрезок АВ, концы отрезка проецируются на плоскость в точки А1 и В1 соответственно. АА1 = 8см,
ВВ1 = 12см. Фигура АВВ1А1 лежит в одной плоскости, пересекающей данную по прямой А1В1.
Проведем прямую АА2 параллельно А1В1. Тогда в прямоугольном треугольнике АВА2 катет ВА2 равен
ВА2 = 12 — 8 = 4 см.
Средняя линия ММ2 этого треугольника равна 2см.
Тогда расстояние от середины отрезка АВ до плоскости равно
ММ1 = ММ2 + М2М1 = 2 + 8 =10см.

Источник