Как найти расстояние от точки до линии

From Wikipedia, the free encyclopedia

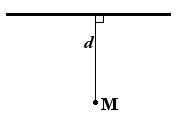
In Euclidean geometry, the distance from a point to a line is the shortest distance from a given point to any point on an infinite straight line. It is the perpendicular distance of the point to the line, the length of the line segment which joins the point to nearest point on the line. The formula for calculating it can be derived and expressed in several ways.

Knowing the distance from a point to a line can be useful in various situations—for example, finding the shortest distance to reach a road, quantifying the scatter on a graph, etc. In Deming regression, a type of linear curve fitting, if the dependent and independent variables have equal variance this results in orthogonal regression in which the degree of imperfection of the fit is measured for each data point as the perpendicular distance of the point from the regression line.

Line defined by an equation[edit]

In the case of a line in the plane given by the equation ax + by + c = 0, where a, b and c are real constants with a and b not both zero, the distance from the line to a point (x₀, y₀) is^[1]^[2]^: p.14

$operatorname{distance}(ax+by+c=0, (x_0, y_0)) = frac{|ax_0+by_0+c|}{sqrt{a^2+b^2}}.$

The point on this line which is closest to (x₀, y₀) has coordinates:^[3]

$x={frac {b(bx_{0}-ay_{0})-ac}{a^{2}+b^{2}}}{text{ and }}y={frac {a(-bx_{0}+ay_{0})-bc}{a^{2}+b^{2}}}.$

Horizontal and vertical lines

In the general equation of a line, ax + by + c = 0, a and b cannot both be zero unless c is also zero, in which case the equation does not define a line. If a = 0 and b ≠ 0, the line is horizontal and has equation y = −c/b. The distance from (x₀, y₀) to this line is measured along a vertical line segment of length |y₀ − (−c/b)| = |by₀ + c|/|b| in accordance with the formula. Similarly, for vertical lines (b = 0) the distance between the same point and the line is |ax₀ + c|/|a|, as measured along a horizontal line segment.

Line defined by two points[edit]

If the line passes through two points P₁ = (x₁, y₁) and P₂ = (x₂, y₂) then the distance of (x₀, y₀) from the line is:^[4]

${displaystyle operatorname {distance} (P_{1},P_{2},(x_{0},y_{0}))={frac {|(x_{2}-x_{1})(y_{1}-y_{0})-(x_{1}-x_{0})(y_{2}-y_{1})|}{sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}}.}$

The denominator of this expression is the distance between P₁ and P₂. The numerator is twice the area of the triangle with its vertices at the three points, (x₀, y₀), P₁ and P₂. See: Area of a triangle § Using coordinates. The expression is equivalent to h = 2A/b, which can be obtained by rearranging the standard formula for the area of a triangle: A = 1/2 bh, where b is the length of a side, and h is the perpendicular height from the opposite vertex.

Line defined by point and angle[edit]

If the line passes through the point P = (P_x, P_y) with angle θ, then the distance of some point (x₀, y₀) to the line is

${displaystyle operatorname {distance} (P,theta ,(x_{0},y_{0}))=|cos(theta )(P_{y}-y_{0})-sin(theta )(P_{x}-x_{0})|}$

Proofs[edit]

An algebraic proof[edit]

This proof is valid only if the line is neither vertical nor horizontal, that is, we assume that neither a nor b in the equation of the line is zero.

The line with equation ax + by + c = 0 has slope −a/b, so any line perpendicular to it will have slope b/a (the negative reciprocal). Let (m, n) be the point of intersection of the line ax + by + c = 0 and the line perpendicular to it which passes through the point (x₀, y₀). The line through these two points is perpendicular to the original line, so

$frac{y_0 - n}{x_0 - m}=frac{b}{a}.$

Thus,

and by squaring this equation we obtain:

a^2(y_0 - n)^2 + b^2(x_0 - m)^2 = 2ab(y_0 - n)(x_0 - m).

Now consider,

${displaystyle {begin{aligned}(a(x_{0}-m)+b(y_{0}-n))^{2}&=a^{2}(x_{0}-m)^{2}+2ab(y_{0}-n)(x_{0}-m)+b^{2}(y_{0}-n)^{2}\&=left(a^{2}+b^{2}right)left((x_{0}-m)^{2}+(y_{0}-n)^{2}right)end{aligned}}}$

using the above squared equation. But we also have,

${displaystyle (a(x_{0}-m)+b(y_{0}-n))^{2}=(ax_{0}+by_{0}-am-bn)^{2}=(ax_{0}+by_{0}+c)^{2}}$

since (m, n) is on ax + by + c = 0.
Thus,

${displaystyle left(a^{2}+b^{2}right)left((x_{0}-m)^{2}+(y_{0}-n)^{2}right)=(ax_{0}+by_{0}+c)^{2}}$

and we obtain the length of the line segment determined by these two points,

${displaystyle d={sqrt {(x_{0}-m)^{2}+(y_{0}-n)^{2}}}={frac {|ax_{0}+by_{0}+c|}{sqrt {a^{2}+b^{2}}}}.}$

^[5]

A geometric proof[edit]

Diagram for geometric proof

This proof is valid only if the line is not horizontal or vertical.^[6]

Drop a perpendicular from the point P with coordinates (x₀, y₀) to the line with equation Ax + By + C = 0. Label the foot of the perpendicular R. Draw the vertical line through P and label its intersection with the given line S. At any point T on the line, draw a right triangle TVU whose sides are horizontal and vertical line segments with hypotenuse TU on the given line and horizontal side of length |B| (see diagram). The vertical side of ∆TVU will have length |A| since the line has slope —A/B.

∆PRS and ∆TVU are similar triangles, since they are both right triangles and ∠PSR ≅ ∠TUV since they are corresponding angles of a transversal to the parallel lines PS and UV (both are vertical lines).^[7] Corresponding sides of these triangles are in the same ratio, so:

$frac{|overline{PR}|}{|overline{PS}|} = frac{|overline{TV}|}{|overline{TU}|}.$

If point S has coordinates (x₀,m) then |PS| = |y₀ — m| and the distance from P to the line is:

$|overline{PR} | = frac{|y_0 - m||B|}{sqrt{A^2 + B^2}}.$

Since S is on the line, we can find the value of m,

$m = frac{-Ax_0 - C}{B},$

and finally obtain:^[8]

$|overline{PR}| = frac{|Ax_0 + By_0 + C|}{sqrt{A^2 + B^2}}.$

A variation of this proof is to place V at P and compute the area of the triangle ∆UVT two ways to obtain that
where D is the altitude of ∆UVT drawn to the hypotenuse of ∆UVT from P. The distance formula can then used to express , , and in terms of the coordinates of P and the coefficients of the equation of the line to get the indicated formula.^{[citation needed]}

A vector projection proof[edit]

Let P be the point with coordinates (x₀, y₀) and let the given line have equation ax + by + c = 0. Also, let Q = (x₁, y₁) be any point on this line and n the vector (a, b) starting at point Q. The vector n is perpendicular to the line, and the distance d from point P to the line is equal to the length of the orthogonal projection of on n. The length of this projection is given by:

$d = frac{|overrightarrow{QP} cdot mathbf{n}|}{| mathbf{n}|}.$

Now,

$overrightarrow{QP} = (x_0 - x_1, y_0 - y_1),$

so $overrightarrow{QP} cdot mathbf{n} = a(x_0 - x_1) + b(y_0 - y_1)$

and $| mathbf{n} | = sqrt{a^2 + b^2},$

thus

$d = frac{|a(x_0 - x_1) + b(y_0 - y_1)|}{sqrt{a^2 + b^2}}.$

Since Q is a point on the line, , and so,^[9]

$d = frac{|ax_0 + by_0 + c|}{sqrt{a^2 + b^2}}.$

Although the distance is given as a modulus, the sign can be useful to determine which side of the line the point is on, in a sense determined by the direction of normal vector (a,b)

Another formula[edit]

It is possible to produce another expression to find the shortest distance of a point to a line. This derivation also requires that the line is not vertical or horizontal.

The point P is given with coordinates ( $x_{0},y_{0}$ ).
The equation of a line is given by y=mx+k . The equation of the normal of that line which passes through the point P is given $y=frac{x_0-x}{m}+y_0$ .

The point at which these two lines intersect is the closest point on the original line to the point P. Hence:

$mx+k=frac{x_0-x}{m}+y_0.$

We can solve this equation for x,

$x=frac{x_0+my_0-mk}{m^2+1}.$

The y coordinate of the point of intersection can be found by substituting this value of x into the equation of the original line,

$y=mfrac{(x_0+my_0-mk)}{m^2+1}+k.$

Using the equation for finding the distance between 2 points, $d=sqrt{(X_2-X_1)^2+(Y_2-Y_1)^2}$ , we can deduce that the formula to find the shortest distance between a line and a point is the following:

${displaystyle d={sqrt {left({{frac {x_{0}+my_{0}-mk}{m^{2}+1}}-x_{0}}right)^{2}+left({m{frac {x_{0}+my_{0}-mk}{m^{2}+1}}+k-y_{0}}right)^{2}}}={frac {|k+mx_{0}-y_{0}|}{sqrt {1+m^{2}}}}.}$

Recalling that m = —a/b and k = — c/b for the line with equation ax + by + c = 0, a little algebraic simplification reduces this to the standard expression.^[3]

Vector formulation[edit]

Illustration of the vector formulation.

The equation of a line can be given in vector form:

Here a is a point on the line, and n is a unit vector in the direction of the line. Then as scalar t varies, x gives the locus of the line.

The distance of an arbitrary point p to this line is given by

{displaystyle operatorname {distance} (mathbf {x} =mathbf {a} +tmathbf {n} ,mathbf {p} )=|(mathbf {p} -mathbf {a} )-((mathbf {p} -mathbf {a} )cdot mathbf {n} )mathbf {n} |.}

This formula can be derived as follows: is a vector from a to the point p. Then is the projected length onto the line and so

{displaystyle mathbf {a} +((mathbf {p} -mathbf {a} )cdot mathbf {n} )mathbf {n} }

is a vector that is the projection of onto the line and represents the point on the line closest to . Thus

{displaystyle (mathbf {p} -mathbf {a} )-((mathbf {p} -mathbf {a} )cdot mathbf {n} )mathbf {n} }

is the component of perpendicular to the line. The distance from the point to the line is then just the norm of that vector.^[4] This more general formula is not restricted to two dimensions.

Another vector formulation[edit]

If the vector space is orthonormal and if the line goes through point a and has a direction vector n, the distance between point p and the line is^[10]

${displaystyle operatorname {distance} (mathbf {x} =mathbf {a} +tmathbf {n} ,mathbf {p} )={frac {left|(mathbf {p} -mathbf {a} )times mathbf {n} right|}{|mathbf {n} |}}.}$

Note that cross products only exist in dimensions 3 and 7.

Notes[edit]

^ Larson & Hostetler 2007, p. 452
^ Spain 2007
^ ^a ^b Larson & Hostetler 2007, p. 522
^ ^a ^b Sunday, Dan. «Lines and Distance of a Point to a Line». softSurfer. Archived from the original on 2021-05-07.
^ Between Certainty and Uncertainty: Statistics and Probability in Five Units With Notes on Historical Origins and Illustrative Numerical Examples
^ Ballantine & Jerbert 1952 do not mention this restriction in their article
^ If the two triangles are on opposite sides of the line, these angles are congruent because they are alternate interior angles.
^ Ballantine & Jerbert 1952
^ Anton 1994, pp. 138-9
^ Weisstein, Eric W. «Point-Line Distance—3-Dimensional». mathworld.wolfram.com. Retrieved 2021-06-06.

References[edit]

Anton, Howard (1994), Elementary Linear Algebra (7th ed.), John Wiley & Sons, ISBN 0-471-58742-7
Ballantine, J.P.; Jerbert, A.R. (1952), «Distance from a line or plane to a point», American Mathematical Monthly, 59 (4): 242–243, doi:10.2307/2306514, JSTOR 2306514
Larson, Ron; Hostetler, Robert (2007), Precalculus: A Concise Course, Houghton Mifflin Co., ISBN 978-0-618-62719-6
Spain, Barry (2007) [1957], Analytical Conics, Dover Publications, ISBN 978-0-486-45773-4
Weisstein, Eric W. «Point-Line Distance—3-Dimensional». MathWorld.

Определение расстояния от точки до прямой

Расстояние от точки до прямой – это длина перпендикуляра, опущенного из точки на прямую. В начертательной геометрии она определяется графическим путем по приведенному ниже алгоритму.

Алгоритм

Прямую переводят в положение, в котором она будет параллельна какой-либо плоскости проекции. Для этого применяют методы преобразования ортогональных проекций.
Из точки проводят перпендикуляр к прямой. В основе данного построения лежит теорема о проецировании прямого угла.
Длина перпендикуляра определяется путем преобразования его проекций или с использованием способа прямоугольного треугольника.

Пример

На следующем рисунке представлен комплексный чертеж точки M и прямой b, заданной отрезком CD. Требуется найти расстояние между ними.

Решение

Согласно нашему алгоритму, первое, что необходимо сделать, это перевести прямую в положение, параллельное плоскости проекции. При этом важно понимать, что после проведенных преобразований фактическое расстояние между точкой и прямой не должно измениться. Именно поэтому здесь удобно использовать метод замены плоскостей, который не предполагает перемещение фигур в пространстве.

Результаты первого этапа построений показаны ниже. На рисунке видно, как параллельно b введена дополнительная фронтальная плоскость П₄. В новой системе (П₁, П₄) точки C»₁, D»₁, M»₁ находятся на том же удалении от оси X₁, что и C», D», M» от оси X.

Выполняя вторую часть алгоритма, из M»₁ опускаем перпендикуляр M»₁N»₁ на прямую b»₁, поскольку прямой угол MND между b и MN проецируется на плоскость П₄ в натуральную величину. По линии связи определяем положение точки N’ и проводим проекцию M’N’ отрезка MN.

На заключительном этапе нужно определить величину отрезка MN по его проекциям M’N’ и M»₁N»₁. Для этого строим прямоугольный треугольник M»₁N»₁N₀, у которого катет N»₁N₀ равен разности (Y_M₁ – Y_N₁) удаления точек M’ и N’ от оси X₁. Длина гипотенузы M»₁N₀ треугольника M»₁N»₁N₀ соответствует искомому расстоянию от M до b.

Второй способ решения

Параллельно CD вводим новую фронтальную плоскость П₄. Она пересекает П₁ по оси X₁, причем X₁∥C’D’. В соответствии с методом замены плоскостей определяем проекции точек C»₁, D»₁ и M»₁, как это изображено на рисунке.
Перпендикулярно C»₁D»₁ строим дополнительную горизонтальную плоскость П₅, на которую прямая b проецируется в точку C’₂ = b’₂.
Величина расстояния между точкой M и прямой b определяется длиной отрезка M’₂C’₂, обозначенного красным цветом.

Похожие задачи:

Определение расстояния от точки до плоскости
Определение натуральной величины отрезка
Расстояние между параллельными прямыми

Источник

Расстояние от точки до прямой на плоскости.

Определение.

Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.

Формула для вычисления расстояния от точки до прямой на плоскости

Если задано уравнение прямой Ax + By + C = 0, то расстояние от точки M(M_x, M_y) до прямой можно найти, используя следующую формулу

d =	\|A·M_x + B·M_y + C\|
√A² + B²

Примеры задач на вычисление расстояния от точки до прямой на плоскости

Пример 1.

Найти расстояние между прямой 3x + 4y — 6 = 0 и точкой M(-1, 3).

Решение. Подставим в формулу коэффициенты прямой и координаты точки

d =	\|3·(-1) + 4·3 — 6\|	=	\|-3 + 12 — 6\|	=	\|3\|	= 0.6
√3² + 4²	√9 + 16	5

Ответ: расстояние от точки до прямой равно 0.6.

Источник

В евклидовой геометрии расстояние от точки до линии — это кратчайшее расстояние от заданной точки до любой точки на бесконечной прямой. Это расстояние перпендикуляра от точки до линии, длина отрезка линии, который соединяет точку с ближайшей точкой на линии. Формулу для его расчета можно вывести и выразить несколькими способами.

Знание расстояния от точки до линии может быть полезно в различных ситуациях — например, для нахождения кратчайшего расстояния до дороги, количественной оценки разброса на графике и т. Д. В регрессии Деминга, тип аппроксимации линейной кривой, если зависимые и независимые переменные имеют одинаковую дисперсию, это приводит к ортогональной регрессии, в которой степень несовершенства аппроксимации измеряется для каждой точки данных как перпендикулярное расстояние точка от линии регрессии.

Содержание

1 Декартовы координаты
- 1.1 Линия, определяемая уравнением
- 1.2 Линия, определяемая двумя точками
2 Доказательства
- 2.1 Алгебраическое доказательство
- 2.2 Геометрическое доказательство
- 2.3 Доказательство проекции вектора
3 Другая формула
4 Векторная формула
5 Другая векторная формула
6 См. Также
7 Примечания
8 Ссылки
9 Дополнительная литература

Декартова координаты

Линия, определяемая уравнением

В случае линии на плоскости, заданной уравнением ax + by + c = 0, где a, b и c являются действительными константы, где a и b не равны нулю, расстояние от линии до точки (x 0,y0) равно

distance ⁡ (ax + by + c = 0, (x 0, y 0)) = | а х 0 + б у 0 + с | а 2 + б 2. { displaystyle operatorname {distance} (ax + by + c = 0, (x_ {0}, y_ {0})) = { frac {| ax_ {0} + by_ {0} + c |} { sqrt {a ^ {2} + b ^ {2}}}}.} $operatorname {distance} (ax + by + c = 0, ( x_0, y_0)) = frac {| ax_0 + by_0 + c |} { sqrt {a ^ 2 + b ^ 2}}.$

Точка на этой прямой, ближайшая к (x 0,y0), имеет координаты:

x = b (bx 0 — ay 0) — aca 2 + b 2 и y = a (- bx 0 + ay 0) — bca 2 + b 2. { displaystyle x = { frac {b (bx_ {0} -ay_ {0}) — ac} {a ^ {2} + b ^ {2}}} { text {and}} y = { frac) {a (-bx_ {0} + ay_ {0}) — bc} {a ^ {2} + b ^ {2}}}.} $x = { frac {b (bx_ {0} -ay_ {0}) - ac } {a ^ {2} + b ^ {2}}} { text {и}} y = { frac {a (-bx_ {0} + ay_ {0}) - bc} {a ^ {2} + b ^ {2}}}.$

Горизонтальные и вертикальные линии

В общем уравнении линии, ax + by + c = 0, a и b не могут быть равны нулю, если c также не равно нулю, и в этом случае уравнение не определяет линию. Если a = 0 и b ≠ 0, линия горизонтальна и имеет уравнение y = -c / b. Расстояние от (x 0, y 0) до этой линии измеряется по отрезку вертикальной линии длиной | y 0 — (-c / b) | = | по 0 + c | / | b | в соответствии с формулой. Аналогично, для вертикальных линий (b = 0) расстояние между той же точкой и прямой составляет | ax 0 + c | / | a |, измеренное по горизонтальному отрезку линии.

Линия, определяемая двумя точками

Если линия проходит через две точки P 1 = (x 1,y1) и P 2 = ( x 2,y2), то расстояние (x 0,y0) от линии составляет:

расстояние ⁡ (P 1, P 2, (x 0, y 0)) = | (y 2 — y 1) x 0 — (x 2 — x 1) y 0 + x 2 y 1 — y 2 x 1 | (у 2 — у 1) 2 + (х 2 — х 1) 2. { displaystyle operatorname {distance} (P_ {1}, P_ {2}, (x_ {0}, y_ {0})) = { frac {| (y_ {2} -y_ {1}) x_ { 0} — (x_ {2} -x_ {1}) y_ {0} + x_ {2} y_ {1} -y_ {2} x_ {1} |} { sqrt {(y_ {2} -y_ { 1}) ^ {2} + (x_ {2} -x_ {1}) ^ {2}}}}.} $operatorname {distance} (P_ {1}, P_ {2}, (x_ {0}, y_ {0})) = { frac {| (y_ {2} -y_ {1}) x_ {0} - (x_ {2} -x_ {1}) y_ {0} + x_ {2} y_ {1} -y_ {2} x_ {1} |} {{ sqrt {(y_ {2}) -y_ {1}) ^ {2} + (x_ {2} -x_ {1}) ^ {2}}}}}.$

Знаменателем этого выражения является расстояние между P 1 и P 2. Числитель равен удвоенной площади треугольника с вершинами в трех точках (x 0,y0), P 1 и P 2. См.: Площадь треугольника § Использование координат. Выражение эквивалентно h = 2 A b { textstyle h = { frac {2A} {b}}} ${ textstyle h = { frac {2A} {b}}}$ , которое можно получить, переставив стандартную формулу для площади треугольник: A = 1 2 bh { textstyle A = { frac {1} {2}} bh} ${ textstyle A = { frac {1} {2}} bh }$ , где b — длина стороны, а h — высота перпендикуляра от противоположная вершина.

Доказательства

Алгебраическое доказательство

Это доказательство действительно только в том случае, если линия не является ни вертикальной, ни горизонтальной, то есть мы предполагаем, что ни a, ни b в уравнении линия нулевая.

Линия с уравнением ax + by + c = 0 имеет наклон -a / b, поэтому любая прямая, перпендикулярная ей, будет иметь наклон b / a (отрицательный обратный). Пусть (m, n) будет точкой пересечения прямой ax + by + c = 0 и прямой, перпендикулярной ей, которая проходит через точку (x 0, y 0). Прямая, проходящая через эти две точки, перпендикулярна исходной прямой, поэтому

y 0 — n x 0 — m = b a. { displaystyle { frac {y_ {0} -n} {x_ {0} -m}} = { frac {b} {a}}.} $frac {y_0 - n} {x_0 - m} = frac {b} {a}.$

Таким образом, a (y 0 — n) — b (x 0 — m) = 0, { displaystyle a (y_ {0} -n) -b (x_ {0} -m) = 0,}и возводя это уравнение в квадрат, мы получаем:

a 2 (y 0 — n) 2 + b 2 (x 0 — m) 2 = 2 ab (y 0 — n) (x 0 — m). { displaystyle a ^ {2} (y_ {0} -n) ^ {2} + b ^ {2} (x_ {0} -m) ^ {2} = 2ab (y_ {0} -n) (x_ {0} -m).}

Теперь рассмотрим,

(a (x 0 — m) + b (y 0 — n)) 2 = a 2 (x 0 — m) 2 + 2 ab (y 0 — N) (Икс 0 — м) + б 2 (Y 0 — N) 2 = (a 2 + b 2) ((x 0 — m) 2 + (Y 0 — N) 2) { Displaystyle (а (x_ {0} -m) + b (y_ {0} -n)) ^ {2} = a ^ {2} (x_ {0} -m) ^ {2} + 2ab (y_ {0} -n) (x_ {0} -m) + b ^ {2} (y_ {0} -n) ^ {2} = (a ^ {2} + b ^ {2}) ((x_ {0} -m) ^ {2} + (y_ {0} -n) ^ {2})}

(a (x_0 - m) + b (y_0 - n)) ^ 2 = a ^ 2 (x_0 - m) ^ 2 + 2ab (y_0 -n) (x_0 - m) + b ^ 2 (y_0 - n) ^ 2 = (a ^ 2 + b ^ 2) ((x_0 - m) ^ 2 + (y_0 - n) ^ 2)

с использованием приведенного выше уравнения в квадрате. Но у нас также есть

(a (x 0 — m) + b (y 0 — n)) 2 = (ax 0 + by 0 — am — bn) 2 = (ax 0 + by 0 + c) 2 { displaystyle (a (x_ {0} -m) + b (y_ {0} -n)) ^ {2} = (ax_ {0} + by_ {0} -am-bn) ^ {2} = ( ax_ {0} + by_ {0} + c) ^ {2}}

, поскольку (m, n) находится на ax + by + c = 0. Таким образом,

(a 2 + b 2) (( x 0 — m) 2 + (y 0 — n) 2) = (ax 0 + by 0 + c) 2 { displaystyle (a ^ {2} + b ^ {2}) ((x_ {0} -m) ^ {2} + (y_ {0} -n) ^ {2}) = (ax_ {0} + by_ {0} + c) ^ {2}}

и получаем длину отрезка определяется этими двумя точками,

d = (x 0 — m) 2 + (y 0 — n) 2 = | а х 0 + б у 0 + с | а 2 + б 2. { displaystyle d = { sqrt {(x_ {0} -m) ^ {2} + (y_ {0} -n) ^ {2}}} = { frac {| ax_ {0} + by_ {0} } + c |} { sqrt {a ^ {2} + b ^ {2}}}}.} $d = sqrt {(x_0 - m) ^ 2 + (y_0 - n) ^ 2} = frac {| ax_0 + by_0 + c |} { sqrt {a ^ 2 + b ^ 2}}.$

Геометрическое доказательство

Диаграмма для геометрического доказательства

Это доказательство действительно, только если линия не горизонтально или вертикально.

Отбросьте перпендикуляр из точки P с координатами (x 0, y 0) на линию с уравнением Ax + By + C = 0. Обозначьте основание перпендикуляра R. Проведите вертикальную линию через точку P и отметьте ее пересечение с данной линией S. В любой точке T на прямой нарисуйте прямоугольный треугольник TVU, стороны которого являются горизонтальными и вертикальными отрезками с гипотенузой TU. по заданной линии и горизонтальной стороне длины | B | (см. диаграмму). Вертикальная сторона ∆TVU будет иметь длину | A | так как линия имеет наклон -A / B.

∆PRS и ∆TVU — похожие треугольники, поскольку они оба являются прямыми треугольниками и ∠PSR ≅ ∠TUV, поскольку они соответствуют углам трансверсали параллельным линиям PS и UV (обе вертикальные линии). Соответствующие стороны этих треугольников находятся в одинаковом соотношении, поэтому:

| P R ¯ | | P S ¯ | = | T V ¯ | | T U ¯ |. { displaystyle { frac {| { overline {PR}} |} {| { overline {PS}} |}} = { frac {| { overline {TV}} |} {| { overline { TU}} |}}.} $frac {| overline {PR} |} {| overline {PS} |} = frac {| overline {TV} |} {| overline {TU} |}.$

Если точка S имеет координаты (x 0, m), то | PS | = | y 0 — m | и расстояние от P до линии:

| P R ¯ | = | у 0 — м | | B | А 2 + В 2. { displaystyle | { overline {PR}} | = { frac {| y_ {0} -m || B |} { sqrt {A ^ {2} + B ^ {2}}}}.} $| overline {PR} | = frac {| y_0 - m || B |} { sqrt {A ^ 2 + B ^ 2}}.$

Поскольку S находится на линии, мы можем найти значение m,

m = — A x 0 — CB, { displaystyle m = { frac {-Ax_ {0} -C} {B}},} $m = frac {-Ax_0 - C} {B},$

и, наконец, получаем:

| P R ¯ | = | A x 0 + B y 0 + C | А 2 + В 2. { displaystyle | { overline {PR}} | = { frac {| Ax_ {0} + By_ {0} + C |} { sqrt {A ^ {2} + B ^ {2}}}}. } $| overline {PR} | = frac {| Ax_0 + By_0 + C |} { sqrt {A ^ 2 + B ^ 2}}.$

Вариант этого доказательства состоит в том, чтобы поместить V в точку P и вычислить площадь треугольника ∆UVT двумя способами, чтобы получить, что D | T U ¯ | = | V U ¯ | | V T ¯ | { displaystyle D | { overline {TU}} | = | { overline {VU}} || { overline {VT}} |}, где D — высота ∆UVT, обращенная к гипотенуза ∆UVT от P. Формула расстояния может быть использована для выражения | T U ¯ | { displaystyle | { overline {TU}} |}, | V U ¯ | { displaystyle | { overline {VU}} |}и | V T ¯ | { displaystyle | { overline {VT}} |}в терминах координат точки P и коэффициентов уравнения линии для получения указанной формулы.

Векторная проекция доказательство

Пусть P будет точкой с координатами (x 0, y 0) и пусть данная линия имеет уравнение ax + by + c = 0. Кроме того, пусть Q = (x 1, y 1) — любая точка на этой прямой, а n вектор (a, b), начинающийся в точке Q. Вектор n перпендикулярно линии, а расстояние d от точки P до линии равно длине ортогональной проекции QP → { displaystyle { overrightarrow {QP}}}на n . Длина этой проекции определяется как:

d = | Q P → ⋅ n | ‖ Н ‖. { displaystyle d = { frac {| { overrightarrow {QP}} cdot mathbf {n} |} { | mathbf {n} |}}.} $d = frac {| overrightarrow {QP} cdot mathbf {n} |} { | mathbf {n} |}.$

Теперь

QP → = (x 0 — x 1, y 0 — y 1), { displaystyle { overrightarrow {QP}} = (x_ {0} -x_ {1}, y_ {0} -y_ {1}),} $overrightarrow {QP} = ( x_0 - x_1, y_0 - y_1),$

поэтому QP → ⋅ N = a (x 0 — x 1) + b (y 0 — y 1) { displaystyle { overrightarrow {QP}} cdot mathbf {n} = a (x_ {0} -x_ {1}) + b (y_ {0} -y_ {1})} $overrightarrow {QP} cdot mathbf {n} = a (x_0 - x_1) + b (y_0 - y_1)$

и ‖ n ‖ = a 2 + b 2, { displaystyle | mathbf {n} | = { sqrt {a ^ {2} + b ^ {2}}},} $| mathbf {n} | = sqrt {a ^ 2 + b ^ 2},$

таким образом

d = | a (x 0 — x 1) + b (y 0 — y 1) | а 2 + б 2. { displaystyle d = { frac {| a (x_ {0} -x_ {1}) + b (y_ {0} -y_ {1}) |} { sqrt {a ^ {2} + b ^ { 2}}}}.} $d = frac {| a (x_0 - x_1) + b (y_0 - y_1) |} { sqrt {a ^ 2 + b ^ 2}}.$

Поскольку Q — точка на прямой, c = — ax 1 — by 1 { displaystyle c = -ax_ {1} -by_ {1}}, и поэтому

d = | а х 0 + б у 0 + с | а 2 + б 2. { displaystyle d = { frac {| ax_ {0} + by_ {0} + c |} { sqrt {a ^ {2} + b ^ {2}}}}.} $d = frac {| ax_0 + by_0 + c |} { sqrt {a ^ 2 + b ^ 2}}.$

Другая формула

Можно создать другое выражение, чтобы найти кратчайшее расстояние от точки до линии. Этот вывод также требует, чтобы линия не была вертикальной или горизонтальной.

Точка P задается с координатами (x 0, y 0 { displaystyle x_ {0}, y_ {0}} $x_ {0}, y_ {0}$ ). Уравнение линии задается следующим образом: y = m x + k { displaystyle y = mx + k}. Уравнение нормали этой линии, проходящей через точку P, задается y = x 0 — xm + y 0 { displaystyle y = { frac {x_ {0} -x} {m}} + y_ {0}} $y = frac {x_0-x} {m} + y_0$ .

Точка, в которой эти две прямые пересекаются, является ближайшей точкой на исходной прямой к точке P. Следовательно:

mx + k = x 0 — xm + y 0. { displaystyle mx + k = { frac {x_ {0} -x} {m}} + y_ {0}.} $mx + k = frac {x_0-x} {m} + y_0.$

Мы можем решить это уравнение относительно x,

x = x 0 + my 0 — мкМ 2 + 1. { displaystyle x = { frac {x_ {0} + my_ {0} -mk} {m ^ {2} +1}}.} $x = frac {x_0 + my_0-mk} {m ^ 2 + 1}.$

Координата y точки пересечения можно найти, подставив это значение x в уравнение исходной строки,

y = m (x 0 + my 0 — mk) m 2 + 1 + k. { displaystyle y = m { frac {(x_ {0} + my_ {0} -mk)} {m ^ {2} +1}} + k.} $y = m frac {(x_0 + my_0-mk)} {m ^ 2 + 1} + k.$

Использование уравнения для определения расстояния между двумя точек, d = (X 2 — X 1) 2 + (Y 2 — Y 1) 2 { displaystyle d = { sqrt {(X_ {2} -X_ {1}) ^ {2} + ( Y_ {2} -Y_ {1}) ^ {2}}}} $d = sqrt {(X_2-X_1) ^ 2 + (Y_2-Y_1) ^ 2}$ , мы можем сделать вывод, что формула для нахождения кратчайшего расстояния между линией и точкой следующая:

d = (x 0 + my 0 — мкм 2 + 1 — x 0) 2 + (mx 0 + my 0 — мкм 2 + 1 + k — y 0) 2 = | к + м х 0 — у 0 | 1 + м 2. { displaystyle d = { sqrt { left ({{ frac {x_ {0} + my_ {0} -mk} {m ^ {2} +1}} — x_ {0}} right) ^ { 2} + left ({m { frac {x_ {0} + my_ {0} -mk} {m ^ {2} +1}} + k-y_ {0}} right) ^ {2}} } = { frac {| k + mx_ {0} -y_ {0} |} { sqrt {1 + m ^ {2}}}}.} ${ displaystyle d = { sqrt { left ({{ frac {x_ {0} + my_ {0} -mk} {m ^ {2} +1}} - x_ {0}} right) ^ { 2} + left ({m { frac {x_ {0} + my_ {0} -mk} {m ^ {2} +1}} + k-y_ {0}} right) ^ {2}} } = { frac {| k + mx_ {0} -y_ {0} |} { sqrt {1 + m ^ {2}}}}.}$

Вспоминая, что m = -a / b и k = — c / b для линии с уравнением ax + by + c = 0, небольшое алгебраическое упрощение сводит это к стандартному выражению.

Векторная формулировка

Иллюстрация векторной формулировки.

Уравнение строки можно представить в векторной форме:

x = a + tn { displaystyle mathbf {x} = mathbf {a} + t mathbf {n}}

Здесь a — это точка на линии, а n — единичный вектор в направлении линии. Затем, когда скаляр t изменяется, x дает геометрическое место линии.

Расстояние от произвольной точки p до этой линии определяется как

расстояние ⁡ (x = a + tn, p) = ‖ (a — p) — ((a — п) ⋅ n) n ‖. { displaystyle operatorname {расстояние} ( mathbf {x} = mathbf {a} + t mathbf {n}, mathbf {p}) = | ( mathbf {a} — mathbf {p}) — (( mathbf {a} — mathbf {p}) cdot mathbf {n}) mathbf {n} |.}

operatorname {distance} ( mathbf {x} = mathbf {a} + t mathbf {n}, mathbf {p}) = | ( mathbf {a} - mathbf {p}) - (( mathbf {a} - mathbf {p}) cdot mathbf {n}) mathbf {n} |.

Эта формула может быть получена следующим образом: a — p { displaystyle mathbf {a} — mathbf {p}}— вектор от p до точки a на линии. Тогда (a — p) ⋅ n { displaystyle ( mathbf {a} — mathbf {p}) cdot mathbf {n}}— это длина проекции на линию, и поэтому

((a — p) ⋅ n) n { displaystyle (( mathbf {a} — mathbf {p}) cdot mathbf {n}) mathbf {n}}

— вектор это проекция элемента a — p { displaystyle mathbf {a} — mathbf {p}}на линию. Таким образом,

(a — p) — ((a — p) ⋅ n) n { displaystyle ( mathbf {a} — mathbf {p}) — (( mathbf {a} — mathbf {p})) cdot mathbf {n}) mathbf {n}}

является компонентом a — p { displaystyle mathbf {a} — mathbf {p}}перпендикулярно к строке. Тогда расстояние от точки до линии будет просто norm этого вектора. Эта более общая формула не ограничивается двумя измерениями.

Другая векторная формулировка

Если векторное пространство ортонормировано и если линия (l) проходит через точку A и имеет вектор направления u → { displaystyle { vec {u}}} vec u , расстояние между точкой P и линией (l) равно

d (P, (l)) = ‖ AP → × u → ‖ ‖ U → ‖ { displaystyle d ( mathrm {P}, (l)) = { frac { left | { overrightarrow { mathrm {AP}}} times { vec {u}} right |} { | { vec {u}} |}}} ${ displaystyle d ( mathrm {P}, (l)) = { frac { left | { overrightarrow { mathrm {AP}}} times { vec {u}} right |} { | { vec {u}} |}} }$

где AP → × u → { displaystyle { overrightarrow { mathrm {AP}}} times { vec {u}}}— это векторное произведение векторов AP → { displaystyle { overrightarrow { mathrm {AP}}}}и u → { displaystyle { vec {u}}} vec u и где ‖ u → ‖ { displaystyle | { vec {u}} |}— векторная норма u → { displaystyle { vec {u}}} vec u .

Обратите внимание, что перекрестные произведения существуют только в измерениях 3 и 7.

См. Также

Примечания

Ссылки

Антон, Ховард (1994), Элементарная линейная алгебра (7-е изд.), John Wiley Sons, ISBN 0-471-58742-7
Ballantine, JP; Джерберт, А. (1952), «Расстояние от прямой или плоскости до точки», American Mathematical Monthly, 59 : 242–243, doi : 10.2307 / 2306514
Ларсон, Рон; Хостетлер, Роберт (2007), Precalculus: A Concise Course, Houghton Mifflin Co., ISBN 0-618-62719-7
Испания, Барри (2007) [1957], Analytical Conics, Dover Publications, ISBN 0-486-45773-7

Дополнительная литература

Деза, Мишель Мари ; Деза, Елена (2013), Энциклопедия расстояний (2-е изд.), Springer, стр. 86, ISBN 9783642309588

Источник

Line defined by an equation[edit]

Line defined by two points[edit]

Line defined by point and angle[edit]

Proofs[edit]

An algebraic proof[edit]

A geometric proof[edit]

A vector projection proof[edit]

Another formula[edit]

Vector formulation[edit]

Another vector formulation[edit]

See also[edit]

Notes[edit]

References[edit]

Further reading[edit]

Определение расстояния от точки до прямой

Расстояние от точки до прямой на плоскости.

Формула для вычисления расстояния от точки до прямой на плоскости

Примеры задач на вычисление расстояния от точки до прямой на плоскости

Содержание

Декартова координаты

Линия, определяемая уравнением

Линия, определяемая двумя точками

Доказательства

Алгебраическое доказательство

Геометрическое доказательство

Векторная проекция доказательство

Другая формула

Векторная формулировка

Другая векторная формулировка

См. Также

Примечания

Ссылки

Дополнительная литература