Долгое время я предпочитала решать задачи на нахождение расстояния от точки до прямой геометрическим способом, поскольку использование метода координат мне казалось очень нерациональным. Но наконец-то я поняла, как изящно, без построения перпендикулярной плоскости решать эту задачу.
Поясню общий ход решения на примере вспомогательной задачи, а потом решим реальную задачу из ЕГЭ по математике.
Вспомогательная задача:
В произвольном треугольнике 
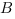

Расстояние от точки 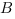

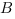


Пусть вершины треугольника имеют координаты:
1. Найдем косинус угла между прямыми, содержащими стороны

Для этого найдем координаты векторов 

Зная координаты векторов, можно найти косинус угла между векторами.
Косинус угла 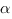
Косинус угла между прямыми равен модулю косинуса угла между направляющими векторами прямых.
Скалярное произведение равно сумме произведений одноименных координат:
Длина вектора 
Длина вектора 
2. Зная 

3. Теперь мы можем найти длину 

Если треугольник 
то 




Решим задачу:
Основанием прямого параллелепипеда 




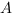

План наших действий:
1. Введем систему координат.
2. Найдем координаты направляющих векторов прямых 

3. Найдем косинус угла между прямыми 

4. Найдем синус угла между прямыми 

5. Найдем расстояние от точки 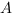

Вспомним свойства диагоналей ромба:
Диагонали ромба
- взаимно перпендикулярны,
- точкой пересечения делятся пополам
- являются биссектрисами углов ромба.
Поместим начало система координат в точку пересечения диагоналей ромба, а оси направим вдоль диагоналей:
Найдем длины отрезков 


Рассмотрим треугольник 

1. Найдем координаты точек
2. Найдем координаты векторов 


3. Найдем длины векторов 

4. Найдем модуль косинуса угла 




5. Найдем синус угла 
6. Pасстояние от точки 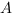

Ответ: 10
И.В. Фельдман, репетитор по математике.
Помогите найти расстояние от точки О до стороны АС.

Вы перешли к вопросу Помогите найти расстояние от точки О до стороны АС?. Он относится к категории Геометрия,
для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот
вариант ответа не полностью вас удовлетворяет, то с помощью автоматического
умного поиска можно найти другие вопросы по этой же теме, в категории
Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном
объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части
сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете
ознакомиться с вариантами ответов пользователей.
Как найти расстояние между двумя точками?
Расстоянием между точками также называют прямую,
у которой одна из точек это начало, а соответственно
другая конец. Найти расстояние между этими
двумя точками, значит найти длину прямой,
связывающей точки.
Есть много разных способов найти расстояние между
двумя точками, но самый универсальный, на мой взгляд,
это найти расстояние взяв за основу Теорему Пифагора.
Исходя из этой теоремы, можно сказать, что в нашем
случае расстоянием(прямой), является гипотенуза,
а чем тогда являются точки, сейчас разберемся.
Формулировка великой Теоремы Пифагора звучит так:
в прямоугольном треугольнике квадрат гипотенузы равен
сумме квадратов катетов. Или же кратко, формулой:
( c^2 = a^2 + b^2 ) где c — это гипотенуза, a и b — катеты.
Формулировка этой теоремы применяется почти всегда и везде,
где нужно найти расстояние от чего-то до чего-то. Сейчас, мы
используя эту теорему найдем расстояние между точками.
Итак, для примера возьмем точки с координатами
первой точки — x1 = 0; y1 = 4, второй точки — x2 =3; y2 = 0.
Как же нам теперь выразить точки через катеты a и b ?
Читайте дальше, все гениальное просто.
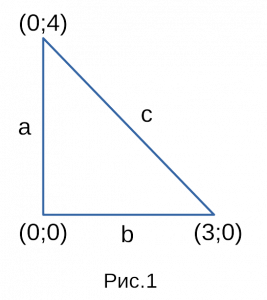
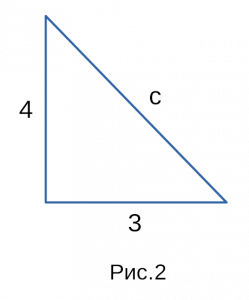
На рисунке 1 мы изобразили для наглядности
прямоугольный треугольник, с координатами
которые мы взяли для примера. На рисунке 2
тот же самый прямоугольный треугольник,
только без координат! Эти два прямоугольных
треугольника идентичные, поэтому вернемся
к Теореме Пифагора.
Заменяем длины катетов a и b, из Теоремы Пифагора,
на разность координат точек. Взгляните на формулу,
которая получилась:
Подставляем наши координаты:
В итоге получилось, что расстояние в нашем примере
равно 5(корень из 25). Как видите все просто, и вы можете
смело применять эту формулу, решая не только задачи,
но и на практике, находя расстояние зная только две точки.
Все формулы для треугольника
1. Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a , b , c — стороны произвольного треугольника
α , β , γ — противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), ( a ):
* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), ( a):
2. Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
a , b — катеты
c — гипотенуза
α , β — острые углы
Формулы для катета, ( a ):
Формулы для катета, ( b ):
Формулы для гипотенузы, ( c ):
Формулы сторон по теореме Пифагора, ( a , b ):
3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b — сторона (основание)
a — равные стороны
α — углы при основании
β — угол образованный равными сторонами
Формулы длины стороны (основания), (b ):
Формулы длины равных сторон , (a):
4. Найти длину высоты треугольника
Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.
H — высота треугольника
a — сторона, основание
b, c — стороны
β , γ — углы при основании
p — полупериметр, p=(a+b+c)/2
R — радиус описанной окружности
S — площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
Расстояние от точки до прямой
Что называется расстоянием от точки до прямой? Как найти расстояние от точки до прямой?
Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из данной точки на прямую.
Таким образом, чтобы найти расстояние от точки до прямой, надо из точки к прямой провести перпендикуляр и найти его длину.
Например, на рисунке 1 расстояние от точки A до прямой a равно длине перпендикуляра AB, опущенного из точки A на прямую a.
Задачи на нахождение расстояния от точки до прямой сводятся к рассмотрению прямоугольного треугольника.
№ 1. Из точки к прямой проведены две наклонные, длины которых относятся как 2:3, а длины их проекций соответственно равны 2 см и 7 см. Найти расстояние от точки до прямой.
Дано: A∉a,
BC и BD — их проекции, BC=2 см, BD=7 см
1) Пусть k — коэффициент пропорциональности. Тогда AC=2k см, AD=3k см.
2) Рассмотрим треугольник ABC — прямоугольный (так как AB — перпендикуляр к прямой a по условию). По теореме Пифагора
3) Аналогично, из треугольника ABD
4) Приравниваем правые части полученных равенств и находим k:
5) Зная k, найдем AB:
№ 2. Из точки к прямой проведены две наклонные, длины которых равны 13 см и 15 см. Найти расстояние от точки до прямой, если разность проекций наклонных равна 4 см.
Дано: A∉a,
AC и AD — наклонные, AC=13 см, AD=15 см,
BC и BD — их проекции, BD-BC=4 см
1) Пусть BC=x см, тогда BD=x+4 см.
2) Рассмотрим треугольник ABC — прямоугольный (так как AB — перпендикуляр к прямой a по условию). По теореме Пифагора
3) Аналогично, из треугольника ABD
4) Приравниваем правые части полученных равенств и находим x:
5) Зная x, найдем AB:
№ 3. Найти расстояние от точки A до прямой a, если известно, что наклонная AF, длина которой равна c, образует с прямой a угол α.
Дано: A∉a,
Треугольник ABF — прямоугольный (так как AB — перпендикуляр к прямой a по условию). AB — катет, противолежащий углу ACB, AF — гипотенуза.
http://www-formula.ru/2011-10-09-11-08-41
Расстояния
Задача на нахождения расстояния в стереометрической фигуре является главной и самой важной из всех. Прежде всего определимся с тем, что имеется ввиду под словом «расстояние», ведь их может быть бесконечно много.
Расстояние между объектами в геометрии – это кратчайшее из расстояний между ними.
Обозначение:
В стереометрии найти расстояние можно между следующими комбинациями фигур:
РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ
Расстояние между точками– это длина отрезка, соединяющего эти точки.
В задачах на стереометрию мы не можем просто воспользоваться линейкой, и длину этого отрезка должны найти аналитически. Поэтому длину отрезка AB между точками A и B находят как сторону треугольника, если отрезок AB удается включить в некоторый треугольник в качестве одной из его сторон.
То есть если в задаче предлагается найти расстояние между точками, нужно задать себе вопрос: «В каком треугольнике этот отрезок является стороной?», затем построить этот треугольник и найти в нем нужную сторону.
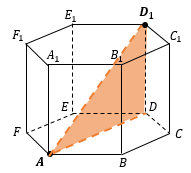
Например:
|
|
|
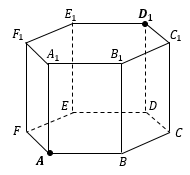
РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПРЯМОЙ
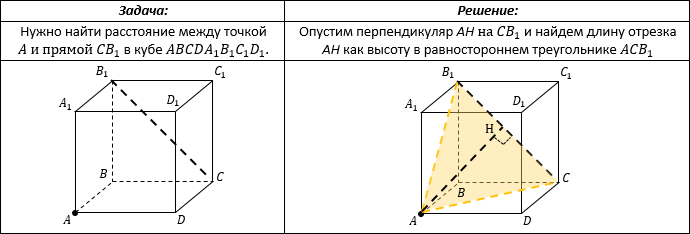
Расстояние от точки до прямой – длина перпендикуляра, опущенного из точки на прямую.
Этот отрезок перпендикуляра можно вычислить, включив его в треугольник (или трапецию) в качестве одной из высот. То есть нужно задать себе вопрос: «В каком треугольнике этот отрезок является высотой?», затем построить этот треугольник и найти в нем высоту.
Например:
РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПЛОСКОСТЬЮ
Существует несколько способов нахождения расстояния от точки до плоскости:
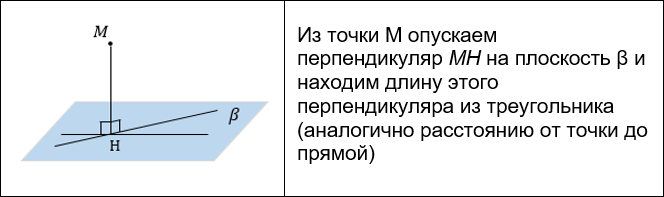
- Построение перпендикуляра из точки на плоскость.
- К этому способу обращаются, если расстояние из точки M на плоскость опускать неудобно, а удобно опустить равный ему перпендикуляр из другой точки, лежащей на одной линии с M.
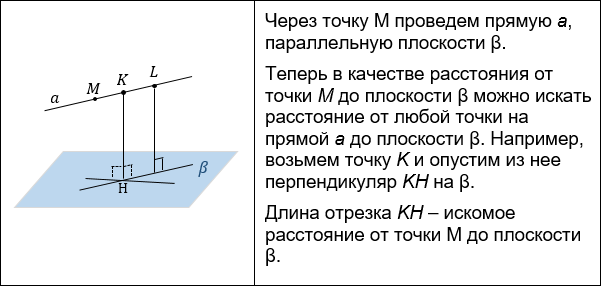
- Построение перпендикуляра из точки прямой к плоскости.
- Построение перпендикуляра из точки плоскости на плоскость.
К этому способу, аналогично, обращаются, если расстояние из точки M на плоскость опускать неудобно, а удобно опустить равный ему перпендикуляр из другой точки, лежащей на одной плоскости с M.
- Через двойное выражение объема.
Расстояние от точки M до плоскости β – это перпендикуляр, опущенный из точки на плоскость, то есть по сути это высота в некоторой пирамиде с вершиной M и плоскостью основания, лежащей на β. Если легко вычислить объем этой пирамиды, используя другое основание и другую высоту, то через этот объем можно найти нужное расстояние.
Например:
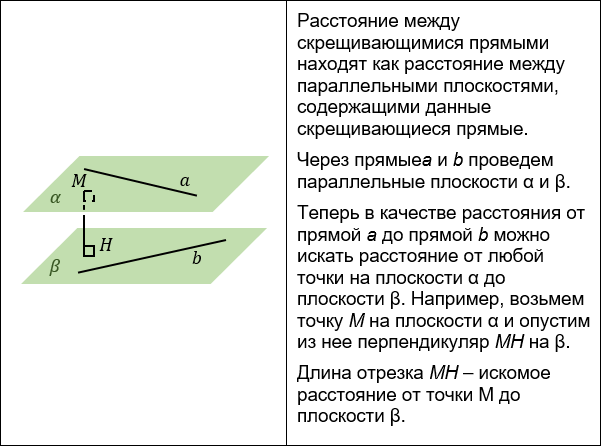
РАССТОЯНИЕ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ
Существует несколько способов нахождения расстояния между скрещивающимися прямыми:
1. Построение взаимного перпендикуляра.
2. Построение параллельной прямой.
К этому способу обращаются, если строить взаимный перпендикуляр неудобно и одна из скрещивающихся прямых уже заключена в удобную плоскость.
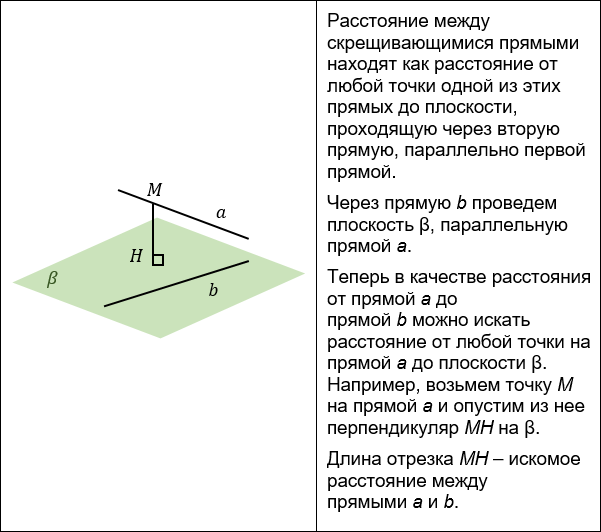
3. Построение параллельной плоскости.
vlsho547
Вопрос по геометрии:
Помогите найти расстояние от точки О до стороны АС

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
sadelatser
Расстоянием от точки до прямой является длина перпендикуляра, проведенного из этой точки к этой прямой. Проведем перпендикуляр ОР.
По условию МО и ON — серединные перпендикуляры к сторонам треугольника ABC. Значит точка О — центр окружности, описанной около треугольника ABC. Значит отрезки OB и OC равны. Значит отрезок ОС =10. Теперь рассмотрим треугольник COP. Он прямоугольный с углом 30 градусов. Значит его катет ОР равен половине гипотенузы ОС. ОР = 5. (рисунок во вложениях)

Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат — это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.