Как найти расстояние от звезды в парсеках - Исправление недочетов и поиск решений вместе с Examum.ru

Наша компания имеет богатый опыт сотрудничества и участия в тендерах с государственными и частными компаниями. Мы предлагаем большой набор готовых решений для образовательных учреждений, а также работаем по индивидуальным техническим заданиям.

Если вы являетесь участником или организатором тендера или госзакупки, заполните, пожалуйста, форму и опишите свой запрос. Наш специалист по работе с корпоративными заказчиками обязательно с вами свяжется. Вы также можете связаться с нами по телефону: +7 (812) 418-29-44 (доб. 117 или доб. 106).

Источник

Random converter

Калькуляторы
Астрономия

Калькулятор расстояния и годичного параллакса

Scheme

Калькулятор определяет расстояние до недалекой звезды в световых годах и парсеках, если известен годичный параллакс этой звезды в угловых секундах. Можно также определить параллакс, если известно расстояние.

Пример: рассчитать расстояние в световых годах до самой яркой звезды звездного неба северного полушария Арктура (α Волопаса) в созвездии Волопаса, если известно что ее параллакс равен 88.83 угловым миллисекундам.

Параллакс

Расстояние

Поделиться ссылкой на этот калькулятор, включая входные параметры

Определение параллакса и формула для расчета расстояния

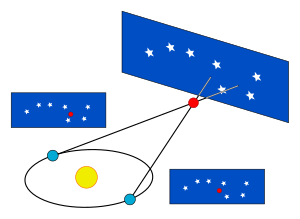
Параллакс — это изменение видимого кажущегося положения объекта, наблюдаемого с разных точек и измеренное как угол (или половинный угол) между направлениями от наблюдателя на объект. Годичный звездный параллакс — это изменение положения звезды, наблюдаемой с двух находящихся на большом расстоянии друг от друга точек. Эти две точки наблюдения расположены на земной орбите, как показано ниже. Параллакс небесного тела можно использовать для нахождения расстояния до него по формуле:

Formula

Здесь D — расстояние до небесного тела, измеренное в парсеках, и p — наблюдаемый годичный параллакс, измеренный в дуговых секундах. Эта формула и используется для расчетов в нашем калькуляторе. Парсек определяется как расстояние до объекта, годичный звездный параллакс которого равен 1 дуговой секунде. Иными словами, парсек — это расстояние, с которого диск размером в 1 а.е. будет иметь угловой размер в 1 угловую секунду.

Годичный параллакс звезды (чертеж не в масштабе); 1 — астрономическая единица (а.е.), то есть расстояние от Земли до Солнца; D — расстояние от центра земной орбиты до звезды S; p — параллакс, измеренный в угловых секундах («)

Подробнее о длине и расстоянии: измерение расстояний в космосе

Общие сведения

Космос огромен — поэтому космические расстояния измеряются не так, как это делается на Земле. В статье о длине и расстояниях мы говорили главным образом об измерении относительно небольших расстояний, которые не трудно себе представить. Однако расстояния в космосе представить себе очень трудно из-за их огромной величины, а привычные метры и километры едва ли годятся для использования в космосе. Для измерения расстояний между планетами и галактиками вряд ли можно использовать измерительные приборы типа рулетки или линейки. Спутниковая навигация в космосе тоже не работает. Поэтому для космоса придется ввести не только новые единицы измерения, но и новые методы измерения этих расстояний.

Измерения с помощью радиолокации

Расположенная на Земле радиолокационная станция (РЛС) посылает СВЧ-излучение в сторону астрономического объекта, расстояние до которого нужно вычислить. Затем измеряется время, которое необходимо, чтобы сигнал достиг объекта и вернулся назад, к РЛС. Зная это время и скорость света в вакууме, можно определить расстояние, умножая скорость на время.

Использовать РЛС для этих измерений удобно не только для определения расстояния до нужного астрономического объекта, но и для оценки скорости изменения этого расстояния (ведь объекты во Вселенной движутся друг относительно друга!). Это, в свою очередь, полезно при слежении за перемещениями объектов в космосе, например, для оценки возможности столкновения астероида с Землей.

Этот метод ограничен астрономическими объектами, которые находятся на небольших расстояниях от Земли. Можно сказать, что он пригоден для объектов, находящихся в пределах Солнечной системы. Это связано с тем, что радиосигнал ослабляется и рассеивается на больших расстояниях. Кроме того, чем больше расстояние, тем больше должен быть объект для того, чтобы его могла «увидеть» радиолокационная станция.

Годичный звездный параллакс

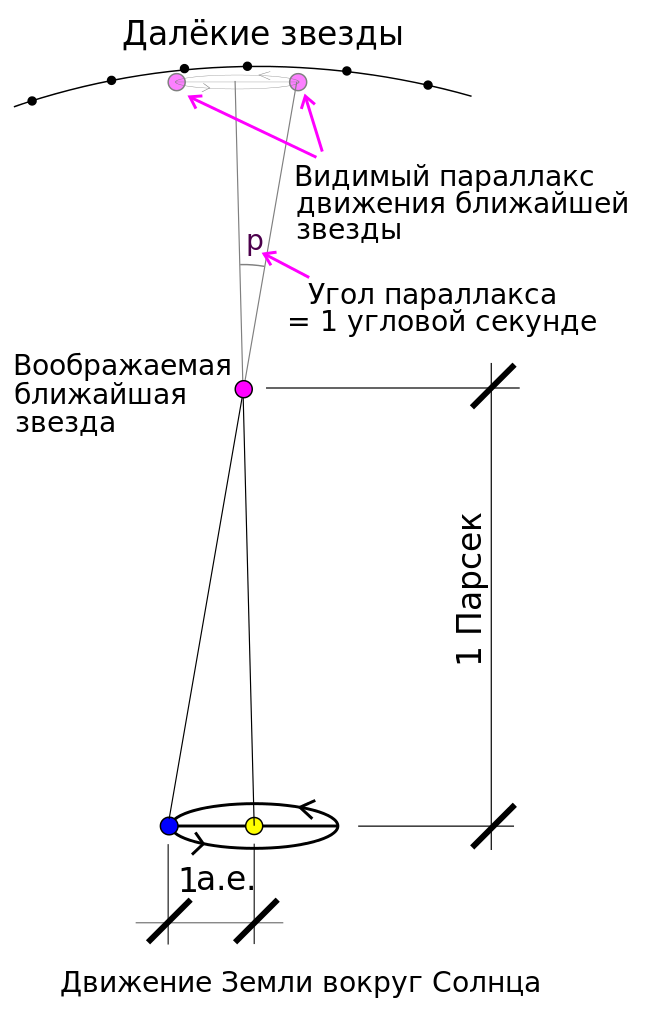
В статье о длине и расстоянии мы уже обсуждали годичный звездный параллакс. Здесь мы кратко рассмотрим это явление, потому что именно параллакс используется для измерения расстояний в космосе. Параллакс — геометрические явление, используемое для определения расстояний. Он хорошо выражен, если наблюдать объект с разных точек зрения относительно удаленного фона. Познать суть параллакса достаточно легко: вытяните перед собой палец или карандаш и закройте один глаз. Отметьте насколько далеко этот палец от другого объекта (скажем, от дерева, если вы на улице, или от шкафа, если вы находитесь в помещении). Теперь закройте этот глаз и откройте другой. Заметили, что палец или карандаш переместился относительно удаленного объекта? Это перемещение и является параллаксом. Если проделать аналогичный эксперимент, удерживая палец ближе к глазам, можно заметить, что расстояние, на которое перемещается палец или карандаш относительно удаленного объекта, стало больше. Чем ближе палец к глазам, тем больше он сдвигается относительно удаленного объекта при рассматривании пальца обоими глазами. Понятно, что это явление можно использовать для измерения расстояния до объекта, в данном случае — пальца.

На этом рисунке два положения Земли обозначены голубыми кружками, а Солнце — оранжевое. А — реальное положение звезды, расстояние до которой необходимо измерить. А2 и А3 — кажущиеся положения этой звезды с двух точек наблюдения относительно удаленной белой звезды DS. Р — параллактический угол. Измеряемое расстояние между Солнцем и звездой, обозначенное оранжевой линией AS, равно одному парсеку, если угол Р равен одной дуговой секунде.

Более подробное математическое объяснение измерения расстояний с помощью параллакса приводится в статье о длине и расстоянии. В общем случае, можно сказать, что расстояния следует измерять, когда Земля находится в двух противоположных точках ее орбиты вокруг Солнца (с интервалом в шесть месяцев, так как Земля делает один оборот вокруг Солнца за один год). Мы используем известное расстояние от Земли до Солнца (точно измеренное и называемое астрономической единицей) и измерим угол, образованный линией, соединяющей Землю в точке первого измерения, звезду, расстояние до которой измеряется, и точкой, в которой находится Земля во время второго измерения. Фактически, нам нужно знать только половину этого угла, которая называется параллактическим углом и обозначена на рисунке буквой P. Таким образом, имеется достаточно информации, чтобы рассчитать расстояние от Земли до звезды с помощью тригонометрических уравнений.

С помощью описанного метода можно измерить расстояние в различных единицах длины, но астрономы предпочитают парсек. Один парсек — это расстояние от Солнца до рассматриваемой звезды, если параллактический угол равен 1 дуговой секунде. Другой единицей длины является световой год (1 парсек = 3,26 светового года), однако эту единицу чаще используют журналисты. Астрономы предпочитают парсеки.

Четыре звезды имеют один и тот же размер, но расположены на разных расстояниях от нас. Звезда в положении 1 находится ближе всего, а звезда в положении 4 на максимальном удалении от нас. В результате мы видим ближние к нам звезды как более яркие, а удаленные — как менее яркие. Если известная их реальная яркость, можно сравнить ее с их кажущейся яркостью и, таким образом, узнать расстояние до них

Как и при радиолокационных измерениях, этот метод ограничен расстоянием, на которое удалена звезда. Если она слишком далеко (более 500 парсеков), то угол, который нужно измерить, слишком мал и измерить его практически невозможно. Поэтому для больших расстояний данный метод не работает.

Цефеиды

Для измерения расстояний в космосе можно использовать определенные типы звезд, называемых Цефеидами. Цефеида — пульсирующая звезда с точной зависимостью светимости (яркости) от периода пульсации. Чем больше этот период, тем выше яркость Цефеид. Эта корреляция между периодом пульсации я светимостью хорошо известна и все Цефеиды ведут себя одинаково. Поэтому, если известен период пульсации, который несложно наблюдать, можно измерить светимость звезды. Мы знаем, что чем дальше звезда, тем меньше ее яркость. Таким образом, если сравнить реальную яркость с кажущейся, можно определить расстояние до звезды.

Пульсация цефеид обусловлена их сжатием и расширением. При этом их яркость изменяется, и для определения периода нужно измерить время между точками с максимальной яркостью. Ядро звезды не изменяет размеры, однако их внешние газовые слои расширяются и сжимаются вследствие флуктуаций давления газа в этих слоях. Сжатие и расширение происходит за счет двух сил: гравитационного притяжения, которое приводит к сближению молекул газа в направлении центра звезды, и давления газа, которое приводит к расширению внешнего слоя.

Схематическое изображение пульсирующей Цефеиды с периодом в два дня. Пики светимости 1 декабря 2010 г., когда звезда начинает постепенно терять яркость. 2 декабря яркость минимальная. Затем звезда снова достигает максимальной светимости 3 декабря и уменьшает светимость 4 декабря и так далее

Когда звезда находится в сжатом состоянии, ее фотоны имеют высокую энергию и в результате давление повышается, что приводит к расширению внешней оболочки звезды. Когда это давление падает и становится меньше гравитационных сил, сжимающих оболочку, звезда сжимается. Затем процесс повторяется.

Цефеиды можно использовать для измерения расстояний до 40 миллионов парсеков, то есть намного больших, чем позволяет метод параллакса. Недостаток метода — цефеиды не так уж часто встречаются.

Сверхновая типа Ia

Еще одним стандартным измерителем расстояния являются сверхновые типа Ia. Идея аналогичная использованию Цефеид: при известной реальной светимости сверхновой в момент взрыва, когда яркость максимальна, можно сравнить ее с видимой яркостью звезды и, таким образом, определить насколько далеко она от нас. Именно эта категория сверхновых интересует нас в связи с тем, что они наиболее хорошо изучены, а их поведение предсказуемо, поэтому максимальная светимость во время взрыва хорошо известна. Эти взрывы происходит с двумя астрономическими объектами — с белыми карликами и еще одним белым карликом или со звездой-гигантом. Белый карлик представляет собой звезду очень высокой плотности в конце ее жизненного цикла, когда эта звезда «всасывает» материю находящихся рядом звезд (в нашем случае — второй звезды) до тех пор, пока не взорвется. Эти взрывы сверхновых позволяет измерять расстояния до галактик, в которых они находятся.

Другие методы измерения расстояний

Имеется еще несколько методов измерения расстояний в космосе. Один из них основан на предположении, что вселенная расширяется с известной скоростью. Если известна скорость, с которой галактики удаляются от нашей галактики, то с помощью закона Хаббла можно рассчитать насколько далеко они от нас. Закон Хаббла гласит, что расстояние до галактики равно скорости галактики, деленной на постоянную Хаббла, которая является известной константой. Скорость галактики можно определить, изучая спектр галактики, а затем, учитывая эффект Доплера, можно определить расстояние. Эффект Доплера, более известный в астрономии как смещение Доплера — это изменение частоты электромагнитного излучения (в нашем случае — света), излучаемого объектом, который движется относительно наблюдателя. При движении в сторону от наблюдателя этот спектр сдвигается в сторону низких частот, то есть в красную сторону, причем степень сдвига зависит от скорости удаления галактики. По смещению можно рассчитать скорость, а затем вычислить расстояние.

Примеры расчета расстояния до некоторых звезд и их звездного параллакса

Параллакс в дуговых миллисекундах и расстояние в световых годах

Канопус (α Киля)

Ригель Кентаурус (α Центавра A)

Сириус (α Большого Пса)

Вега (α Лиры)

Капелла (α Возничего)

Ригель (β Ориона)

Альтаир (α Орла)

Альдебаран (α Тельца)

Антарес (α Скорпиона)

Арктур (α Волопаса)

Unit Converter articles were edited and illustrated by Анатолий Золотков

Источник

From Wikipedia, the free encyclopedia

Parsec
A parsec is the distance from the Sun to an astronomical object that has a parallax angle of one arcsecond (not to scale)
General information
Unit system	astronomical units
Unit of	length/distance
Symbol	pc
Conversions
1 pc in …	… is equal to …
metric (SI) units	3.0857×10¹⁶ m ~31 petametres
imperial & US units	1.9174×10¹³ mi
astronomical units	2.06265×10⁵ au 3.26156 ly

The parsec (symbol: pc) is a unit of length used to measure the large distances to astronomical objects outside the Solar System, approximately equal to 3.26 light-years or 206,265 astronomical units (au), i.e. 30.9 trillion kilometres (19.2 trillion miles).^[a] The parsec unit is obtained by the use of parallax and trigonometry, and is defined as the distance at which 1 au subtends an angle of one arcsecond^[1] (1/3600 of a degree). This corresponds to 648000/π astronomical units, i.e. 1 pc = 1 au/tan(1 arcsec).^[2] The nearest star, Proxima Centauri, is about 1.3 parsecs (4.2 light-years) from the Sun.^[3] Most stars visible to the naked eye are within a few hundred parsecs of the Sun, with the most distant at a few thousand.^[4]

The word parsec is a portmanteau of «parallax of one second» and was coined by the British astronomer Herbert Hall Turner in 1913^[5] to make calculations of astronomical distances from only raw observational data easy for astronomers. Partly for this reason, it is the unit preferred in astronomy and astrophysics, though the light-year remains prominent in popular science texts and common usage. Although parsecs are used for the shorter distances within the Milky Way, multiples of parsecs are required for the larger scales in the universe, including kiloparsecs (kpc) for the more distant objects within and around the Milky Way, megaparsecs (Mpc) for mid-distance galaxies, and gigaparsecs (Gpc) for many quasars and the most distant galaxies.

In August 2015, the International Astronomical Union (IAU) passed Resolution B2 which, as part of the definition of a standardized absolute and apparent bolometric magnitude scale, mentioned an existing explicit definition of the parsec as exactly 648000/π au, or approximately 30.856775814913673×10¹⁵ metres (based on the IAU 2012 exact SI definition of the astronomical unit). This corresponds to the small-angle definition of the parsec found in many astronomical references.^[6]^[7]

History and derivation[edit]

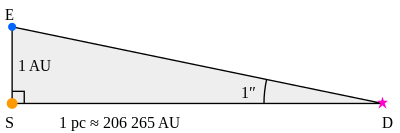
The parsec is defined as being equal to the length of the adjacent leg (opposite leg being 1 AU) of an extremely elongated imaginary right triangle in space. The two dimensions on which this triangle is based are its shorter leg, of length one astronomical unit (the average Earth-Sun distance), and the subtended angle of the vertex opposite that leg, measuring one arcsecond. Applying the rules of trigonometry to these two values, the unit length of the other leg of the triangle (the parsec) can be derived.

One of the oldest methods used by astronomers to calculate the distance to a star is to record the difference in angle between two measurements of the position of the star in the sky. The first measurement is taken from the Earth on one side of the Sun, and the second is taken approximately half a year later, when the Earth is on the opposite side of the Sun. The distance between the two positions of the Earth when the two measurements were taken is twice the distance between the Earth and the Sun. The difference in angle between the two measurements is twice the parallax angle, which is formed by lines from the Sun and Earth to the star at the distant vertex. Then the distance to the star could be calculated using trigonometry.^[8] The first successful published direct measurements of an object at interstellar distances were undertaken by German astronomer Friedrich Wilhelm Bessel in 1838, who used this approach to calculate the 3.5-parsec distance of 61 Cygni.^[9]

Stellar parallax motion from annual parallax

The parallax of a star is defined as half of the angular distance that a star appears to move relative to the celestial sphere as Earth orbits the Sun. Equivalently, it is the subtended angle, from that star’s perspective, of the semimajor axis of the Earth’s orbit. The star, the Sun and the Earth form the corners of an imaginary right triangle in space: the right angle is the corner at the Sun, and the corner at the star is the parallax angle. The length of the opposite side to the parallax angle is the distance from the Earth to the Sun (defined as one astronomical unit, au), and the length of the adjacent side gives the distance from the sun to the star. Therefore, given a measurement of the parallax angle, along with the rules of trigonometry, the distance from the Sun to the star can be found. A parsec is defined as the length of the side adjacent to the vertex occupied by a star whose parallax angle is one arcsecond.

The use of the parsec as a unit of distance follows naturally from Bessel’s method, because the distance in parsecs can be computed simply as the reciprocal of the parallax angle in arcseconds (i.e. if the parallax angle is 1 arcsecond, the object is 1 pc from the Sun; if the parallax angle is 0.5 arcseconds, the object is 2 pc away; etc.). No trigonometric functions are required in this relationship because the very small angles involved mean that the approximate solution of the skinny triangle can be applied.

Though it may have been used before, the term parsec was first mentioned in an astronomical publication in 1913. Astronomer Royal Frank Watson Dyson expressed his concern for the need of a name for that unit of distance. He proposed the name astron, but mentioned that Carl Charlier had suggested siriometer and Herbert Hall Turner had proposed parsec.^[5] It was Turner’s proposal that stuck.

Calculating the value of a parsec[edit]

By the 2015 definition, 1 au of arc length subtends an angle of 1″ at the center of the circle of radius 1 pc. That is, 1 pc = 1 au/tan(1″) ≈ 206,264.8 au by definition.^[10] Converting from degree/minute/second units to radians,

${displaystyle {frac {1{text{ pc}}}{1{text{ au}}}}={frac {180times 60times 60}{pi }}}$

, and

{displaystyle 1{text{ au}}=149,597,870,700{text{ m}}}

(exact by the 2012 definition of the au)

Therefore,

{displaystyle pi ~mathrm {pc} =180times 60times 60~mathrm {au} =180times 60times 60times 149,597,870,700~mathrm {m} =96,939,420,213,600,000~mathrm {m} }

(exact by the 2015 definition)

Therefore,

${displaystyle 1~mathrm {pc} ={frac {96,939,420,213,600,000}{pi }}~mathrm {m} =30,856,775,814,913,673~mathrm {m} }$

(to the nearest metre)

Approximately,

In the diagram above (not to scale), S represents the Sun, and E the Earth at one point in its orbit. Thus the distance ES is one astronomical unit (au). The angle SDE is one arcsecond (1/3600 of a degree) so by definition D is a point in space at a distance of one parsec from the Sun. Through trigonometry, the distance SD is calculated as follows:

${displaystyle {begin{aligned}mathrm {SD} &={frac {mathrm {ES} }{tan 1''}}\&={frac {mathrm {ES} }{tan left({frac {1}{60times 60}}times {frac {pi }{180}}right)}}\&approx {frac {1,mathrm {au} }{{frac {1}{60times 60}}times {frac {pi }{180}}}}={frac {648,000}{pi }},mathrm {au} approx 206,264.81~mathrm {au} .end{aligned}}}$

Because the astronomical unit is defined to be 149597870700 m,^[11] the following can be calculated:

Therefore, 1 parsec	≈ 206264.806247096 astronomical units
≈ 3.085677581×10¹⁶ metres
≈ 30.856775815 trillion kilometres
≈ 19.173511577 trillion miles

Therefore, if 1 ly ≈ 9.46×10¹⁵ m,

Then 1 pc ≈ 3.261563777 ly

A corollary states that a parsec is also the distance from which a disc one astronomical unit in diameter must be viewed for it to have an angular diameter of one arcsecond (by placing the observer at D and a diameter of the disc on ES).

Mathematically, to calculate distance, given obtained angular measurements from instruments in arcseconds, the formula would be:

${displaystyle {text{Distance}}_{text{star}}={frac {{text{Distance}}_{text{earth-sun}}}{tan {frac {theta }{3600}}}}}$

where θ is the measured angle in arcseconds, Distance_earth-sun is a constant (1 au or 1.5813×10⁻⁵ ly). The calculated stellar distance will be in the same measurement unit as used in Distance_earth-sun (e.g. if Distance_earth-sun = 1 au, unit for Distance_star is in astronomical units; if Distance_earth-sun = 1.5813×10⁻⁵ ly, unit for Distance_star is in light-years).

The length of the parsec used in IAU 2015 Resolution B2^[12] (exactly 648000/π astronomical units) corresponds exactly to that derived using the small-angle calculation. This differs from the classic inverse-tangent definition by about 200 km, i.e. only after the 11th significant figure. As the astronomical unit was defined by the IAU (2012) as an exact SI length in metres, so now the parsec corresponds to an exact SI length in metres. To the nearest meter, the small-angle parsec corresponds to 30856775814913673 m.

Usage and measurement[edit]

The parallax method is the fundamental calibration step for distance determination in astrophysics; however, the accuracy of ground-based telescope measurements of parallax angle is limited to about 0.01″, and thus to stars no more than 100 pc distant.^[13] This is because the Earth’s atmosphere limits the sharpness of a star’s image.^{[citation needed]} Space-based telescopes are not limited by this effect and can accurately measure distances to objects beyond the limit of ground-based observations. Between 1989 and 1993, the Hipparcos satellite, launched by the European Space Agency (ESA), measured parallaxes for about 100000 stars with an astrometric precision of about 0.97 mas, and obtained accurate measurements for stellar distances of stars up to 1000 pc away.^[14]^[15]

ESA’s Gaia satellite, which launched on 19 December 2013, is intended to measure one billion stellar distances to within 20 microarcsecond, producing errors of 10% in measurements as far as the Galactic Centre, about 8000 pc away in the constellation of Sagittarius.^[16]

Distances in parsecs[edit]

Distances less than a parsec[edit]

Distances expressed in fractions of a parsec usually involve objects within a single star system. So, for example:

One astronomical unit (au), the distance from the Sun to the Earth, is just under 5×10⁻⁶ pc.
The most distant space probe, Voyager 1, was 0.000703 pc from Earth as of January 2019. Voyager 1 took 41 years to cover that distance.
The Oort cloud is estimated to be approximately 0.6 pc in diameter

Parsecs and kiloparsecs[edit]

Distances expressed in parsecs (pc) include distances between nearby stars, such as those in the same spiral arm or globular cluster. A distance of 1,000 parsecs (3,262 ly) is denoted by the kiloparsec (kpc). Astronomers typically use kiloparsecs to express distances between parts of a galaxy, or within groups of galaxies. So, for example (NB one parsec is approximately equal to 3.26 light-years):

Proxima Centauri, the nearest known star to earth other than the sun, is about 1.3 parsecs (4.24 ly) away, by direct parallax measurement.
The distance to the open cluster Pleiades is 130±10 pc (420±30 ly) from us, per Hipparcos parallax measurement.
The centre of the Milky Way is more than 8 kiloparsecs (26,000 ly) from the Earth, and the Milky Way is roughly 34 kiloparsecs (110,000 ly) across.
The Andromeda Galaxy (M31) is about 780 kpc (2.5 million ly) away from the Earth.

Megaparsecs and gigaparsecs[edit]

Astronomers typically express the distances between neighbouring galaxies and galaxy clusters in megaparsecs (Mpc). A megaparsec is one million parsecs, or about 3,260,000 light years.^[17] Sometimes, galactic distances are given in units of Mpc/h (as in «50/h Mpc», also written «50 Mpc h⁻¹«). h is a constant (the «dimensionless Hubble constant») in the range 0.5 < h < 0.75 reflecting the uncertainty in the value of the Hubble constant H for the rate of expansion of the universe: h = H/100 (km/s)/Mpc. The Hubble constant becomes relevant when converting an observed redshift z into a distance d using the formula d ≈ c/H × z.^[18]

One gigaparsec (Gpc) is one billion parsecs — one of the largest units of length commonly used. One gigaparsec is about 3.26 billion ly, or roughly 1/14 of the distance to the horizon of the observable universe (dictated by the cosmic background radiation). Astronomers typically use gigaparsecs to express the sizes of large-scale structures such as the size of, and distance to, the CfA2 Great Wall; the distances between galaxy clusters; and the distance to quasars.

For example:

The Andromeda Galaxy is about 0.78 Mpc (2.5 million ly) from the Earth.
The nearest large galaxy cluster, the Virgo Cluster, is about 16.5 Mpc (54 million ly) from the Earth.^[19]
The galaxy RXJ1242-11, observed to have a supermassive black hole core similar to the Milky Way’s, is about 200 Mpc (650 million ly) from the Earth.
The galaxy filament Hercules–Corona Borealis Great Wall, currently the largest known structure in the universe, is about 3 Gpc (9.8 billion ly) across.
The particle horizon (the boundary of the observable universe) has a radius of about 14 Gpc (46 billion ly).^[20]

Volume units[edit]

To determine the number of stars in the Milky Way, volumes in cubic kiloparsecs^[b] (kpc³) are selected in various directions. All the stars in these volumes are counted and the total number of stars statistically determined. The number of globular clusters, dust clouds, and interstellar gas is determined in a similar fashion. To determine the number of galaxies in superclusters, volumes in cubic megaparsecs^[b] (Mpc³) are selected. All the galaxies in these volumes are classified and tallied. The total number of galaxies can then be determined statistically. The huge Boötes void is measured in cubic megaparsecs.^[21]

In physical cosmology, volumes of cubic gigaparsecs^[b] (Gpc³) are selected to determine the distribution of matter in the visible universe and to determine the number of galaxies and quasars. The Sun is currently the only star in its cubic parsec,^[b] (pc³) but in globular clusters the stellar density could be from 100–1000 pc⁻³.

The observational volume of gravitational wave interferometers (e.g., LIGO, Virgo) is stated in terms of cubic megaparsecs^[b] (Mpc³) and is essentially the value of the effective distance cubed.

In popular culture[edit]

The parsec was seemingly used incorrectly as a measurement of time by Han Solo in the first Star Wars film, when he claimed his ship, the Millennium Falcon «made the Kessel Run in less than 12 parsecs». The claim was repeated in The Force Awakens, but this was changed in Solo: A Star Wars Story, by stating the Millennium Falcon traveled a shorter distance (as opposed to a quicker time) due to a more dangerous route through the Kessel Run, enabled by its speed and maneuverability.^[22] It is also used ambiguously as a spatial unit in The Mandalorian as opposed to a unit of distance.^[23]

In the book A Wrinkle in Time, «Megaparsec» is Mr. Murry’s nickname for his daughter Meg.^[24]

Notes[edit]

^ One trillion here is short scale, ie. 10¹² (one million million, or billion in long scale).
^ ^a ^b ^c ^d ^e

1 pc³ ≈ 2.938×10⁴⁹ m³

1 kpc³ ≈ 2.938×10⁵⁸ m³

1 Mpc³ ≈ 2.938×10⁶⁷ m³

1 Gpc³ ≈ 2.938×10⁷⁶ m³

1 Tpc³ ≈ 2.938×10⁸⁵ m³

References[edit]

^ «Cosmic Distance Scales – The Milky Way». Retrieved 24 September 2014.
^ B. Luque; F. J. Ballesteros (2019). «To the Sun and beyond». Nature Physics. 15 (12): 1302. Bibcode:2019NatPh..15.1302L. doi:10.1038/s41567-019-0685-3.
^ Benedict, G. F.; et al. «Astrometric Stability and Precision of Fine Guidance Sensor #3: The Parallax and Proper Motion of Proxima Centauri» (PDF). Proceedings of the HST Calibration Workshop. pp. 380–384. Retrieved 11 July 2007.
^ «Farthest Stars». StarDate. University of Texas at Austin. 15 May 2021. Retrieved 5 September 2021.
^ ^a ^b Dyson, F. W. (March 1913). «The distribution in space of the stars in Carrington’s Circumpolar Catalogue». Monthly Notices of the Royal Astronomical Society. 73 (5): 342. Bibcode:1913MNRAS..73..334D. doi:10.1093/mnras/73.5.334. [paragraph 14, page 342] Taking the unit of distance R* to be that corresponding to a parallax of 1″·0 [… Footnote:]
* There is need for a name for this unit of distance. Mr. Charlier has suggested Siriometer, but if the violence to the Greek language can be overlooked, the word Astron might be adopted. Professor Turner suggests Parsec, which may be taken as an abbreviated form of «a distance corresponding to a parallax of one second».
^ Cox, Arthur N., ed. (2000). Allen’s Astrophysical Quantities (4th ed.). New York: AIP Press / Springer. Bibcode:2000asqu.book…..C. ISBN 978-0387987460.
^ Binney, James; Tremaine, Scott (2008). Galactic Dynamics (2nd ed.). Princeton, NJ: Princeton University Press. Bibcode:2008gady.book…..B. ISBN 978-0-691-13026-2.
^ High Energy Astrophysics Science Archive Research Center (HEASARC). «Deriving the Parallax Formula». NASA’s Imagine the Universe!. Astrophysics Science Division (ASD) at NASA’s Goddard Space Flight Center. Retrieved 26 November 2011.
^ Bessel, F. W. (1838). «Bestimmung der Entfernung des 61sten Sterns des Schwans» [Determination of the distance of the 61st star of Cygnus]. Astronomische Nachrichten. 16 (5): 65–96. Bibcode:1838AN…..16…65B. doi:10.1002/asna.18390160502. Archived from the original on 24 June 2007.
^ B. Luque; F. J. Ballesteros (2019). «Title: To the Sun and beyond». Nature Physics. 15 (12): 1302. Bibcode:2019NatPh..15.1302L. doi:10.1038/s41567-019-0685-3.
^ International Astronomical Union, ed. (31 August 2012), «RESOLUTION B2 on the re-definition of the astronomical unit of length» (PDF), RESOLUTION B2, Beijing: International Astronomical Union, The XXVIII General Assembly of the International Astronomical Union recommends [adopted] that the astronomical unit be redefined to be a conventional unit of length equal to exactly 149597870700 m, in agreement with the value adopted in IAU 2009 Resolution B2
^ International Astronomical Union, ed. (13 August 2015), «RESOLUTION B2 on recommended zero points for the absolute and apparent bolometric magnitude scales» (PDF), RESOLUTION B2, Honolulu: International Astronomical Union, The XXIX General Assembly of the International Astronomical Union notes [4] that the parsec is defined as exactly (648 000/) au per the AU definition in IAU 2012 Resolution B2
^ Pogge, Richard. «Astronomy 162». Ohio State University.
^ «The Hipparcos Space Astrometry Mission». Retrieved 28 August 2007.
^ Turon, Catherine. «From Hipparchus to Hipparcos».
^ «GAIA». European Space Agency.
^ «Why is a parsec 3.26 light-years?». Astronomy.com. 1 February 2020. Retrieved 20 July 2021.{{cite web}}: CS1 maint: url-status (link)
^ «Galaxy structures: the large scale structure of the nearby universe». Archived from the original on 5 March 2007. Retrieved 22 May 2007.
^ Mei, S.; Blakeslee, J. P.; Côté, P.; et al. (2007). «The ACS Virgo Cluster Survey. XIII. SBF Distance Catalog and the Three-dimensional Structure of the Virgo Cluster». The Astrophysical Journal. 655 (1): 144–162. arXiv:astro-ph/0702510. Bibcode:2007ApJ…655..144M. doi:10.1086/509598. S2CID 16483538.
^ Lineweaver, Charles H.; Davis, Tamara M. (1 March 2005). «Misconceptions about the Big Bang». Scientific American. 292 (3): 36–45. Bibcode:2005SciAm.292c..36L. doi:10.1038/scientificamerican0305-36. Archived from the original on 10 August 2011. Retrieved 4 February 2016.
^ Kirshner, R. P.; Oemler, A. Jr.; Schechter, P. L.; Shectman, S. A. (1981). «A million cubic megaparsec void in Bootes». The Astrophysical Journal. 248: L57. Bibcode:1981ApJ…248L..57K. doi:10.1086/183623. ISSN 0004-637X.
^ «‘Solo’ Corrected One of the Most Infamous ‘Star Wars’ Plot Holes». Esquire. 30 May 2018.
^ Choi, Charlse (5 November 2019). «‘Star Wars’ Gets the Parsec Wrong Again in ‘The Mandalorian’«. space.com. Retrieved 6 May 2020.
^ «In «A Wrinkle in Time,» what is Mr. Murry’s nickname for Meg?». Retrieved 6 May 2020.

External links[edit]

Guidry, Michael. «Astronomical Distance Scales». Astronomy 162: Stars, Galaxies, and Cosmology. University of Tennessee, Knoxville. Archived from the original on 12 December 2012. Retrieved 26 March 2010.
Merrifield, Michael. «pc Parsec». Sixty Symbols. Brady Haran for the University of Nottingham.

Источник

Парсек – космическая единица измерения, при помощи которой астрономы определяют расстояние к особо отдаленным объектам во Вселенной.

Содержание:

1 Общие сведения
2 История открытия
3 Материалы по теме
4 Как определить парсек
5 Самые популярные примеры расстояний в парсеках
6 О расстояниях наглядно. Нажмите кнопку «Старт»

Общие сведения

Парсек (сокращенное «параллакс секунда») – это внесистемная единица измерений, при помощи которой в космологии измеряют расстояния к особенно отдаленным объектам космического пространства. Данная единица выполняет не только практическую функцию – помогает вычислить расстояние к тому или иному объекту во Вселенной, но и создает астрономам своеобразный комфорт. Судите сами, гораздо проще сказать, что расстояние от Солнца к ближайшей звезде равно 1,3 парсека, чем то, что оно равно 40,7 триллионов километров. Человек, который бы регулярно оперировал цифрами с таким огромным количеством нулей, рано или поздно бы сошел с ума. Таким образом, придумав парсек, ученые значительно упростили вычислительные процессы в астрономии.

Парсек

Парсек – популярная единица измерения в астрофизике. Любителям этой науки хорошо известно, что она равна 3,2616 световым годам. Многие из них свободно могут назвать расстояние к тому или другому отдаленному объекту в парсеках. Но, к сожалению, далеко не все понимают, как появилась на свет данная единица измерения и как ее правильно вычислять.

История открытия

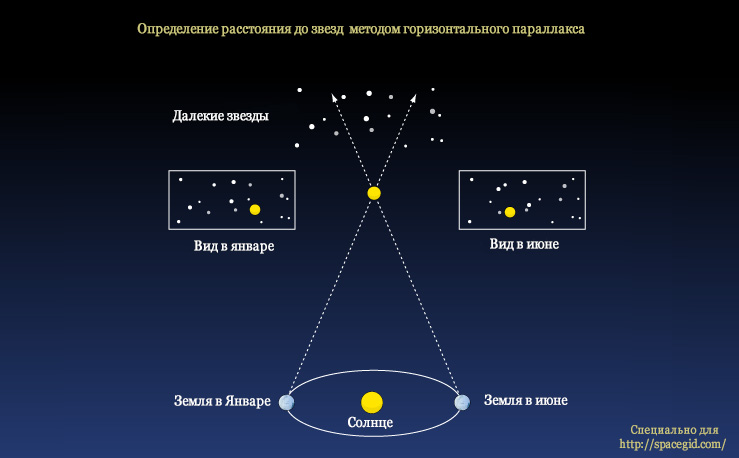
Если расстояния к близким объектам в космосе можно измерить при помощи радиотелескопа с точностью до нескольких сантиметров, то измерить расстояние к удаленным уголкам Вселенной намного сложнее. Тем не менее, ученым нужно было найти способ, как вычислить данную величину и они решили воспользоваться методом горизонтального параллакса, который хорошо известен в геометрии.

Материалы по теме

Суть метода горизонтального параллакса проста: если смотреть на отдаленный объект с разных мест, то на фоне других, более далеких объектов он будет менять свое положение. Зная расстояние между местами, с которых ведется наблюдение, а также угол смещения объекта на фоне отдаленных предметов, можно вычислить расстояние к нему путем геометрических подсчетов. Этой аксиомой решили воспользоваться астрономы; она послужила основой для открытия новой единицы измерения – парсек.

Как определить парсек

Допустим, вы смотрите на звезду и хотите определить расстояние к ней в парсеках. Но для этого вам необходимо знать, что собой являет расстояние в 1 парсек. Данное расстояние представляет собой смещение небесного тела на фоне других, более далеких объектов на угол равный одной угловой секунде при перемещении наблюдателя на половину диаметра земной орбиты.

Кому-то такое определение может показаться сложным для восприятия. В действительности суть определения парсека понять не так уж трудно. Возвращаясь к нашей звезде, расстояние в парсеках к которой мы хотим определить, нам придется произвести два наблюдения за этим объектом с разных точек земной орбиты. Сделать это можно без каких-нибудь космических приборов, а просто дождавшись, когда Земля сама пройдет половину своего годичного пути и станет на противоположную сторону Солнца.

Собственное движение 61 Лебедя за год

Зная длину между точками, откуда производились наблюдения (она равна 1 астрономической единице – расстоянию Земли от Солнца или радиусу орбиты Земли), а также смещение звезды на фоне более дальних звезд и галактик, мы можем вычислить расстояние к ней. Если в наблюдаемом диапазоне звезда сместилась на 1 угловую секунду, расстояние к ней составляет один парсек, если же она сместилась на полсекунды – два парсека. Вопреки догадкам, чем меньше параллакс (смещение) небесного тела, тем больше к нему парсеков.

Самые популярные примеры расстояний в парсеках

Ближайшая к Солнцу звезда Проксима Центавра удалена от него на расстояние 1,3 парсека (пк);
Диаметр нашей галактики Млечный Путь составляет 30 тыс. пк или 30 килопарсеков;
1 астрономическая единица при переводе в парсеки представляет собой очень маленькое число – всего 4,848·10⁻⁶парсека;
Расстояние к ближайшей к нам галактике Андромеда равно 0,77 мегапарсек или 770 000 парсек;
1 парсек равен 30,8568 трлн. км.;
Согласно современным представлениям возраст вселенной 13.7 млрд. лет, а за это время Вселенная увеличилась в размерах до 27 млрд. парсек из-за того, что расширение пространства идет быстрее скорости света.

О расстояниях наглядно. Нажмите кнопку «Старт»

Источник

Наше Солнце справедливо называют типичной звездой, но среди огромного многообразия мира звёзд есть немало таких, которые значительно отличаются от него по физическим характеристикам. Поэтому более полное представление о звёздах даёт такое определение:

звезда — это пространственно обособленный, гравитационно связанный, непрозрачный для излучения космический объект, в котором в значительных масштабах происходили, происходят или будут происходить термоядерные реакции превращения водорода в гелий.

Солнце существует уже несколько миллиардов лет и мало изменилось за это время, поскольку в его недрах всё ещё происходят термоядерные реакции, в результате которых из четырёх протонов (ядер водорода) образуется альфа-частица (ядро гелия, состоящее из двух протонов и двух нейтронов). Более массивные звёзды расходуют запасы водорода значительно быстрее (за десятки миллионов лет). После того как водород израсходован, начинаются реакции между ядрами гелия с образованием устойчивого изотопа углерода-12 и другие реакции, продуктами которых являются кислород и тяжёлые элементы (натрий, сера, магний и т. д.). Таким образом, в недрах звёзд образуются ядра многих химических элементов, вплоть до железа.

У наиболее массивных звёзд прекращение всех возможных термоядерных реакций сопровождается мощным взрывом, который наблюдается как вспышка сверхновой звезды.

Все элементы, которые входят в состав нашей планеты и всего живого на ней, образовались в результате термоядерных реакций, происходивших в звёздах, поэтому звёзды не только самые распространённые во Вселенной объекты, но и самые важные для понимания происходящих в ней явлений и процессов.

Именно термоядерные реакции являются характерной отличительной особенностью звёзд от планет. Поэтому современное определение планеты формулируется так:

планета — небесное тело, обращающееся вокруг звезды или остатка звезды, достаточно массивное, чтобы приобрести сферическую форму под действием собственной гравитации, и своим воздействием удалившее малые тела с орбиты, близкой к собственной, но при этом в её недрах не происходят и никогда не происходили реакции термоядерного синтеза.

Мысли о том, что звёзды — это далёкие солнца, высказывались ещё в глубокой древности. Однако долгое время оставалось неясным, как далеко они находятся от Земли. Ещё Аристотель понимал, что если Земля движется, то, наблюдая положение какой-либо звезды из двух диаметрально противоположных точек земной орбиты, можно заметить, что направление на звезду изменится (рис. 5.12). Это кажущееся (параллактическое) смещение звезды будет служить мерой расстояния до неё: чем оно больше, тем ближе к нам расположена звезда. Но не только самому Аристотелю, но даже значительно позднее Копернику не удалось обнаружить это смещение. Только в конце первой половины XIX в., когда телескопы были оборудованы приспособлениями для точных угловых измерений, удалось измерить такое смещение у ближайших звёзд.

Рис. 5.12. Параллактическое смещение звезды

Рис. 5.13. Годичный параллакс звезды

Годичным параллаксом звезды p называется угол, под которым со звезды можно было бы видеть большую полуось земной орбиты (равную 1 а. е.), перпендикулярную направлению на звезду (рис. 5.13).

Расстояние до звезды

D = ,

где a — большая полуось земной орбиты. Заменив синус малого угла величиной самого угла, выраженной в радианной мере, и приняв a = 1 а. е., получим следующую формулу для вычисления расстояния до звезды в астрономических единицах:

D = .

В 1837 г. впервые были осуществлены надёжные измерения годичного параллакса. Русский астроном Василий Яковлевич Струве (1793—1864) провёл эти измерения для ярчайшей звезды Северного полушария Веги (α Лиры). Почти одновременно в других странах определили параллаксы ещё двух звёзд, одной из которых была α Центавра. Эта звезда, которая с территории России не видна, оказалась ближайшей к нам. Даже у неё годичный параллакс составил всего 0,75ʺ. Под таким углом невооружённому глазу видна проволочка толщиной 1 мм с расстояния 280 м. Поэтому неудивительно, что столь малые угловые смещения так долго не могли заметить.

Расстояние до ближайшей звезды, параллакс которой p = 0,75ʺ, составляет D = = 270 000 а. е. Единицами для измерения столь значительных расстояний являются парсек и световой год.

Парсек — это такое расстояние, на котором параллакс звёзд равен 1ʺ. Отсюда и название этой единицы: пар — от слова «параллакс», сек — от слова «секунда». Расстояние в парсеках равно обратной величине годичного параллакса. Например, поскольку параллакс α Центавра равен 0,75ʺ, расстояние до неё равно 1,3 парсека.

Световой год — это такое расстояние, которое свет, распространяясь со скоростью 300 тыс. км/с, проходит за год. От ближайшей звезды свет идёт до Земли свыше четырёх лет, тогда как от Солнца около восьми минут, а от Луны немногим более одной секунды.

1 пк (парсек) = 3,26 светового года = 206 265 а. е. = 3•1013 км.

К настоящему времени с помощью специального спутника «Гиппаркос» измерены годичные параллаксы более 118 тыс. звёзд с точностью 0,001ʺ.

Таким образом, теперь измерением годичного параллакса можно надёжно определить расстояния до звёзд, удалённых от нас на 1000 пк, или 3000 св. лет. Расстояния до более далёких звёзд определяются другими методами.

После того как астрономы получили возможность определять расстояния до звёзд, выяснилось, что звёзды, находящиеся на одинаковом расстоянии, могут отличаться по видимой яркости (т. е. по блеску). Стало очевидно, что звёзды имеют различную светимость. Солнце кажется самым ярким объектом на небе только потому, что оно находится гораздо ближе всех остальных звёзд.

Светимостью называется полная энергия, излучаемая звездой в единицу времени.

Она выражается в абсолютных единицах (ваттах) или в единицах светимости Солнца.

В астрономии принято сравнивать звёзды по светимости, рассчитывая их блеск (звёздную величину) для одного и того же стандартного расстояния — 10 пк.

Видимая звёздная величина, которую имела бы звезда, если бы находилась от нас на расстоянии D0 = 10 пк, получила название абсолютной звёздной величины M.

Рассмотрим, как можно определить абсолютную звёздную величину M, зная расстояние до звезды D (или параллакс — p) и её видимую звёздную величину m. Напомним, что блеск двух источников, звёздные величины которых отличаются на единицу, отличается в 2,512 раза. Для звёзд, звёздные величины которых равны m1 и m2 соответственно, отношение их блесков I1 и I2 выражается соотношением:

I1 : I2 = .

Для видимой и абсолютной звёздных величин одной и той же звезды отношение блесков будет выглядеть так:

I : I0 = 2,512M – m,

где I0 — блеск этой звезды, если бы она находилась на расстоянии D0 = 10 пк.

В то же время известно, что блеск звезды меняется обратно пропорционально квадрату расстояния до неё. Поэтому

I : I0 = : D2.

Следовательно,

2,512M – m = : D2.

Логарифмируя это выражение, находим

0,4(M – m) = lg 102 – lg D2,

или

M = m + 5 – 5 lg D,

или

M = m + 5 + lg p.

Абсолютная звёздная величина Солнца M☉ = 5m. Иначе говоря, с расстояния 10 пк наше Солнце выглядело бы как звезда пятой звёздной величины.

Зная абсолютную звёздную величину звезды M, легко вычислить её светимость L. Считая светимость Солнца L☉ = 1, получаем:

L = 2,5125 – M,

или

lg L = 0,4(5 – M).

По светимости (мощности излучения) звёзды значительно отличаются друг от друга: некоторые излучают энергию в сотни тысяч раз больше, чем Солнце, другие — в десятки тысяч раз меньше. Абсолютные звёздные величины звёзд наиболее высокой светимости (гигантов и сверхгигантов) достигают M = –9m, а звёзды-карлики, обладающие наименьшей светимостью, имеют абсолютную звёздную величину M = +17m.

Всю информацию о звёздах можно получить только на основе исследования приходящего от них излучения. Наблюдая звёзды, можно заметить, что они имеют различный цвет. Хорошо известно, что цвет любого нагретого тела, в частности звезды, зависит от его температуры. Более полное представление об этой зависимости даёт изучение звёздных спектров. Для большинства звёзд это спектры поглощения, в которых на фоне непрерывного спектра наблюдаются тёмные линии.

Температуру наружных слоёв звезды, от которых приходит излучение, определяют по распределению энергии в непрерывном спектре (рис. 5.14), а также по интенсивности разных спектральных линий. Длина волны, на которую приходится максимум излучения, зависит от температуры излучающего тела. По мере увеличения температуры положение максимума смещается от красного к фиолетовому концу спектра. Количественно эта зависимость выражается законом Ви́на:

λmax = ,

где λmax — длина волны (в см), на которую приходится максимум излучения, а T — абсолютная температура.

Рис. 5.14. Распределение энергии в непрерывном спектре Солнца и чёрного тела при различных температурах

Как оказалось, эта температура для различных типов звёзд заключена в пределах от 2500 до 50 000 К. Изменение температуры меняет состояние атомов и молекул в атмосферах звёзд, что отражается в их спектрах. По ряду характерных особенностей спектров звёзды разделены на спектральные классы, которые обозначены латинскими буквами и расположены в порядке, соответствующем убыванию температуры: O, B, A, F, G, K, M.

У наиболее холодных (красных) звёзд класса M в спектрах наблюдаются линии поглощения некоторых двухатомных молекул (например, оксидов титана, циркония и углерода). Примерами звёзд, температура которых около 3000 К, являются Антарес и Бетельгейзе.

В спектрах жёлтых звёзд класса G с температурой около 6000 К, к которым относится и Солнце, преобладают линии металлов: железа, натрия, кальция и т. д. По температуре, спектру и цвету сходна с Солнцем звезда Капелла.

Для спектров белых звёзд класса A, которые имеют температуру около 10 000 К (Вега, Денеб и Сириус), наиболее характерны линии водорода и множество слабых линий ионизованных металлов. В спектрах наиболее горячих звёзд появляются линии нейтрального и ионизованного гелия.

Различия звёздных спектров объясняются отнюдь не разнообразием их химического состава, а различием температуры и других физических условий в атмосферах звёзд. Изучение спектров показывает, что преобладают в составе звёздных атмосфер (и звёзд в целом) водород и гелий. На долю всех остальных химических элементов приходится не более нескольких процентов.

Измерение положения спектральных линий позволяет не только получить информацию о химическом составе звёзд, но и определить скорость их движения. Если источник излучения (звезда или любой другой объект) приближается к наблюдателю или удаляется от него со скоростью v, то наблюдатель будет регистрировать изменение длины волны принимаемого излучения. В случае уменьшения расстояния между наблюдателем и звездой длина волны уменьшается и соответствующая линия смещается к сине-фиолетовому концу спектра. При удалении звезды длина волны излучения увеличивается, а линия смещается в красную его часть. Это явление получило название эффекта Доплера, согласно которому зависимость разности длин волн от скорости источника по лучу зрения v и скорости света c выражается следующей формулой:

= ,

где λ0 — длина волны спектральной линии для неподвижного источника, а λ — длина волны в спектре движущегося источника.

Эффект Доплера наблюдается в оптической и других областях спектра и широко используется в астрономии.

Полученные данные о светимости и спектрах звёзд уже в начале XX в. были сопоставлены двумя астрономами — Эйнаром Герцшпрунгом (Голландия) и Генри Расселлом (США) — и представлены в виде диаграммы, которая получила название «диаграмма Герцшпрунга—Расселла». Если по горизонтальной оси отложены спектральные классы (температура) звёзд, а по вертикальной — их светимости (абсолютные звёздные величины), то каждой звезде будет соответствовать определённая точка на этой диаграмме (рис. 5.15). В результате обнаруживается определённая закономерность в расположении звёзд на диаграмме — они не заполняют всё её поле, а образуют несколько групп, названных последовательностями. Наиболее многочисленной (примерно 90% всех звёзд) оказалась главная последовательность, к числу звёзд которой принадлежит наше Солнце (его положение отмечено на диаграмме кружочком). Звёзды этой последовательности отличаются друг от друга по светимости и температуре, и взаимосвязь этих характеристик соблюдается весьма строго: самую высокую светимость имеют наиболее горячие звёзды, а по мере уменьшения температуры светимость падает. Красные звёзды малой светимости получили название красных карликов. Вместе с тем на диаграмме существуют и другие последовательности, где подобная закономерность не соблюдается. Особенно заметно это среди более холодных (красных) звёзд: помимо звёзд, принадлежащих главной последовательности и потому имеющих малую светимость, на диаграмме представлены звёзды высокой светимости, которая практически не меняется при изменении их температуры. Такие звёзды принадлежат двум последовательностям (гиганты и сверхгиганты), получившим эти названия вследствие своей светимости, которая значительно превосходит светимость Солнца. Особое место на диаграмме занимают горячие звёзды малой светимости — белые карлики.

Рис. 5.15. Диаграмма «спектр — светимость»

Лишь к концу XX в., когда объём знаний о физических процессах, происходящих в звёздах, существенно увеличился и стали понятными пути их эволюции, удалось найти теоретическое обоснование тем эмпирическим закономерностям, которые отражает диаграмма «спектр — светимость».

Какова светимость звезды ξ Скорпиона, если её звёздная величина 3m, а расстояние до неё 7500 св. лет?

Дано:

m = 3m

D = 7500 св. лет

Решение:

lg L = 0,4(5 – M).

M = m + 5 – 5 lg D, где D = 7500 : 3,26 = 2300 пк.

Тогда M = 3 + 5 – 5 lg 2300 = –8,8.

lg L = 0,4•[5 – (–8,8)] = 5,52.

L — ?

Отсюда L = 330 000.

Ответ: L = 330 000.

Вопросы 1. Как определяют расстояния до звёзд? 2. От чего зависит цвет звезды? 3. В чём главная причина различия спектров звёзд? 4. От чего зависит светимость звезды?

Упражнение 18 1. Во сколько раз Сириус ярче, чем Альдебаран; Солнце ярче, чем Сириус? 2. Одна звезда ярче другой в 16 раз. Чему равна разность их звёздных величин? 3. Параллакс Веги 0,11ʺ. Сколько времени идёт свет от неё до Земли? 4. Сколько лет надо было бы лететь по направлению к созвездию Лиры со скоростью 30 км/с, чтобы Вега стала вдвое ближе? 5. Во сколько раз звезда 3,4 звёздной величины слабее, чем Сириус, имеющий звёздную величину –1,6? Чему равны абсолютные величины этих звёзд, если расстояние до каждой составляет 3 пк?

Источник

1 pc³	≈ 2.938×10⁴⁹ m³
1 kpc³	≈ 2.938×10⁵⁸ m³
1 Mpc³	≈ 2.938×10⁶⁷ m³
1 Gpc³	≈ 2.938×10⁷⁶ m³
1 Tpc³	≈ 2.938×10⁸⁵ m³

Калькулятор расстояния и годичного параллакса

Определение параллакса и формула для расчета расстояния

Подробнее о длине и расстоянии: измерение расстояний в космосе

Общие сведения

Измерения с помощью радиолокации

Годичный звездный параллакс

Цефеиды

Сверхновая типа Ia

Другие методы измерения расстояний

Примеры расчета расстояния до некоторых звезд и их звездного параллакса

History and derivation[edit]

Calculating the value of a parsec[edit]

Usage and measurement[edit]

Distances in parsecs[edit]

Distances less than a parsec[edit]

Parsecs and kiloparsecs[edit]

Megaparsecs and gigaparsecs[edit]

Volume units[edit]

In popular culture[edit]

See also[edit]

Notes[edit]

References[edit]

External links[edit]

Общие сведения

История открытия

Материалы по теме

Как определить парсек

Самые популярные примеры расстояний в парсеках

О расстояниях наглядно. Нажмите кнопку «Старт»